Introduction

Hydrological models are well-established tools applied over the years to simulate and predict the responses of ecosystems to water stress (Bradley 2002; Richter et al. 1996). Coupling cutting-edge hydrological models with advanced support originating from geographic information systems (GIS) and remote sensing (RS) that are integrated with ecological indicators allows the field of model-based analyses to expand into new dimensions, providing new and detailed information, which is required to broaden scientific knowledge of ecosystem functions (Berezowski et al. 2015; Grygoruk et al. 2014; Zhou et al. 2008). A particularly broad field in this regard covers the protection, management and restoration of mires and riparian wetlands, where strict hydrological criteria (water level distribution, duration of water levels, flood extents and volumes) must be fulfilled to assure sustainable habitat conditions or keep greenhouse gases emissions at an acceptable level (Chormański et al. 2009; Fortuniak et al. 2017; Grygoruk et al. 2015; Koreny et al. 1999; Mirosław-Świątek et al. 2016c; Vepraskas and Caldwell 2008). Special attention is paid to the requirements and tolerance of wetland vegetation species to a variability of water levels in a classical (phytosociological) approach (Caldwell et al. 2011). Moreover, the appropriate interpretation of water levels from a modern (trait-based) ecological approach appears to be even more important (Opdekamp et al. 2012). Either way, the most critical hydrological variables determining the status of riparian and mire ecosystems are associated with indices related to groundwater depths (e.g., average groundwater depth within the vegetation path, magnitude of water table fluctuations, minimum and maximum groundwater depths and duration of inundation).

Bearing in mind the possible errors that are associated with results of hydrological modelling, it is currently a standard procedure to assess the sensitivity of models with special regard to model parsimony and the uncertainty of the parameters applied. In this regard, groundwater flow models (e.g., MODFLOW-based or HYDRUS-based approaches) are subjected to a detailed estimation of prediction uncertainty (Hassan et al. 2008). Surprisingly, the most frequent approach is to disregard the uncertainty of the model domain. Among many sources of the uncertainty of groundwater models subjected to extended analysis (Wu and Zeng 2013), especially parameter identification, the influence of the model domain’s uncertainty on modelling results has seldom been tested. In most studies in which the amount and direction of flows or water are the main point of interest, this factor seems to be insignificant, as it has only an indirect effect on the model performance. However, this is not so in the case of water-stress-oriented analyses conditioned mostly on groundwater depths. Here, model uncertainty might be strongly affected by the accuracy of elevation data, and serious methodological difficulties appear when different suitability classes of groundwater depths for certain plant communities fall inside of its confidence intervals. This is especially noticeable for riparian and mire ecosystems, in which the water table is relatively close to the terrain surface, and—importantly—such areas remain hardly accessible for elevation measurements due to a dense vegetation cover, which additionally underpins a relatively lower quality of elevation-assessment products such as digital elevation models (DEMs), even those developed with cutting-edge airborne laser scanning-light detection and ranging (ALS-LiDAR) methodology (Mirosław-Świątek et al. 2016b).

Our study attempts to answer the following research questions: (1) What are the differences between terrain elevations derived from ALS-LiDAR DEM compared to the DGPS-measured values within a lowland floodplain wetland? (2) Does the uncertainty of the groundwater flow model domain, herein referred to as the uncertainty of terrain elevation data, affect modelled values of total hydraulic heads? (3) Is the uncertainty of ALS-LiDAR DEM dependent on land cover type? (4) Is a deterministic approach to the GIS-based and model-based analysis of groundwater depths suitable and reliable enough to be used for ecological purposes such as the reliable assessment of water-level-related habitat indicators? In our paper, we present a detailed study from a complex, temperate European floodplain-mire wetland located in the Biebrza Valley (Poland).

Materials and methods

Study area

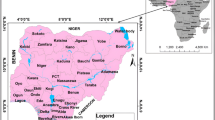
Our study was conducted in the northern stretch of the Lower Basin of the Biebrza Valley (Fig. 1a, b), located in northeastern Poland, which is one of the most famous and ecologically valuable mosaics of riparian and mire ecosystems of Europe (Wassen et al. 2006). The research site is a broad land depression that was shaped in the late Pleistocene by fluvio-glacial waters of the Vistulian Glaciation. The valley is approximately 5 km wide and is filled with sand, on which peat soils of a maximum thickness of 3 m developed in the Holocene. Terrain elevations in the study area vary from 103 to 118.5 m a.s.l. (the latter beyond the river valley). The area is regularly flooded (Grygoruk et al. 2013), consists of numerous natural floodplain lakes (Slapinska et al. 2016), and the main source of water supply to wetlands of this part of the Biebrza Valley is flooding originating from the Biebrza River. The average discharge of the Biebrza River in the stretch analysed reached approximately 22.4 m3/s (Grygoruk et al. 2011). Groundwater levels in the riparian habitats analysed vary from permanent inundation in spring (flood depths up to 1.5 m within the floodplain) down to 1.5 m below the ground in the driest periods. The average annual air temperature is equal to 6.6 °C (Banaszuk 2004), and the average annual total precipitation is as high as 560 mm (Kossowska-Cezak 1984). The area of the valley is densely vegetated by typical riparian plant communities such as sedges, reed-manna grass, reeds, willow and alder shrubs and forests (Fig. 1b).

Fig. 1
figure 1

Study area—Northern part of the Lower Basin of the Biebrza Valley. a Digital Elevation Model (0.6 m spatial resolution) after Mirosław-Świątek et al. (2016b); b distribution of ground elevation measurements in various classes of land cover (plant communities): 1 Caricetum appropinquatae, 2 Caricetum gracilis, 3 Glycerietum maximae, 4 Alder and Willow encroachments, 5 mixed forest, 6 water, 7 Phragmitetum australis, 8 mown meadow and pasture, 9 mosaic of loose tussock sedges and grasses, 10 mosaic of loose tussock and tussock sedges

Full size image

The majority of the study area is agriculturally managed as extensively used meadows of a seasonal mowing regime, but the vegetation remains near natural; no new species have been introduced for agricultural purposes. Additionally, the entire area analysed remains covered by Natura 2000 protection both as a special area of protection (SAP) and as an area of special protection of species (ASP). Biebrza Valley is known for its unique features as a migratory bird habitat (Polakowski et al. 2014) and as an ultimate area of protection of valuable and rare species of birds connected to wetlands (Maciorowski et al. 2014; Oppel et al. 2014). Specific actions related to the appropriate management of this area, such as broad-scale large-track mowing, are considered influential to the microtopography of the wetlands analysed (Banaszuk et al. 2016; Kotowski et al. 2013;), which additionally justifies the need for detailed research on the accuracy of the numerical topographic data for ecohydrological purposes that we undertake in our analysis.

Selection of habitats for the analysis

The key issue of our research was to reveal how the uncertainty of DEM affects the predicted hydrological conditions of habitats using the total hydraulic head computed using the groundwater model. In this regard, we selected individual patches of habitats that had different vegetation structure and could had been characterized with the presence of different species of birds. The habitats selected were categorized into 9 different vegetation types and open water, which was later not considered in our analysis (ref. Fig 1b), namely Caricetum appropinquatae, Caricetum gracilis, Glycerietum maximae, Phragmitetum australis, a mosaic of alder and willow encroachments, mixed forest, mown meadow/grazed pasture, a mosaic of loose tussock and tussock sedges and a mosaic of loose tussock sedges and grasses. Vegetation type classes were delineated on the basis of field measurements and airborne and satellite optical imagery using object-based image analysis (OBIA) by Mirosław-Światek et al. (2016b). The vegetation map was intersected with the preliminary map of Natura 2000 bird species distribution in order to obtain habitat patches consisting of selected vegetation and potential presence of selected birds (BNP 2015). In our analysis, we focused on specific bird species, the behaviour of which is related to particular hydrological conditions (waterlogging, shallow groundwater level), namely Anser albifrons, Aquila clanga, Crex crex, Gallinago gallinago, Porzana porzana and Acrocephalus paludicola. All of the selected bird species represent different behavioural and foraging groups and cover the most representative species present within the Biebrza Valley. Spatial analysis allowed us to select 24 individual patches of habitats with different hydrological requirements (Table 1; Fig. 2a). For each of the habitats we assigned a range of optimum (OPT) and tolerant (TOL) groundwater depths, referred to as the habitat suitability index (HSI) (Table 1). These values were assigned in an arbitrary manner based upon available water-level monitoring data and information on the habitat requirements of both plants and birds and were spatially intersected with maps of groundwater-level monitoring in the Lower Biebrza Basin (Grygoruk 2013; Grzywaczewski et al. 2014; Grzywaczewski et al. 2017; Maciorowski et al. 2014; Okruszko 2005; Oppel et al. 2014; Polakowski et al. 2014).

Table 1 Ecological and hydrological features of selected habitats
Full size table
Fig. 2
figure 2

Groundwater flow model calibration results. a locations of piezometers used for model calibration and habitats selected for the hydrological analysis; b calibration plot

Full size image

It must be noted that any measure similar to the HSI might be affected by averaging input values. The score can be elaborated for distributed input but also averaged over a larger area. In the first case, the measure is evaluated for all point values and then averaged, whereas in the second, the averaging is performed prior to summarizing the areas of habitats. We discuss this issue by comparing the mean of the HSI obtained for water depths at model nodes for a habitat (HSI for point values) with that computed for values averaged over a habitat area (HSI for habitat-averaged water levels).

One should consider the given values of HSI as being indicative only. The given criteria are used in our study as a locally relevant approximation of the hydrological conditions of the habitats analysed. These criteria were used for the analysis of the possible influence of DEM on the final results of hydrological analysis. Although we used local references for wetland habitat criteria, the direct values of tolerant and optimum water levels in riparian wetlands and mires worldwide tend to be at similar levels of magnitude (Mitsch and Gosselink 2015).

Assessment of DEM accuracy in various habitats

ALS-LiDAR methodology and object-based image analysis (OBIA) was applied to develop a high-quality DEM of the research area with the spatial resolution of 1 m (Mirosław-Świątek et al. 2016b). It involved the combined use of airborne and optical satellite imagery, real-time kinematic GNSS (RTK GNSS) elevation measurements, topographical surveys and vegetation height measurements to correct the so-called ‘vegetation effect’ present in ALS LiDAR DEMs resulting from the falsification of terrain elevations caused by very dense wetland vegetation.

One of the goals of our study was to provide a comparative analysis of ALS-LiDAR DEM accuracy compared with field measurements (Fig. 1a) within the extent of various types of land cover (vegetation classes). In the ranges selected, 10 vegetation classes at scattered points (Fig. 1b), we compared field-measured and DEM-derived terrain elevations. The terrain elevations used in the comparative study were measured with the use of the DGPS methodology and resulted in elevation measurements with accuracy as high as ± 0.02 m (Mirosław-Świątek et al. 2016a). The individual value, which in the comparative analysis is considered as a local field measurement (Fig. 1b), due to the microtopography of the wetland analysed, was assessed as an average terrain elevation calculated on the basis of multiple representative point measurements done within the area of 625 m2 (25 m × 25 m—the area of the DEM grid cell). On the basis of differences between the measured and DEM-derived values, we assessed the mean errors of estimation and standard deviations of differences, which were later used as DEM uncertainty boundaries in a Monte Carlo analysis.

Groundwater flow model description

The simple groundwater flow model developed was based on the MODFLOW code (Harbaugh 2005). The model was developed and executed in the ModelMuse Graphical User Interface (Winston 2009). The model covered the entire area of research (ref. Figs 1, 2a) with a grid mesh of 25 m × 25 m, amounting to 441 by 407 (no. of rows by no. of columns) cells. Vertical discretization of the model domain was performed according to the changing lithological structure and consisted of 3 layers representing variably saturated peat (the superficial layer of the model), saturated peat (the middle layer of the model) and saturated sand (the bottommost layer of the model). These layers were simulated as convertible (topmost peat) and confined (deeper peat and sand). A similar setup of model layers was proven to be relevant for the field conditions of the Biebrza Valley (Grygoruk et al. 2014; Grygoruk et al. 2015). For the purpose of our study, we executed the model in a steady state because only the specific situation of the average multi-year hydrologic conditions was needed. The boundary conditions of the model included a simulation of groundwater recharge, river-aquifer interactions and groundwater inflow to the valley from adjacent plateaus. Groundwater recharge was simulated with the RCH package.

The value of groundwater recharge was calculated on the basis of precipitation, interception, evapotranspiration and surface runoff externally from the model in a GIS-based spatial approach and reached levels as high as 135 mm/year. Interaction between the river and groundwater was simulated with the RIV package. Elevations of the water table along the river were linearly interpolated on the basis of field measurements of the water level. The depths of the river were assigned to each of the RIV-package-related model cells on the basis of field-measured data from 35 river channel cross sections. In all of the cells with the active RIV package, the measured bottom of the river was situated below the peat bottom, which indicated good hydraulic connectivity of the river and groundwater of the sandy aquifer, which remains the most important source of groundwater on the regional scale. We assumed that the layer of river bed sediments was 1 m deep, and its hydraulic conductivity is one order of magnitude lower than the hydraulic conductivities of the sandy aquifer, which was tested and proven to be appropriate for the Biebrza Valley groundwater system by Bleuten and Schermers (1994) and Batelaan and Kuntohadi (2002). Lateral inflow to the valley was simulated with the CHD package. The values of water levels along the external (E and W) boundaries of the model domain were assigned on the basis of field observations in 11 piezometers distributed uniformly along the model boundaries. Model calibration was done with the use of field-measured data of groundwater levels in 15 piezometers (Fig. 2a). The root mean squared error (RMSE) of modelled versus observed groundwater levels reached 0.35 m, and the determination coefficient (R2) was equal to 0.77, which was considered satisfactory given the low variability of the groundwater table throughout the modelled area. The calibrated values of the hydraulic conductivities of particular layers were as high as 0.223 m/d for the topmost peat, 0.110 m/d for the saturated peat and 13.2 m/d for the saturated sand. The map of the total hydraulic head of the groundwater table produced with the use of the developed model was used in the assessment of the DEM’s uncertainty influence on modelled wetland habitat conditions.

Uncertainty assessment approach

We investigated the transformation of the uncertainty of the DEM influencing the groundwater flow model. The DEM’s uncertainty is considered here in a probabilistic manner, in which an elevation at each grid node is disturbed by a random term e (Hunter and Goodchild 1997):

$$Z_{i,j} = \hat{Z}_{i,j} + e$$
(1)

where Z i,j denotes the elevation at the (i, j) node and \(\hat{Z}_{i,j}\) the nominal DEM value. It is assumed that the disturbance term e is independent and follows a normal distribution e ∼ N (0, σ k ). The variance \(\sigma_{k}^{2}\) depends on the local DEM accuracy, assessed for each k-th habitat class (Table 2). It can be expected that errors in DEM elevations are spatially dependent (Hunter and Goodchild 1997; Aguilar et al. 2010). However, as the identification of the errors’ autocorrelation is a difficult task and requires many measurement locations, the assumption of the independent disturbance term used here is common in similar studies (e.g., Liu et al. 2012).

Table 2 Differences of field-measured versus ALS-LiDAR DEM-derived ground elevations in selected land cover (vegetation type) classes
Full size table

The effect of the DEM uncertainty was analysed for direct outcomes of the groundwater model—groundwater table elevations H and depth h—and derived from the water table depth, the HSI. The first outcome, groundwater elevation H, does not depend explicitly on the terrain surface and can be considered a measure of the effect of DEM uncertainty on the hydraulic properties of the aquifer. The second outcome, the depth to the water table, defined as the difference between the DEM elevation and the ground water elevation at the given grid node h i,j  = Z i,j  − H i,j explicitly incorporates the DEM disturbance term e: \(h_{i,j} = \hat{Z}_{i,j} - H_{i,j} + e\). Last, the HSI is a piecewise linear function of h.

Comparing the input and output variations, it is possible to assess the sensitivity of the output on introduced disturbances (Archer et al. 1997). High variation suggests a strong influence of DEM uncertainty. Conversely, low variation indicates low sensitivity. Moreover, adding the uncertainty term might lead to a different solution from that based on the nominal values of the DEM. With linear transformations, it is expected that the disturbances do not affect the output mean value:

$$E\left( {M\left( Z \right)} \right) = M\left( {E\left( Z \right)} \right)$$
(2)

where M(·) stands for the model output, E(·) is the expectation operator and Z is a grid matrix of disrupted DEM elevations (eq. Text, note \(E(Z) = \hat{Z}\)). The equation might not necessarily be true, which suggests the presence of non-linear effects that affect the transformation of the uncertainty (Kiczko et al. 2013; Brandyk et al. 2016; Romanowicz and Kiczko 2016). The transformation of DEM uncertainty to the distribution of the outcome values representing hydrological conditions of wetland habitats was investigated using Monte Carlo sampling with 10,000 model realizations. Statistical analyses were performed with respect to habitat classes and characterized by different levels of accuracy of the DEM. The output uncertainty was investigated for the spatially distributed output of the model and values were averaged over an area of a certain plant community.

Results

Elevation differences in selected land cover classes: ALS-LiDAR versus DGPS

A comparison of field-measured to DEM-derived elevations of the riparian wetland analysed showed variable discrepancies (Table 2). The best fit of DEM to field-measured data was recorded with extents of Caricetum gracilis (MAE = 0.23 m; σ k  = 0.26 m), Glycerietum maximae (MAE = 0.26 m; σ k  = 0.33 m) and a mosaic of loose tussock and tussock sedge vegetation (MAE = 0.27 m; σ k  = 0.30 m). The highest discrepancies between the field-measured and DEM-derived ground elevations were surprisingly recorded within mown meadows/grazed pastures (MAE = 0.77 m; σ k  = 0.84 m), Caricetum appropinquatae (MAE = 0.52 m; σ k  = 0.69 m) and mixed forest (MAE = 0.40 m; σ k  = 0.60 m).

Values of σ k calculated on the basis of obtained elevation differences were used in a DEM disturbance uncertainty analysis: the transformation of DEM in Monte Carlo sampling was done in the interval of σ k within the extents of particular land cover (vegetation type) classes (see Fig. 1b).

Influence of DEM uncertainty on habitat parameter assessment

The effect of the DEM disturbance on the calculated total hydraulic heads H (groundwater elevations; Fig. 3a) was found to be unnoticeable. The standard deviation of H did not exceed the value of 3 mm within all of the plant communities analysed. This observation allowed us to conclude that hydrological analysis of groundwater depths in wetlands, which is done with the use of trustworthy elevation data (e.g., field measurements) and spatially diverse H that remain an output from the groundwater flow model (such as the MODFLOW-based approach presented herein), remains a reliable source of data on the hydrological conditions of habitats. This was different in the case of outcomes that directly depended on the DEM elevations: depth to the groundwater table h (Fig. 3b) and the HSI. The depth h, because groundwater elevations H remain almost constant in all samples, has the same uncertainty pattern as the DEM, with the disturbance term e. The computed standard deviations are equal to the assumed standard deviations of the DEM elaborated for each plant community. In Fig. 4, the frequencies of calculated groundwater depths averaged over the habitat area are shown along with the piecewise function of the HSI. As expected, the distribution of h mostly follows the normal distribution of the disturbance e. Depths marked with dashed lines obtained using undisrupted DEM elevations usually fall in the middle of the sample. This is different for areas in which the water table was close to the surface, as in the case of habitat of mixed forest (no. 5, Fig. 4c), where the semi-normal distribution is affected by the constraint limiting it to the positive values (h i,j  ≥ 0), resulting in a peak at the zero height. The uncertainty of the depths h significantly affects the HSI scores due to their nonlinear form. For an example, in Fig. 4a, the undisturbed water depth (for nominal elevations of the DEM) is identified as being within a tolerance of habitat no. 2 (Caricetum appropinquatae, Fig. 4c). This agrees with the frequency bars, which indicate that most of the water depths disturbed with the DEM fall into that category. However, due to the uncertainty, the optimal conditions cannot be excluded, as almost 20% of the samples are present in that class. This is even more noticeable in Fig. 4b, where the depth of the nominal DEM elevations is close to the limit of the class of optimum conditions, and the probabilistic solution suggests that less favourable conditions might be present. In joining information on frequencies of groundwater depths with intervals of HSI classes, it is possible to calculate the overall probability of the given HSI score. In Table 3, the confidence values of the HSI score are elaborated in this manner and given for each vegetation class, both for habitat-averaged and point values of the groundwater depth h. The score of HSI for undisrupted DEM was calculated as a mean value of groundwater depths for all grid cells belonging to a particular habitat (Fig. 3a). In the case of groundwater depths with the disrupted DEM applied, the probability of the particular average values of h was assessed (Fig. 3b). The probability of reaching a particular value of h was also analysed for individual grid cells belonging to the particular habitat (Fig. 3c). For numerous vegetation classes, the HSI score calculated for nominal DEM elevations should be considered with the others, as it has a similar level of confidence. Fig 5 presents the spatial pattern of the confidence of the Optimum (A and D), tolerant (B and E) and unsuitable (C and F) HSI scores. Moreover, comparing the confidence values in Table 2, elaborated with and without averaging, it can be noted that there are significant differences in the results, which reveals that averaging significantly affects the solution. This means that HSI scores computed for point and averaged values are not equivalent.

Fig. 3
figure 3

Habitat conditions analysed in the study: a total hydraulic head of groundwater, b average groundwater depth within the whole habitat calculated as a mean value of groundwater depths (hi for i = 1, …, N) where N is the summary number of cells in the habitat, c groundwater depth in every grid cell that belongs to the habitat. Gray zone stands for the uncertainty of DEM

Full size image
Fig. 4
figure 4

Calculated frequencies (horizontal bars) of the depth to the groundwater table h and HSI classes (gray continuous line) for two plant communities. The dashed line shows the depth for undisrupted DEM. a Habitat Caricetum appropinquatae (no. 2); b Caricetum appropinquatae (no. 3); c Caricetum appropinquatae (no. 5); d Caricetum appropinquatae (no. 6); e Caricetum gracilis (no. 8); f Glycerietum maximae (no. 12)

Full size image
Table 3 The confidence of HSI, accounting for the DEM uncertainty
Full size table
Fig. 5
figure 5

Probability of reaching optimal (a, d), tolerant (b, e) and unsuitable (c, f) groundwater levels within the habitats analysed

Full size image

Discussion

Past research has shown that in areas with dense vegetation, the estimated ground surface elevations derived from ALS LiDAR data are typically higher, although they are subjected to higher uncertainty than those surveyed with GNSS RTK measurements. It was observed that ALS LiDAR accuracy decreases along with an increasing canopy cover. Reutebuch et al. (2003) and Hodgson et al. (2003) indicated that shrub and forest vegetation have a significant influence on laser-beam penetration capabilities. Likewise, Hodgson and Bresnahan (2004) and Hodgson et al. (2003) found elevation errors to be much higher for shrubs compared to other types of vegetation. Reutebuch et al. (2003) obtained the MAE of field-measured and LiDAR-derived terrain elevations within forests as high as 0.31 m. Similarly, in our research, the upward shift for alder and willow encroachments was also observed and was as high as 0.24 m on average (σ k  = 0.35 m; MAE = 0.32 m). One should also consider that the GNSS techniques used in this study due to the specifics of forest areas and high shrubberies could not provide precise information compared to open areas for DTM creation (Ordóñez Galána et al. 2011). This resulted from the negative influence of dense crown cover and wood biomass on the propagation of the GPS signal (Wężyk 2015). Similar issues were identified by numerous authors within areas covered with low vegetation, where laser measurements have a systematic positive height shift compared to the ground surface (e.g., Pfeifer et al. 2004). Hodgson and Bresnahan (2004) compared the LiDAR data with total station and rapid-static GPS measurements. The RMSE for the LiDAR data ranged from 0.22 m for low grass, 0.19 m for high grass, 0.23 m for brush and low trees and up to 0.26 m for deciduous forest. Evans and Hudak (2007) obtained elevation differences equal to 0.31 m for high canopy cover and 0.17 m for low canopy cover. Myszkowski et al. 2009 obtained an upward shift equal to 0.29 m for the low vegetation up to 0.2 m. The main influencing factor here was vegetation height, as the scanning density was very large—0.15 m and 12 points/m2. In our research, the highest (but similar) upward shifts for low vegetation were observed in sedges (Caricetum gracilis) and reeds (Phragmitetum australis and Glycerietum maximae) and on average were equal to 0.15 m (σ k  = 0.40 m; MAE = 0.34 m; RMSE = 0.41) and 0.16 m (σ k  = 0.33 m; MAE = 0.26 m; RMSE = 0.34) respectively. Different results were obtained for Caricetum appropinquatae, for which the average elevation difference was −0.10 m (σ k  = 0.69 m; MAE = 0.52 m; RMSE = 0.61) with a range of values between −1.27 and 0.64 m. When such sedges create compact tussocks, the results can be influenced on the one hand by mistakenly performed measurement of the ground surface with the GNNS RTK method (at the top or between tussocks) and on the other hand by the difficulties of generating DTM with a laser beam, originating once from the top of the tussock and once from the area between them. The largest elevation differences (−0.38 m on average; with a range of values from −1.75 to 1.69 m) and the highest mean absolute error (MAE = 0.77 m; RMSE = 0.83; σ k  = 0.84 m) were observed in the class of ‘mown meadow/grazed pasture’. The disagreement between ALS-LiDAR and DGPS could have resulted from generalizing 1 m DTM into the 25 m DTM used in this paper to keep the final DTM compatible with the grid size applied to the MODFLOW model. The possible errors in DTM creation in this class could have been caused by the presence of dense drainage network overgrown by bushes: generalization of 1 m DTM into the coarser resolution multiplied the error of the terrain elevation in different land-cover classes. The last return values were obtained on the one hand from the ditches and on the other hand from the bushes, which then had an impact on the resulting DTM. This aspect has so far seldom been considered in the literature. In light of the presented results, we advise the careful interpretation of both LiDAR-DEM-based and GNSS RTK-based ground elevation approximations in densely drained areas of peatlands.

The total hydraulic heads of groundwater calculated with the developed MODFLOW-based model changed only to an insignificant extent with respect to the implemented variability of terrain elevation in the Monte Carlo exercise we performed. The σ k obtained from the modelled total hydraulic heads in the ensemble of 10,000 simulations, which reached 0.003 m, indicates a negligibly small sensitivity of the model to changing geometry of the domain, referred to as the use of variable DEMs. This result remains logical and obvious, as the developed MODFLOW model did not account for unsaturated zone flow simulation, where the modification of terrain elevation is likely to affect the results of groundwater head computation to a more decent extent by changing the thickness of the unsaturated zone. However, we consider this observation relevant for approaches that use MODFLOW with additional packages that are capable of simulating—even roughly—the unsaturated zone flow (Grygoruk et al. 2014). In the developed model, terrain elevation affects computed total heads in cases in which total hydraulic heads exceed ground level. This observation remains important when head-dependent flux boundary conditions are applied (e.g., DRAIN package), for which water flux remains a function of terrain elevation and actual groundwater level. Our model simulates steady-state, average conditions from a multi-year period. Although we simulate field conditions of riparian wetlands, in our case, only a few cells of the model faced conditions of groundwater seepage to the level reaching elevations above the ground. To keep the model relatively simple to allow verification of the initial hypotheses, we did not account for the quantification of uncertainties associated with varying elevations of, e.g., the bottom of the river in the RIV package applied. However, we consider this an important topic for further analyses, especially in local, river-stretch-oriented approaches accounting for modelling groundwater-surface water interactions, in which the uncertainty of river bottom elevation may become an issue affecting the modelling results to a considerable extent.

Contradictory to the low uncertainty of modelled total hydraulic heads with respect to the variable terrain elevations, discussed above, the uncertainty analysis of calculated groundwater depths against the changing terrain elevations that resulted from the errors of DEM performed in our study revealed high sensitivity of this parameter to the changing terrain elevations tested in the Monte Carlo approach. Our estimated HSI score referred to the modelled groundwater depths for both undisrupted DEM and the anticipated uncertainty of the DEM in cases of habitats that changed significantly (Table 3; Fig. 6). For example, habitat conditions for biota approached by the HSI score in habitat no. 17 (Mosaic of alder and willow encroachments located within the range of presence of Aquila clanga) were described as ‘tolerant’ in the case in which undisrupted DEM was considered. Accounting for DEM uncertainty and analysing hydrological conditions within this habitat with the use of an averaged h for the entire habitat indicated that the probability of having a ‘tolerant’ value of the HSI reached only 0.53. At the same time, the probabilities of reaching the ‘optimum’ and ‘unsuitable’ values of HSI within this habitat were as high as 0.20 and 0.27, respectively (Table 3). In the case of spatially distributed values of particular probabilities of h occurrence in the grid nodes of the habitats analysed, the results of an HSI score estimation are even more variable. In  the above-discussed habitat no. 17, the probability of HSI being unsuitable for the biota analysed reaches 0.47 and is nearly equal to the probability of HSI being optimal (0.46). In this case, the interpretation of HSI, which was unambiguous and explicit (‘tolerant’) for undisrupted DEM, has lost its unilaterality and remained defined as optimum (with the probability of 46%), tolerant (7%) and, surprisingly, unsuitable (47%). In some cases, in the habitats analysed, the HSI value ‘unsuitable’ was assigned for both undisrupted DEM and the analysis of the probability of h averaged over a particular community area (i.e., habitat no. 10 - Glycerietum maximae).

Fig. 6
figure 6

Confidence intervals of HIS scores computed for grid nodes (spatially diverse) and averaged ground water depths for 24 plant communities (habitat: 1–6 Caricetum appropinquatae; 7–8 Caricetum gracilis; 9–12 Glycerietum maximae; 13–15, 17 mosaic of alder and willow encroachments; 16 mixed forest; 18–19 Phragmitetum australis; 20 mown meadow/pasture; 21 mixed sedges and grasses; 22–24 mosaic of loose tussock and tussock sedges); Opt, Tol and null—stand respectively for the optimal, tolerance and null HSI score derived for undisrupted DEM with averaged values

Full size image

However, when the probability of a particular h occurrence within the individual grid nodes was analysed, the ‘tolerant’ and ‘optimum’ values of HSI were defined with the probability of 0.34 and 0.09 respectively. However, hydrological conditions defined as ‘unsuitable’ are expected with the probability of 0.53. Switching from the analyses of the probability of h averaged over habitats to probabilities of h in particular grid nodes, the results in the majority of habitats analysed the changed probabilities of ‘tolerant’ and ‘optimal’ values of HSI (Fig. 5). For example, in habitat no. 14 (Mosaic of alder and willow encroachments, range of presence of Anser albofrons, Crex crex, Gallinago gallinago and Acrocephalus paludicola), the dominant ‘optimum’ hydrological conditions for biota (a probability of 0.97 in the approach when h is averaged over the habitat) remain ‘optimum’ only for some 56% of the habitat, when the probability of particular values of h in particular grid nodes is analysed (Table 3). This reveals that measures defined in the same manner as the proposed HSI are sensitive to the placement of the averaging operator—prior to or after the measure.

Assessing a habitat’s hydrological conditions on the basis of groundwater depth remains widely applicable in managing wetland environments both in the study area (Chormański et al. 2009) and worldwide (Mitsch and Gosselink 2015). Our discussion of the results of the relevance of DEM quality on groundwater modelling interpretations indicate that neglecting the uncertainty of DEM and different approaches to groundwater depth assessment within wetlands may result in biased ecohydrological analyses. We conclude that groundwater-modelling-based decision support approaches in wetland management can result in wrong decision-making if the quality of the applied DEM is not addressed in studies referring to groundwater depths: habitats that are foreseen to be too dry can in fact be too wet.

Conclusions

  1. (1)

    We compared terrain-elevation data originating from the ALS-LiDAR DEM and from field measurements performed with the use of GNSS GPS to reveal errors in the DEM elevation data. We revealed that the MAE of DEM within the floodplain wetland that was analysed ranged from 0.23 to 0.77 m (σ k varied from 0.26 to 0.84 m respectively) and depended on the types of vegetation.

  2. (2)

    We revealed that the uncertainty of DEM influences MODFLOW-computed groundwater heads in steady-state conditions when the unsaturated zone is not accounted for and groundwater seepage to the surface of the model occurs only to a limited extent. The standard deviation of water levels computed in these conditions did not exceed 0.003 m.

  3. (3)

    We found that the uncertainty of DEM significantly influenced the results of the assessment of the habitat’s hydrological conditions expressed as groundwater depths, herein approximated by the HSI score. In extreme cases, although the averaged HSI assessed in the deterministic manner was defined as ‘unsuitable’, in a probabilistic approach (grid-cell-scale estimation), it reached values of 40% probability, signifying ‘optimum’ or ‘tolerant’. We stress that model-derived average groundwater levels that referred to terrain elevations obtained from the DEM remains a reason for potential, significant errors in the quantification of the hydrological parameters of habitats referred to as depth to groundwater table.

  4. (4)

    For the 24 habitats analysed, we revealed vast differences between the HSI score calculated for the individual grid cells of the model and the HSI score computed as an average value from the set of grid cells located within the habitat patches. This indicates the problem of averaging in the elaboration of measures similar to the HSI.

  5. (5)

    When using groundwater flow models in which DEM was used to determine the geometry of the model domain, magnitudes of groundwater depths referred to as differences between the minimum and maximum values of groundwater table elevations over a certain period remain the most reliable and least uncertain hydrological predictor of habitat conditions.

  6. (6)

    We conclude that groundwater-modelling-based decision support approaches to wetland assessment can result in incorrect management if the quality of DEM used in the analyses is not addressed in studies referring to groundwater depths: habitats that have been foreseen to be too dry can eventually remain too wet.