1 Introduction

On a global scale, urban flooding perseveres to obtrude major challenges hindering the sustainable and healthy development of nations, with the events’ severity and austerity, coupled with its countless repercussions, projected to further intensify, as an aftermath of climate change impacts and rapid urbanisation (Bagiouk et al. 2024; Zhong et al. 2023; Agonafir et al. 2023; Ramezani et al. 2023; Mosavi et al. 2018; Singh et al. 2020). With the Australian nation’s escalating climate vulnerability status, alongside the flourishing statewide urban sprawl influencing increased proportions of impervious areas, the risk of incessant residual urban flooding is imminent, emphasising the need for accurate urban flood forecasting practices (Australian Academy of Science 2021; Bibi and Kara 2023; Ramezani et al. 2023; Wang et al. 2023). However, the process involved in predicting urban catchment flooding is pondered to be emphatically intricate, relating to the complex topographical characteristics and inherent non-linearity correlated with the dominant hydrological procedures of urban catchments (Piadeh et al. 2023; Aziz et al. 2015; Balacumaresan et al. 2023), showcasing high degree of spatial/temporal variability (Anafi et al. 2023), conjoined with limited data availability (Kumar et al. 2023a; Chitwatkulsiri and Miyamoto 2023; Kim & Han 2020; Asadi et al. 2019: Balacumaresan et al. 2023).

Over the years, numerous types of empirical, conventional, and physically based modelling practices have been employed by researchers to comprehend the urban catchment response demonstrated to intense precipitation intensity incidences (Teng et al. 2017; Jodhani et al. 2023; Kumar et al. 2023b; Kim & Han 2020; Jafarzadegan et al. 2023). However, various limitations associated with these different types of practices such as the utilisation/adoption of simplified-mathematical-conceptualisations/approximation of catchment characteristics and governing equations (Hill et al. 2023; Avila et al. 2022; Sezen and Partal 2022; Ghumann et al. 2011; Atashi et al. 2023), heavy reliance/requirement of extensive, detailed high-quality datasets and numerous catchment-specific-parameters specifications for precise model calibration and validation (Mohseni and Muskula 2023; Sayed et al. 2023; Avila et al. 2022; Mishra et al. 2022; Laurenson et al. 2010), internal inconsistencies and model configuration issues etc., (Kemp & Hewa 2023; Avila et al. 2022; Mohseni and Muskula 2023) have limited these models’ prediction accuracy, reliability and favourability (Piadeh et al. 2023; Jehanzaib et al. 2022; Chu et al. 2020; Asadi et al. 2019; Xie et al. 2021; Wang et al. 2022). The 2022 Maribyrnong River flooding debacle in Victoria, serves testament to how limitations associated with conventional modelling practices lead to significant imprecisions and severe underestimation of the likely flood flow quantiles, ensuing in dire communal repercussions, both socially and economically (Melbourne Water 2023, Babister et al. 2023; Balacumaresan et al. 2023). With the risk of incessant residual urban flooding being imminent, in conjunction with the constantly changing climate and cumulative statewide urbanisation, this event serves as one among many, insinuating the critical requirement for enhancements in the present flood flow assessment techniques.

Recently, the hydrological community have been increasingly drawing attention towards potential alternatives to conventional modelling practices, with Artificial Neural Network (ANN) models being one of the most favourable options, with their functionality and reliability being widely evaluated in numerous studies, across an extensive series of applications such as rainfall-runoff modelling, flood forecasting, flood susceptibility assessment and flood mapping (Mosavi et al. 2018; Khosravi et al. 2020; Chapi et al. 2017; Kao et al. 2021; Xie et al. 2021; Perez-Alarcon et al. 2022; Chakrabortty et al. 2021). The study results have collectively highlighted numerous favourable benefits of using ANN models, such as the model’s suitability and competence towards identifying and simulating highly complex, dynamic, non-linear relationships between input-output variables (Sezen & Partal 2022; Yang et al. 2024; Chang et al. 2020), requirement of limited comprehension surrounding the physical processes being modelled, with process generalisation being conducted mainly based upon the data describing input-output parameters (Sezen & Partal 2022; Poulsen et al. 2022; Lin et al. 2020; Daliakopoulos & Tsanis 2016; Calvo-Olivera et al. 2024), the model’s flexibility and versatility in processing multivariate inputs with different characteristics (Sayed et al. 2023; Zhang et al. 2023; Papastefanopoulos et al. 2023; Wu et al. 2021), while also adequately functioning with limited/minimal data availability (Aoulmi et al. 2021; Juan et al. 2017; Perez-Alarcon et al. 2022; Wu et al. 2021) and the high prediction accuracy rate (Lin et al. 2020) etc., to state some, which offset majority of the limitations involved with conventional modelling practices (Takkai Eddine et al. 2024). This indicates that ANN models can be considered as a feasible option for improving the accuracy of the hydrological flow estimation process in urban catchments (Balacumaresan et al. 2023). Therefore, the principal aim of this paper is concentrated upon the incorporation of ANN-modelling-techniques, towards improving the accuracy of the hydrological flow estimation process in urban catchments.

Most of the former research undertaken, primarily explored the widespread employment and prowess of ANN-modelling techniques, in the accurate estimation of expected flood flow quantiles, and the model’s supremacy, with regards to the precision of its predictions and results dependability (Wang et al. 2022; Katipoglu et al. 2023; Samantaray et al. 2023; Sivaparagasam 2010; Perez-Alarcon et al. 2022), when being comparatively evaluated against other machine-learning-based (ML-based) and conventional modelling approaches (Gunathilake et al. 2021; Jimeno-Saez et al. 2018; Katipoglu 2022; Dehghani and Poudeh 2021). Downscaling the research direction towards use of ANN in accurate flood flow estimation, majority of the research is accented towards assessing and enhancing the model’s performance and prediction precision, through the incorporation of various hydrological, hydroclimatic and geomorphological variables as supplementary input variables, alongside rainfall for flood flow estimation (Tao et al. 2024; Jafarzadegan et al. 2023; Asadi et al. 2019; Chang et al. 2020; Lin et al. 2020; Vaheddoost et al. 2023; Madhuri et al. 2021; Wahba et al. 2023; Tamiru et al. 2021; Xie et al. 2021; Ndehedehe et al. 2021; Mokarram et al. 2023; Aoulmi et al. 2021; Wu et al. 2021). However, a common issue pertaining to urban catchments (both globally and nationally) is the lack of sufficient measured/observed data or limited availability of data across urban areas, primarily due to most of the urban catchments remaining ungauged/poorly-gauged/under poor-maintenance (due to high maintenance cost) (Gong et al. 2023), having limited coverage/accessibility to monitoring locations (Zhong et al. 2023), the high costs associated with monitoring sporadic waterlogged locations in accordance with urban landscapes’ complex topography (Zhong et al. 2023; Wang et al. 2018; Pastorek et al. 2023) and/or being located in data scarce/sparse locations (Falah et al. 2019; Ekeu-Wei et al. 2020). Alternative data sources such as remote sensing, crowdsourced data or social media confront challenges in the providence of precise and continuous hydrological data at specific sites across urban areas (Zhong et al. 2023; Darko et al. 2021), while the existence of a panoptic monitoring network across urban locales for monitoring urban-flood-related-data remain scarce (Zhong et al. 2023; Wang et al. 2018; Efraimidou and Spiliotis 2024). Therefore, the requirement for improved modelling techniques, capable of precisely computing the catchment flow, based upon the available minimal data (commonly available hydrological variables such as rainfall and flow) is deemed highly essential, in lieu of the residual urban flooding risk prevalence.

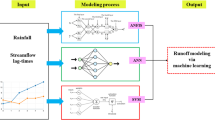
While rainfall remains as the most widely available and heavily utilised hydrological variable in almost any flood-flow-related study/investigation globally (Asadi et al. 2019; Chang et al. 2020; Lin et al. 2020; Dehghani and Poudeh 2021; Arun & Giridhar 2010; Sheikh and Coulibaly 2024; Kumawat et al. 2023; Aoulmi et al. 2021; Ghamariadyan and Imteaz 2021), the incorporation of flow as an input variable in various combinations/capacities/variations has been less common (Ahmad et al. 2024; Feng et al. 2024; Sheikh and Coulibaly 2024; Gholami & Sahour 2022; Sharma et al. 2022; Wu et al. 2021; Nascimento et al. 2022). When relating the flow to the waterbody and the respective catchment characteristics, the effects of upstream catchment flow contributions and its dynamics upon the accelerated flow being generated downstream, given the holistic complexity linked with upstream-downstream associations of hydrological processes in flowing waterbodies, portray a significant role in spatially distributed travel time of the generated catchment runoff (Berhanu et al. 2016; Bunster et al. 2019). Thus, it can be deciphered that the flow contributions from the upstream catchment locations are comprehended to have a collective influence, alongside the rainfall, upon the flow being spawned at the downstream catchment locations, directly impacting various hydraulic parameters such as the flow velocity, travel time and hydraulic radius (Bunster et al. 2019; Berhanu et al. 2016). However, the consideration of upstream catchment flow contributions has mostly been either neglected, or assumed as static, which results in inaccurate depiction of the modelled catchment’s hydrological response (Bunster et al. 2019; Berhanu et al. 2016; Mohammadi 2021). In terms of hydrological research using ANN models, to the best of our knowledge, the incorporation and analysis of the collective influence of upstream catchment flow and the localised rainfall, upon improving the dynamics of the downstream catchment flow estimation process using ANN models in Australian urban catchments has been scarcely explored (Nourani et al. 2014). Therefore, this research aims to address this knowledge gap in research and tackle the need for enhanced modelling techniques, with the primary focus being centred upon using precipitation and upstream-catchment-flow as the main input variables to estimate the expected urban catchment runoff, with the assistance of ANN models, employing two powerful supervised learning algorithms - Bayesian Regularization (BR) and Levenberg Marquardt (LM), the predictive abilities of which, in terms of developing accurate estimates of the expected flood flow will be comparatively evaluated and authenticated against the actual observations. Gardiners Creek catchment, a highly urbanised waterway catchment, located in south-eastern Melbourne, Australia was selected as the case study location. The main objectives of the study are the development of an enhanced accuracy flood flow estimation model, based upon ANN-modelling techniques, employment of the developed model in effective estimation of urban catchment runoff based on minimal data – upstream flow data and/or localised rainfall and studying the collective influence of rainfall and upstream catchment flow upon the dynamics of the flow being spawned downstream. The optimum model dimensions, evaluated on the basis of the respective statistical performance, amongst the numerous simulations that were undertaken, were purported as an alternative consideration for accurate flood flow prediction in urban catchments.

2 Study area and data

2.1 1 Study area

Gardiners Creek catchment, an urban catchment located in Melbourne’s south-eastern suburbs (37° 49’S, 145° 7’E − 37° 50’S, 145° 2’E), withholding a mean imperviousness fraction of 46%,

was designated as the case study location (Fig. 1). The Gardiner Creek’s origin point is at Middleborough Road, flowing over a complete length of over 16.5 km, and outlets to the Yarra River, approximately six kilo-metres from the Melbourne Central Business District (CBD) at Heyington, encircling a total catchment area of 111 km2. The average annual precipitation for the Gardiners Creek catchment is 750 mm, with the mean monthly maximum and minimum temperature vary between 25 oC and 15.3 oC (in summer) and 15 oC and 7.6 oC (in winter) respectively.

Fig. 1
figure 1

Study area (Gardiners creek catchment) and locations of the gauging stations

Full size image

The Gardiners Creek catchment area serves as a multifaceted urban environment, merging and providing accessibility for travelling across multiple Eastern municipalities, specifically Boroondara, Stonnington, Whitehorse and Monash. The catchment area comprises of a mixed land-use distribution inclusive of residential (64%), public use (11%), roads (9%) and other uses (16%). There are a total of seven streamflow gauging stations situated in the vicinity of the Gardiners Creek catchment, where only three of them – Eley Road East Drain at Eley Road (Station ID 229,638 A), High Street Road at Ashwood (Station ID 229,625 A) and Great Valley Road at Gardiner (Station ID 229,624 A) with good-quality, complete datasets, situated within the catchment boundary were nominated for the calibration and validation processes of the ANN model. The placement of all the streamflow gauging stations can be referred to in Fig. 1.

2.2 Data

Quality checked rainfall (in mm) and stream discharge (in m3/s) data available at 6-minute time interval, spanning from 1st January 1980 to 1st December 2021, logged at the multiple gauging stations positioned within the Gardiners Creek catchment area, were provided by Melbourne Water Corporation (https://www.melbournewater.com.au/). There were a total of seven gauging stations located within the vicinity of Gardiners Creek, where their locations were placed using QGIS and GeoCoding tools. The precipitation and flow datasets for all the gauging stations, were evaluated for completeness (complete dataset with no missing values) and data quality based on the data quality guideline provided by Melbourne Water (https://www.melbournewater.com.au/). Based upon the mentioned criteria, three streamflow gauging stations- Eley Road East Drain at Eley Road, High Street Road at Ashwood and Great Valley Road at Gardiner were chosen for the model calibration and validation in the current study. Blackburn North Drive at Kinkora Road (Station ID 229,636 A), despite being situated near the catchment boundary, was not considered due to the incompleteness and poor quality of its respective measured rainfall records, while the available good-quality flow records were utilised as upstream catchment flow contributions to the Eley Road East Drain catchment location. Two of the most recent major historical storm incidences − 4th February 2011 and 6th November 2018, that occurred in the catchment over the past fifteen years, were nominated built upon the flood history archives from the Victorian local flood guide (Victoria State Emergency Services 2022). The storm incidence nomination process is constrained within the last fifteen years to understand the catchment’s present hydrological response stature, amalgamating the bearings of latest catchment features alterations, ecological factors and climate change impacts (Chakrabortty et al. 2021). The selection of the storm incidence data primarily involved considering two days preceding and following the prevalence of the storm incidence, and collectively infusing them along with them storm event data, to obtain an overall comprehension of the current response stature of the catchment to storm events.

The localised precipitation data and the flow contributions from the upstream catchment were considered as the two primary input variables. Regarding flow contributions from the upstream catchment, in any water body, a hydrological event that transpires in the upstream sections, will have a certain level of impacts upon the downstream sections of the water body, namely involving the dynamics and quantity of the flow. Given this encompassive complexity involved with upstream-downstream associations of hydrological processes in water bodies (Berhanu et al., 2016), the effect of upstream flow contributions, collectively alongside the rainfall on the flow being generated at the downstream catchment locations is deemed essential and is thus considered as an additional input variable together with rainfall for the three gauging station locations.

3 Methodology

3.1 Data Pre-processing and Normalization

Every catchment response to rainfall is associated with a lag-time, which however is a natural phenomenon which the ANN is unable to comprehend, Thus, the lag-times need to be adjusted, prior to running the ANN models, i.e., the discharge data needs to be brought backward to associate the respective discharge measurement with the corresponding rainfall magnitude which transpired earlier. In the case of urban catchments especially, this procedure is deemed highly essential, primarily due to the nature of the impervious surfaces influencing the flow velocity and acceding overland flow to reach the prime channel at an intensified pace, which increases the probability for significant over/(under)estimation. Thus, the appropriate lag-times were explored, based upon established studies, and accordingly processed, followed by noise-treatment and filtering of outliers, disregarding any recordings of controversial origin, or imposing minimal influence on the values of the extremes. Prior to the ANN simulation, the datasets are normalised, to warrant for all the dataset’s numeric columns sharing a mutual scale, ensuring all the essential process parameters are equally handled by the ANN model, and ensuring no incidence of computation errors involving varying parameter magnitudes prevails (Balacumaresan et al. 2023; Choudhury et al. 2018). The normalisation of the data is established using the following Eqs. 1,

$${X}_{Norm}=\frac{{X}_{O}- {X}_{min}}{{X}_{max}- {X}_{min}}$$
(1)

Where, \({X}_{Norm}\) is the normalised value, \({X}_{O}\) is the original value and \({X}_{min}\) and \({X}_{max}\) signifies the minimum and maximum values.

3.2 Development of ANN Model

A feedforward multilayer perceptron (MLP) neural network architecture is embraced for the developed model, along with hyperbolic tangent sigmoid function (tansig) being adopted as the neural transfer activation function. The ANN model undergoes the process of training and testing, utilising two supervised learning algorithms – Bayesian Regularization (BR) and Levenberg Marquardt (LM), and the prediction capability and model performance obtained when applying both algorithms are comparatively evaluated. Given the high complexity and non-linearity involved with the urban catchment’s physical processes, the ascertainment of the optimum dimensions of hidden layers and neurons contained within, is deemed highly crucial in offsetting the non-linearity of the physical processes (Khoirunisa et al. 2021; Asokhan and Nakulraj 2020; Choudhury et al. 2018). Accordingly, provided the sensitivity of the calibrated network performance to the hidden layers dimensions, the variance of the hidden layers, and the neurons contained within each layer is repeatedly conducted until the optimal dimensions are found (Balacumaresan et al. 2023). The hidden layer variance procedure was conducted in the format of varying the number of neurons from 1 to 30 for one hidden layer, 2 and 1 to 30 and 29 for two hidden layers and so on continuously for a total of upto six hidden layer, with an increment of one neuron in each layer (Balacumaresan et al. 2023; Choudhury et al. 2018).

Initially, the ANN model underwent training and testing utilising the localised rainfall as the single input variable at all three-locations using both of the selected learning algorithms - LM and BR. This is trailed by re-training the models for the three catchment locations, this time integrating the flow contributions from the respective upstream catchment of the catchment under analysis (Kinkora Road for Eley Road, Eley Road East Drain for Ashwood and Ashwood Road for Gardiners), as a supplementary input variable, along with the rainfall data, for accurate flow estimation. The consideration of the upstream catchment flow mainly involves vindicating for the impacts of upstream flow contributions on the dynamics of the flow being generated at the downstream locations, thus enhancing the flow estimation accuracy and procuring a more realistic catchment response depiction (Balacumaresan et al. 2023). As mentioned in the earlier sections, the storm events dataset for both events comprises of two days preceding and subsequent to the prevalence of the storm event, at 6-minute time intervals, where the dataset was separated using an 80:20 ratio for training and testing datasets respectively, where the training dataset was further segregated with an 80:20 ratio for the training and validation datasets. Accordingly, the number of measured values used for the training and testing datasets were automatically segregated with the ratio of 80:20 for both of the storm events that were modelled.

The performance and the accuracy of the models’ predictions for both daatsets (train/test) will be assessed, using various statistical indexes such as Pearson’s Coefficient of Correlation (R), Coefficient of Determination (R2) and the generalisation error value (MAE), which serves as indicators elucidating the correlation between the predicted output and the actual observations, the goodness-of-fit-achievement and the proportion of variance amidst the actual and predicted outputs (Balacumaresan et al. 2023; Khoirunisa et al. 2021; Asokhan and Nakulraj 2020; Choudhury et al. 2018). Based upon the performance indicators evaluation, the model which showcases no incidence of network overfitting, assures proper value generalisation and possesses the optimum hidden layer dimensions are nominated (Balacumaresan et al. 2023; Choudhury et al. 2018). Following completion, the simulated values undergo denormalization, converting them back to their actual real number format representation and are plotted out in the form of hydrographs. The entire development process of the ANN models was established using Mathworks Matlab software.

4 Results

A comparative performance summary of both ANN models (LM and BR) for both datasets (training and testing), using single (rainfall) and multiple (rainfall and upstream catchment flow) input variables, at all three streamflow gauging stations, in terms of correlation (R, R2) and generalisation error (MAE), for the 6th of November 2018 storm event, have been presented in Table 1 below, while being graphically represented in the following figures, ranging from Figs. 2a, 3, 4, 5, 6 and 7b - Eley Road at East Drain (Figs. 2a and 3b), High Street Road at Ashwood (Figs. 4a and 5b) and Great Valley Road at Gardiners (Figs. 6a and 7b).

Table 1 ANN model performance at downstream catchments using single and multiple input variables for both LM-ANN and BR-ANN models for 6th of November 2018 storm event
Full size table
Fig. 2
figure 2

Comparisons of ANN model results for Eley Road East Drain at Eley Road Retarding Basin catchment location for training dataset for 6th of November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 3
figure 3

Comparisons of ANN model results for Eley Road East Drain at Eley Road Retarding Basin catchment location for testing dataset for November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 4
figure 4

Comparisons of ANN model results for High Street Road at Ashwood catchment location for training dataset for November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 5
figure 5

Comparison of ANN model results for High Street Road at Ashwood catchment location for testing dataset for November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 6
figure 6

Comparisons of ANN model results for Great Valley Road at Gardiners catchment location for training dataset for November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 7
figure 7

Comparisons of ANN model results for Great Valley Road at Gardiners catchment location for testing dataset for November 2018 storm event using: (a) single input variable and (b) two input variables

Full size image

Referring to both Table 1; Figs. 2a, 3, 4, 5, 6 and 7b, the LM and BR-based models’ performances, trained utilising a single input parameter (rainfall), being interpreted in terms of the correlation coefficients for both datasets (train/test), indicates the presence of a moderate association between the dependent (flow) and independent (rainfall) variables. Comparatively, the LM and BR-based models’ performances for both datasets (train/test), trained using multiple input parameters (rainfall and upstream catchment flow) showcases the coexistence of a strong, positive association between the dependent (flow) and independent (rainfall and upstream catchment flow) variables. An in-depth analysis of the correlation for both cases (single and multiple inputs), is undertaken using the coefficient of determination (R2) (expressed as a percentage), where the R2 values for the LM and BR-based models, considering only rainfall as the primary input variable, vary in range between 61.4% and 76.7% (LM) and 52.4% and 72.1% (BR), accenting the achievement of a moderate-goodness-of-fit (as depicted in Figs. 2a, 3, 4, 5, 6 and 7b), stipulating moderate performance in replicating the observed result, with up to 76.7% of the variance proportion in the dependent variable (flow) being attributed to the independent variable (rainfall). In comparison, the R2 values for the LM and BR-based models, considering both rainfall and upstream catchment flow, ranges between 85.5 and 97.4% (LM) and 83.3% and 93.7% (BR), highlighting a significant improvement in both the models’ performances, further emphasized by the higher-goodness-of-fit achievement, as seen in Figs. 2a, 3, 4, 5, 6 and 7b for both datasets (train/test) from the close alignment of the simulated hydrographs with the observed hydrograph. This further signifies that the models have performed well in replicating the observed result, with approximately 95.3% of the variance proportion in the dependent variable (flow) being explained by the independent variables (rainfall and upstream catchment flow).

When assessing the Mean Absolute Error (MAE) values (in m3/s), for both the LM and BR-based models’ performances for both datasets (train/test), the magnitudes of the MAE values, considering only rainfall as the input variable, ranges from 0.686 m3/s to 9.43 m3/s (LM) and 0.697 m3/s to 10.25 m3/s (BR), whereas when both rainfall and the upstream catchment flow are considered, the magnitude of the MAE values ranges from 0.234 m3/s to 4.621 m3/s (LM) and 0.246 m3/s and 4.457 m3/s (BR). The generalization error results infer that consideration of both flow contributions from the respective catchment(s) upstream and rainfall as input variables, in comparison to only using rainfall, results in both models (LM-ANN and BR-ANN) performing well in replicating the observed result, with much lower generalization error (MAE) values, indicating minimal differences between the predicted and observed value, further conforming and offering stronger confidence on the models’ prediction accuracy and results reliability.

When comparatively assessing the performances of the ANN models trained using both the LM and BR training algorithms, it can be inferred from Table 1; Figs. 2a, 3, 4, 5, 6 and 7b, that the LM-ANN model has clearly outperformed the BR-based ANN model in most of the cases, when using both single and multiple input parameters, especially in the testing datasets, showcasing higher correlation coefficients (R2) ranging between 61.4% and 76.7% (single input variable) and 85.5% and 95.3% (multiple input variables), in contrast to the BR-ANN model’s R2 values, which range between 52.4% and 72.1% (single input variable) and 83.3% and 94.3% (multiple input variables). However, regarding the training dataset, the BR-ANN model is shown to have surpassed the performance of the LM-ANN model in some of the cases, when using single and multiple input variables, as shown by the R2 values for the Eley Road East Drain at Eley Road Retarding Basin and Great Valley Road at Gardiners streamflow gauging stations, which were 65.8% and 72.1% (single input variable) and 89.6% and 94.3% (multiple input variables), respectively, in comparison to the LM-ANN model’s R2 values, which were 64.4% and 66.5% (single input variable) and 88.1% and 93.3% (multiple input variables). However, when looking at the MAE values for both the BR-ANN and LM-ANN, it can be noticed that the MAE values for the LM-ANN, ranging between 0.512 m3/s and 7.791 m3/s (single input variable) and 0.234 m3/s and 4.021 m3/s (multiple input variables), are much lower than the MAE values for the BR-ANN in most of the cases, ranging between 0.626 m3/s and 7.397 m3/s (single input variable) and 0.246 m3/s and 4.528 m3/s (multiple input variables), attesting that the LM-ANN model predictions have a high rate of accuracy, with minimal difference between the replicated and observed values. On an overall scale, the LM-ANN model has outperformed the BR-ANN model, with regards to a stronger, positive correlation, higher-goodness-of-fit-achievement and lower generalization error, conforming to the LM-ANN model’s prediction accuracy and results reliability.

The performances of both models (LM/BR) were further evaluated employing another storm event that transpired in the Gardiners Creek catchment - the 4th of February 2011 event, where a summary of the network performance is presented in Table 2, while being graphically illustrated in the Figs. 8a, 9, 10, 11, 12 and 13b – Ele3 Road at East Drain (Figs. 8a and 9b), High Street Road at Ashwood (Figs. 1b and 10a) and Great Valley Road at Gardiners (Figs. 11 and 12a and b).

Table 2 ANN model performance at downstream catchments using single and multiple input variables for both LM-ANN and BR-ANN models for 4th February 2011 storm event
Full size table
Fig. 8
figure 8

Comparisons of ANN model results for Eley Road East Drain at Eley Road Retarding Basin catchment location for training dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 9
figure 9

Comparisons of ANN model results for Eley Road East Drain at Eley Road Retarding Basin catchment location for testing dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 10
figure 10

Comparisons of ANN model results for High Street Road at Ashwood catchment location for training dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 11
figure 11

Comparisons of ANN model results for High Street Road at Ashwood catchment location for testing dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 12
figure 12

Comparisons of ANN model results for Great Valley Road at Gardiners catchment location for training dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image
Fig. 13
figure 13

Comparisons of ANN model results for Great Valley Road at Gardiners catchment location for testing dataset for 4th of February 2011 storm event using: (a) single input variable and (b) two input variables

Full size image

Referring to Figs. 8a, 9, 10, 11, 12 and 13b; Table 2, the results clearly accentuate that both the LM and BR-based ANN models, trained utilising multiple input parameters (rainfall and upstream catchment flow) exhibit a much stronger and exceptional performance for both datasets (train/test), in terms of the higher R2 values ranging between 80.8% and 94.9% (LM) and 79.3% and 93.3% (BR) and the lower generalisation error (MAE) values ranging between 0.273 m3/s and 7.49 m3/s (LM) and 0.457 m3/s and 9.41 m3/s (BR), in comparison to the performance of the LM and BR-based ANN models, trained using a single input parameter (rainfall), exhibiting a comparatively lower, moderate performance for both datasets (train/test), as depicted by the moderate R2 values ranging between 54.3% and 84.1% (LM) and 52.5% and 81.9% (BR) and the higher MAE values ranging between 0.686 m3/s and 9.43 m3/s (LM) and 0.697 m3/s and 10.25 m3/s (BR). In other words, this clearly stipulates that when multiple input variables (rainfall and upstream catchment flow) are utilised, both the LM and BR-based ANN models perform well, in terms of displaying stronger, positive correlation coexisting between the variables, higher-goodness-of-fit-achievement, with upto 94.9% of the variance proportion in the dependent variable (flow) being explained by the dependent variable (rainfall) and also lower generalisation error, indicating that there is minimal difference between the predicted and actual observations, serving testament to the model’s prediction accuracy and result reliability, in contrast to the moderate performance results achieved when utilising only rainfall as the input variable.

When comparatively assessing the performances of the LM-ANN and BR-ANN models against each other, it can be clearly inferred based upon Table 2; Figs. 8a, 9, 10, 11, 12 and 13b, that the LM-ANN model precisely estimates the likely flow at the three selected locations, with regards to the strong positive correlation and the high goodness-of-fit attained between the observed and simulated values, as depicted by the R2 values ranging from 54.3 to 84.1% (single input) and 80.8-94.9% (multiple inputs), in contrast to BR-ANN model’s R2 values, which range from 52.5 to 81.9% (single input) and 79.3-93.3% (multiple inputs), and the low MAE values attained, ranging between 0.686 and 9.43 m3/s (single input) and 0.358–7.49 m3/s (multiple inputs), which were relatively much lower than the BR-ANN model’s MAE values, which range between 0.69 and 10.25 m3/s (single input) and 0.479–9.41 m3/s (multiple inputs), thereby outperforming the BR-ANN model, and offering additional assurance on the LM-ANN’s predictive competence and results accuracy rate, towards potentially adapting it for implementation in accurate estimation of the expected catchment flow. The results are further supported by the findings of Chopra et al. (2015), Romlay et al. (2019), Tabassum & Dar (2020), Heng et al. (2022) and Prasad et al. (2023) all concluding that LM-based ANN models displayed superior performance over BR-ANN models, delivering further assurance that the LM-based ANN model is the most suitable model typle to be contemplated for implementation for conducting urban catchment response studies and in precisely predicting the expected flood flow quantiles.

On an overall scale, based upon the encompassing complexity involved with upstream-downstream linkages of hydrological processes in waterbodies, the addition of upstream catchment flow, collectively alongside rainfall as multiple input parameters, serves its purpose as a delineation, rationalizing the collective impact and contributions of upstream catchment flow alongside rainfall, upon the dynamics of the accelerated flow generated at the downstream catchment/sub-catchment locations, This is clearly evidenced in terms of the variance seen in the models’ results when using only rainfall, where a moderate correlation (0.737–0.917 (LM) and 0.724–0.876 (BR)), moderate-goodness-of-fit achievement (54.3-84.1% (LM) and 52.4-81.9% (BR)) and higher generalization error values (0.512–7.391 m3/s (LM) and 0.626–10.25 m3/s (BR)) was achieved (as seen in Tables 1 and 2; Figs. 2a, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13b), in contrast to the results when upstream flow is considered as an additional variable alongside rainfall, where the results exhibit a much stronger, positive correlation (0.899-0.987 (LM) and 0.891–0.971 (BR)), higher goodness-of-fit achievement (80.8-97.4% (LM) and 79.3-94.3% (BR)) and co-existence of minimal differences between the model predictions and the actual observations (0.234–7.49 m3/s (LM) and 0.246–9.41 m3/s (BR)). Based upon the high positive variation showcased by the results, it can be stated that the inclusion of upstream catchment flow alongside rainfall as a supplementary input variable has significantly contributed to enhancing the performances of both models, elucidating for majority of the variance proportion shown by the flow estimates (as seen in the R2 values from Table 1), improving the models’ prediction accuracy and simulating a more pragmatic response of the urban catchment response to the modelled storm events at the specified streamflow gauging stations’ locations.

Regarding the model’s respective performances, the LM-ANN model has collectively outperformed the BR-ANN model in most of the cases, especially in the testing dataset of the 6th of November 2018 storm event and in both datasets (train/test) for the 4th of February 2011 storm event, when using both single and multiple input variables, as showcased by the results in terms of a higher R2 (54.3-84.1% (single) and 80.8-97.4% (multiple)) and lower MAE values (0.512–7.391 m3/s (single) and 0.234–7.49 m3/s (multiple)), in contrast to the BR-based ANN model’s performance, in terms of the relatively lower R2 (52.4-81.9% (single) and 79.3-94.3% (multiple)) and slightly higher MAE values (0.626–10.25 m3/s (single) and 0.246–9.41 m3/s (multiple)). The BR-based ANN model only outperforms the LM-based ANN model on two instances, which are in the training dataset for the 6th of November 2018 at the Eley Road East Drain and Great Valley Road at Gardiners gauging stations, as showcased by the higher R2 values (65.8% and 72.1% (single) and 89.6% and 94.3% (multiple)), in comparison to the slightly lower R2 values (64.4% and 66.5% (single) and 88.1% and 93.3% (multiple)). However, the magnitude of the generalisation error is slightly higher for the BR-based ANN model (0.626 m3/s and 6.083 m3/s (single) and 0.246 m3/s and 4.028 m3/s (multiple)) in comparison to the error magnitudes of the LM-based ANN model (0.583 m3/s and 5.478 m3/s (single) and 0.234 m3/s and 4.62 m3/s (multiple)), which depicts that despite demonstrating slightly lower correlation and comparatively lower goodness-of-fit-achievement, the LM-ANN model has lower error magnitude, stipulating that the LM-based ANN model has been comparatively more successful in replicating the observed result, with minimal differences between the simulated and the observed values, affirming to the LM-ANN model’s prediction accuracy rate and reliability of results being generated, in contrast to the BR-ANN model. Hence, based upon the results, it can be deduced that the LM-based-ANN model has the potential towards being considered as a feasible alternate solution that can be instigated in the enhancement of the present flood flow estimation practices of urban catchments and towards effectually predicting the catchment runoff, grounded upon the providence of minimal data variables.

5 Conclusion

The rapidly escalating statewide-urban-sprawl and the fluctuating-climate-vulnerability-status of Australia has collectively triggered a continuous risk of residual urban flooding. However, the limited-data-availability, high intricacy and intrinsic-non-linearity allied with the topography and dominant-hydrological-processes of Australian urban catchments, limit the prediction accuracy of conventional modelling practices, flaunting the necessity for enhanced flood forecasting practices. Thus, the prime intention of this research paper was focused upon assessing the effectiveness of ANN models in the enhancement and precise estimation of the expected catchment flood flow, based upon the providence of minimal data variables. Two supervised learning algorithms – BR and LM were utilised in the training of the ANN model for multiple recent significant storm events − 4th of February 2011 and 6th of November 2018, which transpired at the study location, Gardiners Creek catchment, based on high quality datasets from three streamflow gauging stations located within. Two commonly available hydrological variables – localised rainfall and flow contributions from the respective upstream catchment locations, were used for model calibration, where they were incorporated as two sets - single (rainfall) and multiple (rainfall and upstream catchment flow), as a means of comprehending the significance of considering upstream catchment flow in flow estimation at downstream catchment locations.

The comparative assessment results of both models (LM/BR) for both datasets (train/test) for both storm events, exhibit strong positive correlation and high-goodness-of-fit achievement (80.8-97.4% (LM) and 79.3-94.3% (BR)) and much lower generalisation error values (0.234–7.49 m3/s (LM) and 0.246–9.41 m3/s (BR)), when considering the upstream catchment flow along with the rainfall as input variables, in contrast to the moderate correlation and goodness-of-fit achievement (54.3-84.1% (LM) and 52.4-81.9% (BR)) and higher generalisation error values (0.512–7.391 m3/s (LM) and 0.626–10.25 m3/s (BR)) obtained when considering only rainfall as the single input variable. Regarding the comparative performance of both models, the LM-ANN exhibits superiority in most cases, when using both single and multiple input variables, as showcased by the high R2 (54.3-84.1% (single) and 80.8-97.4% (multiple)) values and lower MAE values (0.512–7.391 m3/s (single) and 0.234–7.49 m3/s (multiple)), in contrast to the BR-ANN model’s performance, in terms of the comparatively lower R2 (52.4-81.9% (single) and 79.3-94.3% (multiple)) and slightly higher MAE values (0.626–10.25 m3/s (single) and 0.246–9.41 m3/s (multiple)). Thus, it can be comprehended from the results that the LM-ANN model has clearly outperformed the BR-ANN model, with regards to the higher correlation, better goodness-of-fit-achievement and more accurate flow predictions, in terms of the model being successful in replicating the observed results, with minimal difference between the observed and modelled values, as validated by the lower error values, conforming to the LM-based ANN model’s predictions’ accuracy and reliability of results, highlighting it to be a more optimal option for consideration in enhanced estimation of accurate flood flow quantiles.

On an overall basis, the results clearly accentuate that the incorporation of the flow contributions from the respective upstream catchment(s), together with the rainfall has significantly contributed towards enhancing the models’ respective performances, vindicating for the collective impact and contribution that the upstream catchment flow along with the rainfall has upon the dynamics of the flow being generated at the downstream sub-catchment locations. This is clearly evidenced in terms of the high positive variance shown in the R2 and MAE values, where the higher-goodness-of-fit-achievement and the minimal-magnitude-differences, corroborate for the models’ successful replication of the observed flow and the high prediction accuracy achieved, and substantiating for majority of the variance proportion in the flow (up to 97.4%). Thus, it can be inferred from the results that the collective integration of rainfall and the flow contributions from the respective catchment upstream as input variables for flow estimation provides a more realistic depiction of the urban catchments’ retortment at the specified location to the storm event, accounting for the holistic intricacy allied with the upstream-downstream associations of hydrological procedures, and significantly improving the models’ prediction accuracies and reliability of the predicted results. In terms of the models’ performances, the LM-based-ANN model clearly outperforms the BR-based ANN model, with regards to a stronger correlation, a higher goodness-of-fit-achievement, with minimal error differences between the predicted and actual observations, thus confirming the capability and high effectiveness of the LM-ANN model in the estimation of the expected catchment flood flow, grounded upon the providence of minimal data – deuce variables (localised rainfall and upstream catchment flow) with high prediction accuracy. Thus, the LM-ANN model, alongside the simple methodology associated with the adoption of flow contributions from the respective upstream catchments and rainfall as input variables, investigated in this study, can be considered as a cost-effective solution that can be potentially considered for implementation in catchment studies for regions with limited data availability or situated in data scarce/sparse locations. As part of future works, the developed ANN model, following validation against a benchmark conventional model, will be implemented for estimating the flood flow expected in the same catchment under future climate change scenario using multiple projected greenhouse gas emissions scenarios for various future timescales.