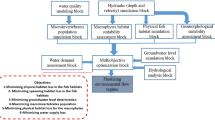
Abstract
The present study proposes and evaluates an integrated framework to assess dam construction and removal, encompassing the simulation of downstream river habitats and reservoir operation in three distinct statuses: conventional reservoir operation optimization, optimal release considering environmental aspects within the optimization model, and natural flow conditions. Fuzzy physical habitat simulation was employed to assess physical habitats, while an ANFIS-based model was utilized to simulate thermal tension and dissolved oxygen tension at downstream habitats. Particle swarm optimization was applied in the optimization models. To evaluate the effectiveness of the proposed framework, results from the optimization system as well as habitat suitability models in the natural flow and current condition were compared using various measurement indices, including the reliability index, vulnerability index, the Nash–Sutcliffe model efficiency coefficient (NSE), and root mean square error (RMSE). The case study results suggest that the reliability of water supply may be diminished under optimal release for environmental and demand considerations. Additionally, optimal release for the environment may not adequately protect downstream aquatic habitats. Therefore, in cases where the preservation of downstream habitats is a priority, dam removal may be a logical solution. Moreover, it is essential to acknowledge that the main limitation of the proposed method is its high computational complexity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rivers play a pivotal role in meeting various water demands, including drinking water and irrigation. Among the hydraulic structures present in rivers, large dams are of paramount importance for water supply, as well as for functions such as electricity generation and flood control (Di Baldassarre et al 2021). However, the burgeoning population poses environmental challenges to river ecosystems (Jones and Bull 2020). This leads to an increase in offstream flow to meet water demands while decreasing instream flow, thereby exacerbating environmental degradation in river ecosystems. The environmental impacts of dams have been extensively discussed in recent decades (e.g., Li et al. 2021), highlighting the need to address issues such as dam removal.
Dam removal has emerged as a challenging issue in recent years, with previous studies discussing its importance and feasibility (e.g., Foley et al. 2017; Major et al. 2017). It is evident that a comprehensive approach, possibly involving complex modeling, is necessary to assess the potential benefits of dam removal on the environment. An integrated framework proves invaluable in evaluating how dam removal could positively impact the environment, considering various aspects. Notably, the assessment of dam removal projects should include an evaluation of their effects on downstream aquatic habitats. Dams represent significant investments in hydraulic infrastructure. Therefore, optimizing reservoir operations post-construction becomes crucial (Ahmad et al. 2014). Optimal reservoir operation aims to maximize benefits, with methodologies like the loss function widely used for optimization. Moreover, incorporating storage loss into the optimization system remains pertinent (full review by Beiranvand and Ashofteh 2023). Despite the challenges posed by the non-linear nature of reservoir operation, various optimization techniques such as linear programming (LP), non-linear programming (NLP), and dynamic programming (DP) have been employed (e.g., Chen 2021). However, advanced computational methods like metaheuristic algorithms are increasingly recommended due to their efficiency (e.g., Yaseen et al. 2019).
Assessing environmental degradation in rivers requires effective tools, with mathematical models being instrumental in evaluating water quality and quantity. Abiotic factors play a crucial role in providing suitable habitats for aquatic life (Ahmadi‐Nedushan et al. 2006). Notably, physical parameters and water quality parameters are vital considerations for environmental assessments, including environmental flow assessment. While univariate methods offer simplicity, more efficient techniques like fuzzy multivariate methods have been developed to account for interactions between physical factors. Expert opinion plays a significant role in simulating physical habitats due to their complexity. Water quality is another critical aspect of river ecosystem management, as it directly impacts aquatic life. Biological activities of aquatic organisms are dependent on water quality parameters such as temperature and dissolved oxygen (Devi et al. 2017). Ensuring suitable water quality is essential for the reproductive success of various fish species, highlighting the importance of considering water quality in environmental management plans.
It is essential to emphasize the research gap and the novel contributions of the present study. The integration of environmental modeling within reservoir operation structures is crucial for assessing the downstream impacts of both dam construction and dam removal. While some previous studies have examined the downstream environmental impacts of dams, there remains a lack of integrated frameworks specifically designed to assess downstream environmental degradation resulting from dam construction or removal. Motivated by this research gap, the primary novelty of this study lies in proposing and evaluating an integrated framework for assessing dam removal, with a focus on downstream environmental degradation encompassing water quality and hydraulic parameters. By incorporating both physical and water quality simulations into reservoir operation optimization, the proposed method offers a comprehensive approach to evaluating the environmental benefits of dam removal. This framework addresses fundamental questions regarding how dam removal can alleviate environmental degradation in downstream river habitats and highlights the critical role of optimal operation in minimizing adverse impacts. Moreover, this study presents an opportunity to enhance simulation–optimization methods for assessing dam removal projects, providing a flexible and adaptable framework that can be upgraded as needed.
2 Application and Methodology
The proposed framework comprises two scenarios for measuring reservoir losses and downstream environmental degradation. Different measurement indices are employed to assess the environmental benefits of dam removal and its impacts within the river basin. The first scenario optimizes release and storage in the reservoir without considering downstream environmental flow, aiming to maximize reservoir benefits. In contrast, the second scenario introduces a novel optimization system that simultaneously minimizes environmental degradation and reservoir losses as well as assuming dam removal to restore natural river flow.
2.1 Physical Habitat Simulation
The previous studies have demonstrated the utility of such simulations in river ecosystem management (Sedighkia et al. 2021a). We utilized 1D fuzzy physical habitat simulation, recognized as one of the most efficient methods for habitat assessment. Notably, the applicability and efficiency of one-dimensional hydraulic modeling for physical habitat simulation have been validated in prior research (Jowett and Duncan 2012). The development of fuzzy habitat rules constitutes a critical step in physical habitat simulation. In our approach, we combined field studies with expert opinions to formulate these rules. Field studies comprised two main components: ecological studies or fish observations and surveying river cross-sections, essential for hydraulic simulation. In this study, electrofishing was employed due to its advantages and the research team's prior experience. Additionally, depth and velocity were concurrently measured in microhabitats using a propeller and metal rule (Harby et al. 2004). It is noteworthy that the Brown trout was selected as the target species in the case study. A representative reach of 1000 m in length was considered for the physical habitat simulation. More details on the fuzzy physical habitat simulation have been addressed in the literature (Noack et al. 2013).
2.2 Thermal Habitat Assessment
Thermal habitat assessment is a crucial component of the proposed framework for analyzing dam removal. A fundamental requirement for achieving this goal is the simulation of stream temperature. While hydrodynamic models like SSTEMP have been developed for this purpose (Ouellet et al. 2020), they lack flexibility when integrated into optimization models. Therefore, a more adaptable and applicable method is needed, and data-driven models present an efficient option.
Neural networks are widely recognized as effective tools for developing robust data-driven models in water quality simulation (Chatterjee et al. 2017; Dumitru and Maria 2013). We employed an adaptive neuro-fuzzy inference system (ANFIS) to simulate stream temperature within the proposed framework (developed by Jang 1993 and more details by Awan and Bae 2014). Table 1 presents the main characteristics of the developed ANFIS-based model for simulating stream temperature, demonstrating the potential complexity of data-driven temperature models.
Subsequently, it is necessary to convert stream temperature into thermal habitat tension. Here, we adopted a biological-based model used by Sedighkia et al. (2019) to assess the thermal habitat tension of the Brown trout within the present framework. However, it is important to note that using other target species may require its own thermal tension model. Figure 1B illustrates the thermal tension curve for the Brown trout utilized in the case study (more details by Sedighkia et al. 2019 and Sedighkia et al. 2021b).
Furthermore, optimization was conducted on a monthly scale, necessitating the use of monthly data from various stations downstream. Additionally, employing an index is crucial for assessing the robustness of the data-driven model. The Nash–Sutcliffe model efficiency coefficient (NSE) was utilized for this purpose, initially developed for measuring the performance of hydrological models (Abbaspour et al. 2015), but applicable to any type of simulation for comparing results with recorded data or observations to validate the model. Equation 1 presents the basic form of this index. To estimate the wetted perimeter in the optimization model, a relationship between wetted perimeter and discharge was developed based on hydraulic modeling by HEC-RAS 1D. A downstream reach with a length of 9000 m was considered in the stream temperature modelling. The following equation shows the NSE mathematical definition.
where mt represents the simulated or modelled parameter, Ot denotes observed or recorded data, Omean is the average of the observed data, and Ti indicates the number of samples.
2.3 Dissolved Oxygen Modelling
Dissolved oxygen (DO) is a critical water quality parameter for river habitats, serving as an indicator of water quality suitability for aquatic life. Other pollutants in the river can impact DO concentration, making it a representative parameter for overall water quality. In this study, we employed an ANFIS-based model to simulate DO concentration. The modeling was conducted on a monthly scale to capture temporal variations. Table 2 presents the main characteristics of the developed data-driven model for simulating dissolved oxygen.
Given that DO levels are influenced by various water pollutants that may be discharged into the river, we included the month (January to December) as one of the inputs in the data-driven model. It is important to note that pollutant rates can vary across months due to agricultural activities in the downstream river basin. Additionally, a DO tension model for the Brown trout, developed by Sedighkia et al. (2019), was adopted within the proposed framework. The outputs of the DO model were converted to DO tension using the biological model. Figure 1A1 and 1A2 illustrate the DO tension curve developed by Sedighkia et al. (2019), which was utilized in the case study.
To assess the robustness of the dissolved oxygen data-driven model, we applied the Nash–Sutcliffe efficiency coefficient (NSE). This index provides a measure of how well the model predictions match the observed data, ensuring the reliability of the modeling approach.
2.4 Optimization Model
In both scenarios, optimization models are required to efficiently manage reservoir operation. In the first scenario, aimed at maximizing reservoir benefits, Eq. 2 was utilized as the objective function. This function minimizes the difference between the target (maximum requested water demand) and the release for demand. Constraints play a crucial role in structuring optimization models. For scenario 1, we incorporated several constraints into the proposed optimization model, including minimum operational storage, maximum storage, and maximum water demand. Specifically, operational storage in the reservoir should not fall below the minimum operational threshold or exceed the reservoir's capacity. Additionally, release for demand must not surpass the maximum requested water demand.
To handle constraints within the metaheuristic optimization framework, penalty functions were employed—a well-established approach utilized in numerous prior studies (developed by Agarwal and Gupta 2005). Three penalty functions were integrated into the optimization model for scenario 1. These penalty functions increase the penalty incurred by the model when constraints are violated in the optimal solution. Equation 6 illustrates the final form of the objective function for the optimization model in scenario 1. Here, C1 to C3 represent constant coefficients determined through initial sensitivity analysis of the optimization model.
where Dt is maximum water demand, Rt is release for demand or total release for environment and demand in the scenario 2, St is storage, Smax is maximum storage or capacity of the reservoir and Smin is minimum operational storage in the reservoir. Moreover, it is necessary to update reservoir storage in each time step that was carried out by the Eq. 7. Overflow was calculated by the Eq. 8 where Et is evaporation from the reservoir, At is area of the reservoir, It is inflow of the reservoir and T is time horizon.
We developed a novel optimization model for scenario 2, aiming to minimize water demand loss, storage loss, and environmental degradation. Therefore, the loss function utilized in the previous optimization model serves as one of the terms in this updated optimization model. Specifically, four main terms were considered: water demand loss, physical habitat loss, thermal habitat loss, and dissolved oxygen loss.
In detail, PHN, THN, and DHN represent the normalized weighted usable area, thermal suitability, and dissolved oxygen suitability in the natural flow, respectively. On the other hand, PHM, THM, and DHM denote the normalized weighted usable area, thermal suitability, and dissolved oxygen suitability in the optimal release for the environment, respectively.
In this optimization model, we also employed the penalty function method. The same penalty functions as in the previous model were utilized. The final form of the objective function for the optimization model in scenario 2 is displayed in Eq. 10. Particle swarm optimization (PSO) stands as one of the classic and widely utilized metaheuristic algorithms in optimization models (Eberhart and Kennedy 1995). Further details regarding the methodology of this algorithm can be found in the literature (Eberhart and Kennedy 1995).
2.5 Measurement Indices
The reliability index was employed to assess the performance of the optimization model in both the first and second scenarios concerning water supply. This index was originally developed by Sedighkia et al. 2021a and further improved by Ehteram et al. in 2018. Equation 11 defines this index. Storage loss is another critical aspect to be evaluated. The vulnerability index was also developed by Sedighkia et al. 2021a. Additionally, we utilized the root mean square error (RMSE) to measure the performance of the optimization models regarding storage loss. Equations 12 and 13 define these indices in terms of measuring storage loss compared to optimal storage in the reservoir.
Furthermore, several indices are necessary to gauge the performance of the optimization models in terms of physical habitat loss, thermal habitat loss, and dissolved oxygen suitability loss. The Nash–Sutcliffe model efficiency coefficient (NSE) and RMSE were employed for this purpose, as shown in the following equations. It is important to note that optimal suitability is compared with the natural condition at the downstream river reach.
2.6 Case Study
The Tajan River is one of the most significant rivers in the southern Caspian Sea basin in Iran, serving as a valuable habitat for numerous fish species. Recognizing the importance of irrigation demand, the Rajaei Dam was constructed upstream of this river. However, water demand is being met by extracting water from the reservoir, potentially impacting downstream river habitats. Currently, the release for environmental purposes is minimal, leading to challenges between regional water authorities and the regional department of environment.
This situation presents a dilemma: dam removal could alleviate severe environmental degradation downstream, but environmental optimization might also reduce such degradation. Given the complexities involved in managing the environmental aspects of this river basin, there was a clear need for an integrated framework to assess dam removal and address the environmental management challenges. Figure 2 illustrates the land use, river network, and the location of the Rajaei reservoir within this basin.
3 Results and Discussion
In the first step, it is necessary to present and discuss the results of the physical habitat simulation. Figure 3 illustrates a sample fuzzy membership function developed for the physical habitats, while Table 3 displays the developed fuzzy habitat rules for the target species, which in this case was the Brown trout. Additionally, Fig. 4 presents the weighted usable area (WUA) curve, which serves as the final output of the physical habitat simulation. This curve was subsequently utilized in the structure of the optimization model in scenario 2. The fuzzy rules indicate that the target species may be sensitive to flow velocity, which is logical considering that high flow velocity increases energy consumption for fish.
In the second step, the validation results of the thermal data-driven model should be presented. Figure 5a displays the validation results of the thermal habitat tension model, with the Nash–Sutcliffe efficiency coefficient (NSE) computed. The NSE value is 0.95, indicating that the model is highly robust in simulating stream temperature. According to the literature, an NSE above 0.4 suggests strong predictive skills for the model (Knoben et al. 2019). However, even an NSE greater than zero can be considered acceptable.
Furthermore, Fig. 5b depicts the validation results of the dissolved oxygen model, with an NSE value of 0.04. While this indicates that the dissolved oxygen model may not be as robust as desired, it is still within an acceptable range. It is important to note that modeling dissolved oxygen can be complex due to the impact of water pollutants and other factors. Previous studies have highlighted that water quality models, such as those for nitrate or dissolved oxygen, may not achieve as high NSE values as runoff models due to the influence of unknown factors and simplifications in the models (Abbaspour et al. 2015).
The large variation in NSE values is justified by the influence of environmental factors on the simulated parameters. For example, changes in land use and point sources of pollution have less effect on water temperature, making its modeling generally easier. Conversely, dissolved oxygen can be highly affected by changes in land use or point sources of pollution, meaning that considering only limited and key inputs in the model may not be sufficient to generate an accurate model, as observed in the present study. Therefore, the performance of the developed model may be justified based on the complexities involved in simulating dissolved oxygen in the stream.
Our case study indicates that modeling dissolved oxygen should be considered a source of uncertainty in the present framework. However, the robustness of the proposed data-driven model may vary from case to case, with some cases exhibiting fewer complexities regarding water quality issues and therefore yielding more robust results.
It should be noted that the Department of Environment conducted undocumented studies, resulting in the development of two linear regression models upstream of the reservoir. Due to the absence of reservoir impact and other pollutants, water temperature and dissolved oxygen concentration were dependent on the air temperature and water temperature, respectively. These equations were utilized in the environmental assessment for the natural flow. Equations 20 and 21 display these regression models. It is worth mentioning that a high dissolved oxygen concentration is the main characteristic of the natural flow in this river basin.
In the third step, the results of the optimization should be presented and discussed. We selected a 72-month period for the simulation in the present study, which posed challenges for both the reservoir and the river basin due to low inflows during certain months. Figure 6a and b illustrate the inflow of the reservoir, optimal release for water demand, and maximum water demand as well as storage time series. It is important to note that the performance of the penalty functions, including minimum operational storage and maximum storage, is robust. The storage time series indicates that the optimization model can maintain the storage between the minimum operational storage and maximum storage, thus indicating acceptable overall performance of the optimization model in scenario 1 regarding storage. However, a detailed analysis of storage loss requires relevant measurement indices, which will be discussed.
Figure 7a displays the release for demand, reservoir inflow, and maximum demand in scenario 2. It appears that considering environmental aspects, with a focus on environmental flow in the optimization model, leads to changes in supplied demand, especially in the first years of the simulated period due to low reservoir inflow. Consequently, low supplied flow in some time steps might pose a challenge for the practical application of the proposed optimization framework in scenario 2. It's worth noting that further analysis of this issue depends on the specific challenges and circumstances of each case study, meaning it may vary on a case-by-case basis. In our case study, the release for demand in each time step was not highly effective. However, the total release over the simulated period was significant. Therefore, using the reliability index seems logical in this case. Nevertheless, engineers may choose different indices in other case studies. More water is supplied in the third, fourth, and fifth years of the simulated period, and utilizing other water resources available in the study area is advisable to compensate for the water supply. Figure 7b presents the storage time series in scenario 2, indicating notable changes in reservoir storage compared to scenario 1. Reduced storage in some simulated time steps is evident, potentially leading to increased storage loss in the optimal release for environment and demand. However, an accurate analysis requires the use of measurement indices.
Furthermore, environmental results should be presented and discussed in scenario 2. Figure 8a illustrates the normalized weighted useable area (NWUA) time series during the simulated period. NWUA was normalized by the maximum WUA for better interpretation of the results in further applications. Significant changes compared to the natural flow are observed. Generally, it appears that using optimal reservoir operation considering environmental aspects may not increase the useable area as much as the natural flow, supporting the argument for dam removal to restore river habitats. However, reducing NWUA is a concern for certain time steps in the simulated period. It's important to note that while NWUA in scenario 2 exceeds that of the natural flow in some time steps, indicating that optimal operation may improve the suitability of physical habitats compared to the natural flow, this occurs only rarely in the case study.
Thermal tension is another aspect that should be discussed. Figure 8b displays the thermal tension time series during the simulated period, comparing thermal tension in the natural flow and the optimal release for the environment and demand by the reservoir. Results indicate that the output of the thermal tension model may be complex, as thermal tension is considerably reduced in some time steps while increased in others. Therefore, the reservoir may have both positive and negative effects within the simulated period. Reservoirs may serve as applicable tools to control thermal tension at downstream habitats in some cases. However, interpreting the results based solely on the thermal tension time series may not be straightforward.
Dissolved oxygen tension is another aspect in the environmental analysis of scenario 2, as displayed in Fig. 8c. Dissolved oxygen tension in the natural flow is close to zero in all time steps. However, the optimal release for the environment and demand indicates that the optimization model may not effectively minimize differences in dissolved oxygen tension in many time steps. Nevertheless, it is undeniable that the performance of the optimization model is adequate in some time steps. It should be noted that regarding the dissolved oxygen model, validation demonstrated that the model is not very reliable in the case study. However, the general trend of the results was acceptable. The high uncertainty of the model may reduce the reliability of the optimization model in terms of dissolved oxygen optimization. Therefore, considering this uncertainty is essential for the final application of the results. However, significant differences between simulated tension in scenario 2 and natural flow in some steps indicate that the results of the optimization model may still be reliable.
As previously mentioned, a thorough discussion of the results and deciding in the case study require the use of measurement indices. Figure 9a displays the reliability index of water demand in both scenarios. A notable decrease in the reliability of water supply is observed in the case study. Specifically, the reliability changes by approximately 15%, indicating a considerable reduction in the economic benefits from the reservoir due to the use of optimal operation considering environmental aspects. Additionally, Fig. 9b and c displays the measurement indices for storage loss, including RMSE and VI. Results demonstrate that the change in storage loss in scenario 2 compared with scenario 1 is not significant. Thus, using optimal reservoir operation considering environmental aspects in the optimization model may not weaken the storage benefits in the reservoir of the case study.
Table 4 presents NSE and RMSE for three environmental aspects in the proposed framework, including physical habitat loss, thermal habitat loss, and dissolved oxygen loss. It's important to note that only positive differences between simulation and optimization in scenario 2 and natural flow were considered to compute the indices. In other words, if physical habitat loss exceeds that of the natural flow in scenario 2, it will be considered equal to NWUA in the natural flow. This approach was applied regarding thermal tension and dissolved oxygen tension as well. NSE for physical habitat loss is -3.43, indicating that the optimization model is not able to provide physical habitat loss as suitable as the natural flow. Moreover, RMSE for physical habitat loss is 0.41, demonstrating a considerable difference between the suitability of physical habitats in the two scenarios. Furthermore, NSE for thermal tension shows that the performance of the optimization model is acceptable in terms of thermal tension. However, RMSE is considerable, indicating that 29% of the thermal tension may render the habitat unsuitable, especially for sensitive species such as the Brown trout. Furthermore, the performance of the optimization model is not defensible in terms of the DO tension based on the computed indices.
Finally, it is possible to assess the feasibility and advantages of the dam removal project in the case study based on all the results. It appears that optimal operation considering environmental flow may not be feasible in the case study. On one hand, the reliability of water supply is reduced, which poses a problem for the regional water authority. On the other hand, optimal operation in scenario 2 may not effectively provide environmental suitability downstream of the reservoir. Hence, it seems that using other options in the case study for water supply, such as storing water in the pools of farms, should be considered if protecting environmental values downstream is the goal. Indeed, dam removal seems necessary to improve the suitability of downstream habitats. However, implementing dam removal may require additional simulations and optimizations. The main advantage of the proposed method is to provide a practical simulation–optimization framework to assess the environmental aspects of dam removal. However, dissolved oxygen results indicate that reducing water pollutants downstream of the reservoirs should also be considered in habitat restoration projects.
Every novel method may have limitations that should be discussed. The main limitation of the proposed framework is its high computational complexity, defined as the required time and memory for using an algorithm in the optimization. Due to the use of an ANFIS-based model in the optimization model, computational complexity is significant. Therefore, using this framework for long-term periods or numerous simulations may require powerful computers and be time-consuming. Additionally, we considered water demand based on the case study in the proposed framework. It's necessary to consider other aspects such as hydropower in future studies. Furthermore, it's essential to consider the uncertainties of the ANFIS-based model for further applications of the results.
4 Conclusions
The present study proposes a novel framework to simulate the environmental aspects of dam removal to facilitate decision-making regarding the necessity and advantages of dam removal projects. Two scenarios were considered, including conventional reservoir operation optimization and optimal operation considering environmental aspects within the optimization model's structure. The first and second scenarios were compared in terms of water supply and storage losses. Additionally, the outputs of scenario 2 were compared with natural flow in terms of physical habitat loss, thermal habitat loss, and dissolved oxygen habitat loss using NSE and RMSE as measurement indices. Based on the results of the case study, the reliability of water supply was significantly reduced in scenario 2, indicating that optimal release considering environmental issues might pose challenges for water demand management in the river basin. Moreover, optimal release considering environmental aspects was not able to reduce tensions and losses as effectively as natural flow. Thus, dam removal is recommended in terms of environmental suitability for downstream aquatic habitats.
Data Availability
Some or all data and materials that support the findings of this study are available from the corresponding author upon reasonable request.
References
Abbaspour KC, Rouholahnejad E, Vaghefi SRINIVASANB, Srinivasan R, Yang H, Kløve B (2015) A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J Hydrol 524:733–752
Agarwal M, Gupta R (2005) Penalty function approach in heuristic algorithms for constrained redundancy reliability optimization. IEEE Trans Reliab 54(3):549–558
Ahmad A, El-Shafie A, Razali SFM, Mohamad ZS (2014) Reservoir optimization in water resources: a review. Water Resour Manage 28(11):3391–3405
Ahmadi-Nedushan B, St-Hilaire A, Bérubé M, Robichaud É, Thiémonge N, Bobée B (2006) A review of statistical methods for the evaluation of aquatic habitat suitability for instream flow assessment. River Res Appl 22(5):503–523
Awan JA, Bae DH (2014) Improving ANFIS based model for long-term dam inflow prediction by incorporating monthly rainfall forecasts. Water Resour Manage 28(5):1185–1199
Beiranvand B, Ashofteh PS (2023) A Systematic Review of Optimization of Dams Reservoir Operation Using the Meta-heuristic Algorithms. Water Resour Manag 1–70
Chatterjee S, Sarkar S, Dey N, Ashour AS, Sen S, Hassanien AE (2017) Application of cuckoo search in water quality prediction using artificial neural network. Int J Comput Intell Stud 6(2–3):229–244
Chen J (2021) Long-term joint operation of cascade reservoirs using enhanced progressive optimality algorithm and dynamic programming hybrid approach. Water Resour Manage 35(7):2265–2279
Devi PA, Padmavathy P, Aanand S, Aruljothi K (2017) Review on water quality parameters in freshwater cage fish culture. Int J Appl Res 3(5):114–120
Di Baldassarre G, Mazzoleni M, Rusca M (2021) The legacy of large dams in the United States. Ambio 50(10):1798–1808
Dumitru C, Maria V (2013) Advantages and Disadvantages of Using Neural Networks for Predictions. Ovidius Univ Ann Ser Econ Sci 13(1)
Eberhart R, Kennedy J (1995) Particle swarm optimization. In Proceedings of the IEEE international conference on neural networks. Citeseer 4:1942–1948
Ehteram M, Karami H, Mousavi SF, Farzin S, Celeste AB, Shafie AE (2018) Reservoir operation by a new evolutionary algorithm: Kidney algorithm. Water Resour Manage 32(14):4681–4706
Foley MM, Bellmore JR, O’Connor JE, Duda JJ, East AE, Grant GE, Anderson CW, Bountry JA, Collins MJ, Connolly PJ, Craig LS (2017) Dam removal: Listening in. Water Resour Res 53(7):5229–5246
Harby A, Baptist M, Dunbar MJ, Schmutz S (2004) State-of-the-art in data sampling, modelling analysis and applications of river habitat modelling: COST action 626 report (Doctoral dissertation, Univerza v Ljubljani, Naravoslovnotehniška fakulteta)
Jang JS (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern 23(3):665–685
Jones IL, Bull JW (2020) Major dams and the challenge of achieving “No Net Loss” of biodiversity in the tropics. Sustain Dev 28(2):435–443
Jowett IG, Duncan MJ (2012) Effectiveness of 1D and 2D hydraulic models for instream habitat analysis in a braided river. Ecol Eng 48:92–100
Knoben WJ, Freer JE, Woods RA (2019) Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol Earth Syst Sci 23(10):4323–4331
Li B, Chen N, Wang W, Wang C, Schmitt RJP, Lin A, Daily GC (2021) Eco-environmental impacts of dams in the Yangtze River Basin, China. Sci Total Environ 774:145743
Major JJ, East AE, O’Connor JE, Grant GE, Wilcox AC, Magirl CS, Collins MJ, Tullos DD (2017) Geomorphic responses to dam removal in the United States–a two-decade perspective. Gravel-Bed Rivers 10(9781118971437):355–383
Noack M, Schneider M, Wieprecht S (2013) The Habitat Modelling System CASiMiR: A Multivariate Fuzzy-Approach and its Applications. Ecohydraulics: an integrated approach, pp.75–91
Ouellet V, St-Hilaire A, Dugdale SJ, Hannah DM, Krause S, Proulx-Ouellet S (2020) River temperature research and practice: Recent challenges and emerging opportunities for managing thermal habitat conditions in stream ecosystems. Sci Total Environ 736:139679
Sedighkia M, Abdoli A, Ayyoubzadeh SA, Ahmadi A (2019) Modelling of thermal habitat loss of brown trout (Salmo trutta) due to the impact of climate warming. Ecohydrol Hydrobiol 19(1):167–177
Sedighkia M, Datta B, Abdoli A (2021a) Optimizing reservoir operation to avoid downstream physical habitat loss using coupled ANFIS-metaheuristic model. Earth Sci Inf 14(4):2203–2220
Sedighkia M, Datta B, Abdoli A, Moradian Z (2021b) An ecohydraulic-based expert system for optimal management of environmental flow at the downstream of reservoirs. J Hydroinf 23(6):1343–1367
Yaseen ZM, Allawi MF, Karami H, Ehteram M, Farzin S, Ahmed AN, Koting SB, Mohd NS, Jaafar WZB, Afan HA, El-Shafie A (2019) A hybrid bat–swarm algorithm for optimizing dam and reservoir operation. Neural Comput Appl 31(12):8807–8821
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. The Authors received no funds for this research work.
Author information
Authors and Affiliations
Contributions
Mahdi Sedighkia is responsible for writing of the manuscript and related programming and calculations. Asghar Abdoli is responsible for field studies and reviewing the research work.
Corresponding author
Ethics declarations
Ethical Approval
Not applicable.
Consent to Participate
Not applicable.
Consent to Publish
Not applicable.
Competing Interests
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sedighkia, M., Abdoli, A. A Simulation–Optimization System to Assess Dam Construction with a Focus on Environmental Degradation at Downstream. Water Resour Manage 38, 2489–2509 (2024). https://doi.org/10.1007/s11269-024-03781-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-024-03781-4