Prior Assumptions for Leak Localisation in Water Distribution Networks with Uncertainties

Abstract

Hydraulic model-based leak (burst) localisation in water distribution networks is a challenging problem due to a limited number of hydraulic measurements, a wide range of leak properties, and model and data uncertainties. In this study, prior assumptions are investigated to improve the leak localisation in the presence of uncertainties. For example, $\ell _2$-regularisation relies on the assumption that the Euclidean norm of the leak coefficient vector should be minimised. This approach is compared with a method based on the sensitivity matrix, which assumes the existence of only a single leak. The results show that while the sensitivity matrix method often yields a better leak location estimate in single leak scenarios, the $\ell _2$-regularisation successfully identifies a search area for pinpointing the accurate leak location. Furthermore, it is shown that the additional error introduced by a quadratic approximation of the Hazen-Williams formula for the solution of the localisation problem is negligible given the uncertainties in Hazen-Williams resistance coefficients in operational water network models.

1 Introduction

Leak detection and localisation is a critical operational task for water companies to minimise water losses. This task is generally carried out in two stages. Firstly, a leak (burst) is detected within a wide area network; and secondly, localisation methods, which are based on the cross-correlation of acoustic signals using lift and shift acoustic sensors, are applied to accurately pinpoint the leak location for the repair works to commence. This two-stage task is costly and labour intensive as it depends on the size of the search area. Furthermore, acoustic cross-correlation for localising leaks is only applied at night. This method delays the leak localisation, which might be operationally critical for medium to large size bursts.

Improvements in sensing over the past decade enable the use of pressure and flow data in combination with a hydraulic model to promptly identify a smaller search area, which significantly reduces the cost of pinpointing leaks (Li et al. 2015). In this manuscript, the problem of leak localisation is investigated using a steady-state hydraulic model and hydraulic data. It is assumed that the presence of leaks has already been detected. The terms leak and burst are used interchangeably.

Because of the small number of measurement locations in comparison to the number of possible leak locations, and the uncertainty in operational hydraulic models, the localisation problem is generally ill-posed, i.e. it is under-determined, and its solution might be sensitive to noise, or not exist at all (Pudar and Liggett 1992). The derivation of a good solution to the localisation problem requires the use of prior assumptions to overcome the ill-posedness. Consequently, most leak localisation methods constrain the number of possible solutions by assuming the occurrence of a single leak only.

The sensitivity matrix method, for example, compares changes in pressure measurements caused by a single leak with the sensitivities of the pressure measurements to the leak flow from every possible leak location (Casillas et al. 2013). Other examples include the use of supervised machine learning techniques (Zhang et al. 2016; Xie et al. 2019), for which a labelled training data set is generated in simulation assuming the occurrence of a single leak at various locations. Note that the simulation of simultaneous leaks would lead to a combinatorial increase in the number of possible leak scenarios. Clustering approaches are applied to group nodes with similar leak signatures in a zone. Classifiers are then trained to attribute new pressure measurements to a leak scenario within a zone and provide good localisation in the case of only one leak. In Xie et al. (2019), the method is also tested on scenarios with two simultaneous leaks and it fails to correctly locate any of the leaks in about 50% of the case study scenarios.

To avoid the use of a labelled training data set, some methods use data gathered under leak-free hydraulic conditions in a water network and compare it with data gathered under a leak scenario to detect and locate a leak (Quiñones-Grueiro et al. 2018; Soldevila et al. 2020). Based on the prior assumption of a single leak, a likely leak node is then identified among the nodes with the the largest pressure residuals (Kallesøe and Jensen 2018). Error-domain model falsification (Moser et al. 2018) and model invalidation (Vrachimis et al. 2021) define uncertainty bounds instead of using machine learning, and both methods assume the existence of a single leak. As a consequence of this prior assumption, the listed methods are not able to locate multiple simultaneous leaks.

Methods, which localise multiple leaks, are rarely studied and involve solving a parameter estimation (inverse) problem. To deal with the under-determined problem, these methods pre-select (Berglund et al. 2017) or group (Sanz et al. 2016) leak candidates, and as a result, the problem becomes even-determined. Alternatively, heuristic optimisation methods are applied, which carry out multiple runs to yield a set of possible leak candidates (Steffelbauer et al. 2014). A method that does not rely on prior assumptions about leak candidates and that locates simultaneously occurring leaks within a single run was proposed in Blocher et al. (2020). To deal with the ill-posedness, $\ell _2$-regularisation is applied for the solution of the inverse problem. However, the proposed method has been investigated with the assumption of perfect data and hydraulic model. The current study extends the work presented by Blocher et al. (2020) by investigating the prior assumptions made by $\ell _2$-regularisation, and it evaluates the performance under model uncertainty.

The main contributions of this manuscript are as follows:

• 1. The localisation performance of the $\ell _2$-regularised problem formulation is investigated under uncertainty. This includes a comparison of the results obtained with data gathered over a different number of time steps, and and with different leak sizes.

• 2. Prior assumptions made by the $\ell _2$-regularised problem formulation to deal with ill-posedness are studied in comparison with $\ell _1$-regularisation. The impact of these prior assumptions is compared with the prior assumptions made by the sensitivity matrix method.

• 3. The problem formulation in Blocher et al. (2020) requires a quadratic approximation (QA) to model the head losses due to friction: Upper bounds for the error introduced by the QA and the error in the Hazen-Williams resistance coefficient are examined in the present paper.

The paper includes five sections. Section 2 presents the effects of regularisation on the solution for the localisation problem. Section 3 describes the case study network and discusses the errors introduced by the QA. Section 4 examines the impact of uncertainty on the localisation performance. Section 5 discusses the prior assumptions made by the $\ell _2$-regularised approach, in comparison with the assumptions made by the sensitivity matrix method. It also presents recommendations for their joint application. Figure and equation numbers that refer to the supplementary Online Resource are preceded by an S.

2 Problem Formulation

2.1 Optimisation Problem Formulation

The problem formulation, as previously defined in Blocher et al. (2020), estimates the unknown leak parameters $\mathbf {c} \in \mathbb {R}^{n_n}$ for all $n_n$ demand nodes in the network, using a hydraulic model and pressure and flow measurements. The objective of the problem formulation is to minimise the weighted sum of a loss function $v(\cdot )$, and a regularisation term $R(\cdot )$,

$$\begin{aligned} \underset{\mathbf {c}\in \mathbb {R}^{n_n}_+}{\text {minimise}}\quad v(\mathbf {c}) + \rho R(\mathbf {c}), \end{aligned}$$

(1)

where $v(\cdot )$ is the squared Euclidean distance between measured and modelled pressures and flows. For ease of notation, $v(\cdot )$ is written here as a function of the leak parameters $\mathbf {c}$. The full problem formulation, which has been extended in this study to include pressure reducing valves (PRVs), is given in Problem S.2, see Online Resource Section 1.

The scalar regularisation parameter $\rho > 0$ in Problem 1 facilitates a trade-off between the minimisation of $v(\cdot )$ or the minimisation of $R(\cdot )$. The regularisation term $R(\cdot )$ enables the inclusion of prior assumptions about the leak parameters to reduce the ill-posedness of the localisation problem. In Blocher et al. (2020), the regularisation term is selected as $R(\mathbf {c}) = ||\mathbf {c}||_2^2$ ($\ell _2$-regularisation). In the following section, the benefits of $\ell _2$-regularisation are demonstrated for an example network and a comparison with $\ell _1$-regularisation is carried out.

2.2 Choice of the Regularisation Term

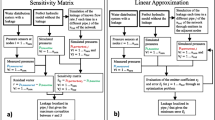
In Fig. 1, a number of leak scenarios and measurements for a network with two demand nodes, and hence two possible leak locations, are illustrated (network details in Online Resource Section 2.1). Figure 1a depicts a set of leak scenarios (cyan asterisks) mapping uniquely onto the head measurements shown in Fig. 1b, see Online Resource Section 2.2 and 2.3. The leak scenario $V_1$ (black diamond in Fig. 1a) corresponds to a single leak located at node 1. Figure 1a also depicts a scenario with a single leak located at node 2 (plotted with a square). As shown in Fig. 1b, measurements within a radius $\kappa$ around the measurement obtained from $V_1$ can be due to a set of different leak scenarios, including scenarios for which the leak is only at node 2.

Fig. 1

Different leak scenarios and corresponding measurements for a network with two nodes

Problem 1 is then re-written to interpret the effect of regularisation:

$$\begin{aligned} \underset{\mathbf {c}\in \mathbb {R}^{n_n}_+}{\text {minimise}}\quad R(\mathbf {c})\\ \nonumber \text {subject to} \; v(\mathbf {c}) \le \kappa . \end{aligned}$$

(2)

For convex functions $v(\cdot )$ and $R(\cdot )$, it can be shown that Problems 1 and 2 are equivalent (Kloft et al. 2009).

Problem 2 provides an interpretation for the benefits of regularisation in case of ill-posedness where the solution is sensitive to noise. Rather than assuming that model and measurements are exact, the scenario with minimum $R(\mathbf {c})$ is chosen among all leak scenarios that are within the uncertainty level $\kappa$ (here, $\kappa \approx 0.2$ m). As an example, an $\ell _1$- and an $\ell _2$-regularised solution are given in Fig. 1a.

This example also illustrates how regularisation further constrains the solution space by making a prior assumption about the solution. Selecting the solution that is minimal in the sense of the $\ell _1$-norm results in the solution where $c_1 = 0$ $\mathrm{m}^{2.5} \cdot \mathrm{s}^{-1}$. If the solution must be minimal in the sense of the $\ell _2$-norm, both $c_1$ and $c_2$ are non-zero. Let us consider all nodes with $c_i > 0$ as leak candidates. The solution with minimal $\ell _1$-norm then risks missing the true leak node, while the solution with minimal $\ell _2$-norm results in a larger set of leak candidates. This observation confirms that $\ell _2$-regularisation is suitable for identifying a search area for prioritising further leak localisation activities in contrast to $\ell _1$-regularisation.

In summary, the prior assumptions made when solving Problem 1 with $R(\mathbf {c}) = ||\mathbf {c}||_2^2$ imply slightly relaxing the constraints imposed by data and model in favour of selecting a solution, which is minimal in the sense of $\ell _2$-norm. This solution is most likely to include the true leak node among a set of candidates, which define a leak search area. The approximation made by Problem 1 is adjusted by the regularisation parameter $\rho$ instead of the uncertainty level $\kappa$. A strategy to choose $\rho$ has been proposed in Blocher et al. (2020), see Online Resource Section 5.

3 Case Study Set-Up and Pipe Parameter Uncertainty

In this section, the case study network used in this study is described. Moreover, the error present in the Hazen-Williams (HW) resistance coefficient is compared with the error that is additionally introduced by a quadratic approximation (QA) to the HW model.

3.1 Case Study Network

Figure 2 shows the benchmarking water network model LTownABnet, which was published by Vrachimis et al. (2020). The hydraulic model is based on a real water network, but the measurements, including model and data uncertainty, are obtained from simulations. The network consists of 799 links, 690 demand nodes, and two source nodes (Inlet1 and Inlet2) with known fixed head. Three PRVs control the pressures. The uncertainties consist of demand and pipe parameter uncertainties, as well as some measurement uncertainty (the measurements are rounded to two digits after the decimal point), and a topological error (pipe p37).

Measurements are available in five minute intervals from 30 demand nodes (pressure) and from PRV1, PRV2 and the pump (flow). As an example, Fig. 2 shows the simulated pressure distribution at 12 pm on 8 January 2018. The total simulated consumption at that time is about $50 \, \mathrm {l/s}$ and the pump is off.

Fig. 2

Simulated pressure distribution at 12 pm on 8 January 2018 in LTownABnet. Pipe p37 is assumed to be open in models $\mathrm{HW}_\mathrm{nom}$ and $\mathrm{HW}_\mathrm{cal}$, while in reality ($\mathrm{HW}_\mathrm{real}$) it is closed

The customer demand is modelled as a multiplicative time series whose parameters are estimated as in Steffelbauer et al. (2020). The resulting demand model is subject to varying levels of uncertainty depending on the time of the day (see Online Resource Section 3.1).

Three sets of pipe parameters (each including roughness coefficient, diameter and length) are available, which are used to calculate HW resistance coefficients: The set of pipe parameters $\mathrm {HW}_\mathrm{real}$ was used to generate the measurements and does not introduce any errors in the head losses. Additionally, a nominal set, $\mathrm {HW}_\mathrm{nom}$, and a calibrated set, $\mathrm {HW}_\mathrm{cal}$, of pipe parameters are available which introduce some pipe parameter uncertainties, see Table S.1. The modelling error introduced by the closed pipe p37 is part of the errors introduced by $\mathrm {HW}_\mathrm{cal}$ and $\mathrm {HW}_\mathrm{nom}$.

3.2 Errors in the Head Loss Models

For a pipe j, the head loss $\Phi _j(\cdot )$ between inlet and outlet is typically described by the non-smooth Darcy-Weisbach (DW) or Hazen-Williams (HW) formulae. For both equations, the relation of $\Phi _j(\cdot )$ and the flow $q_j$ in the pipe j can be written as

$$\begin{aligned} \Phi _j(q_j) = \nu _j q_j \, |q_j|^{n_{exp} - 1}. \end{aligned}$$

(3)

However, these models cause difficulties when solving optimisation problems in water networks with mathematical optimisation techniques. This is due to the rational exponent $n_{exp} = 1.852$ in the case of the HW model, or due to the implicit relation of the resistance coefficient $\nu _j$ and the flow $q_j$ in the case of the DW model. Quadratic approximations (QA) to the head loss models have been proposed to mitigate these issues (Eck and Mevissen 2015; Pecci et al. 2017). As in Blocher et al. (2020), the head loss due to friction is modelled in Problem S.2 using a QA,

$$\begin{aligned} \Phi _{\mathrm {QA},j}(q_j) = q_j (a_j |q_j| + b_j). \end{aligned}$$

(4)

The approximation coefficients $a_j, b_j \ge 0$ are derived such that the absolute errors introduced by the QA with respect to Eq. 3 are minimal, considering the expected flow range for pipe j, see Pecci et al. (2017). Nevertheless, the QA of the HW head losses introduces additional uncertainties which are discussed next.

Pecci et al. (2017) have investigated the error introduced by QA with respect to the true HW model where no uncertainties are considered. Here, the error introduced by the QA is compared with the error already present in the HW resistance coefficient, and analytical upper bounds are provided.

Denote by $\Delta _j$ the relative error in the modelled HW resistance coefficient and by $\nu _{\mathrm {r},j}$ the resistance coefficient corresponding to $\mathrm {HW}_\mathrm{real}$. The modelled resistance coefficient $\nu _j$ is then written as $\nu _j = (1+\Delta _j) \nu _{\mathrm {r},j}$. From Eq. 3, the absolute difference $e_j$ of modelled and real head loss across a pipe j follows as

$$\begin{aligned} e_j = | (1+ \Delta _j) \nu _{\mathrm {r},j} \, q_j^{n_{exp} } - \nu _{\mathrm {r},j} \, q_j^{n_{exp}} | = | \Delta _j \nu _{\mathrm {r},j} \, q_j^{n_{exp} } |. \end{aligned}$$

(5)

Note that $e_j$ increases with the flow in the pipe. Similarly, the absolute error $e_{\mathrm {QA},j}$, introduced by the QA with respect to $\mathrm{HW}_\mathrm{real}$, is written as

$$\begin{aligned} e_{\mathrm {QA},j} = |a_j q_j^2 + b_j q_j - \nu _{\mathrm {r},j} q_j^{n_{exp} } |, \end{aligned}$$

(6)

where $a_j$ and $b_j$ are derived to approximate the modelled HW head loss. Deriving upper bounds for $e_{\mathrm {QA},j}$ yields

$$\begin{aligned} e_{\mathrm {QA},j} \le q_{j,\text {max}}^{n_{exp}} \nu _{\mathrm {r},j} \,\left( \omega _1 + | \Delta _j | \omega _2 \right) , \\ \nonumber \end{aligned}$$

(7)

where $\omega _1 \approx 6.7 \cdot 10^{-3}$, $\omega _2 \approx 1.007$ and $q_{j,\text {max}}$ is the maximum expected flow in pipe j, see Online Resource Section 3.2.

For large errors $|\Delta _j|$, it holds that $\omega _1 \ll |\Delta _j| \omega _2$ and $\omega _2 \approx 1$. For $q_j = q_{j,\text {max}}$, the upper bound in Eq. 7 corresponds then approximately to the error introduced by the modelled HW resistance coefficient, see Eq. 5. For small errors $|\Delta _j|$, $\omega _1$ cannot be considered negligible. However, in that case, the sum $|\omega _1| + | \Delta _j | \omega _2$ is small, and the upper bound on the error is small in comparison to the case where $|\Delta _j|$ is large.

These results suggest that for pipes with large errors in the HW resistance coefficients, the worst QA errors in the head loss estimates are comparable to the worst HW errors. While the same conclusions cannot be drawn for pipes with a small error $|\Delta _j|$, the head loss errors observed for these pipes are expected to be comparatively small. The modelling errors in the hydraulic states will therefore be mostly driven by pipes with large errors $|\Delta _j|$ in the HW resistance coefficients, as confirmed by Fig. S.5. While $\mathrm{QA}_\mathrm{real}$ introduces some errors with respect to $\mathrm{HW}_\mathrm{real}$, the errors are much lower than the errors introduced by $\mathrm{HW}_\mathrm{nom}$ or $\mathrm{HW}_\mathrm{cal}$. The error distribution of $\mathrm{QA}_\mathrm{nom}$ and $\mathrm{QA}_\mathrm{cal}$ is similar to the error distribution of $\mathrm{HW}_\mathrm{nom}$ and $\mathrm{HW}_\mathrm{cal}$.

4 $\ell _2$-Regularisation Under Uncertainty

The objective of the $\ell _2$-regularised Problem 1 (or Problem S.2) is to identify a set of candidate nodes, which includes the true leak node. As a result, this method reduces the leak search area. The localisation performance with regards to that objective is assessed using a quantitative metric proposed in Blocher et al. (2020) and summarised here: The metric $\beta$ assumes that each node i in the network is attributed a value $0 \le u_i \le 1$ by the localisation method. A large attribute suggests that the node is a likely leak candidate. The attributes are derived by normalising the leak coefficients $c_i$ identified by the optimisation. The metric $\beta$ then yields values such that $-1 \le \beta \le 1$. A value of $\beta = 1$ indicates that the true leak nodes have been identified as the only leak candidates. A value of $0< \beta < 1$ suggests that the localisation has successfully reduced the search area, while $\beta \approx 0$ is interpreted as the method not providing useful information. A negative value of $\beta$ indicates that the method guides the leak search in the wrong direction. Note that while $\beta >0$ suggests that the search area has been reduced, the authors consider a result with $\beta \gtrapprox 0.4$ as a good localisation result.

Based on Blocher et al. (2020), the regularisation parameter $\rho$ is selected by simulating a number of different leak scenarios and evaluating the performance $\beta$ of the solution to the $\ell _2$-regularised Problem S.2 for different choices of $\rho$. For LTownABnet we obtain $\rho = 1$ (see Fig. S.6). While the choice of the regularisation parameter $\rho$ may be impacted by uncertainties (see Fig. 1), the selection of $\rho$ by simulating scenarios with uncertainties is impractical in an operational scenario, because a model of uncertainty is often not available. The discussion is hence limited here to $\rho = 1$.

Problem S.2 is solved using the interior point solver IPOPT (v3.12.9) implemented in MATLAB using the interface provided by the OPTI Toolbox (Currie and Wilson 2012).

4.1 Leak Events and Localisation Time Windows

The localisation performance with uncertainty is tested using leaks simulated in 2018 in LTownABnet, which includes three background leaks (p427, p654, p810) with a leak flow between 1.4 and 1.9 l/s and nine further leaks where the leak flow ranges from 4.5 l/s to 9.7 l/s. To obtain scenarios with exactly one unknown leak, leaks are included in the demand model in some cases (Table S.2).

The use of measurements gathered at a single time step is compared with the use of measurements gathered over multiple time steps. In the case of multiple time steps, a 1 hour time window (12 time steps) and a 3 hour time window (36 time steps) are considered. In this work, the analysis is limited to the case of larger leaks (more than 1.4 l/s), which need to be promptly located and repaired, and time windows longer than 3 hours are not investigated. To take into account a change in uncertainty over the day, the leak localisation problem is solved every 30 minutes over a 24 h period. For example, the first 1h time window collects data measured between midnight and 00:55, and the second 1h time window collects data measured between 00:30 and 01:25. This yields 48 solutions per leak event and number of time steps. Testing three different head loss models and three different time window lengths (1, 12 and 36 time steps) results in $48 \times 3 \times 3$ scenarios/solutions per leak event.

To be able to directly compare the localisation performance with uncertainty with the performance assuming perfect hydraulic model and data, measurements are generated (in simulation) for each scenario and model, and the localisation results are evaluated.

4.2 Localisation Performance, Number of Time Steps and Head Loss Uncertainty

The impact of uncertainty on the performance $\beta$ is investigated with regard to the head loss model and the number of time steps, see Fig. 3 with performance profiles for the 12 leak events. Let $\beta _V$ be the localisation performance for leak scenario V in the set of leak scenarios $\mathcal {V}$. The percentage of scenarios, $\mathcal {P} (\tau )$, with a performance $\beta \ge \tau$ is defined as

$$\begin{aligned} \mathcal {P} (\tau ) = 100\frac{|\{ V \in \mathcal {V}: \beta _V \ge \tau \}|}{|\mathcal {V}|}. \end{aligned}$$

(8)

In Fig. 3a, the performance profiles are shown with respect to the number of time steps used. The shape of the profiles obtained for perfect data and model does not change if the number of time steps is increased. However, a comparison with the profiles obtained with uncertainties indicates that uncertainties cause a performance reduction. While in the case of no uncertainties, 97% of scenarios yield a performance $\beta > 0.5$, only 67 to 77% achieve the same performance or better, if uncertainties are present. Additionally, the minimum performance using exact data and model corresponds to $\beta = 0.4$, while with uncertainties, 9% of scenarios yield a performance $\beta \le 0$ in the case of only a single time step, thus missing the leak or guiding the leak search in the wrong direction. The localisation performance with uncertainty improves however if more than one time step is used. Only 4 % of scenarios then yield $\beta < 0$. Using 36 instead of 12 time steps does not yield a significant improvement.

Fig. 3

Performance profiles for the leak scenarios with uncertainties in comparison with profiles obtained for the same leak scenarios when measurements are generated without demand or pipe parameter uncertainties (denoted with a superscript 0)

In Fig. 3b, the performance profiles are sorted according to the head loss model used. As before, if measurements are obtained using exact data and model, the performance profiles differ only slightly in shape. A comparison of the profiles for the different head loss models obtained with uncertainties indicates that the overall performance when using $\mathrm{QA}_\mathrm{real}$, based on the real pipe parameters, is better than the performance of $\mathrm{QA}_\mathrm{nom}$. This is expected since $\mathrm{QA}_\mathrm{nom}$ introduces larger errors. The performance profile obtained when using $\mathrm {QA}_\mathrm{cal}$ indicates that calibration improves the performance with regard to $\mathrm{QA}_\mathrm{nom}$, and even $\mathrm{QA}_\mathrm{real}$ in some scenarios while it performs similarly, or even slightly worse, than $\mathrm{QA}_\mathrm{nom}$ in other scenarios. However, the impact of the additional uncertainty introduced by $\mathrm{QA}_\mathrm{nom}$ and $\mathrm{QA}_\mathrm{cal}$ appears to be small in comparison to the overall performance reduction under uncertainty.

Figure 3 suggests that the localisation performance is reduced in the presence of uncertainties whereby demand uncertainty has the highest contribution. Using multiple time steps for the analysis improves the localisation performance in comparison to using only a single time step.

4.3 Leak Size and Localisation Performance

The performance $\beta$ depends strongly on the leak location (Blocher et al. 2020). With the addition of uncertainties, it is expected that the size of the leak has a greater impact on the performance. The discussion in the following is limited to $\mathrm{QA}_\mathrm{cal}$, which is the hydraulic model used in operational scenarios.

In Fig. 4, the performance values are compared for the twelve leak events, sorted according to their leak size. The data obtained using the same time window length is summarised in a boxplot for each leak event. Each boxplot illustrates the median performance $\beta$ (dash in the centre of a box), and the lower and upper quartiles (lower and upper edges of a box). Consequently, 50% of the performance values are within the box. The length of the whiskers illustrates the spread of the remaining data. However, data points further than 1.5 times the interquartile range away from the lower or upper edge of the box are considered outliers (marked as crosses).

Fig. 4

Impact of uncertainties on the leak localisation performance for each of the 12 leak events. Data is sorted according to the number of time steps

According to Fig. 4, nine of the twelve leak events yield scenarios that result in $\beta \le 0$, which indicates that the leak is not localised correctly. In most cases, $\beta < 0$ appears only in the case of a single time step and corresponds to outliers, which confirms that using multiple time steps improves the robustness of the localisation in the presence of uncertainties. However, in the case of the three background leaks (p427, p654 and p810), a larger number of scenarios yields $\beta \le 0$. The smallest leak, p427, leads to $\beta \le 0$ in more than 25 % of scenarios irrespective of the number of time steps. While the other small leaks, p654 and p810, perform better than p427, their performance values are still low with the majority of scenarios yielding $\beta <0.4$. Moreover, the median performance reduction caused by uncertainty is 0.47 or more for the small leaks, while for the nine larger leaks the median performance is reduced by at most 0.15. These results suggest that the localisation performance is significantly affected by uncertainties when small leaks are considered. Similarly, larger uncertainty levels during the day affect the localisation performance more than the smaller uncertainty levels at night, see Fig. S.7.

In summary, the proposed method is robust to the uncertainties observed in LTownABnet when the leak flow is greater than 4 l/s and multiple time steps are used. Note that there are no leak events with a leak flow between 2 and 4 l/s. In the case of smaller leaks, or only a single time step, the localisation result may still provide useful information, since the median value of $\beta$ is greater than zero for all twelve leak events. However, the localisation method is not reliable in this case as it does not always identify the true leak node among the leak candidates. Finally, these results suggest that the choice of the regularisation parameter, $\rho = 1$, is still suitable given the uncertainties in the network.

5 Leak Search Area Versus Leak Candidate Localisation

The investigation in the previous section has shown that $\ell _2$-regularisation (denoted in the following by IP-R, i.e. regularised inverse problem) can be applied for the localisation of medium to large leaks with uncertainties. The results were evaluated with regard to the performance metric $\beta$, i.e. with regard to the objective of identifying a reduced search area. In this section, the prior assumptions made by IP-R are investigated by comparing it with the sensitivity matrix method (SMM) using the performance metric $\beta$ and a distance metric $\delta$.

In contrast to the objective in the previous section, many published localisation methods aim to identify a node as close as possible to the true leak node. Then, to evaluate the localisation success, the distance $\delta$ of the leak candidate to the true leak nodes is a suitable metric. In this manuscript, distance is measured by using the shortest path between the leak candidate and the leak node, taking into account the pipe length in metres. In contrast to the metric $\beta$, the distance $\delta$ is usually only applied when there is only one true leak, since this is the only case where the relation between a leak candidate and the true leak is well-defined. In the case where no leak candidate is identified, $\delta$ is equal to the network’s diameter, i.e. the longest of all shortest paths between any pair of nodes in the network. A value $\delta = 0$ indicates that the leak has been accurately localised.

5.1 The Sensitivity Matrix Method

Before discussing the different localisation results, the SMM is summarised as follows (Casillas et al. 2013):

The set of nodes where the head (or pressure) is measured is denoted by $\mathcal {M}$. Note that the relation of the head $h_i$ and the pressure $p_i$ at node i is $p_i = h_i - z_i$ where $z_i$ is the elevation of the node. A sensitivity matrix $\mathbf {S} \in \mathbb {R}^{|\mathcal {M}| \times n_n}$ is defined where the ith column consists of the sensitivities $\frac{\partial h_{m}}{\partial \epsilon _i}$ for all nodes $m \in \mathcal {M}$ to a constant leak $\epsilon _i$ at node i. The derivatives in $\mathbf {S}$ are typically approximated numerically, i.e. $\frac{\partial h_{m_j}}{\partial \epsilon _i} \approx \frac{h_{m_j, \epsilon _i} - h_{m_j,0}}{\epsilon _i}$ where $h_{m_j, \epsilon _i}$ is the simulated head at node $m_j$ given a leak $\epsilon _i$ and $h_{m_j, 0}$ is the simulated head in the absence of leaks.

Let $\mathbf {p_{\mathrm {res}}}^T = \left[ (\bar{h}_{m_1} - h_{m_1,0}) \hdots (\bar{h}_{m_m} - h_{m_m,0}) \right] \in \mathbb {R}^{|\mathcal {M}|}$ be the vector of residuals where $\bar{h}_m$ are the head measurements obtained given the leak scenario. The column i of $\mathbf {S}$ is then compared with $\mathbf {p_{\mathrm {res}}}$. To measure similarity for the comparison, the angle $\alpha _i$ between the two vectors is used (Casillas et al. 2013). If multiple time steps are considered, $\alpha _i$ is calculated separately for each time step. Then, the mean angle over all time steps is computed. The node with index l such that $l = \arg \min _{i \in \{1...n_n\}} \alpha _i$ is the main leak candidate, and is used to evaluate the localisation distance $\delta$. To be able to evaluate the performance $\beta$, the mean angles are normalised such that the node l with minimum angle yields an attribute $u_l = 1$ and the node j with the largest angle yields an attribute $u_j = 0$.

In summary, SMM makes the assumption that there is exactly one leak in the network by evaluating the derivatives with regard to one leak. Consequently, it constrains the number of possible solutions for the localisation problem. In contrast to IP-R, it does not require a quadratic approximation to the HW head losses, and it does not require a trade-off between the prior assumption, and fitting the data. However, it relies on a linearisation of the network equations and it is limited to the localisation of only one leak. For the present case study, the approximate derivatives are obtained by simulating leaks of $\epsilon _i = 1.6$ l/s which corresponds to the average background leak flow.

5.2 Leak Localisation with SMM and IP-R

The objective of this study is to examine the different assumptions made by the two methods SMM and IP-R, and to compare their performance using two different metrics. Note that the aim is not to investigate the performance of SMM with uncertainties and then benchmark it against IP-R. The discussion is therefore limited here to the use of the calibrated model and 36 time steps. A diagram summarising the methods and their evaluation is given in Fig. S.9.

In Fig. 5, IP-R is compared with SMM by analysing the performance $\beta$ (Fig. 5a) and the distance $\delta$ (Fig. 5b). The localisation in scenarios with no uncertainties is compared with the localisation with uncertainties.

Fig. 5

Comparison of IP-R and SMM for localisation results obtained using 36 time steps and the calibrated model. Grey lines with superscript 0 indicate performance profiles obtained assuming no uncertainty

Figure 5a shows that overall SMM yields a lower performance $\beta$, with a maximum $\beta = 0.4$, while for IP-R, in the case with no uncertainty, the minimum $\beta$ is equal to 0.45. SMM yields a large candidate set, and thus low performance $\beta$, whereas IP-R successfully discards a large proportion of nodes. However, in the case of IP-R, the true leak node is not always among the nodes with the highest attributes in the candidate set (see the example in Fig. 6).

The performance profiles with uncertainties in Fig. 5a suggest that SMM is less impacted by uncertainties when compared with IP-R. A possible explanation is that the metric $\beta$ is not sensitive to the impact of uncertainties on SMM’s localisation performance, i.e. the entire network is a leak search area, with or without uncertainties. For example, in Fig. 6a about 40 % of nodes yield an attribute greater than 0.9. The performance for IP-R with uncertainties has been discussed in Sect. 4. While IP-R yields $\beta < 0$ for small leaks in some scenarios, IP-R still outperforms SMM in about 90 % of scenarios when using the metric $\beta$.

In Fig. 5b, the distance profile of the main leak candidate to the true leak node is shown. SMM outperforms IP-R both with and without uncertainties. In particular, $50\%$ of the SMM localisation results yield the exact candidate in the case without uncertainties. This is reduced to about 22 % with uncertainties in the hydraulic model and data whereas IP-R never yields the exact candidate. The worst case distance for SMM is 900m while this threshold is exceeded by IP-R in 25 % of scenarios.

As an example, Fig. 6 depicts candidates identified by the different methods. The SMM localisation yields a candidate close to the true leak node ($\delta = 72$ m), where as the IP-R candidate is 370 m away. However, SMM also produces estimates that are far away from the true leak node. For example, the SMM candidate for the leak event p628, Fig. 6, is further than 200 m away from the true leak node for some scenarios, see Fig. S.8, and then closer to the IP-R candidate than to the true leak node.

Fig. 6

Localisation results for leak event p628 at 12 pm (36 time steps and calibrated model)

In summary, SMM performs better than IP-R in terms of reducing the distance to the true leak node for the presented case study, and it is able to correctly isolate the true leak node in a large portion of scenarios. An explanation could be that SMM benefits from making the assumption of the existence of exactly one leak, which is correct for this case study. The sensors in LTownABnet are placed using the sensitivity matrix (Vrachimis and Eliades 2020), which may also be beneficial for the localisation objective of SMM.

IP-R relies on making the assumption that the $\ell _2$-norm of the leak coefficient vector is minimal, which does not include any knowledge about the leak parameters. It discards the majority of non-leak nodes while keeping the true leak node. In terms of identifying a leak search area, IP-R outperforms the SMM. An additional key benefit of IP-R is the localisation of multiple simultaneous leaks (Blocher et al. 2020).

In comparison with the isolation of a single candidate, the identified leak search area enables engineers to optimally plan to reduce the work associated with pin-pointing the exact leak location using acoustic localisation methods. The two objectives described by the two performance metrics $\beta$ and $\delta$ can hence be utilised in parallel to complement each other.

6 Conclusion

This paper investigates the application of prior assumptions for the solution of an ill-posed inverse problem for hydraulic model-based leak localisation in water networks. The considered methods include $\ell _2$ and $\ell _1$-regularisation schemes, and a method based on the sensitivity matrix (SMM). The results show that $\ell _2$-regularisation (IP-R) successfully reduces the leak search area in the presence of model uncertainties which enables the efficient use of manpower to further pin-point the leak location. When a single leak is present, the assumptions made by SMM improve the accuracy of the localisation. The results suggest that a combined use of IP-R and SMM can successfully be applied to reduce the leak search area and increase the localisation accuracy. It is shown that errors introduced by the quadratic approximation within the formulation of IP-R are negligible compared to the uncertainties inherent in models of operational networks. Further work is required to extensively validate the proposed approach in operational water networks.