1 Introduction

Water distribution networks consist of various components such as pipes, pumps, valves and tanks. The networks need to satisfy current and future water demands (Spiliotis and Tsakiris 2012; Korteling et al. 2013; Tsakiris and Spiliotis 2017). The main objective considered when designing water distribution networks is cost minimization subject to adequate water supply and pressure at the demand nodes. However, inevitably some network elements will be unavailable occasionally, for example, due to pipe breakage and pump failure. Therefore, some spare capacity needs to be included to enable the network to perform reasonably well under both normal and abnormal operating conditions. Thus, network resilience is important also (Harrison and Williams 2016; Herrera et al. 2016; Agathokleous et al. 2017). Resilience is characterised by redundancy, failure tolerance and reliability.

Optimizing the design of water distribution networks is an extremely complex problem that is classed as NP-hard (Yates et al. 1984). de Neufville et al. (1971) were among the first researchers who recognised that water system design involved at least two conflicting objectives related to cost minimization and network performance. For many years, conflicting objectives were often aggregated into a scalar function and solved as a single-objective optimization problem.

More recently, evolutionary algorithms have been preferred. Evolutionary algorithms are stochastic search techniques well suited to identifying the Pareto optimal sets in complex multi-objective optimization problems. Many population-based optimization techniques have been employed in the design of water distribution networks. Some examples are genetic algorithms (Holland 1975), differential evolution (Storn and Price 1997), particle swarm (Kennedy and Eberhart 1995), ant colony (Dorigo et al. 1999) and harmony search (Geem et al. 2001).

Elitism is an extremely important feature in evolutionary algorithms that ensures the best solutions in a population are retained for inclusion in the next generation. This ensures that the fittest candidates will be preserved to improve the convergence characteristics (Zitzler et al. 2000). Vector Evaluated Genetic Algorithm (Schaffer 1985), Vector-Optimized Evolution Strategy (Kursawe 1990), Multi-Objective Genetic Algorithm (Fonseca and Fleming 1993), Weight-Based Genetic Algorithm (Hajela and Lin 1992) and Non-Dominated Sorting Genetic Algorithm (Srinivas and Deb 1994) are some examples of non-elitist evolutionary algorithms. Examples of elitist evolutionary algorithms include the Non-Dominated Sorting Genetic Algorithm (NSGA) II (Deb et al. 2002), Distance-Based Pareto Genetic Algorithm (Osyczka and Kundu 1995), Strength Pareto Evolutionary Algorithm (Zitzler and Thiele 1998) and Pareto-Archive Evolution Strategy (Knowles and Corne 2000).

Genetic algorithms are widely employed in the design of water distribution networks (Wu and Simpson 2001; Vairavamoorthy and Ali 2005; Rao and Salomons 2007; Haghighi et al. 2011; Creaco and Pezzinga 2015). Examples include design and rehabilitation (Jayaram and Srinivasan 2008), pump operation scheduling (Goldberg and Kuo 1987), tank siting and sizing (Prasad 2010) and water quality optimization (Munavalli and Kumar 2003).

Many researchers in various disciplines including water distribution employed the nondominated sorting genetic algorithm NSGA II (Yan et al. 2016). The majority of the applications of NSGA II in the area of water distribution considered design optimization through pipe sizing. Different measures of reliability were included in some cases, for example, Prasad and Park (2004), Farmani et al. (2006) and Saleh and Tanyimboh (2016). Some other applications of NSGA II included Farmani et al. (2006) and Prasad (2010) who designed the benchmark network called “Anytown”. Jayaram and Srinivasan (2008) and Siew et al. (2014) investigated design and rehabilitation based on the life cycle cost. In the area of drinking water safety, Preis and Ostfeld (2008) and Weickgenannt et al. (2010) considered contamination detection whilst Jeong and Abraham (2006) focused on the consequences of external attacks.

Due to the high computational burden associated with the reliability calculations, surrogate measures (Forrester et al. 2008; Díaz et al. 2016) have been proposed, for example, flow entropy and resilience index (Awumah et al. 1990, 1991; Tanyimboh 1993; Tanyimboh and Templeman 1993a, b; Todini 2000). The advantage of using such measures is that they are relatively simple functions that do not require repetitive time-consuming hydraulic simulations and can be incorporated in optimization algorithms relatively easily.

The idea of incorporating Shannon’s informational entropy measure of uncertainty in the design of water distribution networks was introduced by Awumah et al. (1990). Tanyimboh and Templeman (1993a, b) formalised the definition of the entropy function for flow networks using the conditional entropy concept (Khinchin 1953, 1957) and multiple probability spaces. Czajkowska and Tanyimboh (2013) demonstrated that the entropy-based solutions derived from multiple operating conditions outperformed those from a single operating condition.

It has been shown that networks designed to carry the maximum entropy flows are more reliable than the traditional minimum cost solution and the relationship between reliability and entropy is strong (Tanyimboh and Templeman 1993b, 2000; Tanyimboh and Kalungi 2008; Tanyimboh and Setiadi 2008). The evidence in the literature shows that higher entropy values increase the uniformity of the pipe diameters (Awumah et al. 1991; Tanyimboh and Templeman 1993b) which, therefore, increases the reliability by increasing the opportunities for flow re-routing (Prasad and Park 2004). Investigations by Gheisi and Naser (2015) and Tanyimboh et al. (2016) demonstrated that flow entropy correlated well with hydraulic reliability and failure tolerance while other surrogate measures were mostly inconsistent.

This article is concerned with the formulation of the maximum entropy model for water distribution networks with multiple operating conditions. The primary aim is to develop and demonstrate a rigorous approach using empirical results. Research on flow entropy hitherto has focused on the peak demands. However, different loading conditions may be critical at various points during the typical 24-h operating cycle and there is a clear need to develop more realistic maximum entropy models applicable to real rather than small hypothetical networks.

2 Entropy Maximizing Design Optimization Approach

Steady state simulation is widely used in the design of water distribution networks. However, there are some important situations in which steady state modelling has weaknesses, e.g. valve operation and analysing energy consumption. Extended period simulation is more realistic. It leads to a better understanding of the characteristics e.g. due to time-varying water demands, and tank water level variations. Moreover, the optimization of pump scheduling or tank sizing and siting require extended period simulations.

Previously it was thought that if the peak daily demands were satisfied then the other operating conditions would be satisfied as well (Vamvakeridou-Lyroudia et al. 2005). However, Prasad (2010) demonstrated that the node pressure constraints have to be considered for all loading conditions. Alperovits and Shamir (1977) observed that the minimum demand periods have to be considered in addition to the maximum daily demand and fire flows. In addition to the fire-fighting and other emergency flows, the loading patterns that are frequently considered include:

  1. (a).

    The maximum daily demand, i.e. the peak demand over a 24-h period.

  2. (b).

    The peak hour demand that usually occurs in the evening of the maximum day.

  3. (c).

    The average daily demand, i.e. the average demand for the average day’s consumption.

  4. (d).

    The minimum daily demand, i.e. the loading pattern when water consumption is at its lowest level and the tanks refill.

2.1 Informational Entropy under Multiple Operating Conditions

Alternative hypotheses for maximizing the entropy when there are multiple operating conditions include: (a) maximizing the largest entropy value across all the operating conditions; (b) maximizing the smallest entropy value across all the operating conditions, to alleviate the worst-case performance; and (c) maximizing the sum of the separate entropies from all the operating conditions.

Collectively, the entropy values for the various operating conditions constitute an entropy vector. Maximizing the largest entropy value implies maximizing the largest element in the entropy vector. On its own, the largest entropy element provides only a partial characterization and thus may not represent the overall performance adequately. It has the potential to overestimate the resilience and, if used in design optimization, could lead to suboptimal results (Czajkowska 2016). This option yields the following objective function.

$$ \operatorname{Maximize}\;f=\mathit{\operatorname{Max}}\left({S}_k,\kern0.5em \forall k\right) $$
(1)

where S k is the entropy of the kth operating condition. Additional details on S k are in the supplementary data.

On the other hand, maximizing the minimum element of the entropy vector would undoubtedly alleviate the worst-case scenario. However, it could underestimate the overall performance and, consequently, yield suboptimal or inconsistent results when used in optimization algorithms (Czajkowska 2016). The objective function based on the minimum entropy element is as follows.

$$ \operatorname{Maximize}\;f=\mathit{\operatorname{Min}}\left({S}_k,\kern0.5em \forall k\right) $$
(2)

where S k is the entropy of the kth operating condition.

Maximizing the sum of the separate entropies aims to achieve a good performance for all the operating conditions collectively.

$$ \operatorname{Maximize}\;f=\sum \limits_k{S}_k $$
(3)

where S k is the entropy of the kth operating condition.

A basic property of entropy as a measure of uncertainty is that the joint entropy of two or more independent probabilistic schemes is the sum of their separate entropies (Shannon 1948, Tanyimboh 1993: 73-77). Accordingly, for independent operating conditions, the joint entropy is the sum of the separate entropies. The appeal of this interpretation lies in the fact that it accounts for all the operating conditions. Furthermore, it does not require any additional assumptions or criteria. Therefore, viewed as a basic property of the network, the logical conclusion is that the sum of the entropies should be maximized. This was the fundamental hypothesis of the research.

2.2 Network Design Optimization Model

Flow entropy may be included in the design optimization of a water distribution network to minimize the cost without sacrificing resilience completely. In this way, redundancy is safeguarded and deployed to the best possible advantage, to help address any unanticipated flow re-routing and short-term increases in demand. The objectives were thus cost minimization and entropy maximization. Only the initial construction cost was considered in this research. Other costs and additional factors may be incorporated relatively easily (Siew et al. 2014). Though relevant, these wider considerations were not the main focus of the investigation.

The constraints were the constitutive equations (i.e. conservation of mass and energy) and the minimum node pressure constraints. The equations for the conservation of mass and energy were satisfied by embedding the EPANET 2 hydraulic simulation model (Rossman 2000) in the evolutionary algorithm. The minimum node pressure constraints were addressed by introducing an additional objective that considers the feasibility of the solutions.

Michalewicz (1995) classified the approaches for addressing constraints in evolutionary algorithms as: (a) repairing, (b) modifying, (c) rejecting and (d) penalizing strategies. The most common practice is to degrade infeasible solutions by applying penalties, with greater constraint violations incurring higher penalties. Excessively high penalties may confine the search to the feasible region of the solution space. However, searching through the feasible and infeasible regions improves the efficiency and yields better solutions than searching in the feasible regions only (Glover and Greenberg 1989). Designing penalty functions and calibrating the associated parameters is a complex task and requires extensive fine-tuning (Dridi et al. 2008). A penalty-free formulation was developed to obviate the difficulties.

According to the maximum entropy formalism, the entropy should be maximized subject to the relevant constraints without introducing any arbitrary assumptions (Jaynes 1957). Hence, the optimization problem may be summarized briefly as follows.

$$ \operatorname{Minimize}\ \mathrm{the}\ \mathrm{cost}\;{f}_1=\sum \limits_i^{np}{C}_i\left({d}_i,{L}_i\right) $$
(4)
$$ \operatorname{Minimize}\ \mathrm{the}\ \mathrm{node}\ \mathrm{pressure}\ \mathrm{deficits}\;{f}_2=\mathit{\operatorname{Max}}\left\langle \max \left[0,\left({H}_n^{req}-{H}_n\right)\right];\kern1em \forall n\right\rangle $$
(5)
$$ \operatorname{Maximize}\ \mathrm{the}\ \mathrm{flow}\ \mathrm{entropy}\;{f}_3=S $$
(6)
$$ \mathrm{Subject}\ \mathrm{to}:{d}_i\in D;\kern1em \forall i $$
(7)

C i (d i , L i ) is the cost of pipe i with diameter d i and length L i while np is the number of pipes. The set D comprises the available discrete pipe diameter options. S is the flow entropy. H n and \( {H}_n^{req} \) are, respectively, the available and required residual heads at node n. The required head corresponds to the pressure above which the demand is satisfied in full. The decision variables are the pipe diameters. The hydraulic simulation model EAPANET 2, that ensures energy and flow conservation, also provides the nodal heads.

3 Solution Methodology

3.1 Solution of the Optimization Problem

NSGA II was employed as it is efficient and used widely by many researchers in various disciplines. The evolutionary optimization procedure in NSGA II (Deb et al. 2002) is based on Pareto-dominance and global elitism. It maintains diversity by seeking an even distribution of the nondominated solutions in the objective space using the crowding distance. The crowding distance is a measure of the spatial distribution of the solutions in the objective space and is based on the average distance between a solution and its neighbours.

The source code of NSGA II (in C++) was modified and linked to the hydraulic simulation model EPANET 2. EPANET 2 (Rossman 2000) is public domain software for modelling water distribution networks that performs both steady state and dynamic simulations, and water quality modelling. A procedure that calculates the flow entropy for any given network configuration was developed, tested and incorporated in the optimization algorithm. The multiobjective optimization algorithm thus produced can handle both single and multiple operating conditions.

While investigating the methodology it was observed that the number of infeasible solutions in the Pareto-optimal sets exceeded the number of feasible solutions. This may be because the nodal head deficit function f 2 in Eq. 5 does not distinguish between solutions with different levels of surplus head, as all feasible solutions have a deficit of zero. Hence, for feasible solutions, the Pareto-dominance is based on the cost and entropy only. By contrast, for infeasible solutions, the Pareto-dominance is based on three objectives. It is known that more solutions become nondominated as the number of objectives increases (Ishibuchi et al. 2015), and this may have contributed to the imbalance between the number of feasible and infeasible solutions in the Pareto-optimal sets achieved.

Therefore, on discarding the infeasible solutions at the end of each optimization run, all the nondominated feasible solutions achieved from the start to the end of the optimization were incorporated in the Pareto-optimal set. Membership of the final Pareto set of feasible solutions was based on Pareto-dominance and the selection was done using additional software developed (in Perl) in the research. Furthermore, the nondominated solutions from all the optimization runs were combined and sorted based on Pareto dominance to obtain a single unified nondominated set.

3.2 Resilience Evaluation Procedure

Two of the criteria used to assess the proposed maximum entropy design approach were the hydraulic capacity reliability and failure tolerance that emphasize different aspects of resilience (Tanyimboh et al. 2001). Pressure-driven analysis (Tsakiris and Spiliotis 2014) based on the logistic pressure-discharge relationship (Tanyimboh and Templeman 2010) was used to simulate the effects of pipe failures.

The definition used for the hydraulic capacity reliability is the network’s ability to fulfil on average the required nodal demands at adequate pressure, under normal and abnormal operating conditions. The pipe failure model used was taken from Cullinane et al. (1992). Also, the pipe failure tolerance provides an estimate of the fraction of the total demand that the network can satisfy on average when one or more components are out of service and its importance was emphasized previously (Gheisi and Naser 2013, 2015).

4 Results and Discussion

4.1 Problem Specifications

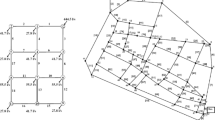
This example is based on the network shown in Fig. 1 that serves part of the city of Ferrara (Creaco et al. 2010, 2012). It consists of 49 nodes, 76 pipes and 29 loops. The total demand is 367 l per second. Each reservoir has a head of 30 m. Manning’s roughness coefficient is 0.015 for all the pipes the total length of which is about 25.2 km. The elevation and minimum required head at the demand nodes are 0 m and 28 m respectively.

Fig. 1
figure 1

Topology of the network investigated. The pipe identifiers are shown in square brackets

Full size image

As the original data for the network had only one loading condition, two fire-flow scenarios were created with reference to the fire flows in Simpson et al. (1994). Under the fire flow conditions, the required residual head at the demand nodes was taken as 14 m, except for the node with a fire-fighting flow for which the required residual head was 8.4 m. The two fire flow conditions correspond to a fire at node 31 for Fire Flow 1 and node 11 for Fire Flow 2. Details of the three loading conditions and the pipe lengths are in Tables 1 and 2, respectively.

Table 1 Nodal demands and required residual heads
Full size table
Table 2 Pipe lengths
Full size table

The available pipe diameter options and their costs per metre (in mm and €/m) are: {(150, 271.94), (200, 299.43), (250, 328.01), (300, 359.54), (350, 399.03), (400, 438.63), (450, 461.34), (500, 502.78)}. There are 8 pipe diameter options, so the solution space comprises 876 or 4.313 × 1068 infeasible and feasible solutions. A 3-bit binary substring with 8 (i.e. 23) substrings was used. The GA parameters were: N E  = 500,000, N G  = 1000, N S  = 500, N R  = 30, p c  = 1.0 and p m  = 1/228 = 0.004 (this is the probability that any single bit would mutate by being reversed from 0 to 1 or vice versa) where 228 is the chromosome length. N E is the maximum number of function evaluations or hydraulic simulations allowed; N G is the number of generations; N S is the population size; N R is the number of independent runs with random initial populations; and p c and p m are the crossover and mutation probabilities. A single-point crossover operator was used to produce two offspring from two parents. The average CPU time for a single optimization run was about 90 min on a PC (Intel Core 2 Duo, 3.5 GHz, 3GB RAM); in other words, 45 h or 1.9 days in total for the 30 optimization runs. The results are summarised in the supplementary data that is available online, in Table C1 in Appendix C.

4.2 Effectiveness of the Optimization Approach

It was thought that the surplus heads at the critical nodes would increase as the entropy increased. However, there was no correlation between the surplus heads and entropy or cost as shown in Fig. 2. The surplus heads were relatively small with an average of 0.027 m. As the pipe diameters were discrete and thus small surpluses were virtually unavoidable given that only eight pipe diameter options were available, the methodology developed can be considered satisfactory with respect to the optimality of the solutions.

Fig. 2
figure 2

Quality of the solutions achieved. The plots are based on 30 optimization runs

Full size image

The results of individual optimization runs revealed apparent gaps in some of the Pareto fronts and an imbalance between the feasible and infeasible solutions. It is possible that the number of feasible solutions for this network is relatively small in comparison to the size of the solution space. It may be noted that the maximum headloss allowed between the supply and demand nodes was only 2 m based on the available head of 30 m at the supply nodes and the stipulated minimum residual head of 28 m at the demand nodes. In fact the present results are consistent with Saleh and Tanyimboh (2016). While the cost and entropy values (for the peak demands) were similar, the present formulation achieved 74 nondominated feasible solutions with 15 million function evaluations in total compared to only 27 nondominated feasible solutions in Saleh and Tanyimboh (2016) with 20 million evaluations in total. Also, the average surplus head was 2.7 cm compared to 3.5 cm in Saleh and Tanyimboh (2016).

In Saleh and Tanyimboh (2016) the least expensive feasible solution cost was €8.011 million and the entropy was 4.7968. The cost of the most expensive solution was €10.285 million and the entropy was 7.2989. Herein, the corresponding values were: €8.074 million and 5.125, for the peak demands, for the least expensive solution; and €10.108 million and 7.127, for the peak demands, for the most expensive solution. Thus the solutions from the proposed methodology are very competitive. In any case, Saleh and Tanyimboh (2016) did not consider multiple operation conditions; so the present solutions have more advantages.

The value of the entropy increased rapidly from the start of the optimization, followed by a second phase with relatively steady progress as shown in Fig. 3a. Only the feasible solutions were included in the results shown in Fig. 3a. The reason is that the entropy values for infeasible solutions are unrealistic, as the flow rates derived from demand-driven analysis are misleading in that the corresponding energy loss due to pipe friction exceeds the total energy of the system. Perhaps this apparent anomaly could be avoided in the future by adopting pressure-driven analysis for more realistic simulations of the infeasible solutions.

Fig. 3
figure 3

Convergence properties. The plots are based on 30 optimization runs

Full size image

Infeasible solutions help drive the optimization, e.g. by sustaining the search near the feasibility boundaries and avoiding a purely interior search that may be suboptimal (Siew et al. 2014). Figure 3b shows the progress of the infeasible solutions. The mean deficit of the solutions increased as the optimization progressed, as the solutions with the smallest deficits (i.e. the solutions located close to the feasible region) improved and eventually became feasible. It was observed that, after decreasing rapidly initially, the number of feasible solutions increased gradually until the end of the optimization (Czajkowska 2016).

4.3 Effectiveness of the Joint Entropy Formulation

Figure 4 shows the trade-off between flow entropy and cost for the non-dominated feasible solutions. There was a positive coefficient of correlation of 0.991 between the flow entropy and the mean diameter. Larger pipe diameters improve the hydraulic reliability by increasing the pipe flow capacities and lowering the pipe failure rates. This is consistent with previous results in the literature. There is evidence also, of strong positive correlation between the flow entropy and uniformity of the pipe diameters that improves flow re-distribution further.

Fig. 4
figure 4

Entropy values from total entropy maximization

Full size image

It is obvious from Fig. 4 that no operating condition had the highest entropy value in all the solutions. For the relatively expensive solutions (€8.5 million and above) Fire Flows 2 and 1 had the highest and lowest entropy values, respectively. On the other hand, Fig. 4 shows that when considering the less expensive solutions (up to €8.5 million) there was no obvious trend. This provides empirical evidence that maximizing the total entropy is the most appropriate approach for multiple operating conditions. Also, the surplus heads for the fire flows in Fig. 5 reveal that none of the fire flows dominated the other in every solution.

Fig. 5
figure 5

Nondominated solutions from total entropy maximization

Full size image

Furthermore, maximizing the largest or smallest entropy value would consider only one operating condition out of three. The operating condition with the largest or smallest entropy could change in successive generations. This could potentially make the algorithm unstable or inefficient through lack of continuity. While the entropy values for different operating conditions were comparable in the present example, there may be significant differences in other situations.

Similar results were achieved on several additional networks in which the total, maximum and minimum entropy maximization approaches were investigated separately. Entropy maximization based on a single loading condition was investigated also. The results showed that multiple operating conditions improved the resilience (i.e. reliability and pipe failure tolerance) and maximizing the sum of the entropies gave the best solutions (Czajkowska 2016).

5 Conclusions

A methodology for flow entropy maximization in the design optimization of water distribution networks under multiple loading conditions was developed and assessed. The empirical results achieved demonstrated that the joint entropy of two or more independent loading conditions is the sum of the separate entropies. It was revealed also that no single loading condition was consistently dominant from the perspective of the flow entropy. The reason is that the critical loading conditions varied from one solution to the next and thus could not be ascertained beforehand. Maximizing the sum of the entropies was, therefore, the most logical approach. These observations are consistent with both the maximum entropy formalism (Jaynes 1957) and the formal definition of the joint entropy of independent probability schemes (Shannon 1948).

A large increase in the number of feasible solutions was achieved compared to previous investigations. It is possible, however, that in the network considered, the total number of feasible solutions is relatively small compared to the size of the solution space. It is also possible that the optimization performed mainly an exterior rather than an interior search within the feasible solution space. Thus some important challenges remain notably the effective incorporation and exploitation of infeasible solutions. Demand-driven hydraulic simulations were used in the optimization. Consequently, the flow entropy values of the infeasible solutions were misleading. Therefore, additional investigations are required. Alternative formulations of the optimization model based on pressure-driven simulation may be worth considering also.