ToTem NRSfM: Object-Wise Non-rigid Structure-from-Motion with a Topological Template

Abstract

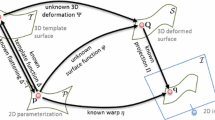
We present a Non-Rigid Structure-from-Motion (NRSfM) method to reconstruct an object whose topology is known. We represent the topology by a 3D shape that weakly resembles the object, which we call a Topological Template (ToTem). The ToTem has two main differences with the template used in Shape-from-Template (SfT). First, the shape in the ToTem is not necessarily feasible for the object, whereas it must be in the SfT template. Second, the ToTem only models shape, excluding the classical texture-map representing colour in the SfT template. These two differences greatly alleviate the practical difficulty of constructing a template. However, they make the reconstruction problem challenging, as they preclude the use of strong deformation constraints between the template shape and the reconstruction and the possibility of directly establishing correspondences between the template and the images. Our method uses an isometric deformation prior and proceeds in four steps. First, it reconstructs point-clouds from the images. Second, it aligns the ToTem to the point-clouds. Third, it creates a coherent surface parameterisation. Fourth, it performs a global refinement, posed as Bundle Adjustment (BA). We show experimentally that our method outperforms the existing methods for its isolated steps and NRSfM methods overall, in terms of 3D accuracy, ability to reconstruct the object’s visible surface and ability to approximate the object’s invisible surface.

Appendices

Appendices

Geometry of the Topological Templates

We describe some basic geometric properties of the parametric shapes in the following paragraphs.

1.1 Planar

We denote the 2D template with ${\textbf{p}} = (x,y) \in \mathbb {R}^2$. Therefore the map $\Delta :\mathbb {R}^2 \mapsto \mathbb {R}^3$ is trivial and given in table 2. The next warp $\psi$ is defined as:

$$\begin{aligned} \psi _{i}(\textbf{P}) = \begin{pmatrix} {X}&{Y}&{Z}&1\end{pmatrix} \underset{4 \times 3}{{\textbf{a}}} + \underset{1 \times {l}}{\rho (\textbf{P}, {\textbf{D}})} \underset{{l} \times 3}{{\textbf{w}}}, \end{aligned}$$

(48)

and the combined warp is:

$$\begin{aligned} \varphi _i(x, y) = \psi _{i} \circ \Delta = \Delta (x,y) {\textbf{a}} + \rho \Big (\Delta (x,y), {\textbf{D}}\Big ){\textbf{w}}. \end{aligned}$$

(49)

Therefore, the derivatives of the warps are:

$$\begin{aligned} \begin{aligned} \varphi _x(x, y) = \begin{pmatrix} 1&0&0&1\end{pmatrix}{\textbf{a}} + \frac{\partial }{\partial x}\Big (\rho \big (\Delta (x,y), {\textbf{D}}\big )\Big ){\textbf{w}} \\ \varphi _y(x, y) = \begin{pmatrix} 0&1&0&1\end{pmatrix}{\textbf{a}} + \frac{\partial }{\partial y}\Big (\rho \big (\Delta (x,y), {\textbf{D}}\big )\Big ){\textbf{w}}, \end{aligned} \end{aligned}$$

(50)

where for the l-th element of $\rho$ we have:

$$\begin{aligned} \frac{\partial }{\partial x}\Big (\rho ^l\big (\Delta (x,y), {\textbf{D}}\big )\Big ) = \frac{X - D_l^X}{\rho ^l\big (\Delta (x,y), {\textbf{D}}\big )} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial }{\partial y}\Big (\rho ^l\big (\Delta (x,y), {\textbf{D}}\big )\Big ) = \frac{Y - D_l^Y}{\rho ^l\big (\Delta (x,y), {\textbf{D}}\big )}. \end{aligned}$$

(51)

Proceeding similarly, the second derivatives of the warps are given by:

$$\begin{aligned} \varphi ^l_{xx}(x, y) =&\frac{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2 - \big ( X - D_l^X \big )^2}{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2} {\textbf{w}}\\ \varphi ^l_{yy}(x, y) =&\frac{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2 - \big ( Y - D_l^Y \big )^2}{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2}{\textbf{w}} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\varphi ^l_{xy}(x, y) = \varphi ^l_{yx}(x, y) \\&\quad = \frac{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2 - \Big ( \big ( X - D_l^X \big ) + \big ( Y - D_l^Y \big ) \Big )^2}{\Big ( \rho ^l\big (\Delta (x,y), {\textbf{D}}\big ) \Big )^2}{\textbf{w}}. \end{aligned} \end{aligned}$$

(52)

1.2 Cylindrical

Following the definition of $\Delta$ from table 2, we obtain $\psi$ as:

$$\begin{aligned}{} & {} \psi _{i}(\textbf{P}) = \begin{pmatrix} {X}&{Y}&{Z}&1\end{pmatrix} \underset{4 \times 3}{{\textbf{a}}} + \underset{1 \times {l}}{\rho (\textbf{P}, {\textbf{D}})} \underset{{l} \times 3}{{\textbf{w}}}. \end{aligned}$$

(53)

$$\begin{aligned}{} & {} \varphi (r,\theta ) = \begin{pmatrix} \sin {\theta }&r&\cos {\theta }&1\end{pmatrix} {\textbf{a}} + \rho \Big (\Delta (r,\theta ), {\textbf{D}}\Big ){\textbf{w}} \end{aligned}$$

(54)

For the case of cylindrical surfaces, we elaborate the computation of the tangent vectors and surface normal of $\psi _{i}$ with some verbosity. Assuming:

(55)

we can compute:

(56)

and ignoring $\upalpha _{14}$ from Eq. (56), we obtain:

$$\begin{aligned} \varphi _r^{\top } = \begin{pmatrix} \upalpha _2&\upalpha _6&\upalpha _{10} \end{pmatrix} +\begin{pmatrix} \lambda ^{r}_{1}&\lambda ^{r}_{2}&\lambda ^{r}_{3} \end{pmatrix}, \end{aligned}$$

(57)

where the assumption that the fourth column of $\check{{\textbf{a}}}$ and $\check{{\textbf{w}}}$ are all zeros gives us ${\textbf{a}}$ and ${\textbf{w}}$ respectively. Similarly:

$$\begin{aligned} \varphi _{\theta }^{\top }= & {} \begin{pmatrix} (\upalpha _1 \cos {\theta } - \upalpha _3\sin {\theta })&(\upalpha _5\cos {\theta } - \upalpha _7\sin {\theta })&(\upalpha _9 \cos {\theta } - \upalpha _{11} \sin {\theta }) \end{pmatrix}\nonumber \\{} & {} + \begin{pmatrix} \lambda ^{\theta }_{1}&\lambda ^{\theta }_{2}&\lambda ^{\theta }_{3} \end{pmatrix}, \end{aligned}$$

(58)

where:

(59)

since $\upalpha _{13}$ and $\upalpha _{15}$ are zeros. Given that $\textbf{N} = \begin{pmatrix} N^{{X}}&N^{{Y}}&N^{{Z}}\end{pmatrix} = \varphi _r \times \varphi _{\theta }$, we have:

$$\begin{aligned} N^{{X}}= & {} (\upalpha _{6} + \lambda ^{r}_{2})(\upalpha _{9}\cos {\theta } - \upalpha _{11}\sin {\theta } + \lambda ^{\theta }_{3}) \nonumber \\{} & {} - (\upalpha _{10} + \lambda ^{r}_{3})(\upalpha _{5}\cos {\theta } - \upalpha _7\sin {\theta } + \lambda ^{\theta }_{2}) \end{aligned}$$

(60)

$$\begin{aligned} N^{{Y}}= & {} - (\upalpha _{2} + \lambda ^{r}_{1})(\upalpha _{9}\cos {\theta } - \upalpha _{11}\sin {\theta } + \lambda ^{\theta }_{3}) \nonumber \\{} & {} + (\upalpha _{10} + \lambda ^{r}_{3})(\upalpha _{1}\cos {\theta } - \upalpha _{3}\sin {\theta } + \lambda ^{\theta }_{1}) \end{aligned}$$

(61)

$$\begin{aligned} N^{{Z}}= & {} (\upalpha _{2} + \lambda ^{r}_{1})(\upalpha _{5}\cos {\theta } - \upalpha _{7}\sin {\theta } + \lambda ^{\theta }_{2})\nonumber \\{} & {} - (\upalpha _{6} + \lambda ^{r}_{2})(\upalpha _{1}\cos {\theta } - \upalpha _{3}\sin {\theta } + \lambda ^{\theta }_{1}), \end{aligned}$$

(62)

where $\textbf{N}$ is the un-normalized vector along the direction of the surface normal, evaluated at $(r,\theta )$. Consequently, the unit normal is expressed as $\hat{\textbf{N}} = \frac{ \varphi _r \times \varphi _{\theta }}{\Vert \varphi _r \times \varphi _{\theta } \Vert }$. We denote the function for unit normal computation as $\mathcal {N}_i(\cdot )$, which takes the j-th coordinate from the flattened template $(r_j,\theta _j)$ and computes the unit normal, given by $\mathcal {N}_i(r_j,\theta _j) = \begin{pmatrix} \hat{N}^{{X}}_{i,j}&\hat{N}^{{Y}}_{i,j}&\hat{N}^{{Z}}_{i,j}&1 \end{pmatrix}$ for the i-th image frame.

1.3 Spherical

For spherical objects, beginning from the initial mapping $\Delta$ described in table 2, the maps $\psi$ and $\varphi$ are obtained following the same form as Eqs. (1) and (54) respectively. The normals to the spherical surface, which are the equivalent of Eqs. (56) to (62), are summarised below. The derivatives of $\varphi$ are given as:

$$\begin{aligned} \tilde{\varphi }_{\theta _1}{} & {} = \begin{pmatrix} \sin {\theta _1}\cos {\theta _2}&-\cos {\theta _1}&\sin {\theta _1}\sin {\theta _2} \end{pmatrix} {\textbf{a}}\nonumber \\{} & {} \quad + \frac{\partial \rho \big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _1}{\textbf{w}} \end{aligned}$$

(63)

$$\begin{aligned} \tilde{\varphi }_{\theta _2}{} & {} = \begin{pmatrix} \cos {\theta _1}\sin {\theta _2}&0&-\cos {\theta _1}\cos {\theta _2} \end{pmatrix} {\textbf{a}} \nonumber \\{} & {} \quad + \frac{\partial \rho \big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _2}{\textbf{w}}, \end{aligned}$$

(64)

where the l-th element of $\frac{\partial \rho \big (\Delta (r,\theta ), {\textbf{D}}\big )}{\partial \theta _1}$ and $\frac{\partial \rho \big (\Delta (r,\theta ), {\textbf{D}}\big )}{\partial \theta _2}$ are given respectively as:

$$\begin{aligned}{} & {} \frac{\partial \rho ^{l}\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _1} \nonumber \\{} & {} \quad = \frac{ \Big ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l \Big )^{\top } \Delta _{\theta _1} }{\rho ^{l}\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )} \quad \text { and } \nonumber \\{} & {} \frac{\partial \rho ^{l}\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _2}\nonumber \\{} & {} \quad = \frac{ \Big ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l \Big )^{\top } \Delta _{\theta _2} }{\rho ^{l}\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}, \end{aligned}$$

(65)

where $\Delta _{\theta _1} = \frac{\partial \Delta }{\partial \theta _1}$ and $\Delta _{\theta _2} = \frac{\partial \Delta }{\partial \theta _2}$ following standard convention. Similar to section 2, the unit normals can be obtained as $\hat{\textbf{N}} = \frac{ \varphi _{\theta _1} \times \varphi _{\theta _2}}{\Vert \varphi _{\theta _1} \times \varphi _{\theta _2} \Vert }$. From Eq. (65), the second derivatives of the warps can be computed as:

$$\begin{aligned} \begin{aligned} \tilde{\varphi }_{\theta _1 \theta _1}&= \begin{pmatrix} \cos {\theta _1}\cos {\theta _2}&\sin {\theta _1}&\cos {\theta _1}\sin {\theta _2} \end{pmatrix} {\textbf{a}}\\&\quad + \frac{\partial ^2 \rho \big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _1^2}{\textbf{w}} \\ \tilde{\varphi }_{\theta _2 \theta _2}&= \begin{pmatrix} \cos {\theta _1}\cos {\theta _2}&0&\cos {\theta _1}\sin {\theta _2} \end{pmatrix} {\textbf{a}}\\&\quad + \frac{\partial ^2 \rho \big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _2^2}{\textbf{w}} \\ \tilde{\varphi }_{\theta _1 \theta _2}&= \tilde{\varphi }_{\theta _2 \theta _1} = \begin{pmatrix} -\sin {\theta _1}\sin {\theta _2}&0&\sin {\theta _1}\cos {\theta _2} \end{pmatrix} {\textbf{a}} \\&\quad + \frac{\partial }{\partial \theta _1}\Big (\frac{\partial \rho \big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _2}\Big ){\textbf{w}}, \end{aligned} \end{aligned}$$

(66)

where:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 \rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _1^2} = \frac{ \Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^2 \Big ( ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top } \Delta _{\theta _1 \theta _1} + \Delta _{\theta _1}^{\top }\Delta _{\theta _1} \Big ) - ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top } \Delta _{\theta _1}}{\Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^3}\nonumber \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 \rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )}{\partial \theta _2^2} = \frac{ \Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^2 \Big ( ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top } \Delta _{\theta _2 \theta _2} + \Delta _{\theta _2}^{\top }\Delta _{\theta _2} \Big ) - ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top } \Delta _{\theta _2}}{\Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^3}\\&\frac{\partial }{\partial \theta _1}\Big (\frac{\partial \rho ^l\big (\Delta (\theta _2), {\textbf{D}}\big )}{\partial \theta _2} \Big ) = \frac{\partial }{\partial \theta _2}\Big (\frac{\partial \rho ^l\big (\Delta (\theta _1), {\textbf{D}}\big )}{\partial \theta _2} \Big ) \\&\quad = \frac{ \Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^2 \Big ( ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top } \Delta _{\theta _1 \theta _2} + \Delta _{\theta _1}^{\top }\Delta _{\theta _2} \Big ) - ( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l )^{\top }( \Delta (\theta _1,\theta _2) - {\textbf{D}}_l) \Delta ^{\top }_{\theta _1} \Delta _{\theta _2}}{\Big (\rho ^l\big (\Delta (\theta _1,\theta _2), {\textbf{D}}\big )\Big )^3}. \end{aligned} \end{aligned}$$

(67)

1.4 General Shapes

We have a combination of two warps, the first one being:

$$\begin{aligned} \Delta (x,y) = \begin{pmatrix} x&y&0&1\end{pmatrix} {\textbf{a}}_{\Delta } {+} \rho (\textbf{p}, {\textbf{D}}) {\textbf{w}}_{\Delta } {=} \begin{pmatrix} X&Y&Z \end{pmatrix} {=} \textbf{P}, \end{aligned}$$

(68)

where the pre-defined warp parameters $({\textbf{a}}_{\Delta }, {\textbf{w}}_{\Delta } )$ are obtained using conformal flattening of some mesh using the method of Sheffer and de Sturler (2001) and Sheffer et al. (2005). The variables $({\textbf{a}}_{\Delta }, {\textbf{w}}_{\Delta } )$ are computed offline and only once per object model. This is followed by the second warp for deformation of the canonical model, given by:

$$\begin{aligned} \psi _{i}(\textbf{P}) =&\begin{pmatrix} {X}&{Y}&{Z}&1\end{pmatrix} \underset{4 \times 3}{{\textbf{a}}} + \underset{1 \times {l}}{\rho (\textbf{P}, {\textbf{D}})} \underset{{l} \times 3}{{\textbf{w}}} \qquad \text { and } \nonumber \\ \varphi _i(x, y) =&\psi _{i} \circ \Delta . \end{aligned}$$

(69)

We are interested in the derivatives of the warps:

$$\begin{aligned} \varphi _x = \begin{pmatrix} \frac{\partial \textbf{P}}{\partial x}&0 \end{pmatrix} + \frac{\partial \rho (\textbf{P}, {\textbf{D}})}{\partial x}{\textbf{w}} \qquad \varphi _y = \begin{pmatrix} \frac{\partial \textbf{P}}{\partial y}&0 \end{pmatrix} + \frac{\partial \rho (\textbf{P}, {\textbf{D}})}{\partial y}{\textbf{w}}. \end{aligned}$$

(70)

Thereafter, we have:

$$\begin{aligned} \begin{pmatrix} \frac{\partial \textbf{P}}{\partial x} \\ \frac{\partial \textbf{P}}{\partial y} \end{pmatrix}= & {} \begin{pmatrix} \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 \end{pmatrix} {\textbf{a}}_{\Delta } + \frac{\partial \rho (\textbf{p}, {\textbf{D}})}{\partial x} {\textbf{w}}_{\Delta } \\ \begin{pmatrix} {0} &{} {1} &{} {0} &{} 0\end{pmatrix} {\textbf{a}}_{\Delta } + \frac{\partial \rho (\textbf{p}, {\textbf{D}})}{\partial y} {\textbf{w}}_{\Delta } \end{pmatrix}\nonumber \\= & {} \begin{pmatrix} \frac{\partial X}{\partial x} &{} \frac{\partial Y}{\partial x} &{} \frac{\partial Z}{\partial x} \\ \frac{\partial X}{\partial y} &{} \frac{\partial Y}{\partial y} &{} \frac{\partial Z}{\partial y} \end{pmatrix} \text {, } \nonumber \\ \begin{pmatrix} \frac{\partial \rho ^l(\textbf{p}, {\textbf{D}})}{\partial x} \\ \frac{\partial \rho ^l(\textbf{p}, {\textbf{D}})}{\partial x}\end{pmatrix}= & {} \begin{pmatrix} \frac{x - D^X_l}{\rho ^l(\textbf{p}, {\textbf{D}})} \\ \frac{y - D^Y_l}{\rho ^l(\textbf{p}, {\textbf{D}})} \end{pmatrix} \forall l \in [1,n], \end{aligned}$$

(71)

and:

$$\begin{aligned}&\begin{pmatrix} \frac{\partial \rho ^l(\textbf{P}, {\textbf{D}})}{\partial x} \\ \frac{\partial \rho ^l(\textbf{P}, {\textbf{D}})}{\partial y} \end{pmatrix} = \begin{pmatrix} \frac{(X - D_l^X)\frac{\partial X}{\partial x} + (Y - D_l^Y)\frac{\partial Y}{\partial x} + (Z - D_l^Z)\frac{\partial Z}{\partial x} }{\rho ^l(\textbf{P}, {\textbf{D}})} \\ \frac{(X - D_l^X)\frac{\partial X}{\partial y} + (Y - D_l^Y)\frac{\partial Y}{\partial y} + (Z - D_l^Z)\frac{\partial Z}{\partial y} }{\rho ^l(\textbf{P}, {\textbf{D}})} \end{pmatrix} \nonumber \\&\qquad \qquad \forall l \in [1,n]. \end{aligned}$$

(72)

Following similar geometric properties, the next frame describes an example of the computation of length along geodesic, specifically for the spherical template:

Jacobian Matrices

We now describe the derivation of analytic Jacobian matrices for all cost functions used in sections 6 and 7.

1.1 Initial Parameterised Reconstruction

The minimisation of Eq. (33) is done analytically and the Jacobian matrix relating the change of $g_{\textrm{data}}$, $g_{\textrm{def0}}$ and $g_{\textrm{def1}}$ w.r.t. $\xi _I \in \mathbb {R}^{1 \times 3l}$, the stacked optimisation parameters, are expressed by the terms:

$$\begin{aligned} \begin{aligned} \textbf{J}_{P} =&\frac{\partial g_{\textrm{data}}}{\partial \xi _I} \text { , } \\ \textbf{J}_{N} =&\frac{\partial g_{\textrm{def1}}}{\partial \xi _I} \quad \text { and } \\ \textbf{J}_{B} =&\frac{\partial g_{\textrm{def0}}}{\partial \xi _I}. \end{aligned} \end{aligned}$$

(75)

Expanding the Jacobian matrices for the j-th row of the matrices $\textbf{J}_{P}$ and $\textbf{J}_{N}$ (corresponding to the j-th row of the error vectors), we obtain the following expressions:

$$\begin{aligned} \begin{aligned} \underset{1 \times 3l}{\underbrace{\textbf{J}_{P,j}}} =&\frac{\partial }{\partial \xi _I} \Big ( \big (\varphi ({\textbf{p}}_j) - {\textbf{Q}}_{j} \big ) \cdot \eta \big (\varphi ({\textbf{p}}_j)\big ) \Big ) \\ =&\frac{\partial }{\partial \xi _I} \Bigg ( \overbrace{\Big ( \underset{1 \times 4}{\underbrace{\begin{bmatrix} \rho \big (\Delta (r_j,\theta _j), {\textbf{D}}\big )&\tilde{\textbf{P}}_j \end{bmatrix} \mathcal {D}^{-1}\begin{bmatrix}\tilde{{\textbf{C}}} \\ \textbf{0}\end{bmatrix}}} - \underset{1 \times 4}{\underbrace{\tilde{{\textbf{Q}}}_{j}}} \Big )}^{\varvec{\mu }_j} \\&\overbrace{\underset{4 \times 1}{\underbrace{\begin{bmatrix} \hat{N}^{X}_j&\hat{N}^{Y}_j&\hat{N}^{Z}_j&1 \end{bmatrix}}}^{\top }}^{\hat{\textbf{N}}_j} \Bigg ) \\ =&\frac{\partial }{\partial \xi _I} (\varvec{\mu }_j \hat{\textbf{N}}_j) = \underbrace{\frac{\partial \varvec{\mu }_j }{\partial \xi _I}}_{1 \times 12l} \underbrace{(\hat{\textbf{N}}_j \otimes \mathbb {1}_{3l})}_{12l \times 3l} + \underbrace{\varvec{\mu }_j}_{1 \times 4} \underbrace{\frac{\partial \hat{\textbf{N}}_j}{\partial \xi _I}}_{4 \times 3l}, \end{aligned} \end{aligned}$$

(76)

where:

(77)

and $\frac{\partial \hat{\textbf{N}}_j}{\partial \xi _I}$ can be obtained from:

$$\begin{aligned} \begin{aligned}&\underbrace{\frac{\partial \hat{\textbf{N}}_j}{\partial \xi _I}}_{4 \times 3l} = \frac{\partial }{\partial \xi _I} \begin{bmatrix} \hat{N}^{X}_j&\hat{N}^{Y}_j&\hat{N}^{Z}_j&1 \end{bmatrix}^{\top } \\&\quad = \frac{1}{\Vert \tilde{\textbf{N}_j}\Vert } \begin{bmatrix} \frac{\partial N^{X}_j}{\partial \xi _I}&\frac{\partial N^{Y}_j}{\partial \xi _I}&\frac{\partial N^{Z}_j}{\partial \xi _I}&0\end{bmatrix}^{\top }\\&\quad - \frac{ \begin{bmatrix} N_j^{X}&N_j^Y&N_j^Z&1 \end{bmatrix}^{\top } \Big ( N_j^X \frac{\partial N_j^X}{\partial \xi _I} + N_j^Y \frac{\partial N_j^Y}{\partial \xi _I} + N_j^Z \frac{\partial N_j^Z}{\partial \xi _I} \Big ) }{(\Vert \tilde{\textbf{N}_j}\Vert )^3}. \end{aligned} \end{aligned}$$

(78)

Thereafter, we are left with the terms $\frac{\partial N^{X}_j}{\partial \xi _I}$, $\frac{\partial N^{Y}_j}{\partial \xi _I}$ and $\frac{\partial N^{Z}_j}{\partial \xi _I}$ which are obtained from Eqs. (56) and (58) by differentiating the expression for the un-normalised normal vector:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial \xi _I} \bigg ( \begin{bmatrix} N^{X}_j&N^{Y}_j&N^{Z}_j \end{bmatrix} \bigg )\\&\quad = \frac{\partial }{\partial \xi _I} \big (\varphi _r \times \varphi _{\theta } \big )\\&\quad = \frac{\partial }{\partial \xi _I} \big ( [\varphi _r]_{\times } \varphi _{\theta } \big ) = \frac{\partial }{\partial \xi _I}\big ( [\varphi _r]_{\times } \big ) \big ( \varphi _{\theta } \otimes \mathbb {1}_{3l} \big ) + [\varphi _r]_{\times }\frac{\partial \varphi _{\theta }}{\partial \xi _I} \\&\quad = \begin{bmatrix} 0 &{} -\frac{\partial \varphi _{r,3}}{\partial \xi _I} &{} \frac{\partial \varphi _{r,2}}{\partial \xi _I} \\ \frac{\partial \varphi _{r,3}}{\partial \xi _I} &{} 0 &{} -\frac{\partial \varphi _{r,1}}{\partial \xi _I} \\ -\frac{\partial \varphi _{r,2}}{\partial \xi _I} &{} \frac{\partial \varphi _{r,1}}{\partial \xi _I} &{} 0\end{bmatrix} \big ( \varphi _{\theta } \otimes \mathbb {1}_{3l} \big )\\&\qquad + [\varphi _r]_{\times } \begin{bmatrix} \frac{\partial \varphi _{\theta ,1}}{\partial \xi _I} \\ \frac{\partial \varphi _{\theta ,2}}{\partial \xi _I} \\ \frac{\partial \varphi _{\theta ,3}}{\partial \xi _I} \end{bmatrix}. \end{aligned} \end{aligned}$$

(79)

From Eq. (56), we have:

(80)

Similarly:

$$\begin{aligned} \begin{aligned}&\frac{\partial \tilde{\varphi _{\theta }}}{\partial \xi _I} = \frac{\partial }{\partial \xi _I} \left( \begin{bmatrix} (\upalpha _1 \cos {\theta } - \upalpha _3\sin {\theta }) \\ (\upalpha _5\cos {\theta } - \upalpha _7\sin {\theta }) \\ (\upalpha _9 \cos {\theta } - \upalpha _{11} \sin {\theta }) \\ (\alpha _{13} \cos {\theta } - \upalpha _{15} \sin {\theta }) \end{bmatrix}^{\top } \right) \\&\quad + \begin{bmatrix} \frac{ D^{\textrm{Z}}_1 \sin {\theta } - D^{\textrm{X}}_1 \cos {\theta } }{\rho ^1(\Delta (r,\theta ), {\textbf{D}})} \\ \vdots \\ \frac{D^{\textrm{Z}}_{l} \sin {\theta } - D^{\textrm{X}}_{l} \cos {\theta }}{\rho ^l(\Delta (r,\theta ), {\textbf{D}})} \end{bmatrix}^{\top } \bar{\varepsilon }_{\lambda } \begin{bmatrix} \mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l} \end{bmatrix} \\&= \begin{bmatrix} \cos {\theta } \\ -\sin {\theta } \end{bmatrix} \frac{\partial }{\partial \xi _I} \bigg ( \begin{bmatrix} \upalpha _{1} &{} \upalpha _{5} &{} \upalpha _{9} &{} \upalpha _{13} \\ \upalpha _{3} &{} \upalpha _{7} &{} \upalpha _{11} &{} \upalpha _{15} \end{bmatrix} \bigg ) \\&\quad + \begin{bmatrix} \frac{ D^{\textrm{Z}}_1 \sin {\theta } - D^{\textrm{X}}_1 \cos {\theta } }{\rho ^1(\Delta (r,\theta ), {\textbf{D}})} \\ \vdots \\ \frac{D^{\textrm{Z}}_{l} \sin {\theta } - D^{\textrm{X}}_{l} \cos {\theta }}{\rho ^l(\Delta (r,\theta ), {\textbf{D}})} \end{bmatrix}^{\top } \bar{\varepsilon }_{\lambda } \begin{bmatrix} \mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l} \end{bmatrix}. \end{aligned} \end{aligned}$$

(81)

Equations (80) and (81) leave us with some more unknown terms in the form of . However, these values can be easily obtained by differentiating Eq. (55) as:

$$\begin{aligned}{} & {} \frac{\partial \check{{\textbf{a}}}}{\partial \xi _I} = \frac{\partial }{\partial \xi _I} \left( \begin{bmatrix} {\alpha }_{1} &{} {\alpha }_{5} &{} {\alpha }_{9} &{} {\alpha }_{13} \\ {\alpha }_{2} &{} {\alpha }_{6} &{} {\alpha }_{10} &{} {\alpha }_{14} \\ {\alpha }_{3} &{} {\alpha }_{7} &{} {\alpha }_{11} &{} {\alpha }_{15} \\ {\alpha }_{4} &{} {\alpha }_{8} &{} {\alpha }_{12} &{} {\alpha }_{16} \end{bmatrix} \right) \nonumber \\{} & {} \quad = \Big ( \tilde{{\textbf{D}}} {\textbf{K}}_{\lambda }^{-1} \tilde{{\textbf{D}}}^{\top } \Big )^{-1} \tilde{{\textbf{D}}} {\textbf{K}}_{\lambda }^{-1} \begin{bmatrix} \mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l}&\mathbb {1}_{l}&\mathbb {0}_{l \times 3l} \end{bmatrix}.\nonumber \\ \end{aligned}$$

(82)

Going back to Eq. (75), the Jacobian matrix $\textbf{J}_{N}$ can be expressed as:

$$\begin{aligned}{} & {} \underbrace{\textbf{J}_{N,j}}_{1 \times 3l} = \frac{ \Big (\hat{N}^X_j - \eta ^{X}\big (\Delta ({\textbf{p}}_j)\big )\Big ) \frac{\partial \hat{N}^X_j}{\partial \xi _I} + \Big (\hat{N}^Y_j - \eta ^{Y}\big (\Delta ({\textbf{p}}_j)\big )\Big ) \frac{\partial \hat{N}^Y_j}{\partial \xi _I} + \Big (\hat{N}^Z_j - \eta ^{Z}\big (\Delta ({\textbf{p}}_j)\big )\Big ) \frac{\partial \hat{N}^Z_j}{\partial \xi _I} }{ \Vert \eta \big (\varphi ({\textbf{p}}_j)\big ) - \eta \big (\Delta ({\textbf{p}}_j)\big ) \Vert }. \end{aligned}$$

(83)

The final Jacobian matrix $\textbf{J}_B$ is a straightforward partial differentiation of Eq. (35).

1.2 Global Refinement

We now discuss the details of the Jacobian matrices involved in the global refinement process from Eq. (39), the Jacobian matrices are given for the original problem, not the efficient one, since the accelerated solutions are easy to derive from the full expanded ones. A single row of the first Jacobian matrix relating the change of $h_{\textrm{rep}}$ to $\varvec{\xi }$ is given by:

(84)

where $\varvec{\kappa }$ and $\varvec{\omega }$ are vectorised uv-coordinates and control handles respectively. Considering the first term and the second set of terms separately, we start with the first term of Eq. (39):

$$\begin{aligned} \begin{aligned}&\frac{\partial h_{\textrm{rep}}}{\partial \kappa } = \frac{\partial }{\partial \kappa } \Big ( \Vert {\textbf{q}}_{i,j} - \Pi \big (\varphi _i({\textbf{p}}_{j})\big ) \Vert \Big ) \\&\quad = \frac{-1}{\Vert {\textbf{q}}_{i,j} - \Pi \big (\varphi _i({\textbf{p}}_{j})\big ) \Vert } \\&\qquad \Bigg ( \bigg ( \Big ( ({\textbf{q}}_{j})_x - \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_x \Big ) \frac{\partial }{\partial \kappa }\Big ( \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_x \Big ) \bigg ) \\&\qquad + \bigg ( \Big ( ({\textbf{q}}_{j})_y - \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_y \Big ) \frac{\partial }{\partial \kappa }\Big ( \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_y \Big ) \bigg ) \Bigg ), \end{aligned} \end{aligned}$$

(85)

assuming the suffix $(\cdot )_x$ or $(\cdot )_y$ gives the x or y coordinate of the 2D point. Given that ${\textbf{Q}}_{i,j} = \varphi _i({\textbf{p}}_j)$ and its homogeneous coordinates are given as $\tilde{{\textbf{Q}}}_{i,j}$, we differentiate both sides of the perspective projection equation w.r.t.  $\kappa$ to obtain:

$$\begin{aligned} \begin{aligned}&\underbrace{\frac{\partial }{\partial \kappa } \Big (\Pi \big (\varphi _i({\textbf{p}}_j)\big ) \Big )}_{2 \times 2m} = \frac{\partial }{\partial \kappa } \left( \begin{bmatrix} \Pi \big (\varphi _i({\textbf{p}}_j)\big )_x \\ \Pi \big (\varphi _i({\textbf{p}}_j)\big )_y \end{bmatrix} \right) \\&\quad = \frac{\partial }{\partial \kappa } \left( \begin{bmatrix} \frac{f_x}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} 0 &{} c_x \\ 0 &{} \frac{f_y}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} c_y \end{bmatrix} f_i^{-1} \tilde{{\textbf{Q}}}_{i,j} \right) \\&\quad = \underbrace{\frac{\partial }{\partial \kappa } \left( \begin{bmatrix} \frac{f_x}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} 0 &{} c_x \\ 0 &{} \frac{f_y}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} c_y \end{bmatrix} \right) }_{2 \times 8m} \\&\quad \underbrace{\big (f_i^{-1} \tilde{{\textbf{Q}}}_{i,j} \otimes \mathbb {1}_{2m}\big )}_{8m \times 2m} + \left( \underbrace{\begin{bmatrix} \frac{f_x}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} 0 &{} c_x \\ 0 &{} \frac{f_y}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} c_y \end{bmatrix}}_{[2 \times 4]}\right. \\&\quad \left. \underbrace{f_i^{-1}}_{4 \times 4} \underbrace{\frac{\partial \tilde{{\textbf{Q}}}_{i,j}}{\partial \kappa }}_{4 \times 2m} \right) . \end{aligned} \end{aligned}$$

(86)

Given that $\frac{\partial }{\partial \kappa }(\frac{f_x}{({\textbf{Q}}_{i,j})_Z} ) = -\frac{f_x}{({\textbf{Q}}_{i,j})_Z^2} \frac{\partial ({\textbf{Q}}_{i,j})_Z}{\partial \kappa }$, to compute Eq. 86), we need the expression for the term $\frac{\partial ({\textbf{Q}}_{i,j})_Z }{\partial \kappa }$, which can be obtained from:

$$\begin{aligned} \begin{aligned}&\underbrace{\frac{\partial \tilde{{\textbf{Q}}}_{i,j}^{\top } }{\partial \kappa }}_{1 \times 8m} = \begin{bmatrix} \frac{\partial ({\textbf{Q}}_{i,j})_X }{\partial \kappa }&\frac{\partial ({\textbf{Q}}_{i,j})_Y }{\partial \kappa }&\frac{\partial ({\textbf{Q}}_{i,j})_Z }{\partial \kappa }&\textbf{0}_{1 \times 2m}\end{bmatrix} \\&\quad = \frac{\partial }{\partial \kappa } \left( \begin{bmatrix} \underbrace{\rho \big (\Delta (r_j,\theta _j), {\textbf{D}}\big )}_{[1 \times l]}&\tilde{{\textbf{Q}}}_{i,j}^{\top } \end{bmatrix} \varepsilon _{\lambda , i}\begin{bmatrix}\tilde{{\textbf{C}}}_i \\ \textbf{0}\end{bmatrix} \right) \\&= \underbrace{ \begin{bmatrix} \frac{\partial }{\partial \kappa } \Big ( \rho \big ( \Delta (r_j,\theta _j), {\textbf{D}}\big ) \Big )&\frac{\partial \sin {\theta _j}}{\partial \kappa }&\frac{\partial r_j}{\partial \kappa }&\frac{\partial \cos {\theta _j}}{\partial \kappa }&0 \end{bmatrix}}_{1 \times 2m(l + 4)} \\&\quad \underbrace{\Bigg ( \bigg (\varepsilon _{\lambda , i}\varepsilon _{\lambda , i}\begin{bmatrix}\tilde{{\textbf{C}}}_j \\ \textbf{0}\end{bmatrix}\bigg ) \otimes \mathbb {1}_{2m}\Bigg )}_{2m(l+4) \times 8m}, \end{aligned} \end{aligned}$$

(87)

and the four terms inside the first $1 \times 2m(l + 4)$ matrix of Eq. (87), for the k-th element of the source points ${\textbf{D}}$, is given by the expressions in the frames below.

Moving to the second set of terms in Eq. 84:

$$\begin{aligned} \begin{aligned}&\frac{\partial h_{\textrm{rep}}}{\partial \varvec{\omega }_i} = \frac{\partial }{\partial \varvec{\omega }_i} \Big ( \Vert {\textbf{q}}_{i,j} - \Pi \big (\varphi _i({\textbf{p}}_{j})\big ) \Vert \Big )\\&\quad = \frac{-1}{\Vert {\textbf{q}}_{i,j} - \Pi \big (\varphi _i({\textbf{p}}_{j})\big ) \Vert } \\&\qquad \Bigg ( \bigg ( \Big ( ({\textbf{q}}_{j})_x - \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_x \Big ) \frac{\partial }{\partial \varvec{\omega }_i}\Big ( \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_x \Big ) \bigg ) \\&\qquad + \bigg ( \Big ( ({\textbf{q}}_{j})_y - \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_y \Big ) \frac{\partial }{\partial \varvec{\omega }_i}\Big ( \Pi \big (\varphi _i({\textbf{p}}_{j})\big )_y \Big ) \bigg ) \Bigg ), \end{aligned} \end{aligned}$$

(93)

where:

$$\begin{aligned}{} & {} \frac{\partial }{\partial \varvec{\omega }_i}\Bigg ( \Pi \big (\varphi _i({\textbf{p}}_{j})\big ) \Bigg ) = \frac{\partial }{\partial \varvec{\omega }_i} \left( \begin{bmatrix} \frac{f_x}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} 0 &{} c_x \\ 0 &{} \frac{f_y}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} c_y \end{bmatrix} \right) \nonumber \\{} & {} \quad \Bigg (f_i^{-1} \tilde{{\textbf{Q}}}_{i,j} \otimes \textbf{1}_{3l} \Bigg ) + \left( \begin{bmatrix} \frac{f_x}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} 0 &{} c_x \\ 0 &{} \frac{f_y}{({\textbf{Q}}_{i,j})_Z} &{} 0 &{} c_y \end{bmatrix}f_i^{-1}\frac{\partial \tilde{{\textbf{Q}}}_{i,j}}{\partial \varvec{\omega }_i} \right) . \end{aligned}$$

(94)

Once again, to compute Eq. (94), we need the expression for the term $\frac{\partial ({\textbf{Q}}_{i,j})_Z }{\partial \varvec{\omega }_i}$, which can be obtained from:

(95)

Obviously, when the indices of $\tilde{{\textbf{Q}}}$ and $\varvec{\omega }$ do not match, the rows of the Jacobian matrix are all zeroes, i.e.  $\frac{\partial \tilde{{\textbf{Q}}}_{{i_1},j}^{\top } }{\partial \varvec{\omega }_{i_2}} = \textbf{0}_{1 \times 12\,l}$ when $i_1 \ne i_2$. Our next objective is to compute the Jacobian matrix relating the change of $E_I$ to $\varvec{\xi }$, providing us with:

$$\begin{aligned}{} & {} \textbf{J}_{I,h} = \frac{\partial }{\partial \varvec{\xi }} \big ( e_{I,h}(\textbf{Q}_{i,j}, \textbf{Q}_{i,q}, d_{j,q}) \big ) \nonumber \\{} & {} \quad = \begin{bmatrix} \frac{\partial }{\partial \kappa } \big ( e_{I,h}(\textbf{Q}_{i,j}, \textbf{Q}_{i,q}, d_{j,q}) \frac{\partial }{\partial \varvec{\omega }} \big ( e_{I,h}(\textbf{Q}_{i,j}, \textbf{Q}_{i,q}, d_{j,q}) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(96)

The two terms on the right most matrix of Eq. (96) are expanded below:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial \kappa } \big ( e_{I,h}(\textbf{Q}_{i,j}, \textbf{Q}_{i,q}, d_{j,q}) \big )\\&\quad = \frac{1}{\zeta _1} \Bigg ( \Big ( (\textbf{Q}_{i,j})_X - (\textbf{Q}_{i,q})_X \Big ) \left( \frac{\partial (\textbf{Q}_{i,j})_X }{\partial \kappa } - \frac{\partial (\textbf{Q}_{i,q})_X}{\partial \kappa } \right) \\&\qquad + \Big ( (\textbf{Q}_{i,j})_Y - (\textbf{Q}_{i,q})_Y \Big ) \left( \frac{\partial (\textbf{Q}_{i,j})_Y }{\partial \kappa } - \frac{\partial (\textbf{Q}_{i,q})_Y}{\partial \kappa } \right) \\&\qquad + \Big ( (\textbf{Q}_{i,j})_Z - (\textbf{Q}_{i,q})_Z \Big ) \left( \frac{\partial (\textbf{Q}_{i,j})_Z }{\partial \kappa } - \frac{\partial (\textbf{Q}_{i,q})_Z}{\partial \kappa } \right) \Bigg ) \\&\qquad - \frac{1}{\zeta _2} \frac{\partial d_{j,q}^2}{\partial \kappa }, \end{aligned} \end{aligned}$$

(97)

where:

(98)

The other term from Eq. (96) is:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial \varvec{\omega }} \big ( e_{I,h}(\textbf{Q}_{i,j}, \textbf{Q}_{i,q}, d_{j,q}) \big ) \\&\quad = \frac{1}{\zeta _1} \Bigg ( \Big ( (\textbf{Q}_{i,j})_X - (\textbf{Q}_{i,q})_X \Big ) \Big ( \frac{\partial (\textbf{Q}_{i,j})_X }{\partial \varvec{\omega }} - \frac{\partial (\textbf{Q}_{i,q})_X}{\partial \varvec{\omega }} \Big ) \\&\qquad + \Big ( (\textbf{Q}_{i,j})_Y - (\textbf{Q}_{i,q})_Y \Big ) \Big ( \frac{\partial (\textbf{Q}_{i,j})_Y }{\partial \varvec{\omega }} - \frac{\partial (\textbf{Q}_{i,q})_Y}{\partial \varvec{\omega }} \Big )\\&\qquad + \Big ( (\textbf{Q}_{i,j})_Z - (\textbf{Q}_{i,q})_Z \Big ) \Big ( \frac{\partial (\textbf{Q}_{i,j})_Z }{\partial \varvec{\omega }} - \frac{\partial (\textbf{Q}_{i,q})_Z}{\partial \varvec{\omega }} \Big ) \Bigg ). \end{aligned} \end{aligned}$$

(99)