Analyzing Ball Bearing Capacitance Using Single Steel Ball Bearings

Abstract

A precise modeling of the capacitance of rolling element bearings is of increasing significance over the last years, e.g. in the context of bearing damage estimation in electric drives. The complexity of a steel bearing as an electrical network makes reliable validation of calculation models under realistic operating conditions nearly impossible. A way to reduce complexity in yet realistic conditions is the use of hybrid bearings with a single steel rolling element. This helps to measure only one current path through the bearing at a time and thus, gives a much clearer picture of the contact capacitance of rolling elements in and out of the load zone. The usage of different materials comes with different thermal expansion coefficients and different elasticities, which cause a significant change in load distribution. For the first time, this work considers both of these effects in calculation and validates them with corresponding experiments using single steel ball bearings.

1 Introduction

A better understanding of the electrical behavior of rolling element bearings is of great interest in various fields of research. First, in inverter fed electrical machines, the bearing’s capacitance has an influence on the resulting voltage drop over the bearing. Hence, a better prediction of the capacitance helps to estimate and reduce the risk of damaging bearing currents [1,2,3,4,5]. Secondly, eligible bearing capacitance models allow the utilization of rolling element bearings as sensors, as the capacitance depends on the bearing load [6, 7] and the lubrication condition [8]. An improvement of the electrical model will enable white box sensor models suitable for arbitrary bearing geometries. Thirdly, capacitance measurements are used for lubrication film measurements and are highly dependent on the quality of the electrical bearing models. Therefore, models are constantly improved [9,10,11,12].

Measuring a bearing’s capacitance is usually done for a whole bearing [4, 13,14,15]. A ball-on-disc tribometer, on the other hand, allows the investigation of a single contact [16,17,18], but is not able to replicate the exact contact geometry between a groove and a ball and the lubrication condition of a real bearing. This work focuses another approach: A regular bearing is used, but all rolling elements except one are replaced by ceramic ones, as realized by Jabłonka [10] and Bechev [19]. Thus, only the steel ball contributes significantly to the total capacitance. This comes at the cost of a change in load distribution due to the different rolling element materials. Jabłonka introduced a static load distribution model considering the different elasticities of the materials.

In this work, a static load distribution model is introduced, that also accounts for different thermal expansion coefficients. This is key to understand the load distribution in such prepared bearings. It correlates the radial load on the bearing to the load on the steel rolling element and therefore enables the interpretation of measured capacitances at a given load.

To achieve this aim purposefully, various assumptions are met, on which the models introduced are based:

• 1. Only the geometry of deep groove ball bearings is considered. Especially different types of rolling elements require separate investigations.

• 2. Pure radial load and therefore symmetry in axial direction is assumed. Expanding the models to accommodate combined loads is possible but yet omitted in this work.

• 3. Centrifugal and hydrodynamic forces are considered in the enhanced model only. Other dynamic effects like the inertia of the rolling elements are neglected as in common load distribution models [20].

• 4. In this work, the bearing’s capacitance is investigated. While the bearing is considered as a parallel circuit of a resistance and a capacitance, at frequencies in and beyond the kHz regime, the capacitance becomes dominant as the resistance is high compared to the capacitance’s impedance.

2 Materials and Methods

The bearing geometry has a major influence on the load distribution. Therefore, all relevant geometry parameters are defined before the load distribution equations are introduced.

2.1 Bearing Geometry

Fig. 1 and Table 1 display all relevant geometry parameters of a deep groove ball bearing used in the following.

Fig. 1

Deep groove rolling bearing’s geometry parameters

Table 1 Geometry parameters of a radial deep groove ball bearing

The minimal ring thicknesses b is an auxiliary quantity to calculate the raceway diameters $D_\textrm{i}$ and $D_\textrm{o}$ in dependency of the manufactured internal radial clearance c, assuming symmetric cross sections of the inner and outer ring,

$$\begin{aligned} b = \frac{D-d-2D_\textrm{RE}-c}{2}. \end{aligned}$$

(1)

The bearing’s operational clearance is affected by the bearing seat fitting. In case of an interference fitting of the shaft, $D_\textrm{i}$ increases by $u_\textrm{i}$ and in case of an interference fitting of the housing, $D_\textrm{o}$ decreases by $u_\textrm{o}$,

$$\begin{aligned} D_\textrm{i}=&d+2b+u_\textrm{i}, \end{aligned}$$

(2)

$$\begin{aligned} D_\textrm{o}=&D-2b-u_\textrm{o}. \end{aligned}$$

(3)

$u_\textrm{i}$ and $u_\textrm{o}$ can be calculated from basic elasto-static equations as in [20].

All geometrical parameters are given at room temperature 20 °C. To account for the thermal expansion, temperature dependent values are calculated for all geometry parameters and their corresponding values,

$$\begin{aligned} l'=l \, \Delta T \, (1+\alpha _\textrm{t}). \end{aligned}$$

(4)

The coefficients of thermal expansion $\alpha _\textrm{t}$ are listed in Table 2.

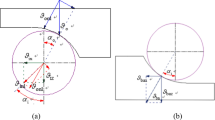
Shifting the inner ring versus the outer ring by $\delta _y$ in the direction of the radial load and by $\delta _x$ perpendicular to $\delta _y$ in radial direction, results in the geometrical configuration seen in Fig. 2. Thus, the separation between the inner and outer ring s at a given position $\psi$ can be calculated. A value of $s>D_{RE}$ corresponds to a clearance and no load on the rolling element. $s<D_{RE}$ describes a deflection of the rolling element leading to a reaction force, cf. Section 2.2. s can be calculated for $\delta _x\ne 0,\; \delta _y\ne 0$ using the auxiliary quantities $\kappa$ and $\psi _\delta$ as follows,

$$\begin{aligned} s&= \frac{\sin (\psi - \psi _\delta )\,\delta _{x}}{\sin \psi _\delta \cdot \sin (\arctan \kappa ) } -R_\textrm{i} + R_\textrm{RE} \quad \text {with} \end{aligned}$$

(5)

$$\begin{aligned} \kappa&= \frac{\sin (\psi - \psi _\delta )\,\delta _{x}}{ \sin \psi _\delta \, \left( R_\textrm{o} - R_\textrm{RE} - \frac{\cos ( \psi - \psi _\delta )}{\sin \psi _\delta }\,\delta _{x}\right) } \quad \text {and} \end{aligned}$$

(6)

$$\begin{aligned} \psi _\delta&= \arctan \left( \frac{\delta _{x}}{\delta _{y}}\right) \quad \text {for} \quad \delta _x\ne 0,\; \delta _y\ne 0. \end{aligned}$$

(7)

In case of a symmetrical rolling element configuration, the displacement of the inner ring in x-direction will be $\delta _x = 0$, therefore, s can be calculated as,

$$\begin{aligned} s= & {} \frac{R_\textrm{o}-R_\textrm{RE}-\cos (\psi ) \, \delta _{y}}{\cos \left( \arctan \left( \frac{\sin (\psi ) \, \delta _{y}}{ R_\textrm{o}-R_\textrm{RE} - \cos (\psi ) \, \delta _{y}}\right) \right) }-R_\textrm{RE}-R_\textrm{i}\nonumber \\{} & {} \text {for} \quad \delta _x=0,\; \delta _y\ne 0. \end{aligned}$$

(8)

Subsequently, the deflection of the rolling element $\delta _\textrm{RE}$ can be calculated,

$$\begin{aligned} \delta _\textrm{RE} = {\left\{ \begin{array}{ll} D_\textrm{RE} - s &{} s \le D_\textrm{RE}\\ 0 &{} \text {else} \end{array}\right. }. \end{aligned}$$

(9)

Fig. 2

Geometric derivation of distance between inner and outer ring s at the angular position $\psi$

Table 2 Material parameters

2.2 Quasi Static Load Distribution

The load-deflection dependency of a ball in a groove depends on the geometry and the materials. The reduced Young’s modulus of a contact of two contact partners 1 and 2 can be calculated from the Young’s moduli $E_1$ and $E_2$ and the Poisson’s ratios $\nu _1$ and $\nu _2$ [21],

$$\begin{aligned} E' = \frac{2}{\frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}}. \end{aligned}$$

(10)

According to Hertz, the deflection constant $K_\textrm{P}$ of two contact surfaces can be calculated as [22],

$$\begin{aligned} K_\textrm{P} = \pi \; k \; E' \sqrt{\frac{2\mathfrak {E}R}{9}} \; \mathfrak {F}^{-1,5}. \end{aligned}$$

(11)

The elliptic integrals $\mathfrak {F}$ and $\mathfrak {E}$ can be determined according to ISO 76 [23]. The ellipticity ratio of the contact ellipse k can be calculated according to Hertz [22]. The reduced radius R is calculated from the radii in the contact [21],

$$\begin{aligned} \frac{1}{R}&= \frac{1}{R_x} + \frac{1}{R_y} \; \text {with} \end{aligned}$$

(12)

$$\begin{aligned} \frac{1}{R_x}&= \frac{1}{R_\textrm{RE}} + \frac{1}{R_\mathrm {i/o}} \; \text {and} \end{aligned}$$

(13)

$$\begin{aligned} \frac{1}{R_y}&= \frac{1}{R_\textrm{RE}} + \frac{1}{R_\mathrm {gi/o}}. \end{aligned}$$

(14)

Subsequently, the deflection constant of a rolling element $K_\textrm{P,RE}$ can be calculated as a series connection of the inner and outer contact, $K_\textrm{P,i}$ and $K_\textrm{P,o}$ respectively [24],

$$\begin{aligned} K_\textrm{P,RE} = \left( \frac{K_\textrm{P,i}^{2/3} \; K_\textrm{P,o}^{2/3}}{K_\textrm{P,i}^{2/3} + K_\textrm{P,o}^{2/3}}\right) ^{3/2}. \end{aligned}$$

(15)

The exponent 3/2 is valid for the point contact, describing the non-linear correlation of deflection and force,

$$\begin{aligned} Q_\textrm{RE} = K_\textrm{P,RE} \; \delta _\textrm{RE}^{3/2}. \end{aligned}$$

(16)

Finally, for each rolling element n in the angular position $\psi _n$, the load $Q_{\textrm{RE},n}$ can be calculated by varying the ring displacement $\delta _x$ and $\delta _y$ and solving the equilibrium of forces iteratively,

$$\begin{aligned} F_\textrm{r} = \sum _{n=1}^Z Q_{\textrm{RE},n} \cos {\psi _n}. \end{aligned}$$

(17)

2.3 Enhanced Model

A systematic flaw of the static model is the discontinuous transition from the loaded to the unloaded zone. Within the load zone the distance between the raceway and the rolling element is calculated using the lubrication film thickness. Towards the end of the load zone forces become extremely small and the film thickness therefore extremely large. Outside the load zone the gap between rolling elements and ring is calculated using the shaft deflection. Thus, barely outside the load zone the distance becomes extremely small. Therefore, capacitance calculation around this transition is not continuous with the static model, cf. Sect. 3.2. Furthermore, it does not allow a calculation of the position of unloaded rolling elements. Thus, the model was enhanced to take hydrodynamic forces on unloaded rolling elements into account. Additionally, the centrifugal force $F_\textrm{c}$ acting on the rolling elements [20] is considered, as it is not negligible for unloaded rolling elements,

$$\begin{aligned} F_\textrm{c} = \frac{1}{2} m \; d_\textrm{m} \; \omega _\textrm{m}^2. \end{aligned}$$

(18)

m is the mass of the rolling element, $d_\textrm{m}$ the pitch diameter of the bearing and $\omega _\textrm{m}$ the orbital speed of the rolling element. Consequently, the load of the inner contact, $Q_\textrm{i} = Q_\textrm{RE}$, and the load of the outer contact, $Q_\textrm{o} = Q_\textrm{RE} + F_\textrm{c}$, have to be differentiated.

Hydrodynamic forces on the rolling elements can be calculated by using Hamrock and Dowsons lubrication film equation for the point contact [21] as a function of the contact load Q. This is possible because all other parameters, the equivalent radius $R_x$ (13), the speed parameter U, the materials parameter G and the ellipticity parameter k are constant for all contacts in the bearing,

$$\begin{aligned}{} & {} H_{0}(Q) = h_0(Q) / R_x = \nonumber \\{} & {} 2.69 \, U^{0.67} \, G^{0.53} \, W(Q)^{-0.067} \, (1-0.61e^{-0.73k}), \end{aligned}$$

(19)

$$\begin{aligned}{} & {} W(Q) = \frac{Q}{E' \; R_x^2}. \end{aligned}$$

(20)

This relation together with the contact deflection $\delta _\textrm{RE}(Q)$ derived from Eq. (16) builds the enhanced model as seen in Fig. 3,

$$\begin{aligned} s = D_\textrm{RE} - \delta _\textrm{RE}(Q_\textrm{i}) - \delta _\textrm{RE}(Q_\textrm{o}) + h_\textrm{0}(Q_\textrm{i}) + h_\textrm{0}(Q_\textrm{o}). \end{aligned}$$

(21)

Analog to the static model, the load distribution is then calculated by solving the equilibrium of forces (17) iteratively.

Fig. 3

Enhanced model using a series connection of load dependent deflection $\delta _\textrm{RE}$ and lubrication film thickness $h_0$

2.4 Capacitance Calculation

Finally, the capacitance of each contact can be calculated using a semi-analytic approach, introduced by the authors in [25]. First, the capacitance $C_\textrm{Hz}$ of the Hertz’ian area $A_\textrm{Hz}$ is commonly calculated with the absolute permittivity of the lubricant $\varepsilon$ as,

$$\begin{aligned} C_\textrm{Hz} = \varepsilon \; \frac{A_\textrm{Hz}}{h_0}. \end{aligned}$$

(22)

Then, opposing commonly used approaches, the geometry is not simplified to the effective radii and uses spherical coordinates $\varphi$ in rolling direction and $\theta$ perpendicular to the rolling direction,

$$\begin{aligned} C_\textrm{out}= & {} 4 \; \varepsilon \int _0^{\varphi _1} \int _{\theta _0(\varphi )}^{\theta _1(\varphi )} \frac{R_\textrm{RE}^2}{h_\textrm{groove}(\theta ,\varphi )} \; \cos {\theta } \; \textrm{d}\theta \; \textrm{d}\varphi \nonumber \\{} & {} \quad + 4 \; \varepsilon \int _0^{\varphi _1} \int _{\theta _1(\varphi )}^{\theta _2(\varphi )} \frac{R_\textrm{RE}^2}{h_\textrm{rim}(\theta ,\varphi )} \; \cos {\theta } \; \textrm{d}\theta \; \textrm{d}\varphi . \end{aligned}$$

(23)

$h_\textrm{groove}$ is the distance between the rolling element surface and groove surface in radial direction. In the second summand, the rim area outside the groove is considered with $h_\textrm{rim}$, the distance between the rolling element and the rim area. The Hertzian theory and the load deflection dependency (Eq. 16) do not result in the exact same contact area. Thus, the calculated distances $h_\textrm{groove}$ may be smaller than in reality. Therefore, areas with $h_\textrm{groove}<h_0$ are omitted. The integration limit $\varphi _1$ is set to $\pi /2$ on the outer ring and less for the inner ring as the convex radius requires a geometrical calculation of the maximum value. The limits in $\theta$-direction are

• $\theta _0(\varphi )$, the edge of the Hertz’ian area,

• $\theta _1(\varphi )$, the edge of the groove and

• $\theta _2(\varphi )$, the edge of the ring.

2.5 Experimental Setup

The experimental setup used to measure the bearings under test is shown in Fig. 4. The radial load on the bearing under test is applied by a hydraulic cylinder. An axial load is not applied as in this paper a contact angle of ${0}^\circ$ is assumed, cf. Sect. 1. An electric motor drives the shaft of the test rig via an electrically insulating dog clutch. The rotational speed was kept constant, as a negligible influence on the load distribution is expected. The speed of $n = {2000}\hbox {min}^{-1}$ is high enough to reach hydrodynamic lubrication but still allows a fine resolution of the capacitance measurement per rotation. For lubrication, the oil is pumped from a reservoir via a heating unit to the test chamber. The oil temperature was chosen in a way that, according to the static model in Sect. 2.2, the load on the single steel ball is equivalent to a ball in the same position of a normal steel bearing. All parameters for the experiments are stated in Table 3.

Table 3 Experimental parameters

Different configurations of bearings, as stated in Table 4, are used in the following. A hybrid bearing with a single steel ball is denoted as a mix(1) bearing. A mix(S) bearing is a hybrid bearing with a steel ball which is slightly smaller than the ceramic balls at room temperature. In a mix(10 S) bearing, two steel balls are mounted, two cage pockets apart, whereas one is of the same size as the ceramic balls and one is smaller.

Three independent bearings of each configuration were assembled and measured to achieve a basic statistical confidence. All bearings are fitted with a glass-fiber reinforced PA66 cage for easier assembly and less stray capacitance. Each assembled bearing underwent a run-in of at least 10h at $F_\textrm{r}={3}{\text {kN}}$, $n={2000}\hbox {min}^{-1}$ and $T_\textrm{oil}={62}$ °C.

Table 4 Test bearing configurations with rolling element materials and estimated diameters at room temperature 20 °C

Fig. 4

Experimental setup for measuring the capacitance of single steel ball rolling bearings

The momentary capacitance of the bearing is measured using an unbalanced AC Wheatstone bridge as shown in Fig. 4. The capacitors are chosen in a similar order as the measurand $C_1 \approx C_2 \approx C_3 \approx {1}\hbox {nF}$. Measured impedances of the capacitors are used to calculate the bearings impedance from the generator voltage $V_\textrm{G}$ and bridge voltage $V_\textrm{M}$. The generator applies a $f_\textrm{G}={20}{\text {kHz}}$ sine voltage with an amplitude of $\hat{V}_\textrm{G}={3}{V}$. Due to the voltage drop across the capacitance $C_1$ the voltage at the bearing decreases to around 1.5V. In the fluid friction regime no non-capacitive current was detected. Therefore, the voltage is considered below the breakdown voltage which is consistent with various studies on the breakdown voltage of similar bearings [26,27,28]. An open adjustment using a hybrid bearing is carried out in order to eliminate all stray capacitances of the test rig as well as the capacitance between the inner and outer ring of the bearing which is not included in the model. A short adjustment is omitted, as the bearing’s impedance $\vert \underline{Z} \vert > {100}{k\,\Omega }$ is high in comparison to the connectors and cables and the measurement circuit is not ideal for measuring small ohmic resistances. Then, the bearing’s capacitance is calculated from the measured impedance $\underline{Z}$ and the angular generator frequency $\omega =2 \pi f_\textrm{G}$ as follows,

$$\begin{aligned} C = - \frac{\textrm{Im}(\underline{Z})}{\omega \vert \underline{Z} \vert ^2}. \end{aligned}$$

(24)

3 Results and Discussion

The developed mathematical model for the load distribution of a deep groove ball bearing is analyzed and compared with measurements. It enables a deeper understanding in the behavior of balls reacting to forces, as well as the interaction between different ball materials and load distribution.

The calculated results from the static model are compared with the enhanced model and improvements are analyzed. The conducted experiments will be directly compared to calculations and similarities are discussed.

Also the superposition of mix(1) and mix(S) bearing signals are compared to mix(10 S) bearing signals and a conclusion about the general procedure of superposition can be done.

3.1 Quasi Static Model

The following figures show the calculated results of the static model with respect to one rotation of the cage. This rotation is equivalent to a full rotation of one ball around the shaft. The ${0}^{\circ }$ position corresponds to the steel ball position in the middle of the load zone and opposite to the radial force.

Figure 5 shows the vertical shaft displacement of a mix(1) and steel bearing over one full cage rotation. The shaft displacement is considered positive in the up direction. That is to intuitively display a downward displacement in the negative direction of the vertical axis.

Fig. 5

Calculated vertical shaft displacement of a steel 6205 bearing compared to a mix-bearing at $F_\textrm{r} = {3}{\,}{\text {kN}}$ and $T = {35}$ °C

Two differences between the steel and mix(1) bearing are noticeable:

First, the shaft displacement of the mix(1) bearing is less than the shaft displacement of the steel bearing. This behavior directly corresponds to the stiffer ceramic material of the mix(1) bearing, which will be less deformed at the same load.

The second difference is the drop of the shaft which only occurs with a mix(1) bearing at ${0}^{\circ }$. The steel ball has to counteract most of the forces at this position, so the deformation is much higher. But the displacement is not reaching the same level as a steel bearing because the ceramic balls next to the steel ball will take some of the load as soon as the deflection is high enough.

Both bearings have a sinusoidal movement of the shaft in common which is caused by different global stiffness behaviors of the bearing during a rotation. Both extremes correspond to one symmetric orientation of the ball bearing. Are two balls equally loaded in the middle of the load zone, the stiffness of these balls add up and the global stiffness increases. A higher global stiffness will prevent a large displacement.

The second symmetric and extreme orientation occurs when only one ball is in the middle of the load zone. The global stiffness in this case is lower and the shaft displacement will be higher. During a rotation of the bearing both of these extreme global stiffnesses will alternate and the sinusoidal movement of the shaft occurs.

The temperature influence on the shaft displacement can be seen in Fig. 6. Both graphs show the behavior of a mix(1) bearing with different oil temperatures. The displacement at 35 °C as seen in Fig. 5 shows a significant deviation from the results with a higher temperature of 60 °C.

With a higher temperature the overall shaft displacement is more negative which is caused by the heat expansion of the whole bearing. Because the outer and inner ring, as well as the shaft and housing are made of steel, they will expand more than the ceramic balls. This causes a greater distance between bearing mid point and contact point of inner ring with the balls.

At temperatures above room temperature the single steel ball has a bigger diameter than the ceramic balls. Thus, at higher temperatures the steel ball will bear more load and cause less displacement when passing the load zone, cf. Figure 6.

Fig. 6

Calculated vertical shaft displacement of two different oil temperatures with a steel 6205 bearing at $F_\textrm{r} = {3}{\,}{\text {kN}}$

The load on each single ball is decisive for the electrical behavior of a bearing. To compare the results of a mix bearing with a steel bearing specific oil temperatures were selected that cause the steel ball of a mix(1) bearing to bear the same load as a ball in a steel bearing in the same position, as mentioned in Sect. 2.5.

Figure 7 shows the load distribution over a full rotation of the steel ball in a mix(1)-bearing as well as the load distribution of a steel ball in a steel bearing. The ceramic balls support the steel ball at the highest loads due to their higher stiffness. Thus, the steel ball in between bears less load.

This figure also shows the load zone of both cases, which is around ${180}^{\circ }$ as the bearing in the bearing seats used is almost play free.

Fig. 7

Calculated load distribution of a single rolling element of a steel 6205 bearing compared to a mix-bearing at $F_\textrm{r} = {3}{\,}{\text {kN}}$ and $T_\textrm{oil} = {35}$ °C

3.2 Enhanced Model

As mentioned in Sect. 2.3, the static model contains a discontinuous transition from the loaded to the unloaded zone. This transition can be seen as spikes in Fig. 8 which shows the total capacitance of a mix bearing over a cage rotation. The spike is caused by the calculation of unloaded rolling elements just outside the load zone. Since the distance between the ball and the raceway is calculated from the static geometry, the distance becomes very small near the load zone. This can cause distances smaller the the lubrication film thickness just inside the load zone, which is not physically accurate.

Fig. 8

Calculated total capacitance of a mix bearing with the static and enhanced model at $F_\textrm{r} = {3}{\,}{\text {kN}}$ and $T_\textrm{oil} = {35}$ °C

The enhanced model shows a continuous transition and overcomes this problem, because the position of the ball is dependent on the lubrication film at any angle. Additionally, the capacitance of the enhanced model outside the loaded zone is smaller because the centrifugal forces $F_\textrm{c}$ are considered. The capacitance between outer ring and ball will increase but in the same time will the capacitance between the inner ring and the ball decrease. A series connection of both capacitances will create a smaller total capacitance compared to two equal capacitances.

3.3 Experiments

After measuring the capacitance and post processing the signal, as described in Sect. 2.5, the measurements and the calculations are compared. All measurements, raw and evaluated, can be found in [29]. Fig. 9 shows the total capacitance of a measured (left) and calculated (right) mix(1) bearing during one cage rotation. The agreement of both is very high, especially for lower temperatures and loads.

At the highest load and temperature spikes occur in the measured signal. These spikes arise most likely due to metallic contact between the ball and race way, as the bearing approaches the mixed lubrication regime at these loads and temperatures. Thus, a change in the phase angle of the measured impedance can be observed, cf. Appendix A, as the ohmic resistance decreases due to the metallic contact.

The capacitance of rolling element outside the load zone is highest for the lowest load, because this case causes less deflection of the shaft and therefore less play for the unloaded rolling elements. This effect can be observed in the measurements as well, even though the difference is less than the standard deviation of the measurement and therefore statistically not significant.

Fig. 9

Measured and calculated total capacitance of a mix(1) bearing at multiple forces and temperatures

Instead of changing the temperature and load simultaneously, Fig. 10 shows the change of maximum capacitance over different temperatures with a constant load of 3kN. Mix(1) and mix(S) bearings are measured as well as calculated to see the influence of different ball sizes.

The rising trend in maximum capacitance for increasing temperature can be seen in both bearing types, for measurements and calculations. Also the difference between both calculated values and the difference between both measured values is comparable.

The biggest difference between both, the calculated and measured values, is the slope and therefore the temperature sensitivity. The current model creates higher impact from the temperature to the capacitance. These measurements show further possibilities to improve the introduced model. More recent lubrication film equations are one possible solution.

The lubrication film is very sensitive to temperature, so different lubrication film equations can generate better results. But also the assumption of a constant temperature difference between inner and outer ring can be a reason for this discrepancy.

Fig. 10

Calculated and measured maximal total capacitance of a mix(1) and a mix(S) bearing at multiple temperatures and $F_\textrm{r} = {3}{\,}{\text {kN}}$

Finally, the assumption that the superposition of all single ball capacitances sum up to the total capacitance of the bearing, is investigated. Figure 11 shows a measured capacitance signal of a mix(10 S) bearing as well as the theoretical signal, when superposing the measured signal of a mix(1) and mix(S) bearing. To generate the approximated mix(10 S) bearing signal in Fig. 11 both measured signals are added up as their respective capacitances are arranged in parallel.

Fig. 11

Measured total capacitance of a mix(10 S) bearing compared to a superposed bearing signal at $F_\textrm{r} = {3}{\,}{\text {kN}}$ and $T = {35}$ °C

Outside the load zone of the mix(S) bearing, a partially negative capacitance was measured. This physically impossible observation is due to the inductance of the test rig as only a compensation for the open circuit was carried out using hybrid bearings. The consideration of the test rig’s inductance would lead to an increase of the small capacitances. Therefore, the superposed signal is in good accordance with the real signal. Thus, under these conditions the superposition of rolling elements is possible.

4 Conclusion

This paper introduced a new model for calculating bearing capacitances while considering not only different Young’s moduli but also different thermal expansion coefficients for different rolling element materials. This enables new insights into properties like the global stiffness for hybrid bearings with a single steel ball. Enhancing this model by considering centrifugal and hydrodynamic forces on rolling elements outside the load zone eliminates discontinuities of the former model, which yields more accurate results.

Measuring the capacitance of corresponding hybrid bearings with a single steel ball bearing showed results in good accordance with the models introduced. Using a modified calculation of the capacitance outside the Hertz’ian area yield this accurate results without relying on any correction factors. However, the temperature dependency is not optimally depicted and is still subject to further improvement.

Then, the usability of single steel ball bearings was further verified by superposing two measurements of two bearings with differently sized single steel balls and then comparing it to a single bearing with the two differently sized balls. Both were in good agreement, indicating that drawing conclusions from a single steel ball bearing can be transferred to multiple steel ball bearings.

Appendix A

1.1 Metallic Contact at High Loads

In Fig. 9 at $F_\textrm{r} = {6}{\,}\text {kN}$ and $T_\textrm{oil} = {62.4}^{\circ }\hbox {C}$ spikes in the measured capacitance can be observed. These spikes are most likely due to metallic contact in the load zone. This leads to an increase in the phase angle of the complex impedance as shown in Fig. 12. The phase increases significantly, although not toward $0^{\circ }$. This is probably due to the small contact area of the metallic contact resulting in a still significant resistance in parallel with a rather large capacitance.

Fig. 12

Measured phase angle of the impedance of a mix(1) bearing at $F_\textrm{r} = {6}{\,}\text {kN}$ and $T_\textrm{oil} = {62.4}^{\circ }\hbox {C}$