A New Film Parameter for Rough Surface EHL Contacts with Anisotropic and Isotropic Structures

Abstract

Numerous tribological contacts worldwide rely on adequate lubrication quality for proper functionality. Despite this, there is no existing approach to accurately predict the state of lubrication. The default model since introduced in the 1960s—the $\Lambda$-ratio, defined as the oil film thickness over the surface roughness height—is unpredictable and may yield erroneous results. Here, we put forward a framework for a new updated film parameter, ${\Lambda }^{*}$, which accounts for the elasto-hydrodynamic lubrication (EHL) effects induced by surface irregularities on the microscopic scale (micro-EHL). This new film parameter was validated in ball-on-disc tribological tests with engineering surfaces comprising isotropic and anisotropic structures. As expected, the new model was found to accurately predict the experimentally measured true mixed and full-film EHL regimes. The ability to accurately predict the mode of lubrication represents a major advance in designing tribological interfaces for optimal efficiency and durability.

1 Introduction

When two non-conformal surfaces under relative motion are brought together under a steady supply of oil, a thin elasto-hydrodynamic lubrication (EHL) film will form [1,2,3,4,5]. The thickness of the film is typically no more than a few hundred nanometres. Despite this modest thickness, its materialization is crucial for the functionality of rotating machinery such as gears, rolling-element bearings and cam followers. Ideally, the developed oil film is thicker than the composite surface roughness height, thus mitigating contact distress by preventing wear of surface irregularities. However, due to economical restrictions typically imposed in the design stage of manufacturing, this situation is seldom the case. In contrast, rough surface EHL contacts are more often forced to operate under various degrees of contact interference. The outcome is precarious since it risks impairing operation through increased friction and reduced service life [6,7,8]. Furthermore, this situation is of substantial environmental concern given that ~ 23% of the total annual energy consumption worldwide originates from friction- and wear-related causes [9]. The need for improved tribological technologies is undoubtedly vast.

At present, well-established theories exist for predicting the EHL film thickness for nominally smooth surfaces [10,11,12]. However, surprisingly little is known about the film-forming mechanisms when surfaces are microscopically rough, and existing design tools are insufficient by means of practical use. This claim is rooted in the fact that the default model in lubrication science and engineering still involves the use of the relatively simple and often critically debated [13,14,15,16,17,18,19,20,21,22,23] $\Lambda$-parameter, i.e., the ratio of the nominal minimum lubricant film thickness and the composite root-mean-square (RMS) surface roughness height, $\Lambda ={h}_{m}/S{q}_{c}$. With this ratio, the regimes of lubrication are typically classified into boundary lubrication (BL) when $\Lambda \le 1$, mixed lubrication (ML) when $1<\Lambda <3$, and EHL when $\Lambda \ge 3$ [2]. While the ratio appears to represent the lubrication quality fairly well when surfaces are mostly Gaussian, particularly with respect to the friction coefficient over the film thickness [20, 24,25,26], it often falls short when following a running-in process—a process causing a gradual change in lubrication quality due to improved surface micro-conformity [27,28,29,30,31]. We have in fact shown in Ref. [22] that when following such a process, a value of $\Lambda =0.24$ may be sufficient for operation under full-film EHL. The reason for this discrepancy is related to the use of surface RMS values in two distinct ways. First, wear occurs mainly at significant peaks, and this is reflected only moderately by surface RMS values. Second, the manifestation of an intermediate, micro-EHL regime [32, 33]—a thin film state that allows for complete separation even when the gap is narrower than the RMS surface height—is possible. Although, mechanistically, this outcome is indeed desirable, a gross miscalculation in lubrication quality is generally not.

Apparently, what is missing in the existing lubrication criteria is a proper way of representing the surface roughness height level, and an additional degree of freedom that accounts for the micro-EHL contribution. Encouragingly, there are some significant aspects of the micro-EHL regime that have been widely established. When a roughness feature enters the EHL contact inlet, the rolling squeeze action causes a local hydrodynamic pressure increase, which subsequently causes the roughness feature to yield elastically from its relaxed state [34,35,36,37,38]. This event constitutes the formation of a local EHL constriction at the asperity scale, which travels through the macro-scale conjunction with the speed of the surface it is attached to. Experimentalists typically refer to this component of the micro-EHL mechanism as the roughness deformation (RD), while theoreticians sometimes refer to it as the particular integral, referring to the steady state solution to the transient EHL problem. The latter discloses further complexity. Indeed, under combined rolling and sliding motion, a transient complementary effect (CE) is invoked upon the deformed roughness, causing the local hydrodynamic pressure and film thickness to become detached [39,40,41,42,43,44]. This transient effect originates from the shear-driven flow that predominates the pressure flow at the approach towards the central zone. The formation and propagation of these components are strongly dependent on the operating conditions and the surface structure. If the asperities are sharp or surfaces are composed of mainly short wavelengths, local hydrodynamic deformations will be limited, and the classical $\Lambda$-ratio may still be sufficient. In contrast, if surfaces are composed of more rounded asperities or long wavelengths, elastic deformations will more easily adhere, and the ML may be postponed [45,46,47]. Consequently, the $\Lambda$-ratio becomes inaccurate, and its use becomes unjustifiable. Clearly, EHL film formation in rough EHL contacts is not governed by the RMS roughness amplitude alone, and since most pertinent aspects of a topography are lacking (e.g., roughness distribution and asperity sharpness), it cannot be utilized for optimizing surfaces for optimal tribological performance. Despite this, it is still being persistently used by researchers and engineers, perhaps due to its convenient applicability and frequent historical use.

Based on the abovementioned shortcomings, we have hypothesized the possibility of whether a new improved film parameter that accounts for the micro-EHL contribution can be deduced based on existing theory. Preferably, this new parameter would be one that is easily accessible for the broader spectrum of researchers not interested in tedious numerical schemes. In fact, the idea is not unrealistic; as early as the late 1960s, it was postulated by Fein and Kreuz [48] that the micro-EHL film that formed under an asperity could be evaluated by semi-analytical theory. At that time, Dowson and Hamrock (D–H) had not yet developed their now-famous EHL formulae, and researchers were forced to rely on much earlier precursors. However, much later in a series of papers published in the 2000s [42, 49,50,51], Spikes et al. picked up on this path laid out some 45 years earlier. Quite conveniently, they managed to experimentally show that modern semi-analytical theories can accurately predict the micro-EHL film thickness of real bumps and ridges.

In the present research, by leveraging the above findings, we have formulated a framework for a new updated film parameter, ${\Lambda }^{*}={h}^{*}/{z}_{0}$. To make this possible, we have from the classical EHL theory deduced a semi-analytical equation that can be used to compute the micro-EHL film formed under hemispherical bumps or ridges oriented either parallel or transverse to the lubricant entrainment. Subsequently, we have evaluated the proposed lubrication parameter through a ball-on-disc tribological setup equipped with real engineering surfaces comprising isotropic and anisotropic structures (roughness lay). As anticipated, the classical $\Lambda$ was found to grossly mispredict the lubrication quality in EHL, whereas through the new film parameter, we have found some strikingly positive agreements with the experimentally verified true ML and full-film EHL regimes. The findings should appeal to readers interested in a much more accurate lubrication quality estimate than offered by the widely used lambda ratio.

2 Materials and Methods

This section outlines details about the classical EHL equations that were employed in the computation of the proposed film parameter and the approach adopted for its experimental validation against real engineering surfaces.

2.1 Film Thickness Equations

Two classical EHL equations were adopted for calculation of the film thickness at the macro- (ball-on-disc) scale [10]; see Eqs. (1) and (2), which represent the Dowson–Hamrock (D–H) minimum and central EHL equations for fully flooded, isothermal, and elliptical EHL contacts.

$$\frac{{h}_{m}}{{R}_{x}^{^{\prime}}}= 3.63{\times U}^{0.68}\times {G}^{0.49}\times {W}^{-0.073}\times \left(1 - {e}^{-0.68k}\right)$$

(1)

$$\frac{{h}_{c}}{{R}_{x}^{^{\prime}}}= 2.69{\times U}^{0.67}\times {G}^{0.53}\times {W}^{-0.067}\times \left(1 - 0.61{e}^{-0.73k}\right)$$

(2)

These equations represent some milestone marks in EHL research, and their accuracy has quite remarkably managed to withstand the test of time, as discussed in more recent work by Lubrecht et al. [11]. The parameter $k$ is an elliptic parameter that can be expressed as $k=1.03\times {\left({R}_{y}^{^{\prime}}/{R}_{x}^{^{\prime}} \right)}^{2/\pi }$. $R^{\prime}$ is the effective radius with sub-indices x and y, denoting the direction parallel and transverse to the lubricant entrainment. The dimensional groupings $U$, $W$, and $G$ are the dimensionless speed, load and material parameters, respectively, given by:

$$U = \frac{{\eta _{0} \times u_{e} }}{{E^{\prime} \times R^{\prime}_{x} }}$$

(3)

$$W = \frac{{w_{z} }}{{E^{\prime} \times R^{\prime^2} _{x} }}$$

(4)

$$G = \alpha ^{*} \times E^{\prime}$$

(5)

where ${u}_{e}=({u}_{b}+{u}_{d})/2$ is the entrainment speed in [m/s]. ${E}^{^{\prime}}=E/(1-{\nu }^{2})$ is the effective elastic modulus for similar materials, with $E$ being the Young’s modulus [Pa] and $\upnu$ being the Poisson’s ratio [-]. ${w}_{z}$ is the applied normal load in [N], and ${\alpha }^{*}$ is the pressure-viscosity coefficient in [m^2/N].

Details of the above input variables are provided in the next section.

2.2 Experimental Details

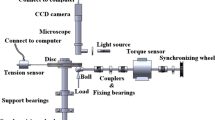
A WAM (Wedeven Associates Machine) ball-on-disc tribological test machine was employed for model verification. EHL lift-off (running-in) tests were conducted to determine the pertinent surface roughness parameters that yield operation in ML and full-film EHL. The procedure is similar to that described in Refs. [22, 23]; hence, only a brief outline will be given here.

Prior to all tests, the machine was first properly calibrated according to the standard protocol, all essential parts were cleaned with heptane and ethyl alcohol, and fresh ball and disc samples were pre-mounted for testing. Approximately 150 mL of test oil was used, and the oil was pre-heated under circulation in a closed looped system until thermal stability at 50 ± 0.24 °C had been established in the oil feed to the contact inlet. The contact was loaded with 1.69 GPa of maximum Hertzian pressure (200 N), and a high degree of sliding, SRR = $({u}_{d}-{u}_{b})/{u}_{e}=$ 1.0, was selected to accelerate the running-in sequence. Using the classical lambda method, it was found that $\Lambda =0.50$ (${h}_{m}=0.142$ µm) was suitable to alter mainly the most prominent asperities and to not risk seizure. For this reason, the entrainment speed was set to 1 m/s.

The ECR signal was monitored to track the evolution in contact performance with time and to determine the completion of running-in (full-film EHL). The interpretation of the signal is based upon the following principles. When the oil film is thin enough to cause rupture at the most prominent asperities, direct metallic junctions are formed, and the ECR signal is < 100% of its maximum value. In contrast, when no metallic junctions are formed under the oil film, the contact is electrically isolated, and the signal value is 100%; thus, operation in the full-film EHL regime is considered. All tests initiated with an ECR value close to 0% due to operation in the ML and were manually terminated once the ECR signal reached > 99.5%, i.e., when the contact reached full-film EHL separation due to reaching a steady state in terms of wear.

The lubricant used was a specially prepared, additive-free [52] PAO (poly-alpha-olephin) provided by Agrol Lubricants, Sweden. The kinematic viscosities at 100 and 40 $^\circ$C were 15.4 and 104 mPa/s, respectively, and the viscosity at the operating temperature was obtained from extrapolation according to ASTM D341. The density at 15 $^\circ$C was reported by the manufacturer to be 0.836 g/cm³. Moreover, the pressure-viscosity coefficient was obtained by linear interpolation to the operating temperature from the PAO data provided in Ref. [53].

The ball and disc specimens were provided by Wedeven Associates Inc., Edgemont, PA, USA. Both test specimens were made of through hardened DIN 100Cr6 (AISI 52100) ball bearing steel of approximately 60 HRC, and a Young’s modulus and Poisson’s ratio of 210 GPa and 0.3, respectively. The disc surface had been polished to a mirror-like isotropic surface finish of 0.003 ± 0.000 µm in surface RMS (mean Sq parameter). The balls were prepared from 13/16 in. grade 10 standard balls to have different surface roughness lay and structures using a honing process developed by the supplier. The roughness patterns were transversal (lay oriented normal to the direction of entrainment), longitudinal (lay oriented in the direction of entrainment), and isotropic. The patterning technology was developed specifically for the current investigation, with the aim to develop different surface roughness structures, but with approximately equal Sq. After selecting the best corresponding balls from each batch comprising a population of ten, we were able to match those specimens that had approximately 0.285 µm Sq (± 0.013 µm). The specific mean Sq values were as follows: transverse (0.283 ± 0.014 µm); longitudinal (0.287 ± 0.016 µm); and isotropic (0.286 ± 0.005 µm). Optical profiles and surface roughness parameters of the different surfaces are shown in the Results section.

2.3 Surface Acquisition and Analysis

A Zygo NewView 7300 3D optical surface profilometer (Zygo Corporation) was employed for acquisition of surface roughness data. Measurements were conducted on two scales: 10 × with 0.5 × FoV and 50 × with 0.5 × FoV. The surface relocation routine developed by the authors in Ref. [22] was employed to obtain roughness data at the same surface area before and after tribological testing. The overall relocation procedure, which comprised the use of MATLAB R2019b (MathWorks) and MountainMaps Premium 7.4 (Digital Surf), was as follows:

• 1. Acquire topographical data of the run-track area before and after test, and implement proper post-processing steps (remove ball form by second degree polynomial, retrieve roughness profile by 0.5 mm robust Gaussian filter).

• 2. Relocate the relevant surface area and correct for lateral and rotational misalignments.

• 3. Correct for biased height scale by minimizing the distance between the unworn areas on either side of the wear track.

• 4. Extract the Hertzian area (worn area) and calculate parameters for surface roughness representation at exactly the same location before and after test.

In addition, surfaces were also evaluated for average representation of surface roughness around the ball and disc run-tracks. For this purpose, the balls were measured circumferentially at 32 evenly distributed areas in the immediate vicinity of the run-tracks before the test and within the run-tracks after the test. For the same purpose, the disc was measured before the test at 3 × 8 radial and circumferential positions, for a total of 24 measurement points. After the test, run-tracks were measured at 8 circumferential disc positions. With the exception of the relocation analysis, the surfaces were post-processed, and roughness parameters were calculated in accordance with the above procedure. Note that for the significantly smoother disc, a 0.08 mm cut-off was employed in the filtering process to preserve the roughness profile after running-in (omit potential run-track shoulders). Changing the cut-off from 0.5 to 0.08 mm made 1 nm difference on the disc pre-test Sq and 9 nm on the transversal case post-test Sq. Hence, insignificant for the ‘single-sided’ EHL contact assumption in the ${\Lambda }^{*}$ analysis (Sect. 4.2).

Regarding the calculation of asperity radii, both motif analysis using MountainMaps and the conventional approach, using the 3-point criterion in MATLAB, was employed to estimate the representative average asperity radii. The analysis of motifs is based on a watercourse/watershed segmentation algorithm that divides the main surface structure into its dominant peaks (or valleys); see elsewhere for details [54, 55]. For this purpose, a 3 by 3 smoothing filter was employed to avoid detection of local peaks other than the core structure, and motifs were merged depending on the following pruning criteria: {if height < 5 × $Sz$, and area < 0.001 mm²}. The former condition is specified in ISO 25178, and the latter was to control the segmentation algorithm from over-segmenting the surface with respect to its main structure (minimum width allowed for a ridge spanning across the Hertzian contact zone was 0.002 × 0.5 mm). Note that to facilitate comparison, a similar filter was used in the calculation of the asperity radii using the conventional approach; see Ref. [56] for more details. With this method, an asperity peak is defined as a point that is higher than its closest two neighbouring points. The peak radius is then calculated by fitting a circumcircle through each point defined as a peak. This computation was performed for all profiles in the x-direction followed by a computation of the average radii according to ${R}_{x,a}=\frac{1}{n}\sum_{i=1}^{n}{r}_{i}$, with ${r}_{i}$ being the asperity radii.

3 Results and Discussion

The theoretical foundation of the proposed film parameter is outlined first. This is followed by a discussion of how the model can be applied to real engineering surfaces. The approach is finally tested for validity against tribological ball-on-disc experiments conducted with real engineering surfaces comprising isotropic and anisotropic roughness structures.

3.1 Theoretical framework

Figure 1 depicts a schematic of a ball-on-disc EHL contact having an arbitrary single surface roughness feature located in the vicinity of the central film thickness zone (${h}_{c}$). For simplicity, we consider the idealised case where non-Newtonian effects, see, e.g., [53, 57], and oil film perturbations caused by sliding (complementarity effect, CE) are neglected. In this case, the ball tangential speed is considered to be equal to the disc speed, i.e., ${u}_{b}={u}_{d}$. When the asperity enters the contact inlet zone, a lubricant squeeze action allows for the formation of a local micro-EHL film as the asperity deforms with magnitude ${\delta }_{a}$. This phenomenon originates from the local pressure increase that causes the asperity to elastically deform to ${z}_{d}$ from its initial relaxed state (out-of-contact) height, ${z}_{0}$. The micro-EHL feature is considered to remain frozen in shape as it travels throughout the contact and when arriving at the outlet constriction (the minimum film thickness, ${h}_{m}$). Thus, within the given assumptions, oil film collapse may be expected to occur if the in-contact (deformed) height of the asperity, ${z}_{d}$, exceeds the available space at the contact outlet, ${h}_{m}$. The criterion for full-film EHL is $\Delta h>0$ (no contact interference), and the criterion for ML is $\Delta h\le 0$ (contact interference).

Fig. 1

Schematic depicting the theoretical framework of the proposed film parameter (not to scale)

Mathematically, the available space at the contact outlet zone can be expressed as:

$${h}_{m}=\Delta h+{z}_{d}$$

(6)

where the deformed asperity height is given from:

$${z}_{d}={z}_{0}-{\delta }_{a}$$

(7)

Substituting Eq. (7) into (6) and rearranging for the contact variable, $\Delta h$, we get:

$$\Delta h={h}_{m}-({z}_{0}-{\delta }_{a} )$$

(8)

Now, from Eq. (8), it is possible to derive a film parameter that resembles the form of the classical lambda ($\Lambda ={h}_{m}/Sq$), consider that:

$$\Delta h=({h}_{m}+{\delta }_{a})-{z}_{0}={h}^{*}-{z}_{0}$$

(9)

Accordingly, it may be realized that full separation (EHL) holds if ${h}^{*}-{z}_{0}>0$, while contact interference occurs if ${h}^{*}-{z}_{0}\le 0$. Thus, a new lambda parameter, ${\Lambda }^{*}$, that accounts for the minimum film thickness and the local micro-EHL film contribution can be defined accordingly:

$${\Lambda }^{*}=\frac{({h}_{m}+{\delta }_{a})}{{z}_{0}}=\frac{{h}^{*}}{{z}_{0}}$$

(10)

with the criteria for oil film breakdown or separation being $\left[1\left(ML\right)>{\Lambda }^{*}\ge 1\left(EHL\right)\right]$. Alternatively, the parameter can be expressed ${\Lambda }^{*}=\frac{{h}_{m}}{({z}_{0}-{\delta}_{a})}=\frac{{h}_{m}}{{z}_{d}}$. As we will see next, ${\delta }_{a}$ is a function of the asperity shape and provides local elasticity to prominent features that risk rupturing the fluid film. In this regard, it is important to emphasize that the limits for the ${\Lambda }^{*}$ lubrication regimes are based on both the geometrical entities of the roughness features and whether actual interference takes place, in contrast to $\Lambda$ in which the limits are more of an arbitrary safety factor in relation to the rigid body surface RMS level, typically 3 $\times$ Sq.

Having defined the expression for ${\Lambda }^{*}$ in Eq. (10), it now only remains to estimate ${h}_{m}$ and ${\delta }_{a}$. The macro-EHL thickness ${h}_{m}$ can be estimated by, for example, the classical D–H equation for circularly and smooth EHL contacts in accordance with standard practice; see Eq. (1) in the Sect. 2. To account for the micro-EHL effect on the surface roughness, there are two different possibilities. For instance, it is possible to correct ${z}_{0}$ for the ${z}_{d}$ using the ‘amplitude reduction theory’ (ART) [37] in the computation of the film quality, i.e., $\Lambda ={h}_{m}/{z}_{d}$. As shown by Morales-Espejel [15] in the context of relating $\Lambda$ to the viscosity ratio ($\kappa$) [58], ${z}_{d}$ may be substituted for the amplitude reduced form of the surface RMS, i.e., $R{q}_{d}$ (or $S{q}_{d}$ in 3D). Here, we propose a different and perhaps even simpler approach.

If the micro-EHL contact is considered to behave as a macro-EHL contact, it is in fact possible to compute ${\delta }_{a}$ from the classical EHL equations as well. Several researchers have made such postulations [48, 59], and others have demonstrated their feasibility through experimental work [49]. Particularly, in Refs. [42, 50, 51], Spikes et al. evaluated three EHL film thickness equations for isotropic (hemispherical bumps), transverse, and longitudinal ridges and found good agreement with optical interferometry measurements in ball-on-disc experiments. Based on their findings, from the ratio of the smooth ball central film thickness and an asperity, it is possible to derive a general expression for ${\delta }_{a}$ that accounts for any asperity geometry:

$$\frac{{\delta }_{a}}{{h}_{c}}={\left(\frac{{u}_{a}}{{u}_{b}}\right)}^{\rm X}{\left(\frac{{R}_{x,a}^{^{\prime}}}{{R}_{x,b}^{^{\prime}}}\right)}^{\alpha }{\left(\frac{{w}_{a}}{{w}_{b}}\right)}^{\beta }\times \kappa$$

(11)

Here, ${u}_{a}$ and ${u}_{b}$ are the entrainment speeds of the asperity (the micro-scale contact) and for the ball (macro-scale contact). ${R}_{x,a}^{^{\prime}}$ and ${R}_{x,b}^{^{\prime}}$ are the asperity and ball effective radii in the entrainment direction. ${w}_{a}$ and ${w}_{b}$ are the effective load acting on an asperity and the ball, and the exponents ${\rm X}$, $\alpha$ and $\beta$ depend on the central film thickness equation used. The variable $\kappa$, which also depends on the specific film thickness equation with ${\gamma }_{1}$, ${\gamma }_{2}$ and ${\gamma }_{3}$, is an ellipticity parameter that in general form can be expressed as:

$$\kappa =\frac{1-{{\gamma }_{1}\times e}^{-{\gamma }_{2}{[{R}_{y,a}^{^{\prime}}/{R}_{x,a}^{^{\prime}}]}^{{\gamma }_{3}} }}{1-{{\gamma }_{1}\times e}^{-{\gamma }_{2}{[{R}_{y,b}^{^{\prime}}/{R}_{x,b}^{^{\prime}}]}^{{\gamma }_{3}}}}$$

(12)

with the additional subscript y referring to the direction transverse to the lubricant entrainment. Note that for isotropic roughness features, $\kappa$ becomes unity. The input variables for Eqs. (11) and (12) are provided in Table 1. If the roughness feature is isotropic (hemispherical bump) or oriented with its principal radius of curvature transverse to lubricant entrainment direction (transversal ridge), then the variables are selected according to case A in Table 1. This is because the variables are based on the Dowson–Hamrock (D–H) central film thickness equation for elliptical contacts [10]; see Eq. (2) in the Sect. 2. Alternatively, in the case when the ridge principal radius of curvature is directed in the entrainment direction (longitudinal ridge), then the variables are selected according to case B in Table 1. In this case, the variables originate from the Dowson–Chittenden (D–C) equation for elliptical contacts [60], which in addition accounts for when the major axis of the Hertzian contact ellipse is directed in the direction of lubricant entrainment. As emphasized by Choo et al. [50, 51], the choice of the elliptical EHL equations is appropriate since both transversal and longitudinal ridges form “micro”-elliptical contacts with a smooth disc. This has been confirmed in several similar investigations, e.g., Refs. [41, 47, 61,62,63,64].

Table 1 Input variables for Eqs. (11) and (12)

Now, by setting the speed and load terms in Eq. (11) to unity (${u}_{a}={u}_{b}$, and the small $\beta$-exponent means that the load term only has a minor influence on film formation), and by substituting Eq. (12) in (11), it may be realized that the radius of curvature at the micro- and macro-scales contributes to the majority of micro-EHL film generation. Accordingly, we introduce a non-dimensional micro-EHL variable, ${f}_{q}$, based entirely on the radii:

$${f}_{q}=\frac{f\left(r\right)}{f\left(R\right)}={\left(\frac{{R}_{x,a}^{^{\prime}}}{{R}_{x,b}^{^{\prime}}}\right)}^{\alpha }\times \frac{1-{{\gamma }_{1}\times e}^{-{\gamma }_{2}{[{R}_{y,a}^{^{\prime}}/{R}_{x,a}^{^{\prime}}]}^{{\gamma }_{3}} } }{1-{{\gamma }_{1}\times e}^{-{\gamma }_{2}{[{R}_{y,b}^{^{\prime}}/{R}_{x,b}^{^{\prime}}]}^{{\gamma }_{3}}}}$$

(13)

where $R$ refers to the macro-contact (ball) radius and $r$ refers to the radii of the roughness features. Thus, conveniently, the micro-EHD film thickness deformation is simply obtained by multiplying this parameter with Eq. (2):

$${\delta }_{a}={{h}_{c}\times f}_{q}$$

(14)

Although there exist different ways of estimating the load ratio, see, e.g., Ref. [65] for a fully deterministic approach and Ref. [66] (Chap. 4) for a Hertzian-based approach, it is worth emphasizing that setting the load term to unity is the most conservative approach in estimating the transition from EHL to ML with ${\Lambda }^{*}$. Hence, with the given assumptions, we have derived an expression that describes the micro-EHL film generation under isotropic and anisotropic roughness by a function that depends solely on the macro-EHL central film thickness and the ratio between the asperity and the ball radii. Finally, inserting Eq. (14) into (10), we obtain a new film parameter that accounts for the micro-EHL using only classical EHL theory.

$${\Lambda }^{*}=\frac{{h}_{m}+{{[h}_{c}\times f}_{q}]}{{z}_{0}}=\frac{{h}^{*}}{{z}_{0}}$$

(15)

For convenience, we have solved the micro-EHL film thickness term ${f}_{q}$ from $r=0$ to $r=R$, with the appropriate exponents in Table 1. Note that $R={R}_{x,b}^{^{\prime}}={R}_{y,b}^{^{\prime}}$ for the ball-disc configuration and that $r={R}_{x,a}^{^{\prime}}={R}_{y,a}^{^{\prime}}$ in the case of hemispherical roughness features. Additionally, under the approximation of infinitely long ridges directed in the transverse direction, then $r={R}_{x,a}^{^{\prime}}$ and ${R}_{y,a}^{^{\prime}}$ are taken as the ball radius, or inversely for longitudinal ridges. The result is presented in Fig. 2 in dimensionless form by $r/R$ on the x-axis. When $r$ tends to $R$, i.e., the smooth ball case, then ${f}_{q}$ tends to unity and ${\delta }_{a}$ tends to ${h}_{c}$. For smaller $r/R$, it can be seen that the asperity radius provides a reduced micro-EHL film in all three cases. The micro-EHL contribution is most pronounced for the case of transversally oriented ridges, followed by hemispherical bumps (isotropic) and longitudinally oriented ridges. The rankings are in agreement with experimental observations reported by, e.g., Kaneta [67], and with deterministic EHL computations made by, e.g., Zhu et al. [65].

Fig. 2

The micro-EHL film contribution, ${f}_{q}$, generated from the asperity radius of curvature of hemispherical bumps (isotropic), and infinitely long ridges oriented either transvers or longitudinal to the lubricant entrainment

Conveniently, if $r$ is known, then all additional computations required to solve ${\Lambda }^{*}$ involve using the classical EHL equations with Eq. (15). Thus, in combination with this chart, it is possible to estimate the state of lubrication for several of the most common roughness patterns in a quite straightforward manner. In general, this can be useful for anyone interested in estimating the adequacy of lubrication without having to solve the full deterministic EHL problem for rough surfaces. In the design of, e.g., transmission assemblies, where it is generally desired to minimize the lubricant viscosity for maximized efficiency, the model may be used to optimize the fluid film breakdown transition with regard to the surface roughness height, roughness lay and asperity sharpness. An example is given in Sect. 4.5.

3.2 Model Extension to Real Surface Roughness

Here, we attempt to extend the previously outlined theory to account for real engineering surfaces. It is appropriate to start by revising the possible parameter that will represent the out-of-contact height, ${z}_{0}$. Since at least the 1960s, tribologists have turned to $Rq$ (RMS) for surface roughness representation with regard to the adequacy of lubrication [68, 69]. However, as understood already in 1933 by Abbott and Firestone [70], wear will naturally not take place in the intermediate or valley portion of the roughness, but rather in the highest peaks. Accordingly, lowering of peaks reflect poorly on the surfaces RMS [22, 23, 26], thus making the Sq-parameter an inappropriate representation of surface roughness height level in general.

Additional deficiencies includes the fact that modelling the composite RMS level as an equivalent rough surface, $S{q}_{c}={\left(S{q}_{1}^{2}+S{q}_{2}^{2}\right)}^{1/2}$, is strictly valid only for statistically independent, random-process Gaussian surfaces with plastically deformed isotropic asperities [18]. This is problematic from an engineering perspective as it implies that the $S{q}_{c}$ is mathematically incorrect for many engineering surfaces and particularly those that have been subjected to running-in during service. In Ref. [18] it was suggested that the sum of the average maximum profile height ($R{z}_{\Sigma }=R{z}_{1}+{\mathrm{Rz}}_{2}$) is a more general and relevant roughness representation than the $S{q}_{c}$ in the computation of $\Lambda$. This is helpful as it directs us away from the Gaussian and isotropic constraints. However, it is questionable whether $Rz$ is a physically meaningful measure to represent the surface roughness peaks, at least with regards to ${\Lambda }^{*}$.

Furthermore, replacing $Rq$ with $Rz$ does not provide an increased sensitivity to wear, plastic deformations and EHD film formation. This we know by careful examination of surfaces before and after running-in using 3D surface relocation techniques developed in our recent research [22, 23]. For example, by re-considering the topographical data obtained in the running-in test termed ‘SRR-case’ in Ref. [23], we find that the $Sz$-parameter ($Rz$ in 3D) only reduced with 6%, while the $Sq$-parameter reduced by 15%. As these changes represent the required topographical changes to onset full-film EHL from an initial state of ML, a large value may be interpreted as a strong indicator for film formation, and vice versa. The insensitivity of the $Sz$-parameter is not surprising given that only the extremes of peaks and valleys are considered in its definition. We shall therefore direct our focus towards another peak parameter.

In Ref. [22] we have highlighted $Spk$ (3D representation of the ISO 13565-2-1996, $Rpk$) as a relevant and highly sensitive parameter for EHD film formation, see also Ch. 7–8 and 10 in Ref. [71] for an even more extensive discussion. Considering the $Spk$ of the same ‘SRR-case’ in Ref. [23], we find a substantial 45% reduction, hence clearly superior to both the $Sq$ and $Sz$ parameters for representation of surface roughness height level. Similar observations were made in Ref. [22]; a reduction in $Sq$ by 20% followed the reduction in $Spk$ by 56%. Moreover, as with the $Rz$-parameter, the $Spk$ is free of the constraints intrinsic for $Sq$. At the same time, it is robust against measurement noise which is in contrast to most extreme surface metrology parameters. Therefore, we shall reject the classical $S{q}_{c}$ as well as the $R{z}_{\Sigma }$, and instead we suggest the $Spk$-parameter derived from the material-area-ratio curve, see Fig. 3a for a schematic definition. The parameter is easy to obtain in any surface metrology software such as, e.g., MountainsMap.

Fig. 3

a Schematic representation of the material-ratio-curve, b graphical representation of the undeformed ball roughness at the EHL-ML transition, i.e., when $\Delta h={h}^{*}-Spk=0$, and c the corresponding representative micro-EHD roughness feature. Full-film micro-EHL occur when $\Delta h\ge 0$ as ${h}^{*}\ge Spk$ (${\Lambda }^{*}\ge 1$), and contact interference when $\Delta h<0$ as ${h}^{*}<Spk$ (${\Lambda }^{*}\ge 1$)

Mathematically, the $Spk$ level may be considered the representative height to the datum of contact interference (smooth disc) by substituting ${z}_{0}$ with $Spk$ in Eq. (9). Thus, and restating it for convince, we get:

$$\Delta h=({h}_{m}+{\delta }_{a})-Spk={h}^{*}-Spk$$

(16)

The micro-geometric representation of the $Spk$-parameter (undeformed roughness) is illustrated in Fig. 3b in relation to the micro-EHD film thickness, ${h}^{*}$, at the transition between EHL and ML. The $Spk$ is consider to represent the peak height of the undeformed surface roughness, see Fig. 3c where a representative $r$ accounts for the development of the micro-EHD film. The representative asperity radius is determined further below. With Eq. (16), we realize that the situation depicted in Fig. 3b and c occurs when $\Delta h=0$ so that ${h}^{*}=Spk$. Additionally, in Fig. 3c it is evident that an increase to either ${h}_{m}$ or ${\delta }_{a}$ yields full film EHL since $\Delta h\ge 0$. On the contrary, a decrease in either ${h}_{m}$ or ${\delta }_{a}$ causes fluid film breakdown since $\Delta h<0$. Clearly, the model seems physical meaningful, and $Spk$ appear to properly represent the height level of those asperities especially susceptible to form a micro-EHL film and possibly to wear in case the film ruptures.

Now, setting Eq. (16) to zero and multiplying with the inverse of $Spk$, the expression for ${h}^{*}$ is obtained. Thus, a general film parameter that accounts for any engineering roughness either with isotropic-/anisotropic-structure and Gaussian/non-Gaussian height distribution, and that account for the micro-EHL, may be expressed:

$${\Lambda }^{*}=\frac{({h}_{m}+{\delta }_{a})}{Spk}=\frac{{h}_{m}+{{[h}_{c}\times f}_{q}]}{Spk}$$

(17)

or more simply:

$${\Lambda }^{*}=\frac{{h}^{*}}{Spk}$$

(18)

As before, full film EHL occurs when ${\Lambda }^{*}\ge 1$, and ML and BL when ${\Lambda }^{*}<1$.

Furthermore, it can be seen in Fig. 3b that occasional peaks may still be in contact due to the way $Spk$ is defined. This is reasonable given that no abrupt transition exists for engineering roughness. The contact is expected to be predominated by rheological effects when ${\Lambda }^{*}\cong 1$, and accordingly, wear and plastic deformations are expected to be negligible by means of practical use. Note also that the schematics in Fig. 3 is illustrated for ‘single-sided-roughness’ for simplicity reasons. Including a ‘two-sided-roughness’ is not a problem. Following the work in Ref. [18], the composite surface peak representation may be obtained by simple summation, i.e., $Spk=Sp{k}_{1}+Sp{k}_{2}$.

Moreover, to compute Eqs. (17) or (18) for an arbitrary engineering surface topography, a representative $R^{\prime}_{{{x \mathord{\left/ {\vphantom {x {y,a}}} \right. \kern-\nulldelimiterspace} {y,a}}}}$ must first be determined for a subsequent determination of ${f}_{q}$, Eq. (13). Several deterministic and statistical approaches exist for this purpose; see, e.g., the works by Kalin [56, 72]. Another and perhaps simpler approach is to fit an arc to a representative asperity by measuring its representative height, ${z}_{a}$, and its corresponding width, along either principal axis x or y, i.e., ${b}_{x/y,a}$. The corresponding radii can then be calculated using trigonometry:

$${R}_{x/y,a}=\frac{{b}_{x/y,a}^{2}}{8{z}_{a}}$$

(19)

By combining Eq. (19) with motif analysis (ISO 25178), we suggest that a more robust ${R}_{x/y,a}$ can be computed in a deterministic manner by making use of the full roughness data set. With this method, the surface is segmented into significant peaks (its core structure), and each peak radius is computed according to Eq. (19) followed by an averaging for a representative ${R}_{x/y,a}$ of the entire surface. More details are provided in the Sect. 2. The proposed method is straightforward using any surface metrology software such as MountainsMap.

3.3 Tribological Tests and Estimation of the Asperity Radii

Tribological tests using a ball-on-disc machine were conducted to evaluate the feasibility of the model applied to real engineering surfaces. The aim of the tests was to obtain details about the topographical changes that are required to onset full-film EHL from an initial state of ML. Subsequently, the representative asperity radii and $Spk$ levels associated with each corresponding lubrication mode were determined. With such knowledge, it is then be possible to validate the proposed film parameter, ${\Lambda }^{*}$, with respect to EHL contacts typically found in various machinery.

Three different high-precision ball specimens were prepared with respect to geometry, roughness and texture (GRT) for the above reasons. The ball surfaces comprised structures having dominant isotropic, longitudinal, and transversal lay, while the mean surface roughness RMS height, Sq, was 0.285 $\pm$ 0.013 µm. The disc surface was prepared mirror smooth with a mean RMS level of 0.003 ± 0.000 µm. These surfaces were operated through a fixed operating conditions running-in sequence until reaching full EHL recovery, similar to the one presented in Refs. [22, 23]; see the Sect. 2 for more details.

3D optical profiles acquired in the same area before and after the test are shown in Fig. 4. Note that the direction of lubricant entrainment is directed upwards in all 3D images (x-axis, see the bottom right Pre-profile in Fig. 4a for the coordinate system). Visual inspection indicates a distinct wear scar, especially in the transverse case, and the roughness features have become blunted. Comparing the pre- and post-test amplitude spectra in all three cases, which refers to the Hertzian contact zone (area of evaluation), it is evident that prominent peaks are greatly reduced with running-in. This is expected since the removal of peaks and increased radii are a widely established outcome associated with the running-in process; see, e.g., [27,28,29,30,31]. Note that all three post-test surfaces had reached an apparent quasi-static steady state, with operation in the full-film micro-EHL regime. Thus, under the given operating conditions, no further (or at least extremely mild) wear was possible. Accordingly, the $Spk$ and ${R}_{x/y,a}$ associated with the ML and full-film EHL regimes can now be determined in accordance with the previous discussion.

Fig. 4

Optical profiler plots showing the same surface areas before and after running-in tests under 10 × objective and 0.5 × FoV: a transversal surface structure with respect to the lubricant entrainment, b longitudinal, and c isotropic. Amplitude distributions are computed within the run-track area (area of evaluation)

From motif analysis, an average ridge width and height were obtained for the transversal pre- and post-test cases according to ${b}_{x,a}=\{0.017, 0.022\}$ mm and ${z}_{a}=\{0.24, 0.17\}$ µm. A verification is made in two steps, first visually and then using a more conventional numerical method. For visual verification, we compare the computed width to a ridge representative for the overall wear track in Fig. 5c; see the 2D profiles and two length scales at mark III. Note that Fig. 5 shows the area labelled I in Fig. 4a under higher resolution (50 × objective with 0.5 × FoV). The pre- and post-test length scales represent the corresponding representative ridges quite well. Note that local maxima, as those two observed in the pre-test 2D profile at III, are merged to render the main surface structure composed of significant ridges. In this regard, the motif analysis provides an average effect on the computed representative ridge radii, and consequently, the overall EHL film generation is associated with the main structure of the surface topography. This is a reasonable approximation given that asperity deformations subside with reduced wavelength [37]. The smallest scale roughness is still accounted for in ${\Lambda }^{*}$ through the $Spk$ parameter.

Fig. 5

High-resolution (50 × and 0.5 × FoV) optical profiler plots showing the transverse case surface area before and after the running-in test: a enlarged area I in Fig. 4, b enlarged area II, and c the x-direction (vertical) 2D profiles of area II, showing deformation of the asperities due to running-in

With the above plausibility check, it is deemed appropriate to substitute the pertinent parameters into Eq. (19) for the second verification step. The corresponding pre- and post-test radii are then $R^{\prime}_{{x,a}} = \left\{ {0.15,0.35} \right\}$ mm. Note that the asperity radii in the y-direction are comparably large and can hence be assumed to be equal to the radius of the ball for convenience, i.e., $R^{\prime}_{{x,a}} = R^{\prime}_{b}$. It can be shown that this makes less than 2 nm on ${\delta }_{a}$.

To further consider the validity of the motif approach, we also computed the asperity radii using a more conventional method [56] (3-point criterion); see Materials and Methods for details. A histogram of the radii retrieved from this procedure is presented in Fig. 6, and the corresponding average pre- and post-test radii are $R^{\prime}_{{x,a}} = \left\{ {0.12,0.65} \right\}$ mm. The pre-test radii agree quite well, while the post-test radii from the 3-point criterion yield distinctly larger average radii, thus suggesting even more hydrodynamic lift. Some variations are, however, expected using different methods [72], and the relatively small deviation between the radius from the motif analysis and 3-point criterion is encouraging and confirms that the method based on motif analysis yields reasonable results.

Fig. 6

Pre- and post-test asperity radii distributions in the transversal case obtained from the conventional method. Sharp radii are replaced with rounder radii due to running-in, which causes increased micro-EHL generation

Repeating the motif analysis method for the longitudinal cases, the following radii are obtained: $R^{\prime}_{{y,a}} = \left\{ {0.19,0.34} \right\}$ mm, which can be compared to those from the 3-point criterion $\{0.14, 0.42\}$ mm. As anticipated, given that the longitudinal structure is distinct with rather consistent wavelengths spanning across the contact, the radii obtained from each method are quite similar. Additionally, a good approximation that follows is to assume infinite-length ridges in the x-direction, and thus, $R^{\prime}_{{x,a}}$ can be taken as $R^{\prime}_{b}$ in the computation of ${\delta }_{a}$. In the isotropic case, the radii obtained from motif analysis are $R^{\prime}_{{x,a}} = \left\{ {0.27,0.49} \right\}$ mm, and those from the 3-point criterion are $\{0.15, 0.50\}$ mm. Hence, these values are in seemingly good agreement. For self-evident reasons, it is appropriate to assume $R^{\prime}_{{x,a}} = R^{\prime}_{{y,a}}$ in the computation of ${\delta }_{a}$.

3.4 Experimental Validation

Having determined the pertinent roughness parameters that correspond to mixed and full-film operation for isotropic and anisotropic surfaces, it is now possible to test the hypothesis of whether an improved film parameter is indeed feasible within the given assumptions.

The results obtained from the above analysis are summarized in Table 2 and Fig. 7. The dimensionless radii, $r/R$, obtained according to the motif method outlined in the previous section, are used to determine the micro-EHL film parameter, ${f}_{q}$, either through Eq. (13) or directly using the chart presented in Fig. 2. The representative inlet induced micro-EHD deformation, ${\delta }_{a}$, for each particular surface is then computed by simply multiplying with the central film thickness (${h}_{c}=0.245$ µm). The proposed film parameter, ${\Lambda }^{*}$, is finally computed through Eq. (17), with the use of ${\delta }_{a}$, the $Spk$ values retrieved from the rough ball pre- and post-test surface areas, and the minimum film thickness (${h}_{m}=0.142$ µm).

Table 2 Summarized results obtained from the proposed model in combination with the ball-on-disc test

Fig. 7

Bar diagram showing the percent of full-film EHL calculated for the ${\Lambda }^{*}$ and $\Lambda$ each respective limits (1 and 3) before and after the test, and for each respective surface. The EHL-ML occurs at 100%, hence any value less than 100% implies contact interference and any value above indicates full-film EHL. Note that Pct. contact interference = 100% − Pct. of full-film EHL

Additionally, to justify our claim that the contact operates under full-film EHL at the end of the tests and to ensure that the calculated values indeed are valid, we monitored the mean electrical contact resistance (ECR) signal over the entire test sequences. These values are presented in the next-to-last column to the right of Table 2. A signal value close to 0% indicates the manifestation of direct metal–metal contact, i.e., frequent ruptures of the lubricant film causing wear and plastic deformation at prominent asperity sites. In contrast, a signal value close to 100% indicates that the contact has attained surface lift-off and thus that contact distress is significantly mitigated by the formation of a virtually fully developed EHL film. In fact, we have seen in our previous research [22] that a signal value > 20% indicates a predominance of EHL effects, with wear too mild to be distinguished using the present surface roughness acquisition routine. The electrical current passing through the contact under such ECR values is most likely due to occasional and rather insignificant surface interferences. Thus, as seen from the table, all the pre-test surfaces can be considered to operate under contact interference, while all the post-test surfaces are considered to have attained full-film EHL. Note that we have chosen to classify the contact state as ML here based on the mild wear and plastic deformations observed in Fig. 4. In a future study it may be appropriate to define meaningful limits that discriminates between the ML and BL regimes.

Now, let us consider the proposed film parameter, ${\Lambda }^{*}$, in Table 2. From this column, it can be seen that the true state of lubrication is very well represented in terms of both ML $\{0.6, 0.8, 0.7\}$ and EHL $\{0.97, 1.1, 1.0\}$ with regards to the transversal, longitudinal and isotropic surfaces, respectively. Recall that the transition between ML and EHL occurs when ${\Lambda }^{*}\cong 1$, in contrast to the classical $\Lambda$, for which the corresponding limit is typically 3. The outcome of the proposed model is in fact quite astonishing, especially when compared to the classical $\Lambda$ that shows a gross mismatch to EHL with $\Lambda =\{0.7, 0.6, 0.6\}$. Furthermore, as anticipated, comparison of the ${\delta }_{a}$ values of $\{48, 29, 45\}$ nm before the test demonstrates that the transversal structure yields more micro-EHL contribution than the longitudinal and isotropic structures. Although, it is also evident in the pre-test ${\Lambda }^{*}$ that more contact interference occurs due to the higher $Spk$ values $\{0.31, 0.21, 0.27\}$ µm. Interestingly, when considering the corresponding post-test ${\delta }_{a}$ values of $\{72, 41, 60\}$ nm, and in particular the percent increases of $\{49, 44, 33\}$ %, it is apparent that all structures improve their micro-EHL film-forming capability with running-in, especially in the transversal case.

To further illustrate the differences in performance between the classical $\Lambda$ and the proposed ${\Lambda }^{*}$, consider Fig. 7. This chart displays both parameters deviation from the EHL-ML transition occurring at 100 percent of full-film EHL, defined from each film parameters criterion for the EHL-ML transition (1 and 3). That is, the bars are calculated either as ‘Pct. of full-film EHL’ $= ({\Lambda }^{*} - 1)/1 \times 100$ or $(\Lambda - 3)/3\times 100$. Note that the corresponding measure for ‘Pct. contact interference’ = 100% − ‘Pct. of full-film EHL’. The red bars are calculated from the pre-test surfaces of Table 2 (col. ${\Lambda }^{*}$ and $\Lambda$) and the blue bars are calculated from the corresponding post-test data.

From Fig. 7, it is clear that the classical $\Lambda$ overall indicates much less EHL than the ${\Lambda }^{*}$, evidently due to lack of any micro-EHD contribution, and possibly due to its vaguely defined criterion for full-film EHL (Sq × 3). Each of the pre-test $\Lambda$’s (red bars) indicate less than 20% full-film EHL before test (or equivalently around 80% contact interference), hence, considerable operation in the BL regime. In contrast, the pre-test ${\Lambda }^{*}$’s indicate a much less adverse lubrication quality, with 60, 80 and 70% of full-film EHL (or 40, 20 and 30% contact interference). This seems more realistic considering the mild topographical changes observed in the optical profiles (Fig. 4). Furthermore, the deficiency of $\Lambda$-ratio is made very clear when considering its marginal improvement in lubrication quality after testing; still approximately 80% contact interference in all cases. This is in vast contrast to the corresponding ${\Lambda }^{*}$ values, which properly tend towards or beyond the true EHL regime occurring at $\ge$ 100%. Only a marginal discrepancy is seen for the transversal case with ~ 3% contact interference (97% full-film EHL). Such a minor error is, however, fairly reasonable given that the wear rate asymptotically tend towards zero at the end of the running-in tests (see, e.g., the s-shaped ECR curves in Refs. [22, 23]).

It is clear that the significantly improved lubrication quality indicated by the ${\Lambda }^{*}$ values with running-in originates from the increased asperity radii. In fact, from the above analysis, it can be realized that as long as the local radii are large (or, equivalently, the wavelengths are long), the surface finish height might not necessarily have to be small, in agreement with the hypotheses of Jacobson [59], for instance. This will be further discussed in the following section.

3.5 Application in Surface Design & Prospects

In large scale manufacturing of tribological surfaces such as gear flanks, there is generally a trade-off between costs and the lubrication quality attained in service. For instance, it is not desirable to design a tribological system too far into the EHL-regime by increasing the lubricant viscosity or by lowering the $Spk$ excessivly. The former, as the viscosity determines the churning and pumping losses in e.g. a gear transmission [73], and the latter since a low $Spk$ generally requires more preparations steps that risk to adversely affect the manufacturing economy. Using the ${\Lambda }^{*}$ it is possible to specify engineering surfaces to promote the transition to full-film EHL in ways not possible with the classical $\Lambda$, particularly, by considering the asperity radii and roughness structure.

Figure 8 demonstrates an example of how the model can be utilized in the design of tribological surfaces intended to achieve EHL performance. Using the same assumptions leading to Fig. 7, we computed the EHL-ML transition for the tree surfaces having transversal, isotropic and longitudinal roughness lay as a function of dimensionless radii and $Spk$. Figure 8a shows the transversal case interference line (red solid line) in three-dimensional space, defined from ${\Lambda }^{*}$. Figure 8b displays the same red solid line but as seen from above, together with the corresponding transition lines obtained from when considering the isotropic and longitudinal surfaces. Note that any point above the EHL-ML transition lines represent contact interference, and any point below represent full-film EHL.

Fig. 8

Engineering design example. Panel a shows ${\Lambda }^{*}$ as a function of dimensionless radii and $Spk$ for surface roughness with a transversal roughness lay (${h}_{m}=0.142$ µm, and ${h}_{c}=0.245$ µm). Panel b shows the EHL/ML transitions for surface roughness with transversal, isotropic and longitudinal roughness lay

Using the geometrical chart of Fig. 8b, it is possible to optimize the EHL-ML transition by controlling merely the $Spk$, asperity radii and roughness lay under the given operating conditions. As an example, consider the transversal case post-test $Spk$ and radius, which are 0.22 µm and 3.5% of the macro-scale radius; see the red dot (Post). Evidently, a predominance in EHL effects applies. However, choosing any of the other structures with equal roughness configurations will cause oil film breakdown. In fact, an asperity radius of either 8.5 or 9.5% of the macro-scale radius is required to generate equal lubrication quality as that of the transversal case; see the IV mark. Any sharper peaks would risk film rupture and consequently impair operation by increased wear and friction.

Thus, clearly, selecting a transversal roughness over an isotropic, and especially a longitudinal, improves an EHL contacts film-forming ability. However, a word of caution; note here that this does not imply that a transversal surface roughness performs better in service than, e.g., a longitudinal. Rather the contrary in fact, the lifespan is most likely considerably shortened with the many more micro-EHL-induced cyclic stresses [7] that arise with the roughness lay oriented transverse to the direction of entrainment, as opposed to that in parallel [74]. The proposed film parameter do not consider the risk of rolling contact fatigue at this stage, and we consider solely the formation of the fluid film in the definition of lubrication quality in this research.

Furthermore, it is of substantial importance to keep the lubrication quality outside of the ML regime with regard to the coefficient of friction (CoF). This may be comprehended by considering the dashed line that represents the drift of the post-test transversal case validation point from that of the pre-test. Because the traction forces over the course of the tribological test have been measured, it is known that the difference in CoF between these two points is approximately 26% (average CoF: 0.064 vs 0.044). Such a significant figure is substantial with respect to contact efficiency, even for a single tribological contact.

From a global perspective, and given that there are more than 10⁹ cars and heavy vehicles in use world-wide [9], the implications of the proposed design scheme are in fact enormous. Holmberg and Erdemir [9] estimated that approximately 20% (103 EJ) of the world’s total annual energy consumption can be attributed to overcoming the friction of tribological contacts. If only a fraction of that could be reduced by tuning the tribological interface in this or similar ways, vast environmental and economic cost savings may be expected.

3.6 Model Assumptions & Limitations

Finally, it is appropriate to discuss some of the simplifications and assumptions being made in the above research.

First, it should be noted that the inlet shear heating effect due to sliding has been neglected in all film thickness computations. This is because the thermal development is marginal under the low-speed conditions used; approximately 4% is estimated using the thermal correction factor given by Gupta [75] and modified by Hili [76] for PAO. However, in technical applications where the EHL/ML transition may occur at higher speeds [26], the inlet heating effect may be significant, and it may be advisable to impose this as an additional safety factor in the criterion for safe operation.

Furthermore, when the smooth surface is moving faster than the rough, film collapse may be expected to occur at the film thickness associated to the CE, rather than at the asperity itself. Recall that the CE travels with the ${u}_{e}$ whilst the RD travels with the ${u}_{b}$ (in this research). Thus, for SRR configuration considered, it is more relevant to consider the film thickness under the CE than that under the RD with respect to film collapse at ${h}_{m}$. However, as the central D–H equation is calculated with the prevailing properties at the contact inlet (sliding is merely a correction), it seems reasonable to associate the ${\delta }_{a}$ to the CE at both SRR = 0 as well as when the SRR = 1 that was the case in the running-in tests. As an example which may serve to clarify this, compare in Ref. [77] the SRR = 0 case with the $\left|\mathrm{SRR}\right|=1$ (disc faster) case the moment the CE is located in the centre of the contact; i.e., Fig. 6 at ${X}_{R}=0$ to Fig. 12 at ${X}_{R}=-1$. Note that for SRR = 0 case, the CE and RD are at the same position as ${u}_{b}={u}_{e}$. Hence, from those simulation results, it is evident that the film thicknesses associated to the RD/CE in pure-rolling is much alike the film thickness associated to the CE in rolling-sliding. Note, however, that any CE decay due to non-Newtonian effects [44, 78] was not accounted for in this research. Neither was the CE wavelength prolongation, i.e., ${\lambda }_{ce}={\lambda }_{x}\times {u}_{e}/{u}_{b}$, which occurs due to the fact the roughness feature is located for a longer time at the EHL inlet zone.

The disc roughness has been assumed to be smooth, both before and after the test in the computation of ${\Lambda }^{*}$. This is justified by the fact that the disc was influenced by very mild wear after running-in. More specifically, the disc roughness increased on average by less than 20 nm after running-in, and consequently, the classical lambda was only influenced by the third significant digit. In a future study, it would be relevant to incorporate a rough disc to examine the feasibility of the model in double-sided rough EHL contacts.

We proposed the motif analysis for the determination of the representative asperity radius as it may be more straightforward than existing numerical approaches (3-point criteria e.g.). If the results shown in Table 2 had been computed with the radius from the 3-point criterion, then all pre-test surfaces would yield somewhat more interference, while all post-test surfaces would yield somewhat more EHL. The overall conclusions would, however, be similar. Additionally, it should be noted that the condition for the ML and FF-EHL transition always occurs at ${\Lambda }^{*}=1$, regardless of the variable taken for ${z}_{0}$ (Spk) in Eq. (17), and the method for determining the asperity radius and the ${f}_{q}$ in Eq. (13).

Finally, and importantly, the proposed ${\Lambda }^{*}$ -model is a measure of the fluid film separation, but not a measure of the fatigue performance. For this, a life-rating model as e.g. that proposed by Gabelli [58] and extended by Morales-Espejel [15] could be employed. This seems like a relevant future step in the development of the ${\Lambda }^{*}$.

4 Concluding Remarks

A new film parameter, ${\Lambda }^{*}={(h}_{m}+{\delta }_{a})/{z}_{0}$, used for estimating the lubrication quality in isotropic and anisotropic patterned and rough elasto-hydrodynamic lubricated (EHL) contacts is proposed. The parameter account for the micro-EHL contribution induced by surface irregularities using classical EHL theory. The model is physically meaningful in the sense that the condition for film collapse is derived upon the basis of whether actual contact interference occurs, in contrast to the classical $\Lambda$ parameter, which is compared to an arbitrary multiple of the surface RMS level. Accordingly, it is proposed that the criterion for safe operation and full-film EHL applies above unity, i.e., ${\Lambda }^{*}\ge 1$, while partial or mixed lubrication (ML) applies when ${\Lambda }^{*}<1$.

Furthermore, the film parameter was tested against ball-on-disc running-in experiments in which the ball surface consisted of real engineering surfaces of either transversal, longitudinal, or isotropic structured roughness lay, and with the opposing surface mirror smooth. The electrical contact resistance (ECR) signal was monitored to determine the true ML and EHL regimes, of which the latter materializes as a result of a running-in. Consequently, this enabled experimental validation of the model.

In all cases, we have found ${\Lambda }^{*}$ to predict the mode of lubrication with surprisingly satisfactory precision. When the ball-disc contact was operated under ML conditions, the new film parameter predicted a 60–80% EHL contribution, and when the contact was operated in full-film EHL, it was found that the parameter accurately predicted a 100% EHL contribution. This was in wide contrast to the classical lambda parameter, which only showed a marginal difference before and after the test and hence incorrectly indicates substantial contact interference even under full-film EHL (~ 20% EHL effect).

In closing, by leveraging some pioneering works in EHL research, we have managed to bring together a simplified theory that accounts for film formation at both the micro- and macro-scales for use in an easily accessible manner. With the proposed film parameter, it is possible for engineers to optimize the oil film in rotating machinery for minimized friction and wear and maximized service life. For instance, if the roughness is properly specified, it is possible to promote the transition to full-film EHL. The prospects for environmental and economic gains are substantial given the vast amount of tribological contacts operating worldwide. Finally, it is our belief that the proposed film parameter is a major step towards substituting the existing one that has been used almost routinely in tribological research since being introduced some 55 years ago.