1 Introduction

Pin-on-disc (PoD) tribological tests are commonly used to investigate the wear behaviour of materials in contact with a sliding motion. The approach is particularly suited to study the relationships existing among wear mechanisms and such parameters like contact pressure, sliding velocity, environmental conditions [1, 2]. Several studies report on the PoD results, concerning investigations on materials for vehicular brake systems for different transportation fields, like road vehicles [3,4,5,6,7] and trains [8, 9]. As automotive brakes are concerned, pads are made of friction materials, comprising a large number of organic and inorganic components, pressed against a rotating disc, typically made of pearlitic cast iron [10]. Dynamometer and road tests are mandatory to obtain design-oriented information and for product certification. However, plain PoD testing is very useful to obtain focused information on the wear mechanisms and on their role on the tribological behaviour of real systems [6, 7, 11,12,13,14]. Moreover, considering the complexity of the formulation of friction materials for brake pads, it is paramount to have a reliable selection tool for the development of novel compositions [10, 15].

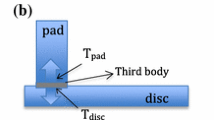
As it is well known, the tribological response of friction materials sliding against cast iron is mainly determined by the characteristics of the friction layer and of its components, i.e., the so-called primary and secondary plateaus [16, 17]. Metallic fibres and hard particles typically act as primary plateaus against which the wear fragments accumulate to form the secondary plateaus. Therefore, wear fragments originate either from a direct wearing out of the friction material and tribo-oxidation of the counterface cast iron or from the damage of the friction layer that forms in between the two mating surfaces [7, 12, 18, 19]. The compactness of the secondary plateaus present in the friction layer is strongly determined by the pin–disc contact temperature during sliding [6, 7, 12, 17, 20]. As shown by Stott and coworkers [21, 22], wear debris may sinter together to form compact and dense layers under the effect of the high local compressive pressures. Of course, the compactness of the secondary plateaus increases with temperature. Therefore, an evaluation of the contact temperature is paramount to understand and to explain the main wear mechanisms [5, 7, 20]. In this regard, it has to be noticed that the local temperature at the friction plateaus, where sliding is really confined, is higher than the average surface contact temperature (or “bulk” temperature according to the nomenclature proposed by Ashby et al. [23]). This parameter is not easy to handle, since it is very difficult to know the actual thermal properties of the friction layers, given its different composition with respect to the base friction material [12, 24,25,26], and its possible fluctuations during the tribological test. The extension of the contact plateaus is also difficult to evaluate a priori as well as their thickness. Contact plateaus range in between 20 and 60% of the nominal area of contact [16, 17, 27]; their thickness ranges from some micrometres up to a few tens of micrometres [7, 8, 16, 17]. In view of these geometrical parameters, the average temperature at the contact plateaus should not be that much higher than the average bulk temperature, and certainly, proportional to it. Therefore, the estimation of the average surface temperature is an important step forward to infer the contact temperature, and, thereby, its role in the sliding wear mechanisms.

Different analytical models have been proposed to estimate the bulk temperature [23, 28,29,30,31,32,33]. A possible approach was proposed by Ashby and coworkers [23]. It is based on the assumption that frictional heat that develops at the pin–disc contact region is removed via heat conduction towards the pin as well as the disc. The surface contact temperature, Ts, can be then calculated from the following relationship:

$$q = \mu p v = q_{\text{Pin}} + q_{\text{Disc}} = k_{1} \frac{{T_{\text{s}} - T_{0} }}{{l_{1} }} + k_{2} \frac{{T_{\text{s}} - T_{0} }}{{l_{2} }}$$
(1)

where q is the frictional heat per unit area generated in the sliding contact, q Pin and q Disc are the portions of heat entering the pin and the disc, respectively, μ is the friction coefficient, p is the applied pressure, v is the sliding velocity, T 0 is the ambient temperature; k 1 and k 2, are the thermal conductivities of the pin and the disc materials, respectively; l 1 and l 2 are the lengths of the heat paths in the pin and in the disc. The assumption that heat is transferred in the disc by conduction only is rather questionable, since the heat flux entering the disc is mainly released by convection from the rotating disc surface [33]. With the approach proposed by Kennedy et al. [33], T s can be therefore evaluated using the following alternative relationship:

$$q = q_{\text{Pin}} + q_{\text{Disc}} = k_{1} \frac{{T_{\text{s}} - T_{0} }}{{l_{1} }} + h \frac{{T_{\text{s}} - T_{0} }}{{\left( {\frac{{r_{0} }}{R}} \right)^{2} }}$$
(2)

where h is the convection coefficient acting on the disc surface, R is the external radius of the rotating disc and r o is the pin radius. Another strategy for calculating T s involves the finite element (FE) modelling, a very powerful method in different fields, including thermal analysis [29, 33,34,35,36], computing capacity and time. A critical aspect in modelling is the selection of the correct contact configuration [30, 32]. In a previous investigation [34], it was demonstrated that the perfect contact model, assuming that the surface temperatures of the contacting bodies are the same, is to be preferred if compared with the other two models: the imperfect contact approach and separated bodies approach.

In the present investigation, PoD tests have been conducted using pins made of a commercial friction material, sliding against pearlitic cast iron discs, coated with a cermet layer, deposited with the HVOF technology [37,38,39,40]. The coatings were deposited to improve wear resistance of the discs, considering that they contribute by up to 50 wt% to the wear of a brake system. Incidentally, the reduction in the disc wear is functional to the reduction in the emissions of airborne wear particles from brake systems, an environmental issue that is becoming increasingly important [3, 4, 14, 41]. The aim of the present study is twofold. In the first place, we aim at modelling the real surface contact temperature in this sliding system with the FE method and the perfect contact approach, in order to understand the role of the disc coating on the contact temperature and consequently on the bulk temperatures achieved during sliding in the pin and the disc. Secondly, we aim at obtaining a simplified analytical equation by extending the Kennedy approach and therefore to get a relation able to provide a quick evaluation of the contact temperature for this kind of tribological couplings. The selected testing conditions are close to mild braking, which occurs when contact temperature is below approximately 200 °C and then no damage of the phenolic binder is observed. Of course, in order to use the obtained information for real applications, a better understanding of the correlations between PoD testing and real braking conditions is required.

2 Pin-on-Disc Testing

For the PoD tests, cylindrical pins with a diameter of 6 mm and a height of 10 mm were machined from a commercial low-steel friction material. In Table 1, the main ingredients of the friction material under study are listed. The hardness of the friction material was measured using a Shore D indentation test, and it was equal to 68. Each pin had a flat end contacting the rotating disc. The discs were 63 mm in diameter and 6 mm in thickness. Two different coatings were thermally sprayed, via high-velocity oxygen-fuel (HVOF) process, on the surface of a traditional pearlitic cast iron discs with a hardness of 235 HV10 and an average surface roughness of 2 µm. The first coating (codenamed: coating A) was made with a WC–CoCr powder containing 86 wt% of WC particles embedded into a Co 10 wt% Cr 4% metal matrix. The second coating was obtained from a Cr3C2–NiCr powder with 75 wt% of Cr3C2 in a 25 wt% NiCr matrix. Figure 1 shows a cross section of coating A. The coating thickness was 70 µm approx., with an average surface roughness in the range 3–3.5 µm, in the as-sprayed conditions. On the basis of a previous study [37], the surface roughness of the coating was reduced by mechanical polish, reaching an average roughness of about 1 µm. Further details of polishing procedure and the roughness optimization can be found in [37]. Each testing disc was inserted in a disc holder with a diameter of 140 mm and a height of 15 mm made of the same pearlitic grey cast iron of the uncoated specimen.

Table 1 Main components of the low-metallic friction material
Full size table
Fig. 1
figure 1

SEM micrograph of the A-coated disc cross section

Full size image

The sliding tests were carried out using an Eyre/Biceri PoD testing rig. The tests were carried out at room temperature (23 °C) and at a sliding speed of 1.57 m/s (corresponding to an angular velocity ω = 52.36 rad/s) for 50 min. The nominal contact pressure between pin and disc was equal to 1 MPa. A run-in step of 10 min in the same experimental conditions was performed before the actual test. This run-in stage was used in previous studies and was sufficient to establish a conformal contact between the pin and the disc [5, 6, 37]. The selected testing parameters aimed at producing mild wear conditions [6, 13, 37]. The wear of the friction material was calculated by measuring the weight loss using an analytical balance with a precision of 10−4 g. The wear data are an average of three repeated tests. The data recorded by the PoD apparatus were the friction coefficient and the pin temperatures. These temperatures were measured by using two K-type thermocouples (class 1) placed at 6.5 mm (T1) and 9.0 mm (T2) far apart from the disc surface. These data were used for the calibration of the FE model.

3 FE Modelling

The theoretical equation governing the heat flow between two contacting bodies is the Fourier’s law [42]:

$$\nabla \cdot \left( {k \nabla T} \right) + q_{v} = \rho c_{p} \frac{{{\text{d}}T}}{{{\text{d}}t}}$$
(3)

where q v is the specific heat generation, k is the thermal conductivity, T is the temperature, ρ is the density of the body in contact and c p is its specific heat.

The FE modelling was performed using the software Ansys v.16 and it was carried out for the entire duration of the tests (3000 s). The simulation is based on the perfect contact approach at the sliding pin–disc interface. A perfect contact was also assumed to exist at the disc and disc-holder interface. The contact between the pin and the pin-holder interface was modelled using a thermal contact conductance, TCC, which was calculated assuming an air gap of thickness × between the two surfaces:

$${\text{TCC}} = \frac{k}{x}$$
(4)

where k is the thermal conductivity of the air at 25 °C in W/m °C (which was set equal to 0.026 W/m °C [42]). On these bases, TCC at the interface between the base of the pin and the pin holder was set to 100 W/m2 °C, whereas the TCC on the lateral side of the pin was considered to be higher, in the range 160–230 W/m2 °C, since the pin diameters had a tolerance equal to ±0.1 mm that affected the pin pin-holder contact during the PoD tests.

After meshing, the model resulted in roughly 92,000 nodes and 32,000 elements. The solid model is based on the SOLID90 elements, while the contact is described by the TARGE174 and CONTA170 surface elements. As known from the literature [34, 36], the Fourier number (F 0) is used to determine the mesh quality.

$$F_{0} = \frac{a \Delta t}{{\Delta x^{2} }}$$
(5)

where a is the thermal diffusivity of the material, Δt is the time increment of the FE simulation and Δx is the element size along the direction of the heat flux. In the present study, the most critical point of the model was the pin made of a material with a very small thermal conductivity, as compared to cast iron’s. Therefore, the size of the pin elements was reduced to guarantee a proper description of the local temperature gradient. The Fourier number, calculated with Eq. (3), was equal to 0.074. According to the literature [36], the recommended F 0 in 3D heat analysis must be lower than 0.17. Therefore, the quality of the mesh was suitable to describe the thermal behaviour of the friction material. Figure 2 shows the element size and the structured mesh used for the FE simulation. The element size in the region of the pin–disc contact was selected of comparable dimensions to avoid computational and convergence problems. In Table 2, the materials properties used in the model are listed.

Fig. 2
figure 2

Mesh used for the FEM simulation

Full size image
Table 2 Materials properties of the different components [34]
Full size table

The thermal load was applied to the disc wear track in the form of a thermal flux, thus assuming that temperature is uniform along the wear track that forms on the disc [32,33,34,35]. The following relation was used:

$$q_{\text{Disc}}^{{}} \left( t \right) = \mu \left( t \right)\, p v \frac{{A_{\text{pin}} }}{{A_{\text{disc}} }}$$
(6)

where µ(t) is the experimental friction coefficient recorded as a function of time, t, p is the nominal contact pressure, v is the sliding speed, A disc is the nominal contact area of the disc and A pin is the nominal contact area of the pin [32,33,34,35].

Figure 3 depicts a schematic representation of the different boundary conditions (thermally insulated surfaces and heat convection coefficient) used in the FE simulation. The FE model was developed to describe the room temperature PoD test, as a consequence of that, the effects of the radiation were assumed to be negligible.

Fig. 3
figure 3

Schematic representation of the boundary conditions applied to the FE model

Full size image

The heat convection coefficients used in the present study were estimated from the literature. Kennedy et al. [33] proposed Eq. (7) to estimate the heat convection coefficient of a rotating disc:

$$h = 2.25 \sqrt \omega$$
(7)

where ω is the angular velocity of the rotating disc. When using Eq. (7), h was found to be 16.28 W/m2 °C. In other studies, regarding the same system, h was found to be higher, in the 50–70 W/m2 °C range [34, 35] and this was attributed to a larger air flux and turbulence created by the geometrical features of a PoD tribometer. In the present study, an intermediate value for the disc heat convection coefficient (h 1) was selected (see Table 3), following the model calibration with the experimental temperature curves. For the same reason discussed above, the heat convection coefficients of the pins were considered higher. With the aim of accounting for the actual air flux, three different values of convection coefficient were used for the pin holder (Table 3): with increasing the distance from the rotating disc, the relative air velocity and turbulence decrease leading to lower heat convection coefficient (see Table 3; Fig. 3 for the definitions).

Table 3 Convection coefficients applied to the different surfaces (see Fig. 3)
Full size table

The above-mentioned model was firstly used to describe the case of the uncoated disc, and then extended to the cases of the coated discs. A 70-µm-thick layer was applied on the upper and on the lower surface of the disc to simulate the coating. The properties of the coatings A and B are listed in Table 4. The previously given boundary conditions were left unchanged.

Table 4 Material properties of the two cermet coatings [literature]
Full size table

4 Results and Discussion

4.1 Friction and Wear Behaviour

As an example, Fig. 4 shows the evolution of the friction coefficient for the test with coating A. It can be seen that during the 50 min test, the steady-state conditions were not achieved. Similar trends were observed in the other two sliding couplings. Therefore, the experimental curves were fitted by means of a third-order polynomial function, and this equation was used in the FE modelling to reduce the experimental scatter in the friction coefficient. The equation is:

$$\mu = A t^{3} + B t^{2} + C t + D$$
(8)

and the experimental values for the constants A, B, C and D are listed in Table 5.

Fig. 4
figure 4

Experimental friction coefficient and its polynomial fit in the case of the coating A

Full size image
Table 5 Summary of the fitting parameters of the discs
Full size table

Table 6 summarizes the values of the average friction coefficients and of the wear data of friction material in the case of the uncoated and coated discs. The wear data listed in Table 6 are typical of a mild form of wear which, as known from the literature [1, 2], is the most common condition for the friction materials in real situations.

Table 6 Wear parameters of the friction material and average friction coefficients
Full size table

4.2 FE Modelling Validation

Figure 5 shows the comparison between the experimental curves of T2, acquired by the pin-on-disc apparatus, and the curves obtained with the FEM simulation.

Fig. 5
figure 5

Comparison of the experimental curves with the FEM-computed curves for a uncoated, b A-coated and c B-coated discs

Full size image

From Fig. 5 it can be noted that the maximum variation from the experimental data is lower than 1 °C. On these basis and additional results that we will present later, we may state that the FE model was properly calibrated and refined and can be then safely used to obtain additional information and predictions.

As an example, Fig. 6 depicts the results of the FE simulation on the uncoated disc at the end of the test. From the simulations, the evolution of the average surface contact temperature, T s, was obtained and the data are shown in Fig. 7. Because of the short test time (50 min.) and in agreement with the evolution of the friction coefficient, the T s values do not reach the thermal steady state, but show a continuously increasing trend. We were not able to measure the disc temperature during the tests, but we measured the disc temperature in the wear track as soon as the tests were stopped, and the experimental values were found to be very close to the values predicted by the FE analysis and displayed in Fig. 7a. For example, a temperature of 55 °C was measured in this way for the test with coating A. This is as a further confirmation of the validity of the adopted FE model.

Fig. 6
figure 6

Results of the FEM simulation in the case of the sliding contact with the grey cast iron disc

Full size image
Fig. 7
figure 7

a Disc track temperatures calculated with the FEM simulation; b determination of ΔT at the end of the tests for coating A, the uncoated disc and coating A with the consideration of an average friction coefficient of 0.47, i.e., typical of the uncoated disc

Full size image

4.3 FE Modelling Predictions

Figure 7 shows the different trend of the temperature curves among the materials under study. This difference correlates nicely with the friction coefficients that are attained during sliding (compare with the average friction coefficients listed in Table 6). However, the temperature rise, ∆T, in the contact region due to sliding is directly proportional to the friction coefficient and also inversely proportional to the thermal conductivities of the materials in contact [23, 33]. In order to understand the role of the friction coefficient and the thermal properties of the materials under investigation, we carried out a FE simulation considering coating A dry sliding against the friction material with a friction evolution equal to that displayed by the uncoated cast iron disc (i.e., with an average friction coefficient of 0.47). The results of the simulation show that ∆T at the end of the test is 27.0 °C. From Fig. 7, it is obtained that ∆T at the end of the test for the uncoated cast iron disc is 24.5 °C, and for coating A is 32.0 °C. This means that in passing from the uncoated cast iron to coating A, while maintaining the same friction coefficient (that of cast iron), ∆T increases by 10.2% due to the decrease in the thermal conductivity introduced by the coating. When maintaining the same coupling, i.e., the coating A against the friction material, and decreasing the friction coefficient, ∆T decreases by 15.6%. These simple calculations show that ∆T is mainly determined by the friction coefficient (being the contact pressure and the sliding velocity unchanged). However, also the coatings play a significant role, even if their thickness is low. This latter point can be explained by considering that the majority fraction of the frictional heat actually flows into the disc. Therefore, we can conclude that under the present conditions cermet coatings affect the temperature field in the sliding bodies by inducing different friction mechanisms at the sliding contacts and also, even if to a lesser extent, by modifying the local thermal properties.

Figure 8 shows the FE-predicted evolution of the pin temperature as a function of the distance from the contact region at the end of the tests. Near the sliding interface, the temperature gradient is linear. This is a further confirmation that close to the heat source the main dissipation mechanism is by unidirectional conduction. By moving far from the contact region, the effects of heat convection and also of the conduction in the pin holder become more important indeed, leading to a deviation from the linearity for the pin temperature profiles.

Fig. 8
figure 8

Trend of the pin temperature as a function of the distance from the contact at the end of the tests

Full size image

Figure 9 shows the predicted evolution with time of the disc temperature, right beneath the wear track. It can be clearly noted that at any time the temperature gradient along the disc cross section is very small. This fact can be explained by considering the high thermal conductivity of the grey cast iron substrate.

Fig. 9
figure 9

Temperatures along the disc profiles for different simulation times

Full size image

Figure 10 finally shows the evolution of the heat partition coefficient, γ, evaluated from the FE simulation results. It is defined as:

$$\gamma \left( t \right) = \frac{{Q_{\text{disc}} \left( t \right)}}{{Q_{\text{disc}} \left( t \right) + Q_{\text{pin}} \left( t \right)}}$$
(9)

where Q Disc is the heat power entering the disc (i.e., Q Disc = q Disc A disc) and Q Pin is the heat power entering the pin (Q Pin = q Pin A pin). It can be seen that the γ values are really close to unity, showing that the most part of the generated heat enters the disc, in agreement with different literature data [24, 25, 32, 34]. In addition, the γ values are very similar at the beginning of sliding and they slightly decrease with time. In order to explain the results, the γ values were estimated using a well-known relationship, reported in the literature [30, 32]:

$$\gamma = \frac{1}{{1 + \frac{{\sqrt {k_{\text{pin}} \rho_{\text{pin}} c_{{{\text{p}}_{\text{pin}} }} } A_{\text{pin}} }}{{\sqrt {k_{\text{disc}} \rho_{\text{disc}} c_{{{\text{p}}_{\text{disc}} }} } A_{\text{disc}} }}}}$$
(10)

where k, ρ and c are the thermal conductivities, densities and specific heats of the materials constituting the pin (in this case the subscript “pin” was used) and the disc (with the subscript “disc”), respectively. In case of the coated discs, the effective thermal conductivity was calculated by summing the thermal resistances of the coating and the cast iron, according to the approach proposed by Ashby et al. [23]. The calculation resulted in a value of the heat partition coefficient equal to 0.997 in all cases, in good agreement with the initial value of the heat partition coefficient calculated using the FE data. The slight decrease of γ with time can be explained through the increase in the disc temperature with time (see Fig. 9) and the corresponding reduction in the capacity of the disc to dissipate heat by conduction.

Fig. 10
figure 10

Partition coefficient calculated with the FEM simulation

Full size image

4.4 Proposal for an Analytical Relationship for the Contact Temperature Evolution

As seen in the introduction, Ashby [23] and Kennedy [33] proposed two different models for the analytical estimation of the surface temperature achieved during the PoD test. The Ashby’s approach, Eq. (1), considers conduction as the main dissipation mechanism. For the calculation of the thermal lengths, Ashby [23] proposed two relationships:

$$l_{1} = l_{\text{pin}} + \frac{{A_{\text{pin}} k_{1} }}{{\sum A_{\text{cont}} R_{\text{cont}} }}$$
(11)

where A cont are the nominal contact areas of the pin with the pin holder and R cont are the heat transfer coefficient of these areas (to a first approximation, l 1 can be set to the length of the pin), and:

$$l_{2} = \frac{{r_{0} }}{\sqrt \pi } \sqrt {\frac{{4 t a_{2} }}{{r_{0}^{2} }}}$$
(12)

where t is the transit time of the slider across the pin and is given by: \(\frac{{\pi r_{0} }}{2v }\), r 0 is the radius of the nominal contact area, a 2 is the thermal diffusivity of the disc and v is the sliding velocity. The final relationship for the calculation of the surface temperature is

$$T_{\text{s}} = \frac{\mu p v}{{\frac{{k_{1} }}{{l_{1} }} + \frac{{k_{2} }}{{l_{2} }}}} + T_{0}$$
(13)

The other approach, proposed by Kennedy et al. [33], considers conduction as the main dissipation mechanism for the pin, and convection as the main mechanism for the disc. The relationship for the calculation of the surface temperature is therefore:

$$T_{\text{s}} = \frac{\mu p v}{{\frac{{k_{1} }}{{l_{1} }} + \frac{h}{{\left( {\frac{{r_{0} }}{R }} \right)^{2} }}}} + T_{0}$$
(14)

The results of the calculations using Eqs. (13) and (14) are shown in Fig. 11 in the case of the uncoated disc. It is noted that the Ashby’s model strongly underestimates the disc surface temperature. This fact was already observed [43, 44] and can be attributed to the fact that the disc temperature continuously increases with time, i.e., each disc volume element in contact with the pin is not able to completely dissipate the heat (by conduction) between two subsequent passes. On the contrary, the Kennedy’s model overestimates the disc surface temperature. This can be explained by considering that steady state was not reached during the tests and part of the heat entering the disc is stored in the disc to rise its temperature. On the bases of the obtained results and of the present arguments, we propose the following equation:

$$Q\left( t \right) = \mu F_{N} v = k_{1} \frac{{(T_{\text{S}} - T_{0} )}}{{l_{1} }}A_{\text{pin}} + h \frac{{\left( {T_{\text{S}} - T_{0} } \right)}}{{\left( {\frac{{r_{0} }}{R}} \right)^{2} }}A_{\text{pin}} + m_{\text{disc}} c_{{{\text{p}}_{\text{disc}} }} \frac{{\left( {T_{\text{S}} - T_{0} } \right)}}{t}$$
(15)

where F N is the applied force and the third term of the equation accounts for the heat storage into the disc during sliding. It is of course an approximate approach that is, however, promising in view of the very small temperature gradients in the disc (Fig. 9). Therefore:

$$T_{\text{S}} \left( t \right) = \frac{Q\left( t \right)}{{\frac{{k_{1} }}{{l_{1} }}A_{\text{pin}} + h A_{\text{disc}}^{\text{tot}} + \frac{{m_{\text{disc}} c_{{{\text{p}}_{\text{disc}} }} }}{t}}} + T_{0}$$
(16)

where A totdisc is the total area of the upper surface of the disc. Figure 12 shows the comparison of the data obtained from the FE simulation and the temperatures calculated with the approach mentioned above, extended also to the coated discs. As can be seen, the modified approach gives results very close to the FE simulation. This approach could be interesting to estimate the average temperature rise of the wear track during a PoD test for both the uncoated and the coated discs when transient conditions represent an important part of the testing time. We can also observe that Eq. (16) depends on time, t, and this explains the time dependency of the partition coefficient γ, as shown in Fig. 10.

Fig. 11
figure 11

Disc surface temperatures calculated by using the different theoretical approaches and the FEM simulation in the case of the uncoated disc

Full size image
Fig. 12
figure 12

Comparison of the FE data and the modified Kennedy approach

Full size image

5 Conclusions

In the present study, the transient thermal analysis of a pin made with a friction material dry sliding against HVOF coated and uncoated pearlitic cast iron disc in a PoD apparatus was investigated by means of a FE analysis. In the modelling, we used the experimental evolution of the friction coefficient that was approximated using a polynomial equation of the third order. The main results could be summarized as follows:

  • A proper calibration of the boundary conditions and, in particular, of the heat convection coefficients is required to obtain a reliable FE model, in a close agreement with the experimental records of the pin temperatures evolutions;

  • In the conditions under study, the two HVOF cermet coatings affect the temperature field in the sliding bodies by inducing different friction mechanisms at the sliding contacts and also, even if to a lesser extent, by modifying the local thermal properties;

  • The heat partition coefficient is close to unity (i.e., most heat is dissipated by the disc), and it slightly decreases with time because of the rise of the disc temperature during sliding because of the reduction in the capacity of the disc to dissipate heat by conduction;

  • A simple analytical relationship for the evaluation of the average contact temperature was obtained by modifying the Kennedy’s approach based on the heat dissipation from the disc by convection. This equation could be used to quickly estimate the contact temperature rise during PoD testing without performing thermal measurements and FE simulations.