1 Introduction

More than 90 % of all rolling bearings are grease-lubricated. Lubricating greases ensure separation of the contacting surfaces through hydrodynamic action, where the lubricant is sheared in between the rolling element–raceway contacts [1]. During the initial operation of the bearing, macroscopic flow (churning) takes place, for a few hours up to about 24 h depending on the internal design of the bearing, operating conditions, percentage filling and rheological properties of the grease. During the churning phase, a fraction of grease will end up next to the running track and another fraction will find its way to other crucial locations inside the bearing, such as under the cage bars, from where the lubricant feed to the bearing contacts takes place, mostly by oil separation [2].

The complexity of the grease and the internal bearing geometry makes it difficult to study the mechanisms of grease lubrication in full rolling bearings. So the research on grease lubrication mechanisms has been mainly done using the ball on flat disk configurations [3–6]. The main drawback of this system is the large difference in time between successive over-rolling and the absence of the true feed and loss mechanisms caused by the difference in geometry and kinematics [2]. Despite these disadvantages, the ball on flat disk configuration can reproduce the contact pressures, temperatures, slide/roll ratios, etc. inside the bearing and most importantly, can be used for measuring film thickness using optical interferometry [3].

The single-point-contact configuration can be used for measuring the grease EHL films accurately down to a few nanometers under fully flooded and starved conditions. In the former, the grease film thickness is higher than expected based on base oil viscosity alone. The thicker lubricant film indicates the presence of thickener material entering the contact [3, 6, 7]. The film thickness can change rapidly due to changes in rheological flow properties caused by, for example, shear degradation of the thickener [8] or due to side flow induced by pressure and centrifugal force [1, 9]. In the absence of a suitable mechanism for track replenishment, the film thickness decreases with time below that estimated by classical EHL theory, which can be ascribed to starvation.

It has been shown earlier that an increase in oil viscosity and thickener concentration contributes to a larger film thickness under fully flooded conditions [10]. Cann assumed that this film thickness may consist of a part formed by elastohydrodynamic action and a part formed by residual layers formed by the thickener [11, 12]. Couronne et al. [4] studied the influence of grease rheology and thickener microstructure on the EHL film. They showed that greases with low elastic moduli were capable of forming thicker films in comparison with greases with higher elasticity. Nevertheless, in their study the thickener microstructure itself was found not to exert any significant influence on the formation of thick lubricant films. On the contrary, Kaneta et al. [6] emphasized the importance of the thickener structure on the film formation. They showed that the thickener microstructure is a dominating parameter influencing the film thickness under fully flooded conditions. Despite the fact that many papers are dedicated to the understanding of grease lubrication, there is still ambiguity on the factors influencing the lubricating ability under fully flooded conditions, which inspired this study. The goal of the present paper is to contribute to the understanding of grease lubrication by studying the effect of rheology, thickener particle geometry and thickener concentration on grease EHL films under fully flooded conditions by using commonly available rolling bearing greases varying the thickener–oil systems. The present paper excludes the ultra-low-speed domain on which recently several papers have been published [8, 13]. The lubrication mechanisms in the low-speed domain are likely to be different from those where hydrodynamic action prevails.

2 Materials and Methods

2.1 Tested Greases and Bled Oils

Six commercially available greases with the most common thickeners and base oils are studied and are designated with respect to their composition. The characteristics of the studied greases are summarized in Table 1. The bled oils were extracted from the greases by using Heraeus Biofuge 17RS centrifuge. The centrifugation was carried out by placing grease sample into a filter crucible with a mesh size of 10 µm. The oil separation test was performed at a temperature of approximately 37–40 °C at a centrifugal acceleration of 360 g.

Table 1 Characteristics of the greases studied
Full size table

2.2 Thickener Concentration Measurements

The thickener content in Table 1 was obtained by dissolving a measured quantity of grease in petroleum ether (PE 40/60) and forcing the dissolved grease to flow through a filter with a mesh size of 2 µm. Next, the filter with the thickener and solvent was subjected to 140 °C for 15 min, to evaporate the solvent. The thickener in the filter was then weighed, and thickener concentration could be obtained from the ratio of the mass of the thickener to that of grease. Measurements were repeated five times to check the repeatability, and the maximum error was found to be less than seven percentage of the weight measurement. The thickener composition in the grease can also be expressed in terms of volume fraction (Table 1), which was obtained by solving Eq. (1)

$$\varphi = \frac{\phi }{{\phi + (1 - \phi )\left( {\frac{{\rho_{g} - (1 - \varphi )\rho_{b} }}{{\rho_{b} \varphi }}} \right)}},$$
(1)

where \(\varphi\) is the volume fraction of the thickener, \(\phi\) is the mass fraction of the thickener, \(\rho_{g}\) is the density of grease (g/cm3), and \(\rho_{b}\) is the density of the base oil (g/cm3).

2.3 Fourier Transform Infrared Spectroscopy (FTIR) Measurements

Absorption spectra of the greases and corresponding bled oils were obtained with a Bruker FTIR TENSOR 27. The spectra have been achieved in a wavenumber range of 400–4000 cm−1 in the absorption mode.

2.4 Film Thickness Measurements

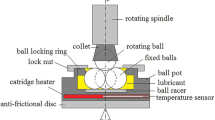
Film thickness measurements were taken under pure rolling conditions with a ball on flat disk test apparatus using optical interferometry (PCS Instruments Ltd), Fig. 1. For more information on the setup, the reader is referred to [12, 14, 15].

Fig. 1
figure 1

Schematic representation of film thickness measurement using optical interferometry

Full size image

The properties of the ball and test conditions are summarized in Table 2. To ensure fully flooded conditions, a grease scoop was used for redistributing and redirecting the grease back onto the rolling track. Nevertheless, the film thickness was found to decrease with time, so to maintain a sufficient and stable film, the fresh grease was fed manually into the contact at each speed increment. The grease and bled oil film thickness measurements were taken by increasing the surface speed from 0.02 to 1 m/s. Two central film thickness measurements were taken, and the data are shown with their 90 % confidence intervals.

Table 2 Ball on flat disk—geometry and testing conditions
Full size table

2.5 Rheological Measurements

Dynamic and steady state rheological characterization of the greases were carried out using an Anton Paar MCR 501 rheometer, using a rough parallel plate system of 25 mm diameter with 1-mm gap (Ra = 2.87 µm). Flow curve measurements were taken using stepped-ramp shear rate, in the range from 10−7 to 1 s−1, for a total measurement duration of 1 h. Oscillatory response at a frequency of 1 Hz was studied from 0.001 to 1000 % strain. To reduce the influence of loading history on the microstructure and to obtain consistent results, a relaxation time of 20 min which was sufficient for the normal force to relax was used after loading the samples.

Viscosity measurements for bled oils were taken using a Brookfield LVTDV-II viscometer at 25 °C. Temperature control was achieved with a precision of ±1 °C using a TAMSON TLC 3 cooled circulator. The experiments were repeated two times to check reproducibility.

2.6 Microstructural Characterization

Microstructural characterization of the lubricating greases was carried out using a scanning electron microscope (SEM) and an atomic force microscope (AFM). For SEM analysis, the grease samples were washed using distilled petroleum ether, dried and gold-coated using JEOL JFC-1300 autofine coater. SEM images were obtained using Neoscope JCM 5000 instrument under high vacuum and at 15 kV. Samples for microstructural characterization using AFM were prepared by carefully scraping the grease on a carbon disk. AFM measurements were taken using a Multimode 8 AFM (Bruker Nano Surfaces, Santa Barbara, CA, USA) with a Nanoscope V controller. Tapping mode AFM images were collected with commercially available silicon cantilevers (NCH and SSS-NCHR, Nanosensors, Neuchatel) with a nominal spring constant of 42 N/m. Repeated measurements and multiple scans were carried out to ensure the reliability of data.

3 Results

3.1 FTIR Measurements

To ensure that the bled oil (obtained using 2- and 10-µm filters) did not contain a significant amount of thickener, a qualitative analysis was performed using FTIR on the bled oils and the corresponding grease samples. The FTIR data and the most salient absorption peaks for the Li/M grease and the corresponding bled oil are shown in Fig. 2 and Table 3, respectively. Comparison of the spectra shows that the peaks relevant for the thickeners (3330, 1580, 1558 and 1420 cm−1) either are absent or are below the detectable limit in the bled oil. However, some differences are observed between the base oil and bled oil viscosity (Table 4). Even for CaS/MS, which showed the highest difference in viscosity, peaks corresponding to the thickeners were not detected using FTIR. This rules out the presence of significant concentrations of thickeners in the bled oil.

Fig. 2
figure 2

FTIR data for Li/M grease and corresponding bled oil at T = 25 °C

Full size image
Table 3 Absorption peaks for Li/M at 25 °C [16, 17]
Full size table
Table 4 Viscosity and pressure–viscosity coefficient of bled oils at T = 25 °C
Full size table

3.2 Determination of Pressure–Viscosity Coefficient (α)

One of the important parameters influencing the film thickness in elastohydrodynamic lubrication is the pressure–viscosity coefficient (α). The α values in Table 4 are obtained by minimizing the error between the central film thickness measurements for bled oils (Fig. 3a–f) and the Hamrock and Dowson [18] film thickness equation (Eq. 2a), as described by Van Leeuwen [19]. The Hamrock and Dowson equation is given by:

$$\frac{{h_{c} }}{{R_{x} }} = 2.69\frac{{U^{0.67} G^{0.53} }}{{W^{0.067} }}\left( {1 - 0.61e^{{ - 0.73k_{d} }} } \right)$$
(2a)
$$k_{d} = 1.03\left( {\frac{{R_{x} }}{{R_{y} }}} \right)^{0.63} ;\quad G = \alpha E';\quad U = \frac{{\eta_{{}} u_{{}} }}{{E'R_{x} }};\quad W = \frac{F}{{E'R_{X}^{2} }};\quad \frac{2}{E'} = \frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }}$$
(2b)
Fig. 3
figure 3

a–f Film thickness as a function of rolling speed for the greases and corresponding bled oils at 25 °C

Full size image

Here, \(h_{c}\) is the central film thickness, \(R_{x}\) is the radius of the ball (m), \(E^{\prime }\) is the reduced modulus of elasticity (Pa), \(\eta_{b}\) is the viscosity of base oil (Pa s), \(u\) is the rolling speed (m/s), \(F\) is the load (N), and \(\alpha\) is the pressure–viscosity coefficient (Pa−1).

The values shown in Table 4 represent only an approximation. The calculated values for \(\alpha\) were found to be higher than reported from high-pressure rheological measurements [20, 21]. However, they lead to an accurate film thickness prediction.

3.3 Central Film Thickness Measurements (h c)

In the range of studied speeds, the bled oil film thickness was found to increase with a slope of ≈0.67, which corresponds to the prediction by the Hamrock and Dowson [18] Eq. (2a). The base oil central film thickness shown in Fig. 3a–f was estimated using the Hamrock and Dowson equation using pressure–viscosity coefficient values of the bled oil. Similar to the bled oils, the log–log film thickness of greases versus speed increased with a slope ≈0.62–0.69 (Fig. 3a–f).

The fully flooded film thickness of the studied greases was found to be higher than their corresponding bled oils. This can be attributed to the presence of thickeners influencing the effective viscosity at the inlet of the contact [3, 22]. The percentage increase in grease film thickness with respect to its corresponding bled oil film thickness was calculated using

$$\Delta h(\% ) = 100 \times \sum\limits_{n = 1}^{N} {\left( {\frac{{\left( {\frac{{h_{\text{grease}} - h_{\text{bledoil}} }}{{h_{\text{bledoil}} }}} \right)_{n} }}{N}} \right)}$$
(3)

Here, \(N\) is the total number of speed increment.

The values obtained using Eq. (3) are shown in Table 4. In general, the grease film thickness was found to be 3–40 % higher than the bled oil film thickness.

3.4 Rheological Characterization

The greases were characterized using continuous shear and oscillatory shear measurements. The flow curve shows a high-viscosity Newtonian region at low shear rates, followed by a shear thinning region marked by a drop in four to five decades in viscosity (Fig. 4a). The viscosity versus shear rate was fitted using the cross model (Eq. 4). As it is not possible to measure the viscosity at very high shear rates with the cone–plate/plate–plate rheometer, it was taken as the effective viscosity of the lubricant in the contact (Table 6). The cross model reads

$$\eta = \frac{{\eta_{0} - \eta_{\infty } }}{{\left( {1 + \frac{{\dot{\gamma }}}{{\dot{\gamma }_{c} }}} \right)^{m} }} + \eta_{\infty }$$
(4)
Fig. 4
figure 4

a Viscosity versus shear rate for a few greases studied at T = 25 °C. b Storage and loss modulus versus stress at a frequency of 1 Hz and T = 25 °C for CaS/M

Full size image

Here, \(\eta_{0}\) is the zero shear rate viscosity/limiting viscosity, \(\eta_{\infty }\) is the viscosity at very high shear rates (in this case, the effective viscosity of the lubricant in the contact, \(\eta_{g}\)), \(\dot{\gamma }_{c}\) is the critical shear rate at which the fluid changes from Newtonian to power law behavior, and \(m\) is the power law index. The parameters obtained using the cross model are summarized in Table 5.

Table 5 Rheological properties obtained from steady state flow curve and oscillatory strain sweep measurements at T = 25 °C
Full size table

The yield stress was obtained from the oscillatory strain sweep as the stress level at which a predefined (0.5 %) deviation from the linear relation between stress and strain was observed. For details, see [23]. Next to the yield stress, the viscoelastic properties (\(G^{\prime }\)—elastic modulus and \(G^{\prime \prime }\)—loss modulus) were measured in oscillating shear at a frequency of 1 Hz (Fig. 4b). The results are listed in Table 5.

3.5 Microstructural Characterization

Two different techniques (SEM and AFM) were used to examine the grease microstructure. Notable differences in the structures were observed between these techniques. Figure 5 shows the microstructure obtained using SEM for the studied greases. The SEM images were obtained by washing away the base oil by using a volatile solvent—petroleum ether. The lithium grease shows a fibrous microstructure with a fine and complex network of twisted fibers [24, 25]. Lithium complex grease also appeared to have a fibrous structure but with fewer junctions between the fibers in comparison with lithium grease [26]. On the other hand, a completely different microstructure was exhibited by calcium sulfonate complex and polyurea grease. Polyurea grease was found to have thickeners in the form of platelets, whereas it was not possible to determine the shape and size of the calcium thickeners that were expected to be spherical [26]. Comparison of the microstructure obtained using SEM and AFM (Fig. 6) suggests that the difference in apparent microstructure might be the result of the washing technique or a result of the soap–solvent interaction, which may lead to the collapse or swelling of the structure [24, 27].

Fig. 5
figure 5

SEM images obtained using washed grease samples with thickener particle dimensions

Full size image
Fig. 6
figure 6

AFM images obtained using the untreated samples with thickener particle dimensions

Full size image

In comparison with SEM, AFM has the advantage of not requiring any sample pretreatment. The grease microstructures obtained using AFM under tapping mode in phase imaging are shown in Fig. 6. The measurements were taken for at least two samples to confirm that the pictures are representative for the microstructure of the corresponding greases. The lithium greases (Li/SS and Li/M) appeared to have a fine twisted cylindrical fiber structure with physical entanglements, whereas lithium complex grease showed a less dense fibrous structure without any physical entanglements, leaving large spaces between the fibers. Calcium sulfonate complex greases (CaS/MS and CaS/M) exhibited a spherical agglomerated structure, and polyurea grease thickeners appeared to be in the form of platelets often separated by a larger distance. However, no significant differences in the thickener particle dimensions are observed using AFM between Li/SS and Li/M, and CaS/M and CaS/MS. A higher degree of physical entanglements was observed for Li/SS over Li/M, and CaS/M showed large spaces between the thickeners in comparison with CaS/MS (not shown). This suggests that there is an influence on the fiber interaction by the thickener concentration and base oil viscosity as is suggested in [28, 29]; however, the effect on the particle shape and size is neglectable.

4 Analysis

FTIR measurements from bled oils showed that the peaks relevant to the thickeners were either absent or below the detectable limit. This means that there was no significant thickener material in the bled oil and that the difference between the bled and base oil viscosity may be ascribed to the presence of additives [5]. This topic was not explored further, as the same additives will be present in their corresponding grease samples.

The average fully flooded film thickness of the greases increased in the order:

$${\text{CaS}}/{\text{M}} > {\text{LiC}}/{\text{PAO}} > {\text{CaS}}/{\text{MS}} > {\text{Li}}/{\text{M}} > {\text{PU}}/{\text{E}} > {\text{Li}}/{\text{SS}}.$$

Under fully flooded conditions, none of the rheological properties listed in Table 5 could be directly related to the ability of the studied greases to produce thick films. Therefore, it is most likely that the microstructure/network is not relevant, but primarily the size and concentration of the thickener particles are. The influence of thickener volume fraction \((\varphi )\) on the percentage increase in film thickness is shown in Fig. 7a. A considerable scatter can be seen in the plot of \(\Delta h(\% )\) versus \(\varphi\). This is in agreement with [10] where a considerable spread in the relative percentage film increase as a function of thickener concentration was observed. The spread in Fig. 7a may be attributed to the difference in the thickener type. This is further analyzed in Fig. 7b where the volume of the individual thickener particles, obtained using AFM, is plotted against \(\Delta h(\% )\). Figure 7b shows that greases with smaller thickener particles give rise to thicker films (CaS/M, CaS/MS, LiC/PAO) in comparison with those with grease particles with larger volume (Li/SS, Li/M and PU/E).

Fig. 7
figure 7

a \(\Delta h(\% )\) versus a thickener volume fraction and b volume of the thickener

Full size image

An additional test was done where the concentration was kept constant, but only the thickener particle size was changed. This was done by working the Li/M grease for 100,000 strokes using an in-house-made grease worker at 25 °C. For details, see [30]. The film thickness and AFM measurements (Fig. 8) show that the film thickness increased with about 20 % with fibers that have become much smaller (from \(V\) = 0.0157 µm3 to \(V\) = 0.0075 µm3).

Fig. 8
figure 8

a Film thickness versus speed for worked and unworked Li/M grease at T = 25 °C, b AFM image for the worked sample

Full size image

Both effects can be combined into a single parameter,\(\left( {\frac{\varphi }{V}} \right)\), the ratio of thickener volume fraction to individual thickener particle volume, and the result is shown in Fig. 9a. A linear relation was found between the percentage increase in film thickness \(\Delta h(\% )\) and \(\frac{\varphi }{V}\) with R 2 = 0.93.

Fig. 9
figure 9

a Percentage increase in film thickness versus \(\frac{\varphi }{V}\) and b percentage increase in effective viscosity versus \(\frac{\varphi }{V}\) for the greases studied. Solid line—linear relation with y-axis intercept equal to zero

Full size image

The relationship is given by:

$$\Delta h(\% ) = 0.61\left( {\frac{\varphi }{V}} \right) + 1.97$$
(5)

These film thickness results can be transferred into a relation between effective viscosity and grease parameters. This makes the results applicable to contacts that are different from the point contact. Moreover, it makes it possible to calculate the fraction of the thickener that travels through the contact using the relations for the viscosity of semi-dilute systems that are known from the literature.

Again, the film thickness measurements are transferred into effective viscosities,\(\eta_{g}\), using Hamrock and Dowson equation, assuming again that the grease pressure–viscosity coefficient is equal to that of its bled oil. The result is shown in Table 6. The percentage increase in effective viscosity was calculated using

$$\Delta \eta (\% ) = \frac{{\eta_{g} - \eta_{bl} }}{{\eta_{bl} }} \times 100 ,$$
(6)

where \(\eta_{g}\) is the effective viscosity of the lubricant in the contact (Pa s) and \(\eta_{bl}\) is the viscosity of bled oil (Pa s).

Table 6 Effective viscosity in the contact, percentage change in effective viscosity and volume fraction and percentage volume fraction of thickener particles traversing the contact
Full size table

The percentage increase in effective viscosity is plotted against \(\left( {\frac{\varphi }{V}} \right)\), and is shown in Fig. 9b. As expected, the effective viscosity of the lubricant in the contact was found to be linearly dependent on \(\left( {\frac{\varphi }{V}} \right)\) with R 2 = 0.96 and reads

$$\Delta \eta (\% ) = 1.9\left( {\frac{\varphi }{V}} \right) - 2.1$$
(7)

Ideally, when \(\varphi \to 0\) there should not be an impact of the thickener on the percentage increase in film thickness and viscosity. However, this was not observed due to nonzero ordinate values in Eqs. (5) and (7). An ideal linear relation which accounts for this is shown in Fig. 9 by taking y-axis intercept as zero, using the same slope from Eqs. (5) and (7).

Not all thickener particles may travel through the contact and contribute to this increase in effective viscosity. By having the effective viscosity, \(\eta_{g}\), the volume fraction (\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi }\)) of the thickener particles that contributed to this increase in viscosity can be approximately calculated using Saito’s equation [31], which accounts for hydrodynamic interactions between the particles. Saito’s equation is given by:

$$\eta_{g} = \eta_{bl} \left[ {1 + \left[ \eta \right]\left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } }}{{1 - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } }}} \right)} \right] ,$$
(8)

where \(\left[ \eta \right]\) is the intrinsic viscosity. The main assumptions that are made to calculate this volume fraction,\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi }\), are that the particles are assumed to be rigid, and that polydispersity of the particles can be neglected.

The intrinsic viscosity,\(\left[ \eta \right]\), which is a measure of the contribution of the dispersed phase to the effective viscosity, depends on the shape of the particles. For spherical particles (calcium sulfonate complex greases), \(\left[ \eta \right] = \frac{5}{2}\), whereas for cylindrical (lithium and lithium complex grease) and disk-shaped particles (polyurea grease), the intrinsic viscosity is given by Eq. (9) and (10), respectively [32].

$$\left[ \eta \right] = \frac{14}{15} + \frac{{f^{2} }}{15(\log 2f - 3/2)} + \frac{{f^{2} }}{5(\log 2f - 1/2)}$$
(9)
$$\left[ \eta \right] = \frac{16}{15}\frac{f}{{\tan^{ - 1} f}}$$
(10)

where \(f\) is the ratio of major to minor dimension.

The volume fraction of the thickeners traversing the contact,\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi }\), obtained using Eq. (8) is shown in Table 6. But it should be noted that these values represent only an approximation. Now, the percentage volume fraction of the thickeners traversing the contact (Table 6) can be calculated using

$$\Delta \varphi (\% ) = \left( {1 - \left( {\frac{{\varphi - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } }}{\varphi }} \right)} \right) \times 100.$$
(11)

The result shows that depending on the nature of the dispersed phase, only a fraction of the thickeners may traverse the contact and can contribute to the overall film thickness. Only a very small fraction of the Li grease thickeners travel through the contact, whereas almost half of the calcium sulfonate complex and polyurea particles will go through. The largest fraction is found for the lithium complex grease.

5 Discussion

The prediction of the EHL film thickness for a grease-lubricated contact often clearly deviates from that of its base oil. There are three regimes in which the lubrication mechanisms are different: ultra-low speed, medium speed and higher speed. At ultra-low speed, the film thickness may increase with decreasing speed [13]. This was modelled using an effective viscosity that is much higher than that of the base oil and is a function of the speed [22]. The higher film thickness may be ascribed to the large increase in viscosity when the shear rate approaches zero and/or to the formation of boundary layers. At medium speeds, the grease film thickness is closer to the base oil film thickness. However, also here the films are usually thicker. Again, the increase in film thickness can be modelled by an increase in viscosity. At these speeds, the films are so thick that the effect cannot be ascribed to the formation of a boundary layer. The shear rates are already so high that the viscosity hardly changes with shear rate. This viscosity can be modelled using Saito’s equation, which describes the increase in viscosity of a fluid containing particles. Equations (5) and (7) describe that small particles in a high concentration have the most pronounced effect. The results shown are applicable to full film lubrication. For rolling bearings, this means during the churning phase. After this, full film only occurs if the speeds are not too high.

6 Conclusions

The grease film thickness was found to be 3–40 % higher than the bled oil film thickness, which is ascribed to an increase in the effective viscosity caused by the presence of thickener particles in the inlet of the contact. No bulk rheological properties characterized by steady and dynamic shear could be related to the grease film thickness. The thickener contribution to the film thickness quantified as \(\Delta h(\% )\) was found to be a function of the thickener concentration and grease particle dimensions obtained using AFM. The degree of film enhancement was found to be proportional to the ratio of the thickener concentration to the average volume of the individual thickener particles and reads

$$\Delta h(\% ) = 0.61\left( {\frac{\varphi }{V}} \right) + 1.97$$

Hence, with the same concentration, smaller thickener particles lead to the generation of thicker films than larger thickener particles. This can be translated into a change in effective viscosity:

$$\Delta \eta (\% ) = 1.9\left( {\frac{\varphi }{V}} \right) - 2.1$$

An analysis of the relation between the effective viscosity and the thickener particle concentration revealed that not all thickener particles travel through the contact. With the limited number of greases that we studied, this varied between 1 and 70 %.