1 Introduction

Kinetic studies of catalytic reactions are an essential part of experimental mechanistic studies, performed to understand these reactions at a molecular level. Kinetic studies reveal how much each parameter affects the rate of a reaction at each time. This information is useful from a practical point of view, and it also allows discerning between different mechanistic proposals. Each mechanistic proposal has a different rate law, which is the equation that indicates the expected effect of each parameter on the rate of a reaction. However, this information is not always easy to extract and interpret for catalytic reactions due to the inherent complexity of their rate laws.

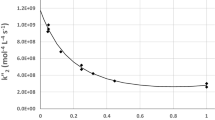
Chemists usually quantify the effect that a parameter has in the rate of a reaction with the order. The IUPAC defines that a reaction is of order α with respect to a substrate A only when the macroscopic rate can be expressed by a power law: r = k[A]α[B]β… [1]. For reactions with more complex rate laws, as catalytic reactions usually have, it is necessary to identify a surrogate power law that best reproduces the real equation at each point (s0.3 in Fig. 1). These surrogate power laws must have the same value (Eq. 1) and the same slope (Eq. 2) as the rate law at that specific point ([A]i). By using these two conditions, it is possible to find a general mathematical description for the order of a reaction in A.

Fig. 1
figure 1

The surrogate power-law function, s0.3, which best fits the real curve, r, at [A] = 0.3 M is the one with an order of 0.4

Full size image
$$r~\left( {{{\left[ A \right]}_i}} \right)~=~{s_i}\left( {{{\left[ A \right]}_i}} \right)~=~{k_i}~{[A]_i}^{{\alpha _i}}$$
(1)
$$\frac{{{\text{dr}}}}{{{\text{d}}[{\text{A}}]}}({[{\text{A}}]_{\text{i}}})=\frac{{ds}}{{{\text{d}}[{\text{A}}]}}({[{\text{A}}]_{\text{i}}})={{\text{k}}_{\text{i}}}{\alpha _{\text{i}}}{\text{ }}[{\text{A}}]_{\text{i}}^{({\alpha _{\text{i}}} - 1)}$$
(2)

From (1):

$${\text{k}}_{{\text{i}}} = \frac{{{\text{r}}\left( {[{\text{A}}]_{{\text{i}}} } \right)}}{{[{\text{A}}]_{{\text{i}}}^{{\alpha _{{\text{i}}} }} }}$$
(3)

From (2) and (3):

$$\upalpha _{{\text{i}}} {\text{ = }}\varepsilon _{{{\text{([A])}}}}^{{\text{r}}} {\text{ = }}\frac{{{\text{dr}}}}{{{\text{d[A]}}}}{\text{([A]}}_{{\text{i}}} {\text{)}} \cdot \frac{{[{\text{A}}]_{{\text{i}}} }}{{{\text{r}}(\left[ {\text{A}} \right]_{{\text{i}}} )}} = \frac{{{\text{d~ln~r}}(\left[ {\text{A}} \right]_{{\text{i}}} )}}{{{\text{d~ln~}}[{\text{A}}]_{{\text{i}}} }}$$
(4)

The alternative mathematical formulas shown in Eq. 4 are known as elasticity coefficient or normalized sensitivity \((\varepsilon _{([A])}^r)\) and are used in mathematics, physics, economics [2], and enzymology [3,4,5,6]. However, this concept has been underused in mechanistic studies of organic and inorganic catalytic reactions. Instead, the analysis of the orders for rate laws has usually been restricted to unrealistic limit cases and therefore really valuable information has been discarded. Currently, there are available free tools to take the derivative of the rate law in order to quickly find the elasticity of any complex rate law equation of a catalytic reaction without requiring advanced knowledge of calculus [7]. Therefore, the normalized sensitivity analysis should get routinely included in the studies of rate laws of catalytic reactions.

2 Examples

There are several scenarios where the use of the normalized sensitivity function can be useful. For the popular unireactant catalytic reaction of Fig. 1 following the Briggs-Haldane kinetics [8], the order of the reaction in substrate A is defined by Eq. (5).

$$\upvarepsilon _{{[{\text{A}}]}}^{{\text{r}}} = \frac{{{\text{K}}_{{\text{M}}} }}{{{\text{K}}_{{\text{M}}} + [{\text{A}}]}}~;{\text{ where}}~~{\text{K}}_{{\text{M}}} ~ = \frac{{{\text{k}}_{{ - 1}} + {\text{k}}_{2} }}{{{\text{k}}_{1} }}$$
(5)

This equation allows us to plot the curve of order in [A] against the concentration of [A] (Fig. 1). Also, the equation makes it evident that the order of the reaction in [A] is independent of the total concentration of catalyst. Therefore, higher concentrations of catalyst do not require higher concentrations of substrate to achieve saturation conditions as it might appear at first glance.

Another usual scenario with complex orders in catalytic reactions results from equilibria involving catalytic species composed by multiple units of catalytic molecules, such as dimers or trimers. Figure 2 shows the analysis of the order in catalyst for a reaction catalyzed by a dimeric species in equilibrium with an inactive monomeric species. In this case, the order in catalyst is between 2 and 1 depending on the range of concentrations of catalyst analyzed, as well as the concentration of substrate and the kinetic constants.

Fig. 2
figure 2

The order in catalyst for a reaction catalyzed by a dimeric species changes from 2 to 1

Full size image

Different reaction mechanisms can lead to the same dependency of the order in catalyst or any other parameter of the reaction. For example, the reaction scheme shown in Fig. 3, where one of the byproducts of one of the steps in the cycle is used as a reactant in a subsequent catalytic step, has the same dependency of the order in catalyst as the reaction previously analyzed in Fig. 2 (indeed, for the values shown, the curves would be identical). This is a good example of how the analysis of the order of the reaction in catalyst facilitates the comparison of rate equations for different reaction mechanisms.

Fig. 3
figure 3

The order in catalyst for a reaction where a byproduct is used as a subsequent reactant changes from 2 to 1

Full size image

The elasticity analysis is especially useful in more complex scenarios. For example, it enables the prediction of the order in catalyst for a reaction where a constant quantity of the catalyst gets irreversibly deactivated by some impurity contained in the reaction media. The analysis in Fig. 4 shows that, in this case, the expected constant first order in catalyst is disturbed at low concentrations close to the concentration of the inhibitor. The lack of awareness of this alternative scenario can mislead some researchers, who may misinterpret the higher order in catalyst at low concentrations of catalyst as the consequence of either having an active dimeric species in equilibria with an out-cycle monomeric inactive species (Fig. 2), or a reaction where one of the byproducts is used as a reactant (Fig. 3).

Fig. 4
figure 4

The order of a reaction in catalyst added in the presence of an irreversible inhibitor

Full size image

3 Conclusions

The elasticity coefficient is the mathematical description of what chemists call order of a reaction. The awareness of this quantitative description of the order of a reaction facilitates the kinetic analysis of complex reaction mechanisms, such as catalytic reactions. A better understanding of the concept “order of reaction” by the catalysis community will enable a better interpretation of kinetic data thus allowing the consideration of alternative mechanisms.