Parameterization of Biot–Willis Effective-Stress Coefficient for Deformation and Alteration of Porous Rocks

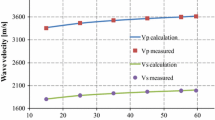
Abstract

The effective stress coefficient is an essential geomechanical parameter required for estimation of the effective stress acting upon the subsurface reservoir porous rock formations and affecting their petrophysical properties. The values of the effective stress coefficient for various rock properties depend on the complex phenomena involving various types of rock deformation and alteration processes. This paper presents a discussion of the relevant factors and an effective method for accurate correlation of the Biot–Willis effective stress coefficient by means of a kinetics-based phenomenological model. This is accomplished by developing a modified power-law equation which describes the variation of the effective stress coefficient by various rock deformation and alteration processes at a macroscopic scale. This equation has five parameters which can be determined using the experimental data obtained by rock testing. The modified power-law equation is derived in a manner to satisfy the low- and high-end limit conditions of the effective stress coefficient exactly, which are the zero and unity values, respectively, for the Biot–Willis effective stress coefficient associated with the bulk volumetric strain. However, many empirical correlations presented in the literature cannot satisfy the low- and high-end limit values of the effective stress coefficient. The modified power-law equation is applied for correlation of the Biot–Willis effective stress coefficient associated with the bulk volumetric strain as functions of porosity, permeability, permeability/porosity ratio, and stress using the experimental data of various porous subsurface rock formations and artificial porous materials. The quality of the correlations is determined by means of the coefficient of regression or correlation and the root mean-square of the difference of the correlation values relative to the measured data. The correlation of the Biot–Willis coefficient with porosity yields the best results compared to the correlations obtained with permeability and permeability/porosity ratio. The stress dependence of the Biot–Willis effective stress coefficient of heterogeneous rock formations involving the slope change and hysteresis effects is correlated to describe the slope discontinuity caused by the deformation process transition and the hysteresis caused by the inertial and delay effects, fully elastic pre-damage, and/or irreversible rock damage during loading/unloading.

Appendix 1 Solution of the Ordinary Differential Equation

The ordinary differential equation described by Eq. (15) can be reformulated as:

$$- \frac{{\alpha_{o} - \alpha_{\infty } }}{{\left( {\alpha_{\infty } - \alpha } \right)^{2} }}\frac{d\alpha }{{dz}} = \frac{d}{dz}\left( {\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }}} \right) = A^{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} B\left( {\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }}} \right)^{{1 - {1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}}$$

(22)

Then, Eq. (22) can be expressed in a more convenient form as:

$$\left( {\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }}} \right)^{{ - 1 + {1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} \frac{d}{dz}\left( {\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }}} \right) = A^{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} B$$

(23)

Consequently, an integration of Eq. (23) gives:

$$\frac{1}{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}}\left( {\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} = A^{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} Bz + C$$

(24)

Application of the end-point limit condition given by Eq. (16) yields the integration constant C as:

$$C = - A^{{{1 \mathord{\left/ {\vphantom {1 B}} \right. \kern-\nulldelimiterspace} B}}} Bz_{o}$$

(25)

Thus, substituting Eq. (25) into Eq. (24) yields an analytical solution as:

$$\frac{{\alpha - \alpha_{o} }}{{\alpha_{\infty } - \alpha }} = A\left( {z - z_{o} } \right)^{B}$$

(26)

Note that this equation also satisfies the end-point limit condition stated by Eq. (17).