Abstract
The application of 3D technology for fabrication of artificial porous media samples improves porous media flow studies. The geometrical characteristics of a porous media pore channel: the channel shape, size, porosity, specific surface, expansion ratio, contraction ratio, and the tortuous pathway of the channel can be controlled through advanced additive manufacturing techniques (3D printing), computed tomography imagery (CT imaging) and image analysis methods. These 3D technologies have here been applied to construct and analyze four homogeneous porous media samples with predefined geometrical properties that are otherwise impossible to construct with conventional methods. Uncertainties regarding the geometrical properties are minimized because the 3D-printed porous media samples can be evaluated with CT imaging after fabrication. It is this combination of 3D technology that improves the data acquisition and data interpretation and contributes to new insight into the phenomenon of fluid flow through porous media. The effects of the individual geometrical properties on the fluid flow are then accounted for in permeability experiments in a Hassler flow cell. The results of the experimental work are used to test the theoretical foundation of the Kozeny–Carman equation and the extended version known as the Ergun equation. These equations are developed from analogies to the Hagen–Poiseuille flow equation. Based on the results from the laboratory experiments in this study, an analytical equation based on the analytical Navier–Stokes equations is presented as an alternative to the Hagen–Poiseuille analogy for porous media channels with non-uniform channel geometries. The agreement between experiment and the new equation reveals that the dissipating losses of mechanical energy in porous media flows are not a result of frictional shear alone. The mechanical losses are also a result of pressure dissipation that arise due to the non-uniformity of the channel geometry, which induced spatial variations to the strain rate field and induce acceleration of the velocity field in the flow through the porous medium. It is this acceleration that causes a divergence from linear flow conditions as the Stokes flow criterion (Re ≪ 1) is breached and causes the convective acceleration term to affect the flow behavior. The suggested modifications of theory and the presented experiments prove that the effects of surface roughness (1) do not alter the flow behavior in the Darcy flow regime or (2) in the Forchheimer flow regime. This implies that the flow is still laminar for the Forchheimer flow velocities tested.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fluid flow through a porous media is a subject of global interest and a topic of extensive research within fields of scientific and industrial nature alike. Within the field of civil engineering, e.g., drinking water supply, water resource management, groundwater heat pump systems, coastal erosion, and water contamination there frequently exists a need to determine the rate of groundwater flow through soil formations. The groundwater flow is assumed to follow the relations given by Darcy’s law (1856) and is governed by the hydraulic conductivity, K (m/s), of the soil. Naturally occurring soil formations have a potential for large spatial variation, and this often requires the determination of a large number of local hydraulic conductivities to adequately describe the over-all field K for an aquifer. Many engineering projects do not have the budget to perform time-consuming and costly field or laboratory permeability tests. Thus, simple predictive methods that estimate the hydraulic conductivity from individual soil samples are still a common and valued approach in the industry.
A range of predictive equations has been developed theoretically or empirically from laboratory tests. Chapuis (2012) has reviewed 45 of the most commonly used predictive methods in engineering and have recommended four of them, one of which is the Kozeny–Carman equation. Common for all the 45 methods is that they relate the hydraulic conductivity or permeability of a soil formation to properties of the solid soil matrix rather than to the pore-space matrix properties directly. This is done because soil samples are often routinely available in many projects. Properties of the soil solids, e.g., the grain size distribution curve, sediment bulk density, soil texture, and form, are properties that are relatively easy to measure compared to in situ pore-space properties. However, the four methods recommended by Chapuis (2012) incorporate simple dimensionless pore-space properties, e.g., the porosity (n) of the bed and the pore channel tortuosity (τ). These pore properties are vital for the accuracy of the methods, but are rarely measured or estimated in practice, at least in Norway. Continuous use of the predictive methods argues that further development and confirmation of their accuracy and applicability are useful for the industry.
The aim of this study is to further investigate how various geometrical properties of a porous media affect its permeability, and thereby improve the empirical equations further. As demonstrated by Chapuis (2012), the in situ pore properties can be difficult to quantify accurately in conventional permeability experiments on natural soils. Natural soils typically consist of a variety of soil particles, with different sizes and shapes, which makes it difficult to evaluate the significance of individual geometrical properties alone. Therefore, the relation between permeability and different geometrical properties of porous media is investigated in detail by applying an additive manufacturing (AM) technique, 3D printing, as a means of fabricating artificial soil samples. Geometries that previously were impossible to construct are now available through AM. AM has recently shown its usefulness in porous media studies (Osei-Bonzu et al. 2018; Gelhausen et al. 2018). In this study, the applied AM technique allows to determine the precise location, shape, and size of all individual particles in a porous media, thus minimizing uncertainties related to the pore-matrix configurations and geometry. The influence of the various pore geometrical properties can then be investigated in a controlled manner. Four different 3D-fabricated homogeneous porous media geometries have been tested in a Hassler flow cell and the results have been used to test the state-of-the-art analytical flow equations of Kozeny–Carman (1937) and Ergun–Orning (1949). These equations are developed based on analogies to the Hagen–Poiseuille equation. As an alternative, a new analytical solution has been developed and is here presented, tested, and compared. The new equation is based on analogies to the analytical solutions of the Navier–Stokes equation and is proposed to be a better explanation for the porous media flow behavior observed in the presented experiments.
2 Theory
The dissipation of mechanical energy that arise as fluids flow through a porous media display a velocity-dependent behavior. At low flow velocities the relation is linear, while at high velocities the flow displays a non-linear behavior. The fundamental equation of fluid flow through a porous media is that of Darcy (1856). Darcy’s law governs the phenomenon in flow conditions where viscous shear forces dominate the dissipating losses of fluid flow through a porous medium. For horizontally directed one-phase flow, the Darcy equation can be stated as Eq. (1) (Hubbert 1940).
where the pressure loss, ΔP (Pa), across the superficial length unit of the porous medium, L (m), is proportional to the superficial velocity of the flow, us (m/s), the viscosity of the fluid, µ (Pa·s), and is inversely proportional to the permeability of the porous medium, k (m2). The superficial fluid velocity is defined as the bulk fluid flow rate, Q (m3/s), divided by the bulk cross-sectional area perpendicular to the flow direction, A (m2). Beyond a certain critical velocity limit the pressure loss diverges from the linear response and must typically be described by a polynomial equation of the second order, of which the Forchheimer equation (Eq. 2) is best known. The second-order term accounts for inertial losses that gradually dominate at progressively higher rates of flow. These losses are proportional to the inertial resistance factor, β (m−1), and the density (ρ kg/m3) of the fluid.
In this paper, the empirical equations of Darcy (1856) and Forchheimer (1930) are linked with that of two analytical solutions of the Navier–Stokes equation. This is done by applying some alternative solutions commonly found in other fields of fluid mechanics. Similar solutions have been attempted by e.g., Brinkman (1947), Hasimoto (1959), Barnea and Mednick (1978), Collins (1976), Sangani and Acrivos (1981), and Happel and Brenner (1983), Wilkinson (1985), and Allen (1985); among others. In this paper, the analytical solution of choice corresponds to that of a horizontally directed, one-phase, incompressible fluid flow in channels, shown in Eq. 3.
where the dissipating forces, F (N), that resist the fluid motion within the flow channel, is a sum of two different force components. The first term on the right-hand side, represented by the dissipation factor C (-), is a linear term and signifies a force dominated by viscous shear stress and pressure dissipation. The dissipating forces that originate from the linear term are proportional to the dynamic viscosity of the fluid, µ (Pa·s), the fluid velocity, V (m/s), and a characteristic length unit, L (m), that describes the channel. For internal flows, such as pipe flows, this is typically the length of the channel.
The second term, represented by the dissipation factor Cd (-), is a non-linear term and signifies the force of convective acceleration. When Eq. 3 is arranged as shown here, the dissipating forces that originate from the non-linear term are dependent on the Reynolds number of the flow (Re). Note that this is not the conventional manner to describe the relation in pipe flows, but it is rendered here in this way because the Reynolds numbers in porous media are small and the main contributor to dissipation originates from the linear term. At high Reynolds numbers the non-linear term dominates, and the equation is typically rearranged in favor of the second-order term (White, 2006). In Eq. 3 the Reynolds number is defined by Eq. 4 where Re (−) signifies a dimensionless number that relates the ratio of inertial forces to viscous forces. The number depends on the velocity, V (m/s), the density, ρ (kg/m3), and the viscosity of the fluid and the characteristic length unit, m (m), of the flow channel geometry.
The linear (C) term and the non-linear (Cd) term of Eq. 3 represent approximate solutions to the incompressible Navier–Stokes equation. The solutions are only valid if the following two assumptions are in force: (1) the effects of gravity affect the hydrostatic pressure component only and does not affect the dynamics of the flow; (2) the flow is steady or quasi-steady. These assumptions imply that the time-dependent term and the Froude number term of the Navier–Stokes equation are negligible small and can be ignored, and that the flow channel exhibits no free-surface effects.
For Eq. 3 to be relevant for porous media it is necessary to define what the various parameters signify and how they are described in relation to each other. In pipe flows and in porous media studies the dissipating force is measured as a loss of pressure across the superficial length of a pipe section or a porous media sample. The force is thus best described as a pressure loss-type equation. The equation should therefore be rearranged to describe a pressure relation, as in Eq. 5, where the loss of pressure, ΔP (Pa), is associated with some characteristic length unit, m (m), that describes how the pressure forces and the friction forces of the fluid motion interact with the channel geometry.
It is clear that both the characteristic length unit, m, and the velocity, V, of both Eqs. 4 and 5 must be defined identically for the equation to be further modified. The manner that these two parameters are defined are often determined according to the problem at hand, and there are certain conventions in different scientific fields (White 2006). In the study of suspended solids, both m and L are typically described as the size or diameter of the solid object, and the velocity is often described by the mean “free stream” velocity. For internal flows, however, such as for pipes, the velocity is typically described by the maximum velocity component within the flow, while m is typically described by Eq. 6. For a uniform circular pipe, the characteristic length unit m simplifies to an expression of the pipe internal radius, ri (m), or diameter, di (m). It should therefore be noted that in Eq. 5, L describes the length of the channel, while m describes the shape of the channel along the channel length L (Schiller 1923).
In the following subsections, a new theoretical method for defining these parameters for a single pore is presented. This expression is then tested if it applies to porous media that consist of numerous pores of equal shape.
2.1 The Stokes flow approximation
Equation 3 shows that if the flow velocity is sufficiently small (Re << 1), the dissipation caused by convective acceleration of the fluid velocity is orders of magnitude smaller than the effects of the linear term (C). The second-order term can then be ignored and Eq. 3 corresponds to the Stokes flow approximation with the general form of Eq. 7 (White, 2006).
Equation 7 states that the dissipating forces, FC, within the flow must balance the dissipating frictional forces, Cf (−), and the dissipating pressure forces, Cp (−), enforced by the motion of a fluid past an object surface. The typical scenario would be a fluid flowing with a mean velocity, Vavg (m/s), past a three-dimensional object of characteristic length, L (m). The balance of dissipating forces is proportional to an unknown dissipation constant (C), which depends on the objects shape and orientation in the flow field. The classical example of this dissipation constant is seen in Eq. 8 for a smooth sphere, e.g., falling in a stagnant fluid or suspended in a uniform velocity field with characteristic length equal to the sphere diameter, d (m), (Fig. 1a).
Principle sketch of the Stokes creeping flow approximation. a A single sphere suspended in a uniform fluid flow field (V) is the classical example. b The velocity field in a pore is spatially bound by the geometry of the pore. The assumption of Dupuit is not correct for the whole pore but should be correct for a section of the pore where the volume ratio equals the area ratio. Equation 13 assumes that the average velocity in Dupuit’s cross-section is equal to the maximum velocity in the pore body cross-section
For a single sphere the dissipating frictional forces are found to be Cf = 2π, and the dissipating pressure forces are found to be Cp = π. The sum of these two coefficients is the Stokes sphere constant shown in Eq. 8. Equation 8 is frequently applied in the field of physical sedimentology and settling of particles (Allen 1985; Raudkivik 1990; Van Rijn 1993). C is found to be similar to 3π for a wide range of geometrical shapes. The C of, e.g., a thin flat circular disk of equal diameter to that of the sphere, but oriented perpendicular to the flow direction, is approximately 15% smaller than the sphere constant. If this disk is oriented parallel to the flow direction the constant is approximately 56% smaller than the 3π sphere constant (White 2006; Çengel and Cimbala 2010). Regarding settling of particles in a fluid, Eq. 8 is considered suitable for a variety of particle shapes provided that the particle sizes are sufficiently small to satisfy the criterion Re < ≈1 (Allen 1985, White 2006) (here the Reynolds number is defined with the particle diameter as the characteristic length unit L and with the mean fluid “free stream “velocity as the velocity component).
Alternatively, Eq. 7 should be valid for a range of particle sizes provided that the velocity is sufficiently small to ensure Re ≪ 1. This is the relevant situation for porous media, where the particles of the media can constitute a range of particle sizes. The corresponding Stokes flow approximation for fluid flow through a single pore is suggested to be Eq. 9, where the characteristic length of the pore channel is defined as the interstitial length, Le (m), of the pore channel (which might be longer than the superficial flow axis).
The shape of the pore geometry along the L is assumed to be described according to the assumptions of Kozeny (1927), which is expressed as Eq. 10 for a single pore. This is the same expression as for Eq. 6, but since a pore channel is not uniform or consistently shaped, the expression does not simplify to an expression related to a diameter of the pore channel.
The corresponding Stokes flow equation for a pore then becomes Eq. 11, where the geometry of the pore is expressed as a ratio of the void volume per unit volume, n (m3·m−3), over the surface area per unit volume, S (m2·m−3).
However, the interstitial velocity within a pore is difficult to quantify in practical experiments and a modification to an average superficial fluid velocity is performed in porous media studies. This is typically done through the application of Dupuit’s assumption (1863, described in Carman (1937)) in Eq. 12.
where the interstitial velocity of the fluid within the porous media, ui (m/s), must be higher than the superficial velocity (Ref. Eq. 1). Dupuit assumed the interstitial velocity to be a function of the porosity (n) of the bed. However, the assumption is assumed valid on the notion that for a randomly packed porous media the voids within a porous media are so “evenly distributed throughout the bed that the fractional free area at any cross-section is constant and equal to the porosity…” (Carman, 1937). Nevertheless, if Dupuit’s assumption is applied to a single pore, this notion is incorrect, and the assumption is not valid. For the flow behavior to satisfy the conservation of mass, the flow velocity must be ever-changing through a pore in response to the contracting and expanding pore channel geometry.
As an alternative, the assumption of Dupuit can be presumed to be correct for a specific slice of pore cross-section within the pore where the slice of pore channel cross-sectional area equals that of the porosity of the whole pore (Fig. 1b). For any pore geometry, this cross-section, hereby termed Dupuit’s cross-section, must be found somewhere in-between the pore body center cross-section and the pore throat center cross-section. If Dupuit’s assumption represent the average interstitial fluid velocity in this cross-section, it is evident that the maximum velocity of the cross-section must be bound by the geometry of the cross-section. The conservation of mass then requires the velocity to be faster anywhere closer to the pore throat region, and slower anywhere closer to the pore body region of the pore. In the case of a uniform channel, e.g., a pipe of uniform cross-section, the relation of the maximum fluid velocity, Umax, and channel geometry is seen in Eq. 13 (Çengel & Cimbala, 2010), where k0 is the channel geometry factor and Ui is the average velocity of the channel.
It is suggested here that if the velocity, V, in Eq. 11 is described similarly to that of the “free stream” velocity in Eq. 8, the same dissipating constant of 3π should result (Fig. 1). This implies that the velocity must be described as the interstitial mean velocity in the pore body. The average pore body cross-section velocity is less than the average velocity in Dupuit’s cross-section. It is therefore assumed that the average velocity in Dupuit’s cross-section is approximately equivalent to the maximum velocity of the pore body cross-section. (Figure 1b). this assumption corresponds to the relation of Eq. 14, where the interstitial velocity of Eq. 12, ui, is thought to resemble the Umax of Eq. 13, and the velocity V of Eq. 11 resembles the average velocity of the channel, Ui.
Combining Eqs. 11, 12, and 14, results in Eq. 15 for the Stokes flow approximation for fluid flow through a pore. The k0 value will here be related to the shape of the pore body region of the pore.
The final corrections needed in the equation are to account for the tortuous pathway of the flow channel. The pore channel might not be oriented parallel to the measuring axis. This causes the actual travel path of the fluid to be longer than the superficial length of the pore. Kozeny (1927) proposed that the longer, tortuous pathway, τ (−), can be expressed by Eq. 16.
Carman (1937) stated that the same correction must be applied to the velocity field. As the point of reference is chosen to be the superficial velocity component, us, it is necessary to account for the flow directions of the interstitial velocity components. Carman (1937) suggested that this should be done according to Eq. 17.
Accounting for the additional distance of travel and the additional velocity with which the fluid progress through the pore, the final form of the Stokes flow approximation becomes Eq. 18. This theoretical approach provides an equation that describes the flow through a pore in relation to the average velocity of the pore body.
In practical experiments, the dissipating constant C will only be revealed if all other parameters are measured and quantified. Among the variables in Eq. 18, the k0 value is the most difficult parameter to determine. It is therefore suitable to define a new coefficient that account for both the C and k0 values in practice. The new coefficient, kS (−), is suggested in Eq. 19 where it is expected that the 3π should be an approximate value for a pore with a non-uniform pore channel.
A well-known alternative to Eq. 18 is the Kozeny–Carman equation (Carman 1937). In this equation, the velocity V component is identified differently and is related to the maximum velocity component within the channel (V is interpreted to resemble Umax of Eq. 13 and not the Ui), as is convention for pipe flow equations where the pipes have uniform cross-sectional shapes (Carman 1937). Their approach corresponds to Eq. 20.
Much of the work of Carman (1937) was founded on the notion that the product of the k0 factor and the tortuosity factor, τ2, is equal to the constant, kC (−). Through his work, Carman (1937) concluded that kC only ranges from 4.84 to 6.13 for porous media with a wide range of particle shapes and sizes, and that an approximate solution for kC for any channel shape or form should be given by Eq. 21. The kC factor is therefore perceived to be a factor that depends on the shape of the flow channel in similar fashion to that of Hagen–Poiseuille flow in pipes.
Table 1 shows a selection of the different k0 values for Eqs. 18, 19, and 21. These values are originally calculated for different cross-section geometries in pipes (Çengel & Cimbala, 2010). The table also presents a range of kS values that would result from Eq. 19, which are limited to 3.67–5.93 for the most relevant channel geometries. The lower limit of 3.14 (π) is obtained for the special case of a rectangular cross-section with infinite axis ratio, which would resemble fluid flow between two plates.
2.2 Including the convective acceleration term
As the fluid flows through the pore, the channel geometry contracts and expands causing convective acceleration to occur. If the Reynolds number is sufficiently large, the non-linear term in Eq. 3 cannot be ignored, meaning that at a particular critical velocity threshold, the acceleration force can no longer be ignored. The characteristic parameters are defined in chapter 2.1, and the non-linear term (Eq. 22) must be arranged accordingly through combination with Eqs. 10, 12, 14, 16, and 17. This provides Eq. 23.
The Cd (−) is a dissipating coefficient that presumably depends on the channel shape, and degree of expansion and contraction along the length axis. A relevant approach for dealing with these effects can be found in fluid mechanics of pipes. A short description is presented here, but the reader is referred, e.g., Çengel & Cimbala (2010) and Idelchik (1994) for further details. The concept of minor losses due to pipe expansion or contraction is developed from the fundamental conservation laws for mass, momentum and energy. The general form of Eq. (24) relates to pipes of uniform internal diameter, di (m) (Eqs. 8–59 in Çengel and Cimbala 2010).
where the total losses of hydraulic head through a pipe, hL,total (m), of length L (m) is due to friction in the pipe, represented by, e.g., the Darcy–Weisbach friction factor in laminar flow, f (−), and due to additional losses caused by an contraction of the flow channel, e.g., a constricting pipe segment like that of Fig. 2a. A constricting segment enforces two losses, both the contraction and the expansion of the segment, and the sum of these losses constitutes the minor loss of the obstruction, KL (−).
Principal sketch of minor losses due to contraction and expansion of the flow channel. a A constricting obstruction in a pipe section of length L causes acceleration of the fluid to occur when the fluid flows through the smaller cross-section. The ratio of the smaller area, Asmall, to the larger area, Alarge, determines the magnitude of minor losses. A smooth angle, θ, of approach dampens the losses. b An equivalent phenomenon occurs in porous media when the fluid flows from one pore to another. The ratio of pore throat area, Asmall, to the pore body area, Alarge, is believed to determine these losses
The loss coefficients, KL, are highly dependent of the pipe geometry, diameter, surface roughness, and the Reynolds number of the flow and are generally larger for expansion segments than for contraction segments. Sharp angles and abrupt changes can cause considerable losses as the fluid is unable to make sharp turns at high velocities, e.g., causing flow separation at the rear of corners or edges (Çengel and Cimbala 2010). Flow separation can occur in areas where the channel size increases and causes the fluid velocity to decrease. According to the Bernoulli equation, the flow develops an adverse pressure gradient along the walls due to the decrease in velocity and this causes the boundary layer to separate from the channel walls (Idelchik 1994).
Semi-empirical equations for pipes exist (Çengel and Cimbala 2010; Crane 1957; Idelchik 1994). For uniform expansion, the loss coefficient, KL-ex (−), can be estimated from Eqs. 25 or 26, with reference to Fig. 2a. The coefficients are based on the velocity of the smallest channel as the reference velocity. The \({\varvec{\alpha}}\) (-) is a kinetic energy correction factor that depends on the flow characteristics. In fully developed turbulent flow the factor is close to 1.05, while in fully developed laminar flow the factor is 2.0. The losses are thus velocity dependent and depend on the Reynolds number of the flow and are relatively greater in laminar flow. In laminar conditions, the range is KL-ex ≈ 0.0-2.0, while in turbulent conditions the expansion losses are typically bound by the range KL-ex ≈ 0.0–1.05.
It is believed that Cd should depend on the constriction ratio similarly to that of KL in pipes. The argument for this is that they both deal with the same geometrical aspects, namely the expansion and contraction of a channel. For these two to be comparable it is vital that both Cd and KL describe the velocity from the same point of reference within the channel. Since the pipe coefficients KL are based on the velocity of the smallest pipe as the reference velocity, a correction of the Cd constant is needed, since the Cd is expressed by the velocity of the larger flow channel. Rearranging the fundamental conservation laws provides the correction 1/a2 where a is defined according to Eq. 27 (Idelchik 1994; Crane 1957).
The modified form of convective acceleration term is then given by Eq. 28, where the dissipation coefficient (CKL) is a coefficient that corresponds to the average velocity of the pore throat region of the pore. In this form, the CKL should therefore be dependent on both the constriction ratio of the channel and the streamlining of the pore channel geometry through the pore throat, similar to that of the KL of pipes.
The final version of Eq. 3 then becomes Eq. 29 including the convective acceleration term.
This equation represents a single pore. For a porous media that consists of numerous pores, these various geometrical factors of Eq. 29 are unique for each pore within the pore matrix. However, if all pores are equal within a homogenous pore matrix, the factors of each pore will be equal to every other pore and Eq. 29 will be able to describe the dissipation of mechanical energy through the whole porous media with a single set of geometrical factors.
A well-known alternative to Eq. 29 is the Ergun equation (Ergun and Orning 1949). The Ergun equation corresponds to Eq. 30. The Ergun equation assumes that the channel geometry of each pore in a porous media is similar to cylindrical channels, as is evident by the k0 = 2 in the linear term and the number 4 in the polynomial term.
The first-order term of the equation is equivalent to that of the Kozeny–Carman equation, but with a fixed k0 factor of 2 (Table 1). The β0 is a factor of geometrical relation and Ergun and Orning (1949) do not explain the β0 factor in relation to pipes of various shapes, as Carman attempts to do for the k0 factor. They do, however, provide the range 1.1 < β0 < 5.6, with most values occurring in the range 2.0–3.3 for randomly packed columns of smooth spheres. Note that the velocity component is represented differently and is only altered according to Eq. 12, which states that the Ergun equation does not directly account for the tortuosity, τ (−), of the porous media.
3 Experimental work and methods
3.1 Sample design
The four particle designs (Fig. 3) were selected to compare various aspects of geometrical relations and their effects on permeability; particle shape (A vs B), size (B vs C), and their packing configuration (B vs D). The geometrical configurations of all the designs result in homogeneous porous medias that should satisfy the assumptions of Kozeny (1927), that the granular beds are equivalent to a “…group of parallel, similar channels…”. All the pores in the samples are thus created equal. The geometries are difficult to achieve in traditional experiments, especially in view of the high porosity medias.
The principal particle design and packing arrangements of the four sample types. a Sample A with 1.0 mm spheres stacked in the cubical arrangement. Pore corresponds to 47.6% porosity. b Sample B with 1.0 mm octahedrons stacked in cubical arrangement. Pore corresponds to 83.3% porosity. c Sample C with 0.50 mm octahedrons stacked in cubical arrangement. Pore corresponds to 83.3% porosity. d Sample D with 1.0 mm octahedrons stacked in two sets of equal cubical arrangements, where the one set is fixed in-between the other without touching the other set. Pore corresponds to 66.6% porosity
The design properties of the four porous media are summarized in Tables 2 and 3. The spherical design (A) comprises 3500 individual 1.0 mm spheres of equal sizes arranged in cubical packing arrangement. This configuration results in a pore shape that corresponds to 47.6% porosity (Fig. 3a). The configuration has traditionally been the subject of fundamental research of fluid flow through porous media, especially in the late nineteenth and early twentieth century (Kozeny 1927; Schriever 1930; Muskat and Botset 1931; Carman 1937) and more recently by Rumpf and Gupte (1971) and Fand et al. (1987). In many of these studies the degree of packing was determined by the porosity of the samples and the exact particle arrangements were never truly clear. Newer studies have investigated this packing arrangement numerically by applying computational methods with the Navier–Stokes equations (Hill et al. 2001). Numerical studies of other geometrical configurations have more recently been carried out by Newman and Yin (2013), Turkuler et al., (2014), Schulz et al. (2019).
The effects of particle angularity on permeability are considered in the second sample design. The angular configuration (B) consists of octahedron particles that are packed identical to that of the spheres (A), where the diagonal length of the octahedron is 1.0 mm. The six points of contact between each octahedron particle and the size of the octahedron are such that it fits within a sphere of equal diameter (Fig. 3b). The number of individual particles and pores is still 3500 (Table 2), but the porosity increases to 83.3%. In sample C the length dimensions of the octahedron particles are reduced by a factor of two, to 0.50 mm, while all other parameters remain unchanged. This increases the number of particles and pores in the sample by a factor of eight and the sample consists of 28,000 individual 0.50 mm particles (Tables 2 and 3). The porosity remains the same as for B, but the flow channels through the sample are smaller and the surface area of the solid matrix is increased by a factor of two.
The final particle configuration, sample D, consists of the same 1.0 mm octahedron particles as sample B (Fig. 3d). The specific geometry created by the octahedron particle beds allow for a second set of equal octahedrons to be fixed in-between the first octahedron configuration of sample B, without the second set touching the first set. The second set introduces a denser form of packing and the configuration corresponds to 66.6% porosity. The inter-fixed particle bed induces a tortuous channel pathway and increases the surface area of the solid matrix by a factor of two. The number of particles in the design is doubled to 7000, but the number of representative pores is increased by a factor of eight, corresponding to 28,000 pores.
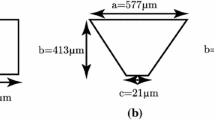
The relative size and shape of the individual pores found in the four samples are shown in Fig. 4. The pore shape of sample A is curved and has the smallest pore throat ratio a = 0.215 by definition of Eq. 27. The pores of sample B & C are cubical and has a pore throat area ratio of a = 0.500. The pore of sample D is subdivided into eight pores of equal shape and size to highlight the internal octahedron particle and the corresponding tortuous pathway of the pore. This helps to show that the pore body of sample D is rectangular (aspect ratio ≈ 2/1). The pore shape is less diverging than the other samples with a pore throat area ratio of a = 0.666.
The corresponding pore shapes and relative sizes of the pores in the porous medias in Fig. 3. The pore throat is red colored. a Sample A pore throat is 0.215 mm2 and the area ratio a = 0.215. b Sample B pore throat is 0.500 mm2 and the area ratio a = 0.500. c Sample C pore throat is 0.125 mm2 and the area ratio a = 0.500. d Sample D pore throat is 0.125 mm2 and the area ratio a = 0.666. The pore is sliced into eight parts to reveal the location of the internal particle and the corresponding tortuous pathway. Two of the pores are shown here
The tortuosity listed in Table 2 applies the definition of τ = Le/L, where the center axis of pore length, Le, is longer than the length of the superficial flow axis, L (Epstein, 1988). For samples A, B, and C the pores are inline with each other and the flow axis and the pores are not tortuous in terms of the definition. The sample D pores are offset by the interfixed particle and the octahedron shape dimensions which provide τ = 1.2247 according to the Pythagorean equation.
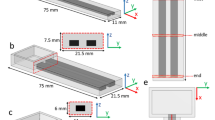
The main design parameters are listed in Table 3. The sample design focuses on preserving the integrity of the pore-space matrix throughout the samples. In classical permeability experiments, the sample material is inserted into a hollow cylinder. The cylinder must have a wide enough diameter to ensure minimum effects from the container wall on the packing arrangement of the material (Fig. 5a) (Carman, 1937; Fand et al. 1987). This issue is avoided in the presented design solution by building the wall and sample material together in parallel. A cylindrical wall will never yield a satisfactory pore-matrix configuration when the particle packing arrangement is cubical (Fig. 5b). A cubical container in which all pores are equal contains the samples in this experiment. This is achieved by cutting the particles along the wall at the interface of the pore boundary and fixing these particles to the container wall (Fig. 5c). This approach allows for the exact calculation of the remaining surface area provided by the container wall and this is included in the over-all sample evaluation in Table 3.
The sample design avoids unwanted effects caused by container wall geometry. a The cylinder container in classical experiments affected the packing arrangement of spheres. b A cylindrical container will affect the pore shape and size in the adjoining layer when the packing arrangement is cubical. c The cubical container in this experiment provides consistent pore shapes and sizes throughout the sample. The cube has an internal dimension of 10.0 mm·10.0 mm in the X-axis and Y-axis. d The complete sample design with sample length of 35.0 mm in the Z-axis. To ensure a good fit for the samples in the Hassler cell, the samples are fabricated with an integrated impermeable cylindrical shell fitting
Six duplicates of each sample were fabricated to show the statistical discrepancies in the final product and to provide a means of control and reference in the permeability testing procedure. To ensure a good fit for the samples in the Hassler cell, the samples were fabricated with an integrated impermeable cylindrical shell fitting (Fig. 5d).
3.2 Sample fabrication
Additive manufacturing (AM), 3D printing, refers to a group of production methods where material is added and constructed successively, often layer by layer. AM is normally divided into seven categories (ISO/ATSM, 2015). The Powder Bed Fusion (PBF) category, with the specific PBF-LB subcategory utilizing laser beam, is the method applied in this study. PBF-LB describes a process where a layer of powder is spread on top of a substrate, thereby selectively being melted into a solid with a laser. These melted stacks will grow into the predefined shape that was described by the computer-aided design model. Building a part layer by layer has the advantage of turning difficult 3D shapes into simple 2D-layer projections that are easier to handle and produce. Each sample was designed and sketched in the Autodesk® Fusion 360™ CAD program. The CAD models were converted to stereolithographic (STL) format and were manufactured in a Concept Laser M2, PBF-LB machine with maraging steel Marlok C1650 powder. The machine is equipped with a 200 W diode pumped Yb:YAG fiber laser with continuous wave mode and a laser beam diameter of 0.150 mm and a wavelength of 1050 nm. The spherical gas-atomized powdered material (Marloc C6150) has a size distributed of 5–22 µm. This size distribution is relatively small compared to standard powder batches and is ideal for geometries that require fine details in the finished product (Vock et al. 2019).
The key to producing fine particle structures is in applying the correct sample design, building sequence, and production parameters in the PBF-LB process. The production parameters have the governing role in the manufacturing. The samples were designed to build 2D projections of the X-axis and Y-axis layer by layer along the Z-axis of the machine (Fig. 5c). It is not trivial to achieve good surface and tolerances in a shape that grows along this Z-axis, as this causes an overhang (Akram et al. 2018; King et al. 2015; Malekipour and El-Mounayri 2018). This mean that the laser beam will inevitably penetrate deeper than intended in the Z-direction, especially if standard production parameters are utilized (Trapp et al. 2017). The result is a surface that is larger than the specified dimensions and the surface has a rougher finish.
It is crucial that the laser beam does not burn through many powder layers but is melting just enough to get an impermeable outer particle shell with an acceptable surface roughness and pore-matrix configuration. The standard PBF-LB production parameters were not appropriate for this study and the customized parameters utilized were provided from an independent, unpublished study where fine geometries were much more important than mechanical strength of the sample. The Marloc C6150 steel has extraordinarily good mechanical properties (Brøtan et al. 2016), which make it unnecessary to discuss the strength of the sample parts for the applied pressures (eight bar) and stresses in the permeability tests. The specimens were built with one contour at 500 mm/s laser speed at 50 W with a layer thickness of 0.03 mm. The inner section had similar parameters with parallel scanlines 45 degrees on to the machine X-axis (Fig. 5c). For each layer the scan lines were rotated 90 degrees. The hatch spacing, which is the distance between the laser scan lines, was set to 0.105 mm. The customized parameters contributed to minimum Z-axis penetration.
3.3 Sample inspection, CT imaging, and image analysis procedures
Due to the specific design of the samples, traditional measuring and control equipment could not be used without destroying the samples. Porosity measuring devices, e.g., Helium or Nitrogen porosity meters, or surface area measurement techniques, e.g., gas adsorption methods (BET), were unsuccessful. To determine the internal properties of the samples, the samples were examined externally in a microscope and inspected internally in a Nikon XT H 225 ST industrial CT scanner.
The CT images and image analysis techniques were utilized for the estimation of sample porosity, internal surface area, and for calculation of the area ratio component, a, that is needed for the empirical correlations. Due to time and funding limitations only the samples A3, B3, B6, C1, and D3 samples could be sufficiently analyzed. These samples were selected randomly from the different duplicates. The large density contrast of the steel particles to the air-filled voids in the samples contribute to high-quality images. The voxel size in the CT images was 22.297 µm in all three dimensions (X, Y, Z) for the image analysis of samples A3, B3, B6, and D3 (similar size as the Marlok C1650 powder). The resolution was improved to 8.466 µm for all three dimensions (X, Y, Z) for sample C1. The CT images were filtered and analyzed with the VGSTUDIO MAX 3.1 software package. A greyscale threshold algorithm was applied to reduce noise and structural artifacts in the CT images and to determine the particle shape, size, and form in the different samples (Fig. 6). The sample porosity and sample surface area of the particle matrix were determined through volume analysis on the voxel data with the marching cubes method. The porosity was measured as a volume ratio of the designated void voxels to the solid voxels. The surface area of the solid voxels provided the surface area data. The CT-image stacks of the various shape matrices were further subjected to image analysis using the ImageJ 1.52a software package on pixel data for comparison. The open space (porosity) was measured as an area measurement by using the “Intermodes” auto threshold method and calculated as the ratio of the measured area to the total image area. This supplied the area ratio component, a, measurements.
3.4 Permeability test procedure, calibration, and equipment
The permeability measurements were conducted with the constant flow rate methodology (McPhee et al., 2015). The absolute–permeability cell setup (Fig. 7) consists of a horizontal oriented, pressurized, 38.0-mm-diameter Hassler cell which is connected in parallel to three circulatory pumps and an outlet reservoir tank. The Hassler cell is customized with two enlarged feeding nodes that incorporate a fixture for the pressure transducers (P1 and P2 (type: GE Druck PTX5072-TA-A3-CA-H1-PA-0-250mbara) with 0.1 kPa accuracy) and an enlarged 11-mm-internal diameter feeding pipe (Figs. 7 and 8). The enlarged feeding pipe ensures negligible parasitic pressure losses from the cell components between the P1 and P2 sensors within the flow rates provided by the pumps. The combination of two VP-12 K Vindum Pumps and one 260D Teledyne ISCO pump provides a complete range of flow rates from 0.0001 to 165.0 ml/min with a pulse-free and continuous mode of rate delivery. The rates utilized in this study are 7.5–165.0 ml/min corresponding to superficial velocities from 0.0012 to –0.0275 m/s. The feeding nodes and the 3D core sample are fixed within the Hassler cell with an airtight rubber sleeve that is pressed around the core and feeding nodes with eight bar confining pressure. The cubical container samples are fabricated with a cylindrical shell fitting to ensure a tight sealing with the rubber sleeve and no leakages along the wall (Fig. 8).
Schematic sketch of the absolute-permeability cell setup. The T1-temperature sensor measured room and oil temperature during the test. The P1 and P2 pressure transducers are mounted in customized fixtures at the ends of the Hassler cell. The pumps are connected in series. The interior of the Hassler cell is shown in Fig. 8
Customized Hassler cell. Left: Picture of test preparations. Sample being inserted into the cell before mounting of the pressure sensors. Right: Schematic sketch of the interior of the cell with a 11-mm-internal diameter fixture for the pressure sensors. The cubical container core samples have a cylindrical shell that fits in the 38 mm diameter chamber and prevents flow outside of the cubical container core. The rubber sleeve is pressed around the fixtures and core sample with eight bar pressure
The circulation fluid was EXXSOL D60 oil at room temperatures (20.2–21.4 °C). The oil density of 790 kg/m3 was measured by an Anton Paar Density Meter, DMA 5000 M at room temperature (21.0 °C). The dynamic viscosity was measured with a SI Analytics KapillaryViscometer D50 to 0.001384 (Pa·s) at room temperature (21.0 °C) and 0.002543 (Pa·s) at (4.5 °C). The oil was dyed red to help locate leakages, from pipefittings etc., during the saturation procedure. The dye had no measurable influence on the density and viscosity measurements. During the saturation sequence, the Hassler cell was turned vertical and flooded from the bottom to help evacuate air from the cavities of the hollow cylindrical shell fittings (Fig. 8). A backpressure technique with an abrupt pressure drop (shocking) was applied to flush trapped air from the interior pore-space matrix. The backpressure was built up and released incrementally from 1–7 bar. The technique was then repeated with the opposite flow direction and vertical orientation. The samples were deemed fully saturated when the initial flow test revealed no zero-shift from the pressure transducer responses in both directions (Fig. 9).
Multipoint test sequence of sample C6 with 24 individual flow rates from 7.5 to 165.0 ml/min. The four main sequences include a “no zero-shift” pause between each sequence to ensure no pressure shift in the sensors. The procedure provides duplicate measurements that confirm each rate measurement and reduce uncertainties in the data analysis
The permeability test followed the multipoint flow rate technique (McPhee et al. 2015), equivalent to the step-test procedure in large-scale aquifer testing (Kruseman et al. 1990). The testing sequence from the C6 sample is presented in Fig. 9 as an example. Each sample test incorporates 24 individual measurements divided into four main sequences of incremental flow rate increases followed by a mirrored flow rate decrease. The mirroring of the sequences provides duplicate measurements that confirm each rate and reduce uncertainties in the regression. Each point of flow rate was run until steady state was reached. The speed of pressure stabilization is a function of the sample length and the permeability of the sample. The time needed for each test was different for each of the four sample types. All samples displayed steady state within 20–40 s. A sequence of zero flow was included between the four main sequences to ensure that no zero-shift of the pressure response had occurred during the test. Each main sequence includes the rate 29.0 ml/min which provides seven measurements of the same reference level to ensure that no pressure shift had occurred between the four sequences (Fig. 9).
To verify k (Eq. 1), kF, and β (Eq. 2) attained with the EXXCOL D60 oil experiments some samples were cleaned with toluene and further tested with distilled water. Most of these tests were not satisfactory because the steel samples showed signs of corrosion upon contact with water. Precipitated iron hydroxide powders (rust) were seen on the particles after the tests. However, some data from these tests are provided to show the general behavioral change observed and to allow for comparison with other published works.
4 Results
4.1 Fabrication results
Details of different A, B, C, and D samples are presented in Fig. 10. The pictures show that surface roughness is the limiting factor for retaining the designed particle shape and form. The powder that border the designed particle surface boundary is partly melted and remolded into the sample during the fabrication. The resulting particle surface is not smooth on the microscopic level but inhibit a certain fraction of the surrounding powder as a rough “coating”. For instance, the fabricated contact point between two individual particles are slightly thicker than the designed specifications (Fig. 10b, c, e, and f), especially affecting the pore throat size of samples A and C more than the samples B and D.
Images of some of the 3D-printed test samples. a Sample A type with cubical container b Close-up of the 1.0 mm spheres. c Sample D type with free pore space between the two sets of octahedrons. d Sample B type without the cubical container. Notice the index finger for scale. e Close-up of the 1.0 mm octahedrons. f Sample C with cubical container
The average estimated properties of porosity, area ratio, and surface area for A3, B3, B6, C1, and D3 are presented in Table 4. CT images of the samples show that the particle size, shape, and configuration were essentially maintained. However, the rough coating of powder along the particle surfaces altered the pore-shape matrix compared to that of the original smooth particle specifications. The particles are slightly larger than intended in the design, especially in regions where they were not bound by a neighboring particle. A selection of different CT images is given in Fig. 11 to show these effects for a single particle bed of each sample. The figure shows three images of each sample. Each image depicts the X-axis and Y-axis (Ref. Fig. 5) of the samples and shows a different cross-sections of a specific particle bed within each sample. The “pore body” image represents the section with the largest channel opening within the pore. The “Dupuit” image shows the section with a channel opening corresponding to the estimated porosity of the bed (Table 4). The “pore throat” image shows the narrowest channel section of the pores in the bed. The alterations are most easily observed for the spheres of A3 which have a thicker connection between neighboring particles of the next bed in the pore body image (Fig. 11). This image should ideally be similar to the B3 image if the spheres were smooth. The contact points between the octahedrons are also thicker than the intended design, but the images of B3 and C1 show that the pore body section of the samples is less affected than A3. This also applies to D3, but here the contact points are seen in the pore throat image. The pore throat images show that the channel openings are smaller than intended. Comparison between the properties of Table 4 to those of the intended design in Table 2 confirms the observed differences. The samples have lower porosities, larger contraction ratios, and rougher and larger surfaces than intended.
Raw-data greyscale CT images. The images depict approximately 9 mm × 9 mm of the X-axis and Y-axis from a typical section of the particle beds of the cubical cores of A3, B3, C1, and D3. The “pore body” cross-section corresponds to the largest channel opening within the pores. The “Dupuit’s” cross-section represents the area ratio corresponding to the porosity given in Table 4. The “pore throat” image shows the narrowest channel section of the pores in the bed. The estimated geometrical data are presented in Fig. 12 and Table 4. The images are yellow markers in Fig. 12
Figure 12 shows the void fraction of the combined CT-image stacks from the same section of the particle bed seen in Fig. 11. The images shown in Fig. 11 are highlighted in yellow markers. The black voids in the CT images are designated as the channel opening along the bed and calculated as a void fraction. The length through the bed is the Z-axis of the samples in Fig. 11. The void fraction data in Fig. 12 confirm that for each 1 mm length of sample, A3 and B3 have one bed of particles and one constriction segment of the channel. Samples C1 and D3 have two. The theoretical void fraction of the intended design is shown as full lines in the figure. Compared to these lines, the samples display smaller void fractions and greater constrictions. The particles are also not fully symmetrical in the Z-axis of the sample, as is indicated by the non-symmetrical void ratios in Fig. 12. The lower half of the particles, e.g., from 0.5 to 1 mm of A3 and B3, are thicker due to the applied fabrication technique and the laser beam seems to have penetrated 2–3 layers beneath the particle boundary.
Estimated void fraction (dotted lines) through a typical section of the particle beds in samples A3, B3, C1, and D3 with reference to Fig. 11. The data start at the pore body cross Sect. (0 mm) and transgress through the pore throat of the bed to the next pore body. The images of Fig. 11 are highlighted in yellow markers along the curves. For each 1 mm length of bed, A3 and B3 have one constriction segment, while C1 and D3 have two. The smooth lines illustrate the theoretical void fractions that would have been the result if the particles were smooth and symmetrical (Fig. 3). The geometrical properties are summarized in Table 4
4.2 Hassler flow cell results
The results of the multipoint flow rate tests with EXXSOL D60 oil are presented in Table 5 and Fig. 13. The least square regression results of the pressure loss versus the flow rate data are obtained for both the linear fit (Darcy–Eq. 1) and the polynomial fit (Forchheimer–Eq. 2). The linear regressions only include the linear data of the test, which was done through iterative testing and comparison of the linear regressions (Fig. 13). The polynomial regression includes all the data points up to the maximum rate of 165 ml/min. All the samples show deviations from linearity after surpassing a threshold, termed critical velocity uc [cm/s] in Table 5. The uc is calculated as the rate of flow where the linear regression yields approximately 1% lower differential pressure loss than the polynomial regression. The uc is calculated from superficial velocity because this velocity is used in the empirical correlations. The onset of uc is observed at lower velocities for sample A and progressively increases in sample B–C–D, respectively. This affects the number of measurements (i) included in the linear regression because the point of divergence is different for the four sample types, while the measurements are conducted on the same intervals. The accuracy of the pressure sensors is displayed in Fig. 13c as a reference and shows that some of the data points of sample B are close to the sensor limits. All other samples were within sensor accuracy range.
Experimental results for the EXXSOL D60 oil multipoint Hassler flow cell tests for samples A, B, C, and D including all the 23 duplicates. The data are plotted as differential pressure loss per unit length versus the superficial velocity, ΔP/L vs. us. The velocity range of the tests is 0.00121–0.0275 m/s (7.25–165 ml/min). Linear least square regression fits are shown in dashed lines in figures a, c, e, and g, while polynomial least square regression fits are shown in full lines in figures b, d, f, and h. Regression results are presented in Table 5
The permeability (k) of samples A1–A5 range from 641 to 738 D (6.33 × 10−10 to 7.18 × 10−10 m2) and samples C1–C6 display the range k = 756–920 D (7.46 × 10−10 to 9.07 × 10−10 m2). The largest k is observed in samples B1–B6 with the range 7 796–9 988 D (7.69 × 10−9 to 9.86 × 10−9 m2), more than one order of magnitude larger than that of the other sample types. The lowest permeabilities are observed in samples D1–D6 with the range of 440–619 D (4.34 × 10−10 – 6.11 × 10−10 m2). This indicates some slight differences in the pore-matrix geometry of the different samples in each sample group, even though the duplicate samples were fabricated in parallel with the same Marlok C1650 powder batch, AM equipment, and laser beam specifications. This is most clear with samples B3 and D4 in Figs. 12g and 13c, which display markedly steeper tangent lines and lower permeability than the others in their respective group.
The permeability k of Eq. 1 is typically slightly less than kF of Eq. 2, most clearly observed for samples A1-A5. The polynomial regression generally offers marginally better R2 than the linear regression, but the higher kF tend to slightly under-estimate the pressure drop at the lowest rate of flow, 7.25 ml/min (0.00121 m/s). The linear regression slightly overestimates the pressure drop compared to the measurements at the lowest rates of 7.25 and 14.5 ml/min (0.00121 and 0.00242 m/s), which suggest that a small portion of non-linear losses are included in the regression. These variations are too small to be seen in Fig. 13, but they insinuate that the correct permeability is presumably found somewhere between the two regressions presented.
The inertial resistance factor (β) of samples A range from 23,608 to 38,861 m−1, which is considerably larger than that of the other sample types. However, the magnitude of the β is dependent of the permeability. For instance, the B1–B6 samples display the lowest β of 903–1 110 m−1, which is more than one order of magnitude smaller than the A1–A5 samples. This is opposite to the observed permeability behavior. To compare the relative magnitude of the β one must evaluate the ratio of the inertial component to the viscous component, βρ/(µ/kF) in Table 5. For A1–A5 the ratios are 9.4–14.9, which is twice as large as those of 5.0–6.1 and 4.58–7.64 for B1–B6 and C1–C6, respectively. The ratio for the B and C samples is twice as large as those of sample D of 2.33–2.76. This is reflected in the curvature of the data in Fig. 13 and corresponds to the same tendency in the observed onset of uc occurring at lower superficial velocities for samples A than samples B–C–D, respectively. This is seen in Fig. 13b where the curvature of the data is more profound for A1–A5 than for other B–C–D samples in Fig. 13d, f, and h.
A multipoint test with distilled water for sample A3 is presented in Fig. 14 to demonstrate the general behavioral change for different fluids. The density of water (998 kg/m3) is higher than the oil density (790 kg/m3), while the viscosity of the oil (1.38 mPa·s) is higher than for water (0.994 mPa·s). The linear data in Fig. 14a for distilled water show lower pressure losses than oil, but the divergence from streamline flow is observed at a lower velocity. This agrees with oil having higher viscosity than water (Table 5). In Fig. 14b the pressure loss for distilled water is higher than for oil after the velocity exceeds approximately 2.3 cm/s. This agrees with water having a higher density than oil. The regression results in Table 5 show that the permeability attained with distilled water is not equal of the oil permeability. Some rust was identified on the steel spheres after the test and this might explain the differences.
Experimental results for the EXXSOL D60 oil and distilled water from the multipoint Hassler flow cell tests of sample A3. The data are plotted as differential pressure loss per unit length versus the superficial velocity. The velocity range of the tests is 0.00121–0.0275 m/s (7.25–165 ml/min). Linear least square regression fits are shown in dashed lines, while polynomial least square regression fits are shown in full lines. Regression results are presented in Table 5. a The pressure losses for distilled water are lower than for oil, but the divergence from linear flow occurs earlier. The stars indicate the onset of critical velocities, uc, of the two experiments. This is expected because of the higher viscosity of oil. b The pressure losses for water surpass that of oil at approximately 2.3 cm/s, due to the higher density of water
4.3 Empirical correlations
The empirical correlations of the experimental data (Eqs. 1 and 2) to the Kozeny–Carman equation (Eq. 20) and the Ergun equation (Eq. 30) are presented in Table 6. It is convention for these equations to be described according to a representative particle diameter of the porous media (Carman, 1937; Ergun and Orning 1949; Fand et al. 1987; Macdonald et al., 1979). This is typically done through introducing the spherical relation of Eq. 31.
where the particle diameter, d (m), the porosity of the bed (n), and a surface factor that account for particle roughness and shape, φ (-), is defined to describe the specific surface area, S. For a single particle the surface factor, φ, is unity for smooth spheres and less than unity for all other shapes. The same convention is therefore presented as an additional equational form (Eqs. 33, 35 and 37) in Table 6, so that the results can be easily compared.
The Kozeny–Carman equations are correlated to the Darcy equation (Eq. 1), which corresponds to Eqs. 32 and 33. The only unknown parameters in Eqs. 32 and 33 are the constants kC and XC, respectively, and these constants are adjusted to achieve a best fit with the regression data of Eq. 1.
Ergun equation is correlated to the Forchheimer equation (Eq. 2), which corresponds to Eqs. 34, 35, 36, and 37. The only unknown parameters in Eqs. 34, 35, 36, and 37 are α0, XE, β0, and YE, respectively, and these constants are adjusted to achieve a best fit with the regression data of the linear and polynomial term in Eq. 2, respectively.
The empirical correlations of the experimental data (Eqs. 1 and 2) to the new analytical Navier–Stokes approximations (Eqs. 18 and 29) are presented in Table 7, with the same input data of Table 6. The Stokes flow approximation are correlated to the Darcy equation (Eq. 1), which corresponds to Eq. 38. Equation 38 has two unknown coefficients, C and k0, and these two parameters are treated as a single unknown coefficient, kS (Eq. 19), which is adjusted to achieve a best fit with the regression data of Eq. 1. Equation 19 is then applied to see how the k0 factor would result should the dissipation coefficient be defined C = 3π.
Equation 29 is correlated to the Forchheimer equation (Eq. 2), which corresponds to Eq. 39 and 40. The unknown parameters in Eq. 39, are C, k0, and these are treated equal to the coefficients in the Stokes flow approximation (Eq. 38) and are adjusted to achieve a best fit with the regression data of the linear term of Eq. 2. The CKL are adjusted to achieve a best fit with the regression data of the polynomial term of Eq. 2.
4.4 Critical Reynolds numbers
Three types of critical Reynolds numbers are presented in Table 8 to allow for comparison with values found in the literature. These numbers are typically utilized to describe when the flow characteristics deviate from linearity. The most common definition is that of Eq. 41, where the characteristic length is described by the diameter of the particle in the bed. Bear (2013) states that this definition provides ReC1 within the range 1–10 for porous media. Table 8 shows that all of the samples achieve numbers within this range. The definition of ReC2 follows the definition suggested by Blake (1922) and is the same definition used by Carman (1937) (Eq. 42). Carman (1937) concluded that Eq. 20 is valid for critical velocities corresponding to ReC2 ≈ 2.0. Table 8 shows that the samples B3 and B6 achieve similar values, while samples A3, C1, and D3 have values less than one. The Reynolds number definition utilized in this paper is presented in Eq. 4 and critical Reynolds numbers of this definition correspond to ReC3 in Eq. 43. Table 8 shows that all samples attain ReC3 < ≈ 1
An alternative definition is presented in Eq. 44 where the divergence from linearity is described as a ratio of non-linear over linear dissipation.
5 Discussion
The presented experiments show that AM in combination with high-resolution CT imaging technology and image analysis software enables the construction and detailed inspection of complex porous media. In this paper it was found that it is the combination of these three different 3D technologies that provide the full benefit of each individual technique. The technologies complement each other because they limit uncertainties in the interpretation of the pore-matrix configuration, especially if compared to conventional porous media studies, e.g., where particles are poured into a cylindrical container. In the presented work, the problem of the container wall affecting the particle arrangement of unconsolidated material is avoided. The exact placement of each particle can be controlled through the design and fabrication of the 3D samples. Since the properties of the design are known they can serve as a reference upon comparison with the final product. After fabrication, the CT imaging and image analysis software can provide a complete and highly accurate rendering of the samples which allows for comparison with the design properties. This allows for testing of geometries that previously would have been impossible to achieve. This demonstrates the potential benefit of combining these 3D technologies in porous media studies.
An issue for metal-based AM fabrication powder materials is the possibility that the material reacts with the fluid. This is observed in the presented experiments for oil and distilled water. The regression results in Table 5 show that the permeability attained with distilled water is not equal to the permeability attained with oil. This suggests that the difference in fluid properties do not fully explain the behavior of the data shown in Fig. 14. Corrosion products (rust) were identified in the samples after the test with distilled water and this is a probable explanation to the different permeabilities of the A3 sample. Other fabrication powder materials that would eliminate the corrosion problem, e.g., Aluminum, Titanium, or other stainless-steel blends or even plastic resins are readily available on the global market. Investigating how these powders react with the testing fluid is therefore recommended before performing the permeability tests.
5.1 Fluid flow through porous media
The Hassler flow cell test results demonstrate that the permeabilities (4.34·10−10 – 9.98·10−9 m2) of the four sample types (which have sand sized particles; d = 1.0 mm and d = 0.5 mm) are within the range of permeabilities associated with unconsolidated sandy soils (Bear, 2013). Medium to coarse sand have permeabilities between 10−11 and 10−9 m2 (Bear 2013; Freeze and Cherry, 1979). The permeabilities of the four sample types (A, B, C, and D) are different and they are also slightly different for each sample within each sample group. The CT images of the five selected samples confirmed that the particle shapes, sizes, and configurations are preserved in the samples (Fig. 11). This argues that the variations of permeability within each group are caused by slight variations in porosity, surface area, and surface roughness of the individual samples in each sample group. Comparison of B3 vs. B6 data in Tables 5, 6, and 7 supports this statement.
For the packing arrangement with the cubical particle bed configuration, the alteration of particle shape from samples A to B displays a large influence on the permeability, from 641–738 D (6.33·10−10 – 7.18·10−10 m2) to 7796–9988 D (7.69×10−9 to 9.86×10−9 m2), respectively (Darcy regression). While this is expected, it is surprising to see that the lowest permeability is observed in samples D with the range of 441–619 D (4.34×10−10 – 6.11×10−10 m2). Both the sample B and D configurations consist of particles with the same size and shape, but the inter-fixed octahedron bed of sample D evidently alters the pore-matrix geometry drastically. The same trend is observed when the size of the particles is reduced from samples B to C. This demonstrates that it is not the particle shape or size that determines the permeability, but the corresponding pore shape and pore size that results from the packing of particles. These observations have good agreement with the literature (e.g., Bear 2013).
The empirical correlations on the linear flow data (Darcy regression in Table 5) show that the Kozeny–Carman equation attains coefficients of similar magnitude to those published by others, kC = 3.92–7.60 (Eq. 32) and XC = 141-274 (Eq. 33). Carman (1937) reports kC values ranging from 4.84 to 6.13 from testing on randomly packed beds of smooth glass spheres. Fand et al. (1987) report XC values ranging from 174 to 184, also from testing on randomly packed beds of smooth glass spheres. Even though the particle shapes, sizes, and packing arrangements of these various sample groups are different, it is interesting to note that the coefficients provided by the Kozeny–Carman equation are very similar. However, the presented experiments demonstrate that the analogy to the pipe geometry factors suggested in Eq. 21 by Carman (1937) is not correct for porous media. The tortuosity (τ) of samples A3, B3 B6, and C1 is unity, while it is 1.2247 for sample D3. The upper limit for the pipe geometry factors is 3.0 (Table 1). Consequently, there are no pipe geometry factors that can describe any of the datasets. The kC coefficient is therefore not a function of the tortuosity factor (τ2) and the pipe geometry factors (k0) in the form of Eq. 21 (corresponding to Eq. 45) for non-uniform pore channels.
In the Darcy flow region, the Stokes flow approximation coefficient kS derived from correlations with the linear regression is identical to the kC of Kozeny–Carman for A3, B3, B6, and C1, where the tortuosity is unity. The main difference is seen in the sample D3 results where the kS coefficient now resembles the other octahedron samples. The resulting geometry factors, k0, for the octahedron particle beds B3 (k0 = 1.81), B6 (k0 = 1.80), and C1 (k0 = 1.80) closely resemble the factor of a square (k0 = 1.78), or closer to a 2 × 1 rectangle (k0 = 1.94) for sample D3 (k0 = 1.86). These coefficients have good agreement with the actual shape of the pore body geometries of the sample configurations (Fig. 3, Fig. 4, and Fig. 11), where the pore bodies of samples B and C are squares, and sample D is rectangular. The geometry factor for sample A3 (k0 = 2.40) does not resemble that of a circle (k0 = 2.0). The geometry factors closest to the k0 value of sample A3 are elliptical or rectangular shapes (Table 1). All the five samples A-D achieve geometry factors within the range of possible values and samples B, C, and D show good agreement with the observed shape of the pore channel. These results argue in favor of the assumption that Eq. 19 can be approximated by the 3π constant (Eq. 46) for non-uniform pore channels.
Mao et al. (2016) note that the “Forchheimer” permeability (kF) is not always equal to the Darcy permeability (k). This is also observed in this study and this affects the empirical correlations. The empirical correlations between the non-linear flow data (Forchheimer regression in Table 5) show that the Ergun equation attains linear coefficients, α0 = 1.87-3.77 (Eq. 34) and XE = 135-271 (Eq. 35), similar to those published by others. The sample A3 value (1.87) agrees with several of the experiments of Ergun & Orning (1949) who report a factor of α0 = 1.8–1.9 for tests with beds of spheres with 30.3–37.2% porosity. The XE = 135 of sample A3 agrees with the data of Rumpf and Gupte (1971) who report XE values from 124-162 on beds of glass spheres with 43.6–64.0% porosity. The non-spherical particles (B, C, and D) attain values of α0 = 2.43-3.77 and XE = 171–271. Dudgeon (1966) report tests on angular sand and gravel particles, where most of the data range approximately from XE = 159 to XE = 546. Similar ranges are also reported by McDonald et al. (1978) and Olatunde and Fasina (2018). The coefficients provided by the Ergun equation are relatively similar for a wide range of particle sizes and shapes. Since the analogy to the pipe geometry factor (circular pipe k0 = 2) is not correct for porous media in this equational form, α0 evidently adopts numerical values that have no logical meaning. Furthermore, the influence of the tortuosity factor (τ2) is not accounted for in the Ergun equation. The α0 will thus at best represent a clustered parameter that account for several erroneously defined geometrical variables.
The coefficient kSF (Eq. 39) derived from correlations with Eq. 29 to the non-linear regression data is identical to twice the size of α0 of the Ergun equation for A3, B3, B6, and C1, where the tortuosity is unity. The main difference is seen in the sample D3 results where the kSF coefficient now resembles that of the other octahedron samples. The resulting geometry factors, k0F, for the octahedron particle beds B3 (k0F = 1.92), B6 (k0F = 1.94), and D3 (k0F = 1.87) closely resemble a 2x1 rectangle (k0 = 1.94). These coefficients are still within the range of possible k0 values (Table 1), but only agree well with the pore body geometries of the samples with D3 configuration (Figs. 3, 4, and 11). Table 7 shows that the values of the kSF coefficients are consistently less than the kS coefficients. In the literature it is often suggested that the differences between Forchheimer permeability (kF) and the Darcy permeability (k) are a result of different flow characteristics within the porous media consisting of a variety of pore sizes (Forchheimer 1930; Carman 1937; Fand et al. 1987; Newman and Yin 2013; Mao et al. 2016). Inertial effects might then occur in the larger pores, while the smaller pores are still in the fully linear region. However, in the presented experiments the pores within each porous media are virtually equal. This suggests that the differences between kF and k might be an effect caused by the best-fit regression method applied to the experimental data.
Based on the results from the provided experiments it is shown that the assumption of Kozeny in Eq. 10 is proven suitable for porous media with homogenous pore matrixes. From a theoretical point of view the assumption is logical if viewed in relation to the assumptions enforced by the Navier–Stokes equation in Stokes flow conditions. In Stokes flow conditions the fluid wraps around the entire surface within the pore channels and the frictional shear forces act on all surface area available to the fluid (White 2006; Çengel and Cimbala, 2010). Applying Kozeny’s assumption is then in accordance with the assumption of Stokes flow. A pore channel’s specific surface area to volume ratio is thus the appropriate characteristic length unit (m) for porous media flows. This is not a controversial conclusion because the expression is essentially the same definition applied in conventional fluid mechanics for pipe flow. For a uniform pipe this characteristic length unit simplifies to an expression in relation to the internal diameter of the pipe (Eq. 6). For a non-uniform pore channel, the expression does not simplify any further. A shape factor (φ in Eq. 31) does seemingly enable the application of the particle diameter as part of the expression, but the diameter of a particle is not the actual characteristic length unit of which the flow behavior relies, a fact that frequently seems to be forgotten.
The new porous media equation (Eq. 29) is based on analogies to the analytical Navier–Stokes equations for pipe flows. In the Darcy flow regime, the analogy of porous media flow to the Stokes flow around a single sphere is perhaps controversial, but the correlation of Eq. 18 to the experimental data shows coefficients (kS) that agree well with experiments (Table 7) and the theory (Table 1). The resulting geometry factor (k0 of Eq. 19) of the four sample types is indeed consistent with the observed shape of the channels in the pore body center region. The success of the analogy presumably relies on the fact that the dissipating forces of the flow are not just a result of frictional shear dissipation alone, as in the Hagen–Poiseuille equation, but also incorporates a significant portion of pressure dissipation. The application of the Stokes sphere constant, 3π, implies that a significant portion (1/3) of dissipation losses are due to pressure dissipation. The pressure dissipation arises due to the non-uniformity of the channel geometry, which induced spatial variations to the strain rate field and induces acceleration of the velocity field within the flow through the porous medium. In uniform straight pipes this type of dissipation does not occur as the cross-section is uniform and there is no change to the velocity field along the pipe in steady-state flows.
Based on the results from the provided experiments it is shown that the effects of particle roughness do not alter the flow behavior in Darcy/Stokes flow conditions. A particle with rough surfaces rather provides more surface area on which the dissipating frictional shear forces of the fluid flow can act. This is evident through comparison between samples B3, B6, and C1 which all yield matching kS coefficients after accounting for surface area and porosity differences. This is also evident through comparison of the presented experiments with those of e.g., Carman (1937), Ergun and Orning (1949) and Fand et al. (1987) and others. The range of coefficients achieved for smooth particles, e.g., kC = 4.18–6.13 for smooth spheres (Carman 1937), is similar to those achieved for the different rough particle arrangements presented here (kC = 3.92–7.60). It is therefore important to describe the specific surface and the porosity of the porous media accurately when utilizing empirical equation for prediction purposes.
Macdonald et al. (1979) suggest that particle roughness should highly affect the flow dynamics in the “high” velocity flow region of the Forchheimer equation. This implies that the β0 and YE of Eqs. 36 and 37 would be expected to be relatively larger if the particle roughness had significant influence on the convective acceleration term. The empirical correlation of sample A3 results in β0 and YE equal to 2.45 and 1.84, respectively. These values are actually lower than the range β0 = 2.5-3.0, reported by Ergun & Orning (1949) on experiments on randomly packed beds of smooth glass spheres and lead shots. The data of Fand et al. (1987) on experiments on randomly packed beds of smooth glass spheres provide YE range of 1.811-1.925. The surface area-to-volume ratio of sample A3 is comparable to what would be expected from a bed of smooth spheres of similar porosity, but the particles are indeed very rough. Much higher factors of β0 and YE would therefore be expected if the particle roughness had significant influence on inertia at the velocities tested. The results thus prove contrary to the predictions of Macdonald et al. (1979).
The β0 and YE of the orthorhombic samples B, C, and D show seemingly random variability in their behaviors (Table 6). The B3 and B6 show low β0 values of 1.10 and 1.06, respectively, while sample C1 shows a high β0 value of 3.04, even though the cubic packing arrangements of the samples are identical. The high β0 of C1 agrees with the predictions of Macdonald et al. (1979) but the lower β0 of B3 and B6 argues that there is some other cause than the surface roughness that affects the behavior. The β0 and YE coefficients of sample D3 are also low and in a similar range to that of B3 and B6. Upon comparison, similar results are seen in, e.g., Dudgeon (1966) in his work on crushed marble and other granular material, or indeed, similar factors are achieved on the data of Becker (1947) on orthorhombic packings. Consequently, the application of the β0 does not yield consistent or logical results and the outcome is therefore difficult to predict. Furthermore, the influence of the tortuosity (τ) is not accounted for in the Ergun equation. The β0 will thus at best represent a clustered parameter that account for several undefined geometrical variables.
The convective acceleration dissipation coefficient CKL (Eq. 40), derived from correlations with the non-linear data of the Forchheimer regression, are small and are similar for all four sample types A-D. These values cannot be easily compared to β0 factors published in the porous media literature, but they are expected to be comparable to similar laminar pipe flows coefficients (KL range between 0.0 and 2.0). The dissipation coefficient CKL of all the samples, A3, B3, B6, C1, and D3, are within the range limits of KL found in the literature of pipes (Çengel and Cimbala 2010; Idelchik 1994; White 2006; Crane 1957). Furthermore, they are very small. These results suggest a low degree of wake formation or flow separation within the pores, and that most of the non-linear pressure dissipation is due to the continuous acceleration and deacceleration of the fluid through the pores. This demonstrates that it is the magnitude of channel contraction (a) that governs the dissipation of mechanical energy in Forchheimer flow, in good agreement with the numerical studies of Newman and Yin (2013).
The spherical particles of sample A3 display the lowest CKL = 0.03 which is probably due to the rounded particle shape and corresponding streamlining of the channel geometry through the pore throat. A specific value for KL-co of 0.03 (Eq. 25), similar to CKL of sample A3, corresponds to, e.g., a well-rounded and smooth pipe contraction segment in turbulent flow conditions (α = 1.05) (Tables 4–8 in Çengel & Cimbala, 2010). The marginally larger CKL coefficients of the octahedron samples B3, B6, and C1 can be explained by a less-streamlined channel geometry through the pore throat with more rapid changes along the pore channel length. It is also interesting to note that sample D3 has the largest CKL = 0.13 even though the β factor for samples D in Eq. 2 is the smallest of all the sample types. This can be explained by additional losses caused by the tortuosity of the channels. The alteration of the predominant flow direction from one pore to the next enforces a change in the velocity field not accounted for by the expansion of the channel alone (note that the modification leading to the τ3 factor in Eq. 29 is not performed to account for this effect).
The CKL coefficient should depend on the flow characteristics within the channel. This means that CKL should include a kinetic energy correction factor (Ref. equation 25 with α = 2.0), which infer that the flow is still fully laminar. This implies that the magnitude of the CKL coefficient is expected to decrease as the flow characteristics turns turbulent and α ≈ 1.05. A decrease of inertia is observed in several “high” velocity experiments, both analytically and numerically (Fand et al. 1987; Hill et al. 2010; Barree and Conway 2005), but this does not necessarily suggest a divergence from laminar flow condition. The divergence might be caused by separation of the laminar boundary layer, as presented and discussed in detail by Idelchik (1994) for conventional pipe flows. The limit of Re > 30–50 for laminar flow separation in pipe diffusers shown by Idelchik (1994) suggests that the laminar boundary layer is still in force for flow conditions similar to those in this study. The application of the CKL coefficient then offers an alternative explanation to the observed behavioral change of flow characteristics at higher Reynolds numbers, as opposed to the theories discussed by Barree and Conway (2005), on the existence of a “minimum permeability plateau” or the application of the cubic velocity term discussed by Firzoozabadi and Katz (1979) or Ezeudembah (1982).
5.2 Limitations of the equations
It is here shown that Eq. 29 works well for porous media consisting of multiple copies of equivalent pores. However, before applying the equation on different porous media, it is important to consider the limitations of the equation regarding the many assumptions underlying the applied modifications of the fundamental Eq. 3. The modifications are highlighted in Eq. 47 with different colors, signifying the modifications associated with the characteristic geometry of the porous media (green), the velocity field (red), the Stoke sphere approximation (blue—linear term), and the concept of minor losses in pipes (blue—non-linear term).

A significant share of the modifications results from the endeavor to describe the interstitial fluid velocity field within the porous media from a measurable superficial fluid velocity component (red color). The velocity modifications are particularly profound in view of the velocity component of the convective acceleration term. The importance of Kozeny’s assumption “…that the granular bed is equivalent to a group of parallel, similar channels…” has a major role in the limitations of the equation. If the channels of the porous media are a group of unparallel and dissimilar channels, as is often the case in natural soils, the modifications of the velocity field are unable to describe the flow relations by a single set of coefficients. A collection of different channel geometries would result in a collection of different velocity fields, each bound by the geometry of that particular pore channel within the porous media. The resulting “global” coefficients would then be an outcome of the average behavior of the sample.
The assumption of Kozeny does, however, not rely on the porous media to be homogeneous in terms of the size and shape distribution of the soil solids of the media. It is the pore-matrix configuration that determines whether the porous media is homogenous. As a consequence, Eq. 29 might function well as long as the mixture of soil particles and their arrangement result in a homogenous pore distribution. An inhomogeneous pore distribution would, however, complicate the matter because the divergence from linear flow occurs earlier for large pores. Additional non-linear dissipation will then occur in parts of the media while other parts will still be fully in the linear flow regime, as Forchheimer (1930) pointed out. It is therefore relevant to consider when the convective acceleration term must be accounted for.
The divergence from linearity is typically assessed through evaluation of the critical Reynolds number of the flow. A variety of critical Reynolds numbers have been presented in Table 8. The critical numbers of ReC1 and ReC2 are both within the expected range of each definition. The Reynolds number definition used in the Stokes approximation (ReC3) is less than one for all samples. This is consistent with the critical number criterion of Re < ≈1 for Stokes flow in general (White, 2006). The criteria of Stokes flow approximation require that the Re ≪ 1 when applying the linear term of Eq. 3 alone on fluid flow problems. Although the ReC1, ReC2, and ReC3 definitions fulfill this requirement experimentally, they do not provide information about the relative magnitude of the inertial versus the viscous component observed in the flow data (Figs. 13 and 14). This is only achieved with the ratio RC, where the samples have ratios between 0.02 and 0.06 (Table 8). This ratio essentially state that the non-linear term is 2–6% of the magnitude of the linear term for the critical velocity used in the equation. This might be a more useful definition for prediction purposes.
Unlike the conventional Reynolds number definitions, the ratio RC incorporates the factors and coefficients (CKL and 1/a2) that account for the constriction and expansion of the pore channel. If a pore channel has a severe constriction, 1/a2 will be a large number, which implies that the divergence from linearity has to occur at relatively lower flow velocities. Alternatively, if there is no contraction of the channel, the CKL (Ref. equation 25) will approach zero, and there will be no divergence from linearity, even at very high flow velocities. Presumably this applies until the onset of turbulence, such as for conventional pipe flows (RePipe ≈ 2300).
6 Conclusion
The presented experiments demonstrate that the application of AM, CT imaging, and image analysis techniques represents an improvement in porous media studies. These 3D technologies enable the study of porous media in a controlled fashion and allow experimental testing on geometries that would otherwise be impossible to achieve with conventional study methods on natural soils or particle beds. Uncertainties regarding the geometrical properties are minimized because the 3D-printed porous media samples can be evaluated with CT imaging after fabrication. This combination of 3D technology improves the data acquisition and data interpretation and contributes to new insight into the phenomenon of fluid flow through porous media.
The presented experiments confirm that the equations of Kozeny–Carman (1937) and Ergun–Orning (1949) can be adjusted to fit the experimental data. However, their underlying fluid mechanical theory do not describe the variation in geometrical properties properly. This is due to the analogy of porous media flows to the Hagen–Poiseuille flow relation, which is seemingly inaccurate for non-uniform pore channels.
The empirical relations of the Darcy equation and the Forchheimer equation can be explained through the analogy to the analytical Stokes flow approximation and the analytical solution of the convective acceleration term of the Navier–Stokes equation. The success of applying the Stokes sphere constant implies that the dissipating forces of the flow are not just a result of frictional shear alone but that a significant portion of dissipation losses are due to pressure dissipation as well. The pressure dissipation arises due to the non-uniformity of the channel geometry, which induced spatial variations to the strain rate field and induced acceleration of the velocity field within the flow through the porous medium. The new analytical Navier–Stoke equation (Eq. 29) provides geometrical coefficients that agree with the observed geometries of the 3D samples. The new equation addresses and, to some extent, modifies some frequently applied assumptions of porous media flow. The conclusions regarding these assumptions are as follows:
-
The assumption of Kozeny is applicable for porous media flow and Eq. 10 is the correct characteristic length unit for application in porous media flow equations.
-
The assumption of Dupuit (1863) on interstitial flow velocity is not the appropriate average velocity found within a non-uniform pore channel. An extension to Dupuit’s assumption is presented, where his assumption is viewed as an approximate value of the maximum velocity in the pore center. Correcting for the channel geometry provides a representative average velocity field of the pore body center. This velocity field is suggested as the analog to the “free stream velocity field” in Stokes flow, which allows for the 3π Stokes constant to apply to porous media flows.
-
A new critical ratio number, RC, that predicts when the Darcy equation deviates from linearity has been suggested. This definition provides diverging limits to the Darcy equation that are in line with the assumptions required for the Stokes flow approximation (Re ≪ 1) and might be useful for prediction purposes.
-
The tortuosity of a pore channel is an individual geometrical property of the porous media and functions as an input variable in Eq. 29.
These modifications of theory along with the experiments presented demonstrate that the effects of surface roughness do not affect the flow behavior in Darcy flow or in Forchheimer flow. The transition from Darcy flow to Forchheimer flow is largely governed by the ratio of constriction of the pore throat and the pore body. This constriction ratio governs the relative acceleration of the fluid and the corresponding inertia that are associated with higher flow velocities in porous media.
In order to evaluate the new theory and equations, there is a need to perform more permeability tests on porous media where the pore geometry is well defined and known. This will probably be achieved soon since the 3D printing and CT imaging technologies are mature enough to provide a means to do so already. Further work should also be focused on porous media with different pore size distributions and pore-shape variations. Combined with investigations of flow conditions into the region of higher Reynolds number flows, this will provide a better understanding of porous media flow and the transition from laminar to the turbulent flow regime in porous media.
References
Akram, J., Chalavadi, P., Pal, D., Stucker, B.: Understanding grain evolution in additive manufacturing through modelling. Addit.Manuf. 21, 255–268 (2018)
Allen, J.R.L.: Principles of physical sedimentology, Allen & Urnwin London, England (1985) ISBN 0045510954
Barnea, E., Mednik, R.L.: A generalized approach to the fluid dynamics of particulate systems part III: General correlation for the pressure drop through fixed beds of spherical particles. Chem. Eng. J. 15(3), 215–227 (1978) ISSN: 0300-9467
Barree, R.D., Conway, M.W.: Beyond beta factors; a model for Darcy, Forchheimer, and trans-forchheimer in porous media. JPT 57(3), 43–45 (2005) ISSN: 01492136
Bear, J.: Dynamics of Fluids in Porous Media., Dover Publications Newburyport, England (2013) ISBN 0-486-13180-7
Becker, J. C.: M.S. thesis, Carnegie Institute of Technology, 1947
Blake, F.E.: The resistance of packing to fluid flow. Trans. Am. Inst. Chem. Eng. 14, 415 (1922)
Brinkman, H.C.: On the permeability of media consisting of closely packed porous particles. Appl. Sci. Res. Amsterdam, A1, 81–86 (1947), ISSN: 0365-7132
Brinkman, H.C.: A calculation of the viscous forces exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34 (1947) ISSN: 0365-7132
Brøtan, V., Åsebø Berg, O., Sørby, K.: Additive manufacturing for enhanced performance of molds, 6th Conference on Learning Factories. Procedia CIRP, 54, 186–190 (2016)
Carman, P.C., Fluid flow through granular beds. Trans IChemE, 15, 150–166 (1937). ISSN: 0263-8762
Çengel, Y. A; Cimbala, J. M. Fluid Mechanics: Fundamentals and Applications, 2nd edn., McGraw-Hill Boston (2010). ISBN 9780071284219
Chapuis, R.P.: Predicting the saturated hydraulic conductivity of soil: a review. Bull. Eng. Geol. Environ. 71, 401–434 (2012). ISSN: 1435-9529. https://doi.org/10.1007/s10064-012-0418-7
Collins, R.E.: Flow of Fluids through Porous Materials, The petroleum publishing company, Thulsa, 1976, ISBN: 0-87814-072-7
Crane Company, Flow of fluids through valves, fittings, and pipe, Crane Company Chicago, 1957
D’arcy, H.P.G., Les Fontaines Publiques de la Ville de Dijon, Victor Dalmont, Paris, (1856)
Dudgeon, C.R.: An experimental study of the flow of water through coarse granular material. La Houille Blanche No. 7, (1966). https://doi.org/10.1051/lhb/1966049
Dupuit, A.J.E.J.: Etudes Théorétiques et Pratiques sur le Mouvement des Eaux, (1863)
Epstein, N.: On tortuosity and the tortuosity factor in flow and diffusion through porous media. CES 44, 777–779 (1989). ISSN: 0009-2509, https://doi.org/10.1016/0009-2509(89)85053-5
Ergun, S., Orning, A.A.: Fluid flow through randomly packed columns and fluidized beds. Ind. Eng. Chem. 41(6), 1179–1184 (1949), ISSN: 0019-7866
Ezeudembah, A.S., Dranchuk, P.M., Flow mechanism of Forchheimer’s cubic equation in high-velocity radial gas flow through porous media. In: Proceedings of SPE Technical Conference and Exhibition, New Orleans (1982)
Fand, R.M., Kim, B.Y.K., Lam, A.C.C., Phan, R.T.: Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluids Eng. 109, 268–273 (1987), ISSN: 00982202. https://doi.org/10.1115/1.3242658
Firzoozabadi, A.; Katz, D.: Analysis of high-velocity gas flow through porous media, JPT 31(2), 211–216 (1979) ISSN: 01492136
Forchheimer, P.: Hydraulic, 3rd edn, p. 60. Teubner Verlagsgesellschaft, Berlin (1930)
Freeze, R.A., Cherry, J.A.: Groundwater. http://hydrogeologistswithoutborders.org/wordpress/1979-english/ (1979)
Gelhausen, M.G., Lenz, D., Krull, F., Korkmaz, V., Agar, D.W:; 3D printing for chemical process laboratories II: measuring liquid-solid mass transfer coefficients. Chem. Eng. Technol. 4, 798–805 (2018), ISSN: 0930-7516, https://doi.org/10.1002/ceat.201700295
Happel, J.; Brenner, H.: Low Reynolds number hydrodynamics with special applications to particulate media. Martinus Nijhoff Publishers, The Hague., The Netherlands (1983) ISBN: 90-247-2877-0
Hasimoto, J.: On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a periodic array of spheres. Int. J. Multiphase Flow 5, 317–328 (1959)
Hill, R.J., Koch, D.J., Ladd, A.J.C.: Moderate Reynold-number flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 243–278 (2001), ISSN: 0022-1120
Hubbert, M.K.: The theory of ground–water motion. J. Geol. 48, 785–944 (1940), ISSN: 00221376. https://doi.org/10.1086/624930
Idelchik, I.E.: Handbook of Hydraulic Resistance, 3rd edn., CRC Press, Boca Raton (1994), ISBN: 0-8493-9908-4.
ISO/ASTM 52900:2015 Additive manufacturing—Part 1: Terminology
King, W., Anderson, A., Ferencz, R., Hodge, N., Kamath, C., Khairallah, S., Rubenchick, A.: Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. (2015). https://doi.org/10.1063/1.4937809
Kozeny, J.: Über kapillare Leitung des Wassers im Boden. Wien Akad, Wiss 136(2a), 271 (1927)
Kruseman, G.P., Ridder, N.A.D., Verweij, J.M.: Analysis and evaluation of pumping test data, Wageningen, International Institute for Land Reclamation and Improvement (1990), ISBN: 9070754207
Macdonald, I.F., El-Sayed, M.S., Mow, K., Dullien, F.A.L.: Flow through porous media—the Ergun equation revisited. Ind Eng Chem Fund, 18(3), 199–208 (1979), ISSN: 01964313
Mao, D., Karanikas, J.M., Fair, P.S., Prodan, I.D., Wong, G.K.: A different perspective on the Forchheimer and Ergun equations. SPE J 21(5), 1501–1507 (2016). ISSN 1086-055
Malekipour, E., El-Mounavri, H.: Common defects and contributing parameters in powder bed fusion AM process and their classification for online monitoring and control: a review. The International Journal of Advanced Manufacturing Technology 95, 527–550 (2018)
Mcphee, C., Reed, J., Zubizarreta, I.: Core Analysis: A Best Practice Guide. Elsevier, (2015), ISBN: 0444635335
Muskat, M., Botset, H.: Physics 1, 27 (1931)
Newman, M.S., Yin, X.: Lattice Boltzmann simulation of non-darcy flow in stochastically generated 2D porous media geometries. SPE J. 18, 12–26 (2013). ISSN: 1086-055X. https://doi.org/10.2118/146689-PA
Olatunde, G., Fasina, O.: Modified Ergun equation for airflow through packed beds of Loblolly Pine Grinds. Kona 36, 232–240 (2018). ISSN: 02884534, https://doi.org/10.14356/kona.2019003
Osei-Bonzu, K., Grassia, P., Shokri, N.: Effects of pore geometry on flowing flow dynamics in 3D-printed porous media. Transp. Porous Med. 128, 903–917 (2018), ISSN: 0169-3913, https://doi.org/10.1007/s11242-018-1103-5
Raudkivik, A.J.: Loose Boundary Hydraulics, 3rd edn. Pergamon Press Oxford, (1990) ISBN 0-08-034074-1
Rumpf, H.C.H., Gupte, A.R.: Einflüsse der Porosität und Korngrößenverteilung im Widerstandsgesetz der Porenströmung. Chem. Ingenieur Technik, 43, 367–375 (1971), ISSN: 0009-286X, https://doi.org/10.1002/cite.330430610
Sangani, A.S., Acrivos, A.: Slow Flow through a periodic array of spheres. Int. J. Multiphase Flow 8, 343–360 (1981)
Schiller, L.: Über den Strömungwiderstand von Rohren verschiedenen Querschnitts und Rauhigkeitsgrades. Z. Angew. Math. Mech. 3, 2 (1923)
Schulz, R., Ray, N., Zech, S., Rupp, A., Knaber, P.: Beyond Kozeny–Carman: predicting the permeability in Porous media. Transport Porous Media (2019). https://doi.org/10.1007/s11242-019-01321-y
Schriever, Trans. Amer. Inst. Min. Metall. Engrs. Pet. Div., Vol. 86, pp. 333, 1930
Trapp, J., Rubenchik, A.M., Guss, G., Matthews, M.J.: In situ absorptivity measurements of metallic powders during laser powder-bed fusion additive manufacturing. Appl. Mater. Today 9, 341–349 (2017)
Turkuler, O., Moghtada, M., Unver, O.: Determination of Kozeny constant based on porosity and pore to throat size ratio in porous medium with rectangular rods. Engineering Applications of Computational Fluid Mechanics 8(2), 308–318 (2014). https://doi.org/10.1080/19942060.2014.11015516
Vock, S., Klöden, B., Kirchner, A., Weissgärber, T., Kieback, B.: Powders for powder bed fusion: a review. Progress in Additive Manufacturing 4, 383–397 (2019)
White, F.M.: Viscous Fluid Flow, 3rd edn. McGraw-Hill Boston, USA (2006). ISBN 9780072402315
Acknowledgements
Open Access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital). This work was conducted as a part of the research project Optimal utilization of groundwater for heating and cooling in Melhus and Elverum (ORMEL). The project is a cooperation between the municipalities of Melhus and Elverum, the Norwegian University of Science and Technology, Asplan Viak AS, and the Geological Survey of Norway. We would like to thank all the involved institutions and persons for cooperation and financial contributions. The authors would like to direct special thanks to Steffen Wærnes Moen, Roger Overå, and Noralf Vedvik for help with customizing the Hassler flow cell and calibration of the measuring equipment. Special thanks to Autodesk® Fusion 360™ for providing the educational CAD license free of charge.
Funding
The Norwegian University of Science and Technology, the Regional Research Funds in Mid-Norway (Grant Number 209074) and the PoreLab Center of Excellence funding scheme (no. 262644) funded this research.
Author information
Authors and Affiliations
Contributions
Conceptualization: SG; Theory: SG; Methodology: SG, VB, EL, OÅB & OTB; Formal analysis: SG; Data curation: SG, VB, EL, OÅB & OT.; Writing—original draft preparation: SG, VB & EL; Visualization: SG, EL, OTB; Writing—review and editing: SG, VB, EL, OTB, OT, RKR, BOH & BSF; Supervision: OT, RKR, BOH & BSF.
Corresponding author
Ethics declarations
Conflict of interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gjengedal, S., Brøtan, V., Buset, O.T. et al. Fluid flow through 3D-printed particle beds: a new technique for understanding, validating, and improving predictability of permeability from empirical equations. Transp Porous Med 134, 1–40 (2020). https://doi.org/10.1007/s11242-020-01432-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-020-01432-x