Uncertainty Quantification of Multiple Gas Transport and Sorption in Porous Polymers

Abstract

A high-fidelity physics-based model of mixed-gas transport coupled with kinetic and equilibrium adsorption is derived, and experiments were performed in order to calibrate and exercise the model. In the literature, a continuum-scale model that couples Fickian diffusion with Henry’s law absorption, and kinetic Langmuir adsorption was previously developed to describe the diffusion and sorption of moisture in porous materials. Here, we expand the model to gases, rather than moisture, derive, and implement a competitive adsorption mechanism into the model to enable mixed-gas sorption. This model facilitates a mechanistic-based understanding of the sorption and diffusion processes of mixed gases in polymeric materials. Diffusion and sorption experiments were conducted for a range of partial pressures; model validation and calibration were carried out by comparing modeled mass uptake and experimental data considering the uncertainties of conceptualized (or assumed) physical processes and system parameters. Uncertainty quantification and sensitivity analysis methods are described and exercised here to demonstrate the capability of this predictive model.

1 Introduction

Gas transport in polymeric materials is of importance to a variety of industries and applications (Dhingra and Marand 1998; Yeom et al. 2000; Harley et al. 2012, 2014; Sun et al. 2015). Quantifying and predicting the coupled sorption and transport of gases in materials enable accurate aging models of multi-material ensembles where gas transport and outgassing are rate determining steps. Advances in laboratory technology (e.g., gravimetric instruments) for experimentally measuring mass uptake and outgassing facilitate data collection and interpretation for coupled gas diffusion and sorption processes. While high-fidelity dynamic models have been developed for evaluating coupled diffusion–sorption mechanisms for water vapor in materials, no such model exists or has been validated for other gases. Unlike water vapor sorption/diffusion models, where the sorption of moisture in dry materials is mostly non-competitive, the sorption of one gas in a material will often necessitate a model capable of assessing the desorption of a competing gas. A mixed-gas transport and sorption model is crucial to the development of technologies to predict the performance of multi-material assemblies as they age.

The most popular procedure for calibrating mass uptake physics is to use the Crank analytical solution (Crank 1975, Eq. (4.23), P50) to a one-dimensional diffusion coupled with a linear absorption (Cox et al. 2001; Harley et al. 2012). This solution requires constant initial and boundary conditions, homogeneous domain, and linear sorption that simplifies the derivation of the standard diffusion equation using an effective diffusivity. These requirements limit the applicability of the model to a rather narrow range of conditions.

In the sorption modeling community, linear absorption (i.e., Henry’s law absorption) serves as the foundation for interpreting experimental data, and many stop there, with no loss of fidelity (Crank 1975). In instances where the sorption mechanisms are more complex, dual- and/or triple-mode sorption models have been developed to include adsorption (e.g., Langmuir) and clustering or pooling (e.g., Zimm and Lundberg 1956; Koros et al. 1977; Koros 1980; Stannett et al. 1980; Huang et al. 2003; Feng 2007; Yanniotis and Blahovec 2009; Li et al. 2013; Harley et al. 2012, 2014). The added complexity of the dual- and triple-mode sorption models, especially when they are coupled with gas transport (advection and diffusion), requires additional computational effort. For this reason, Langmuir adsorption and pooling/clustering are often treated as equilibrium reactions, and both the adsorbed and clustered concentrations can be calculated as secondary state variables that are not directly solved in partial differential equations for transport and ordinary differential equations for reaction kinetics. The dynamic nature of mass uptake in polymeric materials stimulated the study and development of kinetic adsorption models (Harley et al. 2014; Sun et al. 2015; Sharma et al. 2017, 2018).

Langmuir adsorption kinetics are described by rate equations of second-order forward reaction and first-order backward reaction (Harley et al. 2014; Sun et al. 2015). Although the gravimetric sorption and desorption method has been used to study steady-state (equilibrium) mass uptake behavior for a constant boundary concentration and temperature (e.g., Cavenati et al. 2004), the dynamic and transient diffusion and kinetic adsorption have not been well described mathematically. It has been demonstrated theoretically and experimentally that dynamic diffusion and kinetic adsorption play a significant role in mass uptake and outgassing processes (Didierjean et al. 2015). In a closed system (well- stirred cell), where advection and diffusion from system boundaries are not considered, analytical solutions of single-component Langmuir adsorption kinetics can be derived (Islam et al. 2004; Marczewski 2010). However, the dynamic nature of mass uptake in practical applications is mainly due to the time-dependent advection, diffusion, and kinetic adsorption. Without considering transport processes, the batch-mode adsorption kinetics are only applicable to a homogeneous and well-stirred system where advective and diffusive processes differ from the reality of reactive transport in porous media.

Recently, dual- and triple-mode sorption processes (Henry’s absorption, kinetic Langmuir adsorption, and pooling) have been coupled with diffusion (Harley et al. 2014; Sun et al. 2015; Sharma et al. 2017). The dynamic nature of vapor mass uptake has been presented by adsorption reaction rate, diffusivity, and material-specific tortuosity (Sharma et al. 2017). However, the transport model coupled with kinetic Langmuir adsorption was limited to single-gas component (vapor) and does not catch the competitive sorption kinetics of multiple gases in polymeric materials.

Here, we describe the application and modifications of the dynamic triple-mode sorption model in the investigation of uptake and outgassing of gases in a dynamic mixed-gas environment/experiment. The objective is to understand how gas concentrations vary with time and space within several materials due to various driving forces, including advection, diffusion, and reactions. In addition, this work explores and quantifies uncertainties of gas concentrations in terms of uncertain physical processes and system parameters.

2 Theory

2.1 Advection and Diffusion Model for Mixed Gases

The diffusion of moisture with kinetic Langmuir adsorption and equilibrium Henry’s absorption in a porous material was derived and published by Harley et al. (2014) and Sun et al. (2015, 2017) as:

$$\begin{aligned} \frac{\partial C_{\mathrm{T}}}{\partial t}= \frac{\partial \left( C_{\mathrm{H}}+C_{\mathrm{L}}+C_{\mathrm{P}}\right) }{\partial t} =\frac{\partial }{\partial x} \left( D_x\frac{\partial C_{\mathrm{H}}}{\partial x}\right) +\frac{\partial }{\partial y} \left( D_y\frac{\partial C_{\mathrm{H}}}{\partial y}\right) +\frac{\partial }{\partial z} \left( D_z\frac{\partial C_{\mathrm{H}}}{\partial z}\right) \end{aligned}$$

(1)

where $C_{\mathrm{T}}$ [$\hbox {mg g}^{-1}$] is the total sorbed concentration measured as the mass uptake per unit of sample bulk mass, $C_{\mathrm{H}}$ [$\hbox {mg g}^{-1}$] is the mass concentration of the absorbed (i.e., Henry’s mode) water vapor per unit of sample bulk mass, $C_{\mathrm{L}}$ and $C_{\mathrm{P}}$ [$\hbox {mg g}^{-1}$] are, respectively, the adsorbed and pooled concentrations in Langmuir and pooling modes, D [$\hbox {cm}^2\hbox { min}^{-1}$] is the effective diffusion coefficient, t [min] is the time and x, y, z [cm] are the spatial coordinates. In Eq. (1), the absorbed concentration $C_{\mathrm{H}}$ is conceptualized to be mobile.

By introducing an advection term and a formalism to include multiple components, the model in Eq. (1) can be altered and applied to mixed-gas transport in porous materials. The transport equations of mixed gases coupled with kinetic Langmuir adsorption and equilibrium Henry’s absorption (neglecting pooling effect) in a porous material are revised as

$$\begin{aligned} \frac{\partial C_i}{\partial t}= \underbrace{\overbrace{\nabla \cdot \left( D_i\nabla C_i \right) }^{\mathrm{Diffusion}} \overbrace{-\nabla \cdot \left( v_i C_i \right) }^{\mathrm{Advection}}}_{\mathrm{Transport}} \underbrace{-k'_{\mathrm{d},i}\frac{\mathrm {d}C_i}{\mathrm {d}t}}_{\mathrm{Henry's}} \underbrace{-k'_{\mathrm{ad}}\,S\,C_i + k'_{\mathrm{ds}}C_{\mathrm{L},i}} _{\mathrm{Langmuir~kinetics}} \end{aligned}$$

(2)

where the subscript i ($\forall i = 1, 2,\ldots , n$) indicates the $i\hbox {th}$ component among n gas components, $C_i$ [$\hbox {mg g}^{-1}$] is the true mobile gas concentration in terms of sample bulk mass, v [$\hbox {cm min}^{-1}$] is the flow velocity, $k'_{\mathrm{d}}$ [-] is the dimensionless Henry’s law constant, $k'_{\mathrm{ad}}$ [$\hbox {min}^{-1}\hbox {mg}^{-1}\hbox {g}$] and $k'_{\mathrm{ds}}$ [$\hbox {min}^{-1}$] are, respectively, adsorption and de-adsorption rates, $S = C'_{\mathrm{H}}-\sum C_{\mathrm{L},i}$ is the concentration of empty Langmuir sites and $C'_{\mathrm{H}}$ is the Langmuir capacity constant reflecting available reactive surface sites. When $D = 0$, Eq. (2) represents a reactive flow system. When $v = 0$, Eq. (2) describes a diffusion–reaction system.

Henry’s mode concentration, $C_{\mathrm{H}}$ [$\hbox {mg g}^{-1}$], which is also measured in mass of gas component per bulk mass of a material, can be directly treated as a mobile concentration due to its linear dependence of gas-phase (mobile) concentration

$$\begin{aligned} C_{\mathrm{H}}=k'_{\mathrm{d}}\,C =\frac{k'_{\mathrm{d}}\phi }{\rho _{\mathrm{b}}}\,c=k_{\mathrm{d}}\,c, \end{aligned}$$

(3)

in which $k_{\mathrm{d}}=k'_{\mathrm{d}}\phi /\rho _{\mathrm{b}}$ [$\hbox {cm}^3$$\hbox {g}^{-1}$] is the Henry’s law constant used in simulations, $\phi$ [–] is the porosity (the fraction of pore volume over bulk volume), $\rho _{\mathrm{b}}$ [$\hbox {g cm}^{-3}$] is the bulk density and c [$\hbox {mg cm}^{-3}$] represents the mobile gas-phase concentration measured as the mass of a mobile gas per unit of pore volume in a material. c is physically analogous to C with a different unit definition. By assuming that porosity and bulk density of the polymer materials are fixed and not altered by gas transport and reactions, both parameters are implicitly lumped in Henry’s absorption constant, $k_{\mathrm{d}}$.

Considering the retardation of diffusion due to Henry’s absorption, Eq. (2) can be expressed in terms of pore-gas concentration, c:

$$\begin{aligned} \frac{\partial c_i}{\partial t}= \nabla \cdot \left( D_{\mathrm{e},i}\nabla c_i \right) -\nabla \cdot \left( v_{\mathrm{e},i}\,c_i \right) - k_{{\mathrm{ad}},i}\,S\,c_i + \frac{k_{{{\mathrm{ds}}},i}}{k_{{\mathrm{d}},i}} C_{\mathrm{L},i} \end{aligned}$$

(4)

where $D_{\mathrm{e}}= D/(1+k'_{\mathrm{d}})$ and $v_{\mathrm{e}}= v/(1+k'_{\mathrm{d}})$ are the effective diffusion coefficient and flow velocity, $k_{\mathrm{ad}} = k'_{\mathrm{ad}}/(1+k'_{\mathrm{d}})$ is the effective adsorption rate and $k_{\mathrm{ds}} = k'_{\mathrm{ds}}k'_{\mathrm{d}}/(1+k'_{\mathrm{d}})$. Since $k'_{\mathrm{d}}$ is dimensionless, $D_{\mathrm{e}}$, $v_{\mathrm{e}}$, and $k_{\mathrm{ad}}$ keep their original units.

Redefining system parameters, Eq. (4) is mathematically identical to the basic equation developed by Harley et al. (2014) and Sun et al. (2015) except for the advection term and the number of gas components. A generalized computer code (with advection, diffusion, and reaction kinetics) is developed for solving Eq. (4) in MATLAB environment.

2.2 Kinetic Adsorption of Mixed Gases

In the diffusion of a binary gas mixture (two gas components), the presence of one gas may affect the diffusion and adsorption of the other. The diffusion and sorption behavior of the mixed gases in polymeric materials is expected to differ from that of the pure gas components. For example, the porous-medium-specific Langmuir capacity $C'_{\mathrm{H}}$ characterizes the adsorption capacity in a given polymeric material for a particular penetrant. When kinetic diameters are significantly different, we quantify Langmuir capacity in terms of the first gas component with

$$\begin{aligned} C_{\mathrm{L},1} + \alpha _{2,1}C_{\mathrm{L},2}\le C'_{\mathrm{H}}, \quad \alpha _{2,1} = \left( \frac{d_1}{d_2}\right) ^2 \end{aligned}$$

(5)

where $d_1$ and $d_2$ are kinetic diameters and polarizability of two gases and $C_{\mathrm{L},1}$ and $C_{\mathrm{L},2}$ [$\hbox {mg g}^{-1}$] are adsorbed concentrations. If kinetic diameters of two gas components, such as $\hbox {N}_2$ and $\hbox {CO}_2$, are similar (364 and 330 pm for $\hbox {N}_2$ and $\hbox {CO}_2$, respectively, $\hbox {pm} = 10^{-12}\,\hbox {m}$), we may assume that the monolayer adsorption capacities are equal for both components (van der Vaart et al. 2000) and $\alpha \approx 1$.

The Langmuir adsorption and de-adsorption of binary mixed gases are reversible kinetic reactions described by the following equations:

(6)

(7)

where $c_i,~i=1,2$ [$\hbox {mg cm}^{-3}$] are pore-gas concentrations of $\hbox {N}_2$ and $\hbox {CO}_2$, S [$\hbox {mg g}^{-1}$] is the Langmuir empty-site concentration and $k_{{\mathrm{ad}},i}$ [$\hbox {min}^{-1}\hbox {mg}^{-1}\hbox {g}$] and $k_{{{\mathrm{ds}}},i}$ [$\hbox {min}^{-1}$] are adsorption and de-adsorption rates, $i=1,2$, representing $\hbox {N}_2$ and $\hbox {CO}_2$, respectively. Then, the Langmuir concentrations of two gas components are constrained as

$$\begin{aligned} C_{{\mathrm{L}},1} + \alpha _{2,1}C_{{\mathrm{L}},2} = C'_{\mathrm{H}}-S. \end{aligned}$$

(8)

Figure 1 shows a cartoon representation of the relationship between the variables in Eqs. (5)–(7). Red and green balls (above the material surface), representing $\hbox {N}_2$ and $\hbox {CO}_2$ molecules, respectively, compete to occupy the rest of empty sites according to their $k_{\mathrm{ad}}$ and $k_{\mathrm{ds}}$.

Fig. 1

Cartoon showing the relationship between the variables in Eqs. (5)–(7). Red and green balls represent $\hbox {N}_2$ and $\hbox {CO}_2$ molecules, respectively

Since two unknowns $C_{\mathrm{L},1}$ and $C_{\mathrm{L},2}$ are involved in Eq. (8), the empty-site concentration, S, which was solved as a primary state variable in single-gas sorption–diffusion models (e.g., Harley et al. 2014), cannot be treated as a primary variable in the simulation of multi-gas transport. Instead, we treat $C_{\mathrm{L},1}$ and $C_{\mathrm{L},2}$ directly as primary variables and S as the secondary variable. Note that the secondary variables are only involved in intermediate calculations. Then, the ordinary differential equations of Langmuir kinetics are expressed as

$$\begin{aligned} \begin{aligned}&\frac{\mathrm {d}c_1}{\mathrm {d}t} = - k_{{\mathrm{ad}},1}\,S\,c_1 + \frac{k_{{\mathrm{ds}},1}}{k_{\mathrm{d},1}}C_{\mathrm{L},1}\\&\frac{\mathrm {d}c_2}{\mathrm {d}t} = - k_{\mathrm{ad},2}\,S\,c_2 + \frac{k_{{\mathrm{ds}},2}}{k_{\mathrm{d},2}}C_{\mathrm{L},2}\\&\frac{\mathrm {d}C_{\mathrm{L},1}}{\mathrm {d}t} = k_{\mathrm{ad},1}\,k_{\mathrm{d},1}\,S\,c_1 - k_{{\mathrm{ds}},1}C_{\mathrm{L},1}\\&\frac{\mathrm {d}C_{\mathrm{L},2}}{\mathrm {d}t} = k_{\mathrm{ad},2}\,k_{\mathrm{d},2}\,S\,c_2 - k_{{\mathrm{ds}},2}C_{\mathrm{L},2}. \end{aligned} \end{aligned}$$

(9)

When $t\rightarrow \infty$, $\mathrm {d}c_1/\mathrm {d}t = \mathrm {d}c_2/\mathrm {d}t =0$, equilibrium Langmuir isotherm is reached. Then,

$$\begin{aligned} C_{\mathrm{L},1}= & {} b'_1k_{\mathrm{d},1}\left( C'_{\mathrm{H}} - C_{\mathrm{L},1} - \alpha _{2,1}C_{\mathrm{L},2} \right) c_1 \end{aligned}$$

(10)

$$\begin{aligned} C_{\mathrm{L},2}= & {} b'_2k_{\mathrm{d},2}\left( C'_{\mathrm{H}} - C_{\mathrm{L},1} - \alpha _{2,1}C_{\mathrm{L},2} \right) c_2. \end{aligned}$$

(11)

Solving Eqs. (10) and (11), we derive the equilibrium isotherm as

$$\begin{aligned} C_{\mathrm{L},1}= & {} \frac{b'_1k_{\mathrm{d},1}C'_{\mathrm{H}}c_1}{1+b'_1k_{\mathrm{d},1}\,c_1+\alpha _{2,1}b'_2k_{\mathrm{d},2}\,c_2} \end{aligned}$$

(12)

$$\begin{aligned} C_{\mathrm{L},2}= & {} \frac{b'_2k_{\mathrm{d},2}C'_{\mathrm{H}}c_2}{1+b'_1k_{\mathrm{d},1}\,c_1+\alpha _{2,1}b'_2k_{\mathrm{d},2}\,c_2} \end{aligned}$$

(13)

where $b'_1 = k_{\mathrm{ad},1}/k_{{\mathrm{ds}},1}$ and $b'_2 = k_{\mathrm{ad},2}/k_{{\mathrm{ds}},2}$ are affinities of component 1 and 2. For multiple component adsorption, the general of equilibrium isotherm is written as

$$\begin{aligned} C_{\mathrm{L},i}= \frac{b'_ik_{\mathrm{d},i}C'_{\mathrm{H}}c_i}{1+\sum _i \alpha _{i,1}b'_ik_{\mathrm{d},i}\,c_i} \end{aligned}$$

(14)

with $\alpha _{1,1}=1$. When $\alpha _{i,1}=1,~\forall i=1,\ldots , n$, the equilibrium Langmuir concentrations can be simplified as the same as provided by Koros (1980).

2.3 Hysteresis of Henry’s Absorption

Sorption hysteresis has been qualitatively interpreted as the phenomena related to the difference in gas-medium interaction (e.g., capillarity, solubility, material swelling, etc.) between sorption and desorption periods. It will be shown from our experiments (Sect. 4.1) that there is a clear hysteresis for $\hbox {CO}_2$ absorption and de-absorption that must be addressed quantitatively via our modeling. Traditionally, desorption is defined as the release of one substance either from solid surface in Langmuir mode or through the surface in Henry’s mode. To distinguish these desorption modes, we use de-adsorption and de-absorption to represent the desorption, respectively, in Langmuir and Henry’s modes. To accurately describe the different absorption and de-absorption processes, we propose the following equation that is modified from Henry’s law linear function considering a slower $k_{\mathrm{d}}$ and residual sorption:

$$\begin{aligned} C_{\mathrm{H}}= h_0+k_{\mathrm{d}}\,c \frac{{\mathrm {erf}}(a\,c)}{{\mathrm {erf}}(a\,c_{\mathrm{max}})} \quad \forall a> 0 \end{aligned}$$

(15)

where $c_{\mathrm{max}}$ [$\hbox {mg cm}^{-3}$] is the maximum concentration when de-absorption starts, a is the hysteresis parameter measuring how much the de-absorption relation deviates from the Henry’s linear relationship, $h_0$ [$\hbox {mg g}^{-1}$] is the residual absorbed CO$_2$ at the end of the desorption experiment and ${\mathrm {erf}}$ is the error function defined as

$$\begin{aligned} {\mathrm {erf}}(\eta )=\frac{2}{\sqrt{\pi }}\int ^{\eta }_{0} \exp (-\tau ^2) \mathrm{d} \tau . \end{aligned}$$

If the de-absorption still follows the linear relation, Eq. (15) can be modified as

$$\begin{aligned} C_{\mathrm{H}}= h_0+a'\,k_{\mathrm{d}}\,c, \quad a\le 1.0 \end{aligned}$$

(16)

where $a'\,k_{\mathrm{d}}$ is the Henry’s law constant in the de-absorption period and $a'$ is the ratio of de-absorption constant to the absorption constant.

3 Methods

3.1 Experiments

Experiments are conducted using XEMIS (Hiden Isochema 2019) instrument designed by Hiden Isochema, which is equipped as an advanced gas sorption analyzer with next generation microbalance ($1\times 10^{-7}$ g) design for high pressure (to $2.0\times 10^7$ Pa). Sample mass is measured as a function of temperature and pressure allowing for the determination of mass transport and sorption kinetics. The experiments were set up for $\hbox {N}_2$ and $\hbox {CO}_2$ diffusion and sorption in an unfilled polydimethylsiloxane (PDMS, sylgard-184) and a filled PDMS network (M9787). A detailed description of unfilled and filled PDMS samples is given in Harley et al. (2014). Briefly, the filled PDMS network contained approximately 25% wt silica filler while the unfilled PDMS network was synthesized free of filler.

Four sets of experiments were conducted for studying sorption and diffusion processes of mixed $\hbox {N}_2$ and $\hbox {CO}_2$ in two PDMS materials (unfilled and filled). Between experiments, the samples were equilibrated in $\hbox {N}_2$. The sample geometry, properties, and experimental conditions are given in Table 1.

Table 1 Sample properties and experimental conditions

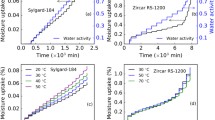
Boundary concentrations of $\hbox {N}_2$ and $\hbox {CO}_2$ are defined as shown in Fig. 2. The partial pressure of $\hbox {CO}_2$ was increased in the uptake period and decreased in the outgassing period gradually in steps of 10% for every 20 min while the partial pressure of N$_2$ was set complementarily. Corresponding mass uptakes are shown in Fig. 3. The second and third experiments are essentially repeated for calibration and prediction purposes at the same temperature, pressure, and under the same boundary condition (solid lines in Fig. 2a).

Fig. 2

Boundary concentration defined for four experiments. a Boundary concentrations for experiments at pressure of 1 atm. b Boundary concentrations for experiments at pressure of 2 atm. Note that the difference between solid and dashed lines in a is due to the temperature difference

Fig. 3

Comparison of measured and modeled mass uptakes of mixed-gas sorption and diffusion experiments. a Mass uptake versus time at pressure of 1 atm and 50 $^{\circ }\hbox {C}$ (Expt. 1), b mass uptake versus time at pressure of 1 atm and 40 $^{\circ }\hbox {C}$ (Expt. 2), c mass uptake versus time at pressure of 2 atm and 40 $^{\circ }\hbox {C}$ (Expt. 4), and d mass uptake versus time at pressure of 1 atm and 40 $^{\circ }\hbox {C}$ (Expt. 3)

3.2 Global Optimization

The calibration of system parameters in Eq. (4) includes several methods to ensure the parameter set for the global minimum of our objective function is identified. Calibration begins with an educated guess on the range for each parameter. Using Latin hypercube (McKay et al. 1979), 1000 parameter sets are generated within the defined range for each parameter. The modeled mass uptake is calculated, with each of the 1000 parameter sets, as a function of absorbed and adsorbed concentrations that are simulated by solving Eq. (4). The calibration of system parameters is defined as a minimization of the integral of absolute difference between modeled and measured mass uptakes:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf{X}}{\text {Minimize}}&{\mathscr {F}}\left( \mathbf{X}\right)&= \frac{1}{t} \int _0^t \bigg | M\left( \mathbf{X}, \tau \right) -{\hat{M}}(\tau ) \bigg | \mathrm{d}\tau \\&\text {Subject to}&\mathbf{X} \in \Omega \\ \end{aligned} \end{aligned}$$

(17)

where $\mathbf{X}$ is the vector of system parameters to be calibrated, $\Omega$ represents the parameter space and $M\left( \mathbf{X}, \tau \right)$ and ${\hat{M}}(\tau )$ are modeled and measured mass uptakes due to diffusion and sorption at time $\tau \in [0, t]$. The best match between model result and experimental data is sorted from all sampling-based simulations and used to verify if it is close to the global minimum optimized using different methods.

The optimized parameter set is seeded into the shuffled complex evolution (SCE) program developed by Duan et al. (1992). The SCE program uses multiple simplexes started from random locations in a parameter space, competitive evolution, and complex shuffling, as a metaheuristic global optimization for solving Eq. (17). This approach has been used successfully in the past to calibrate reactive transport systems in high-dimensional parameter space (e.g., Sharma et al. 2017, 2018).

Although the SCE method is an efficient metaheuristic approach, it does not necessarily guarantee the global optimum. In order to verify global optimization and avoid local minima, a random-perturbation and sampling-based approach was employed. In this approach, a new parameter space is defined as ${\hat{\Omega }} = \hat{\mathbf{X}}\left( 1\pm \delta \right)$ where $\hat{\mathbf{X}}$ is the optimized set of parameters and $\delta$ is a perturbation (e.g., 20%) around the values in $\hat{\mathbf{X}}$.

Using Latin hypercube method (McKay et al. 1979) again in the newly defined space, a number of sample points (i.e., 1000) are generated and simulations are executed on those sample points. The objective function (fitness) ${\mathscr {F}}$ [Eq. (17)] is evaluated and ranked. The best ten parameter sets that minimize ${\mathscr {F}}$ are selected to compare to the optimized parameter set from the previous SCE evaluation. If those ten sets are substantially close to each other and to the SCE optimized set, in comparison with the remaining 990 parameter sets, then the SCE optimized parameter set is verified to be the best. Otherwise, additional optimization with different initial guesses and parameter ranges is suggested. Note that the convergence depends on the perturbation $\delta$, which, in turn, depends on our knowledge on system parameters. Latin hypercube has been demonstrated as an efficient sampling method for representing a high-dimensional parameter space, compared to other sampling methods, such as Monte Carlo approach; it provides a reasonably accurate random distribution for a given number of sample points. Sampling-based simulations are further used to conduct Sobol’ sensitivity analyses that are referred to Sobol’ (1990), Tong (2005), and Saltelli et al. (2008).

3.3 Uncertainty Quantification via Surrogate Models

The model validity and predictability depend on its capability to quantify the uncertainties of model outputs and uncertainty propagation from the initial conditions, environment (i.e., decision variables), conceptual models, and parameters. This could be accomplished in a brute-force fashion by running a large number of physics-based simulations with variable inputs. Unfortunately, the numerical solutions to $C_{\mathrm{H}}$ and $C_{\mathrm{L}}$ used to evaluate Eq. (17) are computationally expensive making a brute-force approach impracticable. A surrogate modeling approach was developed by Sun et al. (2017) where the Langmuir adsorption kinetic model is replaced with a surrogate model making the calculation of $C_{\mathrm{L}}$ orders of magnitude faster. The surrogate modeling approach could be employed to increase simulation efficiency; however, the corresponding solutions can only be used for deterministic simulations, and one would still need to employ a brute-force approach to deal with the range of initial conditions, environment, uncertainties in the parameters, and uncertainties in the models.

An additional challenge, when modeling a dynamic behavior such as reactive transport, is that the modeled output is sensitive to both the present applied boundary conditions and the past conditions. In other words, a dynamic phenomenon possesses a “memory” in which the effect of past conditions (e.g., boundary concentrations) is stored and may alter the response of the material (Sun and Tong 2017). For example, the boundary concentrations in our experiments, as shown in Fig. 2, change with time.

To consider the combined effect of boundary concentrations and uncertain parameters, a dynamic reduced-order model of mass uptake is developed as a function of boundary concentrations and uncertain parameters as

$$\begin{aligned} M(t+\Delta t)&= {{\mathcal {F}}}_0\left[ M(t)\right] +{{\mathcal {F}}}_1\left( \mathbf{X}\right) \nonumber \\&\quad +\,{{\mathcal {F}}}_C\left[ c_C(t)\right] + {{\mathcal {F}}}_N\left[ c_N(t)\right] \end{aligned}$$

(18)

where ${{\mathcal {F}}}$ denotes polynomial equations, ${{\mathcal {F}}}_0\left[ M(t)\right]$ is the function of mass uptake in previous time step, ${{\mathcal {F}}}_1\left( \mathbf{X}\right)$ is the function describing the contribution of non-dynamic material properties and ${{\mathcal {F}}}_C\left[ c_C(t)\right]$ and ${{\mathcal {F}}}_N\left[ c_N(t)\right]$ are functions describing the dependence of mass uptake in the current time step on the boundary concentrations of $\hbox {CO}_2$ and $\hbox {N}_2$, respectively.

4 Results and Analyses

4.1 Experimental Results

We conducted experiments and performed simulations of $\hbox {N}_2$ and $\hbox {CO}_2$ diffusion, sorption, and desorption in the unfilled and filled PDMS. Shown in Fig. 3 are the experimental and modeled mass response curves for the four experiments outlined in Table 1. In experiment 1, the $\hbox {CO}_2$ partial pressure was incrementally increased, resulting in a corresponding decrease in $\hbox {N}_2$ partial pressure, and the sample mass was observed to increase with each step (see Fig. 2a). The curvature at each step enables us to determine the diffusion and sorption kinetics, and the equilibrium points at each step allow for calculation of equilibrium sorption parameters. The weight gain in this experiment is attributed to sorption of $\hbox {CO}_2$, and we assume that the $\hbox {N}_2$ is desorbing.

In the remaining three experiments (i.e., Fig. 3b–d), the $\hbox {CO}_2$ partial pressure was stepwise increased to the point where the atmosphere was 100% $\hbox {CO}_2$ and subsequently decreased (in discrete steps), resulting in a mass increase as $\hbox {CO}_2$ partial pressure rises, and a mass decrease as $\hbox {CO}_2$ partial pressure drops. A comparison of Fig. 3b, d demonstrates an excellent reproducibility of the experiment when the experimental conditions were the same. Comparing Fig. 3c with Fig. 3b, d, it is clear that pressure alters the experimental results, as expected.

In Experiments 2–4, a hysteresis was observed in which the equilibrated mass at each partial pressure did not match between uptake and outgassing. A plot of mass uptake versus $\hbox {CO}_2$ concentration, from Expt. 3, is provided in Fig. 4. At the highest $\hbox {CO}_2$ boundary conditions (i.e., between 1.4 and 1.6 $\hbox {mg cm}^{-3}$), one can see the equilibrated mass in the uptake and outgassing curves match. All the other $\hbox {CO}_2$ boundary conditions display a distinct difference between the equilibrated mass in the uptake curve versus the outgassing curve. This hysteresis is attributed to the slightly different sorption mechanisms of uptake versus outgassing. The relative mass offset between uptake and outgassing, as shown in the inset of Fig. 4, is quantitatively reflected by different $k_{\mathrm{d}}$ values (0.6432 and 0.5854) calibrated using data of Expt. 3. The absorption hysteresis may be explained as the slower microscopic diffusion in the de-absorption period that needs a longer time ($\gg 20$ min) for each partial pressure step to reach equilibrium.

Fig. 4

Mass uptake versus $\hbox {CO}_2$ boundary concentration (Expt. 3) showing absorption hysteresis. The inset shows the relative mass offset between uptake and outgassing periods. The calibrated $k_{\mathrm{d}}$ values of Expt. 3 are 0.6432 and 0.5853, respectively, in uptake and outgassing periods

4.2 Calibrating the $\hbox {N}_2$ and $\hbox {CO}_2$ Sorption and Diffusion Model

Using the approach outlined in the Global Optimization section (Sect. 3.2), the parameters in Eq. (4) were calibrated against the experimental data in Fig. 3. Since the diffusion coefficient is orders of magnitude less sensitive than other sorption parameters to mass uptake (Sun et al. 2015), diffusion coefficients of $\hbox {N}_2$ and $\hbox {CO}_2$ in the unfilled and filled PDMS at 50 $^{\circ }\hbox {C}$ and 40 $^{\circ }\hbox {C}$, respectively, are first calculated using the previously calibrated values (Sun et al. 2015) of vapor diffusion and Graham’s law. In the calibration, it was assumed that the Langmuir capacity for pure $\hbox {N}_2$ and $\hbox {CO}_2$ was the same (i.e., $\alpha _{2,1}=1$). In the seven-dimensional parameter space (i.e., $k_{\mathrm{d}}$ and $b'$ for both $\hbox {N}_2$ and $\hbox {CO}_2$, $C'_{\mathrm{H}}$, and $\hbox {CO}_2$ absorption hysteresis parameters, a and $h_0$), we conducted SCE optimization for Expts. 1, 2, and 4 and random perturbation for Expts. 2, 3, and 4 to obtain and verify the set of calibrated parameters listed in Table 2. Since Expt. 1 (in unfilled PDMS) was conducted in sorption period, only the first five parameters are optimized as shown in the second column of Table 2. The calibrated $k_{\mathrm{d}}$ values for both $\hbox {N}_2$ and $\hbox {CO}_2$ are similar in both filled and unfilled PDMS, which is not surprising as both materials are expected to have similar absorption mechanisms. In contrast, the Langmuir capacity of the unfilled PDMS is 3.75 times smaller than that of the filled PDMS; the most logical explanation is that the cab-o-sil filler increases the surface area for Langmuir adsorption.

In Expt. 3, the repeated Expt. 2, although less measurement uncertainty is observed in the experimental data of mass uptake (Fig. 3d), the calibrated parameter set (that is not listed in Table 2) is almost identical to the set calibrated using Expt. 2. Sampling-based simulations, as described in Sect. 3.2, were performed with 20% perturbation with respect to the optimized parameter sets provide the consistent best fits (columns 5–7, Table 2) for confirming the global minima. Sobol’ total sensitivity indices (TSI) (columns 8–10) indicate that $k_{\mathrm{d}}$ of $\hbox {CO}_2$ is the most sensitive parameter in the defined parameter space. Figure 5 shows the scatter plot of the objective function (Eq. 17) projected in the dimension of $k_{\mathrm{d}}$. In this plot, one can clearly see which $k_{\mathrm{d}}$ value minimizes the objective function for each experiment in the filled PDMS. This convex objective function verifies that the optimized SCE values listed in Table 2 are the global minima. One can see how well the optimized model compares with experimental data in Fig. 3.

Table 2 Calibrated parameters of $\hbox {CO}_2$ and $\hbox {N}_2$ sorption and diffusion in unfilled (Expt. 1) and filled PDMS (Expts. 2, 3, and 4)

Fig. 5

Scatter plot of model fitness (Eq. 17) in the dimension of $\hbox {CO}_2$ Henry’s law constant. Vertical dashed lines show best-fit sample locations (0.7040, 0.7209, and 0.6421) for Expts. 2, 3, and 4, respectively

4.3 Sensitivity Analysis and Uncertainty Propagation of Parameters

The natural question when looking at multiple parameters that influence a dynamic process is which parameters are more sensitive and impactful? To answer this question, a Sobol’ sensitivity analysis of the seven parameters was undertaken. Using Sobol’ total sensitivity indices, one can rank the relative sensitivity of the parameters; the largest number is the most sensitive. The results are included in Table 2 (columns 8–10). One can see, in every experimental parameter set, that the Henry’s absorption constant for $\hbox {CO}_2$ (i.e., $k_{\mathrm{d}}$ for $\hbox {CO}_2$) is the most sensitive parameter.

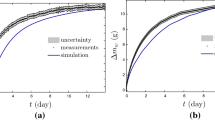
The propagation of uncertainty is critical to making predictions of material gas sorption and diffusion rates in real systems. The optimized parameters in Table 2 will have some degree of uncertainty, in spite of our rigorous parameter calibration process. In order to investigate the outcome of a perturbation in the parameters, we have generated a parameter set that represents 20% perturbation of the optimized parameters and simulated the material mass changes under the conditions of Expts. 2–4 for filled PDMS. Figure 6a shows the mass changes of the calibrated model (red line) and the range of mass changes if the parameters are increased or decreased by 20%. One can see that at low $\hbox {CO}_2$ partial pressures (i.e., earliest and latest time steps), the mass change is relatively insensitive to the uncertainty of the parameters. In contrast, at elevated partial pressures of $\hbox {CO}_2$ (i.e., at 175 min) uncertainty in the parameters can substantially alter the mass uptake due to $\hbox {CO}_2$ sorption. It would have been difficult to see how these different parameters influence the outcome without this visual representation.

Figure 6b shows the relative error between the calibrated model and the $\pm 20\%$ perturbation models; the light blue curve shows the error of the $+20$% perturbation, and the dark blue has the $-20$% relative error. The spikes in the relative error plot correspond to the dynamic portion of mass uptake at each partial pressure condition. What is most interesting is that the relative uncertainty of mass uptake is more than 20% over most of the simulation/conditions. In other words, a 20% uncertainty in the parameters propagates to a larger uncertainty in the mass response.

Fig. 6

Uncertainty of mass uptake in filled PDMS due to 20% perturbation of uncertain parameters. a Uncertain mass uptake. b Relative error of mass uptake

The hysteresis between uptake and outgassing is displayed in Fig. 4. Shown in Fig. 7 are simulations of the outgassing with and without the hysteresis parameters. The uptake stage in both plots (at 1 atm and 2 atm) is a simulation of the parameters using the experimental conditions in Expts. 2 and 4, respectively. The outgassing portions in the latter half of each plot show a simulation in which the hysteresis parameter is set to the optimized parameter (upper curve) and a simulation where the hysteresis parameter is zeroed out (lower curve), resulting in a curve where no hysteresis exists between uptake and outgassing. To enable better visualization of the difference between these two curves, the space between has been shaded. One can clearly see that the lag in $\hbox {CO}_2$ outgassing is compounded during each step and the final stages of outgassing (i.e., when the $\hbox {CO}_2$ partial pressure is lowest) result in the largest disparity between equilibrated mass during uptake and outgassing. One can see the importance and sensitivity of this hysteresis parameter in defining the dynamic outgassing.

Fig. 7

Mass uptake contributed by hysteresis for $\hbox {N}_2$ and $\hbox {CO}_2$ diffusion and sorption in filled PDMS a at pressure of 1 atm (Expt. 2) and b at pressure of 2 atm (Expt. 4)

A surrogate model was developed using the method discussed in the Methods section (Sect. 3.3), in order to reduce the computational resources necessary to perform enough simulations to be statistically relevant for uncertainty quantification. Figure 8a shows the comparison of the emulated (i.e., surrogate) and simulated mass uptakes in all time steps and for all sample points. One can see a one-to-one correlation with a $R^2$ value of 0.99988 indicating an excellent match of the emulated to simulated mass uptakes. In the entire range of uncertain mass uptake shown in Fig. 6a (shaded area), mass uptakes at specific percentiles (confidence levels), such as 1, 33, 67, 99%, can be either simulated using the numerical solution to Eq. (4) or emulated using Eq. (18). As an example, simulated and emulated mass uptakes as functions of time at those four percentiles are compared in Fig. 8b. Although both simulation and emulation provide agreed mass uptakes, the emulation is about 100 times faster than the simulation.

Fig. 8

Comparison of simulated and emulated mass uptakes in filled PDMS at pressure of 1 atm. a Comparison for 2000 sample points at 500 time steps. b Comparison of mass uptakes at 1, 33, 67, and 99 percentiles

4.4 Advection, Diffusion, and Kinetic Reactions

The coupled transport and sorption model developed in this study can be used for assessing material aging and compatibility under dynamic concentrations, including pressure-driven conditions. To verify the implementation of advection operator with the existing diffusion and kinetic reaction operators, we use the analytical solution to a single-component transport (advection and diffusion) coupled with first-order reaction (representing reaction kinetics with a decay rate k) in a semi-infinite column for a constant concentration boundary condition (Bear 1979, P268). The solution is written as the following and coded as

$$\begin{aligned} c = \frac{c_0}{2}\exp \left( \frac{vx}{2D}\right) \left[ \exp (-\beta x)~{\mathrm {erfc}} \gamma ^-+ \exp (\beta x)~{\mathrm {erfc}} \gamma ^+\right] , \end{aligned}$$

(19)

where $c_0$ is the boundary concentration,

$$\begin{aligned}&\beta =\left( \frac{v^2}{4D^2}+\frac{k}{D}\right) ^{1/2}, \quad {\mathrm {erfc}}(\eta )=1-{\mathrm {erf}}(\eta )=\frac{2}{\sqrt{\pi }} \int _{\eta }^{\infty } \exp (-\tau ^2) \mathrm{d} \tau ,\\&\gamma ^-=\frac{x-(v^2+4k~D)^{1/2}t}{2(Dt)^{1/2}}, \quad \gamma ^+=\frac{x+(v^2+4k~D)^{1/2}t}{2(Dt)^{1/2}}. \end{aligned}$$

For given system parameters, $t = 100$ [min], $x = 100$ [cm], $v = 1.0$ [$\hbox {cm min}^{-1}$], $D = 1.0$ [$\hbox {cm}^2\,\hbox {min}^{-1}$], and $k=1.0$ [$\hbox {min}^{-1}$], the analytical and numerical results are compared in Fig. 9. One can see excellent match of the numerical results derived in this work compared with the analytical results of Bear (1979). The largest disparity between the two models occurs at the start of the column (i.e., distance = 0), which is attributed to the spatial discretization in the numerical solution. For the most part, the match between numerical and analytical is excellent, thus increasing our confidence in the rigor of our new numerical model.

Fig. 9

Verification of advection operator coupled with diffusion and reaction operators

Similar to the benchmark problem discussed above, a one-dimensional column of filled PDMS is used for predicting $\hbox {N}_2$ and $\hbox {CO}_2$ concentrations. A constant flow ($v = 0.1$ cm  $\hbox {min}^{-1}$) is assumed from column inlet to outlet, and the time-dependent boundary concentrations of $\hbox {N}_2$ and $\hbox {CO}_2$ from the second experiment (Fig. 2a) of filled PDMS are applied on the column inlet. The time- and space-dependent concentrations of $\hbox {N}_2$ and $\hbox {CO}_2$ in various modes (pore-gas phase, Henry’s, and Langmuir) are obtained using the system parameters calibrated from Expt.  2 in Table 2 (column 3).

Figure 10a shows the pore-gas concentrations as a function of distance in the column, where the boundary concentration (at $x = 0$) is dynamic and matches the dynamic gas concentrations in Expts. 2 and 3 (see Fig. 2a, solid lines). Referring to Fig. 2a, at 100 min, in Expts. 2 and 3, the partial pressure of $\hbox {CO}_2$ in the experimental chamber has undergone four consecutive steps, with equilibration time after each step. The 100-min time point is just prior to the fifth step up in $\hbox {CO}_2$ concentration. As the $\hbox {CO}_2$ partial pressure increased in these experiments, the $\hbox {N}_2$ partial pressure necessarily decreased, and at the 100-min time point, the $\hbox {CO}_2$ concentration was greater than the $\hbox {N}_2$ concentration. The simulation in Fig. 10a shows how this series of concentration changes at the boundary will propagate through the column. Not surprisingly, the concentration at the boundary (i.e., $x = 0$) matches the gas concentration in the experimental chamber. Moving away from the boundary and deeper into the material, one can see the $\hbox {CO}_2$ concentration decreases, which is consistent with the fact that the entire column was initially equilibrated in a pure $\hbox {N}_2$ environment, and the diffusion and sorption mechanisms will result in a gradient of $\hbox {CO}_2$ and $\hbox {N}_2$ concentrations. Correspondingly, the $\hbox {N}_2$ concentration along the length of the column steadily increases. However, at approximately the 7.5 cm point, the $\hbox {N}_2$ concentration also drops, and this is attributed to the advection from the inlet with decreasing boundary concentration of $\hbox {N}_2$ within 100 min.

In the same filled PDMS column with the boundary conditions from Expt. 2, Fig. 10b shows the gas concentrations over the entire duration of the experiment at the mid-plane in the column (i.e., $x = 5$ cm). Not surprisingly, there is a lag in time before the $\hbox {CO}_2$ concentration begins to rise, and this is due to the fact that the gas must advect and diffuse through 5 cm of material before it arrives at this point in the column. Interestingly, the $\hbox {N}_2$ concentration begins to rise approximately 20 min before the $\hbox {CO}_2$. This rise is attributed to the initially high $\hbox {N}_2$ concentration at the inlet. Due to the diffusion and sorption which retard the transport of $\hbox {CO}_2$ and $\hbox {N}_2$ in the material, the peak concentration of $\hbox {CO}_2$ is at approximately 225 min, whereas the peak in $\hbox {CO}_2$ concentration at the boundary is at 175 min (see Fig. 2a, solid lines).

These simulations are merely a demonstration of the impact of diffusion, sorption, and advection in just one dimension, where the boundary condition is dynamic. It is easy to imagine the complexity of a concentration map where the material is three-dimensional, especially in a dynamic environment.

Fig. 10

Prediction of $\hbox {N}_2$ and $\hbox {CO}_2$ concentrations as functions of column distance and time. a Concentrations versus distance from column inlet at $t = 100$ min. b Concentrations versus time at the center of column ($x = 5.0$ cm)

5 Conclusions and Discussion

Transport of mixed gases coupled with kinetic adsorption and equilibrium absorption is a challenging problem with a variety of applications. Previous understanding in competitive sorption is limited to equilibrium isotherms and fails to address the complex dynamic behavior of mass uptake. It has been demonstrated and quantified in this study that dynamic mass uptake is dominated by transient transport and kinetic adsorption. The mathematical model of advection and diffusion of mixed gases coupled with kinetic adsorption and equilibrium absorption has been developed for interpreting complex effects of various physical processes (diffusion, Henry’s absorption, Langmuir adsorption) from data collected from mixed-gas experiments using XEMIS.

In addition to the high-fidelity and physics-based model, we also developed a dynamic reduced-order model to enhance model predictability. Due to large but unquantified uncertainties in conceptual models and parameters, a large number of deterministic models were developed in the uncertain parameter space and further used to train reduced-order models. Uncertainty propagation from inputs to mass uptake is tracked using the reduced-order model. Similar to previous studies of water vapor sorption and diffusion in polymers, the dynamic behavior of mass uptake from mixed $\hbox {N}_2$-$\hbox {CO}_2$ diffusion and sorption is controlled by the $\hbox {CO}_2$ de-adsorption rate and diffusion coefficient. However, the total mass uptake is mainly due to the Henry’s absorption of $\hbox {CO}_2$ according to Sobol’ sensitivity analysis.

Experiments conducted in this work are limited to the interpretation of coupled diffusion and competitive sorption processes. To demonstrate the effect of chemical reactions on material aging properties, diffusion-controlled (or -limited) experiments (e.g., those on gravimetric instruments) may require substantial experimental time. With the implemented advection operator in our simulation code, future experiments will be planned and calibrated in advective and diffusive columns to accelerate kinetic reactions and to explore the mixed-gas transport, sorption, and chemical reactions. The reaction operator developed for modeling the competitive adsorption (reversible kinetics) will be used for identifying and quantifying other reactions once an experiment of reactive transport is completed.