A Hygro-Thermo-Mechanical Multiphase Model for Long-Term Water Absorption into Air-Entrained Concrete

Abstract

Many concrete structures located in cold climates and in contact with free water are cast with air-entrained concrete. The presence of air pores significantly affects the absorption of water into the concrete, and it may take decades before these are fully saturated. This generally improves the long-term performance of such structures and in particular their frost resistance. To study the long-term moisture conditions in air-entrained concrete, a hygro-thermo-mechanical multiphase model is presented, where the rate of filling of air pores with water is described as a separate diffusion process. The driving potential is the concentration of dissolved air, obtained using an averaging procedure with the air pore size distribution as the weighting function. The model is derived using the thermodynamically constrained averaging theory as a starting point. Two examples are presented to demonstrate the capabilities and performance of the proposed model. These show that the model is capable of describing the complete absorption process of water in air-entrained concrete and yields results that comply with laboratory and in situ measurements.

1 Introduction

Durability is a major concern in all concrete structures, but the most important deterioration mechanisms vary depending on the surrounding environment and application. Many of the most common durability issues are closely related to the moisture state inside the structure or to the transport of liquids through it. Both of these are in turn dependent on the pore structure in the concrete material. Concrete structures located in cold climates and in long-term contact with free water, for example hydropower dams, are often cast with air-entrained concrete to reduce the risk of frost damage. This type of concrete contains an artificially created network of large air pores. According to Powers’ hydraulic pressure theory (Powers 1945), frost damage is caused by the hydraulic pressure that arises due to the transport of excess water that is expelled from the freezing sites because the water volume increases by approximately 9% upon freezing. If the artificially created air pores are not fully saturated, they will act as reservoirs into which the excess water can enter and freeze without exerting a high pressure. The overall freezing-induced pressure is thus reduced and consequently also the risk of frost damage. Fagerlund (1977) has, however, shown that a certain threshold value exists, the critical degree of saturation, above which frost damage inevitably occurs. For ordinary air-entrained concrete mixtures, this value ranges between approximately 0.75 and 0.90, which normally means that the entrained air pores at least are partially saturated with water.

The smaller gel and capillary pores in concrete normally absorb water through capillary suction, but the air pores absorb water due to other processes. The long-term absorption of water into air pores is primarily caused by the dissolution of trapped air into the surrounding pore water, which then slowly diffuses towards a free surface. As the air leaves the material, it is replaced by water through suction from the external reservoir. The rate of this process is low, and it may take decades before the air pores are fully saturated. Measurements of moisture distributions in porous materials containing air pores that are in contact with free water show that there is a sharp moisture gradient at the side in contact with water (Rosenqvist 2016; Hall 2007), and these observations have been attributed to the long-term absorption of water into air pores. Fagerlund (1993) presented a theoretical foundation for this long-term water-filling mechanism and derived two models to estimate the degree of water saturation in air pores based on a local diffusion approach between neighbouring air pores of different sizes. This water-filling process has been modelled in several studies, but completely separated from other mass transport processes (e.g. Fagerlund 1993, 2004; Liu and Hansen 2016; Hall and Hoff 2012; Janz 2000; Bentz et al. 2002). A drawback of this approach is that these models cannot describe the long-term moisture distribution in, for example, a water-retaining structure since this is also governed by other transport processes. Furthermore, air pores also absorb water due to freeze–thaw cycles, which can be explained by a mechanism that Coussy (2005) called cryo-suction where water is sucked into air pores due to a depressurization of pore water in the vicinity of ice formed inside air pores. However, in, for example, water-retaining structures, this process is intermittent and often limited to surface regions that are in contact with water and also directly exposed to the ambient climate. In contrast, the aforementioned long-term absorption process is continuously active in all parts of a structure that are in contact with free water.

The absorption of water into small pores caused by capillary suction has been extensively studied in the literature. This unsaturated flow of water can be described by various types of models. A basic approach is to use the Washburn equation where the capillary flow is idealized as taking place in a bundle of parallel capillary tubes (Liu et al. 2014). A more advanced approach is to use a phenomenological diffusion-type model in which the unsaturated flow is described by a single transport coefficient that combines the transport of liquid water and water vapour. Several studies in the literature have shown that this type of model yields results that comply well with measurements (e.g. Bažant and Najjar 1972; Hall 1977; Lockington et al. 1999; Janz 2000; Li and Li 2013). A third type of model that can be used is a coupled multiphase model, in which each phase of the porous medium is treated separately. Concrete is usually divided into three phases: solid, liquid and gas. Governing equations are formulated for each phase either by using a purely macroscopic approach or by starting on the microscale and using averaging theorems to upscale the equations to the macroscale (Hassanizadeh and Gray 1979; Gray and Miller 2005). The major benefit of using a multiphase model is that different transport processes can be formulated separately and also be coupled, which means that different phase changes can be handled efficiently and consistently in the model. This type of model has been used extensively to describe unsaturated flow in concrete for various applications (e.g. Gawin et al. 1995; Chaparro et al. 2015; Johannesson and Nyman 2010; Schrefler and Pesavento 2004; Baroghel-Bouny et al. 2011; Li et al. 2016). Such multiphase models have also been formulated to consider the dissolution of air in the pore water (see e.g. Olivella et al. 1994, 1996; Collin et al. 2002; Khalili and Loret 2001). These concepts were further developed in a model presented by Gawin and Sanavia (2010) to study the effect of the dissolved air on cavitation at strain localization in soil. In their model, the transport of dissolved air was neglected, but they later presented an extended version of the model taking this into account (Gawin and Sanavia 2009). However, unsaturated flow models that also incorporate the long-term water absorption into air pores due to the dissolution and diffusion of trapped air inside these are scarce in the literature on mass transport in concrete.

The purpose of the present study is to develop a hygro-thermo-mechanical multiphase model which includes the slow absorption of water into air pores caused by the dissolution and diffusion of trapped air. Hence, it aims to describe the long-term absorption of water into air-entrained concrete. It should consequently be possible to predict the moisture distributions observed in situ and in laboratory measurements showing sharp moisture gradients towards the surface in contact with free water (Rosenqvist 2016; Hall 2007). The study is limited to the absorption of water and does not, therefore, consider the hysteresis effect in wetting–drying cycles or other processes such as cryo-suction. The rate of water absorption into the air pores is herein described by a diffusion model, where the driving potential is the concentration gradient of dissolved air in the pore water. It is proposed that this concentration is obtained through an averaging procedure, which uses the air pore size distribution as a weighting function.

2 Absorption of Water in Air-Entrained Concrete

The absorption of water into concrete depends largely on the microstructure of the concrete, and especially on its pore structure. The pore network includes a wide range of pore sizes, but these are often divided into two categories, gel pores and capillary pores, following the definition of Powers and Brownyard (1946). The limits of the two categories are somewhat arbitrary in the literature but, according to Jennings et al. (2015), it is reasonable to categorize pores with a radius between 2 and 8 nm as gel pores, while pores with a radius between 8 nm and $10 \, \upmu \hbox {m}$ are defined as capillary pores. A third type of pore can also be identified in many concretes. These pores are larger than the capillary pores, and they will hereafter be referred to as air pores and categorized as pores larger than $10 \, \upmu \hbox {m}$, as is commonly done in the literature (e.g. Fagerlund 1993, 2004; Mayercsik et al. 2016). The gel pores and capillary pores are basically a product of the chemical reactions between cement and water during the hardening of concrete (Jennings et al. 2008), while the air pores are normally caused either by unintended entrapped air in the concrete during mixing or by an air entrainment agent added to the mix in order to create artificial air pores, for example to improve the frost resistance. Since the focus herein is on the long-term absorption of water into air pores, the gel pores and capillary pores are lumped together and called capillary pores, unless otherwise stated.

2.1 Moisture Fixation

The fixation of moisture in concrete is related to both chemically and physically bound water. The first type is due to chemical reactions between cement and water during hardening while the latter is caused by the driving force to reach equilibrium with the ambient environment. At low moisture contents, water is physically bound to the pore surfaces through adsorption, but at high moisture contents, water in the moist air condenses on menisci that are formed in the porous network. For porous materials at equilibrium with the ambient air, the moisture storage capacity is normally described by a sorption isotherm. These also reflect the pore size distribution of the porous medium, and it is possible to transform a sorption isotherm into a pore size distribution and vice versa. A schematic absorption isotherm for air-entrained concrete is shown in Fig. 1. Three regions are indicated in this isotherm, representing different mechanisms of moisture fixation. In the hygroscopic region between relative humidities of 0% and 98%, water is bound by adsorption but also by capillary condensation of water vapour from moist air. For moisture levels above a relative humidity of 98%, water absorption is caused by capillary suction from a free water surface and this region is thus called the capillary region. The distinction between the hygroscopic and capillary regions is, however, fictitious, and in reality they overlap (Fagerlund 2004). At the state denoted capillary saturation in Fig. 1, the relative humidity is 100% and all the capillary pores are saturated with water but the air pores are still filled with gas. When water is absorbed into a porous medium due to capillary suction from a free water surface, air in coarser pores becomes trapped. This follows from the Young–Laplace equation, which states that the capillary suction potential is inversely proportional to the pore size, so that when water in finer pores reaches coarser pores, the suction potential becomes almost zero and the air becomes trapped. Even though the suction potential is by definition zero at this state, the air pores will slowly fill with water until full saturation has been reached, but this is due to dissolution and diffusion of the trapped air; see Sect. 2.3. This process is schematically shown in the absorption isotherm in Fig. 1 as a vertical increase in the degree of saturation at a constant relative humidity of 100%, and it is called the over-capillary region.

Fig. 1

Schematic absorption isotherm for air-entrained concrete, reproduction from (Fagerlund 2004)

Fig. 2

Typical curve from an absorption test on air-entrained concrete, together with a schematic illustration of how a fictitious pore system is filled with water during absorption

2.2 Absorption from a Free Water Surface

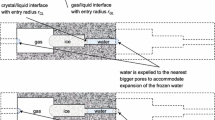
When a concrete surface comes into contact with free water, the concrete starts to absorb water due to capillary suction. A typical curve of an absorption test on a thin air-entrained concrete specimen is shown in Fig. 2. The curve shows the volume of water absorbed by the specimen per unit surface area in contact with water as a function of time. The volume of water absorbed has been shown to be proportional to the square root of time, and the results of absorption tests are normally plotted as a function of this variable instead of linear time (Hall 1977). Two distinct slopes can be identified in the curve, where the initial steep slope corresponds to the fast absorption of water due to capillary suction. The figure also includes a schematic illustration of how a fictitious pore system is filled with water during absorption, where the initial uptake of water corresponds to state A. At the intersection between the two slopes, denoted state B or the nick point, capillary saturation is reached, and the water content thereafter continues to increase with time but at a much slower rate. This part of the curve (state C) corresponds to the filling of the air pores by water, which is governed by dissolution and diffusion of the trapped air. Following the notations in ASTM C1585-13 (2013), the two slopes are denoted initial and secondary absorption and they are expressed in terms of the sorptivity S. This material property was first introduced by Hall (1977) for porous building materials and is defined as

$$\begin{aligned} {S} = \frac{{ I}}{\sqrt{{ t}}} \end{aligned}$$

(1)

where I is the volume of absorbed water normalized with respect to the surface area in contact with water and t is time. Results from several studies have shown that the initial sorptivity depends largely on the initial moisture content and decreases as the initial moisture content increases (e.g. Hall 1989; Li et al. 2011; Castro et al. 2011). The driving potential of the initial absorption is the capillary suction potential, which depends on the smallest pores not yet filled with water. At high initial moisture contents, the smallest pores not filled with water are larger in size compared to an initial state with a lower moisture content. The driving potential, therefore, decreases and the rate of water absorption is slower. This dependence has not, however, been observed for the secondary sorptivity since it is not governed by the capillary suction potential. Multiphase models of the type used in this study have been shown by, for example, Baroghel-Bouny et al. (2011) to accurately describe the initial absorption process from a free water surface in concrete. Multiphase models that also include the long-term secondary absorption of water are, however, scarce in the literature.

2.3 Long-Term Water Absorption

As mentioned previously, the slow secondary absorption of water in air-entrained concrete is a consequence of the air pores being filled with water. This occurs due to a mechanism whereby the trapped air is dissolved in the surrounding pore water and then transported by diffusion to larger pores or to the boundary of the material (Fagerlund 1993; Hall and Hoff 2012; Liu and Hansen 2016). The air bubbles inside the air pores are subjected to an overpressure because of the meniscus that arises at the gas–water interface as a result of the surface tension between the two phases. This overpressure is described by the Young–Laplace equation:

$$\begin{aligned} \Delta P_{\mathrm{ap}} = \frac{2{\upsigma }}{r} \end{aligned}$$

(2)

where $\Delta P_{\mathrm{ap}}$ is the gas overpressure inside the air pores, ${\upsigma }$ is the surface tension between air and water and r is the pore radius. This relationship implies that the overpressure is inversely proportional to the pore radius, and the pressure inside smaller pores is thus higher. According to Henry’s law, the concentration of dissolved air in water is proportional to the absolute gas pressure, and consequently the concentration of air in the pore water surrounding smaller pores is higher. This relationship can be written as

$$\begin{aligned} c_{\mathrm{a}} = \left( P_{0} + \Delta P_{\mathrm{ap}} \right) k_{\mathrm{H}} = P_{\mathrm{ap}} k_{\mathrm{H}} \end{aligned}$$

(3)

where $c_{\mathrm{a}}$ is the concentration of air in the pore water, $P_{0}$ is a reference pressure normally set to 1 atm, $P_{\mathrm{ap}}$ is the absolute gas pressure inside the air pores and $k_{\mathrm{H}}$ is the solubility constant of air in water. Hence, it follows that air diffuses from smaller to larger pores inside the material and ultimately to the outside boundary. As the air diffuses to the outside boundary of the material, it is replaced by water through suction from the outside reservoir. If a material specimen is fully immersed in water, an equilibrium state can only be reached when all the air pores are completely filled with water since the largest pore of the system is the reservoir itself (Janz 2000).

Fagerlund (1993) derived two models that can be used to establish a time-dependent relationship for the degree of water saturation in the air pores, based on the air pore size distribution. Both models consider the local diffusion of air between air pores of different sizes, but they differ in one fundamental assumption. In the first model, it is assumed that all air pores start to absorb water at the same time and at the same rate. Thus, when a pore of a certain size is fully saturated, all larger pores are only partially saturated with water. In the second model, a pore does not start to fill with water until all smaller pores are fully saturated. Furthermore, Fagerlund points out that the second model is more reasonable in a thermodynamic perspective since it represents a lower state of free energy in the system. This was confirmed by comparing values obtained using the two models with experimental results. However, these two models require parameters that are difficult to determine and must consequently be estimated. Hall and Hoff (2012) presented a sharp front model to describe the filling of air pores with water, but also this model requires a number of parameters that must be estimated. In an effort to eliminate these uncertainties, Liu and Hansen (2016) instead developed a geometrical model based on Fagerlund’s work to approximate the time to reach a certain critical degree of saturation within the material. However, this model requires that an absorption test be performed in order to determine some of its parameters.

3 Model for Filling of Air Pores with Water

In the current study, the long-term absorption of water into air pores is described by a global diffusion model; the term “global” is in contrast to the models derived by Fagerlund (1993) which consider local diffusion between neighbouring air pores of different sizes within the concrete material. Fagerlund also described the basis for a global diffusion model, where the concentration gradient is given by the average radius of the remaining air pores not filled with water. No relationships were, however, given to determine this concentration gradient within the material. It is here proposed that this concentration gradient can be determined by averaging the gas overpressure in the air pores not yet filled with water. This averaging procedure to calculate the gas pressure is, however, only applicable and used for moisture states above capillary saturation, i.e. when air is trapped inside the air pores. For moisture states below capillary saturation, the gas pressure is instead governed by the gas flow through the material. Following Fagerlund’s second model, it is assumed that the air pores are consecutively filled with water starting from the smallest air pores. Utilizing a cumulative air pore size distribution as the weighting function and the Young–Laplace equation to calculate the overpressure in a spherical pore of radius r, the average overpressure can be calculated as

$$\begin{aligned} \Delta {\bar{P}}_{\mathrm{ap}} (r_{\mathrm{sat}}) = \frac{\displaystyle \int _{r_{\mathrm{sat}}}^{\infty }\frac{\mathrm{d} {{V}}_{\mathrm{ap}}}{\mathrm{d}r}\frac{2{\upsigma }}{r}\mathrm{d}r}{\displaystyle \int _{r_{\mathrm{sat}}}^{\infty }\frac{\mathrm{d}{{V}}_{\mathrm{ap}}}{\mathrm{d}r}\mathrm{d}r} \end{aligned}$$

(4)

where $\Delta {\bar{P}}_{\mathrm{ap}}$ is the average gas overpressure in the air pores, $r_{\mathrm{sat}}$ is the radius of the largest air pore filled with water and $V_{\mathrm{ap}}$ is the cumulative air pore size distribution. To establish a relationship that describes the current degree of gas saturation as a function of $\Delta {\bar{P}}_{\mathrm{ap}}$, it is first necessary to determine the degree of gas saturation in the air pores as a function of the radius $r_{\mathrm{sat}}$. The latter relationship can be defined as

$$\begin{aligned} {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}(r_{\mathrm{sat}}) = \frac{\displaystyle \int _{r_{\mathrm{sat}}}^{\infty } \frac{\mathrm{d}{{V}}_{\mathrm{ap}}}{\mathrm{d}r}\mathrm{d}r}{\displaystyle \int _{r_\text {min}}^{\infty }\frac{\mathrm{d}{{V}}_{\mathrm{ap}}}{\mathrm{d}r}\mathrm{d}r} \end{aligned}$$

(5)

where ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ is the degree of gas saturation in the air pores ranging from zero to one and $r_{\text {min}}$ is the minimum air pore radius considered. By combining Eqs. (4) and (5), a relationship between $\Delta {\bar{P}}_{\mathrm{ap}}$ and ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ can be established. Its typical shape is shown in Fig. 3 for three different air pore size distributions, which are also used in the numerical examples presented in Sect. 6. Note that all three distributions sum to the same total air pore content, but that they contain different volume fractions of fine air pores. Using Henry’s law defined in Eq. (3), the concentration of dissolved air in the capillary pore water can be determined from the calculated value of $\Delta {\bar{P}}_{\mathrm{ap}}$, while the boundary concentration is determined by the ambient conditions at the free surface. The diffusion of dissolved air can be described by Fick’s second law of diffusion, which in this case can be written as

$$\begin{aligned} \frac{\partial \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}{\varepsilon }_{\mathrm{a}} \rho ^{g}\right) }{\partial { t}} + \nabla \cdot \left( -\tau {\mathbf{D}}_{\mathrm{aw}}\nabla c_{\mathrm{a}} \right) = 0 \end{aligned}$$

(6)

where ${\varepsilon }_{a}$ is the volume fraction of air pores, $\rho ^{g}$ is the air density, $\tau$ is a tortuosity factor accounting for a longer diffusion path inside the porous network and ${\mathbf{D}}_{\mathrm{aw}}$ is the diffusivity tensor of air in water. In Fagerlund’s models, the rate of diffusion of dissolved air is assumed to be uniform in the region that has reached capillary saturation. However, Fagerlund (2004) states that the distance to the free surface obviously has an influence on the long-term rate of absorption since the dissolved air must be transported through a longer path as the thickness increases. This effect is not taken into account in his two models, but is accounted for in our proposed global diffusion model since the diffusion rate depends on the concentration gradient of dissolved air. The proposed model also differs from the sharp front model derived by Hall and Hoff (2012), which assumes a linear concentration gradient over a fully saturated region propagating from the boundary surface.

Fig. 3

Relationship between the average gas overpressure in the air pores $\Delta {\bar{P}}_{\mathrm{ap}}$ and the degree of gas saturation ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ for three different air pore size distributions

The incorporation of the global diffusion model in the set of governing equations representing the complete multiphase system is described in Sect. 4, and the different parameters in Eq. (6) are further described in Sect. 5.3.

4 Multiphase Model of Concrete

The basis for the derivation of the hygro-thermo-mechanical multiphase model is the thermodynamically constrained averaging theory (TCAT) developed by Gray and Miller (2005, 2014), which is a framework that can be applied to a generic multiphase porous medium. Within TCAT, balance equations are first derived at the microscale of the medium and then upscaled through averaging theorems to the macroscale.

Concrete is here considered to be a porous medium consisting of three phases: liquid water (w), gas (g) and solid (s). The gas phase is treated as an ideal mixture of water vapour (W) and dry air (D). The process of dissolving trapped air in the liquid phase is indirectly considered in the multiphase system. In principle, the filling of air pores with water is included as a mass sink in the gas phase, where the removed gas causes a convective flow of liquid water to the air pores, replacing the gas. The rate of this process is controlled by the global diffusion model, which takes into account the dissolution of trapped air. In the following subsections, the governing balance equations for mass, energy and momentum are derived for the complete multiphase porous medium including the effect of the filling of air pores with water. Before deriving the balance equations, the following definitions must be introduced.

The volume fraction of each phase is denoted $\varepsilon ^{{\overline{\overline{\alpha }}}}$ where $\alpha$ denotes one of the three phases, liquid water, gas or solid (w, g, s). It follows that

$$\begin{aligned} \sum _{\alpha } \varepsilon ^{{\overline{\overline{\alpha }}}}=1 \end{aligned}$$

(7)

The total porosity of the medium including both air and capillary pores is denoted $\varepsilon$ and is defined as

$$\begin{aligned} \varepsilon =1-\varepsilon ^{{\overline{\overline{s}}}}\end{aligned}$$

(8)

but the total porosity is divided into air and capillary porosity such that

$$\begin{aligned} \varepsilon =\sum _{\gamma }\varepsilon _{\gamma }\end{aligned}$$

(9)

where $\gamma$ denotes either air pores (a) or capillary pores (c). A pore volume fraction $\eta _{\gamma }$ of each pore type is also introduced:

$$\begin{aligned} \eta _{\gamma }=\frac{\varepsilon _{\gamma }}{\varepsilon } \end{aligned}$$

(10)

The degree of saturation $S^{{\overline{\overline{f}}}}$ of the two fluid phases occupying the pore network in the concrete is defined as

$$\begin{aligned} S^{{\overline{\overline{f}}}}=\frac{\varepsilon ^{{\overline{\overline{f}}}}}{\varepsilon } \end{aligned}$$

(11)

where the index f indicates one of the two fluid phases (w, g). Following the earlier definitions in Eqs. (7) and (8), it can be concluded that

$$\begin{aligned} \sum _{{ f}}S^{{\overline{\overline{f}}}}=1 \end{aligned}$$

(12)

To account for the long-term water absorption into air pores, the total degree of saturation is split between air pores and capillary pores, by weighting the total degree of saturation with respect to the pore volume fractions defined in Eq. (10). Formally, this gives

$$\begin{aligned} S^{{\overline{\overline{f}}}}=\sum _{\gamma }{S}_{\gamma }^{{\overline{\overline{f}}}}= \sum _{\gamma }{\hat{S}}_{\gamma }^{{\overline{\overline{f}}}}\eta _{\gamma }\end{aligned}$$

(13)

where ${S}_{\gamma }^{{\overline{\overline{f}}}}$ and ${\hat{S}}_{\gamma }^{{\overline{\overline{f}}}}$ are the weighted and unweighted degrees of saturation of fluid phase f in pore type $\gamma$, respectively.

The definitions introduced are then used to derive the governing equations of the hygro-thermo-mechanical multiphase model. However, the derivation starts not from the microscale but instead from the macroscopic balance equations for a generic porous medium derived using the TCAT. A complete derivation of the general macroscopic balance equations used herein can, for example, be found in (Gray and Miller 2014). It should, however, be noted that small displacements are assumed, which means that no difference is made between the material and the spatial reference frame.

4.1 Mass Balance Equations

The general macroscopic mass balance for a species i dispersed in an arbitrary phase $\alpha$ can be expressed as

$$\begin{aligned}&\frac{\partial \left( \varepsilon ^{{\overline{\overline{\alpha }}}}\rho ^{\alpha }\omega ^{i{\bar{\alpha }}}\right) }{\partial { t}} + \nabla \cdot \left( \varepsilon ^{{\overline{\overline{\alpha }}}}\rho ^{\alpha }\omega ^{i{\bar{\alpha }}}{\mathbf{v}}^{{\bar{\alpha }}}\right) + \nabla \cdot \left( \varepsilon ^{{\overline{\overline{\alpha }}}}\rho ^{\alpha }\omega ^{i{\bar{\alpha }}}{\mathbf{u}}^{{\overline{\overline{i\alpha }}}}\right) - \varepsilon ^{{\overline{\overline{\alpha }}}}r^{i\alpha }- \sum \mathop {M}\limits ^{i\kappa \rightarrow i \alpha }=0 \end{aligned}$$

(14)

where $\rho ^{\alpha }$ is the density of phase $\alpha$, $\omega ^{i{\bar{\alpha }}}$ is the mass fraction of a species i dispersed in phase $\alpha$ and is defined by ${\rho }^{{{i\bar{\alpha }}}}=\rho ^{\alpha }\omega ^{i{\bar{\alpha }}}$, in which ${\rho }^{{{i\bar{\alpha }}}}$ denotes the mass concentration of species i in phase $\alpha$. The term $r^{i\alpha }$ is a reaction term that can be used to describe chemical reactions between species in the phase while $\mathop {M}\limits ^{i\kappa \rightarrow i \alpha }$ is a source term that accounts for the mass exchange of a species with another phase over an interface $\kappa$. Furthermore, ${\mathbf{v}}^{{\bar{\alpha }}}$ is the velocity of phase $\alpha$, whereas ${\mathbf{u}}^{{\overline{\overline{i\alpha }}}}$ is the diffusive velocity of species i in phase $\alpha$. For a single-species phase, the term $r^{i\alpha }$ and the diffusive flux of species are omitted in the equation. It also follows from the definition above that $\omega ^{i{\bar{\alpha }}}=1$.

Based on the phases and species considered in the multiphase system, a total of four mass balance equations are derived using Eq. (14). It is, however, better to sum the balance equations for water into a single equation that describes the total water content, since the source term expressing the mass exchange between liquid water and water vapour is cancelled out by this operation. This has been done by several researchers, and it means that no explicit constitutive relationship is needed in the model to describe evaporation and condensation (e.g. Gawin et al. 1996; Lewis and Schrefler 1998; Whitaker 1977). Furthermore, the split of the total degree of fluid saturation according to Eq. (13) is introduced in the mass balances. For brevity, only the final form of the mass balance equations is presented.

The mass balance equation for the total water content in the porous medium can be written as

$$\begin{aligned}&\frac{\partial \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{w}\right) }{\partial { t}} + \frac{\partial \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{W\overline{g}}\right) }{\partial { t}} + \frac{\partial \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{w}\right) }{\partial { t}} + \frac{\partial \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{W\overline{g}}\right) }{\partial { t}} \nonumber \\&\quad + \nabla \cdot \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{w}{\mathbf{v}}^{{\overline{ws}}}\right] + \nabla \cdot \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{W\overline{g}}{\mathbf{v}}^{{\overline{gs}}}\right] \nonumber \\&\quad + \nabla \cdot \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{W\overline{g}}{\mathbf{u}}^{\overline{{\overline{W g}}}}\right] + \nabla \cdot \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{w}{\mathbf{v}}^{{\overline{s}}}\right) \nonumber \\&\quad + \nabla \cdot \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{w}{\mathbf{v}}^{{\overline{s}}}\right) + \nabla \cdot \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{W\overline{g}}{\mathbf{v}}^{{\overline{s}}}\right) + \nabla \cdot \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{W\overline{g}}{\mathbf{v}}^{{\overline{s}}}\right) = 0 \end{aligned}$$

(15)

where ${\mathbf{v}}^{{\overline{fs}}}$ is the relative velocity between fluid phase f and the solid skeleton (s) and is defined as

$$\begin{aligned} {\mathbf{v}}^{{\overline{fs}}}={\mathbf{v}}^{{\overline{f}}}-{\mathbf{v}}^{{\overline{s}}}\end{aligned}$$

(16)

The mass balance of dry air (${ D}$) has the same form as the total water balance, but contains only the dry air species

$$\begin{aligned}&\frac{\partial \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{D {\overline{g}}}\right) }{\partial { t}} + \frac{\partial \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{D {\overline{g}}}\right) }{\partial { t}} + \nabla \cdot \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{D {\overline{g}}}{\mathbf{v}}^{{\overline{gs}}}\right] \nonumber \\&\quad +\nabla \cdot \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{D {\overline{g}}}{\mathbf{u}}^{{\overline{\overline{Dg}}}}\right] + \nabla \cdot \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon \rho ^{D {\overline{g}}}{\mathbf{v}}^{{\overline{s}}}\right) + \nabla \cdot \left( {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \rho ^{D {\overline{g}}}{\mathbf{v}}^{{\overline{s}}}\right) = 0 \end{aligned}$$

(17)

The solid phase is assumed to consist of a single species. However, the balance equation is written in a form slightly different from that of the other two and instead expresses the rate of change of the volume fraction of the solid phase as

$$\begin{aligned} \frac{\partial \varepsilon ^{{\overline{\overline{s}}}}}{\partial { t}} = -\frac{1}{\rho ^{s}}\left[ \varepsilon ^{{\overline{\overline{s}}}}\frac{\partial \rho ^{s}}{\partial { t}} + \nabla \cdot \left( \varepsilon ^{{\overline{\overline{s}}}}\rho ^{s}{\mathbf{v}}^{{\overline{s}}}\right) \right] \end{aligned}$$

(18)

From the definition introduced in Eq. (8), it follows that $\partial \varepsilon ^{{\overline{\overline{s}}}}/\partial { t}=-\partial \varepsilon /\partial { t}$, which is utilized in the partial derivatives in Eqs. (15) and (17).

4.2 Energy and Momentum Balance Equations

The general energy balance given by Gray and Miller (2014) contains several terms that can be omitted for porous materials with low permeability, since small velocities of the fluid phases can be assumed in such materials. Furthermore, when dealing with phase changes, it is usually more appropriate to work with enthalpy instead of internal energy (Bear and Bachmat 1990). Hence, the general energy balance is normally simplified for cementitious materials and rewritten in an enthalpy form, as shown by, for example, Sciumé (2013). The enthalpy balance of the complete multiphase system including all considered phases is obtained by summing the contributions from each phase and can be written as

$$\begin{aligned}&(\rho C_{p})_{\mathrm{eff}}\frac{\partial {T}}{\partial { t}} - \nabla \cdot \mathbf{q}+ \Delta H_{\mathrm{vap}}M_{\mathrm{vap}}\nonumber \\&\quad + \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{w}C_{p}^{w}{\mathbf{v}}^{{\overline{ws}}}\right] \cdot \nabla {T} + \left[ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{g}C_{p}^{g}{\mathbf{v}}^{{\overline{gs}}}\right] \cdot \nabla {T} = 0 \end{aligned}$$

(19)

where T is the temperature, $\Delta H_{\mathrm{vap}}= 2257 \, \hbox {kJ/kg}$ is the latent heat of evaporation of water, $\mathbf{q}$ is the conductive energy flux vector and $C_{p}^{\alpha }$ is the specific heat capacity of phase $\alpha$. The term $M_{\mathrm{vap}}$ denotes the mass exchange due to phase changes between liquid water and water vapour and can be obtained through Eq. (14) by deriving the mass balance equation for the liquid water phase. The first term in Eq. (19) is defined as

$$\begin{aligned} (\rho C_{p})_{\mathrm{eff}}= \varepsilon ^{{\overline{\overline{s}}}}\rho ^{s}C_{p}^{s}+ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\varepsilon _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\varepsilon _{\mathrm{a}}\right) \rho ^{w}C_{p}^{w}+ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\varepsilon _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\varepsilon _{\mathrm{a}}\right) \rho ^{g}C_{p}^{g}\end{aligned}$$

(20)

which expresses the effective heat content of the multiphase system.

The linear momentum balance of the multiphase system is also obtained by summation of the contributions from each phase. For concrete, it is usually assumed that the velocities are small and that the timescale of interest is large (days), which means that inertia effects and momentum exchange terms are usually neglected (Pesavento et al. 2016). Taking this into consideration, the momentum balance is given by

$$\begin{aligned} \nabla \cdot \mathbf{t}+\rho \mathbf{g}=0 \end{aligned}$$

(21)

where $\mathbf{t}$ is the total stress tensor of the porous medium, $\mathbf{g}$ is the gravitational acceleration vector and $\rho$ is the total density of the medium. With regard to the defined split of the degrees of saturation in Eq. (13), the total density is defined as

$$\begin{aligned} \rho =\varepsilon ^{{\overline{\overline{s}}}}\rho ^{s}+ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{w}+ \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}\varepsilon + {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\varepsilon \right) \rho ^{g}\end{aligned}$$

(22)

4.3 Summary and Choice of State Variables

The hygro-thermo-mechanical behaviour of air-entrained concrete including the filling of air pores with water can be described by the set of partial differential equations derived above. In total, there are seven governing equations describing the behaviour of the multiphase system: the mass balances of total water content in Eq. (15), dry air in Eq. (17) and solids in Eq. (18), as well as the enthalpy balance in Eq. (19) and the three components of the momentum balance in Eq. (21).

In this study, the following variables are chosen as the state variables of the multiphase model: the capillary pressure $p^{\mathrm{c}}$ in Eq. (15), the gas pressure $p^{g}$ in Eq. (17), the temperature T in Eq. (19) and the displacements $\mathbf{d}$ in Eq. (21). Assuming local equilibrium above the hygroscopic moisture range, the capillary pressure can be defined as

$$\begin{aligned} p^{\mathrm{c}}= p^{g}- p^{w}\end{aligned}$$

(23)

In fact, this relationship can be derived using the second law of thermodynamics (e.g. Gray and Hassanizadeh 1991a; Schrefler and Pesavento 2004). The benefits of using the capillary pressure as state variable, instead of, for example, the water pressure $p^{w}$ or the relative humidity $\varphi$, are thoroughly discussed in, for example, (Gawin et al. 1995, 1996; Baggio et al. 1995; Lewis and Schrefler 1998; Gawin et al. 2006). The main point is that capillary pressure can be used to describe the full range of moisture conditions in porous media, i.e. from fully saturated conditions down to and including the hygroscopic region. More precisely, it can be shown that the capillary pressure is related to a water potential that is formally valid over the entire moisture range and, hence, the definition in Eq. (23) is also valid over the entire moisture range (Lewis and Schrefler 1998). The complete system of governing equations contains many unknowns which, in order to close the system, must be expressed by constitutive equations formulated in terms of the chosen state variables or be defined as constants.

5 Constitutive Relationships

In a formal TCAT analysis, the second law of thermodynamics is used to derive the principle form of the constitutive relationships, and this ensures that the entropy inequality is satisfied (Gray and Miller 2005, 2014). In this study, the constitutive relationships used are, however, taken from the literature, but these have been proven to comply well with experimental results and observations. Many of the relationships have, however, also been derived from the entropy inequality through linearization procedures by others in the literature. Some of the unknowns in the governing partial differential equations have been treated as constants, and they have thus only been given an explicit value in connection with the numerical examples in Sect. 6.

5.1 Equations of State

The volumetric behaviour of each phase in the multiphase system is described by an Equation of State (EOS). For the liquid water and solid phase, these are defined in the same linearized form as was done by Lewis and Schrefler (1998). Assuming that the density of liquid water is a function of both temperature and pressure in the phase, the relationship is given by

$$\begin{aligned} \rho ^{w}= {\rho }_{\mathrm{ref}}^{w} \left[ 1-\alpha ^w\left( {T}-{T}_{\mathrm{ref}}\right) +\frac{1}{K^{w}}\left( p^{w}-{p}_{\mathrm{ref}}^{w}\right) \right] \end{aligned}$$

(24)

where ${\rho }_{\mathrm{ref}}^{w}$ is a reference water density at the reference temperature ${T}_{\mathrm{ref}}$ and reference pressure ${p}_{\mathrm{ref}}^{w}$, $\alpha ^{w}$ is the volumetric thermal expansion coefficient of water and $K^{w}$ is the bulk modulus of water.

The EOS of the solid phase is not only dependent on the temperature and pressure but is also a function of the first invariant of the effective stress tensor $I_{1}^{s}$ and can be written as

$$\begin{aligned} \rho ^{s}= \rho ^{s}_{\mathrm{ref}}\left[ 1- \alpha ^{s}\left( {T}-{T}_{\mathrm{ref}}\right) +\frac{1}{K^{s}} p^{s}+\frac{1}{3\varepsilon ^{{\overline{\overline{s}}}}K^{s}}I_{1}^{s}\right] \end{aligned}$$

(25)

The first invariant of the effective stress tensor $I_{1}^{s}$ takes into account external factors on the solid skeleton and is defined as

$$\begin{aligned} I_1^{s} = 3\left( 1-b\right) K^{s}\left[ \nabla \cdot \mathbf{d}- {{\mathrm{tr}}}\left( {\mathbf{e}}_{\mathrm{th}}\right) + \frac{1}{K^{s}}p^{s}\right] \end{aligned}$$

(26)

where ${{\mathrm{tr}}}\left( {\mathbf{e}}_{\mathrm{th}}\right)$ is the volumetric thermal strain; see Sect. 5.5. The parameter $b$ denotes Biot’s coefficient and is defined by $b=1-\left( K_{T}/K^{s}\right)$, where $K_{T}$ is the bulk modulus of the drained solid skeleton.

The gas phase is assumed to be an ideal gas mixture of water vapour (W) and dry air (${ D}$), and the EOS of the individual gas species is defined by the ideal gas law:

$$\begin{aligned} \rho ^{i\overline{g}}= \frac{M_i}{R{T}}p^{ig}\end{aligned}$$

(27)

where $p^{ig}$ is the partial pressure of species i in the gas phase, $M_{i}$ is the molar mass of species i and R is the universal gas constant. Since no reactions are assumed to occur between the species, the total density and pressure of the gas phase can be described by Dalton’s law as

$$\begin{aligned} \rho ^{g}= \rho ^{W\overline{g}}+ \rho ^{D {\overline{g}}} \end{aligned}$$

(28a)

$$\begin{aligned} p^{g}= p^{W g}+ p^{Dg} \end{aligned}$$

(28b)

5.2 Sorption Equilibrium

Since local thermodynamic equilibrium is assumed at each point in the multiphase system, the state of equilibrium between the liquid water phase and the water vapour in the gas phase can be described by Kelvin’s equation:

$$\begin{aligned} p^{W g}= p_{\mathrm{sat}}^{W g}\exp \left( -\frac{M_{w}}{\rho ^{w}R{T}}p^{\mathrm{c}}\right) \end{aligned}$$

(29)

where $M_{w}$ is the molar mass of water and $p_{\mathrm{sat}}^{W g}$ is the water vapour saturation pressure. There are various empirical relationships describing $p_{\mathrm{sat}}^{W g}$ as a function of temperature in the literature, and here the expression presented by Murray (1967) has been used.

The moisture storage capacity of a porous medium at equilibrium with the ambient environment is usually described by an absorption isotherm, but as outlined earlier, the total degree of saturation has in the present study been split into two separate contributions from capillary pores and air pores. Here, the sorption isotherm describes the moisture storage capacity only up to capillary saturation while the degree of water saturation in the air pores is described by the global diffusion model introduced in Sect. 3. For a concrete specimen fully immersed in water, this means that a global equilibrium is not reached until all the air pores are fully saturated (Janz 2000). If the specimen is partially immersed in water, other equilibrium states are of course possible. Nevertheless, the moisture storage capacity of the capillary pores is described by the analytical expression of van Genuchten (1980):

$$\begin{aligned} {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}=\left[ 1 + \left( \frac{p^{\mathrm{c}}}{l}\right) ^{\frac{m}{1-m}}\right] ^{-\frac{1}{m}} \end{aligned}$$

(30)

where l and m are fitting parameters.

5.3 Long-Term Water Absorption into Air Pores

As outlined in Sect. 3, the long-term water absorption into air pores is described by Fick’s second law of diffusion. The concentration gradient of dissolved air is obtained from the relationship describing ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ as a function of $\Delta {\bar{P}}_{\mathrm{ap}}$ introduced in Sect. 3. This relationship can be established using Eqs. (4) and (5) if the air pore size distribution of the material is known. Utilizing this relationship and Henry’s law defined in Eq. (3), Eq. (6) can be rewritten as

$$\begin{aligned} \frac{\partial \left[ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\left( {\bar{P}}_{\mathrm{ap}}\right) {\varepsilon }_{\mathrm{a}} \rho ^{g}\right] }{\partial { t}}+ \nabla \cdot \left[ - \tau {\mathbf{D}}_{\mathrm{aw}}\nabla \left( k_{\mathrm{H}} {\bar{P}}_{\mathrm{ap}}\right) \right] = 0 \end{aligned}$$

(31)

where ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\left( {\bar{P}}_{\mathrm{ap}}\right)$ is the aforementioned relationship expressed in terms of the average absolute gas pressure in the air pores instead of the overpressure. This pressure is defined as ${\bar{P}}_{\mathrm{ap}}= \Delta {\bar{P}}_{\mathrm{ap}} + P_{0}$, where $P_{0}$ is a reference pressure. In addition, this mass balance equation requires its own state variable, here called an internal variable to separate it from the four chosen state variables of the multiphase system. The natural choice following from Eq. (31) is ${\bar{P}}_{\mathrm{ap}}$.

To close the diffusion model, relationships must be established for the remaining parameters in the equation. The air pore porosity ${\varepsilon }_{a}$ is given by the mass balance equation for the solid phase in Eq. (18) together with the porosity and pore volume fraction defined in Eqs. (8) and (10), respectively. The gas density $\rho ^{g}$ is determined by the ideal gas law at a relative humidity of 100%, where it is assumed that $\Delta {\bar{P}}_{\mathrm{ap}}$ has a negligible effect on the density since its magnitude is small, so that the gas density depends only on the temperature. The tortuosity factor $\tau$ is treated as a constant and normally varies between 0.4 and 0.6 for concrete (Gawin et al. 1999). The diffusivity tensor ${\mathbf{D}}_{\mathrm{aw}}$ is assumed to be temperature dependent and to follow the proportionality relationship defined by Fagerlund (1993). The diffusivity tensor is given by

$$\begin{aligned} {\mathbf{D}}_{\mathrm{aw}}= D_{\mathrm{aw0}}\frac{{T}}{T_0}\mathbf{I}\end{aligned}$$

(32)

where $D_{\mathrm{aw0}}$ is the bulk diffusivity of air in water at the reference temperature $T_0$ and $\mathbf{I}$ is a unity tensor. In this work, the bulk diffusivity is consistently defined as $D_{\mathrm{aw0}}= 2\times 10^{-9} \, \hbox {m}^2/ \, \hbox {s}$ at $T_0 = 298.15 \, \hbox {K}$ (Fagerlund 1993). The solubility constant $k_{\mathrm{H}}$ is temperature dependent and is here determined as was done by Hall and Hoff (2012) under the assumption that air consists of 21% oxygen and 79% nitrogen:

$$\begin{aligned} k_{\mathrm{H}} = \kappa _{\mathrm{H}}\sum n_{\theta }M_{\theta }\exp \left[ A_{\theta }\left( \frac{1}{T} - \frac{1}{T_0} \right) \right] k_{\mathrm{H}\theta }^0 \end{aligned}$$

(33)

where $\theta$ denotes either oxygen $\hbox {O}_2$ or nitrogen $\hbox {N}_2$, $n_{\theta }$ is the gas volume fraction in air, $M_{\theta }$ is the molar mass, $A_{\theta }$ is a constant that is 1300 K for nitrogen and 1500 K for oxygen, $T_0$ is a reference temperature and $k_{\mathrm{H}\theta }^0$ is the solubility of oxygen or nitrogen at the reference temperature. The term $\kappa _{\mathrm{H}}$ governs when air trapped in the air pores starts to dissolve in the surrounding pore water. Before reaching capillary saturation, the air is not trapped and the concentration of dissolved air in the pore water is assumed to be governed by the ambient conditions, but as capillary saturation is reached, the air becomes trapped and starts to dissolve due to the overpressure in the air pores, and $\kappa _{\mathrm{H}}$ is thus defined as

$$\begin{aligned} \kappa _{\mathrm{H}}= {\left\{ \begin{array}{ll} 0 &{} \hbox {if} \, {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}< 1 \\ 1 &{} \hbox {if} \, {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}= 1 \end{array}\right. } \end{aligned}$$

(34)

5.4 Mass and Heat Fluxes

5.4.1 Advective Mass Flux

The advective flux is quantified by describing the relative velocity ${\mathbf{v}}^{{\overline{fs}}}$ of the two fluid phases with the generalized Darcy’s law. This law is commonly used to describe the advective flux within porous media and can be derived using a linearized form of the momentum balance for each fluid phase together with the second law of thermodynamics (cf., Gray and Miller 2014; Sciumé 2013; Gray and Hassanizadeh 1991b; Hassanizadeh 1986). The generalized form of Darcy’s law used in this study is given by

$$\begin{aligned} \varepsilon \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{f}}}}\eta _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{f}}}}\eta _{\mathrm{a}}\right) {\mathbf{v}}^{{\overline{fs}}}= -\frac{k_{\mathrm{r}}^{{ f}}\mathbf{k}}{\mu ^{{ f}}}\left( \nabla p^{f}- \rho ^{f}\mathbf{g}\right) \end{aligned}$$

(35)

where $\mathbf{k}$ is the intrinsic permeability tensor, $\mu ^{{ f}}$ is the dynamic viscosity and $k_{\mathrm{r}}^{{ f}}$ is the relative permeability, which is introduced in order to account for unsaturated flow in the porous medium and varies between zero and one. The dynamic viscosities are considered to be temperature-dependent. In this study, the gas phase viscosity is described by the Sutherland equation and the liquid water phase by the Vogel equation; see Table 1. The relative permeability is usually described with a function that depends on the degree of saturation of each fluid phase. The analytical expressions proposed by van Genuchten (1980) are here used for both the water and the gas phase:

$$\begin{aligned}&k_{\mathrm{r}}^{{ w}} = \left( S^{{\overline{\overline{w}}}}\right) ^{n}\left\{ 1-\left[ 1-\left( S^{{\overline{\overline{w}}}}\right) ^{m}\right] ^{\frac{1}{m}}\right\} ^{2} \end{aligned}$$

(36a)

$$\begin{aligned}&k_{\mathrm{r}}^{{ g}} = \left( 1-{\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\right) ^{n}\left[ 1-\left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\right) ^{\frac{1}{m}}\right] ^{2m} \end{aligned}$$

(36b)

where m and n are fitting parameters. For cementitious materials, a value of 0.5 is normally used for n as reported by Zhang et al. (2015), whereas the value of m is obtained by fitting Eq. (30) to the sorption isotherm. Furthermore, ${\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}$ is used instead of $S^{{\overline{\overline{w}}}}$ in the above expression for the relative gas permeability. The reason for this choice has its origin in the mechanism of filling air pores with water described in Sect. 2.3. Because the trapped air is not considered to be a continuous phase in the porous network at capillary saturation and is transported towards the surface through dissolution and diffusion in the capillary water, there is no advective flow of gas. By choosing ${\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}$ as the independent variable in Eq. (36b), the advective gas flow is eliminated when capillary saturation is reached.

5.4.2 Diffusive Flux

The diffusive flux in the gas phase is only considered below capillary saturation and describes the mass flux of the water vapour (W) and dry air (${ D}$) species through the gas phase. The flux is quantified though the diffusive velocity ${\mathbf{u}}^{{\overline{\overline{ig}}}}$ of the two species and is expressed by Fick’s law. Similarly to Darcy’s law, Fick’s law can also be derived using a linearized momentum balance together with the second law of thermodynamics (cf., Hassanizadeh 1986). The total diffusive mass flux of the two species is expressed as

$$\begin{aligned} {\mathbf{J}}^{{\overline{\overline{ig}}}}= \varepsilon \rho ^{i\overline{g}}\left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\right) {\mathbf{u}}^{{\overline{\overline{ig}}}}= -\rho ^{g}{\mathbf{D}}_{\mathrm{d}}^{ig}\nabla \frac{\rho ^{i\overline{g}}}{\rho ^{g}} \end{aligned}$$

(37)

where ${\mathbf{J}}^{{\overline{\overline{ig}}}}$ is the total diffusive mass flux and ${\mathbf{D}}_{\mathrm{d}}^{ig}$ is the diffusivity tensor. Starting from Dalton’s law defined in Eq. (28), it can be shown that ${\mathbf{D}}_{\mathrm{d}}^{W g}={\mathbf{D}}_{\mathrm{d}}^{Dg}$. Following from this equality, it can also be concluded that the diffusive mass fluxes must sum to zero, i.e. ${\mathbf{J}}^{{\overline{\overline{W g}}}}=-{\mathbf{J}}^{{\overline{\overline{Dg}}}}$. The diffusivity tensor of water vapour inside the partially saturated pore network is defined in the same form as has been done by Gawin et al. (1999) and is given by

$$\begin{aligned} {\mathbf{D}}_{\mathrm{d}}^{W g}= \varepsilon ^{A_{\mathrm{d}}}\left( 1-{\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\right) ^{B_{\mathrm{d}}} f_sD_{\mathrm{v0}}\left( \frac{T}{T_0}\right) ^{C_{\mathrm{d}}}\frac{p_{0}}{p^{g}}\mathbf{I}\end{aligned}$$

(38)

where ${A_{\mathrm{d}}}$, ${B_{\mathrm{d}}}$ and ${C_{\mathrm{d}}}$ are model parameters and ${D_{\mathrm{v0}}}$ is the bulk diffusivity of water vapour in air at the reference temperature ${T_0}$ and pressure $p_{0}$. The parameter $f_s$ is a structure coefficient that accounts for the tortuosity and the Knudsen effect, i.e. the effect of molecules colliding with the solid phase in finer pores. Moreover, to assure that diffusion of water vapour through the gas phase is inactive when the capillary pores in the concrete are saturated, ${\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}$ is used instead of $S^{{\overline{\overline{w}}}}$ in Eq. (38). At this point, the diffusion of gas from air pores occurs instead through the capillary water as described in Sect. 2.3.

5.4.3 Conductive Heat Flux

The conductive heat flux is governed by Fourier’s law:

$$\begin{aligned}&\mathbf{q}= -\lambda _{\mathrm{eff}}\mathbf{I}\nabla {T} \end{aligned}$$

(39a)

$$\begin{aligned}&\lambda _{\mathrm{eff}}= \varepsilon ^{{\overline{\overline{s}}}}\lambda ^{s}+ \varepsilon \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{w}}}}\eta _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}\eta _{\mathrm{a}}\right) \lambda ^{w}+ \varepsilon \left( {\hat{S}}_{\mathrm{c}}^{{\overline{\overline{g}}}}\eta _{\mathrm{c}}+ {\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\eta _{\mathrm{a}}\right) \lambda ^{g}\end{aligned}$$

(39b)

where $\lambda _{\mathrm{eff}}$ is the effective thermal conductivity of the porous medium and $\lambda ^{\alpha }$ is the thermal conductivity of phase $\alpha$. All thermal conductivities are assumed to be constant and therefore independent of temperature variations. The species in the gas phase are not treated separately but are lumped together and described by a single thermal conductivity.

5.5 Stress Tensor

The total stress tensor in Eq. (21) is obtained by summing the contributions of each phase in the multiphase system:

$$\begin{aligned} \mathbf{t}= \varepsilon ^{{\overline{\overline{s}}}}{\varvec{\tau }}^{{\overline{\overline{s}}}}- bp^{s}\mathbf{I}\end{aligned}$$

(40)

where ${\varvec{\tau }}^{{\overline{\overline{s}}}}$ is the effective stress tensor (Lewis and Schrefler 1998). This tensor accounts for the effects of external and internal loads on the solid skeleton of the concrete. It is here assumed that all strains remain small so that the total strain tensor $\mathbf{e}$ can be defined as

$$\begin{aligned} \mathbf{e}= \frac{1}{2}\left[ \nabla \mathbf{d}+ \left( \nabla \mathbf{d}\right) ^{\intercal }\right] \end{aligned}$$

(41)

Based on this definition and taking into consideration the presence of thermal strains, Hooke’s law is used to define the effective stress tensor:

$$\begin{aligned} {\varvec{\tau }}^{{\overline{\overline{s}}}}= {\mathbb {D}}_{\mathrm{e}}:\left( \mathbf{e}- {\mathbf{e}}_{\mathrm{th}}\right) \end{aligned}$$

(42)

where ${\mathbb {D}}_{\mathrm{e}}$ is a fourth-order elasticity tensor and ${\mathbf{e}}_{\mathrm{th}}$ is the thermal strain tensor. The solid phase is assumed in this study to behave as an isotropic linear elastic material where ${\mathbb {D}}_{\mathrm{e}}$ is defined by two material constants, for example Young’s modulus E and Poisson’s ratio $\nu$. The thermal strains of the solid phase are determined as

$$\begin{aligned} {\mathbf{e}}_{\mathrm{th}}= \frac{\alpha ^{s}}{3}\left( {T}-{T}_{\mathrm{ref}}\right) \mathbf{I}\end{aligned}$$

(43)

where $\alpha ^{s}$ is the volumetric thermal expansion coefficient of the solid phase and ${T}_{\mathrm{ref}}$ denotes a reference temperature at which there is no thermal strain. The pressure $p^{s}$ accounts for the pressure exerted on the solid phase by the two fluid phases in the porous network and is defined (cf., Gawin et al. 1995, 1996; Lewis and Schrefler 1998) as

$$\begin{aligned} p^{s}= S^{{\overline{\overline{w}}}}p^{w}+ \left( 1-S^{{\overline{\overline{w}}}}\right) p^{g}\end{aligned}$$

(44)

6 Numerical Examples

To demonstrate the performance and capability of the proposed model to simulate water absorption into air-entrained concrete, two examples are presented. The first is an absorption test where the measured pore size distribution of the air pore system is used to simulate the long-term absorption of water. Furthermore, this pore size distribution is modified to contain a larger volume fraction of either fine or coarse pores, while maintaining the total air pore content constant. The effect of these modifications on the long-term rate of water absorption has been studied. In the second example, the model is applied to a case resembling a front plate in a concrete buttress dam, and the long-term water absorption at different depths below the water level has been studied. The influence of temperature as well as the air pore size distribution on the long-term moisture conditions in the front plate has also been studied.

The system of governing equations is solved using the commercial FE-code Comsol Multiphysics (COMSOL 2016). All governing equations are first converted to their weak form, and integration by parts and the divergence theorem are applied to reduce the order of differentiation. The weak formulations obtained are discretized using the Galerkin method. Time integration is performed with the fully implicit backward differentiation formula (BDF), and the nonlinear equations obtained at each increment are solved using a damped version of the Newton–Raphson method.

6.1 Example 1: Absorption Test

The aim of the first example was to examine whether the model is capable of describing the water absorption process in air-entrained concrete with an emphasis on long-term absorption into air pores. An absorption test performed by Liu and Hansen (2016) was chosen, for which the size distribution of the air pores was also measured. Absorption measurements were performed on concrete specimens with a water–cement ratio (w / c) of 0.45 and approximately 5% air pores. The specimens had a thickness of 12 mm and a cross-sectional area of $100 \times 100 \, \hbox {mm}^2$. Before starting the absorption test, the specimens were preconditioned by drying them in an oven at $50 \, ^{\circ }\hbox {C}$ to a constant weight. After this, the lateral sides were sealed using aluminium foil with butyl rubber to ensure unidimensional absorption. The bottom surface of the specimens was then immersed in 5 mm of water and the mass gain recorded. The geometry of the specimens was discretized using an axisymmetric formulation, where the radius was set to give an equivalent surface area of $100 \times 100 \, \hbox {mm}^2$.

Three different pore size distributions were used in the simulations, where the first corresponded to the measured distribution. The other two are fictitious but they have the same total air pore content with a larger volume fraction of either finer or coarser pores than the measured distribution. These two distributions were also used by Liu and Hansen (2016) in their study of the time to reach a certain critical spacing between air pores in air-entrained concrete. The shape of the cumulative air pore size distribution is described by the relationship:

$$\begin{aligned} V_{\mathrm{ap}} = V_{\mathrm{ap,0}}\exp \left[ -\left( \frac{\chi }{D}\right) ^{\xi }\right] \end{aligned}$$

(45)

where $V_{\mathrm{ap}}$ is the cumulative air pore content, $V_{\mathrm{ap,0}}$ is the total air pore content, $\chi$ and $\xi$ are two fitting parameters and D is the air pore diameter. The three air pore size distributions are plotted in Fig. 4. By utilizing the averaging procedure described in Sect. 3, a relationship between ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ and $\Delta {\bar{P}}_{\mathrm{ap}}$ was established for each of the three distributions. The three relationships obtained are shown in Fig. 3. The absorption isotherm for the tested concrete was not measured, and consequently it has to be estimated. In this work, the shape of the absorption isotherm in Eq. (30) was estimated based on the relationships presented by Xi et al. (1994). The capillary porosity is not explicitly stated, but it can be approximated based on the assumed absorption isotherm and the volume of absorbed water at the nick point in the absorption test. The input parameters are summarized in Table 1.

Fig. 4

Three cumulative air pore size distributions from Liu and Hansen (2016) used in the numerical examples

Table 1 Input parameters used in the numerical examples

The initial moisture content in the specimens was estimated based on the experimental results and on the absorption isotherm used and was found to correspond approximately to a relative humidity of $\varphi =11$%. The initial values of ${\bar{P}}_{\mathrm{ap}}$ at capillary saturation are given by the relationships describing ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}$ as a function of $\Delta {\bar{P}}_{\mathrm{ap}}$, which are obtained from the air pore size distributions using the averaging procedure proposed in Sect. 3. The initial values for the measured, fine and coarse distributions were 104.8 kPa, 106.2 kPa and 103.9 kPa, respectively. The initial temperature in the specimens was set to $20 \, {^{\circ }}\hbox {C}$. The boundary conditions were applied either as Dirichlet- or Neumann-type conditions where the first type constrains a state variable to a fixed value on the boundary, whereas the second type prescribes a flux (q) on the boundary. The applied boundary conditions in the axisymmetric model are summarized in Fig. 5.

Fig. 5

Boundary conditions applied on the axisymmetric model of the absorption test. Note that boundary D is the symmetry axis

A comparison of the simulation results with the measurements performed by Liu and Hansen (2016) is shown in Fig. 6a, where the volume of water absorbed per surface area in contact with water is plotted as a function of the square root of time. It is evident that the proposed model is capable of describing both the initial capillary suction of water and the long-term water absorption into the air pores. However, it should be recalled that the capillary suction part is described by an estimated absorption isotherm which also affects the relative permeabilities due to the chosen constitutive relationships. Consequently, the intrinsic permeability must be fitted to obtain complying results in the capillary suction part and a value of $1.1\times 10^{-18} \, \hbox {m}^{2}$ was found to be satisfactory. It is, however, important to notice that this value is reasonable and complies well with measured intrinsic permeabilities found in the literature for air-entrained concrete (e.g. Wong et al. 2011). However, the main purpose of these simulations is to validate the diffusion model describing the long-term water absorption. The results show that the model predicts the rate of long-term water absorption accurately for the measured pore size distribution using standard values for the air–water diffusivity and tortuosity factor. The simulations also show the effect of refining or coarsening the measured air pore size distribution. In Fig. 6a, the effect does not seem to be significant, but this is due to the quantity of absorbed water and the timescale in the plot. Figure 6b instead shows ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}$ as a function of linear time, and the effect of the different pore size distributions becomes more pronounced. There is a 15% difference in the degree of water saturation for the fine and coarse distributions after 700 h. As discussed in Sect. 2.3, the air pore size distribution has a significant effect on the long-term absorption rate and the simulations indicate that the model is capable of accounting for this effect.

Fig. 6

a Absorbed water according to the simulations using the three distributions and measured absorption data from Liu and Hansen (2016) corresponding to the measured pore size distribution and b degree of water saturation in the air pores ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{w}}}}$ for the three pore size distributions

6.2 Example 2: Water-Retaining Structure

The second example aimed to study moisture conditions in water-retaining structures constructed with air-entrained concrete. Most concrete dams located in cold climates are cast with air-entrained concrete to reduce the risk of frost damage. Hence, it is necessary to consider the mechanism by which air pores are filled with water in an analysis aiming to capture the moisture conditions inside such structures. Unfortunately, few measurements of moisture distributions inside water-retaining structures have been presented in the literature. However, in a recent study by Rosenqvist (2016), moisture profiles inside the front plate of a 60-year-old concrete buttress dam were measured at different depths below the water level. The general shape and design of this type of dam is shown in Fig. 7. Even though no material properties were determined for the concrete except the degree of water saturation equal to capillary saturation ($S_{\mathrm{cap}}$), the simulations can be qualitatively compared to these measurements. The first part of this example, therefore, aims to show that the proposed multiphase model is capable of describing the shape of the observed moisture profiles, which would not be possible if the long-term water absorption process were not included in the model. The second part, on the other hand, aimed to study the influence of temperature and the air pore size distribution on the long-term moisture conditions, as they both have a considerable effect on the mass transport.

6.2.1 Comparison with Measurements

Since the results were to be qualitatively compared with the aforementioned measurements, the dimensions and boundary conditions were chosen to resemble the front plate on which the measurements were performed. The value of $S_{\mathrm{cap}}$ was measured to be 0.79 by Rosenqvist (2016), who also reported that air-entrained concrete with a w / c of about 0.50 was used to construct the dam. The air pore content was assumed to be 5% and to have the same pore size distribution as the measured distribution in the previous example. Based on the measured value of $S_{\mathrm{cap}}$ and the assumed air pore content, the capillary porosity was calculated to be 19%. All other input parameters were assumed to be the same as in Example 1 and are summarized in Table 1. The simulations were performed using a two-dimensional geometry representing a thin strip of the front plate in the buttress dam. Two different depths were considered in the simulations: 0 m, which corresponds to the water surface, and 10.5 m. The front plate thickness increases from 1.2 to 1.3 m between these two depths but a uniform thickness of 1.2 m was used in both simulations. The buttress dam has an insulation wall on the downstream side to reduce the temperature variations over the year, and a mean temperature of $10 \, ^\circ \hbox {C}$ was therefore assumed on this side of the dam. On the upstream side, the water was assumed to have a constant temperature of $4 \, ^\circ \hbox {C}$. The insulation wall also affects the relative humidity in the ambient air in contact with the downstream surface, and this usually has a higher relative humidity than the outside air due to standing water at the bottom. Therefore, an average relative humidity of 90% was assumed on this side. The initial temperature in the structure was set to $10 \, ^\circ \hbox {C}$, and the initial moisture content corresponded to a relative humidity of 85%. At capillary saturation, all the air pores are filled with air and ${\bar{P}}_{\mathrm{ap}}=104.8 \, \hbox {kPa}$ for the assumed air pore size distribution. The only external mechanical load considered in the example was the dead weight of the front plate located above the two studied depths. It was applied as a surface traction ${\tilde{t}}_y$ on the upper boundary of the models. All the boundary conditions applied in the model of the front plate at the two considered depths are summarized in Fig. 7.

Fig. 7

General design of a buttress dam and applied boundary conditions on the thin strips of the front plate. The two values of $p^{w}$ and ${\tilde{t}}_y$ correspond to the two considered depths of 0 m and 10.5 m

Results showing the moisture profiles obtained over the entire front plate thickness after 5 and 60 years are shown in Fig. 8a for the two depths of 0 and 10.5 m. The same plots are shown in Fig. 8b but over a shorter distance from the upstream surface. To enable the profile shapes to be qualitatively compared with the measurements performed by Rosenqvist (2016), his results for 0 and 10.5 m are also plotted in the two figures. It should be noted that measurements are missing for the inner middle part of the front plate, between approximately 0.3 and 0.7 m from the upstream side. This area is illustrated by the dashed lines in the figure. The measurements clearly show that the total degree of water saturation was higher than $S_{\mathrm{cap}}$ close to the upstream surface. Regions located further downstream remain close to capillary saturation but the degree of water saturation continued to decrease towards the downstream surface as water is evaporating to the ambient air at the boundary. It should be noted that similar moisture profiles have been reported by, for example, Hall (2007), who performed absorption measurements in a calcium silicate plug. Generally, the proposed model is capable of describing the overall profile shape over the front plate thickness with a sharp moisture gradient close to the upstream surface because of the long-term water absorption. It is therefore evident that it is necessary to include the water-filling process of air pores when modelling mass transport in water-retaining structures built with air-entrained concrete.

Fig. 8

Moisture profiles obtained from the simulations showing the total degree of water saturation $S^{{\overline{\overline{w}}}}$ compared with measured profiles by Rosenqvist (2016): a over the entire front plate thickness and b over a thickness of 0.4 m from the upstream surface. Note that measurements are missing in the middle part of the front plate, which is indicated by the dashed lines in the figure

The results show that the depth of penetration of the wetting front from the upstream surface increases as the external water pressure increases, which also means that the total water uptake in the structure is higher at greater depths. The results also show that the degree of water saturation, in the case with a higher water pressure, increases at a slightly slower rate in the inner parts that have reached capillary saturation. This behaviour can be explained by longer diffusion paths to a free surface, as was discussed in Sect. 3. However, this observation is contradicted by another series of measurements performed by Rosenqvist (2016), which indicated that the rate of long-term absorption increases with increased depth for fully immersed concrete specimens. Further testing is therefore required to establish the true effect on the long-term water absorption of increasing the water head. In addition, the advective flow of water might also remove some of the dissolved air from the regions where capillary saturation has been reached (Hall and Hoff 2012), but this effect is currently not included in the model.

The measurements show that the front plate at a depth of 0 m was not fully saturated at the upstream surface, probably because the water level fluctuates in the reservoir, and consequently this part of the structure is subjected to wetting–drying cycles. The amplitude of the fluctuation is in most cases small and typically varies between 20 and 30 cm. The shape of the predicted moisture profile at this level after 60 years of constant contact with water differs from the measured profile. If instead the calculated profile after 5 years is compared to the measurements, the general shape complies significantly better. However, to describe these varying moisture conditions adequately, it is necessary to include the hysteresis effect. In addition, since this region is exposed to the ambient environment, it will also frequently be subjected to freeze–thaw cycles, which means that it is also important to consider the cryo-suction of water to get an even more accurate prediction of the moisture conditions in this part of the structure. For regions on the upstream side located at greater depths, neither the hysteresis nor the cryo-suction is important to consider, since these regions are rarely if ever exposed to wetting–drying or freeze–thaw cycles. However, in thin structures without insulation on the downstream side, freezing temperatures may penetrate from that side causing ice to form, with an increased rate of water absorption due to cryo-suction as one possible consequence.

The contribution of the terms related to deformations of the solid phase in the mass balances for total water content and dry air was investigated by running the simulation for 10.5 m with these terms omitted in Eqs. (15) and (17). The calculation of the total volume of water absorbed in the front plate showed that the difference was $<0.2$% after 1 year and decreased even more as time went on. These terms can, therefore, be neglected in the mass balances for the fluid phases, which also means that the traction applied on boundary D has a negligible effect on the moisture distribution in this example. Consequently, the momentum balance can in principle be omitted from the model formulation if the aim is only to study moisture and temperature conditions.

6.2.2 Influence of Temperature

Many of the constitutive equations and material parameters depend on the temperature, and, hence, the balance equations are also temperature dependent. To study the influence of temperature on the long-term moisture conditions in the dam, a series of simulations was performed where the temperature on the downstream side was varied. The studied temperatures were $0 \, ^\circ \hbox {C}$, $10 \, ^\circ \hbox {C}$ and $20 \, ^\circ \hbox {C}$. All other conditions in the simulations were the same as the conditions used in Sect. 6.2.1 for a water depth of 10.5 m. The results of these analyses are shown in Fig. 9 as the degree of water saturation over the front plate thickness after 5 and 60 years.

Fig. 9

Obtained moisture profiles showing the total degree of water saturation $S^{{\overline{\overline{w}}}}$ over the thickness of the front plate for the three studied temperatures on the downstream boundary after 5 and 60 years

As seen in the figure, the temperature effect towards the upstream side is rather small after both 5 and 60 years, even though both the solubility constant $k_{\mathrm{H}}$ and the diffusivity tensor ${\mathbf{D}}_{\mathrm{aw}}$ are temperature dependent. The influence of temperature is, however, more pronounced on the interior parts of the dam, especially after 60 years. At around 0.4 m from the upstream side and further downstream, there is a clear difference between the simulations, where a colder temperature yields a higher degree of saturation. Many of the constitutive relationships and material properties are directly dependent on the temperature, and this influences the results when the downstream temperature is varied in the simulations. Given that the relative humidity is prescribed on the downstream boundary, the state variable $p^{\mathrm{c}}$ is affected by the temperature following Kelvin’s equation. Consequently, $S^{{\overline{\overline{w}}}}$ is affected when the temperature on the boundary is changed, as can be noted in the figure. This of course also affects the advective and diffusive mass fluxes through the front plate since $p^{\mathrm{c}}$, $p^{w}$ and $p^{g}$ are related through the definition in Eq. (23). In conclusion, the results show that the temperature has a considerable influence on the long-term moisture conditions in this case.

6.2.3 Influence of Air Pore Size Distribution

As concluded in Example 1, one of the key parameters affecting the long-term absorption rate is the air pore size distribution. The way in which the air pore size distributions in Example 1 affect the long-term moisture conditions in the front plate was therefore investigated. All input parameters, except for the two additional relationships ${\hat{S}}_{\mathrm{a}}^{{\overline{\overline{g}}}}\left( \Delta {\bar{P}}_{\mathrm{ap}} \right)$ for the fine and coarse distributions, and the boundary conditions were the same as in the analysis for a water depth of 10.5 m in Sect. 6.2.1. The simulation results are presented in Fig. 10, which shows the total degree of water saturation over the thickness of the front plate after 5 and 60 years.

Fig. 10

Calculated moisture profiles showing the total degree of water saturation $S^{{\overline{\overline{w}}}}$ over the thickness of the front plate for the three studied air pore size distributions after 5 and 60 years

As expected, the air pore size distribution has a significant influence on the resulting moisture conditions, where the fine distribution yields an overall higher degree of saturation over the thickness. In contrast to the temperature dependence, a clear difference between the three cases can be seen already after 5 years, and as time passes the difference continues to increase. Comparing the calculated total volume of absorbed water in the air pore system after 60 years for each distribution indicates that the fine distribution has absorbed approximately 19% and 35% more water than the measured and coarse distribution, respectively.

7 Conclusions

This paper presents a hygro-thermo-mechanical multiphase model for air-entrained concrete, which includes the effect of long-term water absorption into air pores. This process is described by a diffusion model, where the driving potential is the concentration of dissolved air in the pore water. An averaging procedure is proposed to obtain a relationship between the degree of gas saturation in the air pores and the dissolved air concentration in the pore water. The procedure utilizes the pore size distribution of the air pore system as a weighting function. The TCAT is used as a basis for the derivation of the multiphase model, where the total degree of saturation is split between capillary pores and air pores.

Two numerical examples have been presented to show the capabilities of the proposed multiphase model. The first focused on verifying that the model could describe the complete absorption process by simulating an absorption test of air-entrained concrete. The effect of refining or coarsening the air pore size distribution was also studied. The results showed good agreement with the measurements, and it was also concluded that the air pore size distributions had an effect on the rate of long-term absorption. A 15% difference in the degree of water saturation of the air pores was observed between the finest and the coarsest air pore size distribution after 700 h. The second example aimed at simulating the moisture conditions at two different depths below the water level, 0 m and 10.5 m, in a water-retaining structure constructed with air-entrained concrete. The simulations were qualitatively compared to measured moisture distributions in the front plate of a buttress dam. The results showed a sharp moisture gradient close to the upstream surface which could be attributed to the long-term water absorption process. This general shape was also verified through the qualitative comparison with the measured moisture distributions. It can, therefore, be concluded that the proposed multiphase model is capable of describing moisture conditions in water-retaining structures cast with air-entrained concrete, which would not be possible without including the long-term water absorption process in the model. Results from the simulations in Example 2 also indicated that the terms related to deformations of the solid phase in the mass balances for the fluid phases can be neglected. Furthermore, the momentum balance in the model can be omitted if the only aim is to study moisture and temperature conditions. The general formulation of the presented model means, however, that it can be used in applications where it is also necessary to describe moisture- and temperature-induced deformations. Moreover, it means that the model can in the future be straightforwardly extended to consider, for example, the effect of damage in the solid skeleton. The second example also showed that the temperature and the air pore size distribution have a considerable influence on the long-term moisture conditions in the front plate.

Apart from the temperature conditions, the risk of frost damage is closely related to the degree of water saturation in the concrete. To reduce this risk, structures located in cold climates are often cast with air-entrained concrete, since such concretes generally have a critical degree of saturation above the state of capillary saturation. It is therefore important to consider the long-term water absorption into air pores when assessing these risks in, for example, hydropower dams, road pavements, piers and bridges. The proposed model provides a means to do this in a general hygro-thermo-mechanical framework and can, therefore, serve as an important aid when making such assessments. However, Example 2  indicates that for certain conditions, the hysteresis effect in wetting–drying cycles and the cryo-suction of water due to freeze–thaw cycles should be considered to improve the performance of the model.