Skip to main content
SpringerLink
Log in

Radial Viscous Fingering in Case of Poorly Miscible Fluids

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

Abstract

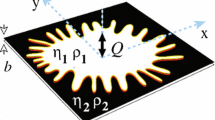
The displacement of a viscous fluid from an annular Hele-Shaw cell with a source of finite radius by a less viscous one is investigated. A special case of poorly miscible fluids is considered when corresponding dimensionless criteria—capillary and Peclet numbers—both tend to infinity. Brinkman model which additionally takes into account small viscous forces in a plane of the cell is used to describe the displacement process. Linear analysis shows a stabilizing effect of viscous forces and reveals a geometrical similarity criterion, namely the ratio of the interface’s radius to the gap between the cell’s plates. The displacement patterns, obtained numerically under Brinkman model, are very sensitive to the discovered criterion. The comparison with available experimental data is acceptable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Chen, J.-D.: Growth of radial viscous fingers in a Hele-Shaw cell. J. Fluid. Mech. 201, 223–242 (1989)

    Article  Google Scholar 

  • Chouke, R.L., van Meurs, P., van der Poel, C.: The instability of slow, immiscible, viscous liquid–liquid displacements in permeable media. Trans. AIME 216, 188–194 (1959)

    Google Scholar 

  • Daripa, P., Pasa, G.: Stabilizing effect of diffusion in enhanced oil recovery and three-layer Hele-Shaw flow with viscosity gradient. Transp. Porous Media 70, 11–23 (2007)

    Article  Google Scholar 

  • Dias, E.O., Alvarez-Lacalle, E., Carvalho, M.S., Miranda, J.A.: Minimization of viscous fluid fingering: a variational scheme for optimal flow rates. Phys. Rev. Lett. 109, 144502 (2012)

    Article  Google Scholar 

  • Gin, C., Daripa, P.: Stability results for multi-layer radial Hele-Shaw and porous media flows. Phys. Fluids 27, 012101 (2015)

    Article  Google Scholar 

  • Hill, S.: Channeling in packed columns. Chem. Eng. Sci. 1, 247–253 (1952)

    Article  Google Scholar 

  • Kim, H., Funada, T., Joseph, D.D., Homsy, G.M.: Viscous potential flow analysis of radial fingering in a Hele-Shaw cell. Phys. Fluids 21, 074106 (2009)

    Article  Google Scholar 

  • Logvinov, O.A.: Stability of the lateral surface of viscous fingers formed when a fluid is displaced from a Hele-Shaw cell. MSU Mech. Bull. 66(2), 25–31 (2011)

    Google Scholar 

  • Logvinov, O.A.: Averaged equations in a Hele-Shaw cell: hierarchy of models. Acta Astronaut. 123, 103–108 (2016)

    Article  Google Scholar 

  • Martyushev, L.M., Birzina, A.I.: Morphological stability of the interphase boundary of a fluid displaced in a finite Hele-Shaw cell. Tech. Phys. Lett. 34(3), 213–216 (2008)

    Article  Google Scholar 

  • Maxworthy, T.: Experimental study of interface instability in a Hele-Shaw cell. Phys. Rev. Ser. A 39(11), 5863–5866 (1989)

    Article  Google Scholar 

  • Nagel, M., Gallaire, F.: A new prediction of wavelength in radial viscous fingering involving normal and tangential stresses. Phys. Fluids 25, 107–124 (2013)

    Article  Google Scholar 

  • Smirnov, N.N., Nikitin, V.F., Maximenko, A., Thiercelin, M., Legros, J.C.: Instability and mixing flux in frontal displacement of viscous fluids from porous media. Phys. Fluids 17, 84–102 (2005)

    Google Scholar 

  • Yee, H.C., Warming, R.F., Harten, A.: Implicit total variation diminishing (TVD) schemes for steady-state calculations. J. Comput. Phys. 57, 27–360 (1985)

    Article  Google Scholar 

  • Zvyagin, A.V., Ivashnev, O.E., Logvinov, O.A.: Effect of small parameters on the structure of the front formed by unstable viscous fluid displacement from a Hele-Shaw cell. Fluid Dyn. 42(4), 518–527 (2007)

    Article  Google Scholar 

Download references

Acknowledgements

The present investigation has been supported by Russian Foundation for Basic Research—Grant 17-08-01032.

Author information

Authors and Affiliations

  1. Faculty of Mechanics and Mathematics, Moscow MV Lomonosov State University, Moscow, 119992, Russia

    Oleg A. Logvinov

Authors
  1. Oleg A. Logvinov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oleg A. Logvinov.

Appendix

Appendix

The coefficients \(\varPi _j, j=0\ldots 5\) and \(\varPhi \) in dispersion relation (16) have the following form:

$$\begin{aligned} \varPhi= & {} 8 (M-1) (\beta _1 + 1) (\beta _2 + 1) n^2 \\&+\, 2 (\beta _1 + 1) (\beta _2 + 1) k^2\left[ M \left( \langle R_2 \rangle ^{2n} + 1 \right) -\left( \langle R_1 \rangle ^{2n} + 1 \right) \right] n \\&-\, 4 (M-1) k \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) (\beta _1 + 1) n \\&-\, 4 (M-1) k \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \langle R_1 \rangle ^{2n} + 1 \right) (\beta _2 + 1) n \\&-\, M k^3 (\beta _2 + 1) \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&+\, k^3 (\beta _1 + 1) \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&+\, 2 (M-1) \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) k^2 \\&\times \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) , \\ \varPi _5= & {} 16 (M-1)^2 (\beta _1 + 1) (\beta _2 + 1), \\ \varPi _4= & {} - 8 (M-1)^2 (\beta _1 + 1) k\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \\&-\, 8 (M-1)^2 (\beta _2 + 1) k\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \langle R_1 \rangle ^{2n} + 1 \right) , \\ \varPi _3= & {} 4 (M-1)^2 k^2\left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \\&\times \,\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&+\, 8 (M-1) k^2 (\beta _1 + 1) (\beta _2 + 1)\left[ \left( \langle R_1 \rangle ^{2n} - 1 \right) -M \left( \langle R_2 \rangle ^{2n} - 1 \right) \right] \\&-\, 16 (M-1)^2 (\beta _1 + 1) (\beta _2 + 1), \\ \varPi _2= & {} 4 (M-1) k^3 M (\beta _2 + 1)\left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&-\, 4 (M-1) k^3 (\beta _1 + 1)\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&-\, 8 (M-1) (\beta _1 + 1) (\beta _2 + 1) k^2\left( M \langle R_2 \rangle ^{2n} - \langle R_1 \rangle ^{2n} \right) \\&+\, 8 (M-1) k (\beta _1 + 1)\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left[ \left( M \langle R_2 \rangle ^{2n} + 1 \right) -\left( \langle R_2 \rangle ^{2n} + 1 \right) \right] \\&+\, 8 (M-1) k (\beta _2 + 1)\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left[ \left( M \langle R_1 \rangle ^{2n} + 1 \right) -\left( \langle R_1 \rangle ^{2n} + 1 \right) \right] , \\ \varPi _1= & {} - 2 (M-1) (\beta _1 + 1) (\beta _2 + 1) k^4\left[ M \left( \langle R_2 \rangle ^{2n} - 1 \right) -\left( \langle R_1 \rangle ^{2n} - 1 \right) \right] \\&-\, 4 (M-1) k^2\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \,\left[ M \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) -\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \right] \\&-\, 4 (M-1) k^2\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \,\left[ 2 \left( M \left( \langle R_1 \rangle ^{2n} + 1 \right) - \left( \langle R_2 \rangle ^{2n} + 1 \right) \right) \right] \\&+\, 4 (\beta _1 + 1) k^3\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \left[ M \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) +\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \right] \\&+\, 4 (\beta _1 + 1) k^3\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \left[ M \left( M \left( \langle R_2 \rangle ^{2n} - 1 \right) - \left( \langle R_1 \rangle ^{2n} + 1 \right) \right) -\left( M \left( \langle R_1 \rangle ^{2n} - 1 \right) - \left( \langle R_2 \rangle ^{2n} + 1 \right) \right) \right] \\&+\, 4 (\beta _2 + 1) k^3\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \left[ M \left( M \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) -\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \right) \right] \\&+\, 4 (\beta _2 + 1) k^3\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \\&\times \left[ M \left( M \left( \langle R_1 \rangle ^{2n} + 1 \right) - \left( \langle R_2 \rangle ^{2n} - 1 \right) \right) -\left( M \left( \langle R_2 \rangle ^{2n} + 1 \right) - \left( \langle R_1 \rangle ^{2n} - 1 \right) \right) \right] , \\ \varPi _0= & {} k^5\left[ M \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) -\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \right] \\&\times \,\left[ M (\beta _2 + 1) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) -(\beta _1 + 1) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \right] \\&+\, 2 (M-1) k^4\left[ - M \left( \langle R_1 \rangle ^{2n} + 1 \right) \left( \langle R_2 \rangle ^{2n} - 1 \right) +\left( \langle R_1 \rangle ^{2n} - 1 \right) \left( \langle R_2 \rangle ^{2n} + 1 \right) \right] \\&\times \,\left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _1 \frac{K_{n-1}(k)}{K_{n}(k)} \right) \left( \frac{I_{n-1}(k)}{I_{n}(k)} - \beta _2 \frac{K_{n-1}(k)}{K_{n}(k)} \right) . \\ \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Logvinov, O.A. Radial Viscous Fingering in Case of Poorly Miscible Fluids. Transp Porous Med 124, 495–508 (2018). https://doi.org/10.1007/s11242-018-1081-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-018-1081-7

Keywords

Search

Navigation