Abstract
The development of the capillary fringe during gravity drainage has a significant influence on saturation and pressure distributions in porous formations (Sarkarfarshi et al. in Int J Greenh Gas Control 23:61–71, 2014). This paper introduces an analytical solution for gravity drainage in an axisymmetric geometry with significant capillary pressure. The drainage process results from the injection of a lighter and less viscous injectant into a porous medium saturated with a heavier and more viscous pore fluid. If the viscous force dominates the capillary and the buoyancy forces, then the flow regime is approximated by differential equations and the admissible solution comprises a front shock wave and a trailing simple wave. In contrast to existing analytical solutions for capillary gravity drainage problems (e.g., Nordbotten and Dahle in 47(2) 2011; Golding et al. in J Fluid Mech 678:248–270 2011), this solution targets the saturation distribution during injection at an earlier point in time. Another contribution of this analytical solution is the incorporation of a completely drained flow regime close to the injection well. The analytical solution demonstrates the strong dependency of the saturation distribution upon relative permeability functions, gas entry capillary pressure, and residual saturation. The analytical results are compared to results from a commercial reservoir engineering software package (\(\hbox {CMG } \hbox {STARS}^{\mathrm{TM}}\)).






Similar content being viewed by others
Abbreviations
- \(\mathbf{u}_\mathrm{w}\), \(\mathbf{u}_\mathrm{n}\) (m/s):
-
Velocity of wetting and non-wetting
- S :
-
Saturation of wetting
- \(S_\mathrm{r}\) :
-
Residual saturation of wetting
- \(S^{b}\) :
-
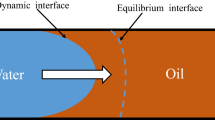
Saturation of top the transition zone (See Fig. 1)
- \(S_\mathrm{c}\) :
-
Top saturation of the front
- \(S_\mathrm{top}\) :
-
Saturation of top of the reservoir
- \(S_\mathrm{ave}\) :
-
Vertical average saturation
- \(\gamma _\mathrm{w}\), \(\gamma _\mathrm{n}\) (Pa/m):
-
Unit weight of wetting and non-wetting
- \(Q_\mathrm{o}\,(\hbox {m}^{2}/\hbox {s})\) :
-
Volumetric rate of injection per unit meter of preformation
- r (m), \(\xi \) :
-
Actual and normalized radius
- z (m), \(\zeta \) :
-
Actual and normalized depth
- t (s), \(\tau \) :
-
Actual and normalized time
- \(r_\mathrm{w}\) (m), \(\xi _\mathrm{w}\) :
-
Actual and normalized well radius
- B (m):
-
Thickness of reservoir
- b :
-
Normalized thickness of the fully drained zone
- R (m):
-
Characteristic length of aquifer radius
- \(P_\mathrm{c}\) (Pa), \(P^{*}_\mathrm{c}\) :
-
Actual and normalized capillary pressure
- \(k_\mathrm{rw}\), \(k_\mathrm{rn}\) :
-
Relative permeability functions
- \(\mu _\mathrm{w}\) (Pa s), \(\mu _\mathrm{n}\)(Pa s):
-
Wetting and non-wetting viscosity
- c :
-
Ratio of wetting viscosity to non-wetting viscosity
- A (kPa):
-
Maximum capillary pressure
- \(\varphi \) :
-
Porosity
- \(\varepsilon \) :
-
Ratio of capillary to viscous force
- \(K\,(\hbox {m}^{2})\) :
-
Intrinsic permeability
References
Barenblatt, G., Entov, V., Ryzhik, M.: Theory of Fluids Flow Through Natural Rock. Kluwer Academic Publisher, Berlin (1990)
Bennion, B., Bachu, S.: Relative permeability characteristics for supercritical CO\(_2\) displacing water in a variety of potential sequestration zones in the western Canada sedimentary basin. In: SPE Annual Technical Conference and Exhibition, Dallas (2005)
Court, B., Bandilla, K.W., Celia, M.A., Janzen, A., Dobossy, M., Nordbotten, J.M.: Applicability of vertical-equilibrium and sharp-interface assumptions in CO\(_2\) sequestration modeling. Int. J. Greenh. Gas Control. 10, 134–147 (2012)
Dake, L.P.: Fundamentals of Reservoir Engineering. Elsevier, Amsterdam (1983)
Dentz, M., Tartakovsky, D.: Abrupt-interface solution for carbon dioxide injection into porous media. Transp. Porous Media 79, 15–27 (2008)
Dusseault, M., Malekzadeh, F.: Sequestration of greenhouse gasses by generating an unstable gas/saline front within a formation. US Patent 9316093 B2 (2016)
Gasda, E.S., Nordbotten, J.M., Celia, M.A.: Vertical equilibrium with sub-scale analytical methods for geological CO\(_2\) sequestration. Comput. Geosci. 13, 469–481 (2009)
Gasda, S.E., Nordbotten, J.M., Celia, M.A.: Vertically averaged approaches for CO2 migration with solubility trapping. Water Resour. Res. 47(5) (2011). doi:10.1029/2010WR009075
Golding, M.J., Neufeld, J.A., Hesse, M.A.: Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270 (2011)
Guo, B., Zheng, M., Celia, H.S.: Axisymmetric flows from fluid injection into a confined porous medium. Phys. Fluids 28(2), 022107 (2016)
Hesse, M., Tchelepi, H., Orr, F.J.: Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60 (2008)
Hinch, E.J.: Method of multiple scales. In: Hinch, E.J. (ed.) Perturbation Methods. Cambridge University Press, Cambridge (1991)
Huppert, H.E., Woods, A.W.: Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69 (1995)
Juanes, R., MacMinn, C., Szulczewski, M.: The footprint of the CO\(_2\) plume during carbon dioxide storage in saline aquifers: storage efficiency for capillary trapping at the basin scale. Transp. Porous Media 82, 19–30 (2009)
Lyle, S., Huppert, H., Hallworth, M., Bickle, M., Chadwick, A.: Axisymmetric gravity currents in a prous medium. J. Fluid Mech. 543, 293–302 (2005)
MacMinn, C., Szulczewski, M.L., Juanes, R.: CO\(_2\) migration in saline aquifers. Part 2: capillary and solubility trapping. J. Fluid Mech. 688, 321–331 (2011)
Malekzadeh, F., Dusseault, M.: A solution for the transition zone isosats in two-phase primary drainage in the presence of gravity. Comput. Geosci. 17, 757–771 (2013)
Malekzadeh, F., Leonenko, Y., Dusseault, M.: Cyclic injection of \({\rm CO}_2\) into saline aquifer with extended interface. Int. J. Glob. Environ. (2017). http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=%20IJGENVI
Nordbotten, M.J., Celia, M.A.: Similarity solution for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327 (2006)
Nordbotten, J.M., Dahle, H.K.: Impact of the capillary fringe in vertically integrated models for \({\rm CO}_2\) storage. Water Resour. Res. 47(2) (2011). doi:10.1029/2009WR008958
Nordabotten, J.M., Celia, M.A., Bachu, A.: Injection and storage of CO\(_2\) in deep saline aquifers. Transp. Porous Media 58, 339–360 (2005)
Pegler, S.S., Huppert, H.E., Neufeld, J.A.: Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620 (2014)
Sarkarfarshi, M., Malekzadeh, F., Gracie, R., Dusseault, M.: Parametric sensitivity analysis for CO\(_2\) geosequestration. Int. J. Greenh. Gas Control 23, 61–71 (2014)
Toro, E.F.: Some properties of the euler equations. In: Toro, E.F. (ed.) Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, pp. 87–114. Springer, New York (2004)
Vilarrasa, V., Bolster, D., Dentz, M., Olivella, S., Carrera, J.: Effects of CO\(_2\) compressibility on CO\(_2\) storage in deep saline aquifers. Transp. Porous Media 85, 619–639 (2010)
Vilarrasa, V., Carrera, J., Bolster, D., Dentz, M.: Semi analytical solution for CO\(_2\) plume shape and pressure evolution during CO\(_2\) injection in deep saline formations. Transp. Porous Media 58, 339–360 (2013)
Wallace, B.: Constrained Optimization: Kuhn-Tucker Conditions. Royal Holloway, Egham (2004)
Yortsos, Y.C.: A theoretical analysis of vertical flow equilibrium. Transp. Porous Media 18(2), 107–129 (1995)
Zheng, Z., Guo, B., Christov, I., Celia, M., Stone, H.: Flow regimes for fluid injection into a confined porous medium. J. Fluid Mech. 767, 881–909 (2015)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Conservative Equation Derivation
By substituting Eq. (9) in Eq. (6), the conservation equation is reduced to
The velocity of water and the injectant in the drained zone can therefore be expressed as follows. Radial derivative of pressure is derived as a function of injection rate and capillary pressure.
Velocity of the wetting phase becomes:
The mass conservation equation becomes:
By a simple vertical averaging, Eq. (9) becomes:
Equation (43) sums the wetting phase conservation equations and incorporates contributions of viscous, capillary and buoyancy forces.
Appendix 2: First-Order Solution
Equation (37) is the first order of the conservation equation. After solving Eq. (36), the zeroth-order solution of the equation is known and Eq. (37) becomes linear.
\(U_{1}^{i}\), \(U_{2}^{i}\), and \(U_{3}^{i}\) are functions of \(o_{0}\) and Eq. (44) is a linear differential equation. By using the method of characteristics and introducing a new variable as \(\omega =\xi -U_{1}^{i} \tau \), Eq. (44) is simplified to
Analytical solution of Eq. (45) is straightforward.
\(o_{1}\) is the first-order correction of saturation. It is possible to evaluate higher-order solutions of the equations resulting from the perturbation method.
Rights and permissions
About this article
Cite this article
Malekzadeh, F.A., Heidari, R. & Dusseault, M. An Analytical Solution for Capillary Gravity Drainage with Dominant Viscous Forces. Transp Porous Med 118, 417–434 (2017). https://doi.org/10.1007/s11242-017-0864-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-017-0864-6