Extracting the collective wisdom in probabilistic judgments

Abstract

How should we combine disagreeing expert judgments on the likelihood of an event? A common solution is simple averaging, which allows independent individual errors to cancel out. However, judgments can be correlated due to an overlap in their information, resulting in a miscalibration in the simple average. Optimal weights for weighted averaging are typically unknown and require past data to estimate reliably. This paper proposes an algorithm to aggregate probabilistic judgments under shared information. Experts are asked to report a prediction and a meta-prediction. The latter is an estimate of the average of other individuals’ predictions. In a Bayesian setup, I show that if average prediction is a consistent estimator, the percentage of predictions and meta-predictions that exceed the average prediction should be the same. An “overshoot surprise” occurs when the two measures differ. The Surprising Overshoot algorithm uses the information revealed in an overshoot surprise to correct for miscalibration in the average prediction. Experimental evidence suggests that the algorithm performs well in moderate to large samples and in aggregation problems where individuals disagree in their predictions.

1 Introduction

Decision-making is often a problem of assessing the chances of uncertain events. Scientists make probabilistic projections on natural phenomena, such as the occurrence of a major earthquake or the effects of anthropogenic climate change. Strategists assess the likelihood of important geopolitical events. Investors form judgments on the risks involved in investments. Economists and policy makers need probabilistic predictions on policy outcomes and macroeconomic indicators. Individual judgments may be subject to biases such as optimism, overconfidence, anchoring on an initial estimate, focusing too much on easily available information, neglecting an event’s base rate, and many more (Kahneman and Tversky 1973; Tversky and Kahneman 1974; Kahneman et al. 1982). Combining multiple judgments to leverage ‘the wisdom of crowds’ is known to be an effective approach in improving accuracy (Surowiecki 2004; Makridakis and Winkler 1983).

The use of collective wisdom involves choosing an aggregation method that combines individual predictions into an aggregate prediction (Armstrong 2001; Clemen 1989; Palan et al. 2019). Previous work found simple averaging to be surprisingly effective, typically outperforming more sophisticated aggregation methods and showing robustness across various settings (Makridakis and Winkler, 1983; Mannes et al. 2012; Winkler et al. 2019; Genre et al. 2013). Intuitively, simple averaging allows statistically independent individual errors to cancel, leading to a more accurate prediction (Larrick and Soll 2006). However, in some prediction tasks, forecasters may have common information through shared expertise, past realizations, knowledge of the same academic works, etc. (Chen et al. 2004). Then, individual errors may become correlated, resulting in a bias in the equally weighted average of predictions (Palley and Soll 2019). In theory, the decision maker in a given task can select and weight judgments such that the errors perfectly cancel out (Clemen and Winkler, 1986; Mannes et al. 2014; Budescu and Chen 2015). However, optimal weights depend on how experts’ prediction errors are correlated and are typically unknown to the decision maker. Some existing methods aim to estimate appropriate weights using past data from similar tasks (Budescu and Chen, 2015; Mannes et al. 2014). The effectiveness of this approach is limited by the availability and reliability of past data. Another line of work proposed competitive elicitation mechanisms (Ottaviani and Sørensen 2006; Lichtendahl Jr and Winkler 2007), which may improve the calibration of the average forecast when forecasters have common information (Lichtendahl Jr et al. 2013; Pfeifer et al. 2014; Pfeifer 2016). Such competitive mechanisms are sensitive to strategic considerations of forecasters (Peeters et al. 2022).

This paper develops the Surprising Overshoot (SO) algorithm to aggregate judgments on the likelihood of an event. I consider a setup where experts form their judgments by combining shared and private information on an unknown probability. When shared information differs from the true probability, experts are likely to err in the same direction, resulting in a miscalibrated average prediction. The SO algorithm relies on an augmented elicitation proposed in recent work (Prelec, 2004; Prelec et al. 2017; Palley and Soll 2019; Palley and Satopää 2022; Wilkening et al. 2022): Experts report a prediction of the probability as well as an estimate of the average of others’ predictions, which is referred to as a meta-prediction. I show that when the average prediction is a consistent estimator, the percentage of predictions and meta-predictions that overshoot the average prediction should be the same. An overshoot surprise occurs when the two measures differ, which indicates that the average prediction is an inconsistent estimator. The SO estimator uses the information in the size and direction of the overshoot surprise to account for the shared-information problem. It does not require the use of past data.

I test the SO algorithm using experimental data from two sources. Palley and Soll (2019) conducted an experimental study where subjects are asked to predict the number of heads in 100 flips of a biased coin. Their experiment implements shared and private signals as sample flips from the biased coin. The second source is Wilkening et al. (2022), who conducted two experimental studies. The first experiment replicates the earlier study by Prelec et al. (2017) which asked subjects true/false questions about the capital cities of U.S. states. However, unlike Prelec et al. (2017) they also ask subjects to report probabilistic predictions and meta-predictions, which allows an implementation of the SO algorithm. In the second experiment, Wilkening et al. (2022) generate 500 basic science statements and ask subjects to report probabilistic predictions and meta-predictions on the likelihood that a given statement is true. Results suggest that the SO algorithm outperforms simple benchmarks such as unweighted averaging and median prediction. I also compare the SO algorithm to alternative solutions for aggregating probabilistic judgments, which elicit similar information from individuals (Palley and Soll 2019; Martinie et al. 2020; Palley and Satopää, 2022; Wilkening et al. 2022). The SO algorithm compares favorably to alternative aggregation mechanisms in prediction tasks where individual predictions are highly dispersed. Experimental evidence suggests that the SO algorithm is especially effective in extracting the collective wisdom from strongly disagreeing probabilistic judgments in moderate to large samples of experts.

This paper contributes to the literature of judgment aggregation mechanisms that utilize meta-beliefs to improve prediction accuracy. The Surprisingly Popular (SP) algorithm picks an answer to a multiple choice question based on predicted and realized endorsement rates of alternative choices (Prelec et al. 2017). The Surprisingly Confident (SC) algorithm determines weights that leverage more informed judgments (Wilkening et al. 2022). The SP and SC algorithms aim to find the correct answer to a binary or multiple-choice question while the SO algorithm produces a probabilistic estimate on a binary event.

Recent work developed aggregation algorithms for probabilistic judgments as well. Pivoting uses meta-predictions to recover and recombine shared and private information optimally (Palley and Soll 2019). Knowledge-weighting constructs a weighted average such that the accuracy of weighted crowd’s aggregate meta-prediction is maximized (Palley and Satopää 2022). Meta-probability weighting also attaches weights to individual predictions where the absolute difference between an individual’s prediction and meta-prediction is considered as an indicator of expertise (Martinie et al. 2020). In testing the performance of the SO algorithm, pivoting, knowledge-weighting and meta-probability weighting are considered as benchmarks. As mentioned above, the SO algorithm performs especially well when individual judgments are highly dispersed. In practice, such problems are likely to be the most challenging ones, where expert judgments disagree substantially and it is not clear how judgments should be aggregated for maximum accuracy.

The rest of this paper is organized as follows: Sect. 2 introduces the formal framework. Sect. 3 develops the SO algorithm and establishes the theoretical properties of the SO estimator. Sect. 4 introduces the data sets and benchmarks we consider in testing the SO algorithm empirically. The same section also presents some preliminary evidence on how overshoot surprises relate to the inaccuracy in average prediction. Sect. 5 presents experimental evidence testing the SO algorithm. Sect. 6 provides a discussion on the effectiveness of the SO algorithm. Section 7 concludes.

2 The framework

The formal framework follows the definition of a linear aggregation problem in Palley and Soll (2019) and Palley and Satopää (2022) with the quantity of interest being a probability. The notation will also be similar to Palley and Soll (2019). Let $Y \in \{0,1\}$ be a random variable that represents the occurrence of an event where $y \in \{0,1\}$ denotes the value in a given realization. Also let $\theta = P(Y = 1)$ be the unknown objective probability of the outcome 1, representing the occurrence of the event. A decision maker (DM) would like to estimate $\theta$. The DM elicits judgments from a sample of $N \ge 2$ risk-neutral agents to develop an estimator, where $N \rightarrow \infty$ represents the whole population.

Agents share a common prior belief over $\theta$ where $\mu _0$ represents the common prior expectation. All agents observe a common signal, given by the average of $m_1$ independent realizations of Y. A subset $K \le N$ of agents are experts who receive an additional independent signal. Without loss of generality, let agents $i \in \{1,2,\ldots ,K\}$ be the experts. An expert’s private signal $t_i$ is the average of $\ell$ agent-specific independent realizations of Y. In the analysis below, we consider the case where $K = N$, i.e. all agents are experts who observe a private signal as well as the common signal. Appendix B presents the same analysis for the case of $K < N$ and shows that the same results are applicable.

Let $\mu _0$ represent $m_0$ independent observations of Y. Also let $m \equiv m_0 + m_1$ and $s \equiv (m_0 \mu _0 + m_1 s_1)/m$. The shared signal s represents a combination of the prior expectation and the common signal. Each agent i follows a belief updating according to Bayes’ rule. Posterior expectation $E[\theta | s,t_i]$ is given by

$$\begin{aligned} E[\theta | s,t_i] = (1-\omega ) s + \omega t_i, \end{aligned}$$

(1)

where $\omega = \ell /(m + \ell )$ denotes the Bayesian weight that represents the informativeness of the private signal $t_i$ relative to the shared signal s¹. The signal structure and $\{m,\ell \}$ are common knowledge to all agents. Agents know that the posterior expectation of any agent i with private signal $t_i$ is given by Equation 1. The parameters $\{m,\ell \}$ and signals $\{s,t_1,t_2,\ldots ,t_N\}$ are unknown to the DM.

Suppose the DM considers the simple average of agents’ predictions as an estimator for $\theta$. Let $x_i$ be agent i’s reported prediction on $\theta$. Suppose all agents report their best guesses, i.e. $x_i = E[\theta | s,t_i]$. Then the average prediction is given by

$$\begin{aligned} \bar{x}_N&= \frac{1}{N} \sum _{i=1}^N x_i = (1-\omega ) s + \omega \frac{1}{N} \sum _{i=1}^N t_i. \end{aligned}$$

Note that $\lim \limits _{N \rightarrow \infty } \bar{x}_N = \bar{x} = (1-\omega ) s + \omega \theta \ne \theta$ if $s \ne \theta$, i.e. average prediction is not a consistent estimator of $\theta$ unless the shared information is perfectly accurate (Palley and Soll 2019). Increasing the sample size does not alleviate the shared-information problem because s is incorporated in $\bar{x}_N$ by each additional prediction. Shared information causes a correlation between predictions and leads to a persistent error in $\bar{x}_N$. Section 3 develops the Surprising Overshoot algorithm, which constructs an estimator that accounts for the shared-information problem.

3 The Surprising Overshoot algorithm

The Surprising Overshoot algorithm relies on an augmented elicitation procedure and the information revealed by the distribution of agents’ reports to construct an estimator. Section 3.1 introduces the elicitation procedure. Sections 3.2 and 3.3 elaborates on the relationship between agents’ equilibrium reports and the resulting average prediction. Section 3.4 develops the SO estimator.

3.1 Belief elicitation

The DM simultaneously and separately asks each agent i to submit two reports. In the first, the agent is asked to make a prediction $x_i \in [0,1]$ on $\theta$. In the second, the agent reports a meta-prediction $z_i \in [0,1]$, which is an estimate of the average prediction of agents $j \in \{1,2,\ldots ,N\} \setminus \{i\}$, denoted by $\bar{x}_{-i} = \frac{1}{N-1} \sum \limits _{j \ne i} x_j$. Agents’ reports are incentivized by a strictly proper scoring rule (Gneiting and Raftery 2007). Let $\pi _{xi} = S_x(x_i,y)$ and $\pi _{zi} = S_z(z_i,\bar{x}_{-i})$ be the ex-post payoffs of an agent i from the prediction and meta-prediction where $S_x$ and $S_z$ are strictly proper scoring rules satisfying $\theta = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{u \in \mathbbm {R}} S_x(u,Y)$ and $\bar{x}_{-i} = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{u \in \mathbbm {R}} S_z(u,\bar{x}_{-i})$. Agent i’s total payoff is given by $\pi _i = \pi _{xi} + \pi _{zi}$.

An agent i’s report is truthful if $(x_i,z_i) = (E[\theta | s,t_i], E[\bar{x}_{-i} | s,t_i])$, i.e. agent i reports her posterior expectations on $\theta$ and $\bar{x}_{-i}$ as prediction and meta-prediction respectively. Truthful reporting represents the situation where reports are truthful for all $i \in \{1,2,\ldots ,N\}$.

Theorem 1

Truthful reporting is a Bayesian–Nash equilibrium in the simultaneous reporting game.

Proofs of all theorems and lemmas are included in Appendix A. Intuitively, Theorem 1 follows from the use of proper scoring rules. Agents are incentivized to report their best estimates on the unknown probability and the average of others’ predictions. In equilibrium, we have $x_i = E[\theta | s,t_i] = (1-\omega )s + \omega t_i$ for all $i \in \{1,2,\ldots ,N\}$. Then, agent i’s equilibrium meta-prediction is given by $E[\bar{x}_{-i} | s,t_i] = (1-\omega ) s + \omega \frac{1}{N-1} \sum \limits _{j \ne i} E[t_j | s,t_i]$. Observe that $E[t_j | s,t_i] = E[E[t_j | \theta ] | s,t_i] = E[\theta | s,t_i]$, i.e. agent i’s expectation on another agent’s signal is her expectation on $\theta$, which is equal to the truthful prediction. Thus, the equilibrium prediction and meta-prediction of an agent i are given by:

$$\begin{aligned} x_i&= (1-\omega )s + \omega t_i, \end{aligned}$$

(2)

$$\begin{aligned} z_i&= (1-\omega )s + \omega x_i, \end{aligned}$$

(3)

In the remainder of this section, I assume truthful reporting and hence, each agent i’s reported predictions and meta-predictions are given by Eqs. 2 and 3 respectively.

3.2 Overshoot rates in predictions and meta-predictions

A prediction or meta-prediction is said to overshoot the average prediction $\bar{x}_N$ if it exceeds $\bar{x}_N$. For any arbitrary agent i, there are two overshoot indicators. For example, if $x_i> \bar{x}_N > z_i$, agent i’s prediction $x_i$ overshoots the average prediction while the meta-prediction $z_i$ does not overshoot.

Lemma 1

(Overshoot in prediction). An agent i’s prediction $x_i$ overshoots $\bar{x}_N$ if and only if her private signal $t_i$ overshoots the average signal $\bar{t} = \sum \limits _{k=1}^N t_k$. For $N \rightarrow \infty$, we have $x_i> \bar{x} \iff t_i > \theta$ where $\bar{x} = \lim \limits _{N \rightarrow \infty } \bar{x}_N$ is the population average of predictions.

Lemma 2

(Overshoot in meta-prediction). An agent i’s meta-prediction $z_i$ overshoots $\bar{x}_N$ if and only if her prediction $x_i$ overshoots the average signal $\bar{t} = \sum \limits _{k=1}^N t_k$. For $N \rightarrow \infty$, we have $z_i> \bar{x} \iff x_i > \theta$ where $\bar{x} = \lim \limits _{N \rightarrow \infty } \bar{x}_N$ is the population average of predictions.

Lemmas 1 and 2 suggest a pattern of predictions as $N \rightarrow \infty$. According to Lemma 1, an agent i’s prediction $x_i$ overshoots $\bar{x}$ if and only if $t_i > \theta$. However, for meta-prediction $z_i$ to overshoot $\bar{x}$, we must have $x_i = (1-\omega ) s + \omega t_i > \theta$. Thus, we do not necessarily have $z_i > \bar{x}_i$ whenever $x_i > \bar{x}$ is satisfied. Consider the following measures computed using predictions and meta-predictions:

$$\begin{aligned} p_x&= \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{i=1}^N \mathbbm {1}(x_i> \bar{x}) \\ p_z&= \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{i=1}^N \mathbbm {1}(z_i > \bar{x}) \end{aligned}$$

The measures $p_x$ and $p_z$ represent the population proportion of predictions and meta-predictions that overshoot the population average $\bar{x}$. I refer to $p_x$ and $p_z$ as the overshoot rate in predictions and meta-predictions respectively. From Lemma 2, we can infer that $p_z$ also corresponds the population proportion of predictions that overshoot $\theta$.

3.3 Overshoot surprise as an indicator of the inconsistency in the average prediction

Overshoot rates in predictions and meta-predictions provide an indicator for a miscalibration in the average prediction $\bar{x}_N$. Theorem 2 establishes a result for the case where $\bar{x}_N$ is a consistent estimator.

Theorem 2

Overshoot rates satisfy $p_x = p_z$ when $\bar{x}_N$ is a consistent estimator of $\theta$

Theorem 2 describes a situation where there is no shared information problem in the average prediction. This corresponds to the special case of $s = \theta$. Then, $\bar{x} = \theta$ and it follows from Lemma 2 that an agent’s prediction and meta-prediction are always on the same side of $\bar{x}$, which implies $p_x = p_z$.

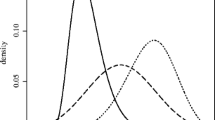
What if $s \ne \theta$ and $\bar{x}_N$ is an inconsistent estimator? Then we have $\bar{x} \ne \theta$ and there could be instances where an agent’s prediction and meta-prediction fall on different sides of $\bar{x}$. Figure 1 below shows one such example:

Fig. 1

An example case where an agent’s meta-prediction $z_i$ overshoots $\bar{x}$ while prediction $x_i$ undershoots. The dashed lines show how $x_i$,$z_i$ and $\bar{x}$ are determined given $\{s,t_i,\theta \}$ from Eqs. 2, 3 and $\bar{x} = (1-\omega )s + \omega \theta$

In the example case, $\bar{x}_N$ is an inconsistent estimator of $\theta$ because $s>\theta$ leads to $\bar{x} > \theta$. Note that we also have $\theta< x_i < z_i$. Intuitively, prediction $x_i$ overestimates $\theta$ because $s > \theta$. Meta-prediction $z_i$ is the combination of agent i’s best estimate on the average signal (which converges to $\theta$ in the limit) and s. Since $x_i$ overestimates $\theta$, by Lemma 2 meta-prediction $z_i$ overshoots $\bar{x}$. However, following Lemma 1, $x_i$ still undershoots $\bar{x}$ because $t_i < \theta$. Therefore, we get $x_i< \bar{x} < z_i$.

Figure 1 suggests that the prediction and meta-prediction of a given agent can be on different sides of $\bar{x}$ when $s \ne \theta$. Then, overshoot rate in predictions ($p_x$) and meta-predictions ($p_z$) may differ.

Definition 1

(Overshoot surprise). An overshoot surprise occurs when $p_z \ne p_x$. The overshoot surprise is positive if $p_z > p_x$ and negative if $p_z < p_x$. The size of the overshoot surprise is given by $\Delta p = p_z - p_x$.

The following result relates overshoot surprise to inconsistency in $\bar{x}_N$:

Theorem 3

Overshoot rates satisfy $p_z \ge p_x$ ($p_z \le p_x$) when $\lim \nolimits _{N \rightarrow \infty } \bar{x}_N > \theta \left( \lim \nolimits _{N \rightarrow \infty } \bar{x}_N < \theta \right)$. Furthermore, $\Delta p$ is a monotonically increasing function of $\lim \limits _{N \rightarrow \infty } (\bar{x}_N - \theta )$.

Theorem 3 establishes that an overshoot surprise is an indicator of the size and direction of the inconsistency in $\bar{x}_N$ resulting from the shared-information problem. A positive overshoot surprise suggests that the average prediction overestimates $\theta$ while a negative overshoot surprise suggests underestimation. Furthermore, the size of the overshoot surprise positively correlates with the asymptotic bias in $\bar{x}_N$. These observations motivate the Surprising Overshoot estimator introduced below.

3.4 The Surprising Overshoot estimator

Let F be the cumulative population density of predictions. Also let the function $Q(q) = inf\{x \in \{x_1,x_2,\ldots ,x_N\} | F(x) \ge q\}$ represent the population quantile of predictions at a given cumulative density $q \in [0,1]$. We can consider $\bar{x}_N$ as an estimator for $Q(1-p_x)$ because $\lim \limits _{N \rightarrow \infty } \bar{x}_N = \bar{x} = Q(1-p_x)$. Section 3.3 suggests that an inconsistency in $\bar{x}_N$ is reflected in how overshoot rates $p_x$ and $p_z$ are related. Consider the case of $p_z > p_x$, i.e. a positive overshoot surprise. Then, $\bar{x}_N$ overestimates $\theta$ in the limit, suggesting that an estimator that converges to a lower quantile of F could be more accurate. Theorem 4 suggests that $Q(1-p_z)$ is the target quantile.

Theorem 4

If there exists at least one $x_i \in \{x_1,x_2,\ldots ,x_N\}$ such that $x_i = \theta$, then $Q(1-p_z) = x_i = \theta$.

Intuitively, if there is at least one perfectly accurate agent in the population, $Q(1-p_z)$ locates her prediction. What if there is no such agent? Then, $Q(1-p_z)$ equals to the prediction(s) that fall closest to $\theta$ among all predictions smaller than $\theta$. In that case, $\theta$ lies at a convex combination of $Q(1-p_z)$ and $inf\{x \in \{x_1,x_2,\ldots ,x_N\}| x > Q(1-p_z) \}$. Theorem 3 showed that $p_z \ne p_x$ when $\bar{x}_N$ is an inconsistent estimator. For example, we have $p_z > p_x$ when $\bar{x}_N$ has an upward asymptotic bias, implying that $Q(1-p_z)$ is a smaller quantile than $\bar{x}$ (which corresponds to $Q(1-p_x)$). Thus, even if $Q(1-p_z)$ differs from $\theta$, it would be closer to $\theta$ than $\bar{x}$ in most cases. Theorem 2 showed that $p_x = p_z$ when there is no asymptotic bias in $\bar{x}_N$. Thus, $Q(1-p_z) = Q(1-p_x) = \bar{x}$ when $\bar{x}_N$ is a consistent estimator.

Theorem 4 applies for the limiting case where the whole population of agents is available. In practice, the DM can only recruit a finite sample of agents. The population distribution F and the quantile function Q are unknown. Thus, $Q(1-p_z)$ cannot be calculated. Let $\hat{F}_N$ be the empirical cumulative distribution function (CDF) and $\hat{Q}_N(q) = inf\{x \in \{x_1,x_2,\ldots ,x_N\} | \hat{F}_N(x) \ge q\}$ represent the corresponding sample quantile function in a finite sample of agents of size N. Also let $\hat{p}_{xN} = \frac{1}{N} \sum \limits _{i=1}^N \mathbbm {1}(x_i > \bar{x}_N)$ and $\hat{p}_{zN} = \frac{1}{N} \sum \limits _{i=1}^N \mathbbm {1}(z_i > \bar{x}_N)$ be the sample overshoot rate in predictions and meta-predictions respectively. The definition below introduces the Surprising Overshoot (SO) algorithm:

Definition 2

(The surprising overshoot algorithm). The Surprising Overshoot algorithm constructs the SO estimator $x_N^{SO}$ for $\theta$ following the steps below:

• 1. Elicit $\{x_1,x_2,\ldots ,x_N\}$ and $\{z_1,z_2,\ldots ,z_N\}$

• 2. Calculate $\hat{p}_{zN} = \frac{1}{N} \sum \limits _{i=1}^N \mathbbm {1}(z_i > \bar{x}_N)$.

• 3. Set $x_N^{SO} = \hat{Q}_N(1-\hat{p}_{zN})$ where $\hat{Q}_N$ is the sample quantile function.

The SO algorithm simply locates the $1 - \hat{p}_{zN}$ quantile of the sample predictions where quantile function is the inverse of empirical CDF. An alternative formulation (elaborated in Sect. 4.4) interpolates between the order statistics to construct a continuous quantile function.

Why should $x^{SO}_N$ be a better estimator than $\bar{x}_N$? Theorem 4 shows that $Q(1-p_z)$ is either equal to or falls very close to $\theta$. If the sample quantile $\hat{Q}_N(1-\hat{p}_{zN})$ converges to the population counterpart for $N \rightarrow \infty$, we would expect very little or no asymptotic bias in $x^{SO}_N$. In contrast, $\bar{x}_N$ could exhibit a substantial asymptotic bias. The SO estimator picks a lower or higher quantile depending on the direction and size of the asymptotic bias in $\bar{x}_N$.

Section 4 presents supporting empirical evidence. Firstly, sample overshoot surprises (calculated using $\hat{p}_{zN}$ and $\hat{p}_{xN}$) strongly correlate with the forecasting errors of average prediction. The sample measures exhibit the pattern predicted by Theorem 3 in the limit. Secondly, the SO estimator produces significantly more accurate estimates than the average prediction. Section 3.5 elaborates on when we expect the SO algorithm to perform well and motivates the empirical analysis.

3.5 Effectiveness of the SO estimator

The SO estimator relies on the empirical distribution of predictions as well as agents’ meta-predictions. This property has implications about the prediction problems where we may expect the SO algorithm to be more effective. To illustrate, consider the two example empirical densities below. Both figures depict predictions from a sample of 10 agents where the sample average prediction is 0.4 while $\theta = 0.25$. In Fig. 2a agents report one of 0.5, 0.3 or 0.1 as prediction. The distribution of predictions in Fig. 2b is more dispersed around the average prediction. Suppose the meta-predictions in each example (not shown on figures) are such that $\hat{p}_{zN} = 0.2$ in both cases. Then the SO estimate is $1-\hat{p}_{zN} = 0.8$ quantile of the empirical density of predictions. The orange bar in each figure locates the SO estimate.

Fig. 2

Two examples of empirical density of predictions

The SO estimate is more accurate in the high dispersion case simply because the 0.2 quantile falls closer to $\theta$. The SO algorithm picks the prediction that corresponds to the sample quantile $1-\hat{p}_{zN}$. So the set of values $x_N^{SO}$ can take depends on the empirical density of predictions. Even when $1-\hat{p}_{zN}$ provides an accurate estimate of the cumulative density at $\theta$, the SO estimate may not be more accurate than $\bar{x}_N$ simply because $1-\hat{p}_{zN}$ quantile of the sample predictions is not close to $\theta$. Such cases are less likely when the sample size is higher and/or the empirical density of predictions is more dispersed, as in Figure 2b. Therefore, we may expect the SO algorithm to perform better in larger samples and when the predictions are more dispersed. Intuitively, high dispersion can be considered as representing prediction tasks where individual judgments disagree, which could occur when the event of interest is highly uncertain and there is no strong consensus among forecasters. The following sections test the SO algorithm using experimental data. In the analyses below, sample size and dispersion of predictions are considered to be the factors of interest.

4 Testing the SO algorithm

This section outlines the empirical methodology and presents some preliminary evidence on overshoot surprises. I use data from various experimental studies to test the SO algorithm. Section 4.1 provides information on the data sets. Section 4.2 gives an overview of the empirical methodology. In testing the SO algorithm, I follow a comparative approach. The analysis will implement various alternative methods as a benchmark and test if the SO algorithm performs significantly better. Section 4.3 introduces the benchmarks. Section 4.4 specifies the types of quantile functions used in implementation of the SO algorithm. Section 4.5 provides some preliminary findings on overshoot surprises and how they relate to the inconsistency in the simple average of predictions.

4.1 Data sets

I use data from three experimental studies². The first data set comes from Study 1 in Palley and Soll (2019). They conducted an online experiment where subjects reported their prediction and meta-prediction on the number of heads in 100 flips of a biased two-sided coin. The actual probability of heads is unknown to the subjects. Prior to submitting a report on a coin, each subject observed two independent samples of flips. One sample is common to all subjects and represents the shared signal. The second sample is subject-specific and constitutes a subject’s private signal. A subject’s best guess on the number of heads in 100 new flips is effectively that subject’s best guess on the unknown bias. Thus, the “Coin Flips” data set includes predictions on an unknown probability and meta-predictions on the average prediction of other subjects.

Study 1 in Palley and Soll (2019) implements three different information structures. All subjects observe the shared signal and a private signal in the ‘Symmetric’ setup while only a subset of subjects observe a private signal in the ‘Nested-Symmetric’ structure. Private signals are subject-specific and unbiased in both structures, which agrees with the theoretical framework of the SO algorithm. The other setup is referred to as the ‘Nested’ structure, in which private signals are not subject-specific. The average of private signals do not converge to the true value, which deviates from the theoretical framework of the SO algorithm. Thus, all results from Coin Flips data in Section 5 exclude ‘Nested’ structure and use the prediction data (48 distinct coins) from the ‘Symmetric’ and ‘Nested-Symmetric’ structures only. For completeness, Appendix E presents an analysis using data from the ‘Nested’ structure.

The Coin Flips data set from Palley and Soll (2019)’s Study 1 allows testing the SO algorithm in a controlled setup. Since the unknown probabilities are known to the analyst, it is possible to calculate prediction errors directly. The number of subjects per coin vary between 101 and 125. Palley and Soll (2019) run a second study where they use the same tasks as in Study 1. However they vary subjects’ incentives and the sample sizes are much smaller. Thus, their second study will not be considered here.

The second source of data involves two experimental studies from Wilkening et al. (2022). The first replicates the experiment initially conducted by Prelec et al. (2017). For each U.S. state, subjects are asked if the largest city is the capital of that state. Prelec et al. (2017) required subjects to pick true or false and report the percentage of other subjects who would agree with them. Wilkening et al. (2022) asked subjects to report probabilistic predictions and meta-predictions on the statement (largest city being the capital city), which allows us to implement the SO algorithm. The “State Capital” data set includes data from 89 subjects in total and each subject answered 50 questions (one per state). In the second experiment, subjects are presented with U.S. grade school level true/false general science statements such as ‘Water boils at 100 degrees Celsius at sea level’, ‘Materials that let electricity pass through them easily are called insulators’ and ‘Voluntary muscles are controlled by the cerebrum’. The “General Knowledge” data includes judgments on 500 such statements in total. Each subject reports a prediction and a meta-prediction on the probability of a statement being true for 100 statements. The number of subjects reporting on a given statement varies between 89 and 95.

4.2 Methodology

The empirical analysis tests the accuracy of the SO algorithm using the prediction and meta-prediction data from the Coin Flips, General Knowledge and State Capital data sets. For each prediction task, I calculate the SO estimate as well as aggregate estimates from the alternative aggregation methods that are considered as benchmarks. Section 4.3 provides information on these benchmarks. In each data set, the performance of a method is based on an average measure of accuracy across all prediction tasks. In the Coin Flips data set, the unknown probability of interest is known to the aggregator. Thus, accuracy is measured by the difference between the estimate and the actual probability. In contrast, the General Knowledge and State Capital tasks have a binary truth. I calculate Brier scores to evaluate the aggregate estimates. In all data sets, the analysis follows a bootstrap approach to compare forecast errors across the aggregation methods. Section 5 elaborates on the accuracy measures and the bootstrap analyses.

Section 3.5 argued that the SO algorithm could be more effective in moderate to large crowds and/or when predictions are more dispersed. In each data set, I generate bootstrap samples of different sizes and evaluate the relative accuracy of the SO estimate as the crowd size increases. Furthermore, the statements in General Knowledge and State Capital data sets differ in terms of the presence of a strong consensus among the predictions. This allows us to investigate how the extent of disagreement in predictions relates to the relative performance of SO algorithm. To illustrate, consider the two example items from the General Knowledge data in Figure 3 below:

Fig. 3

Predictions on two example items from the General Knowledge data

For the item in the left panel, a large proportion of predictions are at 100% and almost all predictions are 50% or higher. The dispersion of predictions is smaller than the item in the right panel, where predictions vary from 0% to 100%. Similar examples can be found in the State Capital data. I classify the items in the General Knowledge and State Capital data sets in three categories (low, medium and high dispersion of predictions) and investigate if the SO estimator is more accurate than the benchmarks under high dispersion. Figure 9 in Appendix C suggests that the dispersion of predictions vary much less across the Coin Flips tasks compared to the General Knowledge and State Capital tasks. The level of dispersion in Coin Flips predictions is relatively low as well. The low, medium and high dispersion categories of tasks would not be distinct in the Coin Flips data and almost all coin flips tasks would qualify as low dispersion considering other data sets. Therefore, the analysis on the effect of dispersion uses the General Knowledge and State Capital data only.

4.3 Benchmarks

The benchmarks in testing the SO algorithm can be categorized in two groups. I will first consider simple benchmarks, namely the simple average and median prediction. Simple averaging is an easy and intuitive aggregation method. The median forecast is also popular because it is more robust to outliers. These simple aggregation methods do not require meta-predictions, which makes them easier to implement. However, as shown in Section 2 with simple averaging, these methods may produce an inaccurate aggregate judgment. As discussed in Section 1, there exists a growing literature which provides more sophisticated solutions to the aggregation problem utilizing meta-beliefs. I consider three advanced benchmarks: Pivoting (Palley and Soll 2019), knowledge-weighting (Palley and Satopää 2022), and meta-probability weighting (Martinie et al. 2020).

The pivoting method first computes simple average of predictions and meta-predictions, $\bar{x}$ and $\bar{z}$ in our notation respectively. Then the mechanism pivots from $\bar{x}$ in different directions. The pivot in the direction of $\bar{z}$ provides an estimate for the shared information while the step in the opposite direction gives an estimate for the average of private signals. These estimates are combined using Bayesian weights to produce the optimal aggregate estimate. The canonical pivoting method requires knowledge of the Bayesian weight $\omega$ to determine the optimal pivot size and aggregation. Palley and Soll (2019) propose minimal pivoting (MP) as a simple variant which adjusts $\bar{x}$ by $\bar{x} - \bar{z}$. The adjustment moves the aggregate estimate away from the shared information and alleviates the shared-information problem. MP does not require the knowledge of $\omega$ but it may only partially correct for the inconsistency in $\bar{x}$.

Knowledge-weighting (KW) proposes a weighted crowd average as the aggregate prediction. The weights are estimated by minimizing the peer prediction gap, which measures the accuracy of weighted crowds’ aggregate meta-prediction in estimating the average prediction. In a similar framework to Section 2, Palley and Satopää (2022) show that minimizing the peer prediction gap is a proxy for minimizing the mean squared error of a weighted aggregate prediction. Intuitively, KW is motivated by the idea that a weighted crowd that is accurate in predicting others could be more accurate in predicting the unknown quantity itself as well. The KW estimate is simply the weighted average prediction of such a crowd. Palley and Satopää (2022) also develop an outlier-robust KW. Since probabilistic judgments are bounded, we may not expect a severe outlier problem. Palley and Satopää (2022) implement the KW method in the Coin Flips data. Their results suggest that standard KW performs better than outlier-robust KW. Thus, I consider standard KW as a benchmark in the analyses below.³

Meta-probability weighting (MPW) aims to construct a weighted average of probabilistic predictions. Martinie et al. (2020) consider a slightly different Bayesian setup where agents receive a private signal from one of the two signal technologies, one for experts and the other for novices. The absolute difference between an agent’s optimal prediction and meta-prediction is higher if the agent’s signal is more informative. Based on this result, the MPW algorithm assigns weights proportional to the absolute differences between their prediction and meta-prediction. It is expected that agents with more informative private signals receive higher weights and the resulting weighted average is more accurate than the unweighted average of predictions.

Similar to the advanced benchmarks listed above, the SO algorithm relies on an augmented elicitation procedure that elicits meta-predictions in addition to predictions. In contrast, the mechanisms in simple benchmarks do not require information from meta-predictions. Thus, we may expect the SO algorithm to significantly outperform simple benchmarks. The advanced benchmarks have similar information demands to the SO algorithm, which makes them appropriate benchmarks for a comparative analysis.

4.4 Implementation of the SO algorithm

The SO algorithm locates a sample quantile according to the quantile function $\hat{Q}_N$. The exact estimate depends on the specification of the quantile function. For robustness, the analysis implements two versions of the algorithm. In the first, the quantile function $\hat{Q}_N(q)$ is a step function given by the inverse empirical CDF. The second implementation interpolates between order statistics to construct a piecewise linear quantile function. To illustrate, suppose we have a sample of 5 predictions given by $\{0.15,0.2,0.3,0.65,0.9\}$. Figure 4 depicts the quantile function corresponding to each implementation:

Fig. 4

Example quantile functions for the implementations of the SO algorithm

Section 5 presents results from the implementation where the quantile function is as in Fig. 4a. Appendix F runs the same analysis, except that the quantile function used in the SO algorithm follows the interpolation approach in Fig. 4b. Both specifications produce very similar results. Therefore, the same conclusions apply.

4.5 Preliminary evidence on overshoot surprises

Section 3 established a relationship between the size and direction of overshoot surprises and prediction errors. The more $p_z$ differs from $p_x$, the higher the overshoot surprise, suggesting a higher miscalibration in the average prediction. Presence of an overshoot surprise relates to the performance of the SO algorithm as well. We may expect a larger error reduction from using the SO algorithm when $|p_z-p_x|$ is larger.

The Coin Flips data set presents an opportunity to investigate whether overshoot surprises correlate with the inconsistency in the average prediction. In this experiment, both the shared signal s and the unknown probability $\theta$ in each coin are generated by the experimenter. Recall from Theorem 3 that a positive (negative) overshoot surprise is associated with $\bar{x} > \theta$ ($\bar{x} < \theta$), which correspond to the case of $s > \theta$ ($s < \theta$). We expect no overshoot surprise if $s=\theta$, resulting in $\bar{x}$ being perfectly accurate. Since the information on s and $\theta$ is available, we can investigate if this pattern is observed in the sample data. Figure 5 shows the relationship between $\Delta \hat{p} = \hat{p}_z - \hat{p}_x$ (size of the sample overshoot surprise) and $s - \theta$. Each dot represents an item (a distinct coin) and the blue line shows the best linear fit.

Fig. 5

The relationship between $s-\theta$ and overshoot surprises ($\Delta \hat{p}$) in prediction tasks. Shaded areas show the regions where the signs of $s-\theta$ and $\Delta \hat{p}$ are as predicted by Theorem 3

Figure 5 shows a strong linear association between $s-\theta$ and overshoot surprise ($\Delta \hat{p}$). Also observe that most of the points are within the shaded regions. A positive (negative) overshoot surprise is much more likely to occur when $s > \theta$ ($s < \theta )$. In addition, $|\Delta \hat{p}|$ is higher when the absolute difference between s and $\theta$ is higher. In accordance with Theorem 3, an overshoot surprise is a strong indicator of the size and direction of the inconsistency in the average prediction. The SO estimator can be thought of as $\bar{x}_N$ adjusted away from the direction of the asymptotic bias where the adjustment is determined by the sign and magnitude of the overshoot surprise. Thus, Figure 5 suggests a potential error reduction from using the SO algorithm. Section 5 explores whether the SO algorithm improves over various benchmarks.

5 Results

This section presents empirical evidence on the performance of the SO algorithm. Section 5.1 implements the SO algorithm and benchmarks in the Coin Flips data. The results demonstrate the accuracy of the SO estimator as the crowd size increases. Section 5.2 implements the SO algorithm and benchmarks in the General Knowledge and State Capital data sets. This section analyzes the accuracy of the SO algorithm at different levels of dispersion in predictions as well as investigating the effect of crowd size. I present evidence suggesting that the SO estimator performs especially well when predictions disagree greatly.

5.1 Coin Flips data

The empirical analysis follows a bootstrap approach similar to Palley and Satopää (2022). For each item (prediction task) in the Coin Flips data set, a subset of subjects of size M is randomly selected to construct a bootstrap sample. Then, for each sample and item I compute the absolute and squared error of aggregate predictions from the benchmarks and the SO algorithm. The average of squared errors across the items gives a measure of the corresponding method’s error in that task. This procedure is run 1000 times for each crowd size $M \in \{10,20,\ldots ,100\}$ to obtain 1000 data points of absolute error and root mean squared error (RMSE) for each aggretaion method. The observations from bootstrap samples allow us to test for differences in errors between the SO algorithm and a benchmark. I consider two measures for comparison. First, I calculate average RMSE across all iterations for each method. Then, it is possible to observe how average RMSE changes across M. Second, I log-transform the absolute errors and calculate pairwise differences for each iteration to construct 95% bootstrap confidence intervals for each M. The differences in log-transformed errors can be interpreted as percentage error reduction (SO estimator vs benchmark). The bootstrap approach also allows us to see the effect of crowd size on the SO estimates.

Figure 6 presents the results of the bootstrap analysis. Figure 6a depicts the average RMSE across iterations while Fig. 6b shows the bootstrap confidence intervals for reduction in log absolute error (the SO estimator vs benchmark). Box plots show 2.5%, 25%, 50%, 75% and 97.5% quantiles in pairwise differences in log-transformed errors. Points above the 0-line represent bootstrap runs where the SO estimate has a lower error.

Fig. 6

Bootstrap analysis on Coin Flips data

Figure 6a shows that the SO algorithm achieves the lowest error in samples of more than 30 subjects. Observe that increasing the sample size has a stronger effect on the SO estimator. Almost all aggregation methods benefit from larger samples due to the wisdom of crowds effect. For the SO algorithm, benefits of a larger crowd are twofold. Not only the wisdom of crowds effect becomes more pronounced, but also a larger sample of predictions typically has a smoother empirical density. Then, the SO algorithm can produce a more precise estimate, as illustrated in Fig. 2.

Figure 6b indicates that the SO algorithm outperforms the simple benchmarks. We also see that the SO algorithm achieves lower errors in most bootstrap samples than the advanced benchmarks. Appendix D provides the 95% bootstrap confidence intervals depicted in Fig. 6b. The SO algorithm improves the accuracy by 30–50% relative to the simple benchmarks. In large samples, the median percentage error reduction with respect to MP, KW and MPW is around 7%, 8% and 25% respectively.

The Coin Flips study elicits judgments in a controlled setup. As discussed in Sect. 4.2, the dispersion of predictions do not differ greatly across tasks. Section 5.2 presents evidence from General Knowledge and State Capital data, where subjects report probabilistic judgments on practical statements. Individual predictions are highly dispersed in some statements while there is a stronger consensus in others. This variety allows an analysis on the effectiveness of the SO algorithm for different levels of dispersion as well as crowd size.

5.2 General Knowledge and State Capital data

Unlike the Coin Flips data, the items in the State Capital and General Knowledge data have a binary truth. I follow a similar approach to Budescu and Chen (2015) and Martinie et al. (2020) and calculate transformed Brier scores associated with the aggregate estimates of each method in each data set. The transformed Brier score of a method i in a given data set is defined as

$$\begin{aligned} S_i = 100 - 100 \sum _{j=1}^J \frac{(o_j - x^i_j)^2}{J}, \end{aligned}$$

where $o_j \in \{0,1\}$ be the outcome of event j, J is the total number of events in the data set and $x^i_j \in [0,1]$ is the aggregate probabilistic prediction of method i on event j. The transformed Brier score is strictly proper and assigns a score within [0, 100]. We want to test whether the SO algorithm achieves a higher transformed Brier score than the benchmarks.

Similar to Sect. 5.1, I follow a bootstrap approach. However, unlike Sect. 5.1 I test the SO algorithm at different levels of dispersion of predictions as well as crowd size. Thus, this section presents results from two different bootstrap analyses. The first is similar to the analysis in Sect. 5.1, except that the transformed Brier score is used as a measure of accuracy. I generate 1000 bootstrap samples of subjects for each crowd size $M \in \{10,20,\ldots ,80\}$ and implement all aggregation methods in each bootstrap sample. The maximum crowd size is set at 80 because the number of subjects varies between 89 and 95. Then, I construct 95% confidence intervals for pairwise differences in transformed Brier scores of the SO estimator and each benchmark. Figure 7 depicts the bootstrap confidence intervals for each data set. An observation above the 0-line indicates that the SO estimator achieved a higher transformed Brier score than the corresponding benchmark in that particular bootstrap sample. Appendix D provides the exact bounds of the intervals shown in Fig. 7.

Fig. 7

Difference in Bootstrapped transformed Brier scores (SO vs benchmark) for each crowd size

Figure 7 suggests that increasing the sample size improves the performance of the SO algorithm relative to the simple average and median prediction in questions with a binary truth as well. A similar result holds for minimal pivoting, but not for knowledge-weighting and meta-probability weighting. The results are in accordance with Fig. 6. Relative accuracy of the SO algorithm (weakly) improves as we move from small to moderate or large samples.

I will now investigate if the SO algorithm is more effective than the alternatives when predictions disagree greatly. We can categorize the General Knowledge and State Capital items in terms of the dispersion of predictions and run the bootstrap analysis within each category. For the main results below, I use standard deviation of predictions as the measure of dispersion in an item. Appendix G replicates the same analysis using kurtosis as the measure and finds very similar results. In the General Knowledge data, I categorize the items in three groups in terms of the standard deviation of predictions: bottom 10%, middle 80% and top 10%. The bottom and top 10% items represent the low and high dispersion items respectively. The State Capital data includes a lower number of items. In order to have a reasonable number of items in each category, the thresholds are set at 25% and 75%. Thus, the low, medium and high dispersion categories in the State capital data are bottom 25%, middle 50% and top 25% in terms of standard deviation in predictions. The bootstrap analysis generates samples and calculates transformed Brier scores separately for each dispersion category. A bootstrap sample consists of items from a category sampled with replacement. Each sample produces a transformed Brier score for each method. I generate 1000 such bootstrap samples in each category and construct 95% confidence intervals for pairwise differences in transformed Brier scores of the SO estimator and each benchmark. Figure 14 in Appendix G presents the same analysis except that the thresholds are set at 33% and 66% in both data sets, which results in an approximately equal number of tasks in each category. Pairwise differences in Brier scores are similar to the results below.

Figure 8 presents 95% bootstrap confidence intervals for pairwise differences in transformed Brier scores. Panels in the 2x3 grid show the results from low, medium or high dispersion items in each data set. Each box plot shows 2.5%, 25%, 50%, 75% and 97.5% quantiles of pairwise differences in transformed Brier scores between the SO estimate and the corresponding benchmark. As in Figure 7, strictly positive pairwise differences would suggest higher accuracy for the SO algorithm than the corresponding benchmark.

Fig. 8

Difference in Bootstrapped transformed Brier scores (SO vs benchmark). The scales on y-axis are allowed to be free in each plot on the 2x3 grid

Appendix D provides the Bootstrap confidence intervals depicted in Figure 8. The confidence intervals show that the SO estimator significantly outperforms simple average and median in moderate and high dispersion items. Furthermore, almost all confidence intervals are strictly above the 0-line in the high dispersion category in each data set. In high dispersion items, the SO algorithm compares favorably to the advanced benchmarks as well.

To summarize, results indicate that the SO algorithm is relatively more effective in moderate to large samples and when individual predictions disagree greatly, resulting in a more dispersed empirical density of predictions. Section 6 provides a further discussion on the strengths and limitations of the SO algorithm.

6 When and why is the SO algorithm effective?

The findings in Section 5 not only document the effectiveness of the SO algorithm but also provides a “user’s manual” for a DM who intends to use an aggregation algorithm to combine probabilistic judgments. The SO algorithm is expected to perform relatively well in moderate to large samples and when the predictions are highly dispersed. Note that the DM knows or can determine the size of the sample of forecasters. Furthermore, the empirical density of predictions is observable to the DM prior to the resolution of the uncertain event. Thus, the decision to implement the SO algorithm can be based on the sample size and the observed dispersion in predictions.

Figures 6 and 7 showed that the forecast errors of the SO algorithm decrease even more rapidly than the benchmarks as the sample size increases. Intuitively, the SO algorithm is more sensitive to the sample size because it relies on the sample density of predictions. The sample quantiles may overlap in very small samples. As the sample size increases, the sample density becomes more representative of the underlying population density and the quantiles could become more distinct. Then, the SO algorithm can produce a more fine-tuned aggregate prediction. The DM should use the SO algorithm if a moderate to large sample of forecasters is available. In very small samples, simple aggregation methods or the MP method may be preferred.

The disagreement between experts is also a factor in the effectiveness of the SO algorithm. Consider a situation where there is a strong consensus among experts: individual predictions are clustered around a certain value (low dispersion). We can imagine two scenarios in which the DM would observe such a pattern. Experts could be highly accurate individually, in which case a simple average of predictions would perform sufficiently well. In the second scenario, predictions are clustered around an inaccurate value. Then, the majority of predictions would be highly inaccurate. Recent work developed algorithms to pick the correct answer to a multiple choice question when the majority vote is inaccurate (Prelec et al. 2017; Wilkening et al. 2022). An analogous solution in aggregating probabilistic judgments may identify a contrarian but well-calibrated prediction and discard others. As discussed in Section 4.3, the KW and MPW mechanisms set individual weights for aggregation. However, these mechanisms are highly unlikely to attach 0 weight to a very high proportion of predictions. The MP method makes an adjustment based on average prediction and meta-prediction. It does not attempt to locate more accurate experts. In theory, the SO algorithm can pick the sample quantile that corresponds to the contrarian prediction. However, the sample quantiles are close to each other when predictions are highly clustered. Thus, the SO algorithm’s adjustment may not be sufficiently extreme. Alternatively, if the DM expects a strong consensus with reasonably well-calibrated individual expert predictions, eliciting the predictions only and using a simple aggregation method could be preferable. Differences in transformed Brier scores at low dispersion in Figure 8 are smaller than the differences at higher levels of dispersion. Simple aggregation methods could be nearly as accurate as the more sophisticated aggregation algorithms at low dispersion.

Now consider a situation of high dispersion in predictions instead. Experts disagree in their predictions and some experts are less accurate (ex-post) than the others. The high dispersion category in General Knowledge and State Capital studies represent this case. Figure 8 suggests that the SO algorithm not only outperforms the simple aggregation methods, but it could also be more effective than the advanced benchmarks as well. The SO algorithm performs well under higher disagreement because the sample quantiles become more distinct, which allows more room for improvement. High dispersion in predictions also allows more precision in the SO estimator. Thus, a DM who observes strong disagreement among individual predictions may prefer the SO algorithm. Note that an aggregation problem can be considered as more tricky when forecasters strongly disagree. The SO algorithm is particularly effective in problems where the DM might need an effective aggregation algorithm the most.

The SO algorithm differs from the other aggregation algorithms in its use of the empirical density of predictions. For a given level of overshoot surprise, the absolute difference between the SO estimator and the average prediction depends on the dispersion in the empirical density of predictions. However, the SO algorithm always produces an aggregate estimate that lies within the range of individual predictions. Recall that the MP method uses a fixed step size to adjust the average prediction. In contrast, the SO algorithm’s adjustment on the aggregate prediction is informed and restrained by the empirical density. This makes the SO estimator more robust to potential over-adjustments, which may reduce the calibration of the aggregate prediction even when it is adjusted in the correct direction.

7 Conclusion

Decision makers frequently face the problem of predicting the likelihood of an uncertain event. Leveraging the collective wisdom of many experts has been shown to be a promising solution. However, the use of collective wisdom is not a trivial solution because there are typically no general guidelines on how individual judgments should be aggregated for maximum accuracy. Forecasters typically have shared information through their training, public knowledge, past observations, knowledge of the same academic works, etc. In such cases, the simple average of predictions exhibits the shared-information problem (Palley and Soll 2019). Recent work developed aggregation algorithms that rely on an augmented elicitation procedure (Prelec 2004; Prelec et al. 2017; Palley and Soll 2019; Palley and Satopää, 2022; Wilkening et al. 2022). These algorithms use individuals’ meta-beliefs to aggregate predictions more effectively. This paper follows a similar approach and proposes a novel algorithm to aggregate probabilistic judgments on the likelihood of an event. The Surprising Overshoot algorithm uses experts’ probabilistic meta-predictions to aggregate their probabilistic predictions. The SO algorithm utilizes the information in meta-predictions and the empirical density of predictions to produce an estimator.

Experimental evidence shows that the SO algorithm consistently outperforms simple averaging and median prediction. I also compared the SO algorithm to alternative aggregation algorithms that elicit meta-beliefs (Palley and Soll 2019; Palley and Satopää 2022; Martinie et al. 2020). The SO algorithm is particularly effective in moderate to large samples of experts and when the empirical density of predictions is highly dispersed. Such high dispersion is more likely to occur in prediction tasks where forecasters strongly disagree in their individual assessment.

In practice, a DM is more likely to need a judgment aggregation algorithm when expert predictions lack a clear consensus. In such decision problems, the DM finds herself with conflicting forecasts with no straightforward way to combine them. The SO algorithm is especially powerful in such challenging aggregation problems because of its effectiveness in aggregating disagreeing judgments. The dispersion in predictions that result from the disagreement among experts works in the algorithm’s favor.

Appendices

Appendices

A. Proofs

1.1 Theorem 1

Let agent $i \in \{1,2,\ldots ,N\}$ be an arbitrary agent. Suppose all agents $j \in \{1,2,\ldots ,N\} \setminus \{i\}$ report truthfully, i.e. $(x_j,z_j) = (E[\theta | s,t_j], E[\bar{x}_{-j} | s,t_j])$ where $\bar{x}_{-j}$ represents the average prediction of all agents excluding j. Truthful reporting is a Bayesian Nash equilibrium if $(x_i,z_i) = (E[\theta | s,t_i], E[\bar{x}_{-i} | s,t_i])$ is agent i’s best response.

Let $(x_i^*,z_i^*) = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{x_i,z_i} E[\pi _i | s,t_i]$ denote the optimal prediction and meta-prediction that maximizes agent i’s expected score given $\{s,t_i\}$ and truthful reporting from other agents. Note that $E[\pi _i | s,t_i] = E[\pi _{xi} | s,t_i] + E[\pi _{zi} | s,t_i]$. Agent i’s prediction does not affect $E[\pi _{zi} | s,t_i]$ as it is completely determined by $z_i$ and $\bar{x}_{-i}$. Similarly, $E[\pi _{xi} | s,t_i]$ is determined by $x_i$ and the realization of Y only. Thus agent i’s meta-prediction has no effect on $E[\pi _{xi} | s,t_i]$. Thus, agent i’s maximization problem is separable where $x_i^* = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{x_i} E[\pi _{xi} | s,t_i]$ and $z_i^* = \mathop {{{\,\mathrm{arg\,max}\,}}}\limits _{x_i} E[\pi _{zi} | s,t_i]$. Recall that $\pi _{xi}$ and $\pi _{zi}$ are maximized at $\theta$ and $\bar{x}_{-i}$ respectively. Then, $x_i^* = E[\theta | s,t_i]$ and $z_i^* = E[\bar{x}_{-i} | s,t_i]$. Truthful report $(x_i,z_i) = (E[\theta | s,t_i], E[\bar{x}_{-i} | s,t_i])$ is agent i’s best response, which completes the proof.

1.2 Lemma 1

Suppose $x_i > \bar{x}_N$ for an agent i. For this agent, we can write

$$\begin{aligned} x_i&> \bar{x}_N \\ (1-\omega ) s + \omega t_i&> (1-\omega ) s + \omega \frac{1}{N} \sum _{k=1}^N t_k \\ t_i&> \frac{1}{N} \sum _{k=1}^N t_k = \bar{t} \end{aligned}$$

For $N \rightarrow \infty$, we have $\displaystyle \bar{t} \rightarrow \theta$ and $\bar{x} = \lim \limits _{N\rightarrow \infty } \bar{x}_N$, so we get $x_i> \bar{x} \iff t_i > \theta$

1.3 Lemma 2

Suppose $z_i > \bar{x}_N$ for an agent i. The following holds for $z_i$:

$$\begin{aligned} z_i&> \bar{x}_N \\ (1-\omega ) s + \omega x_i&> (1-\omega ) s + \omega \frac{1}{N} \sum _{i=k}^N t_k \\ x_j&> \frac{1}{N} \sum _{k=1}^N t_k = \bar{t} \end{aligned}$$

For $N \rightarrow \infty$, we have $\displaystyle \bar{t} \rightarrow \theta$ and $\bar{x} = \lim \limits _{N\rightarrow \infty } \bar{x}_N$, so we get $z_j> \bar{x} \iff x_j > \theta$

1.4 Theorem 2

The sample average $\bar{x}_N$ is a consistent estimator if $\lim \limits _{N \rightarrow \infty } \bar{x}_N = \bar{x} = (1-\omega ) s + \omega \theta = \theta$, which occurs when $s=\theta$ and there is no shared-information problem. Then, $x_i> \bar{x} \iff z_i > \bar{x}$. This follows from Lemma 2 and $\bar{x} = \theta$. Thus, an agent’s prediction and meta-prediction are always on the same side of $\bar{x}$, implying that $p_x = p_z$.

1.5 Theorem 3

Lemmas 1 and 2 suggest that $p_x \equiv \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{i=1}^N \mathbbm {1}(t_i > \theta )$ and $p_z \equiv \lim \limits _{N \rightarrow \infty } \frac{1}{N} \sum \limits _{i=1}^N \mathbbm {1}(x_i > \theta )$. Note that $x_i = (1-\omega )s + \omega t_i > \theta$ holds if and only if $t_i > \theta - ((1-\omega )/\omega )(s-\theta )$. So, we have the following:

$$\begin{aligned} p_x&\equiv \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{i=1}^N \mathbbm {1}(t_i > \theta ) \end{aligned}$$

(4)

$$\begin{aligned} p_z&\equiv \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{i=1}^N \mathbbm {1}\left( t_i > \theta - \frac{1-\omega }{\omega }(s-\theta )\right) \end{aligned}$$

(5)

Consider first the case $\lim \limits _{N \rightarrow \infty } \bar{x}_N > \theta$. We have $(1-\omega )s + \omega \theta > \theta$, which implies $s > \theta$. Then, we must have $p_z \ge p_x$, with $p_z > p_x$ if there exists at least one private signal $t_i \in \left( \theta - \frac{1-\omega }{\omega }(s-\theta ), \theta \right)$ and $p_z = p_x$ otherwise. Now suppose $\lim \limits _{N \rightarrow \infty } \bar{x}_N < \theta$, which occurs when $s < \theta$. Since $s - \theta < 0$, we get $p_z \le p_x$ where the inequality is strict if there is a private signal $t_i$ that satisfies $t_i \in \left( \theta , \theta - \frac{1-\omega }{\omega }(s-\theta ) \right)$.

For the result on $\Delta p$, consider two alternative scenarios $s \in \{s^0,s^1\}$ for any given $s^0$ and $s^1$. Let $\bar{x}^0_N = (1-\omega )s^0 + \omega \bar{t}$ and $\bar{x}^1_N = (1-\omega )s^1 + \omega \bar{t}$ be the average prediction when $s=s^0$ and $s=s^1$ respectively. For any given s, the asymptotic bias in $\bar{x}_N$ is given by $\lim \limits _{N \rightarrow \infty } \bar{x}_N - \theta = (1-\omega )(s-\theta )$. Let $\{p_x^0,p_z^0\}$ and $\{p_x^1,p_z^1\}$ be the overshoot rates for $s = s^0$ and $s=s^1$ respectively. Also let $\Delta p^0 = p_z^0 - p_x^0$ and $\Delta p^1 = p_z^1 - p_x^1$. Equation 4 suggests $p_x^0 = p_x^1$ and the comparison between $\Delta p^0$ and $\Delta p^1$ depends on $p^0_z$ and $p^1_z$ only. First, consider the case $s^1< s^0 < \theta$. We have $\lim \limits _{N \rightarrow \infty } (\bar{x}^1_N - \theta )< \lim \limits _{N \rightarrow \infty } (\bar{x}^0_N - \theta ) < 0$, i.e. there is a negative asymptotic bias in both cases but the bias is stronger for $s = s^1$. Then, we should get $\Delta p^1 \le \Delta p^0$. Since $s^1-\theta < s^0-\theta$, we get $p_z^1 \le p_z^0$ from Equation 5, leading to $\Delta p^1 \le \Delta p^0$. Second case is $\theta< s^0 < s^1$. Then, $0< \lim \limits _{N \rightarrow \infty } (\bar{x}^0_N - \theta ) < \lim \limits _{N \rightarrow \infty } (\bar{x}^1_N - \theta )$, i.e. positive asymptotic bias is stronger for $s = s^1$ and we should have $\Delta p^1 \ge \Delta p^0$. Since $s^1-\theta > s^0-\theta$ Equation 5 suggests $p_z^1 \ge p_z^0$ and hence, $\Delta p^1 \ge \Delta p^0$. Finally, consider $s^0< \theta < s^1$. We have $\lim \limits _{N \rightarrow \infty } (\bar{x}^0_N - \theta )< 0 < \lim \limits _{N \rightarrow \infty } (\bar{x}^1_N - \theta )$, there is a positive bias for $s = s^1$ and negative bias for $s = s^0$. Similar to the second case, it follows from $s^1 - \theta > s^0 - \theta$ that $p_z^1 \ge p_z^0$, which implies $\Delta p^1 \ge \Delta p^0$ as claimed.

1.6 Theorem 4

Lemma 2 established that $z_i> \bar{x} \iff x_i > \theta$ for any agent i in the limit. So, $p_z$ also measures the population proportion of predictions $x_i$ that overshoot $\theta$. Then, $Q(1-p_z) \equiv sup\{x \in \{x_1,x_2,\ldots ,x_N\} | x \le \theta \}$, i.e. $Q(1-p_z)$ corresponds to the highest prediction that does not exceed $\theta$. If there exists $x_i \in \{x_1,x_2,\ldots ,x_N\}$ such that $x_i = \theta$, we must have $Q(1-p_z) = x_i = \theta$ by definition.

B. Mixed sample of experts and non-experts

Without loss of generality, let agents $i \in \{1,2,\ldots ,K\}$ be the experts who observe both the shared signal and a private signal. Agents $i \in \{K+1,K+2,\ldots ,N\}$ are non-experts observe the shared signal s only. Then,

$$\begin{aligned} x_i = {\left\{ \begin{array}{ll} (1-\omega ) s + \omega t_i &{} \text { for } i \in \{1,2,\ldots ,K\} \\ s &{} \text { for } i \in \{K+1,K+2,\ldots ,N\} \end{array}\right. } \end{aligned}$$

Also, we have $z_i = (1-\omega )s + \omega x_i$ for $i \in \{1,2,\ldots ,K\}$ while $z_i = s$ for others. Average prediction is given by $\bar{x}_N = \frac{1}{N} \sum \nolimits _{i=1}^N x_i = (1-\omega ) s + \omega \frac{1}{K} \sum \nolimits _{i=1}^K t_i$.

In this setup, Lemma 1 applies for experts and Lemma 2 apply for all. Consider $i \le K$ first. We have $x_i > \bar{x}_N$ if and only if $t_i > \bar{t}$ where $\bar{t} = \frac{1}{K} \sum \limits _{i=1}^K t_i$. Similarly $z_i> \bar{x}_N \iff x_i > \bar{t}$. For $N \rightarrow \infty$, these conditions become equivalent to Lemmas 1 and 2. Now consider $i > K$. We have$x_i > \bar{x}_N$ iff $s > \bar{t}$. Then, in the limit $x_i> \bar{x} \iff s > \theta$. Also observe that $z_i = (1-\omega ) s + \omega E\left[ \frac{1}{K} \ne \, s \right] = s$ for a non-expert. Since $z_i = x_i = s$, we also have $z_i> \bar{x} \iff x_i = s > \theta$. So, Lemma 2 applies for non-experts as well.

Theorems 2, 3 and 4 also hold in a mixed crowd of experts and non-experts. Consider Theorem 2 first. Average prediction $\bar{x}_N$ is consistent when $s=\theta$. In that case, $\bar{x} = \theta$ and we have $x_i = z_i = \bar{x} = \theta$ for all $i \in \{K+1,K+2,\ldots ,N\}$. From Lemma 2, prediction and meta-prediction of either an experts or a non-experts always falls on the same side of $\bar{x}$, implying that Theorem 2 holds. Next, consider Theorem 3. We always have $x_i = z_i = s$ for all $i \in \{K+1,K+2,\ldots ,N\}$, i.e. a non-experts prediction and meta-prediction are the same. We have $\lim \limits _{N \rightarrow \infty } \bar{x}_N = \bar{x} > \theta$ when $s > \theta$, in which case we also have $x_i = z_i = s > \bar{x}$ for all non-experts. Vice versa is true for $\lim \limits _{N \rightarrow \infty } \bar{x}_N < \theta$, where all non-expert predictions and meta-predictions are smaller than $\bar{x}$. Non-expert reports do not have any effect on the comparison between $p_z$ and $p_z$ because their predictions and meta-predictions are on the same side according to both measures. The proof of Theorem 3 applies for experts, namely agents $i \in \{1,2,\ldots ,K\}$. Since non-experts have no effect on the comparison between $p_z$ and $p_x$, Theorem 3 applies. Finally, consider Theorem 4. For all non-experts, we have $z_i = s > \bar{x}$ if $s>\theta$ and $z_i = s \le \bar{x}$ otherwise. Regardless of whether non-experts overshoot or undershoot in meta-predictions, $Q(1-p_z)$ picks the highest prediction $x_i$ that satisfies $x_i \le \theta$. Only the exact quantile changes. Thus, Theorem 4 applies as well.

C. Dispersion of predictions in different data sets

See Fig. 9.

Fig. 9

Inter-quartile range of predictions across the items in each data set. All predictions are scaled to 0-100%

D. Bootstrap confidence intervals

See Tables 1, 2, 3, 4 and 5.

Table 1 95% Bootstrap confidence intervals depicted in Figure 6b (Coin Flips data)

Table 2 95% Bootstrap confidence intervals depicted in Figure 7, General Knowledge data

Table 3 95% Bootstrap confidence intervals depicted in Figure 7, State Capital data

Table 4 95% Bootstrap confidence intervals depicted in Figure 8, General Knowledge data

Table 5 95% Bootstrap confidence intervals depicted in Figure 8, State Capital data

E. Analysis on the Coin Flips data–Nested structure

Fig. 10

Bootstrap analysis on Coin Flips data

Figure 10 presents the results of a bootstrap analysis (described in Section 5.1) on the Nested structure data. As discussed in Section 4.1, the Nested structure differs from the formal framework of the SO algorithm. Nevertheless, the SO algorithm does not perform significantly worse than any of the benchmarks considered.

F. SO algorithm with interpolated quantile function

See Figs. 11 and 12.

Fig. 11

Results of bootstrap analysis on Coin Flips data

Fig. 12

Pairwise differences in Bootstrapped Transformed Brier scores

G. Robustness checks on Section 5.2

See Figs. 13 and 14.

Fig. 13

Bootstrap differences in Transformed Brier Scores (measure of dispersion: kurtosis)

Fig. 14

Bootstrap differences in Transformed Brier Scores (equal split in categories of dispersion)