Modeling multi-tier heterogeneous small cell networks: rate and coverage performance

Abstract

The rapid growth of small cells is driving cellular network toward randomness and heterogeneity. The multi-tier heterogeneous network (HetNet) addresses the massive connectivity demands of the emerging cellular networks. Cellular networks are usually modeled by placing each tier (e.g macro, pico and relay nodes) deterministically on a grid which ignores the spatial randomness of the nodes. Several works were idealized for not capturing the interference which is a major performance bottleneck. Overcoming such limitation by realistic models is much appreciated. Multi-tier relay cellular network is studied in this paper, In particular, we consider ${\mathscr {K}}$-tier transmission modeled by factorial moment and stochastic geometry and compare it with a single-tier, traditional grid model and multi-antenna ultra-dense network (UDN) model to obtain tractable rate coverage and coverage probability. The locations of the relays, base stations, and users nodes are modeled as a Poisson Point Process. The results showed that the proposed model outperforms the traditional multi-antenna UDN model and its accuracy is confirmed to be similar to the traditional grid model. The obtained results from the proposed and comparable models demonstrate the effectiveness and analytical tractability to study the HetNet performance.

1 Introduction

Cellular networks evolve from planned cells to irregularly dense multi-tier networks to satisfy the exponential growth of the wireless data traffic [45]. Many low power BSs are deployed in congested areas, such as shopping malls, stadiums, coffee shops, and etc, to enhance the network capacity and extend the coverage. The collective coexistence of these low power BSs is termed as small cells and the high power BSs are termed as macrocells, so the resulting network is usually known as a heterogeneous network (HetNet) [15, 28]. As a variety of infrastructure is being deployed including pico, macro and femto BSs [48], as well as fixed relay stations [32], the deployment of cellular network is taking on a massively HetNet character. As a result of network densification, severe interference is generated. Interference management is the main challenge in deploying heterogeneous cellular networks. Some challenges have occurred in the high dense networks such as less coverage, cost, co-channel, and intercell interference due to the increase in the number of connected devices [1]. Hence, the resulting interference is also becoming more complicated.

Deploying small cells significantly converts the current cellular networks into capacity-driven networks with wide-area coverage. However, deploying more small cells introduces interference that can be mitigated by multi-antenna techniques. Due to the singularity of the interference that governing HetNets, prior works on single-input single-output (SISO) transmission [9, 28, 54] cannot be applied directly due to spatial diversity.

Besides cellular network contributions, there is extensive work on multiple-input multiple-output (MIMO) antenna techniques for adhoc networks is analyzed in the literature and similar to our work which can model HetNets. These techniques, such as spatial multiplexing and single-tier MIMO, have been introduced in Vaze and Heath  [47] and multi-user MIMO [1, 39] are finding difficulty in choosing from each tier, the possible number of multi-antenna techniques along with their tractable modeling. In a single-tier multi-antenna network, Di Renzo and Guan  [17] show the importance of multiple receiving antennas to improve the spatial-multiplexing. In Dhillon et al.  [15], the PPP-based heterogeneous model has been extended to MIMO heterogeneous model, a closed-form for average rate was derived in AbdelNabi et al.  [1], Park et al.  [39].

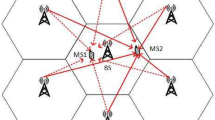
The denser nature of cellular networks makes them increasingly irregular [43]. This depicts small cells opportunistically deployed in hot-spots, and hence highly irregular. As a result, the popular deterministic grid model (see Fig. 1) is increasingly anachronistic in practical deployments. The grid model is quite idealized even for single-tier networks, and sometimes for macrocell locations a perturbed grid model is used [53]. Spatial random model is often a more appropriate model than the deterministic one in characterizing the HetNet. Poisson Point Process (PPP) is being the simplest model among the random spacial models that model the BS locations by two-dimensional point process [35].

Fig. 1

The topology of grid cellular network, where every Voronoi cell represents tier’s coverage area—where the red circle represents tier-1, blue dot represents tier-2 and the black circle represents tier-3 (Color figure online)

However, cellular networks are usually modeled the BSs by arranging them on a line or circle as in the Wyner model or placing them on a grid (with a regular shape), with the user and relay either randomly or deterministically distributed across the network to calculate the signal-to-interference-and-noise ratio (SINR). The resulting SINR consists of multiple random complex variables, without considering the interference randomness in small-cell network [55] and cellular network distribution [51]. These models are not tractable because they are highly idealized, complex system-level simulation is used to evaluate the coverage probability and rate coverage. To reduce the dependence on simulations, SINR closed-form using stochastic geometry was derived [46, 54].

As it is obvious that the Wyner and grid models are not practicable for characterizing the SINR, stochastic geometry has proven to be a useful tool to quantify and model the interference and coverage probability in cellular networks which approximates the actual networks [45]. To provide insight into the operation of the networks, Poisson Point Processes (PPP) model is applied. The PPP model is constituted of BS, relay and user parameters (transmit power and path-loss exponent). Under a homogeneity condition, the BS positions are agnostic to the wireless signal propagation, which makes the power that a relay or user receives from any population of BSs look as if they originated from PPP-distributed BSs [46]. This facilitates the network performance computation metrics such as the coverage probability [39, 53], with its lower and upper bound derivations. Park et al.  [40] studied the effect of two-tier networks with the effect of channel uncertainty. In two-tier network, Khoshkholgh and Leung  [25] compare single and multiuser performance. A comprehensive analysis on the performance metrics such as coverage probability is computed by averaging over all cell sizes and scenarios [2]. The model in Andrews et al.  [2] was studied for multi-tier network [15], and further investigated in Madhusudhanan et al.  [36], Dhillon and Andrews  [13] for single-antenna HetNets. The HetNets PPP-based model of Dhillon et al.  [15] was generalized in Heath et al.  [21], Gupta et al.  [19] to multi-antenna HetNets by deriving the downlink coverage probability. However, the challenge in previous work is incorporating heterogeneous infrastructure such as fixed relays into the system model.

The single antenna PPP-based model presented in Dhillon et al.  [14] for single-tier network and then extended in Novlan et al.  [37] to multi-tier networks, where each BS covers particular Voronoi cell, is regarded as a suitable stochastic model to evaluate the network performance. The ${\mathscr {K}}$-tiers is regarded as a combination of multi-tier and single-tier model in which each tier is modeled by transmission power, density, and path-loss exponent of BSs.

Despite these efforts in characterizing the HetNet i.e., single-tier and multi-tier, the ${\mathscr {K}}$-tier HetNet are relatively unexplored. For these reasons, it is imperative to characterize the randomly distributed performance of two-tier network by using factorial moment and stochastic geometry to derive closed-form bounds for the rate coverage and coverage probability.

2 Motivations and contributions

The rapid proliferation of small cells has triggered an unprecedented data traffic growth in the next cellular generation fifth generation (5G) network. HetNets such as femto, macro, and macro BSs, are introduced as an effective method to address the data traffic growth by deploying small cells to provide better coverage [3]. However, existing works [7, 10, 28] rarely investigated the general ${\mathscr {K}}$-tier MIMO HetNets. In particular, single-tier HetNet [7, 9, 10, 12] and two-tier HetNet [12, 28, 34, 50] were studied, and hence general HetNet framework was not provided. Further, the ${\mathscr {K}}$-tier HetNets with a single antenna was investigated [31, 49], and therefore, the MIMO HetNet was not studied. The authors in [22, 27, 52] consider single-tier MIMO network, and therefore, the spatial dimension which enhances the network throughput per tier was not exploited. Kuang and Liu [27], Xu and Tao  [52], Jiang and Cui  [22] studied the single-tier network, and failed to capture the network heterogeneity. In addition, MIMO techniques are compared in HetNets by using stochastic geometry, but the study did not analyze in detail the SINR distribution [29, 30]. Due to the assumptions and limitations, the proposed closed-forms in Blaszczyszyn and Giovanidis  [7], Chen et al.  [10], Kuang and Liu [27], Xu and Tao  [52], Jiang and Cui  [22], Liu and Yu  [35], Shuminoski and Janevski  [43] are not applicable to general ${\mathscr {K}}$-tier HetNets, with MIMO and multi-tier network. Thus, in the view of prior work, such closed-forms are remaining largely unknown.

In network geometry modeling, multi-tier network design is an important step that increases in complexity. In this paper, factorial moment and stochastic geometry are proposed to reduce complexity and improve rate coverage and coverage probability of the HetNet. Since the HetNet performance is limited by various interferences which degrade the SINR, such as inter-cell and inter-tier interferences, interference modeling is still appealing. In addition, choosing the possible MIMO techniques from each tier with their tractable characterization remains a challenge. The main contributions of this work are given below.

$*$:

First, a comprehensive HetNet that captures important network parameters for ${\mathscr {K}}$-tier and single-tier BSs is developed by using tools from factorial moment and stochastic geometry, in which each tier could be a macrocell, femtocell, or picocell.

$*$:

Then, closed-forms of the user rate coverage and coverage probability have been driven and the plausibility of the model is compared with the traditional grid model and the multi-antenna UDN (Ultra-dense Network) model. When all tiers are having the same SIR threshold, the complementary cumulative distribution function of the received SIR of the random user is regarded as the coverage probability. This can be interpreted as that the coverage probability does not depend upon the BS density.

$*$:

Next, since the locations of the BSs are independent across the tier which generalizes the HetNets based on PPP assumption, the effect of MIMO configuration in canceling the inter-tier interference is considered.

$*$:

Finally, numerical simulations show that the proposed model achieves a significant gain in rate coverage and coverage probability over some comparable models.

Next, Sect. 3, depicts the system and channel models along with SINR derivations. In Sect. 4 the coverage probability is derived, while the rate coverage is given in Sect. 5. Section 6 characterizes the SINR by using the factorial moment to derive the coverage probability for single-tier and multi-tier network. Section 7 offers the numerical results, and Sect. 8 offers the conclusion.

3 Heterogeneous cellular network model

3.1 System model

In multi-tier downlink assisted relay HetNet with multiple independent dual-hop system (Fig. 2). The BSs form a Voronoi tessellation of the plane (see Fig. 3). The communication between user and BS occurs through the relay in the Voronoi cell. To examine what the network perceives, the BSs are located at the origin.

Various classes of different K tiers of BSs are considered, where ${\mathscr {K}}=\{1,2,\ldots ,K\}.$ Table 1 illustrates the system parameters. Each BSs-tier differs for each user in the target SIR $\beta _{k},$ number of antennas $M_{k},$ the deployment density $\lambda _{k},$ and the transmitted power $\textit{P}_{k}.$ These BS-tiers are modeled by an independent and homogeneous Poisson Point Process (PPP) $\varPhi _{k}$ with density $\lambda _{k}.$ Such claim under sufficient channel randomness by theoretical arguments and empirical observations [56] is validated to be accurate for the multi-tier network. To simplify the analysis, we ignore the thermal noise in some scenarios as cellular networks are proven to be interference-limited [46]. The tier access mechanism can be classified as each tier allows all users either registered (open access) or not (closed access) to connect.

Fig. 2

Cellular downlink assisted relay network, in which three-tier network consisting of macro, pico and femtocells network with intended signal and interferences across tiers are shown. Solid lines depict the desired signal, and the dashed lines depict interference

Fig. 3

The Voronoi multi-tier topology, where each Voronoi cell is the coverage area of a tier—where the blue plus sign represent tier-1, red star represents tier-2 and the blue dot represent tier-3 (Color figure online)

Table 1 Illustrates the system parameters

3.2 Channel model

According to Slivnyak’s theorem [11], a typical single-antenna relay or user is located randomly and associated with the closest BS at the origin in the downlink; namely users in the Voronoi cell of a BS are associated with it, resulting in a coverage area that comprises a Voronoi tesselation on the plane, as depicted in Fig. 3. A traditional grid model uniformly places the BSs at the center of the hexagonal model as shown in Fig. 1, and it is evaluated via simulations because it does not lead to a tractable model. The channel power located at $x\in {\mathbb {R}}^{2}$ from the kth-tier user to the relay/BS located at the origin is denoted by $h_{kx}$ and for the interfering link from a kth tier relay/BS located at $k\in {\mathbb {R}}^{2}$ is denoted by $g_{jy}.$ These different channels have different distributions and in general are depending on the multi-antenna technique used by the relay/BS. Various multi-antenna techniques under Rayleigh fading consider that the desired link and interfering link can follow Gamma distribution [25, 54]. Hence $h_{kx}\sim \varGamma (\varDelta _{k},1)$ and $g_{jy}\sim \varGamma (\varPsi _{j},1),$ where $\varDelta _{k}=M_{k}-\varPsi _{k}+1$ and $\varPsi _{j}$ are positive integers that depend upon the multi-antenna techniques used by the BS. In contrast, since there is no beamforming/spatial multiplexing for the Single-Input Single-Output (SISO) channel, the channels $h_{kx}$ and $g_{jy}$ distributions remain the same. The channels $h_{kx}$ and $g_{jy}$ are following Rayleigh fading distribution with exp(1),  which is same as $\varGamma (1,1)$ distribution. For demonstration purpose, we will consider the following two techniques for rate coverage:

• Multi-tier case: in which $\varPsi _{j}=M_{j}$ and $\varDelta _{k}=1,$ where $M_{j}$ is the number of transmit antennas at jth tier. This models tier j, when multi-antenna $M_{j}$ are serving $\varPsi _{j}$ users.

• Single-tier case: in which $\varPsi _{j}=\varDelta _{k}=1,$ $\forall j\in {\mathscr {K}}.$

3.2.1 The effect of propagation loss

Let us define the deterministic path-loss function for SR and RD hops as follows

$$\begin{aligned} \ell \left( \mid x\mid \right) =\left( K\mid x\mid \right) ^{\alpha }, \end{aligned}$$

(1)

where $\alpha >2$ denotes the path-loss exponent and the path-loss constant $K>0.$ Let $S_{X}$ denote the propagation effects such as shadowing with mean ${\mathbb {E}}[S_{x}]=1$ from the origin to X. The $P_{X}$ is representing the signal power that is emitted from the BS at X, let $\{(S_{X},\,P_{X})\}_{X\in \varPhi }\subset {\mathbb {R}}^{+}$ equal distribution to $(S,\,P)$ be independent positive random vectors that constitute X.

Modifying references Liang and Li  [32] and Blasczyszyn et al.  [6], Keeler et al.  [24] to suit our system model, we consider the propagation loss of the Poisson process on ${\mathbb {R}}^{+}$ for SR hop and RD hop, respectively, given as

$$\begin{aligned} \varTheta _{u}= & {} Y_{u}=\left\{ \frac{\ell _{u}\mid X_{u}\mid }{P_{Xu}S_{Xu}},\,X_{u}\in \varPhi _{u}\right\} , \end{aligned}$$

(2)

$$\begin{aligned} \varTheta _{k}= & {} Y_{k}=\left\{ \frac{\ell _{k}\mid X_{k}\mid }{P_{Xk}S_{Xk}},\,X_{k}\in \varPhi _{k}\right\} , \end{aligned}$$

(3)

Lemma 1

Using the random location of nodes and the randomness of channel fading as in Trigui et al.  [46] and applying the mapping theorem [20], the effect of propagation loss Y is considered as a non-homogeneous Poisson point process on ${\mathbb {R}}^{+}$ with intensity measure $\varLambda ([0,t))=at^{\alpha /2},$ where the propagation constant is

$$\begin{aligned} a=\frac{\lambda \pi {\mathbb {E}}\left[ \left( PS\right) ^{\frac{2}{\alpha }}\right] }{K^{2}} \end{aligned}$$

(4)

Despite the distribution of S being arbitrary, we assume that ${\mathbb {E}}\left[ S^{\frac{2}{\alpha }}\right] <\infty$.¹

Proof

for given $\varPhi _{u}$ and $\varPhi _{k},$ apply the displacement theorem for Poisson point process ( [5], Theorem 1.3.9), $\varTheta _{u}$ and $\varTheta _{k}$ constitute a non homogeneous point process on ${\mathbb {R}}^{+}=[0,\infty )$ of intensity measure $\varLambda$ as follows

$$\begin{aligned} \varLambda ([0,s])= & {} {\mathbb {E}}[\varTheta ([0,s])]\nonumber \\= & {} \lambda \int _{{\mathbb {R}}^{2}}Pr\{\ell (\mid z\mid )/S\le s\}dz\nonumber \\= & {} 2\pi {\lambda {\int \limits _{0}^{{\infty }} \mathrm{x}}\mathrm{Pr}\{\ell (\mid \mathrm{z}\mid )/\mathrm{S}\le \mathrm{s}\}\mathrm{dx}}\nonumber \\= & {} 2\pi {\lambda {\int \limits _{0}^{{\infty }} \mathrm{x}}{\mathbb {E}} {[}1\{\ell (\mid \mathrm{z}\mid )/\mathrm{S}\le \mathrm{s}\}{\mathrm{dx}}}\nonumber \\= & {} 2\pi {\lambda {\mathbb {E}}\left[ \int _{0}^{(\mathrm{sS})^{1/\alpha }/\mathrm{K}}\mathrm{xdx}\right] }\nonumber \\= & {} \frac{\lambda \pi {s}^{2/\alpha }}{\mathrm{K}^{2}}{\mathbb {E}}\left[ {S}^{2/\alpha }\right] . \end{aligned}$$

(5)

$\square$

3.3 SINR formulation

The signal-to-interference-plus-noise ratio (SINR) for the SR hop and RD hop is formulated, which allows us to derive the coverage probability.

The SR hop’s SINR of the positive ${\mathbb {R}}^{+}$ for a relay defined as

$$\begin{aligned} \mathrm {SINR}_{\mathrm{k}}\hbox {(X)}\triangleq & {} \frac{\mathrm {F}_{x_{k}}\mathrm {Y}_{\mathrm{k}}^{-1}}{{\sigma }_{k}+\mathrm {I}_{k}- \mathrm {Y}_{k}^{-1}\mathrm {F}_{x_{k}}}, \end{aligned}$$

(6)

$$\begin{aligned} \mathrm {I}_{\mathrm{k}}= & {} \underset{\mathrm {Y}_{\mathrm{k}}\in \varTheta _{\mathrm{k}}}{\sum }\hbox {Y}_{\mathrm{k}}^{-1}\hbox {F}_{\mathrm{x}_{\mathrm{k}}}, \end{aligned}$$

(7)

with an additive white noise power $\sigma _{\mathrm {k}}\ge 0$ and $\mathrm {I}_{\mathrm{k}}$ is the power received from other nodes, $\{F\}_{X\in \varPhi }$ denotes the Rayleigh fading for the two hops with ${\mathbf {E}}[F_{x}]=1$. The term $(\mathrm {I}_{\mathrm{k}}-\hbox {Y}_{\mathrm{k}}^{-1}F_{x_{k}})$ captures the interference that the relay node experienced.

The RD hop’s SINR of a user with an additive white noise power ${\upsigma }_{u}\ge 0$ is given as

$$\begin{aligned} {\mathrm {SINR}}_{\mathrm{u}}\hbox {(X)}\triangleq & {} \frac{\mathrm {Y}_{\mathrm{u}}^{-1}\mathrm{F}_{\mathrm{x}_{\mathrm{u}}}}{{\sigma _{\mathrm{u}}}+\mathrm {I}_{\mathrm{u}}- \mathrm {Y}_{\mathrm{u}}^{-1}\mathrm {F}_{\mathrm{x}_{\mathrm{u}}}}, \end{aligned}$$

(8)

$$\begin{aligned} \mathrm {I}_{\mathrm{u}}= & {} \underset{\mathrm {Y}_{\mathrm{u}}\in \varTheta _{\mathrm{u}}}{\sum }\hbox {Y}_{\mathrm{u}}^{-1}\hbox {F}_{\mathrm{x}_{\mathrm{u}}}, \end{aligned}$$

(9)

where $\mathrm {I}_{\mathrm{u}}$ is the power received from other nodes. The term $(\mathrm {I}_{\mathrm{u}}-\mathrm{Y}_{\mathrm{u}}^{-1}\mathrm{F}_{\mathrm{x}_{\mathrm{u}}})$ is the interference that the user node experienced.² Further, the distribution of $\{Y^{-1}\}$ is an inhomogeneous Poisson point process with intensity $(2a/\alpha )t^{-1-2/\alpha }dt.$

3.3.1 The effect of channel fading

The received power by a user with a single antenna located at $x_{k}\in \varPhi _{k}$, from a BS located at the origin is given by:

$$\begin{aligned} P_{r}=P_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }, \end{aligned}$$

(10)

where $\alpha$ denotes the path-loss exponent. Each user is under power constraint. Assuming that the user is connected to this BS, the SIR formula could be written as follows:

$$\begin{aligned} \mathrm {SIR}(x_{k})=\frac{P_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }}{\sum _{k\in {\mathscr {K}}}\sum _{y\in \varPhi _{j}\backslash x_{k}}P_{j}g_{jy}\parallel y_{j}\parallel ^{-\alpha }+\sigma ^{2}}. \end{aligned}$$

(11)

The first additional term in the denominator $\sum _{k\in {\mathscr {K}}}\sum _{y\in \varPhi _{j}\backslash x_{k}}P_{j}g_{jy}\parallel y_{j}\parallel ^{-\alpha }$ represents the multi-tier interference, while the second term $\sigma ^{2}$ denotes the additive noise power. In our results section, we will show that the interference dominates the noise in the scenarios we have considered. The user is connected and associated with the strongest received signal from a set of BSs (tiers). When the received SIR from a set of BS is higher than the target SIR, the respected user is said to be in coverage. When the SIR from at least one of the $\mathrm {BSs}$ is higher than the target SIR, then a user is said to be in coverage. Mathematically the user is in coverage if

$$\begin{aligned} \mathrm {P}_{\mathrm{c}}= & {} {\mathbb {P}}\left( \underset{k\in {\mathscr {K}}}{\bigcup }\mathrm {SIR}(x_{k})>\beta _{k}\right) \\= & {} {\mathbb {E}}\left[ {\mathbf {1}}\left( \underset{k\in {\mathscr {B}}}{\bigcup }\underset{x_{k}\in \varPhi _{k}}{\bigcup }\mathrm {SIR}(x_{k})>\beta _{k}\right) \right] \end{aligned}$$

where the value of function ${\mathbf {1}}(\varepsilon )=1$ if $\varepsilon >0,$ and ${\mathbf {1}}(\varepsilon )=0$ otherwise. In order to derive the coverage probability for ${\mathscr {K}}$-tier network, we assumed that all BS-tiers are adopting different multi-antenna technique.

4 ${\mathscr {K}}$-coverage probability

The tagged mobile user is said to be in coverage if it is SIR is above the threshold. When all tiers are connecting to at least one BS from any tier without restriction and having the same SIR threshold $\beta ,$ the coverage probability is the complementary cumulative distribution function (CCDF) of the received SIR. With this in mind, we now derive the coverage probability for randomly located users in the ${\mathscr {K}}$th-tier network. Closed-form of the coverage probability bound has been derived with only the approximation of Laplace transform as given in the following Theorem.

Theorem 1

The ${\mathscr {K}}$- coverage probability of a user is denoted by

$$\begin{aligned} \mathrm {P}_{\mathrm{c}}= & {} \sum \limits _{\mathrm{k}\in {\mathscr {K}}}\lambda \int _{{\mathbb {R}}^{2}} \mathrm {exp} \left( -\hbox {C}(\alpha )\left( \frac{\beta _{\mathrm{k}}}{\textit{P}_{\mathrm{k}}}\right) ^{2/\alpha } \parallel \hbox {x}_{\mathrm{k}}\parallel ^{2}\sum \limits _{\mathrm{m=1}}^{{\mathrm{K}}}{\lambda }_{\mathrm{m}} \textit{P}_{\mathrm{m}}^{2/\alpha }\right) \nonumber \\&\mathrm {exp}\left( -\frac{\beta _{\mathrm{k}}\sigma ^{2}}{\textit{P}_{\mathrm{k}}}\parallel \hbox {x}_{\mathrm{k}}\parallel ^{2}\right) \hbox {dx}_{\mathrm{i}}, \end{aligned}$$

(12)

where $C(\alpha )=2\pi ^{2}csc(\frac{2\pi }{\alpha })\alpha ^{-1}.$

Proof

Refer to “Appendix A” . $\square$

Theorem 1 derives the coverage probability for ${\mathscr {K}}$ tier network. As we have established earlier, the user is considered to be in coverage if connected to at least one BS with SIR greater than the threshold. Hence, the coverage probability could be defined by the sum of the mutually exclusive probabilities (events) that one of them may happen at any time. This allows us to express the sum of probabilities over PPP by using an integral of Laplace transform of the interference (i.e., the sum over PPP of the interference leads to a product for it is Laplace function). Since the fading power is exponentially distributed and applying the probability generating functional (PGFL) of PPP, we arrive at the closed form. This result is further simplified for the interference-limited case, where it leads to a simple closed-form shown in the following Corollary.

Corollary 1

In an interference limited scenario, the ${\mathscr {K}}$-tier coverage probability of a tagged user simplified to

$$\begin{aligned} \mathrm {P}_{\mathrm{c}}=\pi \frac{\sum _{\mathrm{i}=1}^{\mathrm{k}\in {\mathscr {K}}} \lambda _{\mathrm{k}}{} \textit{P}_{\mathrm{k}}^{\frac{2}{\alpha }}\beta _{\mathrm{k}}^{-\frac{2}{\alpha }}}{\sum _{\mathrm{j}\in {\mathscr {K}}}\lambda _{\mathrm{j}}{} \textit{P}_{\mathrm{j}}^{\frac{2}{\alpha }} \textit{C}(\alpha )}. \end{aligned}$$

(13)

Proof

Follows from Theorem 1 for interference-limited scenario - no noise $(\varDelta _{k}=1)$.

Setting $k=1$ in the above derived bound in the Corollary, we arrive at single-tier network given by:

$$\begin{aligned} \mathrm {P}_{\mathrm{c}}=\frac{\pi }{\beta ^{\frac{2}{\alpha }}{} \textit{C}(\alpha )}. \end{aligned}$$

(14)

In an interference-limited scenario, we observe that the coverage probability in (14) is dependent on the SIR and independent on the density of BSs. This is explained in Andrews et al.  [2] by the fact that changing the BSs density changes the received interference power with the same factor and thus they cancel each other. Therefore, adding more BSs in any tier can not affect the coverage and therefore the system capacity increases with the number of BSs linearly due to the fact that the user does not differentiate between the tiers because of the SIR equality. Interestingly, changes in the density of transmit power of some BSs tiers is accompanied by changes in the received power that is equalized by the change in interference power.

To compare the ${\mathscr {K}}$th tier with the single-tier case [15], $C(\alpha ,1)$ can be obtained as follows:

$$\begin{aligned} \textit{C}(\alpha ,1)= & {} \frac{2\pi }{\alpha }B\left( \frac{2}{\alpha },\,1-\frac{2}{\alpha }\right) , \end{aligned}$$

(15)

$$\begin{aligned}= & {} \frac{2\pi }{\alpha }\varGamma \left( \frac{2}{\alpha }\right) \varGamma \left( 1-\frac{2}{\alpha }\right) =\frac{2\pi ^{2}csc(\frac{2\pi }{\alpha })}{\alpha }, \end{aligned}$$

(16)

The last step derived from Euler’s formula. Therefore $C(\alpha ,1)$ is the same as $C(\alpha )$ [16]. For the same system parameters, the single-tier coverage is always higher than the ${\mathscr {K}}$th-tier coverage.

However, the single-tier and the ${\mathscr {K}}$th-tier cases are not quite conclusive due to the fact that the single-tier is serving the higher density of users/relays. In order to account for that fact, the system rate which gives the number of bits that are transmitted successfully per second is considered. $\square$

5 Rate coverage

The achievable rate per user is used as a performance evaluation metric, in addition to SIR and the resource allocation to each user served by the best ${\mathscr {K}}$th tier BS that has been allocated by equal resources to their users during given time slots. Each ${\mathscr {K}}$th-tier is using the same frequency resources $W_{k}$ as allocated by the relay or BS in different time slots. Hence, in the downlink, each user served by its respected ${\mathscr {K}}$th-tier BS located at $x_{k}\in \varPhi _{k}$ have been allocated ${\mathscr {O}}_{k}\le W_{k}.$ The mean achievable rate per tier is considered. Specifically, the mean rate is computed for a typical user where adaptive coding is used so each user can set their rate such that they achieve Shannon bound for their instantaneous SIR. The achievable instantaneous rate³$R_{k}$ is given by:

$$\begin{aligned} R_{k}&={\mathscr {O}}_{k}log_{2}(1+SIR(x_{k})). \end{aligned}$$

(17)

In order to model the load on each BS, modeling BSs service areas for different types is required. It is difficult to characterize ${\mathscr {O}}_{k}$ and thus derive a distribution expression for per-user rate [44, 46]. The derived coverage probability (above) will be extended to the per-user rate. It is important to observe that the footprint across the tiers varies tremendously, hence ${\mathscr {O}}_{k}$ for picocell might be higher than the macrocell. In such a scenario, its advisable for the user to connect to picocell, even-though it provides the lowest SIR across the network. Since many applications require minimum rate such as video streaming, this motivates us to introduce the rate coverage which refers to the distribution of rate CCDF.

The rate conditional CCDF for the ${\mathscr {K}}$th-tier is derived in the following Theorem.

Theorem 2

The ${\mathscr {K}}$th-tier rate coverage for user or relay is shown by

$$\begin{aligned} {\mathscr {R}}_{k}= & {} {\mathbb {P}}[R_{k}>\rho ]=\frac{2\pi \lambda _{k}}{A_{k}}\int \limits _{0}^{{\infty }} \sum \limits _{{n=0}}^{{\varDelta _{k}-1}}\frac{1}{n!}(tP_{k}^{-1}x^{\alpha _{k}})^{n}\\&\times e^{-tP_{k}^{-1}x^{\alpha _{k}}N_{k}-\sum \limits _{j=1}^{{k}}\lambda _{j}(t{\hat{P}}_{j})^{\frac{2}{\alpha _{j}}}x^{\frac{2}{{\hat{\alpha }}_{j}}}C_{j}}\underset{{\bar{m}}\in M}{\sum }C({\bar{m}}).\\&\cdot \prod \limits _{l=1}^{{n}}\left( N_{k}{\mathbb {I}}_{l=1}+2 \pi \sum \limits _{j=1}^{{K}}(-1)^{l}D_{j}(l)P_{j}^{l}(t{\hat{P}}_{j})^{\frac{2}{\alpha _{j}}-l}\frac{x^{\frac{2}{{\hat{\alpha }}}}}{x^{l\alpha _{k}}}\right) ^{m_{l}}\\&\cdot xe^{-\pi \sum _{j=1}^{K}\lambda _{j}({\hat{P}}_{j}{\hat{\triangle }}_{j}{\hat{B}}_{j})^{\frac{2}{{\hat{\alpha }}_{j}}}x^{\frac{2}{{\hat{\alpha }}_{j}}}}dx, \end{aligned}$$

where $t=2^{\rho N_{k}/(W_{k}\varPsi _{k})}-1$ and $u_{j}=1/(1+(t/{\hat{\triangle }}_{j}{\hat{B}}_{j}))$ and the number of users served by BS in ${\mathscr {K}}$-th tier $N_{k}=1+(1.28\lambda _{u}A_{k}/\lambda _{k}).$ The proof is similar to single antenna case in Singh et al.  [44], Sadr and Adve  [41] with $\varPsi _{k}=1,$ while hereon $\varPsi _{k}$ depends the multi-antenna transmission.

6 SINR characterization by using factorial moment

We wish to introduce a general framework for studying arbitrary functions of the stationary Poisson Point Process (PPP) formed by the SINR values experienced by a typical user with respect to all BSs in the downlink channel. To meet this end, this process has been completely characterized by deriving explicit, numerically tractable integral expressions for its factorial moment measures. Such framework naturally leads to expressions for the ${\mathscr {K}}$-coverage probability, including the case of random SINR threshold values considered in single-tier and multi-tier network models.

Two useful integrals are presented here for $x\ge 0,$ the first one is the multi-coverage characteristics introduced without considering the effect of fading in Keeler et al.  [24]

$$\begin{aligned} {\mathscr {I}}_{n,\alpha }(x)=\frac{2^{n}\int _{0}^{\infty }u^{2n-1}e^{-u^{2}-u^{\alpha }x\varGamma (1-2/\alpha )^{-\alpha /2}}du}{\alpha ^{n-1}({\bar{C}}(\alpha ))^{n}(n-1)!}, \end{aligned}$$

(18)

where

$$\begin{aligned} {\bar{C}}(\alpha )=\frac{2\pi }{\alpha sin(2\pi /\alpha )}=\varGamma (1-2/\alpha )\varGamma (1+2/\alpha ). \end{aligned}$$

(19)

For simplification

$$\begin{aligned} {\mathscr {I}}_{n,\alpha }(0)=\frac{2^{n-1}}{\alpha ^{n-1}({\bar{C}}(\alpha ))^{n}}. \end{aligned}$$

(20)

while the second one is integral over hyper-cube which is the generalization as shown by (21)

$$\begin{aligned}&{\mathscr {J}}_{n,\alpha }(x_{1},\ldots ,x_{n})\nonumber \\ {}&\quad =\frac{\left( 1+\sum _{j=1}^{n}x_{j}\right) }{n}\nonumber \\&\qquad \underset{[0,1]^{n-1}}{\int }\frac{\prod _{i=1}^{n-1}v_{i}^{i(2/\alpha +1)-1}(1-v_{i})^{2/\alpha }}{\prod _{i=1}^{n}(x_{i}+\eta _{i})}dv_{1}\ldots dv_{n-1}, \end{aligned}$$

(21)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \eta _{1}= v_{1}v_{2}\ldots v_{n-1}\\ \eta _{2}= (1-v_{1})v_{2}\ldots v_{n-1}\\ \eta _{3}= (1-v_{2})v_{3}\ldots v_{n-1}\\ \cdots \\ \eta _{n}= 1-v_{n-1}. \end{array}\right. \end{aligned}$$

(22)

For further simplification, refer to “Appendix B”.

6.1 ${\mathscr {K}}$-coverage probability by using factorial moment

For $Z=SINR$ with SINR level $\mathrm {T},$ the distribution of the coverage number of the user, is defined as the number of either BSs and relays that the user can connect to, namely

$$\begin{aligned} {\mathscr {N}}(T)=\underset{(Z,T)\in {\tilde{\varPsi }}}{\sum }{\mathbf {1}}[\mathrm {Z}>\mathrm{T}]. \end{aligned}$$

(23)

The probability that a relay is connecting to at least one of BSs in the network is known as the ${\mathscr {K}}$-coverage probability, as below

$$\begin{aligned} {\mathscr {P}}^{(k)}={\mathbf {P}}\{{\mathscr {N}}\ge \mathrm {k}\}. \end{aligned}$$

(24)

for a given $\mathrm {T}$, and any $n\ge 1,$ the nth symmetric sum can be given by

$$\begin{aligned} S_{n}(\mathrm {T})={\mathbb {E}}\left[ \underset{x_{1},\ldots ,x_{n}\in {\tilde{\varPsi }}}{\sum }{\mathbf {1}}(\mathrm {Z}_{\mathrm{i}})>\mathrm{T}_{\mathrm{i}} ,\;i=1,\ldots ,n\mid \varPhi \}\right] , \end{aligned}$$

(25)

where for a given $\varPhi ,$ the conditional probability is denoted by ${\mathbf {P}}\{...\mid \varPhi \}.$ Use $S_{0}(\mathrm {T})=1,$ and for a given ${\mathscr {N}}(\mathrm {T})$ BSs, the expected number of ways that the relay can choose from $\mathrm {n}$ BSs to connect with $\mathrm {SINR}>\mathrm{T}$ is denoted by $S_{n}(\mathrm {T}).$ The following Lemma is related to the famous inclusion-exclusion principle [18].

Lemma 2

when ${\mathscr {K}}\ge 1$ we obtain

$$\begin{aligned} {\mathscr {P}}^{(k)}(\mathrm {T})= & {} \sum \limits _{n=k}^{{\infty }}(-1)^{n-k}\left( \begin{array}{c} n-1\\ k-1 \end{array}\right) S_{n}(\mathrm {T}), \end{aligned}$$

(26)

$$\begin{aligned} {\mathbf {P}}\{{\mathscr {N}}(\mathrm {T})=k\}= & {} \sum \limits _{n=k}^{{\infty }}(-1)^{n-k}\left( \begin{array}{c} n\\ k \end{array}\right) S_{n}(\mathrm {T}), \end{aligned}$$

(27)

$$\begin{aligned} {\mathbb {E}}[z^{{\mathscr {N}}(\mathrm {T})}]= & {} \sum \limits _{n=k}^{{\infty }}(z-1)^{n}S_{n}(\mathrm {T}),\quad z\in [0,1], \end{aligned}$$

(28)

$$\begin{aligned} {\mathbb {E}}[{\mathscr {N}}(\mathrm {T})]= & {} S_{1}(\mathrm {T}). \end{aligned}$$

(29)

From the above equation, the right-hand side contains our quantities of interest, which will be evaluated later. Before that, in the following section we evaluate the symmetric sums $S_{n}(\mathrm {T}),$ and observes that the infinite summations in the above expressions reduce to finite sums under reasonable conditions $(S_{n}(\mathrm {T})=0$ for $\mathrm {n}$ large enough).

6.2 Multi-tier network by using factorial moment

In a HetNet, we examine the multi-tier network for ${\mathscr {K}}$-coverage probability and the SINR threshold T that depend only on the BS tier, which could be the BS or relay. For a given m tier of BSs or relays that feature independently homogeneous Poisson Point Process $\{\varPhi _{j}\}$ with densities $\{\lambda _{j}\}$ we have

$$\begin{aligned} {\tilde{\varPhi }}_{j}=\{(X_{j},(S_{X_{j}},P_{X_{j}},\tau _{j}))\}. \end{aligned}$$

(30)

The propagation effect and the BS’s power depends on the tier, and the SINR threshold is changed to non-random such that

$$\begin{aligned} {\mathbb {E}}[(P_{j}S_{j})^{2/\alpha }]<\infty ,\quad j=1,\ldots ,m. \end{aligned}$$

(31)

for $j\ne k$ , the path-loss parameters $\alpha$ and K for the network given that

$$\begin{aligned} \lambda _{j}^{*}=\lambda _{j}{\mathbb {E}}[(P_{j}S_{j})^{2/\alpha }]. \end{aligned}$$

(32)

Using the superposition theorem [26], we denote ${\tilde{\varPhi }}=\bigcup _{j=1}^{m}{\tilde{\varPhi }}_{j}$ the $m-$tier network model.

Corollary 2

for single tier network ${\tilde{\varPhi }}^{*}$with path-loss constant $K=1$ and path-loss exponent $\alpha ,$ such that $P^{*}=1,\;S^{*}=1$ and the BS/relay density $\lambda ^{*}$

$$\begin{aligned} \lambda ^{*}=\sum \limits _{j=1}^{{m}}\lambda _{j}^{*}, \end{aligned}$$

(33)

given that $T^{*}$ is distributed by

$$\begin{aligned} P(T^{*}=\tau _{j})=\frac{\lambda _{j}^{*}}{\lambda ^{*}},\qquad j=1,\ldots ,m. \end{aligned}$$

(34)

Proof

each j tier ${\tilde{\varPhi }}_{j}$ is having ${\tilde{\varPhi }}_{j}^{*}$ as an equivalent tier, setting $P_{j}=1,$ $S_{j}=1$ and density $\lambda _{j}^{*}.$ Following similar steps in Sect. 6.2, let us define

$$\begin{aligned} {\tilde{\varPhi }}_{j}^{*}=\{(X_{j}^{*},(S_{X_{j}}^{*},P_{X_{j}}^{*},\tau _{j}^{*}))\}, \end{aligned}$$

(35)

with density

$$\begin{aligned} \lambda _{j}^{*}=\lambda _{j}{\mathbb {E}}[(P_{j}S_{j})^{2/\alpha }], \end{aligned}$$

(36)

where given $\{(X_{j}^{*})\},$ the marks $\{(\tau _{j}^{*})\}$ are independent (across $X^{*}$), and with a distribution given by

$$\begin{aligned} F_{\tau ^{*}}={\mathbf {P}}(\tau ^{*}\le t)=\frac{{\mathbb {E}}\left[ (P_{j}S_{j})^{2/\alpha }{\mathbf {1}}(\tau ^{*}\le t)\right] }{{\mathbb {E}}\left[ (P_{j}S_{j})^{2/\alpha }\right] }. \end{aligned}$$

(37)

Hence, ${\tilde{\varPhi }}^{*}$ induces the marked SINR process

$$\begin{aligned} {\tilde{\varPsi }}^{*}=&\left\{ \left( Z,\tau ^{*}\right) \right\} \end{aligned}$$

which is equal in distribution to ${\tilde{\varPsi }},$ therefore the factorial moment of $\left\{ Z^{*}\right\}$ are equal to these in $\{Z\}$ with the same propagation process. If two network models induce the same marked propagation processes, then we say they are stochastically equivalent, end of the proof. $\square$

6.3 Single-tier network by using factorial moment

For a single-tier with stationary Poisson point $\varPhi =\{X\}$ and density $\lambda ,$ given a SINR threshold $\tau$, the ${\mathscr {K}}$-coverage probability is derived in Keeler et al.  [24] without fading, whereby the case ($\tau \ge 1$) is considered as a special case of Dhillon et al.  [15], (Theorem 1).

Corollary 3

for single tier network with shadowing moment condition, the condition ${\mathbb {E}}[(PS)^{2/\alpha }]<\infty$ hold, then

$$\begin{aligned} S_{n}=S_{n}(\tau )=\tau _{n}^{-2n/\alpha }{\mathscr {I}}_{n,\alpha }((\sigma /\gamma )a^{-\alpha /2}){\mathscr {J}}_{n,\alpha }(\tau _{n}), \end{aligned}$$

(38)

for $S_{n}=0$ and $0<\tau <1/(n-1),$ where a is shown in (4) and $\tau _{n}$ is given by

$$\begin{aligned} \tau _{n}=\tau _{n}(\tau )=\frac{\tau }{1-(n-1)\tau }, \end{aligned}$$

(39)

Therefore, the k-coverage probability is given by

$$\begin{aligned} {\mathscr {P}}^{(k)}= & {} {\mathscr {P}}^{(k)}(\tau )=\sum \limits _{n=k}^{{\lceil 1/\tau \rceil }}(-1)^{n-k}\left( \begin{array}{c} n-1\\ k-1 \end{array}\right) \tau _{n}^{-2n/\alpha }\nonumber \\&\times {\mathscr {I}}_{n,\alpha }((\sigma )a^{-\alpha /2}){\mathscr {J}}_{n,\alpha }(\tau _{n}), \end{aligned}$$

(40)

For $T\ge 1$ and $k=1$, the above expression reduces to special case of a single-tier network ( [15], Eq. (2)), when $\lceil 1/(\tau )\rceil =1$ and $\tau \ge 1$, the above expression simplifies to

$$\begin{aligned} {\mathscr {P}}^{(1)}(\tau )=\frac{2(\tau )^{-2/\alpha }}{\varGamma (1+\frac{2}{\alpha })} \int \limits _{0}^{{\infty }}ue^{-u^{2}\varGamma (1-2/\alpha )-\sigma a^{-\alpha /2}u^{\beta }}du. \end{aligned}$$

(41)

where the simplified integral expression (41) turns to be the CCDF of the SINR.

7 Numerical results

The simulation and the theoretical procedure for the proposed system analysis are validated in this section. On one hand, the ${\mathscr {K}}$ independent PPPs are generated with the given densities. The serving user is randomly located and the BS or relay is located at the origin, the random channels $h_{xk}$ and $g_{xk}$ with $\beta _{k}=0\,dB.$ A user is said to be in coverage if the target SIR from the BS is greater than the target. Finally, the coverage over sufficient realization of the point process is averaged to compute the coverage probability.

Note that the PPP model is sensitive to the cells that are deployed without planning, such as femtocells and dubious for planned tiers such as macrocells. Hence, to validate the three tiers locations, the macrocells are modeled by a hexagonal grid model while the other tiers are modeled as a PPP model. All multi-tier multi-antenna cases are having 4 transmission antennas per BS i.e. $M_{k}=4,$ $\varPsi _{k}=4$ for all k,  while single-tier case is having $\varPsi _{j}=\varDelta _{k}=1,$ $\forall j\in {\mathscr {K}}.$

On the other hand, the numerical results for the factorial moment are obtained according to the derived analytical result and Monte Carlo simulation as similar to Dhillon et al.  [15], Blaszczyszyn and Keeler  [8]. It is shown that in terms of propagation losses, a Poisson network with constant BS density and random pathloss are equivalent to some network with constant exponents and an isotropic density [8]. Such density increases the complexity of the factorial moment integrals, but they may remain amenable to numerical means. Multi-tier models with variable pathloss values depending on tiers have been studied in Madhusudhanan et al.  [36] and Jo et al.  [23]. In an interference-limited scenario ($\sigma =0$), we set ${\mathscr {K}}=1,$ $PS=1,$ unlike the multi-tier network where $\lambda$ and P will be specified.

To validate our analytical result, the network simulation is generated based on a circular region of radius 10 length units, and $10^{5}$ as the number of network simulation. The path-loss exponent is assumed to be $\alpha =3$ and 5. The shadowing is modeled by a log-normal distribution with expectation 1 dB and 10 dB logarithmic standard deviation. If a user is able to connect to at least one BS with SINR above its threshold, the user is declared to be in coverage. Precisely, the coverage probability is the CCDF of the effective SINR, when SINR threshold is equal across all the tiers.

For a single tier-network, the ${\mathscr {K}}$-coverage probability ${\mathscr {P}}^{(k)}(\tau )$ for ${\mathscr {K}}=1,2,3$ with $\alpha =3$ and $\alpha =5,$ as in Figs. 4 and 5, respectively. This reminds us that the kth strongest signal is related to the coverage probability by the tail distribution function of the SINR.

Fig. 4

For a single-tier network, k-coverage probability $P^{(k)}(\tau )$ for $\alpha =3$

Fig. 5

For a single-tier network, ${\mathscr {K}}$-coverage probability $P^{(k)}(\tau )$ for $\alpha =5$

Figure 6 shows the single-tier coverage probability [24] extended to a two-tier coverage probability network, which leads to SINR derivation for the HetNet, where each tier has the same SINR threshold. Clearly, the single-tier coverage probability is much smaller than the two-tier coverage probability, mainly when the single-tier and two-tier networks are located nearby high power BSs. These results are performance equivalent.

Fig. 6

For two-tier network, the 1-coverage probability ${\mathscr {P}}^{(1)}$ as function of $\tau _{1}$ with $P_{1}=100P_{2},$ $\tau _{2}=1dB$, $\lambda _{u}=\lambda _{k}/2$ for $\alpha =3$ compared to a single-tier network

Figure 7 shows that increasing $\tau ,$ decreases the ${\mathscr {K}}$-coverage probability. It compares the random PPP model to the traditional grid model constituted by a Voronoi tessellation (see Fig. 1). Tier-1 is distributed according to our PPP model, while tier-2 according to grid model. The grid model provides high coverage area across the whole SINR (upper bound). This is because the interference is dominant for the PPP model (lower bound). Since dense cellular networks are interference-limited due to the effect of noise, a gap has been observed when considering the $SNR=10$ and $SNR\rightarrow \infty .$ This validates the assumption that the noise can be ignored in interference-limited scenario.

Fig. 7

$k-$ coverage probability comparison between grid model and our proposed PPP tier model with $\alpha =4$

Figure 8 shows the rate coverage of the proposed model (multi-tier case) versus the grid tier model. All tier locations are drawn from an independent PPP with N interfering tiers. At the lower SIR thresholds, the effect of the interference is not severe, the grid model performs the best, while at higher SIR thresholds, the proposed model is superior due to inter-tier interference cancellation. A similar set for such a network can be found in Dhillon et al.  [15].

Fig. 8

Rate coverage versus target SIR for the proposed model against traditional grid model

Figure 9 compares between K-tiers and single-tier and grid model coverage probabilities with $\alpha =4,$ in interference-limited ${\mathscr {K}}$-tiers network. The K-tiers and single-tier are formed with densities $\lambda _{u}=300,$ and $\lambda _{k}=150,$ respectively. We show that the proposed ${\mathscr {K}}$-tier model provides a lower bound on the coverage probability due to the interference from nearby tiers and is as accurate as the traditional grid model, which provides an upper bound. From the coverage point of view, the grid model is optimal since it perfectly models the BSs as a regular geometry. Further, we observe that there is a gap between the K-tiers and single-tier, this is intuitive because the BSs transmission is enhanced due to the beamforming gain from the multi-antenna deployments, while the BSs single antenna transmission provides no gain.

From a viewpoint of system designers, the ${\mathscr {K}}$-tiers and single-tier coverage regions have an important effect on the cellular network, which differ from the wireless LANs in terms of lower coverage area, less transmission power and interference. When the BS is able to decode the downlink signal but unable to simultaneously connect to the other tier this impacts the handoff algorithm between the BSs. Hence it is important to investigate the tradeoff between ${\mathscr {K}}$-tiers and single-tier in terms of average rate and coverage enhancements.

Fig. 9

Coverage probability K-tier, single-tier and grid model with $\alpha =4,$ $\lambda =[150,\ 300],$ $P_{1}=5$ and $P_{2}=50$

Figure 10 plots the coverage probability of the four antennas BS tiers against the density $\lambda$ and compares it with the multi-antenna UDN (Ultra-dense Network) model (tier-1) [4, 42, 48] and the traditional grid model (tier-1). A total of three tiers are modeled with the first two tiers (${\mathscr {K}}$-tier MIMO and multi-antenna UDN) modeled according to PPP. We notice that tier-1 PPP model is as accurate as the traditional grid model in that it provides upper bound with a gap less than 1 dB from the ${\mathscr {K}}$-tier MIMO and the UDN model provides lower bound with a gap less than1.5 dB from the grid model. This is due to multi-antenna usage by the ${\mathscr {K}}$-tier MIMO to exploit the MIMO capability in boosting the signal. The ${\mathscr {K}}$-tier MIMO performs slightly better than the Multi-Antenna UDN model, whereas the grid model is best suited for higher densities.

Fig. 10

Coverage probability of the proposed model versus the density $\lambda$ with targeted SINR $\beta =0$ dB, for different models

8 Conclusion

As the use of random spatial models to investigate various aspects of HetNet have been experienced in the past few years, it is strongly observed that most of these works focus on multi-tier or single-tier network. This paper presented a comprehensive analysis of the HetNet, in which a tractable model to analyze the ${\mathscr {K}}$-tier HetNet in terms of coverage probability and rate coverage achieved by a typical user is first developed. Second, the coverage probability is evaluated by using factorial moment measures of the point process formed by the SINR values perceived by the user, where each tier differs in terms of number of antenna, target Signal-to-Interference Ratio (SIR), transmitted power, and deployment density. To account for the fact that some transmission techniques provide higher coverage, we derive a ${\mathscr {K}}$-tier and single-tier transmission; by assuming that the BSs are located independently, and to validate its accuracy with the traditional grid model, an extensive comparison with the traditional grid model via numerical simulations was carried out. Due to the additional beamforming gain, the single-tier achieves higher coverage than ${\mathscr {K}}$-tier MIMO. We also showed that the multi-antenna have an effect on reducing the interference from other tiers compared to single-antenna case for an open access scenario.

Appendices

Appendix A

From the coverage probability for K-tier definition:

$$\begin{aligned}&\mathrm {P}_{\mathrm{c}} = {\mathbb {E}}\left[ {\mathbf {1}}\left( \underset{k\in {\mathscr {K}}}{\bigcup }\underset{x_{k}\in \varPhi _{k}}{\bigcup } \mathrm {SIR}(x_{k})>\beta _{k}\right) \right] \nonumber \\&\quad \overset{}{=} {\mathbb {E}}\left[ \left( \underset{\mathrm {k}\in {\mathscr {K}}}{\sum }\underset{\mathrm{x}_{\mathrm{k}} \in \varPhi _{\mathrm{k}}}{\sum }{\mathbf {1}}\left( \mathrm {SIR}(\mathrm{x}_{\mathrm{k}})> \beta _{\mathrm{k}}\right) \right) \right] \end{aligned}$$

(42)

where (42) is drawn from the union bound and following Campbell Mecke Theorem [11] we obtain

$$\begin{aligned} =\underset{k\in {\mathscr {K}}}{\sum }\lambda \int _{{\mathbb {R}}^{2}}{\mathbb {E}}\left[ \mathbf {{\mathbb {P}}}\left( P_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }>\beta _{k}I_{x_{k}}\right) \right] dx, \end{aligned}$$

(43)

Since the channels gain are following Rayleigh distribution that leads to

$$\begin{aligned} =\underset{k\in {\mathscr {K}}}{\sum }\lambda _{k}\int _{{\mathbb {R}}^{2}} {\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}} \left( \frac{\beta _{k}}{P_{k}h_{kx_{k}}}\right) e^{\frac{\beta _{k}\sigma ^{2}}{P_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }}}dx_{k}, \end{aligned}$$

(44)

where ${\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}}(.)$ is the Laplace transform of the interference from the kth tiers. Since all tires are independent

$$\begin{aligned} {\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}}(s)= & {} {\mathbb {E}}_{I}\left[ e^{-sP_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }}\right] \end{aligned}$$

(45)

$$\begin{aligned}= & {} \underset{k\in {\mathscr {K}}}{\prod }{\mathbb {E}}\left[ \underset{x_{k}\in \varPhi _{k}}{\prod }e^{-sP_{k}h_{kx_{k}}\parallel x_{k}\parallel ^{-\alpha }}\right] \end{aligned}$$

(46)

Note also that there is independency between channel powers and BSs locations and following Rayleigh assumption for the channel

$$\begin{aligned} =\underset{k\in {\mathscr {K}}}{\prod }{\mathbb {E}}_{\varPhi _{k}}\left[ \underset{\mathrm {x}_{\mathrm{k}}\in \varPhi _{k}}{\prod } {\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}}\left( P_{k}\parallel x_{k}\parallel ^{-\alpha }\right) \right] \end{aligned}$$

(47)

Using the PGFL of PPP in Chiu et al.  [11], we get

$$\begin{aligned}= & {} \underset{k\in {\mathscr {K}}}{\prod }\mathrm {exp}\left( -\lambda _{k}\int _{{\mathbb {R}}^{2}} \left( 1-{\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}}\left( P_{k}\parallel x_{k}\parallel ^{-\alpha }\right) \right) dx\right) \nonumber \\\end{aligned}$$

(48)

$$\begin{aligned}= & {} \underset{k\in {\mathscr {K}}}{\prod }\mathrm {exp}\left( -\lambda _{k}\int _{{\mathbb {R}}^{2}}\left( 1-\frac{1}{\left( 1+sP_{k}\parallel x\parallel ^{-\alpha }\right) }\right) dx_{k}\right) \nonumber \\ \end{aligned}$$

(49)

Applying Euler’s Beta function $B(x,y)=\int \limits _{0}^{{1}}t^{x-1}(1-t)^{y-1}dt$ to convert the integral and approximates $(1+r^{-\alpha })^{-1}\rightarrow t,$ converting the Cartesian into polar coordinates

$$\begin{aligned} {\mathscr {L}}_{{\mathscr {I}}_{\mathrm {x}_{\mathrm{k}}}}(s)=\mathrm {exp}\left( -s_{x_{k}}^{\frac{2}{\alpha }}\underset{k\in {\mathscr {K}}}{\sum }\lambda _{k}P_{k}^{\frac{2}{\alpha }}C\left( \alpha \right) \right) , \end{aligned}$$

(50)

where $C(\alpha )=\frac{2\pi CSC(\frac{2\pi }{\alpha })}{\alpha }.$ Using (44) and (50) we can derive the coverage probability as follows

$$\begin{aligned} \mathrm {P}_{\mathrm{c}}=&\sum \limits _{\mathrm{k}\in {\mathscr {K}}}{\lambda }_{\mathrm{k}} \int _{{\mathbb {R}}^{2}}\mathrm{exp}\left( -\mathrm{C}(\alpha )\left( \frac{\beta _{\mathrm{k}}}{\textit{P}}_{\mathrm{k}}\right) ^{2/\alpha }\parallel {{\textit{x}}_{k}}\parallel ^{2} \sum \limits _{\mathrm{m}=1}^{{\mathrm{K}}}{\lambda }_{\mathrm{m}}{} \textit{P}_{\mathrm{m}}^{2/\alpha }\right) \nonumber \\&\mathrm{exp}\left( -\frac{\beta _{\mathrm{k}}\sigma ^{2}}{{\textit{P}}_{\mathrm{k}}}\parallel {{\textit{x}}_{k}}\parallel ^{2}\right) \mathrm{dx}_{\mathrm{k}}. \end{aligned}$$

(51)

Appendix B

Simplification on the integral ${\displaystyle {\mathscr {J}}_{n,\alpha }}$

We further simplify the integral ${\mathscr {J}}_{n,\alpha }(x_{1},\ldots ,x_{n})$ as shown in (52). Using $n=1$ the integral reduced to ${\mathscr {J}}_{1,\alpha }(x_{1})=1$ and using $n=2$ reduces the integral to (53). Further simplification leads to closed-form solution in (54),

$$\begin{aligned}&{\mathscr {J}}_{n,\alpha }(x_{1},\ldots ,x_{n}) \nonumber \\&\quad = \frac{1}{n} \sum \limits _{j=1}^{{n}}\underset{[0,1]^{n-1}}{\int }\frac{\prod _{i=1}^{n-1}v_{i}^{i(2/\alpha +1)-1}(1-v_{i})^{2/\alpha }}{\prod _{i=1}^{n}(x_{i}+\eta _{i})}dv_{1}\ldots dv_{n-1}, \end{aligned}$$

(52)

$$\begin{aligned}&{\mathscr {J}}_{2,\alpha }(x_{1},x_{2}) \nonumber \\&\quad = \frac{1}{2} \int \limits _{0}^{{1}}v_{1}^{2/\alpha }(1-v_{1})^{2/\alpha }\left[ \frac{1}{(x_{1}+v_{1})}+\frac{1}{(x_{2}+1-v_{2})}\right] dv_{1}. \end{aligned}$$

(53)

$$\begin{aligned}&\int \limits _{0}^{{1}}\frac{v^{2/\alpha }(1-v)^{2/\alpha }}{x+v}dv \nonumber \\&\quad = \frac{1}{x}B(2/\alpha +1,2/\alpha +1)2^{F_{1}}(1,2/\alpha +1;2(2/\alpha +1);-1/x), \end{aligned}$$

(54)

where $2^{F_{1}}$ is the hyper-geometric function ( [38], Eq. 15.6.1).