Decode-to-cooperate: a sequential alamouti-coded cooperation strategy in dual-hop wireless relay networks

Abstract

An optimal cooperation strategy, decode-to-cooperate, is proposed and investigated for performance improvements in dual-hop wireless relay networks. Based on decode-and-forward (DF) strategy with multiple relay selection, we design a novel scheme such that the source node keeps transmitting sequentially and the selected relays cooperate by transmitting the decoded signal using distributed Alamouti coding. We exploit the multipath propagation effect of the wireless channel to achieve lower probability of error and introduce optimum power allocation and relay positioning. We analyze the scenario when the source to destination direct link is not available and derive a closed form expression for symbol error rate (SER), its upper bound and an asymptotically tight approximation to exploit the performance gain by selecting the optimum relays in a multiple-relay cooperation scheme. Moreover, asymptotic optimum power allocation (based on the SER approximation) and optimal relay positioning are also considered to further improve the SER. The proposed relay selection scheme outperforms cooperative (DF) and non-cooperative schemes by more than 2 dB.

1 Introduction

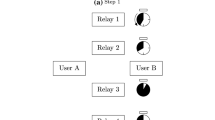
Global increase in multimedia traffic is saturating existing wireless channel capacity, moreover, considering the’ practical limitation in hardware design of hand-held wireless access devices, alludes at exploiting one of the fundamental characteristics of wireless communication i.e., multipath propagation. In order to enhance the performance in single antenna terminal based wireless communication system, i.e., single-input single-output (SISO), a concatenated single-input multiple-output (SIMO) multiple-input single-output (MISO) system could be realized as a virtual antenna array in order to take advantage of the multipath propagation as shown in Fig. 1.

Employing this realization of cooperating terminals is essentially taking advantage of the aforementioned SIMO and MISO systems to gain performance improvements. Cooperative relaying is a useful design to mitigate the effect of wireless fading and exploiting multipath propagation, and as a result achieving optimal performance in dual-hop communication [1]. The aim of this research is to study the affect of multipath propagation in wireless communication by using the basis of transmit diversity [2] to extend our previous work [3]. Considering the aforementioned concatenated SIMO-MISO concept, the selected relay nodes can be used to form a distributed virtual antenna array to serve the users cooperatively.

In [4], the authors proposed exact outage and capacity performance expressions for relay selection and study the diversity achieved based on relay selection. A coalition strength based game theoretic approach is considered for relay selection leading to some useful insights on selection criteria in a multi-relay environment [5]. Performance of the DF strategy with best-relay is investigated [6], where the selected relay is the one with the highest signal-to-noise (SNR). Recently, a study on error probability of DF strategy for a cooperative single relay network was carried out [7], to propose a relay selection scheme with optimized power allocation. In order to generalize the concept of relay selection, diversity analysis of single and multiple relay selection schemes was investigated [8] and based on the simulation results, the performance of multiple relay selection methods was superior than the corresponding single relay selection methods. Multiple antennas based DF relaying is considered [9], to investigate the diversity gain by employing multiple antennas. Performance analysis of single and multiple relay selection indicated marginal gain by selecting more than three relays for the cooperative communication model [10]. Space-time block coded (STBC) cooperative diversity offers larger diversity order than repetition-based algorithms and can be effectively utilized for higher spectral efficiency [11]. Distributed Alamouti code promises higher diversity order and lower error probability and could be employed as a virtual antenna scheme to achieve similar diversity orders and error probability [12].

Effect of network geometry by forming cooperating group of terminals as a result of relay selection, can also lead to substantial performance improvement [13]. Performance based on network geometry can be enhanced by considering power allocation in cooperative communication [7, 14]. Dual hop communication is usually considered in wireless environments where direct source to destination transmission is not possible e.g., IEEE 802.11a despite having higher data rates is prone to multipath fading and only offers one third of the coverage area as compared to IEEE 802.11b. Furthermore, global increase in the number of wireless access users, increases the probability of having more than a single relay available for cooperative communication. Considering this fact and using the concept of cooperative diversity, significant outcomes can be achieved by exploiting the performance of virtual transmit and receive antenna array model through efficient multiple relay selection in a time varying environment.

Fig. 1

Virtual antenna array in SIMO-MISO wireless relay network

Contributions We have proposed,

• An efficient cooperative protocol for dual-hop networks with sequential transmission (from the source) and studied its performance.

• An optimal power allocation and relay positioning strategy for the proposed protocol, such that the performance can be further enhanced.

Organization of the paper In Sect. 2, we present the rationale behind the cooperative strategy and the system model used for the proposed relay selection algorithm. Performance analysis in terms of SER approximation, optimum power allocation and optimal relay position is carried out in Sects. 3, 4, and 5, respectively. Finally, in Sect. 6, we discuss the simulation results and conclude with a brief summary of our work in Sect. 7.

Fig. 2

Cooperative communication using multiple-relays for distributed Alamouti scheme

2 System model

This work extends our previous model [3], by considering Alamouti-coded DF strategy with multiple relay selection as a baseline. Now, we introduce a source $s$ transmitting symbols sequentially, and in the absence of direct source-to-destination link, the destination $d$ seeks help from the nearby relay nodes $r$. In turn, relays that have successfully decoded the information symbols, show willingness to cooperate and going through the process of selection, transmit the information bearing symbols to the destination in a distributed Alamouti fashion, as shown in Fig. 2. We assume a coherent cooperative system where source-to-relay channel state information (CSI) is available at the relays, whereas, destination calculates the relay-to-destination CSI for the selected relays. Considering the absence of the direct link from source to destination, we are still able to achieve full diversity gain using the proposed DC strategy for multiple relay selection and taking into consideration the added advantage of the enhanced SNR for the relay-to-destination link. We employ a time-division multiple access (TDMA) based signal transmission, and consider QPSK modulation.

2.1 Decode-to-cooperate (DC)

The relay selection process is inspired by the original DF strategy [13] with added design considerations. It is based on a minimal handshake between relays and destination. As a result of this, we not only ensure an improved diversity order [3], but also strive towards efficient power consumption and optimal relay positioning. Additionally, this scheme also provide incentive to the participating yet not selected relays by allowing them to conserve energy as only the selected relays transmit the decoded symbols to the destination. The work flow of the proposed DC scheme at the destination node is described in Algorithm 1.

The exchange of control based information for relay selection involves the control channel at the medium access control layer, when the relays receive a negative-acknowledgment (NACK) from the destination, they send a relay ID and the received SNR from the source, indicating that they have decoded the message from the source and are willing to cooperate. The destination accounts for the received SNR from the relays, in addition to the received information form the relay and broadcast the indices of the selected relays. Relays are selected based on the SNR gains at the relays (i.e., source-to-relay link) and the destination (i.e., relay-to-destination links). It is assumed that time incurred for the relay selection process is negligible as compared to the actual data transmission time considering it as preamble time. The selected relays cooperate by transmitting the decoded information are the ones with the maximum SNR gains at the destination (for the source-relay-destination link).

2.2 Cooperative communication based on distributed Alamouti scheme

Let  $h_{m}$ and $g_{m}$ denote quasi-static Rayleigh fading channels from  $s \rightarrow r _{m}$ and $r _{m} \rightarrow d$, respectively. The source $s$ transmits two information bearing symbols $x_k$ in k time slots (where k is even and channel remains constant during this time), then a pair of symbols received at the relays $r _{am}$ and $r _{bm}$ each having their own channel coefficients $h _{am}$ and $h _{bm}$ receive,

$$\begin{aligned} \begin{aligned} \left. \begin{aligned} Z_{(k-1)am}&=x_{k-1}h_{am}\sqrt{P_1}+n_{(k-1)am} \\ Z_{(k)am}&=x_{k}h_{am}\sqrt{P_1}+n_{(k)am} \quad \\ \end{aligned} \right\} Relay~a\\ \left. \begin{aligned} Z_{(k-1)bm}&=x_{k-1}h_{bm}\sqrt{P_1}+n_{(k-1)bm} \\ Z_{(k)bm}&=x_{k}h_{bm}\sqrt{P_1}+n_{(k)bm} \quad \\ \end{aligned} \right\} Relay~b\\ \end{aligned} \end{aligned}$$

(1)

respectively. Where we have, $\forall ~k~\in ~$ $n_{(k)am} \sim \mathcal {N}(0,\sigma ^2)$ and $n_{(k)bm} \sim \mathcal {N}(0,\sigma ^2)$, as normally distributed additive white Gaussian noise with zero mean and variance $\sigma ^2$. $P_1$ refers to the transmission power at the source. The channel between source to $m\text {-th}$ relay $h_m$ is zero-mean independent, circularly symmetric complex Gaussian random variables with variance $\delta _{sm}^2$.

Fig. 3

Illusrating sequential transmission from source, and the received and transmitted symbols at the relays

In the absence of the direct source destination link (i.e., $\delta _{sd}^2=0$), the destination selects two relays and receive information during the next two time slots using a transmit diversity approach [2], which is highlighted in Fig. 3. So, if the destination selects $r _{am}$, $r _{bm}$ as the best relays (Fig. 2), then the received signal at the destination using distributed Alamouti STBC would be,

$$\begin{aligned} \left. \begin{aligned} Y_{(k-1)}=z_{(k-1)am}g_{am}\sqrt{P_2}+z_{(k)bm}g_{bm}\sqrt{P_2}+n_{(k-1)md} \\ Y_{(k)}=-z_{(k)am}^*g_{am}\sqrt{P_2}+ z_{(k-1)bm}^*g_{bm}\sqrt{P_2}+n_{(k)md} \\ \end{aligned} \right\} \end{aligned}$$

(2)

where we have, $\forall ~k~\in ~n_{(k)md}\sim \mathcal {N}(0,\sigma ^2)$ is normally distributed additive white Gaussian noise with zero mean and variance $\sigma ^2$, from the selected relays to destination. $P_2$ refers to the transmission power at the individual relay. The channel between $m\text {-th}$ relay to destination $g_m$ is also zero-mean independent, circularly symmetric complex Gaussian random variables with variance $\delta _{md}^2$. Finally, the destination combines the information bearing symbols as,

$$\begin{aligned} \begin{aligned} \left. \begin{aligned} y_{(k-1)}&= \frac{Y_{(k-1)} g_{am}^*+ Y_{(k)}^* g_{bm}}{|g_{am} |^2+|g_{bm} |^2} \quad \\ y_{(k)}&= \frac{Y_{(k-1)} g_{bm}^*- Y_{(k)}^* g_{am}}{|g_{am} |^2+|g_{bm} |^2} \end{aligned} \right\} \end{aligned} \end{aligned}$$

(3)

These symbols are then decoded using a maximum likelihood (ML) decision rule [2]. We are considering sequentially transmitting source and relay nodes, as illustrated in Fig. 3 and highlighted the decoded symbols only at the selected relays (and not all of the M relays) to avoid complexity. Furthermore, the relays use interference cancellation [15–17] between them to decode the information symbols from source (Fig. 3 gray shaded regions). The selected relays flush the accumulated interference after transmitting the decoded symbols, where as for the relays that were not selected for cooperation, try to decode the next transmission symbols from the source and the previously decoded symbols from the selected relays simultaneously. These relays then, decode the interference and subtract it from the previously decoded symbols to obtain the desired symbols [15], if $\delta _{m_{a1}m_{a2}}^2 \gg \delta _{sm_{a2}}^2$ (i.e., the channel gain between the transmitting and listening relay link is greater as compared to source and listening relay link) or discards the transmission from transmitting relay as noise if $\delta _{m_{a1}m_{a2}}^2 \ll \delta _{sm_{a2}}^2$, before eventually flushing the accumulated interference and start fresh when the source transmits the next symbols sequentially.

3 Probability of error analysis

In this section, we consider symbol error rate (SER) to analyze the error probability performance of the proposed DC strategy. We derive an upper bound and an asymptotic approximation on the error probability for the proposed system with the M-PSK modulation. When M-PSK modulation is used in the system, with instantaneous SNR ($\rho$) and channel coefficients $h_{m}$ and $g_m$, the conditional SER can be given as [18],

$$\begin{aligned}&\mathcal {P}_c^{h_m g_m}= \varPsi (\rho )\nonumber \\&\varPsi _{\rho } \triangleq \int _0^{(\text {M}-1)\pi /\text {M}} exp\left( -\frac{b_{PSK}\rho }{\sin ^2\theta } \right) d\theta \end{aligned}$$

(4)

where $b_{PSK} = \sin ^2(\pi /\text {M})$ and $\text {M}= 2^k$ with k even. The source sends M-PSK symbols, then at the relay, the chance of erroneous decoding is $\varPsi (P_1|h_m|^2/\sigma ^2)$, and the chance of correct decoding is $1 - \varPsi (P_1|h_m|^2/\sigma ^2)$. The channel variances of $h_m$ and $g_m$ are defined by $\delta _{sm}^2$ and $\delta _{md}^2$, respectively. The conditional SER in terms of $h_m$ and $g_m$ could be expressed as,

$$\begin{aligned} \mathcal {P}_{c}^{h_m g_m}= \int _0^{(\text {M}-1)\pi /\text {M}} exp\left( -\frac{b_{PSK}(P_1|h_m|^2 + P_2|g_m|^2)}{\sigma ^2\sin ^2\theta } \right) d\theta \end{aligned}$$

(5)

Given $|h_m|^2$ and $|g_m|^2$ having an independent Rayleigh distribution with $E[|h_m|^2] = \delta _{sm}^2$ and $E[|g_m|^2] = \delta _{md}^2$ respectively, and considering a dual hop communication system where the channel link between the source and destination is not available i.e., $\delta _{sd}^2 = 0$, averaging over the Rayleigh fading channel, the closed form SER [18] of the system can be given as,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{cf}^{w} = F&\left( 1 + \frac{b_{PSK}P_1\delta _{sr_{a}}^2}{\sigma ^2\sin ^2\theta }\right) F \left( 1 + \frac{b_{PSK}P_1\delta _{sr_{b}}^2}{\sigma ^2\sin ^2\theta }\right) \\&+ F \left( 1 + \frac{b_{PSK}P_2\delta _{r_{a}d}^2}{\sigma ^2\sin ^2\theta }\right) \left[ 1 - F \left( 1 + \frac{b_{PSK}P_1\delta _{sr_{a}}^2}{\sigma ^2\sin ^2\theta }\right) \right] \\&\times F \left( 1 + \frac{b_{PSK}P_2\delta _{r_{b}d}^2}{\sigma ^2\sin ^2\theta }\right) \left[ 1 - F \left( 1 + \frac{b_{PSK}P_1\delta _{sr_{b}}^2}{\sigma ^2\sin ^2\theta }\right) \right] \end{aligned} \end{aligned}$$

(6)

where

$$\begin{aligned} F = \frac{1}{\pi }\int _0^{(\text {M}-1)\pi /\text {M}} \frac{1}{x(\theta )} d\theta \end{aligned}$$

(7)

3.1 SER upper bound and asymptotic approximation

The closed form SER in (6) can be numerically evaluated (as it involves a definite integral) but due to its complex nature, we introduce SER upper bound and SER approximation to evaluate the asymptotic performance of the underlined system. So, by removing the negative term in (6) and introducing w,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{ub}^{w} \le F&\left( 1 + \frac{b_{PSK}wP_1\delta _{sr_{a}}^2}{\sigma ^2\sin ^2\theta }\right) \times F \left( 1 + \frac{b_{PSK}wP_1\delta _{sr_{b}}^2}{\sigma ^2\sin ^2\theta }\right) \\&+ F \left( 1 + \frac{b_{PSK}wP_2\delta _{r_{a}d}^2}{\sigma ^2\sin ^2\theta }\right) \times F \left( 1 + \frac{b_{PSK}wP_2\delta _{r_{b}d}^2}{\sigma ^2\sin ^2\theta }\right) \end{aligned} \end{aligned}$$

(8)

where, w is a weight factor depending on the min. max. ratio of the instantaneous SNR ($\rho$) values,

$$\begin{aligned} w = \frac{min(\rho _{sm},\rho _{md})}{max(\rho _{sm},\rho _{md})} \end{aligned}$$

(9)

It is worth mentioning that the quality of the decoded symbols depend on both the source-to-relay and relay-to-destination links, which resulted in the introduction to a weighted approach towards the upper bounded error probability. This weighted approach allows us to study the impact of network geometry on the probability of error and suggest an upper bound on the error probability based on the most stringent requirements. The integrands in the inequality (8) have a maximum value at $\sin ^2(\theta )=1$. Therefore, substituting $\sin ^2(\theta )=1$, we have,

$$\begin{aligned} \mathcal {P}_{ub}^{w}\le & {} \frac{(\text {M}-1)^2{\sigma ^2}^2}{\text {M}^2} \nonumber \\&\times \, \left( \frac{(\sigma ^2+wB_a)(\sigma ^2+wB_b)+ (\sigma ^2+wA_a)(\sigma ^2+wA_b)}{(\sigma ^2+wA_a)(\sigma ^2+wA_b)(\sigma ^2+wB_a)(\sigma ^2+wB_b)}\right) \nonumber \\ \end{aligned}$$

(10)

where $A_a=b_{PSK}P_1\delta _{sr_{a}}^2$, $A_b=b_{PSK}P_1\delta _{sr_{b}}^2$, $B_a=b_{PSK}P_2\delta _{r_{a}d}^2$ and $B_b=b_{PSK}P_2\delta _{r_{b}d}^2$. We derive the probability density function of w (See Appendix), to represent the SER upper bound,

$$\begin{aligned} \mathcal {P}_{ub} \le \int _0^\infty \left( \mathcal {P}_{ub}^w \right) f(w)dw \end{aligned}$$

(11)

So, the upper bound on the SER for the proposed system can be expressed as follow,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{ub} \le&\frac{(\text {M}-1)^2{\sigma ^2}^2}{\text {M}^2}\\&\times \,\left( \frac{(\sigma ^2+B_a)(\sigma ^2+B_b)+ (\sigma ^2+A_a)(\sigma ^2+A_b)}{(\sigma ^2+A_a)(\sigma ^2+A_b)(\sigma ^2+B_a)(\sigma ^2+B_b)}\right) \\&\times \, \frac{\delta _{r_{a}d}^2\delta _{r_{b}d}^2}{\delta _{sr_{a}}^2\delta _{sr_{b}}^2 + \delta _{r_{a}d}^2\delta _{r_{b}d}^2} \end{aligned} \end{aligned}$$

(12)

It could be observed that the upperbound on the error probability depends on the channel quality for source-to-relay and relay-to-destination links. We now compute an asymptotically tight SER approximation if the channel links $h_{m}$ and $g_{m}$ are available, i.e., $\delta _{sr_{a}}^2\ne 0,\delta _{sr_{b}}^2\ne 0,\delta _{r_{a}d}^2\ne 0,\delta _{r_{b}d}^2\ne 0$. According to (6), let us denote the SER as,

$$\begin{aligned} \mathcal {P}_a = I_1\left( \frac{P_1}{\sigma ^2}\right) + I_2\left( \frac{P_2}{\sigma ^2}\right) \end{aligned}$$

(13)

where,

$$\begin{aligned} I_1(x)= F \left( 1 + \frac{xb_{PSK}\delta _{sr_{a}}^2}{\sin ^2\theta }\right) F \left( 1 + \frac{xb_{PSK}\delta _{sr_{b}}^2}{\sin ^2\theta }\right) \end{aligned}$$

(14)

and,

$$\begin{aligned} \begin{aligned} I_2(y) = F&\left( 1 + \frac{yb_{PSK}\delta _{r_{a}d}^2}{\sin ^2\theta }\right) \left[ 1 - F \left( 1 + \frac{xb_{PSK}\delta _{sr_{a}}^2}{\sin ^2\theta }\right) \right] \\&\times F \left( 1 + \frac{yb_{PSK}\delta _{r_{b}d}^2}{\sin ^2\theta }\right) \left[ 1 - F \left( 1 + \frac{xb_{PSK}\delta _{sr_{b}}^2}{\sin ^2\theta }\right) \right] \end{aligned} \end{aligned}$$

(15)

then we have the following results,

$$\begin{aligned} \begin{aligned} \lim _{x\rightarrow \infty } x^2~I_1(x)= \frac{C^2}{b^2_{PSK}\delta _{sr_{a}}^2\delta _{sr_{b}}^2} \\ \lim _{y\rightarrow \infty } y^2~I_2(y)= \frac{C^2}{b^2_{PSK}\delta _{r_{a}d}^2\delta _{r_{b}d}^2} \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} C = \frac{1}{\pi }\int _0^{(\text {M}-1)\pi /\text {M}} {\sin ^2(\theta )} d\theta = \frac{\text {M}-1}{2\text {M}}+ \frac{\sin \frac{2\pi }{\text {M}}}{4\pi } \end{aligned}$$

Therefore, at higher values of x and y, we have the following asymptotically tight approximations,

$$\begin{aligned} I_1(x^2)\approx \frac{1}{x^2}\cdot \frac{C^2}{b^2_{PSK}\delta _{sr_{a}}^2\delta _{sr_{b}}^2}~,~ I_2(y^2)\approx \frac{1}{y^2}\cdot \frac{C^2}{b^2_{PSK}\delta _{r_{a}d}^2\delta _{r_{b}d}^2} \end{aligned}$$

when x and y tend to infinity, the approximated errors are insignificant as compared to the orders of x and y. Replacing x and y with $P_1/\sigma ^2$ and $P_2/\sigma ^2$ respectively and substituting the results in (13), the SER in (6) can be tightly approximated as,

$$\begin{aligned} \mathcal {P}_a \approx \frac{C^2\sigma ^2}{b_{PSK}^2}\left( \frac{1}{P_1^2\delta _{sr_{a}}^2\delta _{sr_{b}}^2} + \frac{1}{P_2^2\delta _{r_{a}d}^2\delta _{r_{b}d}^2}\right) \end{aligned}$$

(16)

4 Optimum power allocation

In order for the cooperation strategy to achieve the desired performance (in terms of probability of error), power should be adequately balanced. In this section, we determine an asymptotic optimum power allocation for the DC cooperation strategy based on the asymptotically tight SER approximation in (16). Specifically, we determine an optimum transmitted power $P_1$ that should be used at the source and $P_2$ at the relay. As the SER approximation in (16) is asymptotically tight at high SNR, it is sufficient to minimize the following term $G(P_1, P_2)$ with the fixed total power constraint, $P_1 + P_2 = P$ in order to optimize the asymptotic SER performance for a single source-relay-destination link,

$$\begin{aligned} G(P_1, P_2) = \left( \frac{1}{P_1\delta _{sm}^2} + \frac{1}{P_2\delta _{md}^2}\right) \end{aligned}$$

(17)

taking derivative of (17) with respect to $P_1$ and setting the resultant expression as 0, we can solve for $P_1$ and $P_2$ from the total power constraint as [18],

$$\begin{aligned} P_1= & {} \frac{ \delta _{md}}{ \delta _{md}+ \delta _{sm}} P \end{aligned}$$

(18)

$$\begin{aligned} P_2= & {} \frac{ \delta _{sm}}{ \delta _{md}+ \delta _{sm}} P \end{aligned}$$

(19)

Here, we consider three scenarios based on network geometry for optimum power distribution in (18) and (19) to comply with fixed total power constraint,

• $\delta _{sm} \gg \delta _{md}$, the source can transmit with less power as the relay is more closer to it but the relay uses most of the power to achieve a desirable SER at the destination.

• $\delta _{sm} \approx \delta _{md}$, the relay is aligned approximately equi-distance from the source and the destination and hence, equal power should be employed at the source and the relay to achieve the desired SER at the destination.

• $\delta _{sm} \ll \delta _{md}$, as the relay is closer to the destination and the confidence in the source-to-relay link is reduced, therefore, most of the power should be employed at the source to achieve a desirable SER at the destination.

5 Optimal relay position

To determine the optimal relay position, we consider the distance between the selected relays and their respective distance from the source and destination. In order to achieve an acceptable SER bound, we tend to bring the selected relays in close proximity within the coverage area of the source, such that the destination lies within the mutual coverage area of the relays. For this, we consider a wireless system with probability density function of the distance l for any uniformly distributed node w.r.t. a central node whose coverage area is defined by a circular cell radius $c_r$ consisting of q sectors as in Fig. 4,

$$\begin{aligned} f(l)=\frac{2l}{c_r^2},~s.t.~0 \le l \le c_r \end{aligned}$$

(20)

Based on the distance between two nodes, where source is at centre and the relays and destination are placed at distance $l_{sm}$ and $l_{md}$, respectively. The information bearing symbols received at the relay and the destination in general,

$$\begin{aligned} \begin{aligned}&Z_{sm} =x_{sm} h_{sm} \sqrt{P_1 l_{sm}^{-\alpha } }+n_{sm} ~(at~Relay)\\&Y_{md} =z_{md}g_{md}\sqrt{P_2 l_{md}^{-\alpha }}+n_{md} ~(at~Destination) \end{aligned} \end{aligned}$$

(21)

where $\alpha$ is the path loss exponent. Furthermore, restricting our discussion to dual-hop wireless networks, we observe the outage probability conditioned on a threshold $\gamma$ when the instantaneous SNR $\rho$ per source-relay-destination link falls below an acceptable rate to decode the signal properly. This criteria will allow us to predict the optimal relay location in terms of distance from the source and the destination. So, the outage probability conditioned on the absence of the direct source-destination link can be given as,

Fig. 4

Illustrating a central source node at a distance l from the relay, with cell radius $c_r$ and showing one sector from $q=4$ sectors

$$\begin{aligned} \mathcal {P}(\rho _{sd} \ll \gamma )= \sum _{\begin{array}{c} \forall selected\\ relays\\ \end{array}} \mathcal {P}(\rho _{sm}\le \gamma ) \mathcal {P}(\rho _{md}\le \gamma ) \end{aligned}$$

(22)

where summation is for the disjoint probability of outage at each selected relay and the multiplicative factor is for independent fading at source-relay and relay-destination links. Then the outage based on the distance between the source-relay-destination can be given as,

$$\begin{aligned} \mathcal {P}(l_{sm},l_{md})= \sum _{\begin{array}{c} \forall selected\\ relays\\ \end{array}} \Big ( 1-f(\gamma ,l_{sm})\Big ) \Big (1-f(\gamma ,l_{md})\Big ) \end{aligned}$$

(23)

where, $f(x,y)=\exp (-\sigma ^2 x y/P_y)$ and $P_y=P_1~\text {when}~y=l_{sm}~\text {and}~P_y=P_2~\text {when}~y=l_{md}$. In order to compute the optimal relay position, we need to find two pairs ($l_{sm}, l_{md}$) of relays for the proposed DC strategy to minimize the conditional probability in (23),

$$\begin{aligned} \begin{aligned} (l_{sm},l_{md})^* = arg~min~\mathcal {P}(l_{sm},l_{md}),\\ s.t.~ 0< l_{sm},l_{md} < c_r \end{aligned} \end{aligned}$$

(24)

the mean square distance between two nodes l units apart with angle $\theta$ can be given as,

$$\begin{aligned} \begin{aligned} f(l_{sm})=E(\Vert l_{sm} - l \exp ^{j\theta } \Vert ^2)~ for ~s \rightarrow r ~link \\ f(l_{md})=E(\Vert l \exp ^{j\theta } - l_{md} \Vert ^2)~ for ~r \rightarrow d ~link \end{aligned} \end{aligned}$$

(25)

where E is the joint statistical expectation over l and $\theta$ (uniformly distributed over $-\pi /q, \pi /q$). Solving for optimal $l_{sm}, l_{md}$, the expected values can be reduced as $(l_{sm})^*=E(l \exp ^{j\theta })$ and $(l_{md})^*=E(l \exp ^{j\theta })$. The optimal relay position to minimize the outage probability can thus be given as,

$$\begin{aligned} \begin{aligned} (l_{sm},l_{md})^*=&\frac{q}{2 \pi }\int \limits _{-\frac{\pi }{q }}^{\frac{\pi }{q}}\int \limits _0^{c_r }l \frac{ (2 l)}{c_r ^2} \left( \sqrt{-1} \sin (\theta )+\cos (\theta )\right) dld\theta \\&\times \frac{q}{2 \pi }\int \limits _{-\frac{\pi }{q }}^{\frac{\pi }{q}}\int \limits _0^{c_r }l \frac{ (2 l)}{c_r^2} \left( \sqrt{-1} \sin (\theta )+\cos (\theta )\right) dld\theta \\ =&\frac{4q^2}{9\pi ^2}\sin \left( \frac{\pi }{q}\right) ^2c_r^2 \end{aligned} \end{aligned}$$

(26)

it can be readily concluded from (26) that the optimal relay position is predominantly dependent on the cell radius ($c_r$) as well as the number of sectors (q) per cell.

Fig. 5

Comparison of the exact SER formulation, its upper bound, and the asymptotically tight approximation for the proposed DC strategy

6 Simulation results

In this section, performance of the proposed DC strategy is analyzed to further investigate the analytical model. A quasi-static Rayleigh fading channel is considered with total transmit power $P = P_1 + P_2$ and SNR = 10 log $[P/\sigma ^2]$, where $\sigma ^2$ is the unit noise variance for both source-to-relay and relay-to-destination links. We take average SER over $k=10,000$ transmissions from the source, in order to evaluate the performance of the proposed sequential scheme. Furthermore, all the results in this section are based on this average.

In Fig. 5, we compare the exact SER (6), the upper bound (12) and the asymptotically tight approximation (16) formulations. We observe that the upperbound and the exact SER have similar diversity order, as both are asymptotically parallel (1 dB margin). However, the tight approximation loosely follows at low SNR, but converges tightly at relatively higher SNR (around 11 dB and above) with the exact SER (6). The upperbound SER indicates the worst performance of the strategy based on the weight parameter defined in Sect. 3.1.

Fig. 6

Comparison of SER of the proposed DC strategy with non-cooperative, cooperative DF with MRC for single relay, and 2$\times$1 Alamouti coding

Fig. 7

SER evaluation with optimum power allocation at the source a $\delta _{sm} = 10, \delta _{md} = 1$, b $\delta _{sm} = \delta _{md} = 1$, c $\delta _{sm} = 1, \delta _{md} = 10$

In Fig. 6, we then compared the SER of the proposed DC strategy, SER of the DF cooperative communication with single relay using maximal-ratio combining (MRC) at the destination [7], SER of $2\times 1$ Alamouti (using 2 transmitters and 1 receiver) scheme [2], and the SER of the non-cooperative source-to-destination transmission. The proposed scheme out-performs the non-cooperative transmission (by more than 5 dB) and the cooperative DF with MRC (by more than 2 dB). It tends to emulates a 2$\times$1 Alamouti transmission, however, lacks behind (almost 3 dB) considering the gain due to identical channel conditions for the two antenna Alamouti scheme as compared to different channel conditions at both the relays in the proposed DC strategy. The proposed scheme, outperforms the cooperative communication scheme (with single relay) and the non-cooperative communication scheme due to the diversity gain it achieves.

Next, we compared the SER for different transmit power levels $P_1$ based on the optimum power allocation formulations in (18) and (19). In order to achieve similar power allocation at both the selected relays, we have assumed similar channel conditions. In Fig. 7, we investigate the SER performance for three different channel conditions. Firstly, we investigate the error probability with increased confidence in the source-to-relay link (i.e., $\delta _{sm} = 10,\delta _{md} = 1$) in Fig. 7a, and hence, observe the asymptotic optimum power allocation ratio’s $P_1/P = 0.3226$ and $P_2/P = 0.6774$. This leads to the conclusion that with increased confidence in the source-to-relay link, employing less power at the source and more at the relay provides the optimum power allocation that efficiently minimizes the error probability. Fig. 7b, when the channel conditions are similar (i.e., $\delta _{sm} = \delta _{md} = 1$), we observe that $P_1/P = 0.5161$ and $P_2/P = 0.4839$ are the asymptotic optimum power ratio’s to comply with the total power constraint. Finally, in Fig. 7c, the optimum power allocation is observed as $P_1/P = 0.6774$ and $P_2/P = 0.3226$, suggesting that reduced confidence on source-to-relay link requires most of the power to be employed at the source to achieve an optimum performance improvement in terms of SER. It is worth noticing that for a given system with pre-established channel conditions, the error probability decreases with increasing SNR, and yet, the optimum power allocation remains the same. It is also observed that identical channel conditions entails least error floor.

In Fig. 8, we present the implications of power allocation for, identical channel conditions (i.e., $\delta _{sm}=\delta _{md}=1$) and, when confidence is reduced on the source-to-relay link (i.e., $\delta _{sm}=1, \delta _{md}=10$). Here, we can easily avoid the case when confidence is reduced on the relay-to-destination link (i.e., $\delta _{sm}=10, \delta _{md}=1$), as Fig. 7a and c, yield similar error probability. We observe that at low SNR (${\le }10$ dB) values both equal power and their respective optimum power allocation yield similar error probability but at relatively higher SNR (15dB and above) the optimum power allocation improves on the SER gain. To achieve an SER of $10^{-3}$ operating under reduced confidence on the source-to-relay link (i.e., $\delta _{sm}=1, \delta _{md}=10$), we achieve a 1dB improvement for the optimal power allocation. Whereas, under identical channel conditions (i.e., $\delta _{sm}=\delta _{md}=1$), optimum power allocation outperforms the equal power allocation by almost 1dB to achieve an SER of $10^{-4}$. In conjunction to the improvement in SER achieved by the optimal power allocation, the relays now operate at lower power as compared to equal power distribution and are still able to cooperate with less error probability. The power conserved at the relays can be further utilized either to improve on the SER, or utilize it for later transmissions.

Fig. 8

SER evaluation of the proposed DC strategy with equal and optimum power allocation at the source and relay

Lastly, we consider the performance of the proposed DC protocol in terms of optimal position of the relay form source and destination with equal and optimum power allocation. Fig. 9 depicts the SER versus the number of sectors q in the circular coverage area under identical channel conditions. The simulations are carried out for an indoor path loss exponent $\alpha =3$ and increasing coverage area or cell radius upto 3 times. We can observe that for unit cell radius the SER decreases with increasing number of sectors (with each sector having atleast a pair of relays for cooperation) but degrades steeply after $q=6$ for both equal and optimum power allocation. The improvement in SER is due to the availability of relays that are in close proximity (as depicted by the shaded region in Fig. 4), however, increasing sectors to a point where the relays from the adjacent sectors can also interfere (inter-sector interference) causes the poor performance as seen in Fig. 9. Furthermore, as we increase the cell radius, a marginal improvement in SER is observed by increasing the number of sectors and similar performance saturation occurs after $q=6$. We also observe further decrease in SER by optimally allocating power to an optimally positioned relay. The improved SER by optimally positioning the relays can ideally be utilized for coverage expansion towards an acceptable SER. This leads to the conclusion that introduction of optimum power allocation and optimal relay positioning can further improve the performance of the proposed DC scheme.

Fig. 9

SER evaluation of the proposed DC strategy for different cell-radius and number of sectors

7 Conclusion

In this paper, we have proposed a novel and optimal DC strategy with multiple relay selection for cooperative communication, when the source-to-destination link is not available i.e., a strict dual-hop network. The proposed DC scheme ensures that relays are adequately selected and efficiently utilized, when the source is sequentially transmitting and the relays transmit the decoded information in order to take part in the cooperative process. Based on the performance analysis, the proposed scheme achieves diversity gain by selecting multiple relays and provides 2 dB improvement over the DF strategy with single relay. It is also observed that optimum power allocation and relay positioning can further enhance the performance of the proposed scheme. Our proposed scheme can therefore be considered as an ideal candidate to incorporate cooperation towards the design of future wireless communication networks, especially high density environments subjected to direct communication constraint. Furthermore, this scheme can also work effectively towards communication in power limited nodes. Future work will focus on assessing performance of the proposed DC strategy with CSI estimation.

Appendix

In order to compute the upper bound on the error probability, we have to derive the probability density function (pdf) of w,

$$\begin{aligned} f(w)= f\left( \frac{min(X,Y)}{max(X,Y)}\right) \end{aligned}$$

(27)

where X and Y are considered as independent exponential variables with densities $ae^{-au}$ and $be^{-bu}$, $u>0$, respectively.

$$\begin{aligned} \mathcal {P}_{ub}\left( \frac{min(X,Y)}{max(X,Y)} \le x\right) = \mathcal {P}(X \le xs) = 1 - e^{-axs} \end{aligned}$$

(28)

Additionally, for $0<x<1$ and $s>0$, a is the variance for the source-to-relay link and b is the variance for the relay-to-destination link. So, by conditioning the law of total probability on Y,

$$\begin{aligned} \begin{aligned}&\mathcal {P}_{ub}\left( \frac{min(X,Y)}{max(X,Y)} \le x\right) \\&\quad = \int _0^\infty \mathcal {P} \left( min(X,s) \le max(X,s)x \right) be^{-bs}ds \\&\quad = \int _0^\infty (1 - e^{-axs})be^{-bs}ds = 1 - \left( \frac{b}{ax+b}\right) , \\&\quad \quad \quad 0<x<1 \end{aligned} \end{aligned}$$

(29)

the pdf of (29) can be obtained by taking its derivative. The probability density function $f_w$ of the min. max. ratio on (0, 1) is given by,

$$\begin{aligned} f_w(x) = \frac{d}{dx} \left( 1 - \left( \frac{b}{ax+b}\right) \right) = \frac{ab}{(ax+b)^2}, 0<x<1 \end{aligned}$$

(30)

which is in conformity,

$$\begin{aligned} \int _0^1 f_w(x)dx = \left( 1 - \left( \frac{b}{ax+b}\right) \right) \mid _0^1 = 1 - \frac{b}{a+b} \end{aligned}$$

(31)

as it is $<1$. It signifies that,

$$\begin{aligned} \begin{aligned}&\mathcal {P}_{ub}(w=1)=\frac{b}{a+b}\text {, and satisfies,} \\&\mathcal {P}_{ub}(w=1)=\mathcal {P} \Big ( min(X,Y)=max(X,Y)\Big ) \mathcal {P}\Big (X=Y\Big ) \end{aligned} \end{aligned}$$

(32)

so therefore, conditioning the law of total probability on X,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{ub}(w=1)&= \int _0^\infty \mathcal {P}\left( \frac{Y}{X}\le u\right) ae^{-au}du \\&= 1 - \frac{a}{a+b}=\frac{b}{a+b} \end{aligned} \end{aligned}$$

(33)

the cumulative density function (cdf) is given as,

$$\begin{aligned} \begin{aligned} F_w(1) - \lim _{x\rightarrow 1^{-}}F_{R}(x)&= 1 - \lim _{x\rightarrow 1^{-}}\left( - 1 - \frac{b}{ax+b}\right) \\&= \frac{b}{a+b} \end{aligned} \end{aligned}$$

(34)

where $F_w(1)=1$ (i.e., having a jump discontinuity at $x=1$) which is the probability $\mathcal {P}_{ub}(w=1)$. The density function of w exists only for $x<1$, and is given as,

$$\begin{aligned} f_w(x) = \frac{ab}{(ax+b)^2}, 0<x<1 \end{aligned}$$

(35)

and

$$\begin{aligned} F_{w}(x) = 1 - \left( \frac{b}{ax+b}\right) , 0<x<1 \end{aligned}$$

(36)

Therefore, the pdf of $w=\frac{min(X,Y)}{max(X,Y)}$, given a and b as the variance of random variable’s x and y, respectively, could be expressed as,

$$\begin{aligned}&f_w(x) = \frac{ab}{(ax+b)^2} + \left( \frac{b}{a+b}\right) \delta (x-1) \end{aligned}$$

(37)

$$\begin{aligned}&\begin{aligned} \mathcal {P}_{ub} \le&\frac{(\text {M}-1)^2{\sigma ^2}^2}{\text {M}^2}\\&\quad \times \int _0^1 \left( \frac{(\sigma ^2+wB_a)(\sigma ^2+wB_b)+ (\sigma ^2+wA_a)(\sigma ^2+wA_b)}{(\sigma ^2+wA_a)(\sigma ^2+wA_b) (\sigma ^2+wB_a)(\sigma ^2+wB_b)}\right) \\&\quad \times \frac{ab}{(aw+b)^2}dw + \frac{(\text {M}-1)^2{\sigma ^2}^2}{\text {M}^2} \\&\quad \times \int _1^1 \left( \frac{(\sigma ^2+wB_a)(\sigma ^2+wB_b)+ (\sigma ^2+wA_a)(\sigma ^2+wA_b)}{(\sigma ^2+wA_a) (\sigma ^2+wA_b)(\sigma ^2+wB_a)(\sigma ^2+wB_b)}\right) \\&\qquad \frac{b}{(a+b)}\delta (w-1) dw \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned}&\begin{aligned}&\frac{(\sigma ^2+wB_a)(\sigma ^2+wB_b)+ (\sigma ^2+wA_a)(\sigma ^2+wA_b)}{(\sigma ^2+wA_a)(\sigma ^2+wA_b)(\sigma ^2+wB_a)(\sigma ^2+wB_b)} \times \frac{ab}{(aw+b)^2} \\&= \frac{Xa}{(\sigma ^2+wA_a)} +\frac{Xb}{(\sigma ^2+wA_b)}+\frac{Xc}{(\sigma ^2+wB_a)} \\&+\frac{Xd}{(\sigma ^2+wB_b)} +\frac{Xe}{(aw+b)^2}+\frac{Xf}{(aw+b)} \end{aligned} \end{aligned}$$

(39)

substituting (10) and (37) in (11), we have an upper bound on the SER as given in (38) and by using partial fraction expansion technique on the first integral term in (38), we can get (39). Finally, ignoring the zero probability component of the expansion and replacing a and b with respective channel variances, we can conclude the SER upper bound of the system as,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{ub} \le&\frac{(\text {M}-1)^2{\sigma ^2}^2}{\text {M}^2} \left( \frac{(\sigma ^2+B_a)(\sigma ^2+B_b)+ (\sigma ^2+A_a)(\sigma ^2+A_b)}{(\sigma ^2+A_a)(\sigma ^2+A_b)(\sigma ^2+B_a)(\sigma ^2+B_b)}\right) \\&\times \frac{\delta _{r_{a}d}^2\delta _{r_{b}d}^2}{\delta _{sr_{a}}^2\delta _{sr_{b}}^2 + \delta _{r_{a}d}^2\delta _{r_{b}d}^2} \end{aligned} \end{aligned}$$

(40)