Capacity of orthogonal space–time block codes in spatially correlated MIMO Weibull fading channel under various adaptive transmission techniques

Abstract

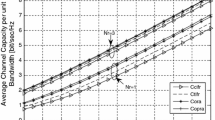
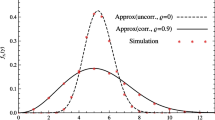
The effect of spatial correlation on channel capacity of orthogonal space–time block codes (OSTBCs) over multiple-input multiple-output Weibull fading under different adaptive transmission scheme is studied. In this paper, we have derive the moment generating function of the OSTBC received signal-to-noise ratio for integer Weibull parameter $\beta$, considering spatial fading correlation. Utilizing the exact expression of the MGF, the probability density function has been simply achieved, thus enabling the exact evaluation of OSTBC capacity under distinct power and rate allocation schemes. Numerical outcomes illustrate the effect of fading severity $\left( \beta \right)$ and fading correlation on the channel capacity and outline the performance differences among the distinctive adaptation schemes. It can be observed that OSTBC system with $opra$ outperform the system with $tifr$ adaptive scheme.

Appendices

Appendix 1

Substituting (15) into (16), the expression for the capacity $\langle {C}\rangle _{ora}$ can be written as

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \mathop {\int }\limits _0^\infty {\text {log}}_{2}\left( 1+\gamma _{s} \right) x\frac{\left( {x\gamma }_{s} \right) ^{j-1}}{\varGamma \left( j \right) }\nonumber \\&\times \,\exp \left( -x\gamma _{s} \right) d\gamma _{s} \end{aligned}$$

(35)

where $x=\frac{\beta Z}{2\overline{\gamma }_{c}\lambda _{m}}$ and $x\frac{\left( {x\gamma }_{s} \right) ^{j-1}}{\varGamma \left( j \right) }\exp \left( -x\gamma _{s} \right)$ can be determined as

$$\begin{aligned} x\frac{\left( {x\gamma }_{s} \right) ^{j-1}}{\varGamma \left( j \right) }\exp \left( -x\gamma _{s} \right) =\sum \limits _{p=0}^{j-1} \frac{\left( {x\gamma }_{s} \right) ^{p}}{\varGamma \left( p+1 \right) } \exp \left( -x\gamma _{s} \right) \end{aligned}$$

(36)

Thus substituting (36) into (35) and by using integration by parts (35) can be written as

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \sum \limits _{p=0}^{j-1} \frac{1}{\Gamma \left( p+1 \right) } \nonumber \\&\times \mathop {\int }\limits _0^\infty \frac{1}{\left( 1+\gamma _{s} \right) }\left( {x\gamma }_{s} \right) ^{p} \exp \left( -x\gamma _{s} \right) d\gamma _{s} \end{aligned}$$

(37)

Let $1+\gamma _{s}=y$, then (37) can be rewritten as

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\mathop {\sum }\limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \mathop {\sum }\limits _{p=0}^{j-1} \frac{x^{p}\exp \left( x \right) }{\varGamma \left( p+1 \right) }\nonumber \\&\times \,\mathop {\int }\limits _1^\infty {\frac{1}{y}\left( y-1 \right) ^{p}\exp \left( -xy \right) dy} \end{aligned}$$

(38)

By using binomial expansion [30], (1.111)] $\left( t+a \right) ^{n}=\sum \nolimits _{k=0}^n \left( {\begin{array}{l} n\\ k\\ \end{array} } \right) t^{k}a^{n-k}$ and [30], (3.381.3)] $\mathop {\int }\nolimits _n^\infty x^{v-1} \text {exp }(-ax)dx=a^{-v}\varGamma \left( v,an \right)$, we get

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \sum \limits _{p=0}^{j-1} \frac{x^{p}\exp \left( x \right) }{\varGamma \left( p+1 \right) }\nonumber \\&\times \,\sum \limits _{q=0}^p \left( {\begin{array}{l} p\\ q\\ \end{array} } \right) \left( -1 \right) ^{p-q}\frac{\varGamma \left( q,x \right) }{x^{q}} \end{aligned}$$

(39)

in which $\varGamma \left( .,. \right)$ represent complementary incomplete gamma function and for q positive integer

$$\begin{aligned} \varGamma \left( q,x \right) =\varGamma \left( q \right) P_{q}\left( x \right) , q\ge 2 \end{aligned}$$

(40)

where $\mathcal {P}_{k}(.)$ is the Poisson sum and defined as [30]

$$\begin{aligned} \mathcal {P}_{k}\left( c \right) =\exp (-c)\sum \limits _{j=0}^{k-1} \frac{c^{j}}{j!} \end{aligned}$$

(41)

For $q=0, \varGamma \left( 0,c \right) =E_{1}\left( c \right)$, in which $E_{1}\left( . \right)$ is the first order exponential integral function $E_{1}\left( c \right) =\mathop {\int }\nolimits _1^{\infty } {\text {exp}(-ct)} / t dt$ [30]. Thus (39) can be written as

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \left[ \sum \limits _{p=0}^{j-1} \frac{\left( -x \right) ^{p}\exp \left( x \right) }{\varGamma \left( p+1 \right) } E_{1}\left( x \right) \right. \nonumber \\&+\sum \limits _{p=1}^{j-1} \frac{\left( -x \right) ^{p}\exp \left( x \right) }{\varGamma \left( p+1 \right) } \nonumber \\&\times \,\left. \sum \limits _{q=1}^p \frac{p!}{q!\left( p-q \right) !} \left( -x \right) ^{-q}\varGamma \left( q \right) P_{q}\left( x \right) \right] \end{aligned}$$

(42)

Thus, in the first term of (42) utilize (41) and in the second term of (42) interchanging the summation, we get

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \left[ \mathcal {P}_{j}\left( -x \right) E_{1}\left( x \right) \right. \nonumber \\&\left. +\sum \limits _{q=0}^{j-1} \frac{\mathcal {P}_{q}\left( x \right) }{q} \sum \limits _{p=q}^{j-1} \frac{\left( -x \right) ^{p-q}}{\left( p-q \right) !} \text {exp}(x) \right] \end{aligned}$$

(43)

$$\begin{aligned} \langle {C}\rangle _{ora}= & {} R_{c}\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \xi _{mj} \left[ \mathcal {P}_{j}\left( -x \right) E_{1}\left( x \right) \right. \nonumber \\&\left. +\sum \limits _{q=0}^{j-1} \frac{\mathcal {P}_{q}\left( x \right) \mathcal {P}_{j-q}\left( -x \right) }{q} \right] \end{aligned}$$

(44)

Appendix 2

Inserting (15) into (19), we get the equation that the maximal cut off SNR $\gamma _{0}$ satisfy

$$\begin{aligned}&\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \frac{\xi _{mj}}{{\Gamma }\left( j \right) \left( \frac{2\overline{\gamma }_{c}}{\beta Z}\lambda _{m} \right) ^{j}} \left[ \frac{1}{\gamma _{0}}\mathop {\int }\limits _{\gamma _{0}}^\infty {\gamma _{s}^{j-1}\text {exp}\left( -\frac{\beta Z\gamma _{s}}{2\lambda _{m}\overline{\gamma }_{c}} \right) } d\gamma _{s} \right. \nonumber \\&\quad \left. -\mathop {\int }\limits _{\gamma _{0}}^\infty {\gamma _{s}^{j-2}\mathrm {exp}\left( -\frac{\beta Z\gamma _{s}}{2\lambda _{m}\overline{\gamma }_{c}} \right) } d\gamma _{s} \right] =1 \end{aligned}$$

(45)

Applying the identity ${\Gamma }\left( n,x \right) =\mathop {\int }\nolimits _x^\infty s^{n-1} e^{-s}ds$, (45) can be rewritten as

$$\begin{aligned}&\sum \limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \frac{\xi _{mj}}{\mathrm {\Gamma }\left( j \right) \left( \frac{2\overline{\gamma }_{c}}{\beta Z}\lambda _{m} \right) ^{j}}\nonumber \\&\quad \times \,\left[ \frac{1}{\gamma _{0}}\frac{{\Gamma }\left( j,\frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}}\gamma _{0} \right) }{\left( \frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}} \right) ^{j}}-\frac{{\Gamma }\left( j-1,\frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}}\gamma _{0} \right) }{\left( \frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}} \right) ^{j-1}} \right] =1\nonumber \\ \end{aligned}$$

(46)

Let $\gamma _{0}=x$ and describing

$$\begin{aligned}&G\left( x \right) =\mathop {\sum }\limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta /2} \frac{\xi _{mj}}{{\Gamma }\left( j \right) \left( \frac{2\overline{\gamma }_{c}}{\beta Z}\lambda _{m} \right) ^{j}} \nonumber \\&\quad \times \left[ \frac{1}{x}\frac{{\Gamma }\left( j,\frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}}x \right) }{\left( \frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}} \right) ^{j}}-\frac{{\Gamma }\left( j-1,\frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}}x \right) }{\left( \frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}} \right) ^{j-1}} \right] -1 \end{aligned}$$

(47)

$$\begin{aligned}&\frac{dG\left( x \right) }{dx}=-\mathop {\sum }\limits _{m=1}^M \sum \limits _{j=1}^{\mu _{m}\beta / 2} \frac{\xi _{mj}}{{\Gamma }\left( j \right) } \left[ \frac{1}{x^{2}}{\Gamma }\left( j,\frac{\beta Z}{2\lambda _{m}\overline{\gamma }_{c}}x \right) \right] \end{aligned}$$

(48)

We have $\frac{dG\left( x \right) }{dx}<0, \forall x>0$ and from (47), we achieve that $\lim _{{x\rightarrow 0}^{+}}{G\left( x \right) }=+\infty$ and $\lim _{{x\rightarrow +{\infty }}}{G\left( x \right) }=-1<0$. The solution of (48) required numerical root finding techniques. $\varGamma (n,t)\approx \Gamma (n)$ for higher value of $t$ and inserting it into (46), we get

$$\begin{aligned} \mathop {\sum }\limits _{m=1}^M \mathop {\sum }\limits _{j=1}^{\mu _{m}\beta /2} {\xi _{mj}\left[ \frac{1}{\gamma _{0}}-\frac{1}{\left( j-1 \right) }\left( \frac{\beta Z}{2\overline{\gamma }_{c}\lambda _{m}} \right) \right] } =1 \end{aligned}$$

(49)

Finally, after some manipulation $\gamma _{0}$ is given in (24).