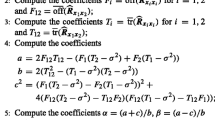1 Introduction

About three main categories of signal recovery algorithms based on the availability of prior information about the mixing process or the mixture are found in statistical wireless signal processing. They are blind, semi-blind and non-blind or normal schemes. Two fundamental properties are emphasized by the adjective “blind”. First is no source signals are observed. Second is no information is available about the mixture. Therefore Blind Source or Signal Separation can be introduced as a process used for recovery of unobserved signals or sources from several observed mixtures. In implementations usually the observation values are obtained by output of a set of sensors. Sensors are designed such that each receives a different combination of the source signals. The core strength of the Blind Source Separation (BSS) model is the weakness of the prior information that made it a versatile tool for extracting the spatial diversity provided by an array of sensors. A statistically strong plausible assumption of independence between the source signals is used to compensate the fact of the lacking of prior knowledge about the mixture.

Interference mitigation and efficient use of resources are two main problems in the air interface communication. Knowledge on interference of radio channels is so important in order to improve the caliber of communication systems. Therefore performance is evaluated based on many parameter and conditions even after they are been commercially deployed. Performance of a digital audio broadcasting in the presence of tonal interference is evaluated in [5]. In one such case, interference management approaches are handled as either exact or approximated solutions of optimization problem [15]. As examples for the case of resource management, two simple allocation methods namely adaptive slot allocation and reservation-based slot allocation are introduced in [2]. Cross-layer resource allocation for real-time services in OFDM based cognitive radio systems is handled as an optimization problem in [19]. Both of them are fair resource allocation mechanisms among different types of services flows based on quality of service characteristics and channel conditions. Both interference management and power allocation for OFDM based cognitive radio systems are modeled as an optimization problem in [9].

The rest of this paper is organized as follows. Motivation for this study, some of the applications and theoretical BSS based approach are presented in general in Sect. 2. In the same section, customized derivations for both OFDM and DS-CDMA systems are also presented. Basic system models with common parameters are described in Sect. 3. Performance evaluations for the both types of systems in terms of bit error rate (BER) simulations along with system parameters are given in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 BSS models

Growth of basic BSS models and algorithms covering various technological sectors are visible. Arrangements having more sensors than sources are of much practical importance [4, 12] where noisy observations and complex signals and mixtures can be included. These derivatives and findings are applicable to the standard narrow band array processing or beamforming models and convolutive mixtures. Because of this they are leading to multichannel blind deconvolution problems. Only stationary non-Gaussian signals can be separated by some of these developments. These kinds of certain limitations pave the way for weaker performance in dealing with some real sources, like audio signals. But different types of approaches and solutions can be seen that take advantage of the nonstationarity of sources to achieve better performance than the classical methods [1].

Genuine motivations for the most of the innovative technological advancements are basic or enhanced human needs or unquenchable curiosity for explorations expanding the conventional boundaries. Biomedical signal analysis and processing (ECG, EEG, MEG) [7, 18] computer vision and image recognition, communications signal processing [17] are some of such most sensitive areas that are significantly associated with major human needs. Borders of the applications connected to them are always being extensively pushed forward. Even though they are not directly connected to any of the basic need, based on economic and other profitable aspects area like geophysical data processing, data mining, acoustics (audio signal processing) and speech recognition are being rapidly developed where a significant active role can be played by BSS principles. In one comparable case separation of multiple speakers from mixtures of them is done using BSS algorithm [13].

2.1 General BSS model

A massive number of successfully completed research studies on linear instantaneous mixtures can be found where the prime intention of conducting them is separation of the sources by combining the observations by means of a matrix adapted for independent output signals. The most vital primary assumption of these techniques is that the sources must be independent [1].

Considering a simple information symbol transfer process, source signal are denoted by \({\mathbf{s}(t)}\), \({\mathbf{s}(t) {=} {[s_1(t), s_2(t), \ldots ,}}\) \({{s_b(t), \ldots , s_B(t) ]}^T}\). \({s_b(t)}\) is the signal element \({b}\) at time \({t}\). \({s_2(t), s_3(t),\ldots , s_b(t), \ldots , s_B(t)}\) are independent or uncorrelated symbols or signals. Signal \({s_1(t)}\) is time correlated. \(\mathbf{A}\) is a \({F \times B}\) matrix and a mixture of coefficient values. The element \({f,b}\) of it is given by \({{ a }_{f,b}}\). \({\mathbf{a}_1}\), \({{\mathbf{a}_1} = {\left[ { a }_{1,1}, { a }_{2,1}, \ldots , { a }_{f,1},\ldots , { a }_{F,1} \right] }^T}\) is the coefficient value matrix of \({s_1(t)}\). Additive independent and identically distributed (iid) white noise is denoted by \({\mathbf{w}(t) = {[w_1(t), w_2(t),}}\) \({{\ldots , w_f(t),\ldots , w_F(t) ]}^T}\), and colored noise is given by \({\mathbf{w}'(t)}\). \({w_i(t)}\) is the noise element \({f}\) at time \({t}\). Then the receive signal matrix \({\mathbf{x}(t)}\), \({\mathbf{x}(t) = {[x_1(t), x_2(t), \ldots , x_f(t),}}\) \({{ \ldots , x_F(t) ]}^T}\) of the basic BSS model at time \({t}\) with \({B}\) unknown input or sources and \({F}\) output or sensor observations can be given as [1, 3] and [10].

$$\begin{aligned} \mathbf{x}(t) = \mathbf{As}(t)+\mathbf{w}(t) = s_1(t)\mathbf{a}_1^{} + \mathbf{w}'(t) \end{aligned}$$
(1)

where \({s_2(t), s_3(t), \ldots , s_b(t), \ldots , s_B(t)}\) are independent or uncorrelated symbols or signals and signal \({s_1(t)}\) is time correlated. When appropriately shaped mapped symbols are considered and the time delay is sufficiently shorter \({c_1^{} = \text{ E } \left\{ s_1(t)s_1(t+\tau ) \right\} \approx \text{ E } \left\{ s_1^2(t) \right\} }\). The differential correlation matrix \({\mathbf{C}(\tau )}\) at a small time difference \({\tau }\) is given [8] as follows,

$$\begin{aligned} \mathbf{C}(\tau ) = \text{ E } \left\{ \mathbf{x}(t)\mathbf{x}^T(t+\tau ) \right\} = c_1^{}\mathbf{a}_1^{}\mathbf{a}_1^T+\mathbf{R}_{\tau } \end{aligned}$$
(2)

where matrix transpose is represented by \({^T}\). The ordinary correlation matrix \(\mathbf{R}\) is,

$$\begin{aligned} \mathbf{R}= & {} \text{ E } \left\{ \mathbf{x}(t)\mathbf{x}^T(t) \right\} \nonumber \\= & {} \mathbf{A} \text{ E } \left\{ \mathbf{s}(t)\mathbf{s}^T(t) \right\} \mathbf{A}^T + \sigma ^2 \mathbf{I } \nonumber \\= & {} c_1^{}\mathbf{a}_1^{}\mathbf{a}_1^T + \mathbf{R}_0 \end{aligned}$$
(3)

Noise variance is given by \({\sigma ^2}\). Assume that \({\left\| \mathbf{R}_0 \right\| > \left\| \mathbf{R}_{\tau } \right\| }\), where \({\left\| \cdot \right\| }\) is Frobenius or 2-norm.

The output \({\mathbf{y}(t)}\) or \(\mathbf{y}\) of the receiver with coefficient \({\mathbf{u}_{rc}}\) is given by,

$$\begin{aligned} \mathbf{y} = {\mathbf{u}_{rc}^T}\mathbf{x} \end{aligned}$$
(4)

The output power \({\text{ E } \left\{ \mathbf{y}^2(t) \right\} }\) is derived by (3) and (4) as,

$$\begin{aligned} \text{ E } \left\{ \mathbf{y}^2(t) \right\} = {\mathbf{u}_{rc}^T}{\mathbf{Ru}_{rc}} \end{aligned}$$
(5)

The energy functions \({J_{1}\left( \mathbf{u}\right) }\) and \({J_{2}\left( \mathbf{u}\right) }\) are given in (6) and (7). \({\mathbf{u}}\) is a variable coefficient value similar to \({\mathbf{u}_{rc}}\). This is a dependent of the measured signal values \({\mathbf{x}(t)}\) or \({\mathbf{x}}\). The differential cross correlation matrix \(\mathbf{C}\) is estimated similar to Eq. (2), \({\lambda _1}\) and \({\lambda _2}\) are the Lagrangian multipliers. Matrix inverse is referred by \({^{-1}}\).

$$\begin{aligned} {J_{1}\left( \mathbf{u}\right) }= & {} \mathbf{u}^T\mathbf{C}^{-1}\mathbf{u} + {\lambda }_1 \left( {\mathbf{I} - \mathbf{u}^T\mathbf{R}^{-1}\mathbf{u}}\right) \end{aligned}$$
(6)
$$\begin{aligned} {J_{2}\left( \mathbf{u}\right) }= & {} \mathbf{u}^T\mathbf{C}^{-1}\mathbf{u} + {\lambda }_2 \left( {\mathbf{I} - \mathbf{u}^T\mathbf{Ru}}\right) \end{aligned}$$
(7)

As the main objective, the interference component of \({\mathbf{w}'(t)}\) is targeted to be suppressed while passing the signal \({s_1(t)\mathbf{a}_1}\). Minimization of the projections of \(\mathbf{u}\) to the effective space spanned by the matrix \({\mathbf{C}^{-1}}\) is tried by the first terms of the (6) and (7). The output power to suchlike inverse method is minimized by \(\mathbf{u}\). Differential correlation matrix \(\mathbf{C}\) contains just time correlated signal part \({s_1(t)\mathbf{a}_1}\). The resulting \(\mathbf{u}^T\mathbf{C}^{-1}\mathbf{u}\) is kept in minimum due to usage of the inverse matrix. Therefore it is expected to pass the signal \({s_1(t)\mathbf{a}_1}\) quite well by \(\mathbf{u}\). Minimization of the projection of \(\mathbf{u}\) to the effective space spanned by the matrix \(\mathbf{R}\) is tried by the second terms. So \({\text{ E } \left\{ \mathbf{y}^2(t) \right\} }\) is targeted to be minimized. But without differential correlation, \(\mathbf{R}\) contains much the interference part represented by \({\mathbf{R}_0}\). Then the desired signal \({s_1(t)\mathbf{a}_1}\) is filtered well again by \(\mathbf{u}\).

A variety of solutions can be achieved in dealing with these cases in the presence of diverse conditions. Many approaches attempting to remove or minimize the effect of noise or interference components can be seen. Here also interference component of the signal is attempted to be removed.

\(\bullet \)   Algorithm 1

Considering the partial derivative \({\frac{\partial J_{1}\left( \mathbf{u}\right) }{\partial \mathbf{u}}=0}\) of (6) defining \({\mathbf{u}_1}\) for the optimization,

$$\begin{aligned} {{\lambda }_1 {\mathbf{u}_1}} = \mathbf{C}^{-1}{\mathbf{Ru}_1} \end{aligned}$$
(8)

Interference signal is filtered out.

Using \({{\lambda }_1 {\mathbf{u}_1}(t) = {\mathbf{g}_1^1}(t)}\) and the iterative fixed point rule as follows,

$$\begin{aligned} {\mathbf{g}_1^1}(t)= & {} \mathbf{C}^{-1}{\mathbf{Ru}_1}(t) \end{aligned}$$
(9)
$$\begin{aligned} {\mathbf{u}^{1}_1}(t)= & {} {\frac{{\mathbf{g}^{1}_1}(t)}{\left\| {\mathbf{g}^{1}_1}(t)\right\| }} \end{aligned}$$
(10)
$$\begin{aligned} {\mathbf{g}_1^2}(t)= & {} \mathbf{C}^{-1}{\mathbf{Ru}_1^1}(t) \end{aligned}$$
(11)

\(\bullet \)   Algorithm 2

Considering the partial derivative \({\frac{\partial J_{2}\left( \mathbf{u}\right) }{\partial \mathbf{u}}=0}\) of (7) defining \({\mathbf{u}_2}\) for the optimization,

$$\begin{aligned} {{\lambda }_2 {\mathbf{u}_2}} = {(\mathbf{CR})^{-1}{\mathbf{u}_2}} \end{aligned}$$
(12)

Interference signal is filtered out.

Using \({{\lambda }_2 {\mathbf{u}_2}(t) = {\mathbf{g}_2^1}(t)}\) and the iterative fixed point rule as follows,

$$\begin{aligned} {\mathbf{g}_2^1}(t)= & {} (\mathbf{CR})^{-1}{\mathbf{u}_2}(t) \end{aligned}$$
(13)
$$\begin{aligned} {\mathbf{u}^{1}_2}(t)= & {} {\frac{{\mathbf{g}^{1}_2}(t)}{\left\| {\mathbf{g}^{1}_2}(t)\right\| }} \end{aligned}$$
(14)
$$\begin{aligned} {\mathbf{g}_2^2}(t)= & {} (\mathbf{CR})^{-1}{\mathbf{u}_2^1}(t) \end{aligned}$$
(15)

For the iteration \({m}\) of any of the solutions in (10) or (14),

$$\begin{aligned} {\mathbf{u}^{m}_c}(t) = {\frac{{\mathbf{g}^{m}_c}(t)}{\left\| {\mathbf{g}^{m}_c}(t)\right\| }} \end{aligned}$$
(16)

where \({\cdot _{1}}\) or \({\cdot _{2}}\) is represented by \({\cdot _{c}}\).

2.2 BSS for OFDM

Higher rate transmission capability, higher bandwidth efficiency and robustness to multipath (including tolerance or persistence to frequency-selective) fading and delay are some of the key factors that brought OFDM techniques to the forefront of the sphere of wireless communications. Two approaches that can be developed with an ambition of improving the symbol recovery using BSS principles for OFDM communications are attempting to remove interference and noise components of the receive signal mixture. Similarly, involvement of a BSS algorithm in a process of symbol recognition focusing to remove interference signals at a basic OFDM receiver is tested.

Wireless communication system consisting a \({N}\) subcarrier (\({N}\)-point inverse discrete Fourier transform (IDFT)/discrete Fourier transform (DFT)) OFDM [6, 14] transmitter and a receiver is considered. Frequency response of the channel state information (CSI) of subcarrier \({n}\) during an OFDM symbol period \({t}\) is signified by \({H_n(t)}\). Impulse response of the channel \({l}\) of the channel tap \({k}\) of the multipath frequency-selective Rayleigh fading channel within the same duration is symbolized by \({h_{k,l}(t)}\). Each tap is modeled with \({L}\) independent paths with exponentially decaying delay profiles.

$$\begin{aligned} H_n(t) = \sum _{k=0}^{N-1}{\sum _{l=0}^{L-1}{h_{k,l}(t)e^{-j{{2{\pi }kn}\over {N}}}}} \end{aligned}$$
(17)

Transmit symbol and normalized additive white Gaussian noise (AWGN) of subcarrier \({n}\) for the period \({t}\) are represented by \({d_n(t)}\) and \({v_n(t)}\) respectively. \({\sigma }\) is the standard deviation to the additive white Gaussian noise. Then the receive signal \({{r}_n(t)}\) on subcarrier \({n}\) during \({t}\) can be expressed as in (18).

$$\begin{aligned} {r_n(t)} = {H_n(t)}d_n(t)+{\left( \frac{\sigma }{\sqrt{2}}v_n(t) \right) } \end{aligned}$$
(18)

Considering the characteristics of a slow fading channel it can be assumed that for a given symbol frame path gain \({{H}_n(t) = {H}_n}\) and \({h_{k,l}(t) = h_{k,l}}\).

$$\begin{aligned} {r_n(t)} = {H_n}d_n(t)+{\left( \frac{\sigma }{\sqrt{2}}v_n(t) \right) } \end{aligned}$$
(19)

The receive signal samples of subcarrier \({n}\) at time period containing symbol \({d_n(t)}\) can be expressed as \({r_n(t), r_n(t+\tau ),}\) ..., \({ r_n(t+(p-1)\tau ), \ldots , r_n(t+(P-1)\tau )}\) where the \({P}\) receive signal samples are taken with small time shifts of \({\tau }\) within each information symbol duration. Therefore the receive signal samples of subcarrier \({n}\) at time period containing symbol \({d_n(t)}\) are denoted by \({r_n(t), r_n(t+\tau ),}\) \({\ldots , r_n(t+(p-1)\tau )}\), \({\ldots , r_n(t+(P-1)\tau )}\). \({\mathbf{r}_n(t)}\) is the row matrix containing these samples as the elements where these samples are equivalent to \({x_1(t), x_2(t), \ldots , x_f(t),}\) \({\ldots , x_F(t)}\) in (1). Symbol sample of \({d_n(t)}\) and AWGN of sample \({p}\) of \({r_n(t)}\) are indicated by \({d_n(t+(p-1)\tau )}\) and \({v_n(t+(p-1)\tau )}\) correspondingly. Similar to (19), sample \({p}\) of receive signal \({r_n(t)}\) is given as,

$$\begin{aligned} r_n\big (t+(p-1)\tau \big )= & {} {H_n}d_n\big (t+(p-1)\tau \big ) \nonumber \\&+~{\left( \frac{\sigma }{\sqrt{2}}v_n\big (t+(p-1)\tau \big ) \right) } \end{aligned}$$
(20)

For any symbol sample on subcarrier \({n}\) within a time duration of a transmit information symbol \({d_n(t)}\), \({d_n(t+(p-1)\tau )}\) \({ = d_n(t)}\).

$$\begin{aligned} r_n\big (t+(p-1)\tau \big )= & {} {H_n}d_n(t) \nonumber \\&+~{\left( \frac{\sigma }{\sqrt{2}}v_n\big (t+(p-1)\tau \big ) \right) } \end{aligned}$$
(21)

The differential correlation matrix \({\mathbf{C}_n(\tau )}\) at a small time difference \({\tau }\) and ordinary correlation matrix \({\mathbf{R}_n}\) for subcarrier \({n}\) according to (2) and (3) are,

$$\begin{aligned} \mathbf{C}_n(\tau )= & {} \text{ E } \left\{ \mathbf{r}_n(t)\mathbf{r}_{n}^{*}(t+\tau ) \right\} \end{aligned}$$
(22)
$$\begin{aligned} \mathbf{R}_n= & {} \text{ E } \left\{ \mathbf{r}_n(t)\mathbf{r}_{n}^{*}(t) \right\} \end{aligned}$$
(23)

Matrix complex conjugate transpose is denoted by \({^{*}}\).

Using the iterative fixed point rule as in (9) and (13), \({{g}^{1}_{c,n}(t)}\) and \({{g}^{m}_{c,n}(t)}\) pairs of subcarrier \({n}\) for the algorithm can be presented,

\(\bullet \)    Algorithm 1

$$\begin{aligned} {g}^{1}_{1,n}(t)= & {} \mathbf{C}^{-1}{\mathbf{R}u_{1,n}}(t) \end{aligned}$$
(24)
$$\begin{aligned} {g}^{m}_{1,n}(t)= & {} \mathbf{C}^{-1}{\mathbf{R}u^{m-1}_{1,n}}(t) \end{aligned}$$
(25)

\(\bullet \)    Algorithm 2

$$\begin{aligned} {g}^{1}_{2,n}(t)= & {} (\mathbf{CR})^{-1}{u_{2,n}}(t)\end{aligned}$$
(26)
$$\begin{aligned} {g}^{m}_{2,n}(t)= & {} (\mathbf{CR})^{-1}{u^{m-1}_{2,n}}(t) \end{aligned}$$
(27)

Coefficient \({{u}^{m}_{c,n}(t)}\) for iteration \({m}\) for subcarrier \({n}\) of any of the solutions given for OFDM is stated as,

$$\begin{aligned} {u}^{m}_{c,n}(t) = {\frac{{g}^{m}_{c,n}(t)}{\left\| {g}^{m}_{c,n}(t) \right\| }} \end{aligned}$$
(28)

Refined receive signal similar to (4) is,

$$\begin{aligned} y_n(t+(p-1)\tau ) = {u}^{m*}_{c,n}(t){r_n\big (t+(p-1)\tau \big )} \end{aligned}$$
(29)

Signal after Equal Gain Combining (EGC) can be expressed as,

$$\begin{aligned} y_n(t) = \frac{{u}^{m*}_{c,n}(t)}{P}\frac{H_n^{*}}{{|{H_n}|}^{2}}\sum _{p=1}^{P}{r_n\big (t+(p-1)\tau \big )} \end{aligned}$$
(30)

A diagonal matrix \({\mathbf{u}_{OFDM}}\) of dimensions \({N \times N}\) is considered. Matrix elements \({{u^{m}_{c,1}}(t), {u^{m}_{c,2}}(t), \ldots , {u^{m}_{c,n}}(t), \ldots ,}\) \({ {u^{m}_{c,N}}(t)}\) are on the diagonal. The column matrix \({\mathbf{x}_{OFDM}}\) where the element \({n}\) can be given by,

$$\begin{aligned} x_n = \frac{1}{P}\frac{{H_{n}^{*}}}{|{H_n}|}\sum _{p=1}^{P}{r_n\big (t+(p-1)\tau \big )} \end{aligned}$$
(31)

The simplified matrix format of the receiver output \({\mathbf{y}(t)}\) or \(\mathbf{y}\) with coefficients \(\mathbf{u}\) for these techniques is given as,

$$\begin{aligned} \mathbf{y}_{OFDM} = \mathbf{u}_{OFDM}^T\mathbf{x}_{OFDM} \end{aligned}$$
(32)

2.3 BSS for DS-CDMA

In most of the CDMA techniques capacity is limited by the amount of interference present in the environment. This interference can be originated from the other users of the system and from external sources radiating power in the same frequency band. It is unlikely to control these types of interferences accurately. Hence many different kinds of remedial approaches can be seen. Here also contributions of pair of BSS algorithms in symbol recovery focusing to remove interference signals at basic DS-CDMA receiver are considered. Comparable approaches to get rid of noise component of the receive signal mixture of the same system functioning under the same conditions can also be demonstrated.

Multipath Rayleigh fading channel used for the synchronous downlink DS-CDMA [6, 16] system is considered. The channel impulse response for the path \({l}\) out of \({L}\) independent paths with exponentially decaying delay profiles at time \({t}\) is denoted by \({A_l(t)}\).

$$\begin{aligned} \mathbf{A}(t) = \sum _{l=0}^{L-1}A_l(t) \end{aligned}$$
(33)

Spreading code element \({j}\) of the user \({k}\) at time \({t}\), transmit symbols of the user \({k}\) at time \({t}\) and normalized additive white Gaussian noise at time \({t}\) are symbolized by \({c_{k,j}(t), d_k(t)}\) and \({n(t)}\) respectively. For the slow fading channel it is assumed that for a given symbol frame path gain \({\mathbf{A}(t) = \mathbf{A}}\). Then the receive signal \({\mathbf{r}_j(t)}\) at time \({t}\) before despreading containing \({K}\) simultaneous users, can be expressed as in (34).

$$\begin{aligned} {\mathbf{r}_j(t)}= & {} \sum _{k=1}^K {\mathbf{A}(t)}c_{k,j}(t)d_k(t)+{\left( \frac{\sigma }{\sqrt{2}}n(t) \right) } \nonumber \\= & {} {\mathbf{A}}\sum _{k=1}^K c_{k,j}(t)d_k(t)+{\left( \frac{\sigma }{\sqrt{2}}n(t) \right) } \end{aligned}$$
(34)

During each spreading code element time period \({P}\) samples are taken with small time shifts of \({\tau }\) from the receive signal. Receive signal samples for a given \({c_{k,j}(t)}\) can be stated as \({r_j(t), r_j(t\!+\!\tau ), \ldots , r_j(t+(p-1)\tau ), \ldots , r_j(t+(P{-}1)\tau )}\) which are similar to \({x_1(t), x_2(t),\ldots , x_f(t),\ldots , x_F(t)}\) in (1). Spreading code element sample of \({c_{k,j}(t)}\), symbol sample of \({d_k(t)}\) and additive white Gaussian noise of sample \({p}\) are denoted by \({c_{k,j}(t+(p-1)\tau )}\), \({d_k(t+(p-1)\tau )}\) and \({n(t+(p-1)\tau )}\) respectively. Sample \({p}\) of receive signal \({\mathbf{r}_j(t)}\) can be mentioned as in (34),

$$\begin{aligned} {r_j\big (t+(p-1)\tau \big )}= & {} {\mathbf{A}}\sum _{k=1}^Kc_{k,j}\big (t+(p-1)\tau \big ). \nonumber \\&d_k\big (t+(p-1)\tau \big ) \nonumber \\&+~{\left( \frac{\sigma }{\sqrt{2}}n\big (t+(p-1)\tau \big ) \right) } \end{aligned}$$
(35)

For any sample within a time duration of a spreading code element \({c_{k,j}(t+(p-1)\tau ) = c_{k,j}(t)}\) and \({d_k(t+(p-1)\tau )}\) \({ = d_k(t)}\).

$$\begin{aligned} {r_j\big (t+(p-1)\tau \big )}= & {} {\mathbf{A}}\sum _{k=1}^K c_{k,j}(t)d_k(t) \nonumber \\&+~{\left( \frac{\sigma }{\sqrt{2}}n\big (t+(p-1)\tau \big ) \right) } \end{aligned}$$
(36)

From (2) and (3),

$$\begin{aligned}&\mathbf{C}(\tau ) = \text{ E } \left\{ \mathbf{r}_j(t)\mathbf{r}_{j}^{*}(t+\tau ) \right\} \end{aligned}$$
(37)
$$\begin{aligned}&\mathbf{R} = \text{ E } \left\{ \mathbf{r}_j(t)\mathbf{r}_{j}^{*}(t) \right\} \end{aligned}$$
(38)
Fig. 1
figure 1

Block diagram of the lowpass equivalent system models a OFDM Systems and b DS-CDMA Systems

Full size image

Applying iterative fixed point rule similar to (9), (13), \({\mathbf{g}^{1}_{c}(t)}\) and \({\mathbf{g}^{m}_{c}(t)}\) pair for two evolutions can be introduced. For the purpose of clarity of the presentation, it is taken as \({\mathbf{h}_{1}(t) = \mathbf{u}_{1}(t)}\) and \({\mathbf{h}_{2}(t) = \mathbf{u}_{2}(t)}\). Rest of the parameters are also changed accordingly,

\(\bullet \)    Algorithm 1

$$\begin{aligned} \mathbf{g}^{1}_{1}(t)= & {} \mathbf{C}^{-1}{\mathbf{Rh}_{1}}(t) \end{aligned}$$
(39)
$$\begin{aligned} \mathbf{g}^{m}_{1}(t)= & {} \mathbf{C}^{-1}{\mathbf{Rh}^{m-1}_{1}}(t) \end{aligned}$$
(40)

\(\bullet \)    Algorithm 2

$$\begin{aligned} \mathbf{g}^{1}_{2}(t)= & {} (\mathbf{CR})^{-1}{\mathbf{h}_{2}}(t)\end{aligned}$$
(41)
$$\begin{aligned} \mathbf{g}^{m}_{2}(t)= & {} (\mathbf{CR})^{-1}{\mathbf{h}^{m-1}_{2}}(t) \end{aligned}$$
(42)

For the iteration \({m}\) of any of the solutions described for DS-CDMA is the same as (16),

$$\begin{aligned} \mathbf{h}^{m}_{c}(t) = {\frac{\mathbf{g}^{m}_{c}(t)}{\left\| \mathbf{g}^{m}_{c}(t) \right\| }} \end{aligned}$$
(43)

Refined receive signal similar to (4) is,

$$\begin{aligned} y_j(t+(p-1)\tau ) = \mathbf{h}^{m*}_{c}(t){r_j(t+(p-1)\tau )} \end{aligned}$$
(44)

Signal after EGC used for despreading can be expressed as,

$$\begin{aligned} \mathbf{y}_j(t) = \frac{\mathbf{h}^{m*}_{c}(t)}{P}\frac{\mathbf{A}^{*}}{|\mathbf{A}|}\sum _{p=1}^{P}{r_j(t+(p-1)\tau )} \end{aligned}$$
(45)

3 System models

Two system models for OFDM and DS-CDMA are separately considered under the same conditions.

3.1 OFDM model

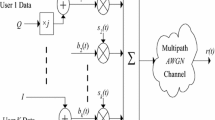
Elementary system model used for discrete time base band simulations is given in Fig. 1a. The single transmit and single receive antenna setup is equipped with an OFDM transmitter and a receiver [6, 14] and it is assumed that systems are properly synchronized under all the conditions. Performance is tested under slow fading frequency-selective Rayleigh downlink channel conditions containing Rayleigh distributed amplitude and uniformly distributed phase values. Receiver is supplemented with lesser complex iterative BSS algorithms with multiple sampling for each receive symbol on each subcarrier. It is assumed that perfect path gain values are available at the receiver. EGC, one of the most stable combining technique is used to treat CSIs. Same system model without multiple sampling is used in order to test and verify the results of standard OFDM system [6, 14].

3.2 DS-CDMA model

Single transmit and single receive antenna discrete time base band DS-CDMA [6, 16] simulation system model is shown in Fig. 1b. \({K}\) users can be handled by the Walsh–Hadamard spreading sequences [16] of the system functioning in synchronous mode. The wireless communication system is operated in a slow fading frequency selective downlink channel. Lesser complex iterative BSS algorithms are employed at the receiver where multiple samples are taken from each receive spread code element. One of the stable conventional combining technique namely EGC is used for remedial actions for the distortions caused by the path gain values and it is assumed that perfect path gain values are available at the receiver. Same system model is used to verify the results of standard downlink synchronous DS-CDMA system with no multiple sampling for receive spread code elements.

4 System parameters and simulation results

System parameters and simulation results for the both categories of techniques are separately presented.

4.1 OFDM systems

Rudimentary or basic 64, 32 and 16 subcarrier OFDM transmitter receiver arrangements with a binary information bit generator and binary phase shift keying (BPSK) symbol mapping are used for carrying our simulations. Symbols are serial to parallel converted among subcarriers after interleaving and sent through the slow fading channel. Multiple signal samples from each symbol received on every subcarrier are taken for the purpose of using with the BSS scheme. By considering the characteristics of the channel [11] and time correlation properties of the binary wave forms [8] samples are taken only within the first 20 % of time duration of an information symbol. Each channel tap is modeled with 4 independent paths and it is assumed that there is no variation of the signal within duration of a symbol due to any other reason other than the channel. Since the system is operated under slow fading conditions the assumption becomes much stronger. Systems with the BSS schemes are configured to be operated a number of iterations using the fixed point rule.

Fig. 2
figure 2

OFDM systems with BSS and EGC a Algorithm 1 and b Algorithm 2

Full size image

In favor of the first set of simulations, variable number of subcarriers for the BSS scheme is considered. Performance results for 16, 32 and 64 subcarriers are obtained for this classification with 15 receive signal samples for each of the receive symbol on every subcarrier. Rest of the parameters and conditions of the model are maintained as the same. Outcome of the operations of the systems namely the OFDM system with the BSS algorithm and the standard OFDM system is presented in Fig. 2. The results of the scheme 1 and 2 worked out for 16, 32 and 64 subcarriers are given by Fig. 2a, b respectively. In this case the algorithms based OFDM systems are competent of outperforming the corresponding standard OFDM systems. But the iterative fixed point rule contributes destructively for the process of recovery of corrupted signals under these parameters.

Corroborative simulations conducted using the explained OFDM substructure with the BSS algorithm with different number of receive samples and standard OFDM system are shown in Fig. 3. Other parameters and conditions are maintained as the same. Performance is scrutinized for the BSS schemes carried out taking 5, 8 and 10 receive signal samples for the each algorithm are presented in Fig. 3a, b respectively. Outcome of the both algorithms with 10 samples is presented in Fig. 3c where the simulation curves of the two schemes fall in the vicinity of each other together with the standard OFDM system. Better bit error rates are demonstrated by the curves of taken for higher signal samples. Hence it could be resolved that a constructive contribution is done by a higher number of samples for the process of refinery of corrupted symbols under these parameters.

4.2 DS-CDMA systems

In order to evaluate performance, a series of simulations are carried out. Systems are operated with 32-users handled by 32 Walsh-Hadamard code matrices [16] with one transmit and one receive antenna setup. Sequences of binary information bits of each user are transformed to binary phase shift keying (BPSK) symbols and sent through the channel. A number of signal samples are taken corresponding to each of the receive spread code element. It is decided to take samples only within the first 20 % of time duration of each spread sequence element by considering the properties of the channel [11] and time correlation properties of the binary wave forms [8]. Each tap is modeled using 4 independent paths. Signal variations due to other reasons are not taken into consideration. This supposition becomes stronger, since the system is operated under slow fading channel conditions. Systems with BSS supplements are configured to be operated number of iterations using the fixed point rule.

Fig. 3
figure 3

OFDM system with BSS and EGC a Algorithm 1, b Algorithm 2 and c two algorithms with 10 samples

Full size image

Simulations are carried out with the BSS add-ons of the each system handling 2, 4, 8, 16 and 32 users. For the each of the receive spread code element, BSS solution are empowered with 5 receive signal samples and 2 iterations where all the other parameters and conditions are maintained as the same. Performance of the DS-CDMA systems with two BSS suggestions and standard DS-CDMA system is presented by Fig. 4 where the results for algorithm 1 and 2 are released in Fig. 4a, b respectively. As in Fig. 4a, b, performance curves of the two derivatives shows clear differences for each of the user case. Suggested algorithms perform well when the user number is higher. It could be observed that the standard DS-CDMA system is capable of outperforming all these algorithms except in one occasion.

Fig. 4
figure 4

32-user DS-CDMA systems with BSS and EGC a Algorithm 1 and b Algorithm 2

Full size image

Multiple variable number of receive samples are taken in the proposed two BSS offshoots. Sample size is changed as 5, 8 and 10 receive signal samples where performance of them is shown in Fig. 3. Rests of the parameters of the setup are maintained as the same. Results for the systems with BSS additives carried out for algorithm 1 and 2 are presented in Fig. 3a, b respectively. Outcome of the both algorithms in the case of 10 samples are shown in Fig. 3c where the simulation curves of them are in the vicinity of each other outperforming the standard or the normal DS-CDMA system. Performance improvement can be seen with the increase of number of receive samples and it is an apparent fact that the process of refinery of corrupted signals is contributed positively by taking a higher number of samples under these parameters.

5 Conclusion

A set of solutions developed based on BSS principles attempting to remove interference signals in a observe mixture in free space communication channels of OFDM and DS-CDMA transmissions was considered. In the case of OFDM performance was evaluated in recovery of information symbols mitigating the deteriorative influences under the categories of variable samples for receive signals and subcarriers for the systems. Similarly in the case of DS-CDMA performance was evaluated under the categories of variable samples for receive signals and variable number of users for the systems. Even though it was not quantified, the algorithms could be introduced as a low computational complexity scheme. More analysis about the algorithms can be done covering Doppler effect to cater to the real environment.