A logic of higher-order preferences

Abstract

If an agent prefers one kind of agents to the other agents, then the agent has first-order preferences. If the agent prefers agents with one kind of preferences to the other agents, then the agent has second-order preferences. The article proposes a sound, complete, and decidable logical system capable of expressing higher-order preferences.

1 Introduction

Logics for reasoning about preferences have been the subject of studies in philosophy, logic, and artificial intelligence for a long time. As with many other modal logics, the focus of the initial works was on finding the right language and writing intuitively acceptable axioms for this language. In the case of preferences, this approach was explored by Halldén (1957),  Åqvist (1962),  Chisholm and Sosa (1966), and  Von Wright (1963). After possible world semantics for modal logics became widely accepted, it became common to start not with intuition, but with a formal semantics of the proposed modality. Following this tradition, van Benthem, Girard, and Roy (2009) consider the modality $[>]\varphi$ meaning “statement $\varphi$ holds in all worlds better than the current one”. The same modality is also investigated in (Liu, 2011) and (Christoff et al., 2021). Even earlier, Lang, van der Torre, and Weydert (2002) considered a conditional version of this modality.

In addition to modality $[>]\varphi$, one can also consider modality $[\not >]\varphi$, meaning “statement $\varphi$ holds in all worlds not better than the current one”.¹ Then, formula $[\not >]\lnot \varphi$ means that all worlds in which $\varphi$ holds are better than the current world. One can combine modalities $[>]$ and $[\not >]$ to express the fact that statement $\varphi$ holds in worlds better than current and only them: $[>]\varphi \wedge [\not >]\lnot \varphi$.

In this article, we study preferences between agents rather than between worlds. Modalities $[>]$ and $[\not >]$ can be adopted for this purpose by using an egocentric logical system (Prior, 1968). In traditional logics, formulae capture properties of possible worlds. In egocentric logics, they capture the properties of agents. As a result, the semantics of an egocentric logic can be defined in terms of a satisfaction relation $a\Vdash \varphi$ between an agent a and a formula $\varphi$ rather than a relation $w\Vdash \varphi$ between a world w and a formula $\varphi$. In such a setting, statement $a\Vdash [>]\varphi$ means that property $\varphi$ holds for all agents better than agent a. Similarly, $a\Vdash [\not >]\varphi$ means that $\varphi$ is true for all agents who are not better than agent a.

Note that modalities $[>]$ and $[\not >]$ capture global preferences on agents, not the preferences of individual agents. The goal of the current work is to study individual preferences of agents about groups of agents. More specifically, we study the relation “agent a prefers any agent with property $\varphi$ to any agent who does not have this property”. If the relation holds, then we write $a\Vdash \textsf{L}\varphi$ and say that agent a “likes” $\varphi$. Thus, we use the word “preference” to refer to a relation on agents and the word “likes” to refer to the modality that captures the properties of the preferences. Modality $\textsf{L}$ can be nested to express higher-order preferences. For example, the statement $a\Vdash \textsf{L}\textsf{L}\text {``is a philosopher''}$ means that agent a likes those who like philosophers. Statement $a\Vdash \lnot \textsf{L}\lnot \textsf{L}\text {``is a philosopher''}$ means that agent a does not like those who do not like philosophers.

In some situations, there is no need for the “likes” modality $\textsf{L}$ because in those situations this modality can be expressed through already studied modality $\textsf{F}$ and its variation $\textsf{NF}$. Modality “for all friends” $\textsf{F}$ was proposed by Seligman, Liu, and Girard (2011) and is also used in (Seligman et al., 2013), (Christoff and Hansen, 2015), and (Christoff et al., 2016). It presupposes that each agent partitions the set of all agents into “friends” and “non-friends”. The statement $a\Vdash \textsf{F}\varphi$ is true if all friends of agent a have property $\varphi$. One can similarly consider the “for all non-friends” modality NF. The statement $a\Vdash \textsf{NF}\varphi$ is true if all non-friends of agent a have property $\varphi$. Let us now go back to preferences and consider an agent a with “good-or-bad” preferences in which agent a divides all agents into “good” and “bad”. Agent a prefers each good agent to each bad agent and has no other preferences. In such a situation, we can call “good” agents to be a’s friends and “bad” agents to be a’s non-friends. Then, the formula $\textsf{L}\varphi$ is equivalent to the formula $\textsf{F}\varphi \wedge \textsf{NF}\lnot \varphi$.

To further illustrate “good-or-bad” preferences, let us consider an example inspired by the quote

“Steve Jobs has a saying that A players hire A players; B players hire C players; and C players hire D players.” (Kawasaki, 2004, p. 101)

Fig. 1

The world according to Steve Jobs

We capture this quote by the diagram depicted in Fig. 1. Here all agents are partitioned into groups A, B, C, and D. The hiring preference relation of each group is depicted in the figure using directed edges. We assume that D-players have no preferences. Note that, in this example, each agent $c\in C$ prefer any D-player to any non-D-player. Thus, by our definition of the “likes” modality,

$$\begin{aligned} c \Vdash \textsf{L}\text {``is a}\,D\hbox { player}'' \hspace{10mm}\forall c\in C. \end{aligned}$$

(1)

Observe from Fig. 1 that the same is not true² for agents who are not C-players:

$$\begin{aligned} x \nVdash \textsf{L}\text {``is a}\,D\hbox { player}'' \hspace{5mm}\forall x\in A\cup B\cup D. \end{aligned}$$

(2)

Note that any agent $b\in B$ prefers any agent in group C to any agent in group $A\cup B\cup D$, see Fig. 1. Thus, taking into account statements (1) and (2), any agent $b\in B$ prefers any agent for whom $\textsf{L}\text {``is a}\, D\text { player''}$ is true to any agent for whom $\textsf{L}\text {``is a} \,D\text { player''}$ is false. Thus, any agent $b\in B$ likes those for whom $\textsf{L}\text {``is a}\,D \text { player''}$ is true:

$$\begin{aligned} b \Vdash \textsf{L}\textsf{L}\text {``is a}\,D\hbox { player}'' \hspace{10mm}\forall b\in B. \end{aligned}$$

In other words, B-players hire those who hire D-players.

Note that although, overall, the structure of the preferences in the Steve Jobs example is not so simple, the preferences of each individual agent are still of “good-or-bad” type. For example, for any agent $b\in B$, the “good” group is C and the “bad” group is $A\cup B\cup D$. Thus, “likes” modality $\textsf{L}$ still can be expressed through modalities $\textsf{F}$ and $\textsf{NF}$.

The situation is different for non “good-or-bad” preferences. For example, consider an agent a who divides all agents into three disjoint groups: “very good”, “good”, and “bad”. Suppose that agent a prefers each “very good” agent to each “good” and each “bad” agent. Also, a prefers each “good” agent to each “bad” agent. Then, a likes all agents in the first group:

$$\begin{aligned} a\Vdash \textsf{L}\text {``is a `very good' agent''} \end{aligned}$$

because a prefers each “very good” agent to any agent in the other two groups. At the same time, agent a also likes all agents in the first two groups:

$$\begin{aligned} a\Vdash \textsf{L}\text {``is not a `bad' agent''} \end{aligned}$$

becuse agent a prefers each agent who is not “bad” to any agent who is “bad”. Next, we will observe that in this setting modality $\textsf{L}\varphi$ is not equivalent to the formula $\textsf{F}\varphi \wedge \textsf{NF}\lnot \varphi$ no matter how we define who are the friends and the non-friends of agent a. Indeed, no matter how we divide agents into friends and non-friends, there is no way to satisfy both of the following formulae:

$$\begin{aligned} a\Vdash \textsf{F}\text {``is a `very good' agent''} \wedge \textsf{NF} \lnot \text {``is a `very good' agent''} \end{aligned}$$

(3)

and

$$\begin{aligned} a\Vdash \textsf{F}\text {``is not a `bad' agent''} \wedge \textsf{NF} \lnot \text {``is not a `bad' agent''}. \end{aligned}$$

(4)

For example, if only “very good” agents are identified as friends, then statement (3) is true, but statement (4) is not. At the same time, if “very good” and “good” agents are identified as friends, then it is the other way around.

In this article, we propose a formal semantics for modality $\textsf{L}$ in the egocentric setting and give a sound, complete, and decidable axiomatization of the properties of this modality. The completeness theorem is using a new technique based on relation $\sqsubseteq$, see Sect. 6.3.

The rest of this article is organised as follows. In Sect. 2, we give a formal definition of a preference model that we use later to give the semantics of modality $\textsf{L}$. In Sect. 3 we describe the syntax and semantics of our language. Section 4 lists the axioms and inference rules of our system. We prove its soundness and completeness in Sect. 5 and Sect. 6, respectively. In Sect. 7, we define “conditional likes” modality, list some of the axioms for it and prove that it is not definable through modality $\textsf{L}$. Section 8 concludes. A preliminary version of this work, containing a model checking algorithm for a richer language, but without the proof of completeness and the discussion of the conditional likes modality, appeared as (Jiang and Naumov, 2022).

2 Preference model

In this section, we introduce the notion of a preference model that serves as a foundation for the semantics of our logical system. In the article, we assume a fixed set of propositional variables $\mathcal {P}$.

Definition 1

A tuple $(\mathcal {A},\{\prec _a\}_{a\in \mathcal {A}},\pi )$ is called a preference model if

• 1. $\mathcal {A}$ is a (possibly empty) finite set of “agents”,

• 2. $\prec _a$ is a strict partial order “preference” relation on $\mathcal {A}$, for each agent $a\in \mathcal {A}$,

• 3. $\pi (p)$ is a subset of $\mathcal {A}$ for each variable $p\in \mathcal {P}$.

Note that, in general, strict and non-strict order relations are definable through each other: $x\preceq y\equiv (x\prec y \vee x=y)$ and $x\prec y\equiv (x\preceq y \wedge x \ne y)$. Thus, it does not matter which of them is chosen as the primitive relation and which is defined through the primitive. Hence, it is not significant that in the above definition we have chosen the strict relation $\prec _a$ as our primitive.

Note that propositional variables, just like all formulae in our language, represent noun-free fragments of propositions such as “is a philosopher”. Prior calls them subject-less predicates (1968). Grove and Halpern use the term relative propositions because they are relative to agents (Grove and Halpern, 1991; Grove & Halpern, 1993; Grove, 1995). To reflect this, item 3 of Definition 1 specifies the valuation $\pi (p)$ of a proposition variable p as a set of agents. Informally, these are the agents for which the propositional variable p is true.

3 Syntax and semantics

The language $\Phi$ of our system is defined by the grammar:

$$\begin{aligned} \varphi :=p\;|\;\lnot \varphi \;|\;\varphi \rightarrow \varphi \;|\;\textsf{L}\varphi , \end{aligned}$$

where $p\in \mathcal {P}$ is a propositional variable. We read $\textsf{L}$ as “likes those who”. We assume that disjunction $\vee$, conjunction $\wedge$, and biconditional $\leftrightarrow$ are defined in our language in the standard way. Next, we define the semantics of our logical system.

Definition 2

For any formula $\varphi \in \Phi$ and any agent $a\in \mathcal {A}$ of a preference model $(\mathcal {A},\{\prec _a\}_{a\in \mathcal {A}},\pi )$, the satisfaction relation $a\Vdash \varphi$ is defined recursively as follows.

• 1. $a\Vdash p$, if $a\in \pi (p)$,

• 2. $a\Vdash \lnot \varphi$, if $a\nVdash \varphi$,

• 3. $a\Vdash \varphi \rightarrow \psi$, if $a\nVdash \varphi$ or $a\Vdash \psi$,

• 4. $a\Vdash \textsf{L}\varphi$, when for all agents $b,c\in \mathcal {A}$, if $b\nVdash \varphi$ and $c\Vdash \varphi$, then $b\prec _a c$.

As we have discussed in Sect. 2, the choice to use strict preference relation $\prec _a$ in Definition 1 is not important. Irrespective of the choice of the primitive relation in Definition 1, one can consider either strict or non-strict preference relation in item 4 of Definition 2. We have chosen to use the strict preference relation there. The non-strict version of the same item will look like:

$$\begin{aligned} a\Vdash \textsf{L}\varphi ,\hbox { when for all agents }b,c\in \mathcal {A},\hbox { if }b\nVdash \varphi \hbox { and }c\Vdash \varphi ,\hbox { then }b\preceq _a c. \end{aligned}$$

(5)

However, note that the assumptions $b\nVdash \varphi$ and $c\Vdash \varphi$ in the above statement imply that $b\ne c$. Thus, statement (5) is equivalent to item 4 of Definition 2 and it does not matter which of them is used in Definition 2. To summarise, although we have chosen to use strict order in Definition 1 and Definition 2, nothing in our results will change if either of those places (or even in both of them) non-strict order is used instead of the strict one.

Some of the existing works on logics of preferences are based on ceteris paribus principle (Von Wright, 1963). If this principle is applied to modality “likes”, then one would say that an agent a likes $\varphi$ if she prefers agents for whom $\varphi$ is true to those for who $\varphi$ is not true, everything else being equal. Capturing the “everything else being equal” assumption semantically is a non-trivial task. One of the possible ways to do it is proposed in (Van Benthem et al., 2009). In this article, we do not use ceteris paribus principle³. Item 4 of the above definition states that an agent a likes $\varphi$ if she prefers each agent for whom $\varphi$ is true to each agent for whom $\varphi$ is not true. This definition is similar to how strong belief is defined in the literature: an agent strongly believes in $\varphi$ if she finds all epistemically possible worlds in which $\varphi$ is true to be more plausible than those where $\varphi$ is false (Baltag and Smets, 2009; Lorini, 2021). Lorini also proposes to define strong desires in a similar way.

We use $\textsf{A}\varphi$ as an abbreviation for the formula $\varphi \wedge \textsf{L}\varphi \wedge \textsf{L}\lnot \varphi$. Because of the next lemma, we read $\textsf{A}$ as “for all agents”.

Lemma 1

$a\Vdash \textsf{A}\varphi$ iff $b\Vdash \varphi$ for all agents $b\in \mathcal {A}$.

Proof

$(\Rightarrow ):$ Suppose that there is an agent $b\in \mathcal {A}$ such that $b\nVdash \varphi$. Note that the assumption $a\Vdash \textsf{A}\varphi$ of the lemma implies that $a\Vdash \varphi$ and $a\Vdash \textsf{L}\varphi$. Then, by item 4 of Definition 2, the assumption $b\nVdash \varphi$ implies that $b\prec _a a$.

At the same time, the assumption $b\nVdash \varphi$ implies $b\Vdash \lnot \varphi$ by item 2 of Definition 2. Note that the assumption $a\Vdash \textsf{A}\varphi$ of the lemma also implies that $a\Vdash \varphi$ and $a\Vdash \textsf{L}\lnot \varphi$. Then, $a\prec _a b$ again by item 4 of Definition 2.

Finally, note that statements $b\prec _a a$ and $a\prec _a b$ are inconsistent because relation $\prec _a$ is a strict partial order by item 2 of Definition 1.

$(\Leftarrow ):$ Suppose that $a\nVdash \varphi \wedge \textsf{L}\varphi \wedge \textsf{L}\lnot \varphi$. Thus, one of the following cases takes place.

Case I: $a\nVdash \varphi$. Then, there is an agent b such that $b\nVdash \varphi$.

Case II: $a\nVdash \textsf{L}\varphi$. Hence, by item 4 of Definition 2, there are agents $b,c\in \mathcal {A}$ such that $b\nVdash \varphi$, $c\Vdash \varphi$, and $b\nprec _a c$. So, there is an agent b such that $b\nVdash \varphi$.

Case III: $a\nVdash \textsf{L}\lnot \varphi$. Thus, again by item 4 of Definition 2, there are agents $b,c\in \mathcal {A}$ such that $b\nVdash \lnot \varphi$, $c\Vdash \lnot \varphi$, and $b\nprec _a c$. Therefore, $c\nVdash \varphi$ by item 2 of Definition 2. $\square$

The lemma below follows from item 4 of Definition 2.

Lemma 2

For any preference model, if $a\Vdash \varphi \leftrightarrow \psi$ for each agent $a\in \mathcal {A}$, then $a\Vdash \textsf{L}\varphi \leftrightarrow \textsf{L}\psi$ for each agent $a\in \mathcal {A}$.

4 Axioms

In this section, we list the axioms and the inference rules of our logical system. In addition to tautologies in language $\Phi$, the system contains the following axioms.

• 1. Reflexivity: $\textsf{A}\varphi \rightarrow \varphi$,

• 2. Distributivity: $\textsf{A}(\varphi \rightarrow \psi )\rightarrow (\textsf{A}\varphi \rightarrow \textsf{A}\psi )$,

• 3. Euclidianity: $\lnot \textsf{A}\varphi \rightarrow \textsf{A}\lnot \textsf{A}\varphi$,

• 4. Substitution: $\textsf{A}(\varphi \leftrightarrow \psi )\rightarrow (\textsf{L}\varphi \rightarrow \textsf{L}\psi )$,

• 5. Coherence of Preferences: $\textsf{L}\varphi \wedge \textsf{L}\psi \rightarrow \textsf{A}(\varphi \rightarrow \psi )\vee \textsf{A}(\psi \rightarrow \varphi )$.

The meaning of the first four axioms above is straightforward. The Coherence of Preferences axiom states that if an agent likes those for whom $\varphi$ is true and also those for whom $\psi$ is true, then either each $\varphi$-agent is a $\psi$-agent or each $\psi$-agent is a $\varphi$-agent. This is the most non-trivial axiom of our system. We prove its soundness in Lemma 10.

We write $\vdash \varphi$ and say that formula $\varphi \in \Phi$ is a theorem of our logical system if it can be derived from the above axioms using the Modus Ponens and the Necessitation inference rules:

$$\begin{aligned} \dfrac{\varphi ,\varphi \rightarrow \psi }{\psi } \hspace{15mm} \dfrac{\varphi }{\textsf{A}\varphi }. \end{aligned}$$

In addition to unary relation $\vdash \varphi$ we also use binary relation $X\vdash \varphi$. We write $X\vdash \varphi$ if formula $\varphi$ is derivable from the theorems of our logical system and the set of additional formulae X using only the Modus Ponens inference rule. It is easy to see that statements $\varnothing \vdash \varphi$ and $\vdash \varphi$ are equivalent. We say that set X is consistent if there is no formula $\varphi \in \Phi$ such that $X\vdash \varphi$ and $X\vdash \lnot \varphi$.

Lemma 3

(Lindenbaum) For any set of formulae X, any consistent subset of X can be extended to a maximal consistent subset of X.

Proof

The standard proof of Lindenbaum’s lemma ((Mendelson, 2009), Proposition 2.14) applies here.$\square$

The proofs of the next three standard lemmas can be found in the appendix.

Lemma 4

(deduction) If $X,\varphi \vdash \psi$, then $X\vdash \varphi \rightarrow \psi$.

Lemma 5

(Transitivity) $\vdash \textsf{A}\varphi \rightarrow \textsf{A}\textsf{A}\varphi$.

Lemma 6

If $\varphi _1,\dots ,\varphi _n\vdash \psi$, then $\textsf{A}\varphi _1,\dots ,\textsf{A}\varphi _n\vdash \textsf{A}\psi$.

5 Soundness

In this section, we prove the soundness of our logical system.

Theorem 1

(soundness) If $\vdash \varphi$, then $a\Vdash \varphi$ for each agent a of each preference model.

The soundness of the Reflexivity axiom as well as of the Modus Ponens and the Necessitation inference rules is straightforward. To improve readability, we prove the soundness of each remaining axiom as a separate lemma.

Lemma 7

(Distributivity) If $a\Vdash \textsf{A}(\varphi \rightarrow \psi )$ and $a\Vdash \textsf{A}\varphi$, then $a\Vdash \textsf{A}\psi$.

Proof

Consider any agent $b\in \mathcal {A}$. By Lemma 1, it suffices to show that $b\Vdash \psi$. Indeed, by the same Lemma 1, the assumptions $a\Vdash \textsf{A}(\varphi \rightarrow \psi )$ and $a\Vdash \textsf{A}\varphi$ imply $b\Vdash \varphi \rightarrow \psi$ and $b\Vdash \varphi$, respectively. Therefore, $b\Vdash \psi$ by item 3 of Definition 2. $\square$

Lemma 8

(Euclidianity) If $a\nVdash \textsf{A}\varphi$, then $a\Vdash \textsf{A}\lnot \textsf{A}\varphi$.

Proof

Consider any $b\in \mathcal {A}$. By Lemma 1, it suffices to show that $b\Vdash \lnot \textsf{A}\varphi$.

Again by Lemma 1, the assumption $a\nVdash \textsf{A}\varphi$ implies that there is an agent $c\in \mathcal {A}$ such that $c\nVdash \varphi$. Thus, $b\nVdash \textsf{A}\varphi$ also by Lemma 1. Therefore, $b\Vdash \lnot \textsf{A}\varphi$ by item 2 of Definition 2. $\square$

Lemma 9

(Substitution) If $a\Vdash \textsf{A}(\varphi \leftrightarrow \psi )$ and $a\Vdash \textsf{L}\varphi$, then $a\Vdash \textsf{L}\psi$.

Proof

Consider any agents $b,c\in \mathcal {A}$ such that $b\nVdash \psi$ and $c\Vdash \psi$. By item 4 of Definition 2, it suffices to show that $b\prec _a c$.

By Lemma 1, the assumption $a\Vdash \textsf{A}(\varphi \leftrightarrow \psi )$ implies that $b\Vdash \varphi \leftrightarrow \psi$ and $c\Vdash \varphi \leftrightarrow \psi$. Hence, $b\nVdash \varphi$ and $c\Vdash \varphi$ by the assumptions $b\nVdash \psi$ and $c\Vdash \psi$, respectively. Therefore, $b\prec _a c$ by item 4 of Definition 2 and the assumption $a\Vdash \textsf{L}\varphi$ of the lemma.$\square$

Lemma 10

(Coherence of preferences) If $a\Vdash \textsf{L}\varphi$ and $a\Vdash \textsf{L}\psi$, then either $a\Vdash \textsf{A}(\varphi \rightarrow \psi )$ or $a\Vdash \textsf{A}(\psi \rightarrow \varphi )$.

Proof

Suppose that $a\nVdash \textsf{A}(\varphi \rightarrow \psi )$ and $a\nVdash \textsf{A}(\psi \rightarrow \varphi )$. Thus, by Lemma 1, there are agents $b,c\in \mathcal {A}$ such that $b\nVdash \varphi \rightarrow \psi$ and $c\nVdash \psi \rightarrow \varphi$. Hence, by item 3 of Definition 2,

$$\begin{aligned} b\Vdash \varphi , \hspace{7mm} b\nVdash \psi , \hspace{7mm} c\Vdash \psi , \hspace{7mm} c\nVdash \varphi . \end{aligned}$$

(6)

By item 4 of Definition 2, the assumption $a\Vdash \textsf{L}\varphi$ of the lemma and parts $c\nVdash \varphi$ and $b\Vdash \varphi$ of statement (6) imply

$$\begin{aligned} c\prec _a b. \end{aligned}$$

(7)

At the same time, by item 4 of Definition 2, the assumption $a\Vdash \textsf{L}\psi$ of the lemma and parts $c\Vdash \psi$ and $b\nVdash \psi$ of statement (6) imply $b\prec _a c$. Hence, $c\nprec _a b$ because $\prec _a$ is a strict partial order relation by Definition 1. This is a contradiction with statement (7).$\square$

6 Completeness and decidability

In this section, we prove the completeness of our logical system and also show that our system is decidable. As usual, the proof of completeness relies on a construction of a canonical model. In modal logic, the worlds of a canonical model are usually defined as maximal consistent sets of formulae. Since the formal semantics of our language, given in Definition 2, defines the satisfaction $\Vdash$ as a relation between an agent and a formula, in our system, the agents play a role somewhat similar to the role of worlds in traditional modal logics. In particular, we define agents as maximal consistent sets of formulae.

There are two major challenges that we faced while constructing the canonical model. First, Definition 1 requires the set of agents $\mathcal {A}$ to be finite. To guarantee the finiteness of the canonical model, we employ the filtration technique. Usually, this technique requires to restrict the language to subformulae of the formulae $\varphi$ for which the canonical model is constructed. This approach fails in our case because the proof of completeness requires us to deal with formulae which are not subformulae of formula $\varphi$. To solve the problem, instead of subformulae of $\varphi$ we consider a larger “saturated” set of formulae. We define the notion of a saturated set and prove its property in Sect. 6.1.

The other challenge in the proof of completeness is to give a definition of the preference relation $\prec _a$ that guarantees that the relation is transitive. We give such a definition and a non-trivial proof of transitivity in Sect. 6.2 as a part of the canonical model description.

At the core of our proof of completeness is the truth lemma proven by induction on the size of a formula. In our case, this lemma states that, in the canonical model, $a\Vdash \psi$ if and only if formula $\psi$ belongs to the maximal consistent set a of formulae. To make the proof of this lemma more readable, we separated the major case in the induction step of the proof into a separate lemma stated and proven in Sect. 6.3. We use this lemma in Sect. 6.4 to prove the truth lemma and to finish the proof of completeness.

6.1 Saturated set

As a part of the proof, we use the technique known as filtration to guarantee that the set of agents in the canonical model is finite. To do filtration, we restrict some formulae to those in a finite “saturated” set $\Phi _0$. Notions similar to our “saturated” set have been used before (Goranko & van Drimmele, 2006, p. 102).

Definition 3

Set of formulae $\Phi _0\subseteq \Phi$ is saturated if it is closed with respect to subformulae and

• 1. if $\varphi \in \Phi _0$ and formula $\varphi$ is not a negation, then $\lnot \varphi \in \Phi _0$,

• 2. if $\textsf{A}\varphi \in \Phi _0$, then $\lnot \varphi \in \Phi _0$,

• 3. if $\textsf{L}\varphi \in \Phi _0$, then $\lnot \varphi \in \Phi _0$.

Lemma 11

Any finite set of formulae can be extended to a finite saturated set of formulae.

Proof

Let $X\subseteq \Phi$ be any finite set of formulae. Consider the set

$$\begin{aligned} \Phi _0=\{\psi ,\lnot \psi \;|\; \psi \hbox { is a subformula of some formula in set }X\}. \end{aligned}$$

Note that set $\Phi _0$ is a finite extension of set X. To finish the proof of the lemma, it suffices to verify conditions 1–3 from Definition 3.

To verify condition 1, consider any formula $\varphi \in \Phi _0$ which is not a negation. Thus, by the choice of set $\Phi _0$, formula $\varphi$ itself must be a subformula of some formula in set X. Therefore, $\lnot \varphi \in \Phi _0$ by the choice of set $\Phi _0$.

To verify condition 3, consider any formula $\textsf{L}\varphi \in \Phi _0$. Again by the choice of set $\Phi _0$, formula $\textsf{L}\varphi$ must be a subformula of some formula in set X. Then, formula $\varphi$ is also a subformula of some formula in set X. Therefore, $\lnot \varphi \in \Phi _0$ by the choice of set $\Phi _0$.

To verify condition 2, consider any formula $\textsf{A}\varphi \in \Phi _0$. Thus, by the definition of modality $\textsf{A}$, it follows that $\varphi \wedge \textsf{L}\varphi \wedge \textsf{L}\lnot \varphi \in \Phi _0$. Then, again by the choice of set $\Phi _0$, formula $\varphi$ must be a subformula of some formula in set X. Hence, $\lnot \varphi \in \Phi _0$ by the choice of set $\Phi _0$. $\square$

6.2 Canonical preference model

In this subsection, we construct a canonical preference model for our logical system. First, for any saturated set of formulae $\Phi _0$, by set $\Phi ^*_0$ we denote the set of formulae

$$\begin{aligned} \Phi ^*_0= & {} \Phi _0\cup \{\textsf{A}\varphi \;|\;\varphi \in \Phi _0\}\cup \{\textsf{A}\lnot \varphi \;|\;\varphi \in \Phi _0\}\nonumber \\{} & {} \cup \;\{\textsf{A}(\varphi \rightarrow \psi )\;|\;\varphi ,\psi \in \Phi _0\} \cup \,\{\lnot \textsf{A}(\varphi \rightarrow \psi )\;|\;\varphi ,\psi \in \Phi _0\}. \end{aligned}$$

(8)

Next, for any saturated set of formulae $\Phi _0$ and any maximal consistent set $a_0\subseteq \Phi ^*_0$, we define canonical preference model

$$\begin{aligned} N(\Phi _0,a_0)=(\mathcal {A},\{\prec _a\}_{a\in \mathcal {A}},\pi ). \end{aligned}$$

Definition 4

$\mathcal {A}$ is the set of all maximal consistent sets $a\subseteq \Phi ^*_0$ such that

$$\begin{aligned} \{\textsf{A}\varphi \;|\;\textsf{A}\varphi \in a_0\}\cup \{\lnot \textsf{A}\varphi \;|\;\lnot \textsf{A}\varphi \in a_0\}\subseteq a. \end{aligned}$$

Lemma 12

$a_0\in \mathcal {A}$.

Our definition of relation $\prec _a$ in the canonical preference model is chosen to match item 4 of Definition 2.

Definition 5

For any agents $a,b,c\in \mathcal {A}$, let $b\prec _a c$ if there is a formula $\textsf{L}\varphi \in \Phi _0$ such that $\textsf{L}\varphi \in a$, $\varphi \notin b$, and $\varphi \in c$.

Note that the transitivity of the relation $\prec _a$ is non-obvious and, perhaps, surprising. We prove it as a part of the lemma below using the axioms of our logical system.

Lemma 13

For each agent $a\in \mathcal {A}$, relation $b\prec _a c$ is a strict partial order on set $\mathcal {A}$.

Proof

We show the irreflexivity and the transitivity of relation $\prec _a$ separately:

Irreflexivity Suppose that there is an agent $b\in \mathcal {A}$ such that $b\prec _a b$. Thus, by Definition 5, there is a formula $\textsf{L}\varphi \in a$ such that $\varphi \notin b$ and $\varphi \in b$, which is a contradiction.

Transitivity Suppose that $b\prec _a c$ and $c\prec _a d$ for some agents $b,c,d\in \mathcal {A}$. Thus, by Definition 5, there are formulae $\textsf{L}\varphi \in \Phi _0$ and $\textsf{L}\psi \in \Phi _0$ such that

$$\begin{aligned} \textsf{L}\varphi \in a, \hspace{5mm} \varphi \notin b, \hspace{5mm} \varphi \in c. \end{aligned}$$

(9)

and

$$\begin{aligned} \textsf{L}\psi \in a, \hspace{5mm} \psi \notin c, \hspace{5mm} \psi \in d. \end{aligned}$$

(10)

By Definition 3, the assumptions $\textsf{L}\varphi \in \Phi _0$ and $\textsf{L}\psi \in \Phi _0$ imply that $\varphi ,\psi \in \Phi _0$. Thus, by Eq. (8),

$$\begin{aligned}&\textsf{A}(\varphi \rightarrow \psi )\in \Phi ^*_0,\hspace{5mm} \textsf{A}(\psi \rightarrow \varphi )\in \Phi ^*_0, \end{aligned}$$

(11)

$$\begin{aligned}&\lnot \textsf{A}(\varphi \rightarrow \psi )\in \Phi ^*_0,\hspace{5mm} \lnot \textsf{A}(\psi \rightarrow \varphi )\in \Phi ^*_0. \end{aligned}$$

(12)

Note that by the Coherence of Preference axiom and propositional reasoning, the part $\textsf{L}\varphi \in a$ of statement (9) and the part $\textsf{L}\psi \in a$ of statement (10) imply

$$\begin{aligned} a\vdash \textsf{A}(\varphi \rightarrow \psi )\vee \textsf{A}(\psi \rightarrow \varphi ). \end{aligned}$$

Hence, either $\textsf{A}(\varphi \rightarrow \psi )\in a$ or $\textsf{A}(\psi \rightarrow \varphi )\in a$ by the maximality of set $a\subseteq \Phi ^*_0$ and the statement (11). We consider these two cases separately:

Case I $\textsf{A}(\varphi \rightarrow \psi )\in a$. Then, $\lnot \textsf{A}(\varphi \rightarrow \psi )\notin a$ because set a is consistent. Thus, $\lnot \textsf{A}(\varphi \rightarrow \psi )\notin a_0$ by Definition 4 and the assumption $a\in \mathcal {A}$ of the lemma. Hence, $\textsf{A}(\varphi \rightarrow \psi )\in a_0$ by statements (11) and (12) and because $a_0$ is a maximal consistent subset of $\Phi ^*_0$. Then, $\textsf{A}(\varphi \rightarrow \psi )\in c$ by Definition 4 and the assumption $c\in \mathcal {A}$. Then, $c\vdash \varphi \rightarrow \psi$ by the Reflexivity axiom and the Modus Ponens inference rule. Thus, $c\vdash \psi$ by part $\varphi \in c$ of statement (9). Note that the assumption $\textsf{L}\psi \in \Phi _0$ implies that $\psi \in \Phi _0$ because by Definition 3 set $\Phi _0$ is closed with respect to subformulae. Therefore, $\psi \in c$ because set c is a maximal consistent subset of $\Phi _0$, which contradicts part $\psi \notin c$ of statement (10).

Case II $\textsf{A}(\psi \rightarrow \varphi )\in a$. Then, $\lnot \textsf{A}(\psi \rightarrow \varphi )\notin a$ because set a is consistent. Thus, $\lnot \textsf{A}(\psi \rightarrow \varphi )\notin a_0$ by Definition 4 and the assumption $a\in \mathcal {A}$ of the lemma. Hence, $\textsf{A}(\psi \rightarrow \varphi )\in a_0$ by statements (11) and (12) and because $a_0$ is a maximal consistent subset of $\Phi ^*_0$. Then, $\textsf{A}(\psi \rightarrow \varphi )\in d$ by Definition 4 and the assumption $d\in \mathcal {A}$. Then, $d\vdash \psi \rightarrow \varphi$ by the Reflexivity axiom and the Modus Ponens inference rule. Thus, $d\vdash \varphi$ by part $\psi \in d$ of statement (10). Note that the assumption $\textsf{L}\varphi \in \Phi _0$ implies that $\varphi \in \Phi _0$ because by Definition 3 set $\Phi _0$ is closed with respect to subformulae. Hence, $\varphi \in d$ because set d is a maximal consistent subset of $\Phi _0$. Therefore, $b\prec _a d$ by Definition 5 using parts $\textsf{L}\varphi \in a$ and $\varphi \notin b$ of statement (9). $\square$

Definition 6

$\pi (p)=\{a\in \mathcal {A}\;|\; p\in a\}$ for each propositional variable $p\in \mathcal {P}$.

The canonical preference model $N(\Phi _0,a_0)=(\mathcal {A},\{\prec _a\}_{a\in \mathcal {A}},\pi )$ is now completely defined.

6.3 Auxiliary lemma

At the core of our proof of completeness is “truth” (or “induction”) Lemma 15. In this subsection, we prove an auxiliary lemma used during the induction step of the proof of Lemma 15.

Lemma 14

For any agent $a\in \mathcal {A}$ and any formula $\textsf{L}\varphi \in \Phi _0$, if $\textsf{L}\varphi \notin a$, then there are agents $b,c\in \mathcal {A}$ such that $\varphi \notin b$, $\varphi \in c$, and $b\nprec _a c$.

Proof Outline. To prove the existence of agents b and c, we construct two consistent sets, $X_{k'}$ and Y and define agents c and b as maximal consistent extensions of sets $X_{k'}$ and Y, respectively.

Defining sets $X_{k'}$ and Y is not a trivial task. First, we introduce a total order $\sqsubseteq$ on a certain class of formulae $\varDelta$. Then, we use this total order to define a finite sequence of sets of formulae $X_0,X_1,\dots ,X_n$. Finally, we choose set $X_{k'}$ to be the last consistent set in this sequence. We use index $k'$ of set $X_{k'}$ in the sequence $X_0,X_1,\dots ,X_n$ to define set Y.

Once sets $X_{k'}$ and Y are chosen and extended to maximal consistent sets c and b, we verify that the two later sets satisfy the conditions of the lemma.

Proof

Consider the set of formulae

$$\begin{aligned} \varDelta =\{\delta \in \Phi _0\;|\;\textsf{L}\delta \in a\}. \end{aligned}$$

(13)

Next, we define a binary relation $\sqsubseteq$ on set $\varDelta$. For any formulae $\delta ,\delta '\in \varDelta$, let

$$\begin{aligned} {\delta \sqsubseteq \delta '\hbox { iff }\textsf{A}(\delta \rightarrow \delta ')\in a}. \end{aligned}$$

(14)

Claim Relation $\sqsubseteq$ is a total preorder on set $\varDelta$.

Proof of Claim We need to show that the relation is reflexive, transitive, and total.

Reflexivity Consider any formula $\delta \in \varDelta$. It suffices to show that $\delta \sqsubseteq \delta$. Indeed, the formula $\delta \rightarrow \delta$ is a propositional tautology. Thus, by the Necessitation inference rule,

$$\begin{aligned} \vdash \textsf{A}(\delta \rightarrow \delta ). \end{aligned}$$

(15)

At the same time, the assumption $\delta \in \varDelta$ implies that $\delta \in \Phi _0$ by Eq. (13). Hence, $\textsf{A}(\delta \rightarrow \delta )\in \Phi ^*_0$ by Eq. (8). Then, $\textsf{A}(\delta \rightarrow \delta )\in a$ by statement (15) and because a is a maximal consistent subset of $\Phi ^*_0$. Therefore, $\delta \sqsubseteq \delta$ by statement (14).

Transitivity Consider any formulae $\delta _1,\delta _2,\delta _3\in \varDelta$ such that $\delta _1\sqsubseteq \delta _2$ and $\delta _2\sqsubseteq \delta _3$. It suffices to show that $\delta _1\sqsubseteq \delta _3$. Indeed, by statement (14), the assumptions $\delta _1\sqsubseteq \delta _2$ and $\delta _2\sqsubseteq \delta _3$ imply that

$$\begin{aligned} \textsf{A}(\delta _1\rightarrow \delta _2)\in a \;\;\; \text{ and } \;\;\; \textsf{A}(\delta _2\rightarrow \delta _3)\in a. \end{aligned}$$

(16)

Note that the formula

$$\begin{aligned} (\delta _1\rightarrow \delta _2) \rightarrow ((\delta _2\rightarrow \delta _3)\rightarrow (\delta _1\rightarrow \delta _3)) \end{aligned}$$

is a propositional tautology. Thus, by the Necessitation inference rule,

$$\begin{aligned} \vdash \textsf{A}((\delta _1\rightarrow \delta _2) \rightarrow ((\delta _2\rightarrow \delta _3)\rightarrow (\delta _1\rightarrow \delta _3))). \end{aligned}$$

Hence, by the Distributivity axiom and the Modus Ponens inference rule,

$$\begin{aligned} \vdash \textsf{A}(\delta _1\rightarrow \delta _2) \rightarrow \textsf{A}((\delta _2\rightarrow \delta _3)\rightarrow (\delta _1\rightarrow \delta _3)). \end{aligned}$$

Then, by the Modus Ponens inference rule and the part $\textsf{A}(\delta _1\rightarrow \delta _2)\in a$ of statement (16),

$$\begin{aligned} a\vdash \textsf{A}((\delta _2\rightarrow \delta _3)\rightarrow (\delta _1\rightarrow \delta _3)). \end{aligned}$$

Thus, by the Distributivity axiom and the Modus Ponens inference rule,

$$\begin{aligned} a\vdash \textsf{A}(\delta _2\rightarrow \delta _3)\rightarrow \textsf{A}(\delta _1\rightarrow \delta _3). \end{aligned}$$

Hence, by the Modus Ponens inference rule and part $\textsf{A}(\delta _2\rightarrow \delta _3)\in a$ of statement (16),

$$\begin{aligned} a\vdash \textsf{A}(\delta _1\rightarrow \delta _3). \end{aligned}$$

(17)

The assumption $\delta _1,\delta _3\in \varDelta$ implies that $\delta _1,\delta _3\in \Phi _0$ by Eq. (13). Hence, we have $\textsf{A}(\delta _1\rightarrow \delta _3)\in \Phi ^*_0$ by Eq. (8). Then, $\textsf{A}(\delta _1\rightarrow \delta _3)\in a$ by statement (17) and because a is a maximal consistent subset of $\Phi ^*_0$. Therefore, $\delta _1\sqsubseteq \delta _3$ by statement (14).

Totality Consider any formulae $\delta _1,\delta _2\in \varDelta$. It suffices to show that either $\delta _1\sqsubseteq \delta _2$ or $\delta _2\sqsubseteq \delta _1$. Indeed, by Eq. (13), the assumption $\delta _1,\delta _2\in \varDelta$ implies that $\textsf{L}\delta _1\in a$ and $\textsf{L}\delta _2\in a$. Thus, by the Coherence of Preferences axiom and propositional reasoning,

$$\begin{aligned} a\vdash \textsf{A}(\delta _1\rightarrow \delta _2)\vee \textsf{A}(\delta _2\rightarrow \delta _1). \end{aligned}$$

(18)

At the same time, the assumption $\delta _1,\delta _2\in \varDelta$ implies $\delta _1,\delta _2\in \Phi _0$ by Eq. (13). Hence, $\textsf{A}(\delta _1\rightarrow \delta _2)\in \Phi ^*_0$ and $\textsf{A}(\delta _2\rightarrow \delta _1)\in \Phi ^*_0$ by Eq. (8). Then, statement (18) implies that either $\textsf{A}(\delta _1\rightarrow \delta _2)\in a$ or $\textsf{A}(\delta _2\rightarrow \delta _1)\in a$, because set a is a maximal consistent subset of $\Phi ^*_0$. Therefore, either $\delta _1\sqsubseteq \delta _2$ or $\delta _2\sqsubseteq \delta _1$ by statement (14).

Note that set $\varDelta$ is finite by Eq. (13) and because set $\Phi _0$ is finite. Let

$$\begin{aligned} \delta _1\sqsubseteq \delta _2\sqsubseteq \dots \sqsubseteq \delta _n \end{aligned}$$

(19)

be any ordering of set $\varDelta$ with respect to relation $\sqsubseteq$. Note that there might exist formulae $\delta ,\delta '\in \varDelta$ such that $\delta \sqsubseteq \delta '$ and $\delta '\sqsubseteq \delta$. Thus, ordering (19) might be not unique. We fix any such ordering.

For any integer k, such that $0\le k\le n$, define a set of formulae

$$\begin{aligned} X_k=\{\varphi \}\cup \{\lnot \delta _1,\dots ,\lnot \delta _k\}\cup \{\textsf{A}\psi \;|\;\textsf{A}\psi \in a_0\}\cup \,\{\lnot \textsf{A}\chi \;|\;\lnot \textsf{A}\chi \in a_0\}. \end{aligned}$$

(20)

Claim Set $X_0$ is consistent.

Proof of Claim Suppose the opposite. Thus, there are formulae

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\in a_0 \end{aligned}$$

(21)

such that

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\vdash \lnot \varphi .\end{aligned}$$

Hence, by Lemma 6,

$$\begin{aligned} \textsf{A}\textsf{A}\psi _1,\dots ,\textsf{A}\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _t\vdash \textsf{A}\lnot \varphi . \end{aligned}$$

Then, by Lemma 5 and the Modus Ponens inference rule applied m times,

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _t\vdash \textsf{A}\lnot \varphi . \end{aligned}$$

Thus, by the Euclidianity axiom and the Modus Ponens inference rule applied t times,

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\vdash \textsf{A}\lnot \varphi . \end{aligned}$$

Hence, by assumption (21),

$$\begin{aligned} a_0\vdash \textsf{A}\lnot \varphi . \end{aligned}$$

(22)

The assumption $\textsf{L}\varphi \in \Phi _0$ of the lemma implies that $\varphi \in \Phi _0$ by Definition 3. Hence, $\textsf{A}\lnot \varphi \in \Phi ^*_0$ by Eq. (8). Then, $\textsf{A}\lnot \varphi \in a_0$ by statement (22) and because set $a_0$ is a maximal consistent subset of $\Phi ^*_0$. Thus, $\textsf{A}\lnot \varphi \in a$ by Definition 4. Hence, by the definition of modality $\textsf{A}$,

$$\begin{aligned} \lnot \varphi \wedge \textsf{L}\lnot \varphi \wedge \textsf{L}\lnot \lnot \varphi \in a. \end{aligned}$$

(23)

Note that $\lnot \lnot \varphi \leftrightarrow \varphi$ is a propositional tautology. Thus, $\vdash \textsf{A}(\lnot \lnot \varphi \leftrightarrow \varphi )$ by the Necessitation inference rule. Hence, $\vdash \textsf{L}\lnot \lnot \varphi \rightarrow \textsf{L}\varphi$ by the Substitution axiom and the Modus Ponens inference rule. Hence, $a\vdash \textsf{L}\varphi$ by Eq. (23) and propositional reasoning. Therefore, $\textsf{L}\varphi \in a$ by the assumption $\textsf{L}\varphi \in \Phi _0\subseteq \Phi ^*_0$ of the lemma and because a is a maximal consistent subset of $\Phi ^*_0$, which contradicts the assumption $\textsf{L}\varphi \notin a$ of the lemma.

Set $X_0$ is consistent by the claim above. Let $k'$ to be the maximal $k\le n$ such that $X_k$ is consistent. Consider the set of formulae

$$\begin{aligned} Y= & {} \{\lnot \varphi \}\cup \{\delta _{k'+1},\dots ,\delta _{n}\}\cup \{\textsf{A}\psi \;|\;\textsf{A}\psi \in a_0\}\cup \,\{\lnot \textsf{A}\chi \;|\;\lnot \textsf{A}\chi \in a_0\}. \end{aligned}$$

(24)

Claim Set Y is consistent.

Proof of Claim We consider the following two cases separately:

Case I $k'<n$. Then, set $X_{k'+1}$ is inconsistent by the choice of integer $k'$. Suppose that Y is also inconsistent. Thus, there are formulae

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s\in a_0 \end{aligned}$$

(25)

$$\begin{aligned}{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t\in a_0 \end{aligned}$$

(26)

such that

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s, \lnot \delta _{k'+1},\lnot \delta _{k'},\lnot \delta _{k'-1},\dots , \lnot \delta _{1}\vdash \lnot \varphi ,\\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t, \delta _{k'+1},\delta _{k'+2},\delta _{k'+3},\dots , \delta _{n}\vdash \varphi . \end{aligned}$$

Hence, by the Modus Ponens inference rule applied $k'$ times to the first statement and $(n-k-1)$ times to the second one,

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s,\\{} & {} \hspace{10mm}\lnot \delta _{k'+1},\lnot \delta _{k'+1}\rightarrow \lnot \delta _{k'},\lnot \delta _{k'}\rightarrow \lnot \delta _{k'-1},\dots , \lnot \delta _{2}\rightarrow \lnot \delta _{1}\vdash \lnot \varphi ,\\ \\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{10mm}\delta _{k'+1},\delta _{k'+1}\rightarrow \delta _{k'+2},\delta _{k'+2}\rightarrow \delta _{k'+3},\dots , \delta _{n-1}\rightarrow \delta _{n}\vdash \varphi . \end{aligned}$$

Then, by Lemma 4 applied to both statements,

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s,\\{} & {} \hspace{10mm}\lnot \delta _{k'+1}\rightarrow \lnot \delta _{k'},\lnot \delta _{k'}\rightarrow \lnot \delta _{k'-1},\dots , \lnot \delta _{2}\rightarrow \lnot \delta _{1}\vdash \lnot \delta _{k'+1}\rightarrow \lnot \varphi ,\\ \\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{10mm}\delta _{k'+1}\rightarrow \delta _{k'+2},\delta _{k'+2}\rightarrow \delta _{k'+3},\dots , \delta _{n-1}\rightarrow \delta _{n}\vdash \delta _{k'+1}\rightarrow \varphi . \end{aligned}$$

Thus, by the law of contraposition applied $(k'+1)$ times to the first statement,

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s,\\{} & {} \hspace{10mm}\delta _{k'}\rightarrow \delta _{k'+1},\delta _{k'-1}\rightarrow \delta _{k'},\dots , \delta _{1}\rightarrow \delta _{2}\vdash \varphi \rightarrow \delta _{k'+1},\\ \\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{10mm}\delta _{k'+1}\rightarrow \delta _{k'+2},\delta _{k'+2}\rightarrow \delta _{k'+3},\dots , \delta _{n-1}\rightarrow \delta _{n}\vdash \delta _{k'+1}\rightarrow \varphi . \end{aligned}$$

Hence, by Lemma 6 applied to both statements,

$$\begin{aligned}{} & {} \textsf{A}\textsf{A}\psi _1,\dots ,\textsf{A}\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _s,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'}\rightarrow \delta _{k'+1}),\textsf{A}(\delta _{k'-1}\rightarrow \delta _{k'}),\dots , \textsf{A}(\delta _{1}\rightarrow \delta _{2})\vdash \textsf{A}(\varphi \rightarrow \delta _{k'+1}),\\ \\{} & {} \textsf{A}\textsf{A}\psi '_1,\dots ,\textsf{A}\textsf{A}\psi '_\ell ,\textsf{A}\lnot \textsf{A}\chi '_1,\dots ,\textsf{A}\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'+1}\rightarrow \delta _{k'+2}),\textsf{A}(\delta _{k'+2}\rightarrow \delta _{k'+3}),\dots , \textsf{A}(\delta _{n-1}\rightarrow \delta _{n})\vdash \textsf{A}(\delta _{k'+1}\rightarrow \varphi ). \end{aligned}$$

Then, by Lemma 5 and the Modus Ponens inference rule applied m times to the first statement and $\ell$ times to the second statement,

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _s,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'}\rightarrow \delta _{k'+1}),\textsf{A}(\delta _{k'-1}\rightarrow \delta _{k'}),\dots , \textsf{A}(\delta _{1}\rightarrow \delta _{2})\vdash \textsf{A}(\varphi \rightarrow \delta _{k'+1}),\\ \\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\textsf{A}\lnot \textsf{A}\chi '_1,\dots ,\textsf{A}\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'+1}\rightarrow \delta _{k'+2}),\textsf{A}(\delta _{k'+2}\rightarrow \delta _{k'+3}),\dots , \textsf{A}(\delta _{n-1}\rightarrow \delta _{n})\vdash \textsf{A}(\delta _{k'+1}\rightarrow \varphi ). \end{aligned}$$

Thus, by the Euclidianity axiom and the Modus Ponens inference rule applied s times to the first statement and t times to the second statement,

$$\begin{aligned}{} & {} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'}\rightarrow \delta _{k'+1}),\textsf{A}(\delta _{k'-1}\rightarrow \delta _{k'}),\dots , \textsf{A}(\delta _{1}\rightarrow \delta _{2})\vdash \textsf{A}(\varphi \rightarrow \delta _{k'+1}),\\ \\{} & {} \textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t,\\{} & {} \hspace{5mm}\textsf{A}(\delta _{k'+1}\rightarrow \delta _{k'+2}),\textsf{A}(\delta _{k'+2}\rightarrow \delta _{k'+3}),\dots , \textsf{A}(\delta _{n-1}\rightarrow \delta _{n})\vdash \textsf{A}(\delta _{k'+1}\rightarrow \varphi ). \end{aligned}$$

Observe that $\textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _s\in a$ by Definition 4 and the assumptions $a\in \mathcal {A}$ and (25). Similarly, $\textsf{A}\psi '_1,\dots ,\textsf{A}\psi '_\ell ,\lnot \textsf{A}\chi '_1,\dots ,\lnot \textsf{A}\chi '_t\in a$ by the assumption (26). Hence,

$$\begin{aligned}{} & {} a,\textsf{A}(\delta _{k'}\rightarrow \delta _{k'+1}),\textsf{A}(\delta _{k'-1}\rightarrow \delta _{k'}),\dots , \textsf{A}(\delta _{1}\rightarrow \delta _{2})\vdash \textsf{A}(\varphi \rightarrow \delta _{k'+1}),\\{} & {} a,\textsf{A}(\delta _{k'+1}\rightarrow \delta _{k'+2}),\textsf{A}(\delta _{k'+2}\rightarrow \delta _{k'+3}),\dots , \textsf{A}(\delta _{n-1}\rightarrow \delta _{n})\vdash \textsf{A}(\delta _{k'+1}\rightarrow \varphi ). \end{aligned}$$

Recall that $\delta _1\sqsubseteq \delta _2\sqsubseteq \dots \sqsubseteq \delta _n$ by assumption (19). Then,

$$\begin{aligned} \textsf{A}(\delta _1\rightarrow \delta _2), \dots , \textsf{A}(\delta _{n-1}\rightarrow \delta _n)\in a \end{aligned}$$

by statement (14). Thus,

$$\begin{aligned}{} & {} a\vdash \textsf{A}(\varphi \rightarrow \delta _{k'+1}), \end{aligned}$$

(27)

$$\begin{aligned}{} & {} a\vdash \textsf{A}(\delta _{k'+1}\rightarrow \varphi ). \end{aligned}$$

(28)

Note that formula

$$\begin{aligned} (\varphi \rightarrow \delta _{k'+1}) \rightarrow ((\delta _{k'+1}\rightarrow \varphi )\rightarrow (\delta _{k'+1}\leftrightarrow \varphi )) \end{aligned}$$

is a propositional tautology. Hence,

$$\begin{aligned} \varphi \rightarrow \delta _{k'+1}, \delta _{k'+1}\rightarrow \varphi \vdash \delta _{k'+1}\leftrightarrow \varphi \end{aligned}$$

by the Modus Ponens rule applied twice. Then,

$$\begin{aligned} \textsf{A}(\varphi \rightarrow \delta _{k'+1}), \textsf{A}(\delta _{k'+1}\rightarrow \varphi )\vdash \textsf{A}(\delta _{k'+1}\leftrightarrow \varphi ) \end{aligned}$$

by Lemma 6. Thus, $a\vdash \textsf{A}(\delta _{k'+1}\leftrightarrow \varphi )$ by statements (27) and (28). Hence, by the Substitution axiom and the Modus Ponens inference rule,

$$\begin{aligned} a\vdash \textsf{L}\delta _{k'+1}\rightarrow \textsf{L}\varphi . \end{aligned}$$

Equation (13) implies that $\textsf{L}\delta _{k'+1}\in a$ because $\delta _{k'+1}\in \varDelta$. Then,

$$\begin{aligned} a\vdash \textsf{L}\varphi . \end{aligned}$$

Recall that $\textsf{L}\varphi \in \Phi _0\subseteq \Phi ^*_0$ by the assumption of the lemma. Thus, $\textsf{L}\varphi \in a$ because a is a maximal consistent subset of $\Phi ^*_0$, which contradicts the assumption $\textsf{L}\varphi \notin a$ of the lemma.

Case II $k'=n$. Suppose that set Y is not consistent. Thus, there are formulae

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\in a_0 \end{aligned}$$

(29)

such that

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\vdash \varphi . \end{aligned}$$

Hence, by Lemma 6,

$$\begin{aligned} \textsf{A}\textsf{A}\psi _1,\dots ,\textsf{A}\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _t\vdash \textsf{A}\varphi . \end{aligned}$$

Then, by Lemma 5 and the Modus Ponens inference rule applied m times,

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\textsf{A}\lnot \textsf{A}\chi _1,\dots ,\textsf{A}\lnot \textsf{A}\chi _t\vdash \textsf{A}\varphi . \end{aligned}$$

Thus, by the Euclidianity axiom and the Modus Ponens rule applied t times,

$$\begin{aligned} \textsf{A}\psi _1,\dots ,\textsf{A}\psi _m,\lnot \textsf{A}\chi _1,\dots ,\lnot \textsf{A}\chi _t\vdash \textsf{A}\varphi . \end{aligned}$$

Hence, by assumption (29),

$$\begin{aligned} a_0\vdash \textsf{A}\varphi . \end{aligned}$$

Recall that $\textsf{L}\varphi \in \Phi _0$ by the assumption of the lemma. Hence, $\varphi \in \Phi _0$ by Definition 3. Then, $\textsf{A}\varphi \in \Phi ^*_0$ by Eq. (8). Thus, $\textsf{A}\varphi \in a_0$ because $a_0$ is a maximal consistent subset of $\Phi ^*_0$. Hence, $\textsf{A}\varphi \in a$ by Definition 4 and the assumption $a\in \mathcal {A}$. Then, $\varphi \wedge \textsf{L}\varphi \wedge \textsf{L}\lnot \varphi \in a$ by the definition of modality $\textsf{A}$. Hence, by propositional reasoning,

$$\begin{aligned} a\vdash \textsf{L}\varphi . \end{aligned}$$

Recall that $\textsf{L}\varphi \in \Phi _0\subseteq \Phi ^*_0$ by the assumption of the lemma. Thus, $\textsf{L}\varphi \in a$ because a is a maximal consistent subset of $\Phi ^*_0$, which contradicts the assumption $\textsf{L}\varphi \notin a$ of the lemma.

Claim $X_{k'},Y\subseteq \Phi ^*_0$.

Proof of Claim Consider any formula $\zeta \in X_{k'}\cup Y$. It suffices to show that $\zeta \in \Phi ^*_0$. By Eqs. (20) and (24), it is enough to consider the following three cases:

Case I $\zeta \equiv \varphi$ or $\zeta \equiv \lnot \varphi$. Assumption $\textsf{L}\varphi \in \Phi _0$ of the lemma implies that $\lnot \varphi \in \Phi _0$ by item 3 of Definition 3. Then, $\varphi \in \Phi _0$ because set $\Phi _0$ is closed with respect to subformulae. Therefore, $\varphi , \lnot \varphi \in \Phi _0\subseteq \Phi ^*_0$.

Case II $\zeta \equiv \delta$ or $\zeta \equiv \lnot \delta$ for some formula $\delta \in \varDelta$. Then, $\textsf{L}\delta \in a$ by Eq. (13). Thus, $\lnot \delta \in \Phi _0$ by item 3 of Definition 3. Hence, $\delta \in \Phi _0$ because set $\Phi _0$ is closed with respect to subformulae. Therefore, $\delta , \lnot \delta \in \Phi _0\subseteq \Phi ^*_0$.

Case III $\zeta \in a_0$. Then, $\zeta \in \Phi ^*_0$ because set $a_0$ is a subset of $\Phi ^*_0$.

Let sets b and c be any maximal consistent subsets of $\Phi ^*_0$ that contain sets Y and $X_{k'}$, respectively. Such subsets exist by the above claim and Lemma 3. Note that $b,c\in \mathcal {A}$ by Definition 4 and Eqs. (24) and (20). Also, $\lnot \varphi \in Y\subseteq b$ by Eq. (24). Then, $\varphi \notin b$ because set b is consistent. Additionally, $\varphi \in X_{k'}\subseteq c$ by Eq. (20).

Claim $b\nprec _a c$.

Proof of Claim Suppose that $b\prec _a c$. Thus, by Definition 5, there is a formula $\textsf{L}\delta \in \Phi _0$ such that $\textsf{L}\delta \in a$,

$$\begin{aligned} \delta \notin b, \end{aligned}$$

(30)

and

$$\begin{aligned} \delta \in c. \end{aligned}$$

(31)

Hence, $\delta \in \varDelta$ by Eq. (13) and because set $\Phi _0$ is closed with respect to subformulae. Recall that chain (19) is the ordering of all formulae in $\varDelta$. Let $\delta =\delta _{i}$ for some $i\le n$. We consider the following two cases separately:

Case I $i\le k'$. Then, $\lnot \delta =\lnot \delta _i\in X_{k'}\subseteq c$ by Eq. (20) and the choice of set c. Hence, $\delta \notin c$ because set c is consistent, which contradicts statement (31).

Case II $i> k'$. Then, $\delta =\delta _i\in Y\subseteq b$ by Eq. (24) and the choice of set b, which contradicts statement (30). $\square$

This concludes the proof of the lemma.

6.4 Final steps

Lemma 15

$a\Vdash \varphi$ iff $\varphi \in a$ for each agent $a\in \mathcal {A}$ and each formula $\varphi \in \Phi _0$.

Proof

We prove the lemma by induction on the structural complexity of formula $\varphi$. If formula $\varphi$ is a propositional variable, then the required follows from item 1 of Definition 2 and Definition 6. If formula $\varphi$ is a negation or an implication, then the required follows from items 2 and 3 of Definition 2, the induction hypothesis, and the maximality and the consistency of the set a in the standard way.

Finally, let formula $\varphi$ have the form $\textsf{L}\psi$.

$(\Rightarrow ):$ Assume that $\textsf{L}\psi \notin a$. Then, by Lemma 14, there are agents $b,c\in \mathcal {A}$ such that $\psi \notin b$, $\psi \in c$, and $b\nprec _a c$. Thus, $b\nVdash \psi$ and $c\Vdash \psi$ by the induction hypothesis. Therefore, $a\nVdash \textsf{L}\psi$ by item 4 of Definition 2.

$(\Leftarrow ):$ Assume that $\textsf{L}\psi \in a$. Consider any agents $b,c\in \mathcal {A}$ such that $b\nVdash \psi$ and $c\Vdash \psi$. By item 4 of Definition 2 it suffices to show that $b\prec _a c$. Indeed, by the induction hypothesis, assumptions $b\nVdash \psi$ and $c\Vdash \psi$ imply that $\psi \notin b$ and $\psi \in c$. Then, $b\prec _a c$ by Definition 5 and the assumption $\textsf{L}\psi \in a$ of the case. $\square$

We are now ready to prove the completeness of our logical system. Recall that we used the filtration technique to guarantee that the set of agents is finite. As a result, we can prove the completeness, but not strong completeness of our system.

Theorem 2

(completeness) If $a\Vdash \varphi$ for each agent a of each preference model, then $\vdash \varphi$.

Proof

Suppose that $\nvdash \varphi$. Consider the singleton set $\{\lnot \varphi \}$. By Lemma 11, it can be extended to a finite saturated set $\Phi _0$. Let $\Phi ^*_0$ be the extension of $\Phi _0$ defined by Eq. (8). Assumption $\nvdash \varphi$ implies that set $\{\lnot \varphi \}$ is consistent. Then by Lemma 3, there is a maximal consistent subset $a_0\subseteq \Phi ^*_0$ such that $\{\lnot \varphi \}\subseteq a_0$. Consider the canonical preference model $N(\Phi _0,a_0)$. By Lemma 12, set $a_0$ is an agent in the network $N(\Phi _0,a_0)$. Note that, by the choice of set $a_0$, we have $\lnot \varphi \in \{\lnot \varphi \}\subseteq a_0$. Thus, $\varphi \notin a_0$ because set $a_0$ is consistent. Therefore, $a_0\nVdash \varphi$ by Lemma 15.$\square$

We conclude this section with an observation that our logical system is decidable, which follows from the completeness theorem.

Theorem 3

Set $\{\varphi \in \Phi \;|\;\vdash \varphi \}$ is decidable.

Proof

The set $\{\varphi \in \Phi \;|\vdash \varphi \}$ is recursively enumerable because it is axiomatisable. Also, the set $\{\varphi \in \Phi \;|\nvdash \varphi \}$ is recursively enumerable because our logical system is sound and complete with respect to the preference models with finite sets of agents. Therefore, the set $\{\varphi \in \Phi \;|\vdash \varphi \}$ is decidable. $\square$

7 The logic of conditional likes

In the previous sections, we considered such unconditional likes statements as “a likes logicians” and “a likes philosophers”. In this section, following Lang et al. (2002), we consider conditional likes statements such as “among all philosophers, a likes logicians”. We write the last statement as

$$\begin{aligned} a\Vdash \textsf{L}(\hbox {``is a logician''}\,|\,\hbox {``is a philosopher''}). \end{aligned}$$

Below, we formally introduce the syntax and the semantics for a language with conditional likes modality $\textsf{L}(\cdot \,|\,\cdot )$ and discuss possible axioms for conditional likes. We also show that unconditional likes modality $\textsf{L}$ is definable through conditional likes modality but not the other way around.

7.1 Syntax and semantics

The language $\Phi ^+$ that we consider in this section is defined by the grammar:

$$\begin{aligned} \varphi :=p\;|\;\lnot \varphi \;|\;\varphi \rightarrow \varphi \;|\;\textsf{L}(\varphi \,|\,\varphi ). \end{aligned}$$

We read $\textsf{L}(\varphi \,|\,\psi )$ as “likes those who have property $\varphi$, among those who satisfy condition $\psi$”. We again assume that disjunction $\vee$, conjunction $\wedge$, and biconditional $\leftrightarrow$ are defined in our language in the standard way. We also assume the same about constant $\top$.

The semantics of formulae in language $\Phi ^+$ could be defined by replacing item 4 of Definition 2 with

$$\begin{aligned} a\Vdash \textsf{L}(\varphi \,|\,\psi ), \,when\, \forall \,b,c\,(if\, b\Vdash \lnot \varphi \wedge \psi \,and\, c\Vdash \varphi \wedge \psi , \,then \,b\prec _a c). \end{aligned}$$

(32)

Note that the conditions $b\Vdash \lnot \varphi \wedge \psi$ and $c\Vdash \varphi \wedge \psi$ imply that $b\ne c$. Thus, just like it was in the case of unconditional likes, a replacement of the strict relation $\prec _a$ in the above statement with the no-strict relation $\preceq _a$ results in an equivalent definition of the conditional likes modality. See our discussion after Definition 2. Observe also that formulae $\textsf{L}(\varphi \,|\,\top )$ is equivalent under the above semantics to the formula $\textsf{L}\varphi$. Thus, the logical system that we consider in this section could be considered to be an extension of the logical system for unconditional likes modality from the previous section. As before, “for all agents” modality $\textsf{A}\varphi$ can be defined as $\varphi \wedge \textsf{L}(\varphi \,|\,\top )\wedge \textsf{L}(\lnot \varphi \,|\,\top )$.

7.2 Axioms

Below are some of the universally true properties that can be expressed in the language $\Phi ^+$.

• 1. $\textsf{L}(\varphi _1\,|\,\psi _1)\wedge \textsf{L}(\varphi _2\,|\,\psi _2)\rightarrow \textsf{L}(\varphi _1\wedge \varphi _2\,|\,\psi _1\wedge \psi _2)$,

• 2. $\textsf{L}(\varphi _1\,|\,\psi _1)\wedge \textsf{L}(\varphi _2\,|\,\psi _2)\rightarrow \textsf{L}(\varphi _1\vee \varphi _2\,|\,\psi _1\wedge \psi _2)$,

• 3. $\textsf{L}(\varphi _1\wedge \varphi _2\,|\,\psi )\rightarrow \textsf{L}(\varphi _1\,|\,\varphi _2\wedge \psi )$,

• 4. $\textsf{L}(\varphi _1\vee \varphi _2\,|\,\psi )\rightarrow \textsf{L}(\varphi _1\,|\,\lnot \varphi _2\wedge \psi )$.

Note, however, that unlike unconditional likes modality, which has a relatively simple axiomatisation, conditional likes modality has much less trivial and harder-to-express properties. An example of them is

$$\begin{aligned} \bigwedge _{0\le i< n}\textsf{L}(\varphi _i\,|\,\psi _i)\rightarrow \bigvee _{0\le i< n}\textsf{A}\lnot (\varphi _i\wedge \psi _i\wedge \lnot \varphi _{i'}\wedge \psi _{i'}), \end{aligned}$$

where, for each i, integer $i'<n$ is such that $i'\equiv i+1 \pmod n$. We believe that this property does not follow from properties 1–4 listed in the beginning of this subsection and that it cannot be reduce to a combination of some simple principles.

We prove the soundness of this principle in the theorem below. A complete axiomatisation of modality $\textsf{L}(\varphi \,|\,\psi )$ remains an open question.

Theorem 4

For an arbitrary preference model $(\mathcal {A},\{\prec _a\}_{a\in \mathcal {A}},\pi )$, any agent $a\in \mathcal {A}$, any $n\ge 1$, and any formulae $\varphi _0,\dots ,\varphi _{n-1}, \psi _0,\dots ,\psi _{n-1}$, if $a\Vdash \textsf{L}(\varphi _i\;|\;\psi _i)$ for each $i<n$, then there is $i< n$ such that

$$\begin{aligned} a\Vdash \textsf{A}\lnot (\varphi _i\wedge \psi _i\wedge \lnot \varphi _{i'}\wedge \psi _{i'}), \end{aligned}$$

where $i'<n$ is such that $i'\equiv i+1 \pmod n$.

Proof

Towards contradiction, suppose that

$$\begin{aligned} a\Vdash \textsf{L}(\varphi _i\;|\;\psi _i), \hspace{5mm}\forall \, i<n \end{aligned}$$

(33)

and

$$\begin{aligned} a\nVdash \textsf{A}\lnot (\varphi _i\wedge \psi _i\wedge \lnot \varphi _{i'}\wedge \psi _{i'}), \end{aligned}$$

for each $i<n$, where $i'<n$ is such that $i'\equiv i+1 \pmod n$. Thus, by Lemma 1, for each $i<n$ there is an agent $b_i\in \mathcal {A}$ such that

$$\begin{aligned} b_i\nVdash \lnot (\varphi _i\wedge \psi _i\wedge \lnot \varphi _{i'}\wedge \psi _{i'}), \end{aligned}$$

where $i'<n$ is such that $i'\equiv i+1 \pmod n$. Hence, by item 2 of Definition 2,

$$\begin{aligned} b_i\Vdash \varphi _i\wedge \psi _i\wedge \lnot \varphi _{i'}\wedge \psi _{i'}, \end{aligned}$$

where $i'<n$ is such that $i'\equiv i+1 \pmod n$. Then,

$$\begin{aligned}&b_0\Vdash \varphi _0\wedge \psi _0,&b_0\Vdash \lnot \varphi _1\wedge \psi _1,\\&b_1\Vdash \varphi _1\wedge \psi _1,&b_1\Vdash \lnot \varphi _2\wedge \psi _2,\\&b_2\Vdash \varphi _2\wedge \psi _2,&b_2\Vdash \lnot \varphi _3\wedge \psi _3,\\&\dots&\dots \\&b_{n-2}\Vdash \varphi _{n-2}\wedge \psi _{n-2},&b_{n-2}\Vdash \lnot \varphi _{n-1}\wedge \psi _{n-1},\\&b_{n-1}\Vdash \varphi _{n-1}\wedge \psi _{n-1},&b_{n-1}\Vdash \lnot \varphi _{0}\wedge \psi _{0}. \end{aligned}$$

These statements can be rearranged as,

$$\begin{aligned}&b_0\Vdash \lnot \varphi _1\wedge \psi _1,&b_1\Vdash \varphi _1\wedge \psi _1,\\&b_1\Vdash \lnot \varphi _2\wedge \psi _2,&b_2\Vdash \varphi _2\wedge \psi _2,\\&b_2\Vdash \lnot \varphi _3\wedge \psi _3,&b_3\Vdash \varphi _3\wedge \psi _3,\\&\dots&\dots \\&b_{n-2}\Vdash \lnot \varphi _{n-1}\wedge \psi _{n-1},&b_{n-1}\Vdash \varphi _{n-1}\wedge \psi _{n-1},\\&b_{n-1}\Vdash \lnot \varphi _{0}\wedge \psi _{0}&b_0\Vdash \varphi _0\wedge \psi _0. \end{aligned}$$

Thus, by assumption (33) and statement (32),

$$\begin{aligned} b_0\prec _a b_1\prec _a b_2\prec _a \dots \prec _a b_{n-1}\prec _a b_0. \end{aligned}$$

Therefore, $b_0\prec _a b_0$ because relation $\prec _a$ is transitive by Definition 1, which contradicts $\prec _a$ being a strict partial order by the same Definition 1. $\square$

Fig. 2

A preference model

7.3 Undefinability

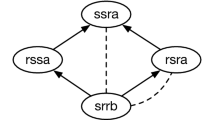
In this section, we show that conditional likes modality $\textsf{L}(\cdot \,|\,\cdot )$ is not definable in our original language $\Phi$. To achieve this, we consider the preference model depicted in Fig. 2. It has four agents: a, b, c, and d. The only preference in the model is that agent c prefers agent a over agent d. Without loss of generality, we assume that the language has only two propositional variables: p and q. Finally, let $\pi (p)=\{a\}$ and $\pi (q)=\{a,d\}$. In other words, propositional variable p is true only about agent a and propositional variable q is true only about agents a and d, see Fig. 2. We will show that agents b and c are indistinguishable in language $\Phi$ and that they are distinguishable in a language containing conditional likes modality $\textsf{L}(\cdot \,|\,\cdot )$.

We start the proof with two auxiliary lemmas. The first of them is true because relation $\prec _b$ is empty.

Lemma 16

If X and Y are any two sets of agents in the preference model depicted in Fig. 2 such that $X\cup Y=\{a,b,c,d\}$ and $x\prec _b y$ for all $x\in X$ and all $y\in Y$, then either set X or set Y is empty.

The second auxiliary lemma is true because agents b and c are not in relation $\prec _c$ with any other agents.

Lemma 17

If X and Y are any two sets of agents in the preference model depicted in Fig. 2 such that $X\cup Y=\{a,b,c,d\}$ and $x\prec _c y$ for all $x\in X$ and all $y\in Y$, then either set X or set Y is empty.

Proof

If $b\in X$, then set Y must be empty because $b\nprec _c y$ for any $y\in \{a,b,c,d\}$, see Fig. 2. Similarly, if $b\in Y$, then set X must be empty. $\square$

Lemma 18

$b\Vdash \varphi$ iff $c\Vdash \varphi$ for any formula $\varphi \in \Phi$.

Proof

We prove the statement by induction on the structural complexity of formula $\varphi$. If formula $\varphi$ is propositional variable p or q, then the statement holds by item 1 of Definition 2 and because $b,c\notin \pi (p)$ and $b,c\notin \pi (q)$. If formula $\varphi$ is a negation or an implication, then the statement of the lemma follows from the induction hypothesis and either item 2 or item 3 of Definition 2 in the standard way.

Suppose that formula $\varphi$ has the form $\textsf{L}\psi$.

$(\Leftarrow ):$ Suppose that $c\Vdash \textsf{L}\psi$. Consider sets

$$\begin{aligned} X= & {} \{x\in \mathcal {A}\;|\;x\nVdash \psi \},\\ Y= & {} \{y\in \mathcal {A}\;|\;y\Vdash \psi \}. \end{aligned}$$

The assumption $c\Vdash \textsf{L}\psi$ implies that $x\prec _c y$ for each agent $x\in X$ and each agent $y\in Y$ by item 4 of Definition 2. Then, either $X=\varnothing$ or $Y=\varnothing$ by Lemma 17. Hence, $b\Vdash \textsf{L}\psi$ again by item 4 of Definition 2.

$(\Rightarrow ):$ The proof is similar, but it uses Lemma 16 instead of Lemma 17. $\square$

The next lemma follows from statement (32) and the specification of the model in Fig. 2.

Lemma 19

$b\nVdash \textsf{L}(p\,|\,q)$ and $c\Vdash \textsf{L}(p\,|\,q)$.

The next theorem follows from the last two lemmas.

Theorem 5

Modality $\textsf{L}(\cdot \,|\,\cdot )$ is not definable in language $\Phi$.

8 Conclusion

We have proposed an egocentric approach to reasoning about higher-order preferences. Unlike the previous works on preference and desire logics, the egocentric approach allows us to express higher-order preferences using nested statements of the form “agent a likes those who like philosophers”. We have considered unconditional and conditional modalities capturing such preferences. We have observed that unconditional modality is definable through conditional, but not the other way around. Our main technical result is a sound, complete, and decidable logical system describing the properties of the unconditional likes modality.

An interesting direction for future research is to introduce the distinction between de re and de dicto likes. An agent might like a group of people because they are philosophers or the group liked by the agent just happens to consist of philosophers.

Appendix

To keep this article self-contained, in this appendix, we prove the standard lemmas mentioned in Sect. 4.

Lemma 4If $X,\varphi \vdash \psi$, then $X\vdash \varphi \rightarrow \psi$.

Proof

Suppose that sequence $\psi _1,\dots ,\psi _n$ is a proof from set $X\cup \{\varphi \}$ and the theorems of our logical system that uses the Modus Ponens inference rule only. In other words, for each $k\le n$, either

• 1. $\vdash \psi _k$, or

• 2. $\psi _k\in X$, or

• 3. $\psi _k$ is equal to $\varphi$, or

• 4. there are $i,j<k$ such that formula $\psi _j$ is equal to $\psi _i\rightarrow \psi _k$.

It suffices to show that $X\vdash \varphi \rightarrow \psi _k$ for each $k\le n$. We prove this by induction on k through considering the four cases above separately.

Case I: $\vdash \psi _k$. Note that $\psi _k\rightarrow (\varphi \rightarrow \psi _k)$ is a propositional tautology, and thus, is an axiom of our logical system. Hence, $\vdash \varphi \rightarrow \psi _k$ by the Modus Ponens inference rule. Therefore, $X\vdash \varphi \rightarrow \psi _k$.

Case II: $\psi _k\in X$. Then, similar to the previous case, $X\vdash \varphi \rightarrow \psi _k$.

Case III: formula $\psi _k$ is equal to $\varphi$. Thus, $\varphi \rightarrow \psi _k$ is a propositional tautology. Therefore, $X\vdash \varphi \rightarrow \psi _k$.

Case IV: formula $\psi _j$ is equal to $\psi _i\rightarrow \psi _k$ for some $i,j<k$. Thus, by the induction hypothesis, $X\vdash \varphi \rightarrow \psi _i$ and $X\vdash \varphi \rightarrow (\psi _i\rightarrow \psi _k)$. Note that formula

$$\begin{aligned} (\varphi \rightarrow \psi _i)\rightarrow ((\varphi \rightarrow (\psi _i\rightarrow \psi _k))\rightarrow (\varphi \rightarrow \psi _k)) \end{aligned}$$

is a propositional tautology. Therefore, $X\vdash \varphi \rightarrow \psi _k$ by applying the Modus Ponens inference rule twice. $\square$

Lemma 5$\vdash \textsf{A}\varphi \rightarrow \textsf{A}\textsf{A}\varphi$.

Proof

Note that formula $\textsf{A}\lnot \textsf{A}\varphi \rightarrow \lnot \textsf{A}\varphi$ is an instance of the Reflexivity axiom. Thus, by contraposition, $\vdash \textsf{A}\varphi \rightarrow \lnot \textsf{A}\lnot \textsf{A}\varphi$. Then, taking into account that $\vdash \lnot \textsf{A}\lnot \textsf{A}\varphi \rightarrow \textsf{A}\lnot \textsf{A}\lnot \textsf{A}\varphi$ by the Euclidianity axiom, one can conclude that

$$\begin{aligned} \vdash \textsf{A}\varphi \rightarrow \textsf{A}\lnot \textsf{A}\lnot \textsf{A}\varphi . \end{aligned}$$

(34)

At the same time, $\lnot \textsf{A}\varphi \rightarrow \textsf{A}\lnot \textsf{A}\varphi$ is an instance of the Euclidianity axiom. Thus, $\vdash \lnot \textsf{A}\lnot \textsf{A}\varphi \rightarrow \textsf{A}\varphi$ by contraposition. Hence, $\vdash \textsf{A}(\lnot \textsf{A}\lnot \textsf{A}\varphi \rightarrow \textsf{A}\varphi )$ by the Necessitation inference rule. Thus,

$$\begin{aligned}\vdash \textsf{A}\lnot \textsf{A}\lnot \textsf{A}\varphi \rightarrow \textsf{A}\textsf{A}\varphi \end{aligned}$$

by the Distributivity axiom and the Modus Ponens inference rule. The last statement, together with statement (34), implies the statement of the lemma by the laws of propositional reasoning. $\square$

Lemma 6If $\varphi _1,\dots ,\varphi _n\vdash \psi$, then $\textsf{A}\varphi _1,\dots ,\textsf{A}\varphi _n\vdash \textsf{A}\psi$.

Proof

By Lemma 4 applied n times, the assumption $\varphi _1,\dots ,\varphi _n\vdash \psi$ implies that

$$\begin{aligned} \vdash \varphi _1\rightarrow (\varphi _2\rightarrow \dots (\varphi _n\rightarrow \psi )\dots ). \end{aligned}$$

Thus,

$$\begin{aligned} \vdash \textsf{A}(\varphi _1\rightarrow (\varphi _2\rightarrow \dots (\varphi _n\rightarrow \psi )\dots )) \end{aligned}$$

by the Necessitation inference rule. Hence, by the Distributivity axiom and the Modus Ponens inference rule,

$$\begin{aligned} \vdash \textsf{A}\varphi _1\rightarrow \textsf{A}(\varphi _2\rightarrow \dots (\varphi _n\rightarrow \psi )\dots ). \end{aligned}$$

Then, $\textsf{A}\varphi _1\vdash \textsf{A}(\varphi _2\rightarrow \dots (\varphi _n\rightarrow \psi )\dots )$, again by the Modus Ponens inference rule. Therefore, $\textsf{A}\varphi _1,\dots ,\textsf{A}\varphi _n\vdash \textsf{A}\psi$ by applying the previous steps $(n-1)$ more times. $\square$