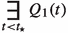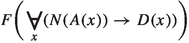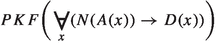Abstract
The Operator Argument against eternalism holds that having non-vacuous tense operators in the language is incompatible with the claim that every proposition has its truth-value eternally. Assuming that (1) there are non-vacuous tense operators, (2) tense operators operate on propositions and (3) tense operators which operate on eternal entities are vacuous, it may be argued that eternalism is false. In this paper, I examine the Operator Argument. The goal is threefold. First, I want to present some aspects of the debate in a more elaborate way, especially those concerning formal matters. Secondly, I will argue that eternalism can escape the Operator Argument. There are two main strategies for handling the Operator Argument. The first one is based on replacing temporal operators with object-language quantifiers. The second rejects the identification of compositional semantic value with assertoric content. My third goal is to show that none of them is as good as the strategy that adopts Timestamp Semantics (Fritz in Philosl Stud 176:2933–2959, 2019 https://doi.org/10.1007/s11098-018-1158-8). I am going to argue that the quantificational treatment of tenses is compatible with temporalism and that the arguments for rejecting the identification of compositional semantic value with assertoric content provide, in fact, a motivation for the temporalist position. At the end, I will develop Timestamp Semantics by providing a novel formalization of it, and defend it against three potential counter-arguments.
Similar content being viewed by others
1 Introduction
Propositions are one of the central notions in philosophy of language. Roughly speaking, propositions are what is said in a given act of assertion. It is often assumed that propositions play a lot of different roles. They are much more than only assertoric contents. In the standard picture, they are the primary bearers of truth-values, the objects of beliefs (and of propositional attitudes in general), the referents of that-clauses, and the compositional semantic values of sentences in a given context. One of the fundamental questions is whether there are any entities that can play all these roles. The assumption that there are such entities is called Propositional Multitasking (Weber, 2012).
Let us begin with the claim that propositions are truth-bearers. In the standard possible worlds framework, propositions are true or false not absolutely, but only relative to a possible world. For example, the proposition that 2+2=4 is true at all possible worlds, while the proposition that Andrzej Duda won the election in 2015 in Poland is true at the actual world and false at the possible world in which Bronisław Komorowski was elected. There is an analogical issue concerning time: are propositions true at some times and false at others, or do they keep their truth-values eternally? Although it is commonly assumed that the truth-values of propositions vary across worldsFootnote 1, the analogical issue concerning time is a matter of some controversy. At first glance, it seems that eternalism, i.e., the thesis that all propositions keep their truth-values eternally, is very plausible. For example, if I assert that it is raining, I mean that it is raining at some particular time – the time of the utterance. Therefore, if what I said is true, it follows that it is raining at time \(t_c\), i.e, the time of utterance, but then what I said is true at all times because it is true at all times that it is raining at time \(t_c\). If this is correct, then propositions – if true at all – are true eternally. This is part of Twardowski’s famous argument against relativism (1900, pp. 151–153). On the other hand, there are a lot of arguments against eternalism, but they are similar in spirit: each one of them is designed to show that eternal entities are not suitable for one of the roles required by Propositional Multitasking.Footnote 2 One of these arguments is the Operator Argument, which aims to show that eternal entities cannot serve as compositional semantic values of sentences in a given context of utterance.
In this paper I will examine the Operator Argument. The goal is threefold: First, I want to present some aspects of the debate in a more elaborate way, especially those concerning formal matters. Secondly, I will argue that eternalism can escape the Operator Argument. There are two main strategies for handling the Operator Argument. The first one is based on replacing temporal operators by object-language quantifiers. The second rejects the identification of compositional semantic value with assertoric content. My third goal is to show that none of them is as good as the strategy that I will propose. I am going to argue that (1) the quantificational treatment of tenses is compatible with temporalism, and (2) the arguments for rejecting the identification of compositional semantic value with assertoric content provide, in fact, a motivation for the temporalist position. My strategy is to show that it is possible to postulate temporal operators that operate on eternal propositions in a non-trivial way. To that end, I will develop the theory called Timestamp Semantics, which was introduced in a paper by Fritz et al. (2019). The theory’s core idea is to represent propositions as pairs \(\langle S, t\rangle \), where S is the set of indices (the traditional Kaplanian content), and t is contextually provided time – usually the time of the utterance. I will provide a formalization of the theory and defend it against three potential objections.
The structure of the paper is as follows. In the second section, I introduce some formalism and basic definitions. In the third, I reconstruct the Operator Argument in detail. I discuss possible answers to the argument, each of which is associated with rejecting one of the key assumptions. What is more, I will show how temporalism can be smuggled into the quantificational framework and criticize the so-called “two-content strategy”. Finally, I will defend Timestamp Semantics – a particular answer to the Operator Argument – against three potential objections. I will end with presenting a new formalization of that theory. Thus, I will argue that an eternalist can successfully escape the Operator Argument.
2 Setting the stage: definitions
Let us start by introducing a basic formal system which may be considered part of Kaplan’s Logic of Demonstratives (1989a, pp. 541–546). To keep things simple, let us focus on a language \({\mathcal {L}}_D\), which contains only sentential variables (\(\Phi \)), two truth-functional connectives (\(\wedge \), \(\lnot \)) and four intensional operators: P (“it was the case that”), F (“it will be the case that”), N (“it is now the case that”), Y (“yesterday, it was the case that”).
Definition 1
A \({\mathcal {L}}_D\)-model is a triple \(\langle {\mathcal {T}}, \le , V \rangle \), where
-
\({\mathcal {T}}\) is a nonempty set—the set of times.
-
The ordering \(\le \) on \({\mathcal {T}}\) is linearFootnote 3, i.e., for each \(a,b,c \in {\mathcal {T}}\) we have: (1) \(a \le a\); (2) \(a \le b\) and \(b\le c\) implies that \(a \le c\); (3) \(a \le b\) and \(b \le a\) implies \(a=b\); (4) \(a \le b\) or \(b \le a\).
-
The relation < on \({\mathcal {T}}\) is defined in the following way
$$\begin{aligned} a < b \iff (a \le b)~\wedge ~ \lnot (a = b). \end{aligned}$$ -
V is a function \(V:\Phi \rightarrow {\mathcal {P}}({\mathcal {T}})\), where \({\mathcal {P}}({\mathcal {T}})\) is the set of all subsets of \({\mathcal {T}}\).
Throughout the paper I will assume, following Kaplan (1989a, p. 543), that the set of times \({\mathcal {T}}\) is the set of integers, i.e., \({\mathcal {T}} = {\mathbb {Z}}\). This is not meant to be a metaphysical claim about the nature of time. Rather, this assumption is made to avoid technical difficulties that are not important from our point of view. In Kaplan’s framework, contexts are represented as sequences of parameters that are needed to generate content.
-
If we think of the formal role played by context within model-theoretic semantics, then we should say that context provides whatever parameters are needed. From this point of view, context is a package of whatever parameters are needed to determine the referent (Kaplan, 1989b, p. 591).
For simplicity, in our case we can assume that contexts are points in time, i.e., elements of the set \({\mathcal {T}}\). The important message from Kaplan is that we must relativize truth not only to a context but also to an index. Since in our language \({\mathcal {L}}_D\) there are tense operators only, it is enough to postulate only a time parameter in the semantic index.
Definition 2
A sentence \(\phi \) is true in \({\mathcal {L}}_D\)-model \(\mathfrak {A}\) as uttered in a context of utterance \(t_c\) and evaluated at a point t:
-
\(\mathfrak {A}, t_c, t \vDash p\) iff \(t \in V(p)\) for \(p \in \Phi \);
-
\(\mathfrak {A}, t_c, t \vDash \lnot \phi \) iff it is not the case that \(\mathfrak {A}, t_c, t \vDash \phi \);
-
\(\mathfrak {A}, t_c, t \vDash \phi \wedge \psi \) iff \(\mathfrak {A}, t_c, t \vDash \phi \) and \(\mathfrak {A}, t_c, t \vDash \psi \);
-
\(\mathfrak {A}, t_c, t \vDash P\phi \) iff there is \(t_1 < t\) such that \(\mathfrak {A}, t_c, t_1 \vDash \phi \);
-
\(\mathfrak {A}, t_c, t \vDash F\phi \) iff there is \(t_1 > t\) such that \(\mathfrak {A}, t_c, t_1 \vDash \phi \);
-
\(\mathfrak {A}, t_c, t \vDash N\phi \) iff \(\mathfrak {A}, t_c, t_c \vDash \phi \);
-
\(\mathfrak {A}, t_c, t \vDash Y\phi \) iff \(\mathfrak {A}, t_c, t_c - 1 \vDash \phi \).Footnote 4
To get a truth value of \(\phi \) in a context, we must evaluate it with respect to the parameters that are supplied by the context of utterance. Thus, given a \({\mathcal {L}}_D\)-model \(\mathfrak {A}\), we may say that a sentence \(\phi \) is true in a context \(t_c\) if and only if \(\mathfrak {A}, t_c, t_c \vDash \phi \). Having this, we can define a proposition expressed by \(\phi \) in a given context of utterance. For Kaplan, a proposition is a set of all indices at which a sentence is true. This is captured by the following definition.
Definition 3
The Kaplanian proposition expressed by \(\phi \) in \({\mathcal {L}}_D\)-model \(\mathfrak {A}\) and context of utterance \(t_c\) is a set \({\mathbb {P}}_{\phi , t_c} \subseteq {\mathcal {T}}\) such that
Equivalently, one can take as a Kaplanian proposition the characteristic function of the set \({\mathbb {P}}_{\phi , t_c}\). Note that since Kaplan’s original language LD also contains modal operators, he represents propositions as characteristic functions of sets of pairs \(\langle w, t\rangle \). This complication is not needed for our purposes. As was mentioned, the important assumption concerning propositions is Propositional Multitasking.
Definition 4
Propositional Multitasking (PM)Footnote 5 is the assumption that there are entities – propositions – which play all the following roles:
-
1.
they are the primary bearers of truth-values;
-
2.
they are the objects of propositional attitudes (such as beliefs);
-
3.
they are the contents of speech acts;
-
4.
they are the compositional semantic values of sentences in a given context of utterance;
-
5.
they are the referents of that-clauses.
Now, let me introduce the formal language which will be helpful in analyzing the Operator Argument.Footnote 6 We need time variables (\(t, t_1, t_2,...\)), proposition variables (\(p, q, p_1, q_1, p_2, ...\)) and universal quantifier \(\forall \), which bounds variables of both kinds. The existential quantifier is defined in the standard way: \(\exists := \lnot \forall \lnot \). We also need a binary relation between propositions and times Tr(p, t), which is understood as “proposition p is true at time t”. Having all this, we can define eternalism in a formal way.
Definition 5
Eternalism (ET) is the thesis that all propositions keep their truth-values eternally.

One might be tempted to think that temporalism is a thesis that is as strong as eternalism, that is, it is the thesis that all propositions change their truth-values through time. However, unless something more is said, temporalism understood in such a way is trivially false, since every tautological sentence expresses a proposition that is always true. Thus, I assume that temporalism is the thesis that at least some propositions change their truth-values over time. Clearly, temporalism as understood in such a way is the negation of eternalism.
Definition 6
Temporalism (TP) is the thesis that there is a proposition that is true at some time but false at another.

Note that, according to Definition 3, Kaplanian propositions are sets of times. For example, the proposition that it is raining in Kraków is the set of all times at which it is raining in Kraków. Obviously, there are times at which it is raining at Kraków and there are also times at which this is not the case. Thus, if we take Tr(p, t) as \(t \in p\), then at least some Kaplanian propositions are temporal in the sense of the above definition.
3 The operator argument reconstructed
In this section I will reconstruct the Operator Argument, whose aim is to show that (ET) is false.Footnote 7 Let us start with the three key assumptions.
-
(A1)
There are non-redundant tense operators.
-
(A2)
Tense operators operate on propositions.
-
(A3)
Tense operators which operate on eternal entities are redundant.
The first assumption states that tenses are best represented by intensional operators rather than by quantifiers in the object language. For example, in our framework, the past tense gets the following treatment:
where P is the past tense operator. To see how this works on a concrete example, assume that \(\phi \) stands for “Jakub is a policeman”. Then, the sentence “Jakub was a policeman” is true as uttered at \(t_c\) and evaluated at t if and only if “Jakub is a policeman” is true at some time \(t_1\) prior to t. Although we have an existential quantifier in the analysis of the past tense, it appears not in the logical form but in the truth-conditions of tensed sentences.
The second assumption (A2) is that tense operators operate on propositions. This can be seen as a consequence of (A1)+(PM): there are tense operators, according to (A1), which operate on compositional values of sentences in contexts; however, according to (PM), these are propositions.
One point is worth mentioning here. At first glance, it may seem that operators operate on formulas, since the operator P takes as an argument a formula \(\phi \) and produces another formula, namely \(P\phi \). However, the proposition expressed by \(P\phi \) in a given context of utterance can be seen as obtained from the proposition expressed by \(\phi \) in this context. Our Kaplanian propositions provide a good illustration of this mechanism:

Thus, it is natural to think that operators operate on propositions and extend the formal definition of every operator O in the way that \(O({\mathbb {P}}_{\phi , t_c}) = {\mathbb {P}}_{O\phi , t_c}\).
This indicates that the notion of operating that we have in mind is something like following: X operates on Ys if and only if there is a function \(f_X\) associated with X such that for each \(y \in Y\), \(f_X(y)\) is well-defined. The Principle of Compositionality (defined later on) will clarify these issues.
The third assumption (A3) is that tense operators are redundant if applied to eternal entities. The classical illustration of this phenomenon involves applying the past tense operator to a time-specified proposition such as It is raining at \(t_1\) in Kraków. After applying the past tense operator to that proposition, we get the proposition that it was the case that it is raining at \(t_1\) in Kraków, which is true if and only if it is raining at \(t_1\) in Kraków. Thus, the past tense operator has no effect at all when applied to a time-specific eternal proposition. For example, Kaplan states this assumption very clearly:
-
If we built the time of evaluation into the contents (thus removing time from the circumstances, leaving only, say, a possible world history, and making contents specific as to time), it would make no sense to have temporal operators. (...) Temporal operators applied to eternal sentences (those whose contents incorporate a specific time of evaluation) are redundant. Kaplan (1989a, p. 503).
Both premises (A1) and (A3) say something about the redundancy of operators. Thus, to make things precise we need a clear notion of redundancy. It seems that a plausible notion of redundancy is captured by the following definition.Footnote 8
Definition 7
The operator O is redundant with respect to a time if and only if for all propositions p the truth-value of Op is the same as the truth-value of p at any time t.

Consider the example presented above once again. In our framework, the time-specified proposition p – that it is raining at \(t_1\) in Kraków is either the set \({\mathcal {T}}\) or \(\emptyset \), depending on whether it is raining at \(t_1\) in Kraków. Since \(P({\mathcal {T}}) = {\mathcal {T}}\) and \(P(\emptyset ) = \emptyset \), we conclude that P is redundant with respect to p in the sense of Definition 7. The Operator Argument proceeds as follows:
-
(P1)
By way of contradiction, assume that (ET) is true.
-
(P2)
By (P1) and (A2), tense operators operate on eternal entities.
-
(P3)
By (P2) and (A3), tense operators are redundant.
-
(P4)
Obviously (P3) contradicts (A1). Therefore, (ET) is false and (TP) is consequently true.
It seems that if one accepts all the assumptions (A1)–(A3), then one is committed to temporalism, namely the thesis that some propositions vary in truth-value across time. In the following subsections I will discuss possible answers to the Operator Argument. Each strategy is connected with rejecting one of the assumptions (A1)–(A3).
3.1 Tense operators are redundant
The first strategy of replying to the Operator Argument is associated with rejecting premise (A1). It may be argued that tense operators should be replaced by object-language quantifiers. When we do not have tense operators in our theory, we can remove the time parameter from the semantic index; since propositions are sets of indices, there is no problem in thinking that propositions are eternal.Footnote 9 This line of response is adapted by King (2003). Let us examine this strategy in detail. Consider the sentence \(\phi =\)“Jakub was a policeman”. According to the quantificational account, it has the following logical form:
-
\(\phi \)’s LFFootnote 10:
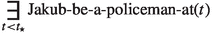
where \(t_{\star }\) is the time of the utterance. To capture this in formal terms, we need to introduce another language \({\mathcal {L}}_{\exists }\), which contains at least the set of time variables \((\Phi _{t})\), the set of predicates of arity 1, (\({\mathcal {Q}} = \{Q_{i} \}_{i \in {\mathbb {N}}}\)), and existential quantifier (\(\exists \)).
Definition 8
A \({\mathcal {L}}_{\exists }\)-model is a triple \(\langle {\mathcal {T}}, \le , {\mathcal {I}} \rangle \), where
-
\({\mathcal {T}}\) is a nonempty set—the set of times.
-
The ordering \(\le \) on \({\mathcal {T}}\) is linear.
-
The relation < is defined in the standard way.
-
For each predicate \(Q_i \in {\mathcal {Q}}\), the function \({\mathcal {I}}\) returns the set \({\mathcal {I}}_{Q_i} \subseteq {\mathcal {T}}\).
We need to introduce the semantics for our language \({\mathcal {L}}_{\exists }\). The following notation will be helpful.
Definition 9
For a function \(f : X \rightarrow Y\), \(x \in X\) and \(y \in Y\) let us define function \(f_{x}^y : X \rightarrow Y\) in the following way
To handle the quantifiers, we need to relativize the truth to the assignments of values to the variables. The language \({\mathcal {L}}_{\exists }\) does not contain temporal operators, so we do not need to postulate a time parameter within the index. However, we need to change the formal definition of the context a little bit. In quantificational analysis, as will soon become clear, it is not enough to have a time in order to generate the content of a sentence: an assignment f is also needed. Thus, it is reasonable to assume that the context supplies such an assignment. As Kaplan puts it
-
Taking context in this more abstract, formal way – as providing the parameters needed to generate content – it is natural to treat the assignment of values to free occurrences of variables as simply one more aspect of context (1989b, p. 591).
In consequence, I will represent any context of utterance c as an ordered pair \(\langle f, t_c \rangle \)Footnote 11. Now, we can define truth clauses for complex sentences.
Definition 10
A sentence \(\phi \) is true in \(\mathcal {L_{\exists }}\)-model \(\mathfrak {A}\), under an evaluation \(f : \Phi _t \rightarrow {\mathcal {T}}\), uttered in a context \(c = \langle f, t_c\rangle \):
-
\(\mathfrak {A}, f, t_c \vDash t_1 = t_2\) iff \(f(t_1) = f(t_2)\);
-
\(\mathfrak {A}, f, t_c \vDash Q_i(t_1)\) iff \(f(t_1) \in {\mathcal {I}}_{Q_i}\);
-
\(\mathfrak {A}, f, t_c \vDash \lnot \phi \) iff it is not the case that \(\mathfrak {A}, f, t_c \vDash \phi \);
-
\(\mathfrak {A},f, t_c \vDash \phi \wedge \psi \) iff \(\mathfrak {A},f, t_c \vDash \phi \) and \(\mathfrak {A},f, t_c \vDash \psi \);
-
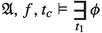 iff there is \(t_2 \in {\mathcal {T}}\) such that \(\mathfrak {A}, f_{t_1}^{t_2}, t_c \vDash \phi \).
iff there is \(t_2 \in {\mathcal {T}}\) such that \(\mathfrak {A}, f_{t_1}^{t_2}, t_c \vDash \phi \).
King’s proposal may be viewed as a version of eternalism, since he agrees with the central idea of Kaplanian propositions – that propositions are sets of indices. Within an index, as King claims, there is no time parameter, so propositions cannot change truth-values through time.Footnote 12 As we shall see, this particular idea – the idea that propositions are sets of indices – is crucial to the fact that his proposal is a version of eternalism. Let us see how this framework works on a particular example. Consider again the sentence \(\phi \)=“Jakub was a policeman” as uttered at \(t_c\). According to King, it has the following logical form.
-
\(\phi \)’s LF:
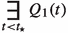
where \(t_{\star }\) denotes the time of utterance \(t_c\), and \(Q_1\) denotes the predicate “Jakub-be-a-policeman-at”. But what is the exact relation between \(t_{\star }\) and \(t_c\)? We have two possible cases. Either \(t_{\star }\) is a constant symbol whose referent is \(t_c\), or it is a variable such that \(f(t_{\star }) = t_c\). It is not clear from King’s paper what exactly \(t_{\star }\) is. However, assuming that it is a constant symbol suggests that in our language we need a constant symbol for each time of utterance. Since time is continuous, it is doubtful that such a language is possible; more importantly, it is doubtful that English is such a language. This seems to suggest that \(t_{\star }\) is a variable,Footnote 13\(^{,}\)Footnote 14 so in what follows, I will assume that \(t_{\star }\) is a variable. Now, having said all this, we can calculate the truth-conditions of \(\phi \) in a given context of utterance \(c = \langle f, t_c\rangle \):

This is equivalent to
Since \({f}_{t}^{t_1}(t) = t_1\) and \({f}_{t}^{t_1}(t_{\star }) = f(t_{\star }) = t_c\), we conclude that the truth-conditions are such that \(\phi \) is true if and only if there is a time \(t_1\) which is earlier than \(t_c\) and such that Jakub is a policeman at \(t_1\). Since, according to the operator analysis, \(\phi \) has a logical form Pq, where \(q \in \Phi \), we conclude that, according to the operator analysis, the truth-conditions of \(\phi \) in a context \(t_c\) are exactly the same as on King’s account. In the same spirit, we can replace temporal operators P, F, N with \(\exists (t < t_{\star })\), \(\exists (t > t_{\star })\), \(\exists (t = t_{\star })\), respectively. In consequence, we really do not need temporal operators at all. However, the quantificational analysis, if formalized as above, does not imply eternalism. Intuitively, this is because \(t_{\star }\) in the logical form is a variable. Since it is a variable, its value can change through the assignments. Thus, if one is willing to agree that propositions can change truth-values with respect to assignments, one can smuggle temporalism into the quantificational analysis. One elegant way to do this is to replace the notion of a Kaplanian proposition with the following notion.
Definition 11
Temporal diagonal propositionFootnote 15 expressed by a sentence \(\phi \) in a given \({\mathcal {L}}_{\exists }\)-model \(\mathfrak {A}\) is the set
According to this definition, propositions are sets of contexts. If for a temporal diagonal proposition p, we define

then it is easy to see that (TP) is true. This is captured by the fact that \(f(t_{\star }) = t_c\), so the referent of \(t_{\star }\) does not remain constant through different contexts.Footnote 16 To illustrate this, consider once again the sentence \(\phi \)=“Jakub was a policeman”. According to the quantificational analysis, the (Kaplanian) proposition expressed by the sentence \(\phi \) as uttered at \(t_c\) is that there is a time prior to \(t_c\) at which Jakub is a policeman. Clearly such a proposition is eternal. However, the temporal diagonal proposition expressed by \(\phi \) is that there is an earlier time at which Jakub is a policeman, and such a proposition is genuinely temporal. Similar remarks can be found in Dever (2015, pp. 7–10), Ninan (2010, pp. 372–378), but these authors show their ideas by using the \(\lambda \)-abstractor, which, as we have seen, is not needed. The conclusion is that even if we agree with King that operators should be replaced with quantifiers, that does not automatically mean that eternalism is true. By rejecting the notion of Kaplanian propositions, one can smuggle temporalism into the quantificational account.Footnote 17 Contrary to this, let us assume that the notion of Kaplanian proposition is favored for other reasons. Why should we replace operators with quantifiers? King presents three main arguments for such a move.
The first argument (King, 2003, pp. 215–217, 238) is concerned with tensed sentences with temporal adverbials. Consider, for example, the sentence \(\phi \) = “Yesterday, Jakub turned off the stove”. If we treat both “Yesterday” and the past tense as intensional operators, then we have two possible readings of \(\phi \):
- (\(\phi _1\))::
-
Y(P(Jakub turns off the stove)),
- (\(\phi _2\))::
-
P(Y(Jakub turns off the stove)).
Obviously, the sentence \(\phi \) is not ambiguous at all, but the bizarre result of the operator analysis is that it should be. What is worse, the reading \((\phi _1)\) is not even a plausible reading:
where \(\psi \) stands for “Jakub turns off the stove”. Thus, \(\phi _1\) is true if there is a time before a day prior to the time of utterance at which Jakub turned off the stove. Note that the reading (\(\phi _2\)) gives the correct prediction:
But this is just a coincidence produced by the fact that operator Y ignores the time parameter of the index.Footnote 18 On the other hand, given the quantificational analysis, it is natural to treat “Yesterday” as a restriction of the domain of quantification. Therefore – or so the argument goes – the quantificational analysis is more adequate than the operator analysis.
In my opinion, this argument is not convincing. It rests on the assumption that time adverbials such as “Yesterday” are necessarily – given the operator analysis – treated as intensional operators. It seems to me that, given the operator analysis of tenses, one is not forced to make such claims. In fact, it is natural to think that “Yesterday” picks out the past tense operator “It was the case that” and returns as a result the more complex operator “Yesterday, it was the case that”. If this is right, then we have only one possible reading of \(\phi \) which gives correct truth-conditions. This argument is developed by Brogaard (2012, pp. 78–101). I conclude that King’s argument does not threaten the operator analysis of tenses.
The second argument against the operator analysis of tenses is concerned with Partee’s (1973) observation that the past tense in English does not always behave in the same way as the operator P. Consider the sentence “Jakub had breakfast” as uttered at time \(t_c\). According to the operator analysis, it is true if and only if Jakub had breakfast at any time prior to \(t_c\). For example, it is true if Jakub had breakfast two years ago, but in most contexts it clearly means that Jakub had breakfast at some particular contextually provided time (or time interval) prior to \(t_c\) (usually, it means that Jakub had breakfast today). According to King, accounting for this phenomenon is problematic for the operator analysis:
-
Thus, it looks as though here the tense in some way picks out a particular contextually determined past time (or interval of time). But in so doing, it is hardly behaving like a standard past tense operator (King, 2003, p. 216).
Unfortunately, King gives only a short comment on how quantificational analysis can handle such examples:
-
If we think that the past tense (...) picks out a particular past time, we could suppose that in context of utterance the existential quantification over times (...) is further restricted just as happens in cases like ‘All the beer is in the fridge.’ (King, 2003, p. 240).
It seems that, according to King, in such cases context provides an additional feature: the restriction of the domain of quantification of the existential quantifier, which occurs in the logical form of the sentence uttered. This indicates that, according to the quantificational analysis, the sentence “Jakub had breakfast” has the following logical form

where \(t_p\) is the contextually provided time of the breakfast. I will not analyze this idea in detail, but I want to note that, in principle, there is no reason that the operator analysis cannot mimic this strategy. Although there is no quantifier in the logical form according to the operator analysis, there is one in the truth-conditions of the sentence in the past tense. This additional feature – the restriction of the domain of quantification – can be seen as going directly to the truth-conditions of the proposition itself, not through its logical form. If this is right, then this restriction can be seen as an example of the so-called unarticulated constituentFootnote 19. The proponent of the quantificational analysis may respond here in the spirit of Stanley (2000). The argument would be that the time of the event in question (and similarly, the restriction of the domain of quantification in the general case) must be a part of the logical form because it can be bound by some operator. In our case, the time that is picked out in “Jakub had breakfast” can be bound by the expression “Each time I was in Paris” as in the case of “Each time I was in Paris, Jakub had breakfast”. The time of the breakfast varies with the temporal values introduced by the operator “Each time I was in Paris”. This indicates that the logical form of “Each time I was in Paris, Jakub had a breakfast” should be something like

Therefore, the objector would conclude that the time must be a value of some variable present in the logical form, because there is no binding without such a variable.Footnote 20 If this is right, then the time of Jakub’s breakfast cannot be an example of unarticulated constituent because, by definition, unarticulated constituents are not traceable to the logical form. Does this kind of argumentation work? I do not think so. Firstly, as Recanati (2002, pp. 325–326) persuasively argued, this kind of reasoning proves too much. Consider a sentence \(\alpha =\)“The policeman stopped the car”. Since the manner of stopping the car can be bound by the operator “in some way or another” (as in the example “in some way or another, the policeman stopped the car”), this implies that in the logical form of \(\alpha \) there is a variable representing the manner of stopping. This seems to be counter-intuitive. Secondly, note that the logical form of “Each time I was in Paris, Jakub had breakfast” is not obtained from the logical form of “Jakub had breakfast” because \(L_1\) is not equivalent to

This observation casts doubts on the assumption that the mere fact that operators such as “Each time I was in Paris” can be applied to sentences such as “Jakub had breakfast” implies that there must be a temporal variable in the logical form of the sentence. In fact, the expression “Each time I was in Paris” can (1) contribute the so-called variadic function, i.e., the function which maps the temporal proposition “Jakub-have-breakfast” onto a property of times “Jakub-have-breakfast-at(t)”,Footnote 21 and (2) bind the newly introduced time variable t. If that is the case, there is no time variable in the standalone case of “Jakub had breakfast”, but there is one in “Each time I was in Paris, Jakub had breakfast” because the variable is both introduced and bound by the operator “Each time I was in Paris”. Observe that the temporalist can think that operator “Each time I was in Paris” picks out the past tense operator and returns as a result the more complex operator “Each time I was in Paris, it was the case that”. In such a case, the logical form of “Each time I was in Paris, Jakub had breakfast” would be the following
where “Jakub-have-breakfast” is the temporal proposition true at all times t such that Jakub has breakfast at t.
Even if the unarticulated constituents account fails, the proponent of the operator analysis has another more standard strategy of replying to King’s problem: she may claim that in the discussed cases the contextually provided time is not a part of what is said or of a proposition, but it is implicated via conversational implicatures (Grice, 1975). In our example, it is said that Jakub had breakfast at some time prior to \(t_c\), but it is implicated that Jakub had breakfast today. The implicature can be recovered from Gricean maxims: if the speaker did not want to communicate that Jakub had a breakfast today, she would break the maxim of relevance. In conclusion, the operator analysis can account for the discussed phenomenon.
King’s third argument in favor of quantifiers is that quantificational analysis is simpler, more elegant and less ad hoc than operator analysis. Consider the following sentences:
- (\(s_1\)):
-
One day, all persons alive now will be dead.
- (\(s_2\)):
-
Once all persons alive then would be dead.
According to the operator analysis, they get the following logical forms:
- (\(s_1\))’s:
-
LF:
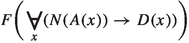
- (\(s_2\))’s:
-
LF:
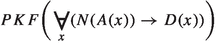
where P is the past tense operator, F is the future tense operator, N is the “now” operator, A, D are predicates which stand for “alive” and “dead”, and K is Vlach’s (1973) operator defined in the following way.
Definition 12
The truth of \(K\phi \) in a \({\mathcal {L}}_D\)-model \(\mathfrak {A}\) as uttered at \(t_c\) and evaluated at t is given by the equivalence:
Intuitively, the operator K picks out the time to which ‘then’ refers to. In our case, the operator stores the time introduced by a past tense operator that embeds it.
I am not going to analyze \((s_1)\) and \((s_2)\) in detail since it would require some extra elements to be introduced in our language \({\mathcal {L}}_D\)Footnote 22 which are not important from our point of view. The operator analysis can account for the truth-conditions of (\(s_1\)) and (\(s_2\)). However, the problem is that
-
even though (\(s_1\)) and (\(s_2\)) appear to have the same number and sort of syntactic constituents combined in the same ways, and they differ only in tense and the words ‘now’ and ‘then’, they have very different LFs: (\(s_1\))’s LF contains two operators and \((s_2)\)’s LF contains four! Surely this looks ad hoc and presupposes a very messy relation between the surface structures of sentences and their LFs. King (2003, p. 222).Footnote 23
Brogaard (2012, p. 101) proposes a solution with the use of the “complex operator strategy”. She suggests that “one day” picks out the future tense operator and returns a more complex operator “one day, it will be the case”; “once” picks out the past tense and returns a more complex operator “It once was the case that”. Consequently, one can have an elegant account of (\(s_1\)) and (\(s_2\)).
-
(\(s_1\)): For all persons x, it will be one day that (x does not exist).
-
(\(s_2\)): It once was the case that (for all persons x, it will be the case that (x does not exist)).
This indicates that operator analysis is able to paraphrase \(s_1\) and \(s_2\) in a way that is not ad hoc nor complicated.
Zeman (2013) provides some arguments against the complex operator strategy. His main worry is that there is not much positive evidence for the claim that the operator analysis is the best on the market. This leads to the question:
-
if there is no positive syntactic evidence for basic tense operators being sentential, what grounds do we have to claim that composite ones are sentential? (Zeman, 2013, p. 326)
Zeman’s suggestion is that we do not have any such grounds. It is true that there is not much positive evidence for such claims, but this worry equally applies also to the quantificational analysis. As it has been shown in this section, all the data that allegedly support the quantificational account can be accommodated by the operator treatment of tenses. Thus, there is not much positive evidence that the quantificational formalization of tenses is the best choice. The conclusion of this section is that King’s arguments by themselves are not decisive. The operator analysis still seems to be an option.
3.2 Tense operators do not operate on propositions
The second strategy is to reject premise (A2). The claim is that tense operators do not operate on propositions. In practice, rejecting (A2) is done by rejecting (PM). Tense operators operate on semantic values of sentences in contexts, so it follows that the semantic values of sentences in contexts cannot be propositions. Thus, we reject Propositional Multitasking. This strategy is argued for in Lewis (1980), Rabern (2012), Yli-Vakkuri (2013). The conclusion is that our theory is more complex because we have two types of entities involved – two types of contentFootnote 24: one that is compositional and plays the role of the semantic values of sentences in contexts; and one that is non-compositional and plays the role of the contents of assertionsFootnote 25. The motivation for such a move comes from the Principle of Compositionality. There seems to be a tension between this principle and the (ET)+(PM) package.
The Principle of Compositionality. For each n-place syntactic operator O, there is a function \(h_O\) such that, for all \(X_1\), \(X_2\), ..., \(X_n\) such that \(O(X_1, X_2, ..., X_n)\) is defined,
where m is the function that maps an expression X to its meaning.Footnote 26
The Principle of Compositionality states, roughly, that the meaning of a complex expression is determined by the meaning of its parts and how they are combined. What is the “meaning” in our definition? It is the semantic value of a given expression in a given context of utterance. Assuming (PM), this is also the assertoric content. Consider the following example. Let \(X_1\) be the sentence “it is raining”; let \(X_2\) be the sentence “it is raining now”; and let O be the past tense operator. According to (ET), in a given context of utterance \(X_1\) and \(X_2\) express the same proposition, thus \(m(X_1) = m(X_2)\). By the Principle of Compositionality, we get
This means that the propositions expressed by the sentences \(O(X_1)\) = “it was raining” and \(O(X_2)\) = “it was the case that it is raining now” in that context are the same. However, they are clearly not: the first is true if and only if there is a past time at which it is raining; the second is true if and only if it is raining at the time of the utterance. The conclusion is that (ET)+(PM) is incompatible with the Principle of Compositionality.
Rabern’s suggestion (2012) is that we should reject (PM) as it is stated by claiming that compositional semantic values and propositions are two different kinds of entities. Firstly, the compositional semantic values of sentences in contexts are sets of indices; they are what we call Kaplanian propositions. However, propositions are defined in some other way. If we assume that we have modal operators in the language and the world parameter in the semantic index, it is natural to claim that the proposition expressed by the sentence \(\phi \) in the context c is the set of possible worlds w such that \(\phi \) is true as uttered at c and evaluated at the time of utterance \(t_c\) and world w. In this sense, propositions are not compositional semantic values of sentences, but they are determined by them.
There are two main concerns regarding this strategy.Footnote 27 The first is connected with the motivation from the Compositionality Principle. It seems natural for the temporalist to claim that the Principle of Compositionality strengthens her point, i.e., that the argument presented above shows that one should reject (ET). From such a point of view, we have two arguments for temporalism and no arguments against it, so the strategy of rejecting (A2) seems ad hoc.
The second concern is that the two-content strategy violates Ockham’s Razor. What motivates (PM) is that by assuming it we end up with a very simple theory – we have only one kind of entity to play all the theoretical roles. However, given the discussed proposal, we have two kinds of contents. The intuition of Ockham’s Razor is that, other things being equal, simpler theories should be preferred. In this spirit, the temporalist may argue that her theory is simpler and, consequently, that rejecting (A2) is a road not worth pursuing. The conclusion is that the two-content strategy is not as innocent as it may look.
3.3 Tense operators may operate on eternal entities
The third strategy is to reject assumption (A3). Lots of authors have overlooked this type of response. For example, Brogaard (2012) recognizes that premise (A3) is needed for the Operator Argument to be valid, but she does not discuss rejecting it and she analyses only the two previous strategies. In this section, I will show how this strategy can be obtained by adopting Timestamp Semantics (Fritz et al., 2019, pp. 2939–2941). Timestamp Semantics is the theory for \({\mathcal {L}}_D\) which results in replacing the codomain of V, i.e., the set \({\mathcal {P}}({\mathcal {T}})\), with the product \({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}\) in Definition 1. This entails that the notion of Kaplanian proposition must also be abandoned. It is natural to replace it with the notion of the timestamp proposition.
Definition 13
The timestamp proposition expressed by \(\phi \) in \({\mathcal {L}}_D\)-model \(\mathfrak {A}\) and context of utterance \(t_c\) is an ordered pair \(\langle {\mathbb {P}}_{\phi , t_c}, t_c \rangle \), where \({\mathbb {P}}_{\phi , t_c}\) is a Kaplanian proposition expressed by \(\phi \) in \(t_c\).
Intuitively, the proposition expressed by it is raining, as uttered at t, is represented in Timestamp Semantics by \(\langle S, t\rangle \), where S is the set of all times at which it is raining. We say that a timestamp proposition \(p = \langle S, t \rangle \) is true at a time \(t'\) if and only if \( t \in S \). Thus, the truth at a point does not depend on a point \(t'\), but only on proposition p. Formally, we can represent truth as a relation Tr such that
We can define the past tense operator P, which operates on timestamp propositions in a very natural way:
And consequently, for any operator O:
Fact 1
A feature of Timestamp Semantics is that it violates (A3) but retains (A1), (A2) and (ET).
Proof
Recall that the underlying set of times is the set of integers, i.e., \({\mathcal {T}} = {\mathbb {Z}}\).
Claim 1
Timestamp Semantics retains (ET).
Proof

Thus (ET) is true:

\(\square \)
Claim 2
Timestamp Semantics retains (A2).
Proof
Since operator P operates on pairs \(\langle {\mathbb {P}}_{\phi , t_c},t\rangle \), which are timestamp propositions, (A2) is trivially satisfied. \(\square \)
Claim 3
Timestamp Semantics retains (A1).
Proof
I will show that tense operator P is non-redundant. Consider a Kaplanian proposition \(S = \{ 3, 5\}\). Then \(P(S) = \{ n \in {\mathbb {Z}} : n > 3\}\). Take any \(t' \in {\mathcal {T}}\). Since \( 4 \notin S\), it follows that \(\lnot Tr( \langle S, 4 \rangle , t')\). On the other hand, we have \( 4 \in P(S)\), so \( Tr( \langle P(S), 4 \rangle , t' )\). Thus we have
Therefore, it is not the case that

This means that operator P is non-redundant. \(\square \)
Claim 4
Timestamp Semantics violates (A3).
Proof
A direct consequence of claims 1 and 3. \(\square \)
There are two points worth mentioning here. Firstly, we should note that defining Timestamp Semantics in a model-theoretic way is at least hard, since Timestamp Semantics rejects the claim that for any temporal operator O and proposition p, the truth-value of Op at any time is determined solely by the truth-values of p at various times. This principle may be formalized as follows.

To see that this principle is not satisfied within Timestamp Semantics, consider \(S = \{1,3\}\) and two eternally true propositions \(p=\langle S, 3\rangle \) and \(q=\langle S, 1\rangle \). Obviously, for the past tense operator P, we have \(P(S) = \{ n\in {\mathbb {Z}} : n > 1 \}\), thus \(Pp=\langle P(S), 3\rangle \) is true at any time (since \(3\in P(S)\)), but \(Pq = \langle P(S), 1\rangle \) is false at any time (since \(1 \not \in P(S)\)). Secondly, according to Timestamp Semantics, tense operators are not truth-functional, i.e., it is not the case that if two contents p and q have the same truth-value at a given time, then the truth-values of Op, Oq are the same at that time. More formally,

The above counterexample shows that this rule is not satisfied, but bear in mind that Kaplanian temporalism also rejects it. To see this, consider two Kaplanian propositions \(p = \{3,4\}\) and \(q = \{4, 5\}\). We see that Tr(p, 4) and Tr(q, 4) holds. It follows that \(Tr(p, 4) \leftrightarrow Tr(q, 4)\) also holds. We can calculate \(P(p) = \{n \in {\mathbb {Z}}: n > 3\}\) and \(P(q) = \{ n \in {\mathbb {Z}} : n >4 \}\). In consequence, Tr(Pp, 4) holds, but Tr(Pq, 4) does not. This means that tense operators are intensional in Timestamp Semantics for the same reason that they are intensional in Kaplan’s semantics. To sum up, adopting Timestamp Semantics is a way to reject (A3) and retain (ET). Timestamp Semantics does this by replacing the notion of Kaplanian proposition with the notion of a timestamp proposition. In the next chapter, I will discuss three potential arguments against Timestamp Semantics in detail. I will show that they are not conclusive.
4 The case of timestamp semantics
In this section I will provide the motivation for considering Timestamp Semantics as a valuable position available on the market, and then consider three potential arguments against Timestamp Semantics. I will argue that none of them is conclusive and, consequently, that eternalists can escape the Operator Argument by adopting Timestamp Semantics.
4.1 Motivation for timestamp semantics
I believe that Timestamp Semantics is worth investigating, mainly because it captures the intuition that a sentence can have a tensed logical form while simultaneously expressing an eternal proposition. For instance, according to Timestamp Semantics, the sentece “Jakub was a policeman” has the logical form P(Jakub is a policeman), where P is the past tense operator “it was the case that”. However, it expresses an eternal proposition, which is true if and only if there is a time t prior to the time of the utterance at which Jakub is a policeman. Note that all sentences have tenseless logical form according to quantificational analysis. This is a crucial difference between these two frameworks.
Note also that the debate between eternalism and temporalism is semantic rather then syntactic. It is a debate about whether propositions can change their truth-values over time; it is not about whether sentences have tenseless logical form. This indicates that there should be an eternalist-friendly semantic theory which is consistent with tensed language. Timestamp Semantics is such a theory: it does not translate each sentence to a tenseless language, it only provides eternalistic truth-conditions.Footnote 28
4.2 The transparency principle
The first argument against Timestamp Semantics is that it violates the transparency principle. Consider the proposition \(p = \langle S, t \rangle \), expressed by “it is raining”, as uttered at t. The strange thing about Timestamp Semantics is that
-
whether that content is true at a time – say, last Tuesday – has nothing to do with how the weather is at that time. By contrast, it seems that whether it was raining last Tuesday has everything to do with how the weather was last Tuesday. But, of course, the content of ‘It is raining’ as uttered now is that it is raining, so there is an odd disconnect between whether that it is raining is true at a given time and whether it is raining at that time. In some sense, this violates a transparency principle for relational truth (Fritz et al., 2019, pp. 2941–2942).
Now, I will present this argument more precisely. For a start, we need a clear formulation of the transparency principle. The authors propose the following.
The transparency principle. At any time t, a content p is materially equivalent to p being true at t.

Let us assume that I uttered “It is raining” on 15:00, 01.06.2022, while standing on the main square in Kraków. According to Timestamp Semantics, the content expressed by “It is raining” on 15:00, 01.06.2022 is \(p = \langle S, t_c\rangle \) where S is the set of all times at which it is raining in Kraków and \(t_c = 15:00, ~01.06.2022\). If we agree with the authors that content p is the content that it is raining in Kraków, then the transparency principle implies that

However, this is equivalent to

Let us consider time \(t_1\) (e.g., last Tuesday) at which it is not raining in Kraków. The transparency principle implies that it is true that
However, this is not the case because at \(t_1\) the left-hand side of the equivalence is false (it is not raining in Kraków at \(t_1\)), but the right-hand side is true because \(t_c \in S\); so, by our previous definitions, \(Tr(\langle S, t_c \rangle , t_1)\) holds. Thus, Fritz et al. (2019) conclude that Timestamp Semantics is in trouble because it violates the transparency principle.
The problem with this reasoning is that it seems to assume what it aims to prove. From the eternalists’ point of view, the content of the considered assertion is not just that it is raining. It is rather something like it is raining at 15:00, on 01.06.2022 in Kraków. When evaluated at different times, this content does not change its truth-valueFootnote 29. To strengthen this intuition, we may imagine that on 02.06.2022 I ask whether what I said on 01.06.2022 was true. It seems that the answer has nothing to do with how the weather was on 02.06.2022. Rather it depends on the actual weather on 01.06.2022.
This indicates that, according to eternalists, (T1) is not a proper instance of the transparency principle, whose actual prediction is that

which is equivalent to

which clearly holds because t in \(Tr(\langle S, t_c \rangle , t)\) is irrelevant. The conclusion is that the transparency principle does not posit a genuine problem for eternalists.
The objector may reply here that this is not the formulation of the transparency principle which she had in mind. One such possible reformulation is as follows: At any time t, the content that would be expressed by \(\phi \) uttered at t is equivalent to the content actually expressed by \(\phi \) being true at t. Eternalism is at odds with such a principle because the content that would be expressed by “it is raining” at \(t_1\) is that it is raining in Kraków at \(t_1\), which of course is not equivalent to the content p being true at \(t_1\).Footnote 30 However, the eternalist may answer that the transparency principle is just false when formulated like this. The reformulation looks reasonable only if we assume temporalism from the beginning, so this reformulation does no better than the starting argument.
4.3 Now \(\phi \) vs. \(\phi \)
The other controversial thing concerning Timestamp Semantics is that, while being eternalist-friendly, it denies that, in a given context of utterance, the two sentences \(\phi \) and \(N\phi \) express the same proposition. To see this, assume that \(\phi \) stands for “it is raining” and is uttered at \(t_c\). According to Timestamp Semantics, the proposition \(p_1\) expressed by \(\phi \) is the ordered pair \(p_1 = \langle {\mathbb {P}}_{\phi , t_c}, t_c\rangle \). The sentence “it is raining now” is formalized by \(N\phi \), and the proposition \(p_2\) expressed by it is the ordered pair \(p_2 = \langle {\mathbb {P}}_{N\phi , t_c}, t_c \rangle \). Note that
However, the set \({\mathbb {P}}_{\phi , t_c}\) is the set of times at which it is raining. Therefore, it is not equal to \(\emptyset \) nor \({\mathcal {T}}\). It follows that \({\mathbb {P}}_{\phi , t_c} \ne {\mathbb {P}}_{N\phi , t_c}\), and this implies that \(p_1 \ne p_2\). The conclusion is that, in a given context, the sentences \(\phi \) and \(N\phi \) always express different propositions. At first glance, this consequence in unwelcome. Many philosophers started from this assumption when providing motivation for accepting eternalism. For example, Richard (1982, p. 337) explicitly invokes this intuition:
-
For the eternalist, a sentence like ‘Nixon is president’ contains an ‘implicit reference’ to a time: in his view, the use of (1) [’Nixon is president’] at time t expresses what the use of ‘Nixon is now president’ expresses relative to t. The second proposition, however, is eternal, i.e., it is either always true or always false.
This intuition is also a part of Twardowski’s (1900, p. 151) argument against relativism. He claims that
-
when I assert that it is raining while standing on High Castle Hill in Lwów, I obviously do not have in mind just any rain, falling at just any place and time; I voice a judgment about the rain falling here and now. I do not articulate this explicitly because there is no danger of being misunderstood, since it is under the mentioned conditions that I assert that it is raining; still, I do in fact have in mind the rain falling here and now. So, if I want to express the judgment without abbreviating it, I must say “It is raining here and now”.
However, I believe that the proponent of eternalism is not forced to make the claim that \(\phi \) and \(N\phi \) must express the same proposition. Eternalism is the thesis that all propositions keep their truth-value eternally. This is captured by Timestamp Semantics. Note that Timestamp Semantics can accommodate the intuition that what is said by \(\phi \) and \(N\phi \) is in some sense “the same”, since the truth of \(p_1\) is equivalent to the truth of \(p_2\):
-
(1)
Since \(p_1 = \langle {\mathbb {P}}_{\phi , t_c}, t_c \rangle \), we have \(Tr(p_1, t')\) is equivalent to \(t_c \in {\mathbb {P}}_{\phi , t_c}\).
-
(2)
By previous observations \(t_c \in {\mathbb {P}}_{\phi , tc}\) is equivalent to \({\mathbb {P}}_{N\phi , t_c} = {\mathcal {T}}\).
-
(3)
The condition \({\mathbb {P}}_{N\phi , t_c} = {\mathcal {T}}\) is equivalent to \(t_c \in {\mathbb {P}}_{N\phi , t_c}\), because \({\mathbb {P}}_{N\phi , t_c}\) is either \(\emptyset \) or \({\mathcal {T}}\).
-
(4)
From \(p_2 = \langle {\mathbb {P}}_{N\phi , t_c}, t_c \rangle \), we get that \(Tr(p_2, t')\) is equivalent to \(t_c \in {\mathbb {P}}_{N\phi , t_c}\).
The conclusion is that Rabern’s motivation for rejecting (A2) is equally good motivation for adopting the semantic theory by which \(\phi \) and \(N\phi \) express different propositions. Timestamp Semantics has this feature: as we noted, the eternalist may claim that, in a given context of utterance, \(\phi \) and \(N\phi \) express different propositions.
It may be argued that, by postulating two distinct propositions for \(\phi \) and \(N\phi \) in a given context, Timestamp Semantics results in a more complex theory than classical eternalism. This is true only at first glance: the classical eternalist will probably take the strategy of rejecting (A2). As I mentioned previously, this move also violates Ockham’s Razor. It seems to me that, from the point of simplicity, Timestamp Semantics does better than the two-content strategy because it breaks Ockham’s Razor’s intuition only in the quantitative sense (it does not postulate different kinds of content – only a greater number of contents of the same kind), while the two-content strategy breaks it in the qualitative sense.
What is more, one can handle Weber’s (2012, pp. 206–209) substitution argument as well. According to eternalism – or so the argument goes – the two sentences it is raining and it is raining at \(t_c\) express the same proposition if uttered at \(t_c\). However, if we apply the past tense operatorFootnote 31, then by the Principle of Compositionality we should get two sentences that express the same proposition. Unfortunately, the proposition that it was raining is not the same as the proposition that it was the case that it is raining at \(t_c\). Weber concludes that the eternalist is in trouble. An eternalist may reply in the same vein as in the case of “Now”. Consider the following definition.
Definition 14
The truth of \(At~ t_1 : \phi \) in a \({\mathcal {L}}_D\)-model \(\mathfrak {A}\) as uttered at \(t_c\) and evaluated at t is given by the equivalence:
This definition implies that the Kaplanian proposition expressed by \(At~ t_1 : \phi \) is either the set \({\mathcal {T}}\) or \(\emptyset \), depending on whether \(\mathfrak {A}, t_c, t_1 \vDash \phi \). Thus, as in the case of “now”, the eternalist concludes that the two sentences it is raining and it is raining at \(t_c\) do not express the same proposition even if uttered at \(t_c\).
The final worry here may be that, according to the considered account, the sentences “it is raining now” and “it is raining at t” (assuming that they are both uttered at t) express the same proposition. This seems to be a problem since one may believe that it is raining now, without believing that it is raining at t and vice versa.Footnote 32 Since propositions are objects of beliefs, these two should express different propositions and, given our account, they do not, which is a violation of (PM). These issues go beyond the scope of this paper, but I want to note that these sentences cause also a problem for Kaplan-style temporalism and classical eternalism.
4.4 Rejecting premise (A2)
The final argument against Timestamp Semantics is that it seems that the Timestamp Semantics rejects (A3) by some kind of formal “cheating”. After all, do operators really operate on timestamp propositions? The intuition is that they do not: Kaplanian propositions are parts of timestamp propositions, and tense operators operate on timestamp propositions in virtue of how they operate on Kaplanian propositions. Thus, it seems that tense operators do not “genuinely” operate on timestamp propositions. It follows that Timestamp Semantics is the two-content strategy in disguise, or so the argument goes.
The response here is that operators operate on semantic values of sentences; by definition of Timestamp Semantics, these are elements of the set \({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}\) and not of the set \(\mathcal {{\mathcal {T}}}\). Since propositions are pairs \(\langle S, t \rangle \), they really are semantic values of sentences in contexts, so Timestamp Semantics does not reject the identification of compositional semantic values with assertoric contents. In consequence, Timestamp Semantics retains both (PM) and (A2). To complete the defence, we should define how the compositional semantic value of complex sentences is constructed from the values of their parts. I will present the formal details in the final part of the paper.
4.5 Formal details
I will follow a suggestion from Fritz et al. (2019, p. 2941, footnote 11.) and base my formalization of Timestamp Semantics in the formalism of Neighborhood Models (Pacuit, 2017). For simplicity, let us assume that we have a language \({\mathcal {L}}\) containing sentential variables (\(\Phi \)), two truth-functional connectives (\(\wedge \), \(\lnot \)) and one temporal operator H (“it has always been the case that”). The operator P can be defined in the standard way: \(P:= \lnot H \lnot \).
Definition 15
A timestamp \({\mathcal {L}}\)-model is an ordered set \(\mathfrak {M} = \langle {\mathcal {T}}, {\mathcal {N}}_H, {\mathcal {C}}, V \rangle \), where
-
\({\mathcal {T}}\) is a non-empty set of times;
-
For the temporal operator H, the set \({\mathcal {N}}_{H} \subseteq {\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}\) is the set of propositions;
-
\({\mathcal {C}}\) is a non-empty set of contexts;
-
\(V : \Phi \times {\mathcal {C}} \rightarrow {\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}\) is a valuation function.
In the standard version of Neighborhood Semantics, instead of the set \({\mathcal {N}}_H\), there is a function \({\mathcal {N}}_H : {\mathcal {T}} \rightarrow {\mathcal {P}}({\mathcal {T}})\), such that for each time \(t \in {\mathcal {T}}\), \({\mathcal {N}}_H(t)\) is the set of all propositions that are necessary (in the relevant sense) at t. Since we are considering eternalism, we want to remove the time parameter from the semantics index. Thus, we should also remove the time parameter from the definition of \({\mathcal {N}}_H\). This indicates that when constructing an eternalist-friendly Neighborhood Semantics, we should define the function \({\mathcal {N}}_H\) as constant. Thus, we treat it as a set. We can define it in the following way.
Definition 16
The set \({\mathcal {N}}_H\) is defined as
where \(R^{\rightarrow }(t) = \{t' \in {\mathcal {T}} : t' < t\}\).
The set \({\mathcal {N}}_H\) is the set of all such propositions in which the first element (the set of times) contains all the times that are earlier than the distinguished time (i.e., the second element). The semantics for the eternal case is analogical to the classic case.
Definition 17
A sentence \(\phi \) is true in a timestamp \({\mathcal {L}}\)-model \(\mathfrak {M}\) and a context c.
-
\(\mathfrak {M}, c \vDash p \) iff \( V(p,c) = \langle S, t \rangle \) and \(t \in S\);
-
\(\mathfrak {M}, c \vDash \lnot \phi \) iff it is not the case that \(\mathfrak {M}, c \vDash \phi \);
-
\(\mathfrak {M}, c \vDash \phi \wedge \psi \) iff \(\mathfrak {M}, c \vDash \phi \) and \(\mathfrak {M}, c \vDash \psi \);
-
\(\mathfrak {M}, c \vDash H\phi \) iff \([\phi ]^{\mathfrak {M},c} \in {\mathcal {N}}_H\).
We do not have the time parameter in the index, but we relativize the truth of sentences to the context of utterance, which is similar to the case of Kaplanian semantics.
Note that in the above definition, we mimic the classic case for the truth of sentences of the form \(H\phi \). Thus, we must define the compositional semantic value of any sentence \(\phi \). The intuition is that we want to mimic the classic case in this respect as well. To do this, the following notation would be helpful.
Definition 18
Operations \(\cap : ({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}) \times ({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}) \rightarrow ({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}})\) and \(\lnot : ({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}) \rightarrow ({\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}})\).
-
\(\lnot \langle S, t \rangle = \langle {\mathcal {T}} \setminus S, t \rangle \);
-
\(\langle S, t \rangle \cap \langle S', t \rangle = \langle S\cap S', t\rangle .\)
Now, the definition of the compositional semantic value is the same as in the classic case.
Definition 19
Compositional semantic value of \(\phi \) in a timestamp \({\mathcal {L}}\)-model \(\mathfrak {M}\) and a context c:
-
\( [p]^{\mathfrak {M}, c} = V(p,c); \)
-
\([\lnot \phi ]^{\mathfrak {M},c} = \lnot [\phi ]^{\mathfrak {M},c};\)
-
\([\phi \wedge \psi ]^{\mathfrak {M},c} = [\phi ]^{\mathfrak {M},c} \cap [\psi ]^{\mathfrak {M},c}\);
-
\([H\phi ]^{\mathfrak {M},c} = m_{{\mathcal {N}}_H}([\phi ]^{\mathfrak {M},c})\).
What remains is the function \(m_{{\mathcal {N}}_H}\). Note that in the classic case, the function \(m_{{\mathcal {N}}_H}\) takes a proposition as an argument and gives another proposition as an output. We can use this intuition, having in mind that in the eternal case propositions are sets of times together with a time determined by the context of utterance. The following definition captures this quite well.
Definition 20
The function \(m_{{\mathcal {N}}_H} : {\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}} \rightarrow {\mathcal {P}}({\mathcal {T}}) \times {\mathcal {T}}\) is defined as follows
For each proposition \(\langle X, t\rangle \), the function \(m_{{\mathcal {N}}_H}\) returns the proposition that contains the set of all times \(t'\) such that all times earlier than \(t'\) belong to X and time t.
This definition completes our framework. Let us illustrate that the truth conditions of the sentences \(H\phi \) are correct. For simplicity, let us assume that the time of the utterance is \(t_c\) and that \([\phi ]^{\mathfrak {M},c} = \langle S, t_c\rangle \).
Let us assume that the proposition expressed by \(\phi \) at c is that it is raining in Kraków. In such a case, S denotes the set of all times at which it is raining in Kraków. The sentence \(H\phi \) expresses the proposition that it has always been the case that it is raining in Kraków; according to our analysis, it is true at c if each time \(t' < t_c\) belongs to the set S; that is, if at each time \(t' < t_c\) it is raining in Kraków. The truth-conditions are correct.
Previously, we defined the timestamp proposition using the notion of a Kaplanian Proposition. The important thing to note is that the compositional semantic value of a sentence in a given context c is the proposition expressed by that sentence in c.
Fact 2
For each \(\mathfrak {M}\), \(\phi \), c it is the case that
where \({\mathbb {P}}_{\phi , t_c}\) is the Kaplanian proposition expressed by \(\phi \).
Proof
Proof by induction on the complexity of \(\phi \).
-
1.
\([p]^{\mathfrak {M},c} = V(p,c) = \langle {\mathbb {P}}_{p, t_c}, t_c \rangle \) by definitions.
-
2.
\([\lnot \phi ]^{\mathfrak {M},c} = \lnot [\phi ]^{\mathfrak {M},c}\). By induction, \([\phi ]^{\mathfrak {M},c} = \langle {\mathbb {P}}_{\phi , t_c}, t_c \rangle \) and thus \(\lnot [\phi ]^{\mathfrak {M},c} = \lnot \langle {\mathbb {P}}_{\phi , t_c}, t_c \rangle = \langle {\mathcal {T}} \setminus {\mathbb {P}}_{\phi , t_c}, t_c \rangle = \langle {\mathbb {P}}_{\lnot \phi , t_c}, t_c \rangle \).
-
3.
\([\phi \wedge \psi ]^{\mathfrak {M},c} = [\phi ]^{\mathfrak {M},c} \cap [\psi ]^{\mathfrak {M},c} = \langle {\mathbb {P}}_{\phi , t_c} ,t_c\rangle \cap \langle {\mathbb {P}}_{\psi , t_c}, t_c \rangle = \langle {\mathbb {P}}_{\phi , t_c} \cap {\mathbb {P}}_{\psi , t_c}, t_c \rangle = \langle {\mathbb {P}}_{\phi \wedge \psi ,t_c}, t_c \rangle \).
-
4.
\([H \phi ]^{\mathfrak {M},c} = m_{{\mathcal {N}}_H}([\phi ]^{\mathfrak {M},c}) = m_{{\mathcal {N}}_H}( \langle {\mathbb {P}}_{\phi , t_c}, t_c \rangle ) = \langle \{ t' \in {\mathcal {T}} : \langle {\mathbb {P}}_{\phi , t_c}, t' \rangle \in {\mathcal {N}}_H \}, t_c \rangle = \langle \{t' \in {\mathcal {T}} : R^{\rightarrow }(t') \subseteq {\mathbb {P}}_{\phi , t_c}\} , t_c\rangle = \langle \{t'\in {\mathcal {T}} : \forall _{t'' < t'} t'' \in {\mathbb {P}}_{\phi , t_c} \}, t_c\rangle = \langle {\mathbb {P}}_{H\phi , t_c}, t_c \rangle \).
\(\square \)
According to this fact, compositional semantic values of sentences in a given context of utterance are (timestamp) propositions, thus the Propositional Multitasking assumption holds. This also proves that the Principle of Compositionality is satisfied. It follows that the argument which says that the Timestamp Semantics is the two content strategy in disguised is misplaced.
5 Conclusion
In this paper, I have argued that there is an elegant way for the eternalist to deal with the Operator Argument. I followed a suggestion from Fritz et al. (2019) and adopted Timestamp Semantics. Unfortunately, Fritz et al. rejected their own proposal and decided to go with the two-content strategy after all. I claimed that allowing for temporal operators that operate on eternal entities in a non-vacuous way is a better solution. Firstly, the alleged motivation for the two-content strategy is also motivation for the temporalist position. It seems natural for the temporalist to claim that the Principle of Compositionality strengthens her point, i.e., that substitution arguments show that one should reject eternalism. From such a point of view, we have two arguments for temporalism and no arguments against it, so the strategy of rejecting (A2) seems ad hoc. Secondly, the assumption that propositions do not serve as compositional semantic values results in a more complex theory, thus it violates Ockham’s Razor’s intuition. What is more, King’s (2003) strategy of using quantifiers is not as good as one might think since it also allows for temporal propositions. Finally, I discussed three potential counterarguments to my proposal. The important message is that the eternalist is not obliged to claim that the two sentences \(\phi \) and it is now the case that \(\phi \) express the same proposition, even when uttered in the same context. Such a move allows us to handle substitution arguments of various kinds (Weber, 2012; Rabern, 2012). In the last section I presented the full formalization of Timestamp Semantics, and showed that it is compositional in the desired sense.
Notes
For example, (Perl, 2015) argues that the objects of at least some beliefs must be temporal.
I do not claim here that time is linear. This assumption is made only to keep things simple.
This definition makes sense only if we assume that \(t_c - 1\) is well defined, which is guaranteed by the assumption that \({\mathcal {T}} = {\mathbb {Z}}\). One potential problem with defining yesterday in such a manner is that the operator N means something like “today” rather than “now”. If \(t_c\) designates the present moment, it follows that \(t_c-1\) denotes the previous moment, which is not what “yesterday” means. One possible way out is to represent times not as integers but as real numbers. In such a case, if \(t_c\) is the present moment, \(t_c - 1\) might represent the moment that was exactly 24 hours before the present moment, which is much closer to “yesterday”. These matters are not essential for the operator argument; so, for simplicity, I will stick with Kaplanian definitions.
See (Weber, 2012, pp. 200–202) for a discussion.
See (Fritz et al., 2019, pp. 2938–2939).
My reconstruction is similar to Brogaard’s (2012, pp. 117–119). A more general reconstruction can be found in (Cappelen & Hawthorne, 2009: 71–72), but the authors take the Operator Argument to be an argument against (PM), not against (ET). Thus, in the context of this paper, a Brogaard-style reconstruction fits better.
See (Fritz et al., 2019, pp. 2938–2939).
One may wonder what is left in the semantic index according to this proposal. On the standard picture, there are modal operators in the language and thus, there is a world parameter within the index. I left it out for the purpose of presentation.
I am using LF as an abbreviation for “logical form”.
It will soon become clear that a particular choice of the assignment makes little difference, with the notable exception that we request that \(f(t_{\star })=t_c\). More about this later on.
Again, it may seem that this makes no sense, since in our semantic theory for \({\mathcal {L}}_{\exists }\) we do not relativize truth to any indices. As it was said before, the claim is that there is a world parameter within the index, but no time parameter. Therefore, King’s proposal is that propositions are sets of possible worlds.
It seems that this argument is not consistent with my assumption that \({\mathcal {T}} ={\mathbb {Z}}\) since the set \({\mathbb {Z}}\) is not continuous. However, this assumption is not essential to the quantificational analysis, and since “Yesterday” is not treated as an intensional operator, we do not really need it while considering \({\mathcal {L}}_{\exists }\)-models.
One might think that this is too hasty. At least one more possibility is still on the table: to treat \(t_{\star }\) similarly to Kaplan’s treatment of “Here” and “I” (1989a, pp. 541–546). In such a case, \(t_{\star }\) functions as 0-argument operator – the denotation of \(t_{\star }\) depends upon the context of utterance c and is equal to \(t_c\). This kind of formalism simplifies the framework: in such a formulation, there is no need to put the assignment function into the context because the function parameter is no longer used to generate content.
See (Rabern & Ball, 2019, pp. 406-407).
Note that when one treats \(t_{\star }\) as a 0-argument operator, then these definitions also simplify.
-
1.
\( {\mathbb {P}}_{\phi } = \{ t_c \in {\mathcal {T}} : \mathfrak {A}, f, t_c \vDash \phi \}\)
-
2.
\( Tr(p, t) \equiv _{def} t \in p\)
-
1.
One counter-intuitive feature of such an account is that the proposition that it is raining now is also temporal.
This fact alone may indicate that “yesterday” does not behave as an intensional operator. After all, one may argue that intensional operators should be sensitive to the parameter of the index.
Recanati (2002, p. 305) provides a very similar example.
For a detailed discussion concerning variadic functions, see Recanati (2002, pp. 318–322) or Zeman (2018). Interestingly, Recanati (2002, pp. 72–74) suggested that tenses may be neither operators nor quantifiers – they may function as variadic operators themselves. Zeman (2018) provides a more detailed introduction of such an account.
Namely, the set of individual variables together with the set of predicates. To see how this can be done, see (Kaplan, 1989a, pp. 541–546).
The notation was changed to be consistent with the paper.
Thus, following Brogaard (2012), I will sometimes refer to the strategy of rejecting (A2) as “the two-content strategy”.
These two are sometimes called “ingredient sense” and “assertoric content”, respectively (Dummett, 1973, p. 447).
Some additional arguments against it may be found in Brogaard (2012, pp. 119–129).
Therefore, Timestamp Semantics seems to be in accordance with the spirit of the new B-theory of time (Oaklander, 1994).
This may be controversial. For example, it may be claimed that the content that it is raining at 15:00 on 01.06.2022 in Kraków has no truth-value before this date, and is true or false after. I will not consider this issue here, since it is connected to the problem of future contingents, which is beyond the scope of this paper.
This is because p is the content actually expressed by \(\phi \), i.e., that it is raining in Kraków at \(t_c = 15:00, ~01.06.2022\).
Weber originally uses “it is always the case” operator, but there is no substantial difference between these two variants of the argument.
References
Brogaard, B. (2012). Transient truths: An essay in the metaphysics of propositions. Oxford: Oxford University Press.
Cappelen, H., & Hawthorne, J. (2009). Relativism and monadic truth. Oxford: Oxford University Press.
Dever, J. (2015). Eternalism, temporalism, neutralism. Inquiry: An Interdisciplinary Journal of Philosophy, 58(6), 608–618. https://doi.org/10.1080/0020174X.2015.1059112
Dummett, M. (1973). Frege: Philosophy of Language. London: Gerald Duckworth.
Fritz, P., Hawthorne, J., & Yli-Vakkuri, J. (2019). Operator arguments revisited. Philosophical Studies, 176, 2933–2959. https://doi.org/10.1007/s11098-018-1158-8
Grice, H. (1975). Logic and conversation. In P. Cole & J. Morgan (Eds.), Syntax and semantics 3: Speech Acts (pp. 64–75). New York: Academic Press.
Janssen, T. M. V. (1997). Compositionality. In J. van Benthem & A. ter Meulen (Eds.), Handbook of logic and language (pp. 417–473). Amsterdam: Elsevier.
King, J. C. (2003). Tense, modality, and semantic values. Philosophical Perspectives, 17, 195–245. https://doi.org/10.1111/j.1520-8583.2003.00009.x
Kaplan, D. (1989). Demonstratives. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan (pp. 481–563). Oxford: Oxford University Press.
Kaplan, D. (1989). Afterthoughts. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan (pp. 565–614). Oxford: Oxford University Press.
Lewis, D. K. (1980). Index, context, and content. In S. Kanger & S. Öhman (Eds.), Philosophy and grammar (pp. 79–100). Amsterdam: Reidel. https://doi.org/10.1007/978-94-009-9012-8_6
Maunu, A. (2003). No belief is contingently true. Auslegung, 26(2), 67–75. https://doi.org/10.17161/AJP.1808.9517
Ninan, D. (2010). Semantics and the objects of assertion. Linguistics and Philosophy, 33(5), 355–380. https://doi.org/10.1007/s10988-011-9084-7
Oaklander, L. N. (1994). A defense of a new Tenseless theory of time. In L. N. Oaklander & Q. Smith (Eds.), The new theory of time (pp. 57–68). New Haven: Yale University Press.
Pacuit, E. (2017). Neighborhood semantics for modal logic. Berlin: Spinger.
Pagin, P., & Westerståhl, D. (2010). Compositionality I: Definitions and variants. Philosophy Compass, 5(3), 250–264. https://doi.org/10.1111/j.1747-9991.2009.00228.x
Partee, B. H. (1973). Some structural analogies between tenses and pronouns in English. The Journal of Philosophy, 70(18), 601–609. https://doi.org/10.2307/2025024
Perl, C. (2015). An argument for temporalism and contingentism. Philosophical Studies, 172, 1387–1417. https://doi.org/10.1007/s11098-014-0355-3
Perry, J. (1979). The problem of the essential indexical. Noûs, 13(1), 3–21. https://doi.org/10.2307/2214792
Perry, J., & Blackburn, S. (1986). Thought without representation. Proceedings of the Aristotelian Society, Supplementary Volumes, 60, 137–166. https://doi.org/10.1093/aristoteliansupp/60.1.137
Prior, A. (1959). Thank goodness that’s over. Philosophy, 34(128), 12–17.
Rabern, B. (2012). Against the identification of assertoric content with compositional value. Synthese, 189, 75–96. https://doi.org/10.1007/s11229-012-0096-9
Rabern, B., & Ball, D. (2019). Monsters and the theoretical role of context. Philosophical Phenomenological Research, 98, 392–416. https://doi.org/10.1111/phpr.12449
Recanati, F. (2002). Unarticulated constituents. Linguistics and Philosophy, 25, 299–345. https://doi.org/10.1023/A:1015267930510
Recanati, F. (2007). Perspectival thought: A plea for moderate relativism. Oxford: Oxford University Press.
Richard, M. (1982). Tense, propositions, and meanings. Philosophical Studies, 41, 337–351. https://doi.org/10.1007/BF00353884
Schaffer, J. (2012). Necessitarian propositions. Synthese, 189(1), 119–162. https://doi.org/10.1007/s11229-012-0097-8
Stanley, J. (2000). Context and logical form. Linguistics and Philosophy, 23, 391–434. https://doi.org/10.1023/A:1005599312747
Twardowski, K. (1900). O tzw. prawdach względnych. In Księga Pamiątkowa Uniwersytetu Lwowskiego ku uczczeniu pięćsetnej rocznicy Fundacji Jagiellonskiej Uniwersytetu Krakowskiego (pp. 64–93). Lwów. English translation: On So-Called Relative Truths. In K. Twardowski (1999). On actions, products and other topics in philosophy. J. Brandl & J. Woleński (Eds.), Amsterdam: Rodopi, pp. 147–170.
Vlach, F. (1973). ‘Now’ and ‘then’: A formal study in the logic of tense anaphora, Ph.D. thesis, University of California, Los Angeles.
Weber, C. (2012). Eternalism and propositional multitasking: In defence of the operator argument. Synthese, 189, 199–219. https://doi.org/10.1007/s11229-012-0092-0
Yli-Vakkuri, J. (2013). Propositions and compositionality. Philosophical Perspectives, 27, 526–563. https://doi.org/10.1111/phpe.12025
Zeman, D. (2013). Temporalism and composite tense operators. Disputatio, 5(37), 323–328. https://doi.org/10.2478/disp-2013-0025
Zeman, D. (2018). Temporal variadic operators. Proceedings of the XXIII World Congress of Philosophy, 38, 51–55. https://doi.org/10.5840/wcp23201838829
Acknowledgements
This research was supported by a grant from the National Science Centre (Poland), no. 2020/39/D/HS1/00810. I am grateful to Katarzyna Kijania-Placek, Jacek Wawer, and two anonymous reviewers of this journal for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The author declares that he has no conflicts of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Węgrecki, J. The operator argument and the case of timestamp semantics. Synthese 202, 198 (2023). https://doi.org/10.1007/s11229-023-04411-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-023-04411-z




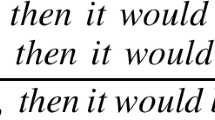
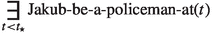
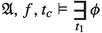 iff there is
iff there is