Skip to main content
SpringerLink
Log in

Particles, fields, and the measurement of electron spin

  • Published:
Synthese Aims and scope Submit manuscript

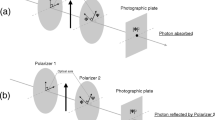
Abstract

This article compares treatments of the Stern–Gerlach experiment across different physical theories, building up to a novel analysis of electron spin measurement in the context of classical Dirac field theory. Modeling the electron as a classical rigid body or point particle, we can explain why the entire electron is always found at just one location on the detector (uniqueness) but we cannot explain why there are only two locations where the electron is ever found (discreteness). Using non-relativistic or relativistic quantum mechanics, we can explain both uniqueness and discreteness. Moving to more fundamental physics, both features can be explained within a quantum theory of the Dirac field. In a classical theory of the Dirac field, the rotating charge of the electron can split into two pieces that each hit the detector at a different location. In this classical context, we can explain a feature of electron spin that is often described as distinctively quantum (discreteness) but we cannot explain another feature that could be explained within any of the other theories (uniqueness).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. Stern–Gerlach spin measurements play a central role in textbook treatments of the philosophy of quantum physics, such as Albert (1992), Lewis (2016), Norsen (2017), Maudlin (2019), Barrett (2020).

  2. Stern and Gerlach saw their experiment as demonstrating “directional quantization,” though this was not initially applied to electron spin as that idea had not yet entered quantum theory (Gerlach and Stern 1922; Weinert 1995; Sauer 2016; Schmidt-Böcking et al. 2016). Now, it is common to present the experiment as showing that electron spin is quantized. I will use the term “discrete” instead of “quantized” because “quantized” suggests “quantum” and, as we will see, the outcomes of Stern–Gerlach experiments can be discrete in theories that are not quantum.

  3. For philosophical discussion and comparison of rigid body classical mechanics (used in Sect. 2), point particle classical mechanics (used in Sect. 3), and continuum mechanics (used in Sect. 6), see Wilson (1998, (2013).

  4. We will not examine relativistic classical theories of a point electron in this article (see Wen et al. 2016; Barandes 2019a, b and references therein).

  5. Here and throughout I adopt Gaussian cgs units.

  6. For the definition of magnetic moment in terms of current density, see Jackson (1999, sec. 5.6).

  7. Keeping the electron’s angular momentum and magnetic moment fixed, the electron will have to rotate faster the smaller it is. For a sufficiently small radius, its edges would have to move faster than the speed of light (Tomonaga 1997, p. 35; Griffiths 2005, problem 4.25; Rohrlich 2007, p. 127; Sebens 2019). Let us assume that the electron is large enough that it does not have to rotate so rapidly.

  8. See Uhlenbeck (1976, p. 47), Pais (1989, p. 39), Jackson (1999, p. 187), Griffiths (2013, problem 5.58).

  9. See Sebens (2019).

  10. This expression for the magnetic field follows (Griffiths 2005, p. 181).

  11. See Feynman et al. (1964, sec. 15.6), Lange (2002, ch. 5).

  12. See Feynman et al. (1964, sec. 34.3), Landau and Lifshitz (1971, sec. 45), Alstrøm et al. (1982), Griffiths (2005, sec. 4.4.2).

  13. The spherical electron of Sect. 2 had a magnetic moment as well, but it was not intrinsic. It was the result of flowing charge. Similarly, the spherical electron had angular momentum that was the result of flowing mass.

  14. Although we can derive the additional term in the force law that must be postulated and the equation for the torque that must be added by analyzing the theory of electromagnetism with rigid bodies, these features must be included as part of the fundamental dynamical laws in this theory of electromagnetism with point particles.

  15. Griffiths (2013, p. 378) considers this modification to the Lorentz force law to incorporate intrinsic magnetic moment and remarks: “I don’t know whether a consistent theory can be constructed in this way, but in any event it is not classical electrodynamics, which is predicated on Ampère’s assumption that all magnetic phenomena are due to electric charges in motion, and point magnetic dipoles must be interpreted as the limits of tiny current loops.” Barandes (2019a, (2019b) analyzes such modifications to the force law, considering intrinsic magnetic dipole moments, intrinsic electric dipole moments, and also other multipole moments.

  16. For a point electron, this potential energy cannot be derived from the total energy in the electromagnetic field (as in Sect. 2). Instead, this potential energy can be calculated by considering the work that must be done to rotate a point magnetic dipole in an external magnetic field (Griffiths 2013, problem 6.21) or the work required to bring the dipole to a given location from infinity (Good and Nelson 1971, p. 227). Or, it can be calculated by asking what potential would generate the additional term in the modified Lorentz force law (19) when one takes its negative gradient (Jackson 1999, sec. 5.7).

  17. For a general derivation from the theory of electromagnetism with rigid bodies of the law for torque that should be included in a theory with point bodies that possess intrinsic magnetic moments and angular momenta, see Jackson (1999, sec. 5.7).

  18. When the electron’s location is not relevant, its spin state is sometimes just specified by two complex numbers. We will not analyze the electron using that simplified representation in this article.

  19. See Bjorken and Drell (1964, eq. 1.34), Berestetskii et al. (1971, eq. 33.7), Dürr and Lazarovici (2020, eq. 1.28).

  20. This approximation is used in Griffiths (2005, example 4.4), Ballentine  (2014, sec. 9.1), Dürr and Lazarovici (2020, sec. 1.7.1).

  21. See Platt (1992).

  22. Similar examples of time evolution for gaussian wave packets appear in Griffiths (2005, problem 2.43), Ballentine (2014, problem 5.8).

  23. This effect is discussed in Griffiths (2005, example 4.3), Ballentine (2014, sec. 12.1). Larmor precession is often ignored in simplified and idealized presentations of Stern–Gerlach experiments. This precession is particularly relevant in repeated series of Stern–Gerlach setups, such as two-path experiments. For example, one often assumes that if an x-spin up electron passes through the Stern–Gerlach magnetic field and then the two wave packets that diverge are brought back together, a subsequent x-spin measurement will show that the electron is x-spin up (when in actuality the electron’s spin has been rotated by the first magnetic field). This kind of simplified treatment appears in Albert (1992, pp. 7–11), Maudlin (2019, pp. 22–25), Barrett (2020, ch. 2).

  24. For detailed introductions to these interpretations of quantum mechanics, see the references in footnote 1.

  25. Albert (1992, ch. 7), Bohm and Hiley (1993, ch. 10), Dürr and Teufel (2009, sec. 8.4), Norsen (2014, p. 346), for example, do not attribute an intrinsic magnetic moment to the electron itself.

  26. This point is explained clearly in relation to collapse theories by Maudlin (2019, pp. 101–102) and in relation to Bohmian mechanics by Norsen (2014).

  27. Bjorken and Drell (1964, p. 11) explain the interaction term as an operator version of the classical potential energy of a point charge in a static electromagnetic field (Feynman et al. 1964, sec. 15.6). This raises a number of questions, as we noted earlier (in Sect. 2) that potential energies are insufficient for achieving conservation of energy in classical electromagnetism and, putting that aside, the additional potential energy associated with the electron’s intrinsic magnetic moment (20) has not been included.

  28. See Bjorken and Drell (1964, sec. 1.4), Berestetskii et al. (1971, sec. 33), Bohm and Hiley (1993, sec. 10.4), Ryder (1996, sec. 2.6), Nowakowski (1999).

  29. This assumption focuses our attention on positive energy modes, allowing us to set aside questions regarding the interpretation of negative energy modes (sometimes addressed by introducing an infinite “sea” of negative energy electrons—the Dirac sea).

  30. By setting \(\phi \) equal to zero we are choosing to ignore the electric field that would be present in the frame where the electron begins at rest (a choice that was explained in Sect. 2).

  31. The state in (41) also appears in Sebens (2019, eq. 36). Note that by taking a non-relativistic approximation we have ended up with a wave function that is not normalized.

  32. See Pauli (1925, (1946), Tomonaga (1997, ch. 2), Morrison (2007), Giulini (2008), Regt and Henk (2017, sec. 7.4).

  33. See, for example, Gross (1966), Glassey and Strauss (1979), Flato et al. (1987).

  34. I have argued elsewhere that we should modify equations like (45) and (46) so that the negative frequency modes of the Dirac field are associated with negative charge and positive energy (Sebens 2020). However, we don’t have to be worry about that here because the negative frequency modes are not important in the non-relativistic approximation that we are using (Bjorken and Drell 1964, p. 10).

  35. For an examination and defense of the idea that forces can be exerted upon fields, see Sebens (2018).

  36. Consider, for example, working backwards through the proofs in Jackson (1999, sec. 6.7), Griffiths (2013, sec. 8.2).

  37. For philosophical discussion of self-interaction, see Lange (2002), Frisch (2005), Earman (2011), Lazarovici (2018), Maudlin (2018), Hartenstein and Hubert (forthcoming).

  38. Hypothetical forces holding the electron together have been called “Poincaré stresses.” See Feynman et al. (1964, ch. 28), Rohrlich (1973), Pearle (1982), Schwinger (1983), Jackson (1999, ch. 16), Rohrlich (2007, sec. 6.3), Griffiths (2012, sec. 5).

  39. The electron’s contribution to the electromagnetic field is also relevant for a precise calculation of the total angular momentum of the electron itself and the electromagnetic field that surrounds it, as there is angular momentum in both the Dirac and electromagnetic fields (Sebens 2019).

  40. This assumption is part of our non-relativistic approximation (Bjorken and Drell 1964, p. 39; Sebens 2019, sec. 5).

  41. This current density is discussed in Ohanian (1986, sec. 4), Sebens (2019, eq. 31).

  42. This section has focused on magnetic moment and the flow of charge. Angular momentum results from the flow of relativistic mass, or you could say the flow of energy (as relativistic mass is proportional to energy). This flow is analyzed in Ohanian (1986), Sebens (2019).

  43. See footnote 15 for Griffiths’ statement of this criticism.

  44. Depending on the way the particle approach is executed, positrons may either be viewed as fundamental particles or as holes in the Dirac Sea. Both options have been explored by scholars working to extend Bohmian mechanics to quantum field theory, the former by Dürr et al. (2004, (2005) and the latter by Bohm himself (Bohm 1953, p. 275; Bohm and Hiley 1993, ch. 12) and more recently by Colin and Struyve (2007), Deckert et al. (2019).

  45. For more on the particle and field approaches to quantum field theory, see the references in Sebens (2019, footnote 2).

  46. Wave functionals over Grassmann-valued fields are used in Floreanini and Jackiw (1988), Jackiw (1990), Hatfield (1992), Valentini (1992, (1996). The issues mentioned above are discussed in Struyve (2010, sec. 9.2), Struyve (2011, sec. 3.3), Sebens (2020, appendix A).

  47. For discussion of the various difficulties involved in extending the interpretations of quantum mechanics from Sect. 4 to relativistic quantum field theory, see Wallace (2008), Barrett (2014), Maudlin (2019, ch. 7), Dürr and Lazarovici (2020, ch. 11–12).

  48. See Wallace (2008, (2018, (2020), Wallace (2012, sec. 1.7).

  49. See Struyve (2010), Struyve (2011), Tumulka (2018) and references therein.

  50. See also Kaloyerou (1994, sec. 4).

  51. This table is modeled on Feynman’s table distinguishing the behavior of bullets, water waves, and electrons (Feynman 1967, figure 31).

References

  • Albert, D. (1992). Quantum mechanics and experience. Cambridge: Harvard University Press.

    Google Scholar 

  • Alstrøm, P., Hjorth, P., & Mattuck, R. (1982). Paradox in the classical treatment of the Stern–Gerlach experiment. American Journal of Physics, 50(8), 697–698.

    Article  Google Scholar 

  • Ballentine, L. E. (2014). Quantum mechanics: A modern development (2nd ed.). Singapore: World Scientific.

    Book  Google Scholar 

  • Barandes, J. A. (2019a). Can magnetic forces do work? arXiv preprint arXiv:1911.08890.

  • Barandes, J. A. (2019b). On magnetic forces and work. arXiv preprint arXiv:1911.00552.

  • Barrett, J. A. (2014). Entanglement and disentanglement in relativistic quantum mechanics. Studies in History and Philosophy of Modern Physics, 48, 168–174.

    Article  Google Scholar 

  • Barrett, J. A. (2020). The conceptual foundations of quantum mechanics. Oxford: Oxford University Press.

    Google Scholar 

  • Bedingham, D., Dürr, D., Ghirardi, G., Goldstein, S., Tumulka, R., & Zanghì, N. (2014). Matter density and relativistic models of wave function collapse. Journal of Statistical Physics, 154, 623–631.

    Article  Google Scholar 

  • Berestetskii, V. B., Lifshitz, E. M., & Pitaevskii, L. P. (1971). Relativistic quantum theory, part 1. Oxford: Pergamon Press.

    Google Scholar 

  • Bjorken, J. D., & Drell, S. D. (1964). Relativistic quantum mechanics. Cambridge: McGraw-Hill.

    Google Scholar 

  • Bohm, D. (1953). Comments on an article of Takabayasi concerning the formulation of quantum mechanics with classical pictures. Progress of Theoretical Physics, 9(3), 273–287.

    Article  Google Scholar 

  • Bohm, D., & Hiley, B. J. (1993). The undivided universe: An ontological interpretation of quantum theory. Abingdon: Routledge.

    Google Scholar 

  • Bohm, D., Hiley, B. J., & Kaloyerou, P. N. (1987). An ontological basis for the quantum theory. Physics Reports, 144(6), 321–375.

    Article  Google Scholar 

  • Chuu, C.-P., Chang, M.-C., & Niu, Q. (2010). Semiclassical dynamics and transport of the Dirac spin. Solid State Communications, 150, 533–537.

    Article  Google Scholar 

  • Colin, S., & Struyve, W. (2007). A Dirac sea pilot-wave model for quantum field theory. Journal of Physics A, 40(26), 7309–7341.

    Article  Google Scholar 

  • de Regt, H. W. (2017). Understanding scientific understanding. Oxford: Oxford University Press.

    Book  Google Scholar 

  • Deckert, D.-A., Esfeld, M., & Oldofredi, A. (2019). A persistent particle ontology for quantum field theory in terms of the Dirac sea. The British Journal for the Philosophy of Science, 70(3), 747–770.

    Article  Google Scholar 

  • Dewdney, C., Holland, P. R., & Kyprianidis, A. (1986). What happens in a spin measurement? Physics Letters A, 119(6), 259–267.

    Article  Google Scholar 

  • Dürr, D., Goldstein, S., Norsen, T., Struyve, W., & Zanghì, N. (2014). Can Bohmian mechanics be made relativistic? Proceedings of the Royal Society A, 470, 20130699.

    Article  Google Scholar 

  • Dürr, D., Goldstein, S., Tumulka, R., & Zanghì, N. (2004). Bohmian mechanics and quantum field theory. Physical Review Letters, 93(9), 090402.

    Article  Google Scholar 

  • Dürr, D., Goldstein, S., Tumulka, R., & Zanghì, N. (2005). Bell-type quantum field theories. Journal of Physics A: Mathematical and General, 38(4), R1–R43.

    Article  Google Scholar 

  • Dürr, D., & Lazarovici, D. (2020). Understanding quantum mechanics: The world according to modern quantum foundations. Berlin: Springer.

    Book  Google Scholar 

  • Dürr, D., & Teufel, S. (2009). Bohmian mechanics. Berlin: Springer.

    Google Scholar 

  • Earman, J. (2011). Sharpening the electromagnetic arrow(s) of time. In C. Callender (Ed.), The Oxford handbook of philosophy of time (pp. 485–527). Oxford: Oxford University Press.

    Google Scholar 

  • Feynman, R. P. (1967). The character of physical law. Cambridge: MIT Press.

    Google Scholar 

  • Feynman, R. P., Leighton, R. B., & Sands, M. (1964). The Feynman lectures on physics (Vol. II). Boston: Addison-Wesley Publishing Company.

    Google Scholar 

  • Flato, M., Simon, J., & Taflin, E. (1987). On global solutions of the Maxwell–Dirac equations. Communications in Mathematical Physics, 112, 21–49.

    Article  Google Scholar 

  • Floreanini, R., & Jackiw, R. (1988). Functional representation for fermionic quantum fields. Physical Review D, 37(8), 2206.

    Article  Google Scholar 

  • Frisch, M. (2005). Inconsistency, asymmetry, and non-locality: A philosophical investigation of classical electrodynamics. Oxford: Oxford University Press.

    Book  Google Scholar 

  • Gerlach, W., & Stern, O. (1922). Der experimentelle nachweis der richtungsquantelung im magnetfeld. Zeitschrift für Physik, 9, 349–352.

    Article  Google Scholar 

  • Giulini, D. (2008). Electron spin or “classically non-describable two-valuedness”. Studies in History and Philosophy of Modern Physics, 39(3), 557–578.

    Article  Google Scholar 

  • Glassey, R. T., & Strauss, W. A. (1979). Conservation laws for the classical Maxwell–Dirac and Klein–Gordon–Dirac equations. Journal of Mathematical Physics, 20(3), 454–458.

    Article  Google Scholar 

  • Good, R. H, Jr., & Nelson, T. J. (1971). Classical theory of electric and magnetic fields. Cambridge: Academic Press.

    Google Scholar 

  • Griffiths, D. J. (2005). Introduction to quantum mechanics (2nd ed.). Upper Saddle River: Pearson Prentice Hall.

    Google Scholar 

  • Griffiths, D. J. (2012). Resource letter EM-1: Electromagnetic momentum. American Journal of Physics, 80, 7–18.

    Article  Google Scholar 

  • Griffiths, D. J. (2013). Introduction to electrodynamics (4th ed.). Upper Saddle River: Pearson.

    Google Scholar 

  • Gross, L. (1966). The Cauchy problem for the coupled Maxwell and Dirac equations. Communications on Pure and Applied Mathematics, 19, 1–15.

    Article  Google Scholar 

  • Hartenstein, V., & Hubert, M. (forthcoming). When fields are not degrees of freedom. The British Journal for the Philosophy of Science. https://academic.oup.com/bjps/advance-article/doi/10.1093/bjps/axy060/5073892.

  • Hatfield, B. (1992). Quantum theory of point particles and strings. Frontiers in physics (Vol. 75). Boston: Addison-Wesley.

    Google Scholar 

  • Holland, P. (1993). The quantum theory of motion. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  • Jackiw, R. (1990). Analysis on infinite-dimensional manifolds—Schrödinger representation for quantized fields. In O. Éboli, M. Gomes, & A. Santoro (Eds.), Field theory and particle physics (pp. 78–143). Singapore: World Scientific.

    Google Scholar 

  • Jackson, J. D. (1999). Classical electrodynamics (3rd ed.). New York: Wiley.

    Google Scholar 

  • Kaloyerou, P. N. (1994). The causal interpretation of the electromagnetic field. Physics Reports, 244, 287–358.

    Article  Google Scholar 

  • Landau, L. D., & Lifshitz, E. M. (1971). The classical theory of fields (3rd ed.). Oxford: Pergamon Press.

    Google Scholar 

  • Lange, M. (2002). An introduction to the philosophy of physics: Locality, energy, fields, and mass. Oxford: Blackwell.

    Google Scholar 

  • Lazarovici, D. (2018). Against fields. European Journal for Philosophy of Science, 8(2), 145–170.

    Article  Google Scholar 

  • Lewis, P. J. (2016). Quantum ontology: A guide to the metaphysics of quantum mechanics. Oxford: Oxford University Press.

    Book  Google Scholar 

  • Maudlin, T. (2011). Quantum non-locality and relativity (3rd ed.). New York: Wiley-Blackwell.

    Book  Google Scholar 

  • Maudlin, T. (2018). Ontological clarity via canonical presentation: Electromagnetism and the Aharonov–Bohm effect. Entropy, 20(6), 465.

    Article  Google Scholar 

  • Maudlin, T. (2019). Philosophy of physics: Quantum theory. Princeton: Princeton University Press.

    Book  Google Scholar 

  • Morrison, M. (2007). Spin: All is not what it seems. Studies in History and Philosophy of Modern Physics, 38, 529–557.

    Article  Google Scholar 

  • Norsen, T. (2014). The pilot-wave perspective on spin. American Journal of Physics, 82(4), 337–348.

    Article  Google Scholar 

  • Norsen, T. (2017). Foundations of quantum mechanics. Berlin: Springer.

    Book  Google Scholar 

  • Nowakowski, M. (1999). The quantum mechanical current of the Pauli equation. American Journal of Physics, 67, 916–919.

    Article  Google Scholar 

  • Ohanian, H. C. (1986). What is spin? American Journal of Physics, 54(6), 500–505.

    Article  Google Scholar 

  • Pais, A. (1989). George Uhlenbeck and the discovery of electron spin. Physics Today, 42(12), 34–40.

    Article  Google Scholar 

  • Pauli, W. (1925). Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Zeitschrift für Physik, 31(1), 765–783.

    Article  Google Scholar 

  • Pauli, W. (1946). Exclusion principle and quantum mechanics. Nobel lecture for 1945 nobel prize in physics. Berlin: Springer.

    Google Scholar 

  • Pearle, P. (1982). Classical electron models. In D. Teplitz (Ed.), Electromagnetism: Paths to research (pp. 211–295). Oxford: Plenum Press.

    Chapter  Google Scholar 

  • Platt, D. E. (1992). A modern analysis of the Stern–Gerlach experiment. American Journal of Physics, 60(4), 306–308.

    Article  Google Scholar 

  • Rohrlich, F. (1973). The electron: Development of the first elementary particle theory. In J. Mehra (Ed.), The physicist’s conception of nature (pp. 331–369). Dordrecht: D. Reidel Publishing Company.

    Chapter  Google Scholar 

  • Rohrlich, F. (2007). Classical charged particles (3rd ed.). Singapore: World Scientific.

    Book  Google Scholar 

  • Ryder, L. H. (1996). Quantum field theory (2nd ed.). Cambridge: Cambridge University Press.

    Book  Google Scholar 

  • Sauer, T. (2016). Multiple perspectives on the Stern–Gerlach experiment. In T. Sauer & R. Scholl (Eds.), The philosophy of historical case studies. Studies in the philosophy and history of science 319. Boston: Springer.

    Google Scholar 

  • Schmidt-Böcking, H., Schmidt, L., Lüdde, H., Trageser, W., Templeton, A., & Sauer, T. (2016). The Stern–Gerlach experiment revisited. The European Physical Journal H, 41, 327–364.

    Article  Google Scholar 

  • Schwinger, J. (1983). Electromagnetic mass revisited. Foundations of Physics, 13(3), 373–383.

    Article  Google Scholar 

  • Sebens, C. T. (2018). Forces on fields. Studies in History and Philosophy of Modern Physics, 63, 1–11.

    Article  Google Scholar 

  • Sebens, C. T. (2019). How electrons spin. Studies in History and Philosophy of Modern Physics, 68, 40–50.

    Article  Google Scholar 

  • Sebens, C. T. (2020). Putting positrons into classical dirac field theory. Studies in History and Philosophy of Modern Physics, 70, 8–18.

    Article  Google Scholar 

  • Struyve, W. (2010). Pilot-wave theory and quantum fields. Reports on Progress in Physics, 73(10), 106001.

    Article  Google Scholar 

  • Struyve, W. (2011). Pilot-wave approaches to quantum field theory. Journal of Physics: Conference Series, 306, 012047.

    Google Scholar 

  • Tomonaga, S. (1997). The story of spin. Chicago: University of Chicago Press.

    Google Scholar 

  • Tumulka, R. (2006). A relativistic version of the Ghirardi–Rimini–Weber model. Journal of Statistical Physics, 125(4), 821–840.

    Article  Google Scholar 

  • Tumulka, R. (2018). On Bohmian mechanics, particle creation, and relativistic space-time: Happy 100th birthday, David Bohm!. Entropy, 20(6), 462.

    Article  Google Scholar 

  • Uhlenbeck, G. E. (1976). Fifty years of spin: Personal reminiscences. Physics Today, 29(6), 43–48.

    Article  Google Scholar 

  • Valentini, A. (1992). On the pilot-wave theory of classical, quantum and subquantum physics. Ph.D. thesis, ISAS, Trieste, Italy.

  • Valentini, A. (1996). Pilot-wave theory of fields, gravitation, and cosmology. In J. T. Cushing, A. Fine, & S. Goldstein (Eds.), Bohmian mechanics and quantum theory: An appraisal (pp. 45–66). Cambridge: Kluwer Academic.

    Chapter  Google Scholar 

  • Wallace, D. (2008). Philosophy of quantum mechanics. In D. Rickles (Ed.), The Ashgate companion to contemporary philosophy of physics (pp. 16–98). Abingdon: Routledge.

    Google Scholar 

  • Wallace, D. (2012). The emergent multiverse. Oxford: Oxford University Press.

    Book  Google Scholar 

  • Wallace, D. (2018). Lessons from realistic physics for the metaphysics of quantum theory. Synthese. https://doi.org/10.1007/s11229-018-1706-y.

  • Wallace, D. (2020). On the plurality of quantum theories: Quantum theory as a framework, and its implications for the quantum measurement problem. In F. Steven & S. Juha (Eds.), Scientific realism and the quantum. Oxford: Oxford University Press.

    Google Scholar 

  • Weinert, F. (1995). Wrong theory-right experiment: The significance of the Stern–Gerlach experiments. Studies in History and Philosophy of Modern Physics, 26(1), 75–86.

    Article  Google Scholar 

  • Wen, M., Bauke, H., & Keitel, C. H. (2016). Identifying the Stern–Gerlach force of classical electron dynamics. Scientific Reports, 6, 31624.

    Article  Google Scholar 

  • Wilson, M. (1998). Classical mechanics. In E. Craig (Ed.), Routledge encyclopedia of philosophy. Abingdon: Routledge.

    Google Scholar 

  • Wilson, M. (2013). What is “classical mechanics” anyway? In R. Batterman (Ed.), The Oxford handbook of philosophy of physics (pp. 43–106). Oxford: Oxford University Press.

    Google Scholar 

Download references

Acknowledgements

Thank you to Valia Allori, Jacob Barandes, Jeffrey Barrett, Mario Hubert, and the anonymous reviewers for helpful feedback and discussion.

Author information

Authors and Affiliations

  1. Division of the Humanities and Social Sciences, California Institute of Technology, 1200 E California Blvd, Pasadena, CA, USA

    Charles T. Sebens

Authors
  1. Charles T. Sebens
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Charles T. Sebens.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sebens, C.T. Particles, fields, and the measurement of electron spin. Synthese 198, 11943–11975 (2021). https://doi.org/10.1007/s11229-020-02843-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11229-020-02843-5

Keywords

Search

Navigation