Abstract
In this paper we discuss the extent to which the very existence of substructural logics puts the Tarskian conception of logical systems in jeopardy. In order to do this, we highlight the importance of the presence of different levels of entailment in a given logic, looking not only at inferences between collections of formulae but also at inferences between collections of inferences—and more. We discuss appropriate refinements or modifications of the usual Tarskian identity criterion for logical systems, and propose an alternative of our own. After that, we consider a number of objections to our account and evaluate a substantially different approach to the same problem.
Similar content being viewed by others
Notes
Essentially, \(\mathsf{B}\)-matrices are algebraic structures which generalize regular logical matrices, in that they do not present an algebra with a distinguished set of designated elements, but rather with two distinguished sets—one of accepted and one of rejected elements. For a more detailed discussion of these results, see Blasio (2017) and Blasio et al. (2018).
For a more detailed explanation of why \(\mathbf {ST}\) is usually referred to as Strict-Tolerant logic, in the context of three-valued logics defined using the strong Kleene algebra, see footnote 11 below.
To wit, think of a paradoxical sentence p and a false sentence q: then the inference from p and \(p \supset q\) to q is not valid in \(\mathbf {LP}\).
Though we hope the context will make things clear enough, we will always clearly state whether, for example, Roman capital letters A, B, C represent formulae, or inferences.
This phenomenon, however, is not limited to \(\mathbf {ST}\) or other convoluted systems, but actually pertains to many other logics. In this respect, see, e.g., Rosenblatt (2019a).
From a proof-theoretic point of view, this will amount to the addition of the so-called truth-rules, that is:
$$\begin{aligned} \frac{\Gamma , Tr(\langle A \rangle ) \Rightarrow \Delta }{\Gamma , A \Rightarrow \Delta } \qquad \frac{\Gamma \Rightarrow Tr(\langle A \rangle ), \Delta }{\Gamma \Rightarrow A, \Delta } \end{aligned}$$Before moving on to these issues, let us also stress that it could be possible to find out which is the proof-theoretic counterpart to local metainferential validity, for example, in the context of sequent calculi. Until now, we have not developed an account of this sort, but someone specially interested in looking at logical systems from a proof-theoretic point of view might be intrigued to look into these issues.
Another way to present \(\mathbf {ST}\)’s validity requires talking about strict and tolerant satisfaction or truth—which explains why this is known as a Strict-Tolerant consequence relation. A valuation v satisfies tolerantly a formula A if and only if \(v(A) \in \{1, \frac{1}{2}\}\), and satisfies it strictly if and only if \(v(A) \in \{ 1 \}\). Then, a valuation v satisfies an inference \(\Gamma \Rightarrow \Delta \) in \(\mathbf {ST}\) if and only if if v strictly satisfies every \(B \in \Gamma \), then v tolerantly satisfies at least one \(A \in \Delta \). Finally, an inference from \(\Gamma \) to \(\Delta \) is valid in \(\mathbf {ST}\) if and only if for every valuation v, if v satisfies strictly every \(B \in \Gamma \), then v satisfies tolerantly some \(A \in \Delta \). Nevertheless, it is worth mentioning that this is not the only way \(\mathbf {ST}\)’s supporters explain their position. They prefer to talk about strict and tolerant assertion rather than talking about strict and tolerant satisfaction, or strict and tolerant truth. As Fjellstad (2016) explains, the reason why they use the idea of strict and tolerant assertion instead of any of the last two (pair of) notions, is to avoid revenge paradoxes related to the notions of “strictly true” and “strictly false’ in the context of truth-theories based on \(\mathbf {ST}\).
In a similar fashion, the logic \(\mathbf {TS}\)—short for Tolerant-Strict logic—, that will also play a key role in this paper, is also usually presented in terms of the notions of strict and tolerant satisfaction. Specifically, a valuation v satisfies an inference \(\Gamma \Rightarrow \Delta \) in \(\mathbf {TS}\) if and only if if v tolerantly satisfies every \(B \in \Gamma \), then v strictly satisfies at least one \(A \in \Delta \). Thus, an inference from \(\Gamma \) to \(\Delta \) is valid in \(\mathbf {TS}\) if and only if for every valuation v, if v satisfies tolerantly every \(B \in \Gamma \), then v satisfies strictly some \(A \in \Delta \).
The same criterion of validity applies to metametainferences as to metainference. Thus, when assessing the validity of metametainferences or metainferences of level 2, this feature is readily established in the same way in which metainferences of level 1 are ruled in or out in \(\mathbf {ST}\), i.e. in a local way.
We should note that validity for inferences both in \(\mathbf {ST}\) and \(\mathbf {TS}\) is not, and cannot be defined in terms of the usual account of preservation of distinguished values. For what is worth, preservation is both a transitive and a reflexive relation, and inferential validity is neither transitive in \(\mathbf {ST}\) nor reflexive in \(\mathbf {TS}\). Notwithstanding this fact, validity in \(\mathbf {ST}\) and in \(\mathbf {TS}\) can be understood in terms of certain relations between distinguished values “for the premises” and distinguished values “for the conclusions”—as seen in, e.g., Malinowski (1990), Frankowski (2004), Chemla et al. (2017), and Ripley (2013b). We would like to thank an anonymous reviewer for urging us to clarify these matters.
Obviously, \({\overline{\mathbf {ST}}} = \mathbf {TS}\) because each one of these logics switches the standards for premises and conclusions that every valuation should meet in order for the inference to be sound in that logic. Thus, \(\mathbf {ST}\)’s standard for premises is a strict one—i.e., \(\{ 1 \}\)—, while its standard for conclusions is tolerant —i.e., \(\{ 1, \frac{1}{2} \}\). Conversely, \(\mathbf {TS}\)’s standard for premises is a tolerant one—i.e., \(\{ 1, \frac{1}{2} \}\)—, while its standard for conclusions is strict —i.e., \(\{ 1 \}\). More concretely, since we explained that \(\mathbf {ST}\) can be understood as \(\mathbf {{K}_{3}}/\mathbf {LP}\), the logic \(\mathbf {TS}\) can thereby be understood as the system \(\mathbf {LP}/\mathbf {{K}_{3}}\).
We would like to thank Francesco Paoli for suggesting a terminology along these lines, and for discussion concerning these issues.
An anonymous reviewer suggest to take into account Brandom’s incompatibility semantics into account for this purpose. Although that might be an interesting option that we would be eager to explore in the future, our clarification is mostly directed at highlighting the work that, e.g., Cobreros et al. (2019), Scambler (2019), and Rosenblatt have been doing on antivalidity, as opposed to mere invalidity. Moreover, there are some pieces of work that discriminate invalidities from the negation of validities. In particular, we are thinking about Meadows (2014) and Pailos and Tajer (2017). Nevertheless, those articles deals with the validity paradox, and not specifically with how a logic should be defined, which is what we are mostly interested in this work.
See, for example Cobreros et al. (2014), however, these authors’ disregard for metainferences is due to their taking metainferences to be properties under which the set of valid inferences of a given logic is closed under, whereas we think of them as logical inferences on their own right. This highlights the logical import of these objects for us, and the secondary role they have for these authors.
Confirmation of the former might be already out, as the unpublished manuscript (Thomas 2015) by Morgan Thomas appears to show.
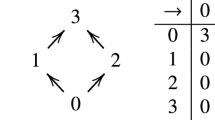
Which can be depicted as below. For more on the connection between paraconsistency and metainferential validity in \(\mathbf {ST}\), see Barrio et al. (2018b).
$$\begin{aligned} \frac{\Rightarrow B}{\Rightarrow A \quad \Rightarrow \lnot A} \end{aligned}$$For more on this, see Blok and Jónsson (2006).
We would like to thank an anonymous reviewer for urging us to consider this option. If this option is considered, however, we may as well ask why a defendant of the Blok–Jónsson framework (like Dicher and Paoli) would opt for a generalization of said account but still claim that the derivability relation—i.e., the internal consequence, the set of derivable sequents—does not codify validity in the target calculus—because it might be a substructural consequence relation. From our point of view, the openness to this generalization undermines the reasons for rejecting the identification of the provable sequents of a calculus with the valid inferences of the logic associated with such a calculus.
We present this version of Monotonicity because we are working in a multi-conclusion framework. Nevertheless, we are aware that usually it is only Left-Weakening that is required to classify a logic as monotonic.
We would like to than an anonymous reviewer for suggesting us to consider this option.
An anonymous reviewer suggests that Dicher and Paoli might, in the end, not be as challenged by these objections as we think they are. The reason for this would be that they could have a cogent understanding (for instance, a bilateralist reading along the lines of Ripley 2013a) both of the internal and of the external consequence relations associated with substructural sequent calculus. To this we reply that we do not doubt that such an option is available. What we do doubt is that their endorsement of the Blok–Jónsson framework allows them to place logic at both levels, whereas for them either the internal or the external consequence relation does not induce a proper consequence relation—philosophically speaking. On the other hand, since we do not embrace such a framework, we can so to say “see” proper consequence relations at more than one level, i.e., by looking at inferences, metainferences, metametainferences, and more.
References
Barrio, E., Pailos, F., & Szmuc, D. (2018a). Substructural logics, pluralism and collapse. Synthese,. https://doi.org/10.1007/s11229-018-01963-3. (Forthcoming).
Barrio, E., Pailos, F., & Szmuc, D. (2018b). What is a paraconsistent logic? In M. Jacek & C. Walter (Eds.), Contradictions, from consistency to inconsistency (pp. 89–108). Berlin: Springer.
Barrio, E., Pailos, F., & Szmuc, D. (2019). A hierarchy of classical and paraconsistent logics. Journal of Philosophical Logic,. https://doi.org/10.1007/s10992-019-09513-z. (Forthcoming).
Barrio, E., Rosenblatt, L., & Tajer, D. (2015). The logics of strict-tolerant logic. Journal of Philosophical Logic, 44(5), 551–571.
Blasio, C. (2017). Revisitando a Lógica de Dunn-Belnap. Manuscrito, 40(2), 99–126.
Blasio, C., Marcos, J., & Wansing, H. (2018). An inferentially many-valued two-dimensional notion of entailment. Bulletin of the Section of Logic, 46, 233–262.
Blok, W., & Jónsson, B. (2006). Equivalence of consequence operations. Studia Logica, 83(1), 91–110.
Chemla, E., Egré, P., & Spector, B. (2017). Characterizing logical consequence in many-valued logics. Journal of Logic and Computation, 27(7), 2193–2226.
Cobreros, P., La Rossa, E., & Tranchini, L. (2019). (I Can’t Get No) Antisatisfaction. https://www.researchgate.net/publication/333353209_I_Can’t_Get_No_Antisatisfaction.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2012). Tolerant, classical, strict. Journal of Philosophical Logic, 41(2), 347–385.
Cobreros, P., Egré, P., Ripley, D., & van Rooij, R. (2014). Reaching transparent truth. Mind, 122(488), 841–866.
Dicher, B., & Paoli, F. (2017). ST, LP, and tolerant metainferences. In C. Başkent & T. M. Ferguson (Eds.), Graham priest on dialetheism and paraconsistency. Dordrecht: Springer. (Forthcoming).
Dicher, B., & Paoli, F. (2018). The original sin of proof-theoretic semantics. Synthese,. https://doi.org/10.1007/s11229-018-02048-x. (Forthcoming).
Fitting, M. The strict/tolerant idea and bilattices. (Unpublished manuscript).
Fjellstad, A. (2016). Naive modus ponens and failure of transitivity. Journal of Philosophical Logic, 45(1), 65–72.
Frankowski, S. (2004). Formalization of a plausible inference. Bulletin of the Section of Logic, 33(1), 41–52.
French, R. (2016). Structural reflexivity and the paradoxes of self-reference. Ergo, 3(5), 113–131.
Galatos, N., Jipsen, P., Kowalski, T., & Ono, H. (2007). Residuated lattices: An algebraic glimpse at substructural logics., Studies in logic and the foundations of mathematics Amsterdam: Elsevier.
Girard, J.-Y. (1987). Proof theory and logical complexity. Napoli: Bibliopolis.
Hjortland, O. T. (2013). Logical pluralism, meaning-variance, and verbaldisputes. Australasian Journal of Philosophy, 91(2), 355–373.
Humberstone, L. (1996). Valuational semantics of rule derivability. Journal of philosophical logic, 25(5), 451–461.
Keefe, R. (2014). What logical pluralism cannot be. Synthese, 191(7), 1375–1390.
Kleene, S. C. (1952). Introduction to metamathematics. Amsterdam: North-Holland.
Malinowski, G. (1990). Q-consequence operation. Reports on Mathematical Logic, 24(1), 49–59.
Meadows, T. (2014). Fixed points for consequence relations. Logique et Analyse, 57, 227.
Pailos, F., & Tajer, D. (2017). Validity in a dialetheist framework. Logique et Analyse, 70(238), 191–202.
Paoli, F. (2002). Substructural logics: A primer. Dordrecht: Kluwer.
Priest, G. (1979). The logic of paradox. Journal of Philosophical logic, 8(1), 219–241.
Priest, G. (2006). Logic: One or many? In J. Woods & B. Brown, (Eds.), Logical consequence: Rival approaches. Proceedings of the 1999 conference of the society of exact philosophy, Hermes, Stanmore.
Read, S. (2006). Monism: The one true logic. In D. de Vidi & T. Kenyon (Eds.), A logical approach to philosophy: Essays in memory of Graham Solomon. Dordrecht: Springer.
Read, S. (2010). General-elimination harmony and the meaning of the logical constants. Journal of Philosophical Logic, 39(5), 557–576.
Restall, G. (2000). An introduction to substructural logics. Abingdon-on-Thames: Routledge.
Ripley, D. (2013a). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–164.
Ripley, D. (2013b). Revising up: Strengthening classical logic in the face of paradox. Philosophers’ Imprint, 13(5), 1–13.
Ripley, D. (2015). Anything goes. Topoi, 34(1), 25–36.
Rosenblatt, L. Bilateralism and invalidities. (Manuscript).
Rosenblatt, L. (2019a). Non-contractive classical logic. Notre Dame Journal of Formal Logic. (Forthcoming).
Rosenblatt, L. (2019b). On structural contraction and why it fails. Synthese,. https://doi.org/10.1007/s11229-019-02241-6. (Forthcoming).
Scambler, C. (2019). Classical logic and the strict tolerant hierarchy. Journal of Philosophical Logic,. https://doi.org/10.1007/s10992-019-09520-0. (Forthcoming).
Scott, D. (1971). On engendering an illusion of understanding. The Journal of Philosophy, 68(21), 787–807.
Shapiro, L. (2016). The very idea of a substructural approach to paradox. Synthese,. https://doi.org/10.1007/s11229-016-1230-x. (Forthcoming).
Shapiro, Lionel. (2016). LP, K3 and FDE as substructural logics. In P. Arazim & T. Lavička (Eds.), The logica yearbook 2014 (pp. 257–272). London: College Publications.
Shoesmith, D., & Smiley, T. (1978). Multiple-conclusion logic. Cambridge: Cambridge University Press.
Tarski, A. (1983). On the concept of logical consequence. In J. Corcoran (Ed.), Logic, semantics, metamathematics: Papers from 1923 to 1938 (2nd ed., pp. 409–420). Indianapolis, IN: Hackett.
Thomas, M. (2015). A Kripke-style semantics for paradox-tolerant, nontransitive intuitionistic logic. https://www.academia.edu/6198058/A_Kripke-style_semantics_for_paradox-tolerant_nontransitive_intuitionistic_logic.
Williamson, T. (1987). Equivocation and existence. Proceedings of the Aristotelian Society, 88, 109–127.
Zardini, E. (2013). Naive modus ponens. Journal of Philosophical Logic, 42(4), 575–593.
Acknowledgements
We would like to thank Bogdan Dicher, Francesco Paoli, Greg Restall, Dave Ripley, and the members of the Buenos Aires Logic Group for discussing previous versions of this work with us. In addition, special thanks go to the anonymous reviewers for this journal whose suggestions helped to substantially improve the paper, and to the editors of the special issue for their patience and help throughout the editorial process.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Barrio, E.A., Pailos, F. & Szmuc, D. (Meta)inferential levels of entailment beyond the Tarskian paradigm. Synthese 198 (Suppl 22), 5265–5289 (2021). https://doi.org/10.1007/s11229-019-02411-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02411-6