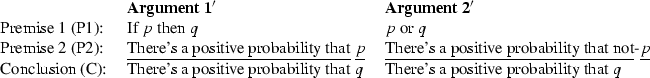Every day one comes across somebody who says that of course his view may not be the right one. Of course his view must be the right one, or it is not his view.
- G. K. Chesterton, Orthodoxy
Abstract
I argue that believing that p implies having a credence of 1 in p. This is true because the belief that p involves representing p as being the case, representing p as being the case involves not allowing for the possibility of not-p, while having a credence that’s greater than 0 in not-p involves regarding not-p as a possibility.
Similar content being viewed by others
Notes
In Dodd (2011) I defend an analogous view about knowledge, namely that If S knows p, then the probability of p on S’s evidence is 1.
Throughout this paper, please read my quotation marks as corner quotes where appropriate.
I’m going to assume ‘probably’ means having a probability greater than 0.5. Applied to credence, therefore, it means having a credence greater than 0.5. I actually believe that’s what it means. However, if the reader disagrees, thinking perhaps that 0.5 is too low of a probability, that won’t affect any of the arguments in this paper. If one substitutes n for 0.5, where n is the minimum probability required for a proposition to be ‘probably’ true, all the arguments I give can be adapted to fit the change, and will still go through.
I’m assuming that one way speakers can use sentences of the form ‘Probably p’ is to express their credences. In fact, I think speakers do use probabilistic language to do this sometimes. That such sentences are used for this purpose is defended by contemporary philosophers of language (for an overview of how to think like this about ‘probably’ and similar operators, see Yalcin 2012). On the other hand, Holton (2014) disagrees. He thinks that we don’t ever use probabilistic language to express credences, but only to talk about probabilistic facts in the world. Holton also denies that we have any probabilistic attitudes like credences at all, although we do have attitudes about probabilities. His view of probabilistic language is plausible if it’s plausible that we lack credences. While Holton denies that we have probabilistic attitudes, he is happy to acknowledge that we have various degrees of confidence and uncertainty in what we regard as open possibilities. I think Holton would deny that degrees of confidence can modeled with the probability calculus—thus they’re not probabilistic attitudes—even where such modeling is thought of just as a useful idealization. I suspect it’s here where our disagreement chiefly lies. If we do lack probabilistic attitudes (for instance, because degrees of confidence shouldn’t be thought of probabilistically) as Holton thinks, then we lack credences and then obviously we can’t use probabilistic language to express them. But if, contra Holton, we do have credences—i.e., degrees of confidence that can be modeled with the probability calculus—then it seems we should be able to use probabilistic language to express them. Why wouldn’t we be able to? What would be stopping us? If my assumption is granted that we do have credences, then it is hard to see why we wouldn’t be able to utilize probabilistic language to express them. I’ll be assuming in this paper that we can do this.
Some readers may favor an expressivist (non-truth conditional) account of the semantics of sentences involving the doxastic use of ‘probably’ I’m focusing on. Such readers will be attracted to expressivist accounts of epistemic modals generally no doubt. Such readers may object to my talk of a judgment that ‘Probably p’, and maybe also object to speaking of an assertion of ‘Probably p’. Here and in what follows, where I talk about judging or asserting ‘Probably p’, feel free to substitute a different, expressivist-friendly locution for using such sentences (e.g., using the sentence on a particular occasion to express the speaker’s attitude). In spite of my use of words like ‘judging’ and ‘asserting’, in fact my arguments in this paper don’t presuppose that expressivist views about epistemic modals are false (or that they’re true).
Argument 1 was discussed by Yalcin (2008).
For those who want to analyze these arguments in terms of dynamic logic, where the order of the premises can affect an argument’s validity, this claim is only true if (P1) and (P2) occur in the order in which I present them (i.e., with (P1) first). I’m grateful to Hans Kamp and Johan van Bentham for drawing my attention to this point. I wish to remain neutral on the question of whether these arguments should be analyzed dynamically.
One might worry that because ‘acceptance’ is a term of art, the fact that we find Arguments 1–3 compelling shouldn’t lead us to conclude that (Commitment) is true. For instance, perhaps we find the arguments compelling only because we take the assertion of their first premise to express the speaker’s knowledge, rather than mere belief. The idea is that we think the speaker is committed to one of the arguments’ conclusions only insofar as s/he knows its first premises, and we don’t think s/he’s committed to its conclusion when s/he merely believes the premise. I have a couple responses. First, consider a case where the speaker asserts the premises of one of Arguments 1–3, but we (unlike the speaker) know that she doesn’t know the first premise, though she sincerely believes it. In this case, I still have an equally strong intuition that she is committed to accepting the argument’s conclusion. This intuition cannot be accounted for by the principle that knowledge of the argument’s premises, but not mere belief, commits one to its conclusion. Second response. The arguments’ second premises and conclusions are used to express the speaker’s credences. Whatever it is about knowing the arguments’ first premise that helps affect a commitment to their conclusions, it must be what knowledge implies about the speaker’s doxastic state. After all, it seems it would have to be the doxastic state the speaker is in in virtue of knowing the argument’s first premises that combines with the doxastic state described in the second premise to commit the speaker to the argument’s conclusion. What doxastic state is there, which is implied by knowing something, and which would do the relevant work here? Whatever doxastic state it is, it has to be one that involves having a certain credence: as we shall see, a speaker is committed to the arguments’ conclusions in virtue of being committed to their second premises just in case s/he has a credence of 1 in their first premises. So what doxastic state is there, which is implied by knowing the arguments’ first premises, which when combined with the speaker’s commitment to premises 2 commits her to the arguments’ conclusions, and which commits her to their conclusions in virtue of requiring her to have a credence of 1? The most obvious answer to this question is belief. Note that on most analyses of knowledge, the only doxastic state that knowing implies is belief. An exception is Williamson (2000), who thinks that knowledge itself is a mental state. So someone who, like Williamson, thought of knowledge as a mental state, could reject (Commitment), claiming that the reason we find Arguments 1–3 compelling is that we imagine the speaker to know the first premise, and not merely believe it, and unlike belief knowledge does require having a credence of 1. I have two replies to this response. First, even on a Williamsonian view, I don’t see the motivation for claiming that knowledge but not belief requires having a credence of 1. Second, the view that knowledge requires having a credence of 1 is itself a striking thesis.
As a referee pointed out, the example that McGee (1985) presented as a counterexample to modus ponens is a potential counterexample to (Commitment) applied to Argument 1. The following seems possible: I believe if a Republican wins the election, then (if it’s not Reagan, it will be Anderson), and also I accept that probably a Republican will win. Yet at the same time I don’t accept that probably (if a Republican wins the election, it will be Anderson). Point taken. I am very unsure about what to say about McGee’s original example (like this one, but with the probability operators missing) as a counterexample to modus ponens, and I’m equally unsure about what to say about this putative counterexample to (Commitment) applied to Argument 1.
As I explain in the Appendix, due to uncertainty about how to think about the probability of an indicative conditional, I can’t demonstrate that this holds for Argument 1. I provide evidence that it holds for Argument 1, and I demonstrate that it holds for Arguments 2 and 3.
Arguments 1–3 are examples of a general phenomenon. I leave it as an exercise for the reader to show that for the following three arguments, the analogue of (Commitment) is plausible, and that like Arguments 1–3 this is the case iff believing their first premises (P1) means having a credence of 1 in (P1).
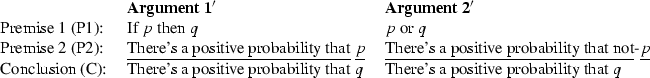

For instance, DeRose (1996), Hawthorne (2004), and Williamson (2000) amongst others have noted this fact. However, Hawthorne (2004) also notes some cases in which we are willing to assert ‘lottery propositions.’ The writers just mentioned all take the typical unassertability of lottery propositions to motivate a knowledge norm of assertion. However, their unassertability can also be explained by a belief norm combined with (Certainty). I think this explanation is better than the explanation in terms of the knowledge norm because it generalizes to explain (Commitment), while the knowledge norm explanation doesn’t, unless we add to that explanation the view that knowledge involves having a credence of 1. But it’s not clear why knowledge should involve having a credence of 1 unless (Certainty) is true. (Since knowledge implies belief, we can explain (Commitment) in terms of the knowledge norm if we accept (Certainty). But accepting (Certainty) enables us to explain it in terms of a mere belief norm too.) Note that accepting my explanation of the unassertability of lottery propositions doesn’t prevent us from accepting the knowledge norm of assertion.
For instance, when he originally stated the Paradox, Kyburg (1961) just took it to be obvious that we do believe that individual tickets won’t win.
As with Arguments 1–3, if we analyze these arguments using dynamic logic, this claim is true only if the arguments occur in the order I presented them in (with (P1) occurring first).
The explanations offered in this subsection will make some readers think of (Stalnaker 1978, 1998)’s influential theory of the interaction of assertion and context. According to Stalnaker, a conversational context C is represented as a set of presuppositions which the speaker and audience share, and these presuppositions leave open a set of possible worlds—the set of worlds compatible with the presuppositions. These are the live possibilities for the conversation. When a sentence is asserted in C that expresses the proposition p and the conversational participants accept the assertion, they update the context by removing all the not-p possibilities from the set of live possibilities. (They will update by eliminating other possibilities too, like the ones ruled out by conversational implicatures.) Note that after a proposition p is accepted by the conversational participants, all the open possibilities in C will be p-possibilities. In this sense, every accepted proposition is necessary. Stalnaker’s theory can explain why asserting (Moore)’s right conjunct seems like a retraction of the assertion of its left conjunct, and why in accepting the premises of Arguments 4–6 conversational participants will thereby be committed to the Arguments’ conclusions.
If we think of assertion as the outward expression of belief, then it’s natural to extend what Stalnaker says about modeling the acceptance of a proposition by participants in a conversation to a way of modeling the acceptance of a proposition by an individual thinker. (This is an extension and not a part of Stalnaker’s theory. Stalnaker denies that in order for conversational participants to accept an assertion for the purposes of conversation, they have to believe it.) In short, the modeling technique may be applied to beliefs. When S comes to believe p, we update the set of possibilities S regards as open (S’s doxastic possibilities) by deleting all the not-p-possibilities from this set. When S comes to believe that p, S no longer regards any not-p-possibilities as open. In this sense, every proposition believed by S is necessary for S, and thus (BIDN) is true.
Finally, we can see Arguments 4–6 (and Arguments 1–3) as examples of what Stalnaker (1975) called “reasonable inferences.” An inference from P to Q is a reasonable inference iff accepting (in the Stalnakerian sense just outlined) a set of premises P eliminates every not-Q possibility, for any conversational context. As Stalnaker explains, the inference from P to Q might be a reasonable inference even though P doesn’t entail Q. (Stalnaker argued that p or q doesn’t entail if not-p then q, while it’s a reasonable inference from p or q to if not-p then q).
The example is from Strevens (1999).
For according to (CDPL), credences are distributed only over doxastic possibilities. So if p is doxastically necessary, S has all of her credence in p and no credence in not-p. Assuming that S’s credences all add up to 1 (as is required by the probability calculus), her credence in p will be 1.
I take it that we have a pre-theoretical grasp of what a representation is, and what assertoric force is. We understand pre-theoretically the difference between representations that are put forward as true, and those that are not: we understand the difference between an assertion and a supposition, and the difference between a news report that purports to tell us about real events (assertoric force), and mere make believe or fiction (no real assertoric force). My claim is that, for our pre-theoretical concepts of representation and assertoric force, an assertoric representation of p doesn’t leave open the possibility that not-p. That a representation that is put forward as true rules out all counterpossibilities I take to be a significant fact about assertoric representations.
Fantl and McGrath (2009) call this the truth standard for belief. They make the same point that I’m about to make, namely that the truth standard doesn’t hold for high but non-maximal credence.
Of course there are scoring rules for probabilities (e.g., the logarithmic and Brier rules), and they’re even sometimes called “accuracy measures”. Such scoring rules provide a way of measuring how well a probabilistic model or assignment fares, but they don’t score the model/assignment as simply accurate or inaccurate. They don’t do that, and a probability assignment or model isn’t simply accurate or inaccurate, true or false. Note that any assignment of probabilities can always receive a higher logarithmic or Brier score except for the assignment that assigns a probability of 1 to all truths and a probability of 0 to all falsehoods. But maps, assertions, beliefs, etc.—representations of the way the world is—can be simply accurate or inaccurate, correct or mistaken. This is a difference between probabilities and representations.
Take the Lockean view of belief to be the view that a state of belief is identical to a state of having a credence above a threshold \(\tau \) (\(\tau < 1\)). According to the Lockean view, there are states of believing p that are identical to states of having a credence greater than \(\tau \) but less than 1 in p. The fact that beliefs can be simply mistaken or correct but credences less than 1 can’t be gives us a simple Leibniz’s Law argument against the Lockean view. Let S be a state of belief that is also a state of having a credence between \(\tau \) and 1. Since S is a belief, it has the property of being correct or being wrong. Since S is a state of having a non-maximal credence, it must lack that property. Contradiction.
This is also Fantl and McGrath’s explanation.
Note the assumption of (CDPL) here.
The response to this objection I’m about to give is also given by Clarke (2013, p. 9ff).
I don’t bet. I’m very confident that I won’t accept any bets this year. Does that mean I’ll accept a bet (or regard a bet as fair) on the proposition that I won’t except any bets this year? Obviously not!
I’m grateful to an anonymous referee for requesting that I deal with this as a separate objection.
The doctor has a high credence that Mike needs his limb amputated. Is she also confident that this is what he needs? In some sense, yes, given that her credence is high. But perhaps it’s also true that she’s full of doubt, given that she has very strong feelings of doubt. Perhaps the words ‘confident’, ‘doubt’, ‘certain’, ‘uncertain’, etc., are all ambiguous. There’s a sense of ‘confidence’ where it’s simply credence, but there’s another sense of ‘confidence’ that has more to do with inner feelings. I’m inclined to think that ‘confidence’, ‘doubt’, etc. are ambiguous in this way. If so, then (Certainty) doesn’t rule out the compatibility of belief with a kind of doubt.
There is an extensive discussion in the literature on assertion, knowledge attributions, contextualism, and subject sensitive invariantism, about whether a speaker can sincerely and felicitiously assert ‘The broken egg will stay there on the floor’ in a context in which the possibility of the egg reconstituting itself has been acknowledged to be real. That discussion validates what I just claimed: it may be that one can’t make the assertion while simultaneously acknowledging the counterpossibility. It’s far from obvious that one can.
I’m grateful to an anonymous referee for pressing this objection.
Clarke’s view also involves accepting (Certainty). Leitgeb (2014) has developed a model of belief that doesn’t imply (Certainty), but which also claims that what one believes depends on which possibilities one is aware of. Like Clarke and Leitgeb, I accept a version of subject-sensitive invariantism about belief.
Note that the above argument’s conclusion is not that (Certainty) implies that beliefs are simply indefeasible. At best it only shows that it follows from (Certainty) that beliefs cannot be defeated by evidence in which the subject had a positive prior credence. From the point of view of (Certainty), this would only include evidence compatible with the subject’s prior beliefs. However, I’m going to proceed by taking it for granted that a belief’s justification can be defeated by evidence that doesn’t contradict any of the subject’s prior beliefs.
In addition to Weisberg’s argument, Artzenius (2003) gives some cases where it seems one shouldn’t update one’s credences by conditionalization.
We classically conditionalize on evidence e by setting our new credences \(P_e(p)\) to the values of our prior conditional credences P(p|e). In Jeffrey conditionalization, one’s credences over a partition \(e_i\) of the probability space changes from \(P_{old}(e_i)\) to \(P_{new}(e_i)\), and then one sets one’s new credences in each proposition p to \(\sum _i P_{old}(p|e_i)P_{new}(e_i)\). Classical conditionalization is a limiting case of Jeffrey conditionalization, wherein \(P_{new}(e_i) = 1\).
See Weisberg (2009). As presentation of his argument for this conclusion would take up too much space, I refer the reader to his paper.
I am grateful for the feedback I received on this paper from audiences at the Universities of Aberdeen, St Andrews, Copenhagen, Nancy, Edinburgh, Stirling, Texas-San Antonio, Konstanz, and at Queens University Belfast. I especially would like to thank Mike Almeida, Johan van Bentham, Tony Brueckner, Mikkel Gerken, Hans Kamp, Aidan McGlynn, Peter Milne, Dilip Ninan, Crispin Wright, and Elia Zardini. I was able to develop the ideas in this paper while a postdoctoral fellow of the AHRC-funded Basic Knowledge Project (2007–2012), led by Crispin Wright. I am grateful to Professor Wright, the other members of the Project, and to the members of the Arché Research Centre (St Andrews) and the Northern Institute of Philosophy (Aberdeen) for their collegiality and support.
For a nice summary of many of the objections to the material conditional analysis of indicative conditionals, see Abbott (2005).
References
Abbott, B. (2005). Some remarks on indicative conditionals. In K. Watanabe & R. B. Young (Eds.), Proceedings from semantics and linguistic theory (SALT). Ithaca, NY: CLC Publications.
Adams, E. (1965). The logic of conditionals. Inquiry, 8, 166–197.
Arlo-Costa, H. (2010). Review of F. Huber and C. Schmidt-Petri (eds.), Degrees of Belief. Notre Dame Philosophical Reviews, 2010
Artzenius, F. (2003). Some problems for conditionalization and reflection. The Journal of Philosophy, 100(7), 356–370.
Bradley, D., & Leitgeb, H. (2006). When betting odds and credences come apart: More worries for dutch book arguments. Analysis, 66, 119–127.
Clarke, R. (2013). Belief is credence one (in context). Philosopher’s Imprint, 13(11), 1–18.
de Finetti, B. (1990). Theory of probability. New York: Wiley.
DeRose, K. (1996). Knowledge, assertion and lotteries. Australasian Journal of Philosophy, 74(4), 568–580.
Dodd, D. (2011). Against fallibilism. Australasian Journal of Philosophy, 89, 665–685.
Douven, I. (2002). A new solution to the paradoxes of rational acceptability. British Journal for Philosophy of Science, 53(3), 391–410.
Edgington, D. (1995). On conditionals. Mind, 104, 235–329.
Eriksson, L., & Hájek, A. (2007). What are degrees of belief? Studia Logica, 86, 183–213.
Fantl, J., & McGrath, M. (2009). Knowledge in an uncertain world. Oxford: Oxford University Press.
Frege, G. (1918). Der Gedanke: Eine logische Untersuchung. Beiträge zur Philosophie des deutschen Idealismus, 1, 58–77.
Hawthorne, J. (2004). Knowledge and Lotteries. Oxford: Oxford University Press.
Holton, R. (2014). Intention as a model for belief. In M. Vargas & G. Yaffe (Eds.), Rational and social agency: Essays on the philosophy of Michael Bratman. Oxford: Oxford University Press.
Jackson, F. (1979). On assertion and indicative conditionals. Philosophical Review, 88(4), 565–589.
Jeffrey, R. (1964). If. Journal of Philosophy, 61, 702–703.
Kripke, S. (1979). A puzzle about belief. In N. Salmon & S. Soames (Eds.), Propositions and attitudes (pp. 102–149). Oxford: Oxford University Press.
Kyburg, H. E. (1961). Probability and the logic of rational belief. Middleton, CT: Wesleyan University Press.
Leitgeb, H. (2014). The stability theory of belief. Philosophical Review, 123(2), 173–204.
Levi, I. (1991). The fixation of belief and its undoing: Changing beliefs through inquiry. Cambridge: Cambridge University Press.
Levi, I. (2004). Mild contraction: Evaluating loss of information due to loss of belief. Oxford: Oxford University Press.
Lewis, D. (1976). Probabilities of conditionals and conditional probabilities. Philosophical Review, 85, 297–315.
McGee, V. (1985). A counterexample to modus ponens. Journal of Philosophy, 82, 462–471.
Pollock, J. (1995). Cogntive carpentry: A blueprint for how to build a person. Cambridge: MIT Press.
Quine, W. (1951). Two dogmas of empiricism. Philosophical Review, 60, 20–43.
Ramsey, F. P. (1964). Truth and probability. In H. E. Kyburg & H. E. Smokler (Eds.), Studies in subjective probability (pp. 61–92). New York: Wiley.
Rieger, A. (2006). A simple theory of conditionals. Analysis, 66(3), 233–240.
Ryan, S. (1996). The epistemic virtues of consistency. Synthèse, 109, 121–141.
Stalnaker, R. (1970). Probability and conditionals. Philosophy of Science, 37(1), 64–80.
Stalnaker, R. (1975). Indicative conditionals. Philosophia, 5, 269–286.
Stalnaker, R. (1978). Assertion. In P. Cole (Ed.), Syntax and semantics 9. New York: Academic Press.
Stalnaker, R. (1998). On the representation of context. Journal of Logic, Language and Information, 7(1), 3–19.
Strevens, M. (1999). Objective probability as a guide to the world. Philosophical Studies, 95, 243–275.
Weisberg, J. (2009). Commutativity or holism? A dilemma for conditionalizers. The British Journal for the Philosophy of Science, 60, 793–812.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Yalcin, S. (November 2008). Probability operators. Unpublished lecture at the Arché Research Centre: University of St. Andrews.
Yalcin, S. (2012). Bayesian expressivism. Proceedings of the Aristotelian Society, 112(2), 123–160.
Author information
Authors and Affiliations
Corresponding author
Appendix 1: Arguments 1–3
Appendix 1: Arguments 1–3
For Arguments 1–3, assume that p and q aren’t logically equivalent, and that ‘probably’ is used to express the fact that the speaker has a credence greater than 0.5 in the relevant proposition.

Recall my notion of ‘acceptance’: one accepts (P1) in Arguments 1–3 iff one believes it, and one accepts (P2) and (C) iff one has a credence greater than 0.5 in the relevant proposition. In Sect. 2 I claimed that
-
(Commitment) In accepting Arguments 1–3’s premises, one is thereby committed to accepting their conclusions, on pain of inconsistency.
In other words, the following set of attitudes is jointly inconsistent: acceptance of (P1) in one of Arguments 1–3, acceptance of (P2) in the same Argument, and rejection of (C) in the same Argument.
In this appendix, I show with respect to Arguments 2 and 3 that (Commitment) is true iff believing their (P1) involves having a credence of 1 in (P1) (Appendices 1.1 and 1.2). Because of a lack of consensus about how to think about the probability of indicative conditionals, I won’t be able to show the same thing for Argument 1. In Appendix 1.3 I show that it holds if the probability of an indicative conditional \(p \rightarrow q\) is the probability of q conditional on p. For those who deny that the probability of a conditional is a conditional probability, I provide some evidence that (Commitment) holds only if believing (P1) involves having a credence of 1 in it.
In the rest of this appendix, let’s call the premise (P1), (P2), and the conclusion (C) of Argument x ‘(P1)\(_x\)’, ‘(P2)\(_x\)’, and ‘(C)\(_x\)’. Thus, for instance, premise (P2) of Argument 2 will be referred to as ‘(P2)\(_2\)’ and the conclusion of Argument 1 will be called ‘(C)\(_1\)’.
1.1 Appendix 1.1: (Commitment) holds for Argument 2 iff accepting (P1)\(_2\) means having a credence of 1 in (P1)\(_2\).
First suppose that accepting (P1)\(_2\) means having a credence of 1 in (P1)\(_2\): \(P(p \vee q) = 1\). Then \( P(\lnot p \& \lnot q) = 0\). Since the acceptance of (P2)\(_2\) (i.e., \(P(\lnot p) > 0.5\)) is equivalent to \( P(\lnot p \& q) + P(\lnot p \& \lnot q) > 0.5\), it follows that \( P(\lnot p \& q) > 0.5\), and thus that \(P(q) > 0.5\), which means that (C)\(_2\) is accepted. Therefore, if (P1)\(_2\) and (P2)\(_2\) are both accepted, and if accepting (P1) \(_2\) means having a credence of 1 in (P1) \(_2\), it follows that (C)\(_2\) is accepted. (Commitment) holds for Argument 2 if accepting (P1) \(_2\) means having a credence of 1 in (P1) \(_2\).
Suppose instead that although (P1)\(_2\) is accepted, \(P(p \vee q) < 1\). Given this supposition, it’s consistent with the fact that \(P(\lnot p) > 0.5\) [(P2)\(_2\) is accepted], that \(P(q) < 0.5\) [(C)\(_2\) isn’t accepted]. I think the reader will be able to see this through the following example. Say \(P(p \vee q)\) = 0.99. As the reader can verify, (P2)\(_2\) will be accepted while (C)\(_2\) won’t be for the following probability distribution:
-
\( P(\lnot p \& \lnot q) = 0.01\) [equivalent to our supposition that \(P(p \vee q)\) = 0.99]
-
\( P(\lnot p \& q) = 0.499\) [\(P(\lnot p) = 0.01 + 0.499 = 0.509 > 0.5\)]
-
\( P(p \& \lnot q) = 0.4909\)
-
\( P(p \& q) = 0.0001\) [\(P(q) = 0.499 + 0.0001 = 0.4991 < 0.5\)]
(Commitment) holds for Argument 2 only if accepting/believing (P1)\(_1\) involves having a credence of 1 in (P1)\(_1\). Combine this fact with what was demonstrated in the first paragraph and we have: (Commitment) for Argument 2 is true iff accepting/believing (P1)\(_2\) requires having a credence of 1 in (P1)\(_2\).
1.2 Appendix 1.2: (Commitment) holds for Argument 3 iff accepting (P1)\(_3\) means having a credence of 1 in (P1)\(_3\).
Recall that (P1)\(_3\) is p, (P2)\(_3\) is \(P(q) > 0.5\) [‘Probably q’] and (C)\(_3\) is \( P(p \& q) > 0.5\) [‘Probably (p & q)’].
Say \(P(p) = 1\) and \(P(q) > 0.5\). Then \( P(q) = P(p \& q) > 0.5\). Therefore, if accepting/believing p (i.e., (P1)\(_3\)) involves having a credence of 1 in p, then (Commitment) holds for Argument 3.
On the other hand, if accepting/believing (P1)\(_3\) doesn’t require having a credence of 1 in (P1)\(_3\), (Commitment) doesn’t hold for Argument 3. I think the reader will see that this is so by considering the following probability distribution.
-
\( P(\lnot p \& \lnot q) = 0.002\)
-
\( P(\lnot p \& q) = 0.008\)
-
\( P(p \& \lnot q) = 0.495\)
-
\( P(p \& q) = 0.495\)
In this example, \(P(p) = 0.495 + 0.495 = 0.99\), \(P(q) = 0.495 + 0.008 = 0.503 > 0.5\) (so (P2)\(_2\) is accepted), but since \( P(p \& q) < 0.5\), (C)\(_3\) isn’t accepted.
(Commitment) holds for Argument 3 if accepting/believing p involves having a credence of 1 in p, and it holds only if accepting/believing p involves having a credence of 1 in p.
1.3 Appendix 1.3: Argument 1
Recall that (P1)\(_1\) is if p then q [\(p \rightarrow q\)], (P2)\(_1\) is \(P(p) > 0.5\) [‘Probably p’], and (C)\(_1\) is \(P(q) > 0.5\) [‘Probably q’].
For Arguments 2 and 3 I argued directly that (Commitment) was true for them iff in accepting/believing each argument’s (P1), one has a credence of 1 in (P1). The problem with arguing in the analogous way for Argument 1 is that in doing so I would have to make an assumption about what the probability of (P1)\(_1\) is. But (P1)\(_1\) is an indicative conditional, and it’s controversial what the probability of an indicative conditional is.
What is the probability of an indicative conditional \(p \rightarrow q\)? We might take indicative conditionals just to be material conditionals (Jackson (1979), Rieger (2006)). In that case, Argument 1 becomes logically equivalent to Argument 2. Then my argument in Appendix 1.1 regarding Argument 2 also shows that (Commitment) is true for Argument 1 iff accepting/believing (P1)\(_1\) requires having a credence of 1 in (P1)\(_1\). While the thesis that indicative conditionals are material conditionals isn’t a popular idea amongst contemporary philosophers and linguists,Footnote 38 it is widely accepted that indicative conditionals entail material conditionals. If modus ponens is valid for indicative conditionals, then \(p \rightarrow q\) entails the material conditional \(p \supset q\).
If one denied that material conditionals entail indicative conditionals, that could be because one thought that indicative conditionals don’t have truth conditions, and thus strictly speaking don’t entail anything (assuming that entailment involves necessary truth-preservation). Another popular and plausible idea is “Stalnaker’s Thesis”: the probability of an indicative conditional \(p \rightarrow q\) is the probability of q conditional on p (Adams 1965; Jeffrey 1964; Edgington 1995; Stalnaker 1970). Lewis (1976) is often taken to have shown that Stalnaker’s Thesis can’t be maintained if indicative conditionals have truth conditions. Those who deny that indicative conditionals have truth conditions typically are motivated by a desire to hang on to Stalnaker’s Thesis. I know of no contemporary philosophers or linguists who deny that indicative conditionals have truth conditions and also deny Stalnaker’s Thesis. Thus most will maintain one of the following two things about indicative conditionals:
-
(i)
\(p \rightarrow q\) has truth conditions and entails \(p \supset q\).
-
(ii)
\(p \rightarrow q\) lacks truth conditions, and \(P(p \rightarrow q) = P(q|p)\) [Stalnaker’s Thesis is true].
First, I’ll argue that on the assumption of Stalnaker’s Thesis, (Commitment) is true for Argument 1 iff \(P(q|p) = 1\). Then we’ll see what happens if (i) is true.
Let’s assume Stalnaker’s Thesis. Now suppose that believing (P1)\(_1\) means having a credence of 1 in (P1)\(_1\): \(P(p \rightarrow q) = 1\). By Stalnaker’s Thesis, this means that (if \(P(p) > 0)\) \( P(q|p) = P(q \& p)/P(p) = 1\). Equivalently, \( P(q \& p) = P(p)\). Therefore, if \(P(p) > 0.5\), then \( P(q \& p) > 0.5\), which entails that \(P(q) > 0.5\). Therefore, if accepting/believing (P1)\(_1\) means having a credence of 1 in (P1)\(_1\), then accepting (P1)\(_1\) and (P2)\(_1\) implies accepting (C)\(_1\). On the other hand, say one can believe/accept (P1)\(_1\) while having a credence in (P1)\(_1\) that’s less than 1. Consider the following probability distribution:
-
\( P(\lnot p \& \lnot q) = 0.4985\)
-
\( P(\lnot p \& q) = 0.0005\)
-
\( P(p \& \lnot q) = 0.002\)
-
\( P(p \& q) = 0.499\)
For the above probability distribution, \(P(q|p) = 0.499/(0.499 + 0.002) \approx 0.996\). \(P(p) = 0.499 + 0.002 = 0.501 > 0.5\), and thus (P2)\(_1\) is accepted. However, \(P(q) = 0.499 + 0.0005 = 0.4995 < 0.5\), and thus (C)\(_1\) is not accepted. Hopefully from this example the reader can glean how, assuming Stalnaker’s Thesis, (Commitment) doesn’t hold for Argument 1 if believing/accepting (P1)\(_1\) doesn’t require having a credence of 1 in \(p \rightarrow q\). Yet previously we saw that (assuming Stalnaker’s Thesis) if accepting/believing (P1)\(_1\) involves having a credence of 1 in (P1)\(_1\), then (Commitment) holds for Argument 1. Therefore, assuming Stalnaker’s Thesis, (Commitment) holds for Argument 1 iff accepting/believing (P1)\(_1\) requires having a credence of 1 in (P1)\(_1\).
Let’s now examine the possibility that (i) above is true instead of Stalnaker’s Thesis. If we interpret indicative conditionals as material conditionals, then Argument 1 is equivalent to Argument 2. Furthermore, however we interpret the conditional in (P1)\(_1\), it follows from what was shown in Appendix 1.1 that (Commitment) holds for Argument 1 only if believing (P1)\(_1\) requires P(\(p \supset q\)) = 1. Assuming that \(p \rightarrow q\) entails \(p \supset q\), the fact that accepting/believing (P1)\(_1\) requires \(P(p \supset q) = 1\) is predicted by the thesis that believing/accepting \(p \rightarrow q\) requires \(P(p \rightarrow q) = 1\) (since if \(P(P) = 1\), then for every Q that P entails, \(P(Q) = 1\)). But why would accepting/believing (P1)\(_1\) require \(P(p \supset q) = 1\) if believing/accepting (P1)\(_1\) did not require \(P(p \rightarrow q) = 1\)? It’s hard to see why it would. While the fact that (Commitment) holds for Argument 1 only if believing (P1)\(_1\) involves P(\(p \supset q) = 1\) is predicted by the thesis that believing/accepting (P1)\(_1\) requires P(\(p \rightarrow q\)) = 1, it’s mysterious from the point of view that believing/accepting (P1)\(_1\) does not have this requirement.
Call the thesis that (Commmitment) holds for Argument 1 iff one’s credence in (P1)\(_1\) is 1 ‘(*)’. Arguing for (*) is more problematic than arguing for its analogues for Arguments 2 and 3, because in order to argue for (*), we have to make some assumptions about the probability of an indicative conditional. Nevertheless, we’ve at least gotten some good evidence for (*). Almost everyone is willing to grant either that \(p \rightarrow q\) entails \(p \supset q\), or else that Stalnaker’s Thesis is true. If Stalnaker’s Thesis holds, then we’ve seen that (*) is true. On the other hand, (Commitment) holds for Argument 1 only if accepting/believing (P1)\(_1\) requires \(P(p \supset q) = 1\). If we assume that \(p \rightarrow q\) entails \(p \supset q\), then this fact is predicted by (*), but it’s otherwise mysterious.
Rights and permissions
About this article
Cite this article
Dodd, D. Belief and certainty. Synthese 194, 4597–4621 (2017). https://doi.org/10.1007/s11229-016-1163-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1163-4