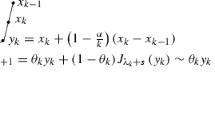Abstract
In a Hilbert framework, we introduce a new class of fast continuous dissipative dynamical systems for approximating zeroes of an arbitrary maximally monotone operator. This system originates from some change of variable operated in a continuous Nesterov-like model that is driven by the Yosida regularization of the operator and that involves an asymptotic vanishing damping. The proposed model (based upon the Minty representation of maximally monotone operators) is investigated through a first-order reformulation that amounts to dynamics involving three variables: a couple of two variables that lies in the graph of the considered operator, along with an auxiliary variable. We establish the weak convergence towards zeroes of the operator for two of the trajectories, as well as fast convergence to zero of their velocities. We also prove a fast convergence property to zero for the third trajectory and for its velocity. It turns out that our model offers a new and well-adapted framework for discrete counterparts. Several algorithms are then suggested relative to monotone inclusions. Some of them recover some recently developed inertial proximal algorithms that incorporate a correction term in addition to the classical momentum term.
Similar content being viewed by others
Data Availability
We do not analyse or generate any datasets, because our work proceeds within a theoretical and mathematical approach. One can obtain the relevant materials from the references below.
References
Abbas, B., Attouch, H., Svaiter, B.F.: Newton-like dynamics and forward-backward methods for structured monotone inclusions in Hilbert spaces. J. Optim. Theory Appl. 161(2), 331–360 (2014)
Alvarez, F., Attouch, H., Bolte, J., Redont, P.: A second-order gradient-like dissipative dynamical system with Hessian driven damping. Application to Optimization and Mechanics. J. Math. Pures Appl. 81(8), 747–779 (2002)
Attouch, H., Bolte, J., Redont, P.: Optimizing properties of an inertial dynamical system with geometric damping: Link with proximal methods. Control. Cybern. 31, 643–657 (2002)
Attouch, H., Cabot, A.: Convergence of a relaxed inertial forward-backward algorithm for structured monotone inclusions. App. Math. Optim. 80, 547–598 (2019)
Attouch, H., Chbani, Z., Fadili, J., Riahi, H.: First-order optimization algorithms via inertial systems with Hessian driven damping. Math. Programm. https://doi.org/10.1007/s10107-020-01591-1, arXiv:1907.10536 (2019)
Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. 168(1–2), 123–175 (2018)
Attouch, H., László, S.C.: Continuous Newton-like inertial dynamics for monotone inclusions. Set-valued and variational Analysis. https://doi.org/10.1007/s11228-020-00564-y (2020)
Attouch, H., Peypouquet, J.: Convergence of inertial dynamics and proximal algorithms governed by maximally monotone operators. Math. Program. 174, 391–432 (2019). https://doi.org/10.1007/s10107-018-1252-x
Attouch, H., Peypouquet, J., Redont, P.: Fast convex minimization via inertial dynamics with Hessian driven damping. J. Diff. Equat. 261, 5734–5783 (2016)
Brezis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, Math Stud, 5, North-Holland, Amsterdam (1973)
Brezis, H.: Function Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2010). https://doi.org/10.1007/978-0-387-70914-7
Cabot, A., Engler, H., Gadat, S.: On the long time behavior of second order differential equations with asymptotically small dissipation. Trans. Amer. Math. Soc. 361, 5983–6017 (2009)
Cabot, A., Engler, H., Gadat, S.: Second order differential equations with asymptotically small dissipation and piecewise flat potentials. Electr. J. Differ. Equat. 17, 33–38 (2009)
Kim, D.: Accelerated proximal point method for maximally monotone operators. Math. Programm. 190, 57–87 (2021)
Labarre, F., Maingé, P.E.: First-order frameworks for continuous Newton-like dynamics governed by maximally monotone operators. Set-Valued Var. Anal. https://doi.org/10.1007/s11228-021-00593-1 (2021)
Maingé, P.E.: Accelerated proximal algorithms with a correction term for monotone inclusions. Appl. Math. Optim. 84, 2027–2061 (2021)
Maingé, P.E.: Fast convergence of generalized forward-backward algorithms for structured monotone inclusions. J. Convex Anal. 29(3) (2022)
May, R.: Asymptotic for a second order evolution equation with convex potential and vanishing damping term. Turk. J. Math. 41(3). https://doi.org/10.3906/mat-1512-28 (2015)
Minty, G.J.: Monotone (nonlinear) operators in Hilbert spaces. Duke Math. J. 29, 341–346 (1962)
Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Amer. Math. Soc. 73, 591–597 (1967)
Shi, B., Du, S.S., Jordan, M.I., Su, W.J.: Understanding the acceleration phenomenon via high-resolution differential equations. arXiv:1810.08907v3 (2018)
Su, W., Boyd, S., Candès, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: theory and insights. Neural Inf. Process.Syst. 27, 2510–2518 (2014)
Acknowledgements
The authors would like to thank the two anonymous referees for their careful reading of the manuscript and their insightful comments and observations.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
1.1 A.1 Basic Properties on the Parameters
Proposition A.1
Let ν(t) = t + ν0 (for some constant ν0) and let {𝜃(.), ω(.)} be given by (1.9)–(1.10a) along with some positive constants \(\kappa \in (0, \infty )\) and 𝜖 ∈ (0, 1). Then the parameters {α(.), β(.), b(.)} defined in (1.6) satisfy (as \(t \to \infty \)): \(\alpha (t) \sim (1+ \kappa e)t^{-1}\), \(\beta (t) \sim \kappa \) and \(b(t) \sim (1-\epsilon )s_0 \kappa ^2t^{-1}\).
Proof
In view of \(\theta (t)=\frac {\kappa \nu (t) -\dot {\nu (t)}}{\nu (t)+ e }\) (from (1.9)) (hence \( \theta (t)=\kappa -\frac { \dot {\nu }(t)+\kappa e}{\nu (t) + e}\)), while taking ν(t) = t + ν0 and setting e0 = e + ν0, we readily get
As a result, by \(\alpha (t):= \kappa -\theta (t)-\frac {\dot {\theta }(t)}{{\theta }(t)}\) (from (1.6)), together with (A.1) and (A.3) we obtain
Moreover, by \( \omega (t)= \frac {s_0}{e+\nu (t)}\left (\kappa (1-\epsilon )-\frac {\dot {\nu } (t) }{\nu (t)} \right )\) (from (1.10a)) and ν(t) = t + ν0, we get
Then, by \(\beta (t):=-\frac {\dot {\theta }(t)}{{\theta (t)}}+ \kappa +\omega (t)\) (from (1.6)), namely by β(t) = α(t) + 𝜃(t) + ω(t), and remembering (as \(t \to \infty \)) that \(\theta (t) \sim \kappa \) (from (A.1)), α(t) → 0 (from (A.4)) and that ω(t) → 0 (from (A.5)), we get \(\beta (t) \sim \kappa \). In addition, using again the above expression of ω(.) yields
It follows that
Consequently, by \(b(t):=\omega (t) \left (\kappa +\frac {\dot {\omega }(t)}{ \omega (t)}- \frac {\dot {\theta }(t)}{{\theta (t)}} \right ) \), or equivalently by \(b(t)=\omega (t) \left (\alpha (t)+ \theta (t) + \frac {\dot {\theta }(t)}{{\theta (t)}} \right ) \), and reminding (as \(t \to \infty \)) that \(\frac {\dot {\theta }(t)}{{\theta }(t)} \to 0\) (from (A.3)), α(t) → 0 (from (A.4)) and that \(\omega (t) \sim \frac {s_{0}\kappa (1-\epsilon )}{t}\) (from (A.5)), we deduce that \( b(t) \sim \frac {s_{0}(1-\epsilon )\kappa ^{2}}{t}\)□
1.2 A.2 Proof of Proposition 2.1.
Let us prove that (i1) ⇒ (i2). Given a C1 × C1 solution (x(.), ζ(.)) to (2.1) with x(.) + ζ(.) of class C2, we set for t ≥ 0,
It is immediate that (2.1b) can be rewritten as
Then, by integrating (A.9) on [0, t] and by differentiating (A.8), while noticing that \(\dot {x}(0)+\dot {\zeta }(0) + z(0)=0\) (from the above definition of z), we successively obtain
Multiplying (A.10a) by β(t) and adding the resulting equality to (A.10b), we obtain
Now, we denote \(y(t)=\frac {1}{\theta (t)}z(t)+x(t)-\frac {\omega (t)}{\theta (t)}\zeta (t)\) (since 𝜃(.) is positive), which can be rewritten as (A.12a), and differentiating (A.12a) readily implies (A.12b):
Thus (A.11a), in light of (A.12a), can be written as.
which proves (A.13). Using also the definitions of α(.), β(.) and b(.) given by (1.6) \((\text {namely}, \alpha (t) =-\frac {\dot {\theta }(t) }{\theta (t)} + \kappa -\theta (t), \beta (t) = -\frac {\dot {\theta }(t)}{\theta (t)} + \kappa +\omega (t) \text { and } b(t)= \omega (t) \left (\kappa + \frac {\dot {\omega }(t)}{\omega (t)}-\frac {\dot {\theta }(t)}{\theta (t)}\right ))\), we are led to the elementary results below:
Hence, by (A.11b) together with (A.12) and (A.14a), we get
This, in light of (A.13) and 𝜃(.) > 0, yields \(\dot {y}(t)+\kappa (y(t)-x(t))=0\), namely (2.2c). Finally, by (A.13) and the previous result, we infer that (2.2) is verified altogether with the initial conditions x(0) = x0 (according to (i1)) and \(y(0) = x_{0}-\frac {1}{\theta (0)}(q_{0}+ \omega (0)\zeta _{0})\) (thanks to (2.2b) at time t = 0).
Let us prove that (i2) ⇒ (i1). (2.2b) can be written as \(\dot {x}(t)+\dot {\zeta }(t) = - \theta (t)\big (y(t)- x(t) \big ) - \omega (t)\zeta (t)\).
This, in light of x(.), y(.), ω(.), 𝜃(.) and ζ(.) being of class C1, entails that \(x(.)+\zeta (.) \in C^{2}([0,\infty );{\mathscr{H}})\). Thus, we can differentiate (2.2b) which gives us
while, from (2.2c) we have \(\dot y(t)= -\kappa \big (y(t)-x(t) \big )\). It follows that (A.15) can be written as
Furthermore, as \(\dot {x}(t)+\dot {\zeta }(t) + \theta (t) \big (y(t)-x(t) + \frac {\omega (t)}{\theta (t)}\zeta (t)) = 0\) (from (2.2b)), we equivalently deduce that \(y(t)-x(t)=-\frac {1}{\theta (t)}(\dot {x}(t)+\dot {\zeta }(t))- \frac {\omega (t)}{\theta (t)} \zeta (t)\), which, by (A.16), entails
hence taking into account the expression of α(.), β(.) and b(.) defined in (1.6) amounts to (2.1b). In addition, the initial condition on y(.) in (i2) writes
which, in light of (2.2b) at time t = 0, entails
This ends the proof
1.3 A.3 The Yosida Regularization
Some useful properties of the Yosida regularization are recalled through the lemma below established in [15] (see also [8, 10, 11]).
Lemma A.1
Let γ, δ > 0 and \(x, y \in {\mathscr{H}}\). Then for z ∈ A− 1({0}), we have
Proof
The proof of (A.17) can be found in [8]. Let us prove (A.18). To get this we simply have
hence
Consequently, by \( \|A_{\gamma }x\|\le \frac {1}{\gamma } \|x-z\|\) and using (A.17), we obtain
that is the desired inequality □
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Maingé, PE., Weng-Law, A. Fast Continuous Dynamics Inside the Graph of Maximally Monotone Operators. Set-Valued Var. Anal 31, 5 (2023). https://doi.org/10.1007/s11228-023-00663-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11228-023-00663-6
Keywords
- Asymptotic behavior
- First-order differential equation
- Dissipative systems
- Maximal monotone operators
- Minty’s representation
- Cocoercive operators
- Yosida approximation
- Nesterov-like acceleration