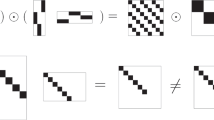Skip to main content
SpringerLink
Log in

Distributed non-negative matrix factorization with determination of the number of latent features

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

The holistic analysis and understanding of the latent (that is, not directly observable) variables and patterns buried in large datasets is crucial for data-driven science, decision making and emergency response. Such exploratory analyses require devising unsupervised learning methods for data mining and extraction of the latent features, and non-negative matrix factorization (NMF) is one of the prominent such methods. NMF is based on compute-intense non-convex constrained minimization, which, for large datasets requires fast and distributed algorithms. However, current parallel implementations of NMF fail to estimate the number of latent features. In practice, identifying these features is both difficult and significant for pattern recognition and latent feature analysis, especially for large dense matrices. In this paper, we introduce a distributed NMF algorithm coupled with distributed custom clustering followed by a stability analysis on dense data, which we call DnMFk, to determine the number of latent variables. The results on synthetic data and the classical Swimmer data set demonstrate the accuracy of model determination while scaling nearly linearly across multiple processors for large data. Further, we employ DnMFk to determine the number of hidden features from a terabyte matrix.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Alexandrov BS, Alexandrov LB, Iliev FL, Stanev VG, Vesselinov VV (2018) Source identification by non-negative matrix factorization combined with semi-supervised clustering. US Patent App. 15/690,176

  2. Alexandrov BS, Stanev VG, Vesselinov VV, Rasmussen KØ (2019) Nonnegative tensor decomposition with custom clustering for microphase separation of block copolymers. Stat Anal Data Min ASA Data Sci J 12(4):302–310

    MathSciNet  Google Scholar 

  3. Alexandrov BS, Vesselinov VV (2014) Blind source separation for groundwater pressure analysis based on nonnegative matrix factorization. Water Resour Res 50(9):7332–7347

    Google Scholar 

  4. Alexandrov LB, Nik-Zainal S, Wedge DC, Aparicio SA, Behjati S, Biankin AV, Bignell GR, Bolli N, Borg A, Børresen-Dale AL et al (2013) Signatures of mutational processes in human cancer. Nature 500(7463):415

    Google Scholar 

  5. Alexandrov LB, Nik-Zainal S, Wedge DC, Campbell PJ, Stratton MR (2013) Deciphering signatures of mutational processes operative in human cancer. Cell Rep 3(1):246–259

    Google Scholar 

  6. Amari Si, Cichocki A, Yang HH (1996) A new learning algorithm for blind signal separation. In: Advances in neural information processing systems, pp 757–763

  7. Barlow H (1989) Unsupervised learning. Neural Comput 1(3):295–311. https://doi.org/10.1162/neco.1989.1.3.295

    Article  Google Scholar 

  8. Battenberg E, Wessel D (2009) Accelerating non-negative matrix factorization for audio source separation on multi-core and many-core architectures. In: ISMIR, pp 501–506

  9. Baum LE, Petrie T (1966) Statistical inference for probabilistic functions of finite state markov chains. Ann Math Stat 37(6):1554–1563

    MathSciNet  MATH  Google Scholar 

  10. Benesty J, Chen J, Huang Y, Cohen I (2009) Pearson correlation coefficient. In: Noise reduction in speech processing, Springer, New York, pp 1–4

  11. Beutel A, Talukdar PP, Kumar A, Faloutsos C, Papalexakis EE, Xing EP (2014) Flexifact: scalable flexible factorization of coupled tensors on hadoop. In: Proceedings of the 2014 SIAM International Conference on Data Mining, SIAM, pp 109–117

  12. Bishop CM (1999) Bayesian PCA. In: Advances in neural information processing systems, pp 382–388

  13. Brunet JP, Tamayo P, Golub TR, Mesirov JP (2004) Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci 101(12):4164–4169

    Google Scholar 

  14. Chan E, Heimlich M, Purkayastha A, Van De Geijn R (2007) Collective communication: theory, practice, and experience. Concurr Comput Pract Exp 19(13):1749–1783

    Google Scholar 

  15. Chennupati G, Azad RMA, Ryan C (2015) Performance optimization of multi-core grammatical evolution generated parallel recursive programs. In: Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, pp 1007–1014

  16. Cichocki A, Phan AH, Zhao Q, Lee N, Oseledets I, Sugiyama M, Mandic DP et al (2017) Tensor networks for dimensionality reduction and large-scale optimization: part 2 applications and future perspectives. Found Trends® Mach Learn 9(6):431–673

    MATH  Google Scholar 

  17. Cichocki A, Zdunek R, Amari Si (2007) Hierarchical ALS algorithms for nonnegative matrix and 3d tensor factorization. In: International Conference on Independent Component Analysis and Signal Separation, Springer, New York, pp 169–176

  18. Cichocki A, Zdunek R, Phan AH, Si Amari (2009) Nonnegative matrix and tensor factorizations: applications to exploratory multi-way data analysis and blind source separation. Wiley, Hoboken

    Google Scholar 

  19. Deerwester SC, Dumais ST, Furnas GW, Harshman RA, Landauer TK, Lochbaum KE, Streeter LA (1989) Computer information retrieval using latent semantic structure. US Patent 4,839,853

  20. Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the em algorithm. J R Stat Soc Ser B (Methodol) 39(1):1–22

    MathSciNet  MATH  Google Scholar 

  21. Dong C, Zhao H, Wang W (2010) Parallel nonnegative matrix factorization algorithm on the distributed memory platform. Int J Parallel Program 38(2):117–137

    MATH  Google Scholar 

  22. Donoho D, Stodden V (2004) When does non-negative matrix factorization give a correct decomposition into parts? In: Advances in neural information processing systems, pp 1141–1148

  23. Fairbanks JP, Kannan R, Park H, Bader DA (2015) Behavioral clusters in dynamic graphs. Parallel Comput 47:38–50

    MathSciNet  Google Scholar 

  24. Févotte C, Cemgil AT (2009) Nonnegative matrix factorizations as probabilistic inference in composite models. In: 2009 17th European Signal Processing Conference, IEEE, pp 1913–1917

  25. Franke B, Plante JF, Roscher R, Lee EsA, Smyth C, Hatefi A, Chen F, Gil E, Schwing A, Selvitella A et al (2016) Statistical inference, learning and models in big data. Int Stat Rev 84(3):371–389

    MathSciNet  Google Scholar 

  26. Gemulla R, Nijkamp E, Haas PJ, Sismanis Y (2011) Large-scale matrix factorization with distributed stochastic gradient descent. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, pp 69–77

  27. Golub GH, Reinsch C (1971) Singular value decomposition and least squares solutions. In: Linear algebra, Springer, New York, pp 134–151

  28. Hartigan JA, Wong MA (1979) Algorithm as 136: a k-means clustering algorithm. J R Stat Soc Ser C (Appl Stat) 28(1):100–108

    MATH  Google Scholar 

  29. Huang K, Sidiropoulos ND, Liavas AP (2016) A flexible and efficient algorithmic framework for constrained matrix and tensor factorization. IEEE Trans Signal Process 64(19):5052–5065

    MathSciNet  MATH  Google Scholar 

  30. Iliev FL, Stanev VG, Vesselinov VV, Alexandrov BS (2018) Nonnegative matrix factorization for identification of unknown number of sources emitting delayed signals. PloS One 13(3):e0193974

    Google Scholar 

  31. Jolliffe I (2011) Principal component analysis. Springer, New York

    MATH  Google Scholar 

  32. Kanna R (2019) Parallel low-rank approximations with non-negativity constraints (PLANC). https://github.com/ramkikannan/planc. Accessed 03 Sep 2019

  33. Kannan R, Ballard G, Park H (2016) A high-performance parallel algorithm for nonnegative matrix factorization. In: Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP’16, ACM, pp 9:1–9:11

  34. Kim J, Park H (2008) Toward faster nonnegative matrix factorization: a new algorithm and comparisons. In: 2008 Eighth IEEE International Conference on Data Mining, IEEE, pp 353–362

  35. Kim J, Park H (2011) Fast nonnegative matrix factorization: an active-set-like method and comparisons. SIAM J Sci Comput 33(6):3261–3281

    MathSciNet  MATH  Google Scholar 

  36. Koitka S, Friedrich CM (2016) nmfgpu4r: GPU-accelerated computation of the non-negative matrix factorization (NMF) using CUDA capable hardware. R Journal 8(2):382–392

    Google Scholar 

  37. Korenius T, Laurikkala J, Juhola M (2007) On principal component analysis, cosine and euclidean measures in information retrieval. Inf Sci 177(22):4893–4905

    MathSciNet  MATH  Google Scholar 

  38. Kubjas K, Robeva E, Sturmfels B (2015) Fixed points EM algorithm and nonnegative rank boundaries. Ann Stat 43:422–461

    MathSciNet  MATH  Google Scholar 

  39. Kysenko V, Rupp K, Marchenko O, Selberherr S, Anisimov A (2012) GPU-accelerated non-negative matrix factorization for text mining. In: International Conference on Application of Natural Language to Information Systems, Springer, New York, pp 158–163

  40. Laurberg H, Christensen MG, Plumbley MD, Hansen LK, Jensen SH (2008) Theorems on positive data: on the uniqueness of NMF. Comput Intell Neurosci 2008:764206

    Google Scholar 

  41. Lee DD, Seung HS (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755):788–791

    MATH  Google Scholar 

  42. Liao R, Zhang Y, Guan J, Zhou S (2014) Cloudnmf: a mapreduce implementation of nonnegative matrix factorization for large-scale biological datasets. Genom Proteom Bioinform 12(1):48–51

    Google Scholar 

  43. Liu C, Yang Hc, Fan J, He LW, Wang YM (2010) Distributed nonnegative matrix factorization for web-scale dyadic data analysis on mapreduce. In: Proceedings of the 19th International Conference on World Wide Web, ACM, pp 681–690

  44. Lopes N, Ribeiro B (2010) Non-negative matrix factorization implementation using graphic processing units. In: International Conference on Intelligent Data Engineering and Automated Learning, Springer, New York, pp 275–283

  45. MacKay DJ et al (1994) Bayesian nonlinear modeling for the prediction competition. ASHRAE Trans 100(2):1053–1062

    Google Scholar 

  46. Mejía-Roa E, García C, Gómez JI, Prieto M, Tirado F, Nogales R, Pascual-Montano A (2011) Biclustering and classification analysis in gene expression using nonnegative matrix factorization on multi-GPU systems. In: 2011 11th International Conference on Intelligent Systems Design and Applications, IEEE, pp 882–887

  47. Mejía-Roa E, Tabas-Madrid D, Setoain J, García C, Tirado F, Pascual-Montano A (2015) NMF-mGPU: non-negative matrix factorization on multi-gpu systems. BMC Bioinform 16(1):43

    Google Scholar 

  48. Moon GE, Sukumaran-Rajam A, Parthasarathy S, Sadayappan P (2019) PL-NMF: parallel locality-optimized non-negative matrix factorization. CoRR arxiv: abs/1904.07935

  49. Paatero P, Tapper U (1994) Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 5(2):111–126

    Google Scholar 

  50. Rousseeuw PJ (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20:53–65

    MATH  Google Scholar 

  51. Sanderson C, Curtin R (2016) Armadillo: a template-based C++ library for linear algebra. J Open Sour Softw 1(2):26

    Google Scholar 

  52. Spearman C (1904) “General Intelligence” objectively determined and measured. Am J Psychol 15(2):201–292

    Google Scholar 

  53. Stanev V, Vesselinov VV, Kusne AG, Antoszewski G, Takeuchi I, Alexandrov BS (2018) Unsupervised phase mapping of X-ray diffraction data by nonnegative matrix factorization integrated with custom clustering. NPJ Comput Mater 4(1):43

    Google Scholar 

  54. Stanev VG, Iliev FL, Hansen S, Vesselinov VV, Alexandrov BS (2018) Identification of release sources in advection-diffusion system by machine learning combined with green’s function inverse method. Appl Math Modell 60:64–76

    MathSciNet  MATH  Google Scholar 

  55. Sun DL, Fevotte C (2014) Alternating direction method of multipliers for non-negative matrix factorization with the beta-divergence. In: 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, pp 6201–6205

  56. Sun M, Zhang X et al (2015) A stable approach for model order selection in nonnegative matrix factorization. Pattern Recognit Lett 54:97–102

    Google Scholar 

  57. Syed AM, Qazi S, Gillis N (2018) Improved SVD-based initialization for nonnegative matrix factorization using low-rank correction. arXiv preprint arXiv:1807.04020

  58. Tan VYF, Févotte C (2009) Automatic relevance determination in nonnegative matrix factorization. In: SPARS’09—signal processing with adaptive sparse structured representations, Inria Rennes—Bretagne Atlantique

  59. Vesselinov VV, Alexandrov BS, O’Malley D (2018) Contaminant source identification using semi-supervised machine learning. J Contam Hydrol 212:134–142

    Google Scholar 

  60. Wold S, Sjöström M, Eriksson L (2001) Pls-regression: a basic tool of chemometrics. Chemom Intell Lab Syst 58(2):109–130

    Google Scholar 

  61. Wu S, Joseph A, Hammonds AS, Celniker SE, Yu B, Frise E (2016) Stability-driven nonnegative matrix factorization to interpret spatial gene expression and build local gene networks. Proc Natl Acad Sci 113(16):4290–4295

    Google Scholar 

  62. Yin J, Gao L, Zhang ZM (2014) Scalable nonnegative matrix factorization with block-wise updates. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Springer, New York, pp 337–352

Download references

Acknowledgements

This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001.

Funding

This study was funded by U.S. Department of Energy National Nuclear Security Administration under Contract No. DE-AC52-06NA25396 through LANL Laboratory Directed Research and Development (LDRD) Grant 20190020DR.

Author information

Authors and Affiliations

  1. Information Sciences (CCS-3) Group, Los Alamos National Laboratory (LANL), Los Alamos, NM, 87545, USA

    Gopinath Chennupati, Erik Skau & Hristo Djidjev

  2. Theoretical Division (T-1) Group, Los Alamos National Laboratory (LANL), Los Alamos, NM, 87545, USA

    Raviteja Vangara & Boian Alexandrov

Authors
  1. Gopinath Chennupati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Raviteja Vangara
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erik Skau
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hristo Djidjev
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Boian Alexandrov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gopinath Chennupati.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

See Tables 3, 4.

Table 3 Execution times for distributed clustering and Silhouette calculation using DnMFk on two data matrices: Data 3 (\(57{,}600 \times 38{,}400\)) and Data 4 (\(129{,}600 \times 51{,}840\))
Full size table
Table 4 Execution times for distributed clustering and Silhouette calculation using DnMFk on two data matrices: Data 1 (\(2^{21} \times 10 \times 10\)) and Data 2 (\(2^{20} \times 50 \times 10\))
Full size table

See Figs. 14, 15 and 16.

Fig. 15
figure 15

k Scaling for clustering and silhouette—the runtimes of clustering and silhouette across 10 perturbations of DnMFk. The matrices are \(2^{21}\times k\times 10\) and \(2^{20}\times k\times 10\), where the k vary as {2, 4, 8, 16, 32, 64, 128, 256}. The execution time increases linearly with k at a fixed processor count

Full size image
Fig. 16
figure 16

Find the number of hidden features in 0.5 TB matrix of \(8{,}388{,}608 \times 8192\). DnMFk find k as 5, which agrees with the ground truth. DnMFk takes 13.6 h on 2048 processors with an average reconstruction error of \(5.8\%\)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chennupati, G., Vangara, R., Skau, E. et al. Distributed non-negative matrix factorization with determination of the number of latent features. J Supercomput 76, 7458–7488 (2020). https://doi.org/10.1007/s11227-020-03181-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-020-03181-6

Keywords

Search

Navigation