Doubly robust estimation of optimal treatment regimes for survival data using an instrumental variable

Abstract

In survival contexts, substantial literature exists on estimating optimal treatment regimes, where treatments are assigned based on personal characteristics to maximize the survival probability. These methods assume that a set of covariates is sufficient to deconfound the treatment-outcome relationship. However, this assumption can be limited in observational studies or randomized trials in which non-adherence occurs. Therefore, we propose a novel approach to estimating optimal treatment regimes when certain confounders are unobservable and a binary instrumental variable is available. Specifically, via a binary instrumental variable, we propose a semiparametric estimator for optimal treatment regimes by maximizing a Kaplan–Meier-like estimator of the survival function. Furthermore, to increase resistance to model misspecification, we construct novel doubly robust estimators. Since the estimators of the survival function are jagged, we incorporate kernel smoothing methods to improve performance. Under appropriate regularity conditions, the asymptotic properties are rigorously established. Moreover, the finite sample performance is evaluated through simulation studies. Finally, we illustrate our method using data from the National Cancer Institute’s prostate, lung, colorectal, and ovarian cancer screening trial.

Appendices

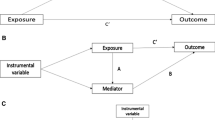
Appendix A: Illustration of the IV-related assumptions

Recall that the IV-related assumptions are assumptions A2-A7 and Fig. 1 gives an illustration of these assumptions. Among these assumptions, assumptions A2-A5 are the core assumptions for all IV-based methods and assumptions A6-A7 are required for the identifiability of the final estimand (Wang et al. 2022; Cui and Tchetgen Tchetgen 2020; Qiu et al. 2021; Wang and Tchetgen Tchetgen 2018). Assumption A2 states that the variable $U$ is sufficient to account for the unmeasured confounding. Assumption A3 requires that the IV is associated with the treatment conditional on ${\varvec{L}}$. Assumption A4 states that the direct causal effect from $Z$ to $T$ is all mediated by the treatment $A$. Assumption A5 ensures that, conditional on ${\varvec{L}}$, the causal effect of $Z$ on $T$ is unconfounded by $U$ because $U$ has no causal effect on $Z$. Assumption A7 posits that in a model for the probability of being treated conditional on ${\varvec{L}}$ and $U$, there exists no additive interaction between $Z$ and $U$. An example that satisfies this assumption is the additive probability model $\pi (A=1|Z,{\varvec{L}},U)=g(Z,{\varvec{L}})+ h(U,{\varvec{L}})$, where $g$ and $h$ are measurable functions such that the range of the function $\pi (A=1|Z,{\varvec{L}},U)$ is a subset of the interval $[0,1]$. The additive probability model can capture certain types of real-world data (Caudill 1988). Another interpretation of the assumption can be given as follows. Define the counterfactual treatment under the IV $Z=z$ as $A(z)$. In randomized trials where $Z\! \perp \! \! \! \perp A(z)|(L, U)$ and $Z\! \perp \! \! \! \perp A(z)|L$, or in observational studies under the same assumptions, the assumption A7 can be rearranged as $E[A(1)-A(0)|{\varvec{L}}, U]=E[A(1)-A(0)|{\varvec{L}}]$. Based on the relationship between the instrument $Z$ and the treatment $A(Z)$, we can segment the population into four adherence type: compliers $(A(1)=1, A(0)=0)$, always-takers $(A(1)=1, A(0)=1)$, never-takers $(A(1)=0, A(0)=0)$, and defiers $(A(1)=0, A(0)=1)$ (Imbens and Angrist 1994; Angrist et al. 1996). Then assumption A7 holds if the adherence type is determined by the observed covariates ${\varvec{L}}$, such as age and disease history.

In our case, no unmeasured confounding assumption is problematic as health status is a confounder. However, the IV assumptions are more likely to be accepted. The IV relevance condition is convincing because the adherence rate is approximately 85%. This indicates a strong relationship between the screening assignment ($Z$) and the treatment ($A$). Regarding the exclusion restriction assumption, the screening assignment itself does not directly affect the health of individuals. Instead, its effect is mediated by its influence on the treatment an individual receives, which ensures the exclusion restriction assumption. Since the IV we utilized here is the randomization procedure itself, it is independent of ${\varvec{L}}, U$ and each person has the same probability $0.5$ of being assigned to the screening group. As a result, both the IV independence and IV positivity assumptions are satisfied. To achieve the independent adherence type assumption, it is necessary to include a list of variables that can predict the adherence type in our analysis. In our case, we use age, colorectal polyps, and diabetes to characterize the non-adherence due to health status. Other important variables are listed in Sect. 5.

Appendix B: Intuition underlying the IWKME-IV

We now provide more details on the intuition underlying our estimator (2) of the counterfactual survival function. Our primary goal is to estimate the counterfactual survival function $P(T^*(d_{\varvec{\eta }}({\varvec{L}}))> t)$ via the Kaplan–Meier-like estimator as follows, where $\prod _{s \le t}$ is a product-based counterpart of the usual sum-based integral of calculus (Gill and Johansen 1990). It requires a consistent estimator for the differential of the counterfactual cumulative distribution function $dP(T^*(d_{\varvec{\eta }}({\varvec{L}}))\le s)$ and another estimator for the counterfactual survival function $P(T^*(d_{\varvec{\eta }}({\varvec{L}}))\ge s)$, where $s\le t$.

$$\begin{aligned} {\widehat{S}}^*_{KM}(t;\varvec{\eta })=\prod _{s \le t}\left\{ 1-\frac{d P(T^*(d_{\varvec{\eta }}({\varvec{L}}))\le s)}{P(T^*(d_{\varvec{\eta }}({\varvec{L}}))\ge s)}\right\} \end{aligned}$$

To be concise, we illustrate the intuition behind constructing the estimator (2) with an example of constructing the estimator of the counterfactual survival function $P(T^*(d_{\varvec{\eta }}({\varvec{L}}))\ge s)$. Let $d_{\varvec{\eta }}({\varvec{L}})=1$, and for simplicity, omit the consideration of censoring and baseline covariates ${\varvec{L}}$. Therefore, our goal is to find a good estimator of ${P}(T^*(1)\ge s)$. Note that

$$\begin{aligned}&{P}(T^*(1)\ge s)\nonumber \\ =&E\left\{ P(T^*(1)\ge s|U)\frac{\pi (A=1|Z=1,U)-\pi (A=1|Z=0,U)}{\pi (A=1|Z=1)-\pi (A=1|Z=0)}\right\} \nonumber \\ =&E\left\{ P(T^*(1)\ge s|U)\frac{(2Z-1)\pi (A=1|Z,U)}{f(Z|U)(\pi (A=1|Z=1)-\pi (A=1|Z=0))}\right\} \nonumber \\ =&E\left\{ P(T^*(1)\ge s|U)\frac{(2Z-1)I\{A=1\}}{f(Z|U)(\pi (A=1|Z=1)-\pi (A=1|Z=0))}\right\} \nonumber \\ =&E\left\{ P(T^*(1)\ge s|Z,A,U)\frac{(2Z-1)I\{A=1\}}{f(Z)(\pi (A=1|Z=1)-\pi (A=1|Z=0))}\right\} \nonumber \\ =&E\left\{ \frac{I\{T^*(1)\ge s\}(2Z-1)I\{A=1\}}{f(Z)(\pi (A=1|Z=1)-\pi (A=1|Z=0))}\right\} \nonumber \\ =&E\left\{ \frac{I\{T\ge s\}(2Z-1)I\{A=1\}}{f(Z)(\pi (A=1|Z=1)-\pi (A=1|Z=0))}\right\} , \end{aligned}$$

(4)

where the first equality follows the independent adherence type assumption A7, the second equality is from the law of total probability, and the fourth equality follows from assumptions A2, A4, and A5. With the identification equation (4) above, we can construct ${\widehat{P}}(T^*(1)\ge s)$ mentioned below as an estimator of ${P}(T^*(1)\ge s)$. It is the same as the denominator part of our estimator (2) when there is no censoring, the baseline covariates ${\varvec{L}}$ are omitted, and $d_{\varvec{\eta }}({\varvec{L}})=1$.

$$\begin{aligned}&{\widehat{P}}(T^*(1)\ge s) \\ =&\frac{1}{n}\sum _{i=1}^n \frac{I\{T_i\ge s\} I\{A_i=1\} (2Z_i-1)}{{\widehat{f}}(Z_i)({\widehat{\pi }}(A_i=1|Z_i=1)-{\widehat{\pi }}(A_i=1|Z_i=0))} \end{aligned}$$