1 Introduction

This paper reports on progress in the analysis of the archival data base from the observations made at the 150-foot tower telescope at the Mt. Wilson Observatory (MWO). A new method of determining large-scale flow velocities and their variations is presented, along with results showing the close association between surface velocities deviations going E-W (east-west) and N-S (north-south). These new results will help in the study of the nature of the solar dynamo, which is currently under intense study using complementary helioseismic and feature tracking methods. Those methods also yield E-W and N-S transverse velocities that apply to a range of solar interior depths. Small time-dependent variations derived from these velocities are of particular interest.

Early in the study of solar and stellar structure it was recognized that rotation requires the presence of a meridional flow called Eddington-Sweet currents (Eddington, 1929; Sweet, 1950). Associated with this rotation induced effect is an enhancement of the brightness at the poles that is not observed at the scale predicted. The solar shape and its relationship with the level surfaces of the gravitational potential played an important part in the debate over gravity theory (see the summary by Gough, 1976). A review by Paternò (2010) provides a history of the early measurements of meridional circulation. With the extensive application of helioseismology to the Sun’s interior velocities, a variety of time- and space-dependent phenomena have been studied and reviewed by Gizon et al. (2020), Choudhuri (2021), Hathaway, Upton, and Mahajan (2022), and Hanasoge (2022). Measuring the meridional circulation requires global stability of the measuring technique, which has not generally been available with the systems based on filtergrams. For example, the work by Gizon et al. (2020) includes a temporal filter step to remove features with lifetimes less than 5 years, and the work by Hathaway, Upton, and Mahajan (2022) is based on feature tracking and does not represent the solar surface. The review by Hazra et al. (2023) gives an extensive discussion of the relationship between meridional circulation and the solar dynamo.

The totality of the collected magnetogram/Dopplergram observations is a resource that allows the study of the temporal variation in the solar rotation rate (Howard, 1976a; Howard et al., 1983a; Gilman and Howard, 1984a; Howard, 1984; Gilman and Howard, 1984b). An important finding of these studies was the identification of an E-W moving pattern of velocity, which Howard and Labonte (1980), LaBonte and Howard (1982b,a), and Howard (1983) called the torsional oscillations. Proposals by Schüssler (1981) and Yoshimura (1981) suggested the torsional oscillations are produced by Lorenz forces from the solar cycle magnetic fields. The work by Howard (1983), however, pointed out that the torsional oscillations occur at times and places where there are no strong magnetic fields.

The torsional oscillations have been confirmed through helioseismology observations (Kosovichev and Schou, 1997; Schou, 1999; Howe et al., 2000; Getling, Kosovichev, and Zhao, 2021; see also the review provided by Howe, 2009). Global dynamo modeling by Guerrero et al. (2016) found that magnetic tension at the tachocline lower boundary of the convection zone can generate a dynamo wave that propagates to the solar surface. Subsequently, Kosovichev and Pipin (2019) found support for this idea from a principal component analysis (Jolliffe, 2013) of the zonal acceleration derived from global helioseismology.

The analysis of the present paper raises additional questions – a) “What is the direction of the flow?” and b) “What is the reference function that we should subtract?” The time scale for changes in the flow is an important part of characterizing the motion. For the torsional oscillations, a differential rotation function is subtracted. Assuming the flow variations we find are related to the solar cycle, we need to subtract a similar background circulation function, which we will refer to as the static meridional circulation function. We find both the differential rotation function and the static meridional circulation function by averaging over the full time span of the record we are using. Data outside our time frame could alter these functions, which would alter the variations we determine. We will show in this paper that the E-W and N-S pair of flows have variations, which are both parts of the torsional oscillations.

The full nature of the torsional oscillations has not been evident because only the east-west component of the velocity vector was part of the variation. Addition of a north-south velocity component as part of the process may help identify the underlying cause. Although surface meridional circulation due to rotation generally originates in the equatorial zone and moves toward the poles, the work by Ulrich (2010), especially Figure 6, showed that there are periods when the flow is toward the equator. That work also showed that there are strong year-to-year changes.

The study by Komm, Howe, and Hill (2018) found some evidence of equatorward motion of the N-S flow. More extensive studies by Komm, Howe, and Hill (2018, 2020) and Getling, Kosovichev, and Zhao (2021) have found variations in the N-S flow in bands that migrate toward the solar equator during the solar cycle. They have correlated the regions on the Sun with magnetic activity with the strength of these N-S flows. There is a general confirmation of the model by Spruit (2003) wherein excess emission in magnetic regions causes cooling and sinking of the matter in magnetized areas. Studies by Komm, Howe, and Hill (2020) and Getling, Kosovichev, and Zhao (2021) have found evidence in support of this model, but there remains the difficulty that the motions are present before there are strong magnetic fields. Our new method of analysis shows that the variations in the E-W and N-S components are closely related throughout the solar cycle.

2 Early Record – Why Starting in 1983?

The digital data record of the 150-foot tower telescope at the Mt. Wilson Observatory begins in 1967, and our project aims to utilize this full record. Solar differential rotation rates have typically been represented by a three term series in \(\sin (\phi )\), where \(\phi \) is the latitude and the lead term is \(A\). Our Equation 1 below is typical. However, the calibration of the \(A\) coefficient was flawed in the years prior to 1983. The calibration of the early observations came from a displacement of the entrance slit a known distance so that a known signal was introduced. This approach, introduced by Babcock (1953) as part of the magnetograph design, involved the controlled displacement of the spectral line from its centered position and the measurement of the resulting artificial signal. Because of variations in the size of the displacement, the calculated calibration coefficients were not stable, thus the determined \(A\) rotation rates and the calibration coefficients are inversely related. While a correction to the \(A\) values can be derived by assuming the calibration coefficient is fixed, the earlier data remain less reliable and we have concentrated on the data obtained after 1983.

3 Initial Reductions of Surface Velocities

3.1 Background

The instrument and measuring system setup and calibration for the Mt. Wilson magnetograph is well described by Howard (1976b), Howard, Boyden, and Labonte (1980) and Howard et al. (1983b); details of the setup and operation of the system can be found in those references. We review some of these details because they influence the results we describe here.

The 150-foot tower system is a digital Babcock (Babcock, 1953) magnetograph. The solar image is fed by a two-mirror coelostat, the first flat mirror compensating for diurnal rotation, while the second flat mirror is controlled by a guiding ring above the focal plane that generates its control signal with four pickups carried on the guiding ring. This control system is described by Howard (1976b). The primary solar image is formed on the plane of the entrance slit to the 75-foot Littrow spectrograph. The guiding system causes the solar image to scan over the entrance slit in a boustrophedonic (back and forth) pattern so that the whole Sun is sampled. The exit slits are the entrance faces of the fiber-optic light pipes which bring the spectral samples to the photomultiplier detectors. As described by Howard et al. (1983b) and discussed below, the signal samples are digitized into four quantities that, together with the position of the stage carrying the photomultipliers, allow the calculation of the Doppler shift and the Zeeman splitting, which in turn gives the magnetic-field strength. The current spectral sampling system is described by Ulrich et al. (1991).

The data from the 150-foot tower project applies to the solar surface yielding magnetic field \(B\), Doppler velocity \(V\), and line intensity \(I\) as functions of heliographic latitude \(\phi \), central meridian angle \(\delta L\), which is the westward angle from the central meridian to the pixel, and time \(t\). An important property of this dataset from the 150-foot tower is its early start date. A complication dealt with in the reduction of this data comes from the fact that observed data is not on a regular grid of spatial position, and the temporal spacing is irregular both within individual observations and between successive observations. Consequently, interpolations are required to produce tables of the observable quantities in regularly spaced grids.

The polarization analysis uses a rapidly oscillating KD*P crystal combined with a Glan–Thompson prism to alternate the state of circular polarization allowed through the spectrograph. The spectral sampling is done by rectangular shaped fiber-optic light pipes whose long dimension entrance windows are along a line of constant wavelength which is roughly perpendicular to the dispersion direction. Paired samples of the spectrum from the red, \(R\), and blue, \(B\), wings of the sampled line are sent to two photomultiplier tubes, whose current strength is digitized yielding values stored in four registers: \(R^{+},R^{-},B^{+},B^{-}\), where the superscript indicates the polarization state. At regular intervals, the sum values are recorded on disk and the registers are cleared. Each data record includes the four sample values, the time along with the location of the servoed stage carrying the sampling rectangles and the position of the servos controlling the position of the solar image. These packets of data are recorded sequentially on a magnetic disk. At the end of the observation, these records get transferred to magnetic tape. These files have a name structure where the letter “M” is followed by YYYYMMDD_HHHH_MM.01, where YYYY is the year, MM is the month, DD is the day, and HHHH_MM is the time. We refer to these as the 01 files.

While the 01 files include all the necessary information, they are in a difficult-to-use format - each data element has a different time, the spacing between the scan lines is not constant, and the elements are not lined up vertically. We address these problem in steps: 1) Each file is converted to an internal format, which we call an MVI file. This file contains three images that are shifted by differential rotation to be at the same time and to compensate for the imperfect guiding system. These shifts produce a rectangular grid. These images show the magnetic, velocity, and intensity variables. 2) For each day, the pixels of the MVI images are shifted at constant latitude using the local rotation rate to a fixed time and averaged together. 3) A set of fits files is created for each average and a text file called VMREC is written. The VMREC file is derived by applying geometric corrections to the background limb shift function (see Section 4), along with first guess differential rotation and meridional circulation laws to yield position-dependent line-of-sight velocity deviation and magnetic field variables as functions of \(x,y\) indicies \(i\), \(j\). Steps to derive an update to the flow functions from the VMREC file are described in the following sections. The MVI files can be retrieved from the data management system JSOC/MDI/HMI at Stanford University.

3.2 Differential Rotation and Meridional Flow

A primary output of the observing program at the 150-foot tower telescope has been the study of the time dependence of the solar surface velocities. The system provides Doppler shifts of the spectral line, which are converted to rotation rate and N-S flow velocity using the spherical trigonometry algorithms from Howard and Harvey (1970). In addition, we modify the sign for the N-S velocity by reversing the sign in the southern hemisphere so a positive value represents flow toward the poles. The largest feature of these velocities is the differential rotation, which has a large east-west component. Flow variability with small amplitude cannot be detected superposed on the differential rotation unless the main pattern is subtracted. This has been done using a polynomial with the coefficients \((A,B,C)\) in the representation

$$ \Omega (\phi ,t) = A(t)+B(t)\sin ^{2}(\phi )+C(t)\sin ^{4}(\phi ) \; \text{ in units of }\mu \,{\mathrm{rad{\,} s^{-1}}}, $$
(1)

where \(\Omega \) is the rotation rate and \(\phi \) is the heliographic latitude. For many years this polynomial was fitted to each observation. This representation is imprecise since there is no expectation that the flow should have this structure. To address this concern while still detecting small and variable structures, we have run the 01 files through a new initial reduction, with the modification that the \(B,C\) pair of coefficients is held fixed. This produces a new archive of MVI files and other products from which we can retrieve the observed flows, but which has a static, first guess differential rotation offset curve subtracted. The curve we have used is:

$$ \Delta \Omega _{0}(\phi )=-0.409999\times [\sin ^{2}(\phi ) + 1.0216295\times \sin ^{4}(\phi )]\; \text{ in units of }\mu \,{\mathrm{rad{\,} s^{-1}}}. $$
(2)

Note that the subtracted quantity is negative, so the rotation rate is increased to become more nearly constant with latitude. The flow remaining after Equation 2 has been applied can be described by either a rotation velocity deviation \(\delta V_{\mathrm{rot}}\) or as an angular rotation rate deviation \(\delta \omega \). The conversion from angular rotation rate deviation to rotation velocity deviation is:

$$ \delta V_{\mathrm{Rot}}(\phi ,t)=\delta \omega (\phi ,t)\times {\mathrm{R}}_{\odot } \cos (\phi )\ . $$
(3)

We use Equation 3 to convert rotation rates or rotation rate deviations to rotation velocities or rotation velocity deviations and vice versa as needed.

We observe the line-of-sight velocity \(V_{\mathrm{los}}\) at each point. Using the geometry described by Howard and Harvey (1970), we convert this velocity to a rotation rate \(\Omega (\phi ,t)\) and a rotation rate deviation:

$$ \delta \omega _{0}(\phi ,t) = \Omega (\phi ,t)-\Delta \Omega _{0}( \phi )\ . $$
(4)

The values of \(\delta \omega _{0}(\phi ,t)\) along with magnetic field strength and line intensity can be read into standard fits files, which we pick to be daily averages with dimension \(256\times 256\) in \(\delta L\) and \(\phi \).

The differential rotation rate offset from Equation 2 was adopted in 1987 and those coefficients do not accurately represent the rotation rate over the full time series. Consequently, we work with a reference rotation rate shown in Equation 5 and we get rotation rate deviations relative to the actual 30-year average in Equation 6

$$ \delta \omega _{\mathrm{ref}}(\phi ) = < \Omega (\phi ,t)>_{\mathrm{average}}- \Delta \Omega _{0}(\phi ), $$
(5)
$$ \delta \omega (\phi ,t) = \delta \omega _{0}(\phi ,t) - \delta \omega _{\mathrm{ref}}(\phi ).\ $$
(6)

In order to recover the rotation rates themselves, we have to use the sum

$$ \Omega (\phi ,t) = \delta \omega (\phi ,t)+\delta \omega _{\mathrm{ref}}( \phi )+\Delta \Omega _{0}(\phi ).\ $$
(7)

The original program reduction yielded the first guess angular rotation rate as in Equation 1, whereas our new reduction yields local line-of-sight velocity deviations relative to the projection of the 30-year average rotation rate. The new rotation velocity deviation is then

$$ \delta V_{\mathrm{rot}}={\frac{{\mathrm{d}}\delta V_{\mathrm{los}}}{{\mathrm{d}}\sin ( \delta L)}}\ . $$
(8)

This equation provides a value of \(\delta V_{\mathrm{rot}}\) for each pixel of the image.

The first guess background meridional flow law adopted at the same time as the differential rotation and is:

$$ V_{\mathrm{mer}}(\phi ,t) = [\cos ({\delta L})\sin (\phi )\cos (B_{0})- \cos (\phi )\sin (B_{0})]\{G\sin (\phi )+H\sin (2\phi )\}, $$
(9)

where \(G=-28.692\,{\mathrm{m\,s}}^{-1}\) and \(H=35.240\,{\mathrm{m\,s}}^{-1}\). The N-S velocity deviation we seek, \(\delta V_{\mathrm{N}\text{-}\mathrm{S}}\), is relative to this function corrected the same way as \(\delta V_{\mathrm{rot}}\). This function was subtracted during the initial reduction and has to be restored now as part of the determination of the 30-year average.

4 New Rotation Rate Algorithm

The method we used previously starts with the initial reduction with the algorithm described by Howard et al. (1983b), which uses pixels from most of the solar disk including those near the limb. The intensity gradient approaching the limb causes scattered light to have a significant effect on the determined rotation law. The amount of scattered light in each solar image is determined by recording intensity values for pixels near but outside the limb. The average from such pixels is used to quantify the scattered light, which, after correlation with the measured rotation rate, allows the derivation of a correction to the rotation rate. For observations with high scattered light, the correction can be large. Our new method avoids the need for this correction.

The scattered light correction is important near the limb due to the steep gradient in intensity as the limb is approached. The position of each pixel is defined by \(\phi \) and \(\delta L\). The new method avoids the steep gradient zone by requiring \(|\sin (\delta L)|<0.85\), which leaves out the near-limb pixels. The heliographic geometry and resolution of the observed Doppler velocities into rotation and meridional circulation were described by Howard and Harvey (1970) and Thompson (2006).

Our task of determining the E-W and N-S flow rates is complicated by another effect known as the limb shift. Due to correlations between vertical velocity and spectral line intensity due to temperature changes, photospheric spectral lines are shifted as a function of the angle the emergent ray makes relative to the local vertical. Both the flow fields and the limb shift contribute to the Doppler shift velocity, \(V_{\mathrm{los}}\), of each pixel, and we wish to isolate only the material flow. We find the limb shift by using an equatorial band 4∘ wide out of the velocity array before the subtraction of the differential rotation. These entries are minimally influenced by the N-S flow and symmetrically influenced by the E-W flow, so we can use this band to derive the limb shift function. The relationship between the limb shift and the E-W and N-S material flows was discussed in detail by Ulrich et al. (1988).

As described in Section 3, the scanning system at the 150-foot tower at Mt. Wilson produces a data file VMREC which gives position indices \(i\) and \(j\) along with daily averages of the line-of-sight component of the rotation velocity deviations, and line-of-sight magnetic-field strength in \(256\times 256\) arrays. Our working quantities are the line-of-sight component of the rotation velocity deviations \(\delta V_{\mathrm{los}}\) and the magnetic fields. We calculate these for the latitude bands 4∘ wide defined below using our new method.

The new method begins by using the latitude \(\phi \) to define bands, each \(4^{\circ}\) wide:

$$ j_{\mathrm{band}} = {\mathrm{Round}}((\phi +82)/4), $$

and collects pixels within each band. We refer to \(j_{\mathrm{band}}\) as the band number. The selected pixels also have \(|\sin (\delta L)|<0.85\). The Doppler shift velocities for each daily observation and each latitude band are then fitted by a quadratic function of \(\sin (\delta L)\) yielding three coefficients \((\alpha ,\beta ,\gamma )\):

$$ V_{los}(\delta L)=\alpha +\beta \sin (\delta L)+\gamma \sin ^{2}( \delta L)\ , $$
(10)

where \(\alpha \) is the daily offset velocity due to the N-S flow, \(\beta \) gives the daily rotation velocity deviation, and \(\gamma \) allows the flexibility to match the other two coefficients. The rotation rate deviation, \(\delta V_{\mathrm{rot}}(\phi ,t)\), is then found from the average of the \(\beta \) values over six Carrington rotations.

Each daily result is influenced by supergranulation noise. The only way to reduce this noise is through averaging. For that reason, we combine the daily results for \(\delta V_{\mathrm{E}\text{-}\mathrm{W}}\) and \(\delta V_{\mathrm{N}\text{-}\mathrm{S}}\) in 6 or 12 Carrington rotation averages. When we use six CR averages, we apply an even-odd filter (0.25, 0.50, 0.25) to the time series to remove the effect of polar tilt from the final series.

As an example, we show in Figure 2 the \(\sin (\delta L)\) dependent points from October 28, 2003 at 20:00 UT with each point value and the fit to Equation 10. This is the same day and latitude band shown in Figure 1. This particular day corresponds to Carrington rotation 2009 with a Carrington longitude of 300∘ and year 2003.8222. The fit coefficients for latitude band 16 for this day are \(\alpha =17.431, \beta =2.874, {\mathrm{\ and\ }} \gamma = -71.142\), all with units of m s−1 since the \(\sin (\delta L)\) factor is dimensionless.

Figure 1
figure 1

This figure shows a sample daily average magnetogram from October 28, 2003. The average is formed by spatial interpolating to a rectangular of dimension \(256\times 256\) in \(\delta L\) and \(\phi \) and temporal shifting of each pixel using differential rotation to the point at 20:00 UT. The pixel positions marked out with an \(X\) are those included in the algorithm for determining the rotation rate. The grid scale causes these pixels to be small, but they can be seen in the enlargement below the main image. These pixels are in latitude band number 16, which covers the range \(20^{\circ }\mathrm{S}<\phi <16^{\circ }\mathrm{S}\). In addition, accepted pixels have \(|\sin (\delta L)|<0.85\) and an absolute magnetic-field strength \(|B|\) less than 30G. In the enlargement, it can be seen that along the lines where the magnetic field changes sign, there are a number of included pixels because the field direction is nearly horizontal. Due to the small number of such pixels and the difficulty of their identification, we have left them in the reduction. Although this figure shows the magnetogram, subject to the field strength limit, the velocities for the shown pixels are extracted at the corresponding points on the Dopplergram.

Full size image
Figure 2
figure 2

This is the sample latitude band shown in Figure 1. Each selected pixel is shown with an \(X\) symbol at its line-of-sight velocity \(V_{\mathrm{los}}\) and sine central meridian angle, \(\sin (\delta L)\). The red line is the quadratic fit to those pixels and the fitting coefficients \(\alpha \) and \(\beta \) are shown by the blue arrows. The value of \(\beta \) is indicated by the very small but non-zero slope of the arrow. The rms variation of both \(\alpha \) and \(\beta \) is about 15 ms−1 overall and the value of \(\beta \) is unusually small in this case. This figure is for a single day of observation, while the quantities used for measurement of the surface flows are averages over six Carrington rotations.

Full size image

5 Data Reduction Steps

The initial step carries out the latitude band fit described in the preceding section for the 7939 days of observation in the record. Each day produces a line of output with 42 entries of \(\alpha \) and \(\beta \). These are combined into a Microsoft Excel file, which is output into two text files, one for the northern hemisphere and one for the southern hemisphere. Entries in these files are Null if fewer than eight points are in the latitude band or if the slope is greater than 100 ms−1.

The time series for each latitude band is cleaned independently using a procedure based on the variance. The variance for each group of 120 points is calculated and a quadratic function of time is fitted to them. The point with the largest absolute deviation from the fit is found and removed, and the variance is recalculated. If this variance has decreased by more than 8%, the point is replaced by the fitted value and next largest deviation is found and removed. The test is repeated until the variance changes by less than 8%. The last deleted point is then restored and the analysis moves to the next group of 120 points. For each latitude band’s time sequence, we have about 50 points out of the 7939 that are removed this way. The points removed, however, would have a strongly adverse effect on the derived velocities if left in. The highest latitude sequences have fewer observations due to the requirement that the velocities stay below 100 ms−1 or due to the failure to have more than eight observations at each accepted latitude and time. The same cleaning process is applied to the N-S flow velocities.

Additionally, the rotation rate as a function of time and latitude is calculated by dividing the rotation velocities by \({\mathrm{R}}_{\odot }\cos (\phi )\). Next, we compute the 30-year averages of the rotation velocities, the rotation rates, and the poleward flow velocities. The 30-year averages of the rotation rates are given in Table 1. The north-south difference in this table is likely of solar origin. The poleward velocity deviations have been treated similarly to the rotation rate deviations, except we have reversed the sign of the N-S velocity and its deviations in the southern hemisphere, so that poleward velocities are positive in both hemispheres. In addition the initial reductions subtracted the final term with \(G\) and \(H\) in Equation 10 of Ulrich et al. (1988) as indicated above in Equation 9. To get the average poleward flow velocity, we have to combine this term and the average offset of the arrays in the archive. This sum, including the sign reversal, is shown in Figure 3.

Figure 3
figure 3

This figure shows the 30-year average of the poleward velocity as a function of latitude. This average is the combination of the offset during the initial reduction and the average of the individual offsets determined with this new method. See the discussion of the sign convention in the text of Section 5. This average does not have error bars because it is used as an offset. Also, the variations during the 30 years come from time dependence, not instrumental errors. An estimate of the measurement uncertainty for the circulation velocity can be obtained from Figure 5, which suggests a value of 0.2 m s−1. That same value can be used for both parts of Figure 4 except for the band parallel to the equator, where the poleward velocity deviations have much larger errors.

Full size image
Table 1 This table gives the angular rotation rate from Equation 7 as a function of latitude band, averaged over the 30 years of this data set. The error of the mean, \(\delta \Omega \) EoM, is also given based on the variance of the data values and the number of points included. To convert these values to nHz, multiply by 1000/(2\(\pi \)) = 159.155.
Full size table

The conversion of the line-of-sight velocity to a poleward flow velocity is based on the assumption that motion is along level surfaces. In fact, the supergranulation can include motion in a radial direction as the material rises or falls through the photosphere. Any radial velocity component then gets divided by \({\mathrm{R}}_{\odot }[\sin (\phi )\cos (B_{0}) - \cos (\phi )\sin (B_{0})]\) which goes to zero along an E-W line through the apparent disk center. The magnification of these radial velocities then produces a significant noise contribution, so that the circulation velocities equatorward of about \(\pm 10^{\circ}\) are not reliable. This is evident in the error plots shown in Figure 5.

6 Rotational and Meridional Flow Maps

The last step in the reduction is the summing of the rotational and poleward velocity deviations for each latitude band into temporal bins of 6 Carrington rotations in duration. For each bin of six Carrington rotations, we obtain 42 values of rotational velocity deviations and 42 values of poleward velocity deviations. Because the time interval for six Carrington rotations is not an even fraction of the year, the x-axis points drift relative to the year.

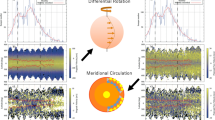
The flow deviation grids can be plotted as flow maps. These maps are shown in Figure 4. The similarity between the patterns of speed-up and slow-down for these two flows is remarkable. The white lines were drawn by eye on the rotational flow map to correspond roughly with the location of the rotational velocity deviation maxima. The lines were then transfered to the poleward velocity deviation map to allow comparison of the spatial-temporal patterns. The combined flow patterns are what constitute the surface pattern of the torsional oscillations. The patterns have greater regularity than has been seen before and the poleward velocity deviation extends to higher latitudes than shown by Getling, Kosovichev, and Zhao (2021).

Figure 4
figure 4

The velocity deviations shown in these two figures have been derived according to the algorithms described in the previous sections. Temporal filtering with a (0.25, 0.5, 0.25) even/odd filter was applied to both maps prior to plotting. The two components, rotational velocity deviations and poleward velocity deviations, together constitute the process known as the torsional oscillations. The dashed white line traces the latitude of the maximum speedup at each time on the rotational velocity deviation map. These line locations are transfered to the same latitudes in the poleward velocity deviation map. For latitudes near 10∘, the time of maximum poleward flow speed in this second map is a year or so after the position of this line, but for most of the plot the times coincide.

Full size image

7 Time Slice Plots – Solar Cycle Dependence

The 2D color plots in Figures 4 and 5 give an overall view of the behavior of the rotational velocity deviation and the poleward velocity deviation. However, the forms of the functions are not readily apparent. There are several shifts in \(\delta V_{\mathrm{pol}}\) occurring at different latitudes, and showing too many curves on a single plot leads to a spiderweb-like result where the consistent features cannot be seen. We have previously noted (Ulrich, Tran, and Boyden, 2022) that \(\delta V_{\mathrm{pol}}\) has a polar reversal indicating upwelling at sunspot minimum. Based on this idea, we have segregated the time slice plots based on the strength and sign of the high latitude poleward velocity deviations. The phase of the solar cycle is well followed with this discriminant.

Figure 5
figure 5

The velocity deviation errors shown in these two figures have been derived along with the six Carrington averages shown in Figure 4. The same temporal filtering as was used in Figure 4 was used on the derived errors. The two components, rotational velocity deviation errors and poleward velocity deviation errors, are also similarly defined.

Full size image

The main source of noise for the resulting six Carrington rotation averages is the supergranulation, which has a lifetime of about a day. The variance of each binned quantity along with the number of days of observation allows an estimate of the error of the mean using Gaussian statistics. This error of the mean is given in Table 1 and is plotted in Figure 5. Note that the colors used for coding the errors of the mean are about a factor of 10 lower than those used to code the velocity deviations. The errors are much smaller than the deviations, except for a band with \(|\phi |<10^{\circ}\), where the radial component of the supergranulation due to rising and falling flows produces a spurious poleward velocity. Surface flows crossing the equator cannot be studied using our algorithm due to this effect. However, for latitudes outside this band, the errors are quite small compared to the determined values. Although the errors increase near the poles, the values of the deviations also increase, so the significance of the measurement remains high. The error is large near 2010 due to the Station fire, which prevented observations for about nine months that year.

Figure 6 shows the time slice plots segregated according to the time within the solar cycle, which picks the selection very well according to the high latitude values of \(V_{\mathrm{pol}}\). The large number of lines prevents showing of error bars which would overlap in many places, creating a confusing plot. Figure 6A is at the times of minimum with the strongest polar outflow. The active region bands near \(15^{\circ}-20^{\circ}\) N-S have equatorial direction flows as well. Figure 6B and Figure 6C are transitioning toward solar maximum with the high latitudes showing poleward flow and the active region bands also developing stronger poleward flow. Figure 6D is after solar maximum, but still has the active region bands flowing poleward, while the high latitudes are still strongly poleward in their flow. Figure 6E and Figure 6F are transitioning to solar minimum, with the high-latitude flow becoming equatorward in Figure 6F. In both of these figures, the active latitude bands are equatorward in their flow. It is worth noting that the time between solar maximum and solar minimum was longer for Cycle 23 than for Cycle 22, yet the dynamics of the poleward flow continued to follow the pattern as minimum was approached in Cycle 23.

Figure 6
figure 6

Time slice plots of \(\delta V_{\mathrm{pol}}\) versus latitude for 12 Carrington rotation averages. To prevent confusing plots, the errors of measurement are not shown, but can be estimated from Figure 5. The curves are color coded and the times of the averages are show on the left, with the characters of the times having the same color as the lines. The times are the start and end for each temporal average. The choice of panel for showing each plot was based on both the high latitude flow value and the active latitude flow value. The spacing started with two lines per panel, but then some lines needed to be moved forward or backward to maintain the most nearly similar shapes.

Full size image

8 Conclusions

This study has yielded poleward flow velocities at latitudes which are much closer to the poles compared to what has been available before. The pattern seen in Figure 3 is consistent with expectations for the meridional flow between latitudes of 15∘ and 60∘. Nearer the equator, the determination is uncertain due to the possible vertical flow, which is interpreted by our formulations as the projection of a flow along a level surface. The strong negative values in Figure 3 are no doubt the result of a subsidence at the equator. Near the poles, the return flow from the time variable circulation currents dominates the observed poleward flow and includes periods when the polar upwelling generates strong equatorward flows. We hope that the new observational results will help the development of a more complete theory of the solar circulation.

The torsional oscillations are well studied and it is well known that the migration of the pattern from high latitudes to the equator requires most of two solar cycles. This study has shown that the poleward flow deviations and the rotational flow deviations are well synchronized during these cycles. The torsional oscillations evidently involve motions in the N-S direction as well as the E-W direction. The high-latitude polar outflow at sunspot minimum found by Ulrich, Tran, and Boyden (2022) extends to a polar inflow at sunspot maximum. The pattern of high-latitude flow deviations is dependent on the phase of the sunspot cycle and can provide a new way of predicting the time remaining before the next sunspot minimum.