1 Introduction

Coronal plasma is optically thin for EUV and X-ray emissions. Coronal structures observed at these wavelengths appear projected onto the plane of the sky. The determination of the three-dimensional (3D) shape of coronal structures is in general not trivial. Structuring, mainly in the form of flux tubes, reflects the topology of the local magnetic field, since the corona is an environment with low plasma-\(\beta \), that is the magnetic pressure dominates over the thermal one.

Coronal loops in active regions outline the local magnetic-field lines and are subject to transverse oscillations, which have been detected in the last decade under different forms of kink motion and damping (Goddard et al., 2016; Pascoe et al., 2016; Nechaeva et al., 2019). Understanding the geometry of coronal loops is important for various reasons: e.g. better determination of the magnetic-field structure, a more reliable discrimination between horizontal or vertical polarisation. Coronal loops, which can be approximated by the field of a virtual point-like dipole below the solar surface, can be considered as a simple circular or elliptical shape. For example, the magnetic-field lines of a dipole are plotted in Figure 1, and two horizontal dotted lines mark the hypothetical position of the photosphere. Above these lines, the curves may appear at a first approximation as circular or elliptic sections. Such a representation for coronal loops is certainly idealized. The magnetic field in the solar corona is non-potential: current flows affect the structure of the magnetic field and can twist loops and make them non-planar. Finding the shape of coronal loop is extremely relevant in the context of coronal seismology. Strong uncertainties in the loop length inevitably affect the estimate of the phase speed of a certain observed MHD wave mode.

Figure 1
figure 1

Example of magnetic-field lines (continuous lines) from a dipole located at the origin, whose magnetic axis is directed perpendicular to the plane defined by the \(x\)- and \(z\)-axes. Length is given in arbitrary units. The dotted lines at \(z=0.5, 1.0\) represent the hypothetical photospheric level. Some field lines emerging from the photosphere can approximately be represented by an ellipse or a semi-circle (coloured dashed lines).

Full size image

The reconstruction of loops or any other solar feature requires at least two distinct points of observations located in space in order to retrieve the position of a feature by geometric triangulation. When only one point of observation was available, as in the 1990s with the Solar and Heliospheric Observatory (SOHO), the technique of dynamic stereoscopy (Aschwanden et al., 1999) was adopted. The launch of the twin Solar TErrestrial RElations Observatory (STEREO) spacecraft in 2006 has permitted taking advantage of two simultaneous points of observations. Stereoscopy is used for retrieving information on the position of a structure in 3D space. The principles of stereoscopy and their relevance to the reconstruction of coronal loops are described in the context of the STEREO mission (which consists of two identical spacecraft observing the Sun) by Inhester (2006). Furthermore, different tools were developed for performing triangulation of corona features, e.g. scc_measure.pro or sunloop.pro, available in the SolarSoftWare (SSW) and written in the IDL language. On the other hand, analysis of scientific data in Python has recently caught the interest of the community and a distribution of software package devoted to the analysis of solar data named Sunpy has been released (Barnes et al., 2020). A package dedicated to 3D reconstruction seems to be missing.

In this work, we aim at presenting a first version of a tool for geometric triangulation developed in Python and fitting the geometry of coronal loops and other features by using the technique of principal component analysis (PCA). By the method of PCA, coronal loops are modelled and fitted to a planar section of a circle or an ellipse. Section 2 presents the concept of geometric triangulation and the Python routines, Section 3 presents the curve-fitting technique with the principal component analysis, and Section 4 lists some examples of applications and analysis of the 3D geometry of some coronal features. A discussion and conclusions are given in Section 5.

2 Geometric Triangulation

We developed a graphic tool in Python, triangulate.py, which allows for a user to perform geometric triangulation of solar features as an alternative to the IDL routine scc_measure.pro in SSW. The principles of geometric triangulation applied to simultaneous observations of a coronal structure are given by Inhester (2006). Aschwanden et al. (2008) applied geometric triangulation to reconstruct the profile of coronal loops observed with STEREO-A and -B by the Extreme UltraViolet Imager (EUVI), describing in detail all the necessary steps to apply to data for performing triangulation (e.g. rotation of the solar images to the same axis, scaling to the same pixel resolution). The tool written in the Python language is not a mere copy and translation from IDL of the algorithm scc_measure.pro, but a simple imitation of the basic operative steps based on the principles of epipolar geometry. We provide a description of these steps as follows.

First of all, we fixed the reference frame in which we want to express the 3D coordinates of a feature of interest, that is Heliocentric Earth EQuatorial (HEEQ) coordinates: the \(\hat{z}\)-axis is directed along the solar North rotation axis, the \(\hat{x}\)-axis points towards the intersection between the solar Equator and the central meridian as seen from Earth, and the third axis is found as \(\hat{\boldsymbol {y}} = \hat{\boldsymbol {z}} \times \hat{\boldsymbol {x}}\). Let OBS-1 refer to an arbitrary observer. We define a heliocentric reference frame for OBS-1 with the Cartesian axes defined as follows (we use upper case letters for the axes to distinguish them from the HEEQ coordinate system): the \(\hat{Z}_{1}\)-axis points from the Sun’s centre to OBS-1, the \(\hat{Y}_{1}\)-axis is perpendicular to \(\hat{Z}_{1}\) and in a plane containing both the \(\hat{Z}_{1}\) and the solar rotation axis. The \(\hat{X}_{1}\)-axis is perpendicular to \(\hat{Z}_{1}\) and \(\hat{Y}_{1}\) pointing towards solar West. When we identify a feature in a solar image, for example in the image given by OBS-1 in Figure 2, we get its helio-projective coordinates (HPC) in angular units, e.g. \(\zeta _{1}\) and \(\eta _{1}\). Given the HPC coordinates, we can trace the line-of-sight (LoS) in the heliocentric coordinate system relative to the observer \((\hat{X}_{1}, \hat{Y}_{1}, \hat{Z}_{1})\) and having the coordinates of the LoS \(X_{1}\) and \(Y_{1}\) as a function of \(Z_{1}\):

$$\begin{aligned} X_{1} = & {(d_{1} - Z_{1}) \tan \zeta _{1}} \end{aligned}$$
(1)
$$\begin{aligned} Y_{1} = & {(d_{1} - Z_{1}) \tan \eta _{1}} \end{aligned}$$
(2)

with \(d_{1}\) the distance of the observer from the Sun. \(Z_{1}\) moves along the Sun–observer line with the positive orientation towards the observer, and can range within a reasonable interval of values, for example \([-2~\mathrm{R_{\odot}}, 2~\mathrm{R_{\odot}}]\). We used 1001 points to define the LoS in OBS-1. Then we convert these points from the observer-oriented reference frame for OBS-1 to the HEEQ coordinate system (points of coordinates (\(x_{\mathrm{LOS}}, y_{\mathrm{LOS}}, z_{\mathrm{LOS}}\))). The conversion consists of a double rotation of the observer-oriented reference frame to the HEEQ one. This can be achieved by the following matrix operation:

$$ \begin{bmatrix} x_{\mathrm{LoS}} \\ y_{\mathrm{LoS}} \\ z_{\mathrm{LoS}} \end{bmatrix} = \mathbf{M}(\phi _{1}) \mathbf{M}(\theta _{1}) \begin{bmatrix} {X_{1}} \\ {Y_{1}} \\ {Z_{1}} \end{bmatrix} , $$
(3)

with

$$ \mathbf{M}(\theta _{1}) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta _{1} & \sin \theta _{1} \\ 0 & -\sin \theta _{1} & \cos \theta _{1} \end{bmatrix} $$
(4)

and

$$ \mathbf{M}(\phi _{1}) = \begin{bmatrix} -\sin \phi _{1} & 0 & \cos \phi _{1} \\ \cos \phi _{1} & 0 & \sin \phi _{1} \\ 0 & 1 & 0 \end{bmatrix} $$
(5)

with \(\theta _{1}\) and \(\phi _{1}\) the latitude and longitude of OBS-1 in the HEEQ reference frame, respectively.

Figure 2
figure 2

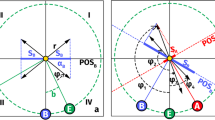
Scheme showing the principle of triangulation with two observers 1 (left panels) and 2 (right panels). Top: The axes in black mark the HEEQ coordinate system. The red and blue axes identify the heliocentric reference frames of OBS-1 and OBS2, respectively. A feature of interest is located in the 3D space (green dot) having HEEQ coordinates \((x_{P},y_{P},z_{P})\). The projections onto the PoS of the observer result in HPC coordinates \((\zeta _{1}, \eta _{1})\) and \((\zeta _{2}, \eta _{2})\), respectively. The PoS, according to the locations of the observers, in general lies out of the solar-rotation axis (\(\hat{z}\)-axis). Bottom panels: view of the PoSs of the two observers perpendicularly to the observer–Sun line (continuous line). The resulting vertical image axis for OBS-1 is aligned with the projection of the solar-rotation axis \(\hat{z}\), whilst for OBS-2 it is tilted a few degrees.

Full size image

Now, it is necessary to define where the LoS from OBS-1 crosses the solar feature under interest. For this we use the second view, that from OBS-2. The LoS is deprojected into the field of view of OBS-2 by converting its points, expressed in HEEQ coordinates, into the heliocentric reference frame for OBS-2. We use the inverse of Equation 3, that is:

$$ \begin{bmatrix} X_{2} \\ Y_{2} \\ Z_{2} \end{bmatrix} = \mathbf{M}(\theta _{2})^{-1} \mathbf{M}(\phi _{2})^{-1} \begin{bmatrix} x_{\mathrm{LoS}} \\ y_{\mathrm{LoS}} \\ z_{\mathrm{LoS}} \end{bmatrix} , $$
(6)

with \(\theta _{2}\) and \(\phi _{2}\) the HEEQ latitude and longitude of OBS-2. Once the LoS has been de-projected into HPC coordinates \((\gamma , \delta )\) in the FoV of OBS-2, the choice of the second point is constrained at the location where the LoS crosses the solar feature under interest. The procedure to triangulate the selected points and compute the 3D coordinates \((x_{P} , y_{P} , z_{P} )\) is illustrated in Figure 3.

Figure 3
figure 3

Scheme showing the LoS from an observer de-projected into the FoV of the other one. The LoS is defined by a grid of equispaced points between \([-2~\mathrm{R_{\odot}}, 2~\mathrm{R_{\odot}}]\). The distances and proportions here have been exaggerated in order to illustrate the procedure for determining the 3D heliocentric coordinates. Following the LoS, the user selects a point of coordinates \((\zeta _{2}, \eta _{2})\). This will not lie on the LoS, but it is between the two closest points \((\gamma _{A}, \delta _{A})\) and \((\gamma _{B}, \delta _{B})\). Given these, a projection of \((\zeta _{2}, \eta _{2})\) on the LoS is determinated \((\zeta _{2}', \eta _{2}')\) and a normalised distance \(\epsilon \) is computed. This factor \(\epsilon \) will then be used to determine the 3D Cartesian coordinates of the point by Equations 8, 9, 10.

Full size image

The de-projected LoS in OBS-2 is defined on a discrete sequence of points (the black dots along the continuous line in Figure 3) (proportions are exaggerated to better present the procedure). When we select the point where the de-projected LoS crosses, the loop is manually located in the image as \((\zeta _{2}, \eta _{2})\). It may well miss the de-projected LoS by a small amount and we therefore project the manual tie-point onto the deprojected LoS (epipolar line) to obtain \((\zeta '_{2}, \eta '_{2})\), which will fall between the LoS points \((\gamma_{A}, \delta_{a})\) and \((\gamma_{B}, \delta_{B})\). The distance between \((\zeta _{2}, \eta _{2})\) and \((\zeta '_{2}, \eta '_{2})\) in the figure is exaggerated for clarity. Having these coordinates we can calculate the distance \(\epsilon \) from \((\gamma _{A}, \delta _{A})\) and express it as a fraction of the interval size where \((\zeta _{2}', \eta _{2}')\) falls, i.e.

$$ \epsilon = \frac{\sqrt{(\zeta _{2}' - \gamma _{A})^{2} + (\eta _{2}' - \delta _{A})^{2}}}{\sqrt{(\gamma _{B} - \gamma _{A})^{2} + (\delta _{B} - \delta _{A})^{2}}}. $$
(7)

The Cartesian triplet in HEEQ is then computed by assuming linearity when projecting the 3D LoS in the FoV of OBS-2. Specifically, having the 3D points \((x_{\mathrm{LoS},A}, y_{\mathrm{LoS},A}, z_{\mathrm{LoS},A})\) and \((x_{\mathrm{LoS},B}, y_{\mathrm{LoS},B}, z_{\mathrm{LoS},B})\) associated with the HPC points \((\gamma _{A}, \delta _{A})\) and \((\gamma _{B}, \delta _{B})\), we can find:

$$\begin{aligned} x_{P} = & \epsilon (x_{\mathrm{LoS},B} - x_{\mathrm{LoS},A}) + x_{ \mathrm{LoS},A}, \end{aligned}$$
(8)
$$\begin{aligned} y_{P} = & \epsilon (y_{\mathrm{LoS},B} - y_{\mathrm{LoS},A}) + y_{ \mathrm{LoS},A}, \end{aligned}$$
(9)
$$\begin{aligned} z_{P} = & \epsilon (z_{\mathrm{LoS},B} - z_{\mathrm{LoS},A}) + z_{ \mathrm{LoS},A}. \end{aligned}$$
(10)

The triangulation procedure is analogous if the user inverts the observers, i.e. if they choose first a point in OBS-2 and then selects the second point along the LoS traced in the FoV of OBS-1.

3 Curve Fitting: Principal Component Analysis

After the user has collected an ensemble of data points sampling the shape of a coronal structure, for example a coronal loop, the next step is finding the best curve that fits the data. We adopt the principal component analysis (PCA), whose theoretical basis and applications are described in detail by Nisticò, Verwichte, and Nakariakov (2013). In this section, we give a summary of how to apply the technique and run it in Python. A Python module has been developed named stereoscopy.py, containing a set of functions aiming at performing the PCA computation and at plotting the results for the different projections.

3.1 The Principal Component Analysis

The PCA reduces the correlation in the data and returns the basic information. This is achieved by diagonalising the covariance matrix built from a set of data points. From a geometrical point of view, applying the PCA to an ensemble of points sampling for example a loop in a 3D heliocentric reference frame means to transform them into a natural coordinate system for the loop itself, which would be represented by the loop plane and the major and minor radii that determine the profile (circular or elliptical). On the other hand, PCA can be also applied to 1D features, such as streamers of jets. For better clarity, we provide a summary of the PCA technique in the case of a set of \({(x_{\mathrm{P},i}, y_{\mathrm{P},i}, z_{\mathrm{P},i})}\) coordinates defining a certain coronal loop. Before constructing the covariance matrix \(\mathbf{C}\), it is advised to refer the points to a midpoint \((x_{\mathrm{M}}, y_{\mathrm{M}}, z_{\mathrm{M}})\), which is determined as the half distance between the loop footpoints. After the definition of the midpoint, the relative coordinates are computed:

$$\begin{aligned} x_{i} = {x_{{P},i}} - x_{{M}} , \end{aligned}$$
(11)
$$\begin{aligned} y_{i} = {y_{{P},i}} - y_{{M}} , \end{aligned}$$
(12)
$$\begin{aligned} z_{i} = {z_{{P},i}} - z_{{M}} . \end{aligned}$$
(13)

This operation is equivalent to translating the heliocentric reference frame from the Sun’s centre to the loop midpoint. The covariance matrix is defined as

$$ \mathbf{C} = \frac{1}{N} \begin{bmatrix} \sum _{i=1}^{N} x^{2}_{i} & \sum _{i=1}^{N} x_{i} y_{i} & \sum _{i=1}^{N} x_{i} z_{i} \\ \sum _{i=1}^{N} x_{i} y_{i} & \sum _{i=1}^{N} y_{i}^{2} & \sum _{i=1}^{N} y_{i} z_{i} \\ \sum _{i=1}^{N} x_{i} z_{i} & \sum _{i=1}^{N} y_{i} z_{i} & \sum _{i=1}^{N} z_{i}^{2} \end{bmatrix} $$
(14)

and then diagonalised in order to maximise the variances (i.e. the elements on the diagonal) and minimise the elements off the diagonal by solving the associated eigenvalue problem: \(\mathrm{det}|\mathbf{C} - \lambda \mathbf{I}| = 0\). The eigenvalues and the corresponding eigenvectors are computed in Python with the function eig of the Numpy library (Harris et al., 2020). Once computed, the eigenvalues are sorted in ascending order. We name each eigenvalue \(\lambda _{n}\), \(\lambda _{a}\), \(\lambda _{b}\) and the corresponding eigenvectors: \(\boldsymbol{e}_{n}\), \(\boldsymbol{e}_{a}\), \(\boldsymbol{e}_{b}\). The result of diagonalisation can lead to different geometrical interpretations or models, according with the values of the eigenvalues that are obtained. In general, the eigenvectors have a precise geometrical meaning and represent the axes where the variances of the dataset are maximised. From a geometric point of view, the eigenvectors represent the axes of an ellipsoid, which can be reduced to a planar or linear distribution of points, depending on the largest values taken by the eigenvalues.

For example, in the case of curvi-linear and planar features, such as coronal loops, one dimension associated to the smallest eigenvalue [\(\lambda _{n}\)] is negligible with respect to the others. The eigenvector \(\boldsymbol{e}_{n}\) represents the vector normal to the loop plane, while the others two eigenvectors \(\boldsymbol{e}_{a}\) and \(\boldsymbol{e}_{b}\) identify the vectors along the minor and major radii of the loop, which have values \(r_{a} = \sqrt{2 \lambda _{a}}\) and \(r_{b} = \sqrt{2 \lambda _{b}}\). The dataset can be re-projected onto a new reference frame, which is rotated with respect to the original translated heliocentric reference frame. Such a re-projection consists in a coordinate transformation, whose matrix is defined by the components of the eigenvectors.

On the other hand, in the case of a quasi-straight-line data point distributions, PCA will result in only one large eigenvalue. The associated eigenvector will simply indicate the direction, in which the points are distributed in the original coordinate system. Some examples are given in the next sections.

4 Applications and Data Analysis

We apply the PCA fitting method to some observations. We focus on three observations as follows: a coronal loop observed in a quiet-Sun region on 21 January, 2013 and already studied by Nisticò, Verwichte, and Nakariakov (2013), Nisticò, Anfinogentov, and Nakariakov (2014), and Duckenfield et al. (2018) (Observation No. 1); some loops in the active region observed on 13 February, 2011, and listed in the catalog of Nechaeva et al. (2019) (Observation No. 2); a coronal jet (Observation No. 3) listed in the catalog from Nisticò et al. (2009). The principal component analysis results are presented in Table 1.

Table 1 Midpoint coordinates in the HEEQ coordinate system, the eigenvalues from PCA, and the minor and major axes \(r_{a}\) and \(r_{b}\) for data points sampling the coronal features. All values are reported in units of \(\mathrm{R}_{\odot}\).
Full size table

4.1 Observation No. 1

The 3D shape of the coronal loop has already been discussed by Nisticò, Verwichte, and Nakariakov (2013). It represents a good target for testing the Python script triangulate.py and comparing the outputs with the SSW routine scc_measure.pro. The loop is found in a quiet region and is made of several finer threads, which experience transverse oscillation. The loop was also studied by Duckenfield et al. (2018), who found the presence of multiple harmonics in the oscillations. In Figure 4 we present a one-time snapshot of the observations. The top panel of Figure 4 shows the graphical interface of the triangulate.py tool. It consists of two windows showing the region with the loop of interest as seen from the Atmospheric Imaging Assembly (AIA) of the Solar Dynamics Observatory (SDO) (left) and the Extreme UltraViolet Imager (EUVI) of STEREO-A (right). To increase the appearance of the loop in the FoV of the instruments, we subtracted from the images those taken five minutes before (because of the cadence of STEREO/EUVI). The graphical interface presents some buttons that can be used for interacting with the images and enable to activate the cursor of the mouse, picking a point (for example, the red point in the AIA FoV), and drawing the line-of-sight in the other FoV (the associated line-of-sight in white in the EUVI FoV). More details are provided in the Appendix. The ensemble of 3D points sampling the coronal loop is shown in the middle panels for three different orientation of the HEEQ coordinate system: in red, points obtained from the Python tool, in blue, those found with the SSW/IDL routine scc_measure.pro. Both distributions lie along the same path, indicating that the Python tool works well and returns similar results. The red dots are fitted by the PCA. First, the points are refered to a midpoint, which ideally lies on the loop base line. Since the loop is sampled for its entirety, we calculated the midpoint as the half distance of the two extreme points at the loop footpoints. The best-fitting curve is plotted as a red-dashed line, and it is found in the local reference frame of the loop after having determined the principal components. The blue and red arrows represent the axes of the ellipse: in blue the major and in red the minor radii. The green arrow represents the normal to the loop plane. The coronal loop in the local reference frame is plotted in the bottom panel of Figure 4. The best curve is found as:

$$\begin{aligned} x_{l} = & r_{a} \cos \theta , \end{aligned}$$
(15)
$$\begin{aligned} y_{l} = & r_{b} \sin \theta , \end{aligned}$$
(16)
$$\begin{aligned} z_{l} = & 0 \end{aligned}$$
(17)

with \(\theta =[0,2\pi ]\), and \((x_{l}, y_{l}, z_{l})\) coordinates of the points in the local reference frame. The best-fitting curve can be referred to the HEEQ reference frame by a simple change of basis and spatial translation as follows:

$$ \begin{bmatrix} x_{h} \\ y_{h} \\ z_{h} \end{bmatrix} = \mathbf{M}(\boldsymbol{e}_{n}, \boldsymbol{e}_{a}, \boldsymbol{e}_{b}) \begin{bmatrix} x_{l} \\ y_{l} \\ z_{l} \end{bmatrix} + \begin{bmatrix} x_{M} \\ y_{M} \\ z_{M} \end{bmatrix} , $$
(18)

with \((x_{M}, y_{M}, z_{M})\) being the midpoint coordinates and the change of basis matrix defined as (please note the that components of the eigenvectors are in the HEEQ reference frame):

$$ \mathbf{M}(\boldsymbol{e}_{n}, \boldsymbol{e}_{a}, \boldsymbol{e}_{b}) = \begin{bmatrix} e_{a,x} & e_{b,x} & e_{n,x} \\ e_{a,y} & e_{b,y} & e_{n,y} \\ e_{a,z} & e_{b,z} & e_{n,z} \end{bmatrix} $$
(19)
Figure 4
figure 4

Analysis of Observation No. 1. Top: SDO/AIA (left) and STEREO/EUVI-A FoVs containing the observed coronal loop. Middle: data points sampling the shape of the coronal loop from the triangulate.py tool (in red) and from the scc_measure.pro procedure (in blue). The PCA is applied only to the red points. The eigenvectors are plotted in different colours. The dashed red line is the fitting curve. Bottom panels: the data points sampling the loop in the local reference frame. The continuous red line is the fitting curve.

Full size image

4.2 Observations No. 2

The active region under interest was observed face-on from SDO/AIA and side-viewed from STEREO/EUVI-A (Figure 5) and was the site of a flare that triggered kink oscillations (Nechaeva et al., 2019). The loops of the active regions overlap in some parts. In general, the triangulation procedure is efficient when the same structure is clearly distinguishable by both observers, which in this case may be particularly difficult. The entire path of the loops is seen in the SDO/AIA perspective, while in STEREO/EUVI-A the loops are so squashed that it is difficult to clarify which leg lies in front of the other. However, by drawing the LoS of one observer onto the other, one could in principle guess the orientation of the loop and its height. For this case, a technique described by Verwichte, Foullon, and Van Doorsselaere (2010) would be more suitable considering the perspectives of the active regions from the observers. In any case, we applied the triangulation tool in order to retrieve the geometry of the large loop observed in the North of the active region. To increase the appearance of the loops, we processed the images by adopting a high-pass filtered image, which was obtained by subtracting from the normal intensity image the Gaussian smoothed one with \(\sigma = 2.0 \) pixels.

Figure 5
figure 5

Analysis of Observation No. 2. Top: high-pass filtered images for the active region observed by SDO/AIA 193 (left) and STEREO/SECCHI/EUVI 195 (right). The tie-points are given in red and are numbered from 0 to 8, in order to associate the corresponding loop legs in both the FoV. The fitting loop from PCA is overplotted in blue. The loop footpoints are given as green triangles. In the left panel, the solar limb as viewed by STEREO is overplotted in red. Middle: 3D reconstructed loop in three different projection in the HEEQ coordinate system. Bottom: reconstructed loop in the local reference frame.

Full size image

The loop is marked by a series of tie-points that were collected with the triangulate.py routine (Figure 5). When collecting the points, we identified the right loop leg viewed by SDO/AIA with the upper one in STEREO/EUVI-A. However, since the epipolar line drawn from the SDO FoV crosses both the legs of the loop in the STEREO-A image, the ambiguity about the location of the legs is still present. Therefore, we performed a second triangulation by reversing the position of the loop legs (Figure 6).

Figure 6
figure 6

Analysis of Observation No. 2, but with a reverse orientation of the loop legs, with respect to what was shown in Figure 5. Top: high-pass filtered images for the active region observed by SDO/AIA 193 (left) and STEREO/SECCHI/EUVI 195 (right). The 3D tie-points are given as red dots and number from 0 to 8. The fitting loop from PCA is overplotted in blue. The loop footpoints are given as green triangles. In the left panel, the solar limb as viewed by STEREO is overplotted in red. Middle: 3D reconstructed loop in three different projections in the HEEQ coordinate system. Bottom: reconstructed loop in the local reference frame.

Full size image

In both cases, we collected nine tie-points which sample the loop profiles. Each tie point is highlighted with a number in Figure 5 and 6, which help with the association of the loop legs observed with AIA and EUVI-A. The loop footpoints are only visible in the AIA FoV, and their identification also becomes difficult because of the presence of many overlapping loop threads. We got the coordinates in the helioprojective coordinate system: the eastern footpoint was chosen with coordinates (\(-80, -194\)) arcsec, while the western one having coordinates (\(9, -194\)) arcsec. The heliocentric position of the midpoint is determined by a simple average of the two footpoints coordinates and is given in Table 1. The PCA works well with a few points, and a nice elliptical shape is found in both cases, with the major radius of the ellipse about 2.5 times greater than the minor radius. However, the ambiguity about which reconstruction fits the loops is not solved. The 3D-reconstructed loops differs only in the orientation, determined by the azimuthal angle formed by the footpoint baseline. Furthermore, in both cases the footpoints of the reconstructed loops deviate from the locations were chosen, and which are plotted as green triangles in Figures 5 and 6. This particular case shows how geometric triangulation results can be difficult and the removal of any ambiguity in the loop shape can be tackled by adopting automatic tracing methods (Aschwanden, De Pontieu, and Katrukha, 2013; Gary, Hu, and Lee, 2014).

4.3 Observations No. 3

In this example, we demonstrate how to apply the principal component analysis to coronal features that are not curved, like coronal loops, but different such as coronal jets, which appear as narrow ejections of plasma. We can triangulate the shape of the jet with a series of points sampling its entire length. The advantage in using the PCA relies on the possibility to infer the direction of propagation of the ejected plasma. Indeed, since a coronal jet is a collimated column of plasma, the PCA applied to an ensemble of tie-points should return as usual three eigenvectors, but two of them, which are associated with very small eigenvalues, are representative of the cross-section of the jet; the third one, associated with the largest eigenvalue, defines the direction of propagation (i.e. the direction where there is the largest spread of the data points). In a more general context, 3D reconstruction of jets is useful for recovering the 3D kinematics (Patsourakos et al., 2008) or for understanding the eventual deflection due to magnetic field (Nisticò et al., 2015).

In the following case, we carried out geometric triangulation for a jet observed by STEREO and listed in the catalogue of Nisticò et al. (2009). The top panel of Figure 7 presents the jets as seen in the 171 Å channels of EUVI-B (left) and EUVI-A (right). We used normal intensity images: there was no need to apply any filtering since the jet emission was clearly seen. The red plus points are those determined with triangulate.py and sample the entire visible length of the jet. A further point is shown at the eastern leg of the jet base in STEREO-B and the associated LoS in STEREO-A for demonstrative purpose.

Figure 7
figure 7

Top: triangulate.py graphical interface for the coronal jet observed with STEREO. Bottom: the 3D points in the different orientations of the HEEQ coordinate system.

Full size image

Before applying the PCA, we subtract the coordinates of a reference point, which is located at almost half the height of the jet, from the data. The PCA returns an eigenvector (the blue arrow in the bottom panels of Figure 7) directed in the same way as the points are distributed (given in magenta colour). The length of the eigenvector in green is intentionally exaggerated and does not reflect the true length determined by the corresponding eigenvalue. The direction of propagation of the jet can be compared to the radial direction. By considering a radial unit vector \(\hat{\boldsymbol{e}}_{r}\) from the midpoint of the data point distribution, we found that the angle formed with respect to the unit vector \(\hat{\boldsymbol{e}}_{b}\) is about 178.5 deg. The vector \(\hat{\boldsymbol{e}}_{b}\) is directed oppositely to the direction of the ejected plasma, hence the plasma jet moves almost radially away. It is worthwhile to mention some wiggles in the distribution of the data points as seen in the middle panels. Such a wiggle is not seen in the images (at the time of the observations, because of the small angle separation between the spacecraft, the plane-of-sky of the observers is close to that of the plane Y–Z of the HEEQ reference frame). The wavy shape is probably due to the uncertainties in picking the points that sample the jet. However, future analysis of other events may relate the wave-like structure of a jet to transverse oscillations, as already found in some jet observations (Cirtain et al., 2007) and theoretically described by Vasheghani Farahani et al. (2009). 3D reconstruction as a function of time will give more details on the evolution of kink oscillations in coronal jets.

5 Discussion and Conclusions

In this work, we present a graphic tool coded in Python named triangulate.py that allows performing geometric triangulation of coronal features observed from two different vantage points. The concept of the tool is equivalent to that of the SSW/IDL routine scc_measure.pro, based on manual tie-point reconstruction. The main purpose is to provide a software for non-IDL users, who mainly work with Python and the SunPy package for the analysis of solar image data. Furthermore, following Nisticò, Verwichte, and Nakariakov (2013), we have also defined some functions in Python, collected in a module stereoscopy.py, for i) performing the principal components analysis of a set of 3D coordinates sampling a certain coronal feature, and ii) plotting the reconstructed shape into different projections of the HEEQ coordinate system. We present the results of applying the triangulation routine to different observational targets: two coronal loops (Observations No. 1 and 2) and one jet (Observation No. 3). In Observation No. 1, we compared the outputs of the Python program triangulate.py with the SSW/IDL routine scc_measure.pro. Both algorithms give very similar results.

The PCA method is adopted for recovering the 3D shape of coronal structure. The tie-points that are sampled with triangulate.py form a cloud of points. The PCA defines a reference frame for which the cross correlations of the data-point components vanish. Three positive eigenvalues of different values are obtained from the covariance matrix of the tie points. In the case when one eigenvalue dominates all others, we have a nearly linear shape of the point cloud. In this case, the root mean square of the fitting can be represented by

$$ \sigma _{\mathrm{fit}} = \sqrt{\lambda _{n} + \lambda _{a}}, $$

which is the distance of the points from the line along the eigenvector \({\boldsymbol{e}}_{b}\). In the case when two eigenvalues dominate the smallest \(\lambda _{n}\), the cloud is distributed near a plane. Then \(\lambda _{n}\) is just the root-mean-square distance of the data points from the plane. We now interpret the two largest eigenvalue, \(\lambda _{a}\) and \(\lambda _{b}\), as the radii of the loop ellipse (or a circle in the case \(\lambda _{a} = \lambda _{b}\)). The loop shape is well reconstructed if the data points are distributed more or less regularly along the entire loop profile (Observation No. 1 is an example for such a case). The uncertainties associated with the eigenvectors and eigenvalues from the PCA are not straightforward to determine. Sonnerup and Scheible (1998) in the context of minimum and variance analysis of magnetic-field measurements (equivalent to the PCA) provide three different methods for evaluating uncertainties of the principal components, including the possibility of bootstrap techniques. When tracing coronal features, a major source of error is associated with the correct identification of the same structure in both the perspectives. In addition, the correct determination of the loop footpoints (hence the associated centre of the loop or midpoints) contributes to the goodness of the fit (for example, Observation No. 2). For simplicity, we propose that the uncertainties of the loop radii \(r_{a}\) and \(r_{b}\) are determined by the distance of the data point from the ellipse along the radial direction, i.e.:

$$ \sigma _{r_{a}} = \sqrt{ \frac{\sum _{i} (x_{i} - r_{a} \cos \theta _{i})^{2}}{N}} $$

with \(\cos \theta _{i} = x_{i}/\sqrt{x_{i}^{2}+y_{i}^{2}}\), and

$$ \sigma _{r_{b}} = \sqrt{ \frac{\sum _{i}(y_{i} - r_{b} \sin \theta _{i})^{2}}{N}}, $$

with \(\sin \theta _{i} = y_{i}/\sqrt{x_{i}^{2}+y_{i}^{2}}\). The values of the uncertainties are reported in Table 1 for Observations No. 1 and 2.

Observation No. 2 is an example where the interpretation of two largest eigenvalues as the radii of the loop ellipse does not work optimally because the data points do not cover the entire loop profile. This leads to an overestimation of the major axis of the loop. In such a case, the data points projected into the plane normal to \({\boldsymbol{e}}_{n}\) may be better fitted directly to an ellipse; e.g. the least-square-fit proposed by Gander, Golub, and Strebel (1994) may then yield an elliptic loop shape with a smaller distance to the data points.

Three-dimensional reconstruction of coronal structures plays a relevant aspect with the recently launched Parker Solar Probe (PSP) and Solar Orbiter. The Wide-Field Imager (WISPR) instrument onboard PSP acquires off-Sun-centred observations in white light of the solar corona and inner heliosphere (Vourlidas et al., 2016). The problem of geometric triangulation with WISPR was presented by Liewer et al. (2019) and Nisticò et al. (2020). Remote-sensing instruments onboard Solar Orbiter such as the Metis coronagraph (Antonucci et al., 2020), the Extreme Ultraviolet Imager (EUI: Rochus et al., 2020), and the Heliospheric Imager (Howard et al., 2020) observe both in white light and ultra-violet wavelengths. For example, multi-instrument observations are fundamental for understanding the 3D evolution of coronal mass ejections. PCA could be helpful for retrieving the symmetry axes of CMEs that can be modelled as ellipsoids. In addition, Zhukov et al. (2021) have used geometric triangulation with SDO/AIA and the Solar Orbiter/EUI data to estimate the height of coronal EUV brightenings, also called as campfires.