Corrugation Instability of a Coronal Arcade

Abstract

We analyse the behaviour of linear magnetohydrodynamic perturbations of a coronal arcade modelled by a half-cylinder with an azimuthal magnetic field and non-uniform radial profiles of the plasma pressure, temperature, and the field. Attention is paid to the perturbations with short longitudinal (in the direction along the arcade) wavelengths. The radial structure of the perturbations, either oscillatory or evanescent, is prescribed by the radial profiles of the equilibrium quantities. Conditions for the corrugation instability of the arcade are determined. It is established that the instability growth rate increases with decreases in the longitudinal wavelength and the radial wave number. In the unstable mode, the radial perturbations of the magnetic field are stronger than the longitudinal perturbations, creating an almost circularly corrugated rippling of the arcade in the longitudinal direction. For coronal conditions, the growth time of the instability is shorter than one minute, decreasing with an increase in the temperature. Implications of the developed theory for the dynamics of coronal active regions are discussed.

1 Introduction

Arcades of plasma loops are a typical feature of solar coronal active regions. Examples of coronal arcades are sets of postflare loops in two-ribbon flares and closed magnetic configurations overlying eruptive magnetic ropes. Arcades are key ingredients of the standard model of a flare and an inverse-polarity prominence equilibrium. Dynamical processes in arcade structures are important for understanding several key basic processes in the corona, such as energy balance and release, and prominence formation and evolution. Often, these processes are observed to evolve quasi-periodically. For example, light curves of solar and stellar flares often have quasi-periodic pulsations that could be associated with oscillatory processes (e.g. Nakariakov and Melnikov, 2009) in the flaring arcades. A transverse oscillatory motion with a period of about 1000 s in an arcade situated above an emerging magnetic rope was detected by Kim, Nakariakov, and Cho (2014). Consecutive ignition of quasi-periodic hard X-ray emission with a period of about a minute, propagating along the magnetic polarity inversion line in a flaring arcade, was observed in a solar flare by Grigis and Benz (2005) and Bogachev et al. (2005). A similar effect was detected in the microwave emission of a solar flare (e.g. Kim et al., 2013). A recent comprehensive statistical analysis demonstrated that phenomenon is associated with successive triggering of the energy release process in different loops of the flaring arcade (Kuznetsov et al., 2016). Oscillatory processes in the magnetic arcades supporting quiescent prominences might also be responsible for prominence oscillations (Arregui, Oliver, and Ballester, 2012).

A likely mechanism for the oscillatory processes in arcades is connected with magnetohydrodynamic (MHD) oscillations that have been intensively modelled for more than two decades (see, e.g. Goossens, Erdélyi, and Ruderman, 2011, for a comprehensive review). Several studies have addressed perturbations in the plane perpendicular to the arcade axis. In particular, the propagation of fast magnetoacoustic waves in coronal potential arcades, excited by photospheric footpoint motions, was studied in Cadez, Oliver, and Ballester (1996). The excitation of resonant shear Alfvén oscillations in coronal arcades driven by toroidal footpoint motions was described by Ruderman et al. (1997). Oliver, Hood, and Priest (1996) considered a general two-dimensional arcade equilibrium structure with no longitudinal magnetic field component, and derived governing equations for the coupled slow and fast modes, while the Alfvén mode was decoupled from the magnetoacoustic modes. The propagation of impulsively generated Alfvén waves in an arcade was numerically modelled by Chmielewski et al. (2014). Magnetohydrodynamic waves in sheared coronal arcades, including propagation along the axis of the arcade, were studied by e.g. Arregui, Oliver, and Ballester (2004b,a) in the zero-$\beta$ limit, and the properties of coupled fast and Alfvén modes were established. Slow waves propagating along the axis of an arcade, i.e. along the neutral line, have been proposed as a candidate process to explain the progression of flaring energy releases along the neutral line that are typical for two-ribbon flares (Nakariakov and Zimovets, 2011). Fast waves guided by a plasma arcade have been considered as a possible mechanism for kink oscillations in coronal active regions (Hindman and Jain, 2015).

Much less attention has been received by MHD instabilities in plasma arcades, which may also be responsible for the progression of flaring energy releases along the neutral line in two-ribbon flares. Another interesting topic that requires understanding regarding MHD instabilities in arcades is the abrupt destabilisation that could trigger a coronal mass ejection. Likewise, the source of the filamentation of an arcade, i.e. the appearance of corrugated fine structure that is often detected in post-flare plasma arcades, is of interest. These processes require consideration of MHD perturbations that have a characteristic scale along the arcade axis (i.e., across the field) much shorter than the lengths of the loops that form the arcade. These perturbations, with a spatial scale much shorter than the parallel field-aligned scale when the field is azimuthal, could be referred to as corrugated perturbations, and the associated instability could be called a corrugation instability. On the other hand, as these perturbations have a small scale across the field, they could also be referred to as ‘‘ballooning’’, but this term must be used with caution in the coronal context, as this term is usually applied in solar physics to perturbations with a high azimuthal wave number $m$.

In solar physics, only a few studies have been dedicated to ballooning modes so far. These works were mainly dedicated to the study of slightly twisted magnetic ropes, where the ballooning perturbations were associated with high values of $m$. Ruderman (2007) carried out a theoretical analysis of long-wavelength non-axisymmetric modes, including ballooning modes, of a compressible zero-beta weakly twisted magnetic rope surrounded by a straight and homogeneous magnetic field. The main attention was paid to the kink mode. Karami and Bahari (2012) generalised this study and addressed the oscillation period ratios of different harmonics. Costa and González (2006, 2008) developed an energy-principle-based formalism for the estimation of the non-axisymmetric mode parameters, i.e. $m>0$. Cheremnykh et al. (2017) showed that in a thin magnetic tube with a curved magnetic field, the stable $m=1$ mode is dominant when the azimuthal magnetic field outside the tube is absent. However, in the presence of an external magnetic field, this mode becomes unstable (Cheremnykh, Kryshtal, and Tkachenko, 2017). Stepanov, Kopylova, and Tsap (2008) and Tsap et al. (2008) demonstrated that the ballooning instability of arch-shaped twisted magnetic ropes might cause the formation of helmet-shaped structures in the lower solar corona, and might also produce a quasi-periodic modulation of gyrosynchrotron emission in flares.

On the other hand, the theory of the ballooning oscillations and instability of highly twisted magnetic ropes, relevant to the study of the corrugation instability of an arcade, has been intensively elaborated in the context of the terrestrial magnetosphere. Gold (1959) suggested very early on that the hot plasma MHD instability (later coined the ballooning instability) can explain various eruptive phenomena in the terrestrial magnetotail. Walker (1987) showed that the MHD modes in the ballooning limit are represented by the coupled Alfvén and slow magnetosonic branches, while the fast magnetosonic mode is evanescent. Burdo, Cheremnykh, and Verkhoglyadova (2000) showed that the coupling of the Alfvén and slow magnetoacoustic modes gives rise to a ballooning instability in the dipole field. These authors also formulated for the first time the instability criterion outside the local approximation. Cheremnykh and Parnowski (2004), Agapitov, Cheremnykh, and Parnowski (2008) and Leonovich and Kozlov (2013b) considered the instability in a plasma with an inhomogeneity along the field lines. Ma, Hirose, and Liu (2014) studied the instability in the Hall-MHD framework. Klimushkin, Mager, and Pilipenko (2012) and Mager and Klimushkin (2017) generalised the theory of ballooning perturbations accounting for kinetic effects. The exploitation of the coronal–magnetospheric analogy opens up interesting opportunities for knowledge transfer (Nakariakov et al., 2016).

The aim of this paper is to further develop the linear theory of corrugated perturbations in a plasma arcade with an arbitrary radial profile of the equilibrium quantities. The shear of the magnetic field is neglected. Mathematically, this work is based on the set of equations for the coupled Alfvén and slow magnetoacoustic modes derived in Klimushkin (1997, 1998) and Cheremnykh and Danilova (2011), and the formalism developed for the study of the spatial structure of the unstable modes in the terrestrial magnetosphere (Klimushkin, 2006; Klimushkin and Chen, 2006; Mazur, Fedorov, and Pilipenko, 2013; Cheremnykh, Klimushkin, and Kostarev, 2014; Cheremnykh, Klimushkin, and Mager, 2016). In Section 2 we review the derivation of the governing equations that describe the radial structure of the perturbations. Section 4 addresses the derivation and study of the dispersion relation for the coupled Alfvén and slow modes with large longitudinal wave numbers perpendicular to the field, which determines the wave vector radial component in the WKB approximation. In Section 5 we study the possibility of mode trapping in the radial direction across the magnetic shells, derive the eigenvalues of the perturbations, consider the conditions under which the modes are unstable, and estimate the growth rates. In Section 6 we summarise the results and discuss their possible observational manifestations.

2 Governing Equations

Consider a coronal arcade as half of a plasma cylinder with an azimuthal magnetic field. The magnetic field component along the axis of the cylinder is neglected. The plasma is considered to be of finite $\beta$. Thus, in the magnetic geometry in our model corresponds to a z-pinch, with the magnetic surfaces represented by nested coaxial cylinders (Figure 1). In the solar coronal context, a similar model with a purely poloidal magnetic field has recently been used by Kaneko et al. (2015). The azimuthal angle $\varphi$ shows the direction along the field lines. At $\varphi=0, \pi/2$, which corresponds to the photosphere, the line-tying boundary conditions are applied. The longitudinal $y$ coordinate is directed along the cylinder axis, i.e. the magnetic neutral line. All parameters of the equilibrium are taken to depend only on the radial coordinate $r$, that is, the field line curvature radius. The coordinates $\varphi$, $y$, and $r$ are locally orthogonal to each other. In the following, we focus on ideal MHD processes.

Figure 1

Model representing a twisted magnetic rope filled with a plasma, as a cylinder. The coordinates $y$, $\varphi$, and $r$ are directed along the cylinder axis, along the magnetic field line, and in the radial direction, respectively. The horizontal line denotes the photosphere with the line-tying boundary conditions.

The plasma equilibrium condition has the form

$$ \nabla P = \frac{1}{c} {{\boldsymbol {J}}} \times{ {\boldsymbol {B}}}, $$

(1)

where $P$, ${{\boldsymbol {J}},}$ and ${{\boldsymbol {B}}}$ are the equilibrium values of the plasma pressure, electric current density, and magnetic field, respectively. It is convenient to introduce the parameters $\kappa= P^{-1} \mathrm{d}P/\mathrm{d}r$, that is, the reciprocal spatial scale of the radial non-uniformity of the plasma pressure, and $\beta= 8 \pi P/ B^{2}$, that is, the ratio of the plasma pressure to the magnetic pressure. With this notation, the equilibrium condition can be written as

$$ \frac{\beta}{2} \kappa+ \frac{1}{B} \frac{\mathrm{d}B}{\mathrm {d}r} + \frac{1}{r} =0. $$

(2)

In the following, we consider $\beta$, $\kappa$, and $B$ as smooth functions of the radial coordinate $r$.

Within the approximation of infinite plasma conductivity, the component of the wave electric field ${\boldsymbol {E}}$ along the ambient magnetic field is zero. In the ballooning approximation, a two-dimensional field ${\boldsymbol {E}}$ is non-rotational (e.g. Klimushkin, 1997), that is, it can be represented as a two-dimensional gradient of some scalar (“a potential”):

$$ {{\boldsymbol {E}}} = - \nabla_{\perp}\Phi . $$

(3)

As the other field variable, the quantity

$$ \Theta= \frac{\sqrt{4 \pi\gamma P}}{c k_{y}} \nabla\cdot\boldsymbol {\xi} $$

(4)

can be used, where $\boldsymbol{\xi}$ is the plasma displacement vector, and $\gamma$ is the adiabatic index.

Owing to the assumed plasma uniformity with respect to the $y$ direction, we can perform a Fourier transform of any perturbed quantity $F$ as

$$ F(r,y,\varphi,t)=F(r,\varphi) \exp{(-i \omega t + i k_{y} y )}. $$

(5)

Here, the quantity $k_{y}$ is the component of the wave number along the axis of the arcade. The dependence of $F$ on the radial coordinate $r$ is determined by the specific equilibrium radial profiles of $P$, ${{\boldsymbol {J}},}$ and ${{\boldsymbol {B}}}$, and the boundary conditions at $r=0, \infty$. In the following, we focus on the ballooning limit that is based on the assumption that the characteristic spatial scale of the perturbations across the field, i.e. in the $y$ and $r$ directions, are small in comparison with the spatial scales of the equilibrium quantities. A necessary condition for this is a high $k_{y}$ value: $k_{y} \gg\kappa$.

Considering that the perturbations with spatial scale in the radial direction are much smaller than the local radius of the field curvature, we can use the WKB approximation with respect to the radial coordinate $r$. That is, the $r$ dependence of the perturbations can be represented in the form $\exp{i \int k_{r}(r, \omega) \mathrm{d}r}$, where $k_{r}$ is the radial component of the wave vector. The perpendicular component of the wave vector $k_{\perp}$ is $k_{\perp}^{2}=(k_{r}^{2}+k_{y}^{2})^{1/2}$.

A set of the MHD equations under these assumptions was obtained for an arbitrary geometry by Klimushkin (1997, 1998) and later, but independently, by Cheremnykh and Danilova (2011) and Mazur, Fedorov, and Pilipenko (2012). For the cylinder geometry, it can be written as

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \biggl( \frac{1}{r^{2}} \frac{\partial ^{2}}{\partial\varphi^{2}} + \frac{\omega^{2}}{V_{\mathrm{A}}^{2}} \biggr) \Phi- \beta\frac{\kappa}{r} \Phi= \frac{2 \omega}{r} \frac{V_{\mathrm{S}}}{V_{\mathrm{A}}} \Theta, $$

(6)

$$ V_{\mathrm{S}}^{2} \biggl( \frac{1}{r^{2}} \frac{\partial^{2}}{\partial \varphi^{2}} + \frac{\omega^{2}}{V_{\mathrm{C}}^{2}} \biggr) \Theta= \frac{2 \omega}{r} \frac{V_{\mathrm{S}}}{V_{\mathrm{A}}} \Phi. $$

(7)

Here $V_{\mathrm{A}}$, $V_{\mathrm{S}}$, and $V_{\mathrm{C}}$ are the Alfvén, sound, and tube (cusp) speeds, defined as

$$ V_{\mathrm{A}}^{2} = \frac{B^{2}}{4 \pi\rho}, \ V_{\mathrm{S}}^{2} = \frac{\gamma P}{\rho}, \ V_{\mathrm{C}}^{2} = \frac{V_{\mathrm{A}}^{2}V_{\mathrm{S}}^{2}}{V_{\mathrm{A}}^{2}+V_{\mathrm{S}}^{2}}, $$

where $\rho$ is the undisturbed plasma density.

Equations 6 and 7 determine the structure of the Alfvén and slow modes coupled with each other through the field line curvature; we recall that in the limit $k_{y} \gg\kappa$, the fast mode is evanescent (e.g. Walker, 1987). The equations must be supplemented with boundary conditions. On the azimuthal coordinate, the line-tying boundary conditions must be applied (Hood, 1986), which means that the plasma displacement ${\boldsymbol {\xi}}$ must vanish on the photosphere, where $\varphi=0$ and $\pi$:

$$ {\boldsymbol {\xi}}|_{\varphi=0, \pi}=0. $$

(8)

As the transverse displacement is proportional to the wave electric field, the condition ${\boldsymbol {\xi}}_{\perp}=0$ results in

$$ \Phi|_{\varphi=0, \pi}=0. $$

(9)

The parallel along the field displacement is related to the $\Theta$ function as

$$ \frac{\omega^{2}}{V_{\mathrm{C}}^{2}} \frac{\omega}{ck_{y}} \xi_{\parallel}= - \frac{\sqrt{4 \pi\gamma P} }{\omega} \frac{\partial\Theta }{\partial\varphi} $$

(e.g. Klimushkin, 1998). Then, the equality ${\boldsymbol {\xi}}_{\parallel}=0$ imposes the boundary condition for the $\Theta$ function:

$$ \frac{\partial\Theta}{\partial\varphi} \biggl| _{\varphi =0, \pi} =0. $$

(10)

Equations 6 and 7 supplemented with boundary conditions 9 and 10 are the governing equations used for the analysis presented in the paper.

3 Alfvén and Slow-Mode Eigenfunctions

Equations 6 and 7 describe the coupling of Alfvén and slow modes. We consider two auxiliary problems connected with uncoupled modes.

We designate $\Phi_{N}$ a solution of the boundary problem stated by the Alfvén mode equation

$$ \biggl( \frac{1}{r^{2}} \frac{\partial^{2}}{\partial\varphi^{2}} + \frac {\omega^{2}}{V_{\mathrm{A}}^{2}} \biggr) \Phi_{N}= 0, $$

(11)

with the boundary conditions

$$ \Phi_{N}|_{\varphi=0, \pi}=0, $$

(12)

where $N$ is the parallel (field-aligned) integer harmonic number. The function $\Phi_{N}$ is normalised as

$$ \langle\Phi_{N} \Phi_{N'} \rangle=\delta_{NN'}, $$

(13)

where $\langle... \rangle= \int_{0} ^{\pi}(...) \mathrm {d} \varphi$.

Eigenfunctions of problems 11 and 12 are

$$ \Phi_{N} =\sqrt{\frac{2}{\pi} } \sin N \varphi, $$

(14)

and the corresponding eigenfrequencies are

$$ \Omega_{\mathrm{A}N} =\frac{NV_{\mathrm{A}}}{r} . $$

(15)

Likewise, we designate $\Theta_{N}$ as a solution of the boundary problem stated by the slow-mode equation

$$ \biggl( \frac{1}{r^{2}} \frac{\partial^{2}}{\partial\varphi^{2}} + \frac {\omega^{2}}{V_{\mathrm{C}}^{2}} \biggr) \Theta_{N}= 0 , $$

(16)

with the boundary conditions

$$ \frac{\partial\Theta}{\partial\varphi} \biggl| _{\varphi =0, \pi} =0 $$

(17)

normalised as

$$ \langle\Theta_{N} \Theta_{N'} \rangle=\delta_{NN'}, $$

(18)

where $N$ and $N'$ are two integers. Under these conditions, the eigenfunction is

$$ \Theta_{N} = \sqrt{\frac{2}{\pi} } \times \left\{ \textstyle\begin{array}{l@{\quad }l} 1/\sqrt{2} , & \mbox{if} \ N=0 ,\\ \cos{N \varphi} , & \mbox{if} \ N>0; \end{array}\displaystyle \right. $$

(19)

and the corresponding eigenfrequency is

$$ \Omega_{\mathrm{C}N} =\frac{NV_{\mathrm{C}}}{r} . $$

(20)

Note that the cases $\omega=\Omega_{\mathrm{A}N}$ and $\omega =\Omega_{\mathrm{C}N}$ correspond to well-known Alfvén and slow-mode resonances, respectively (e.g. Cheng et al., 1993; Klimushkin, 1997, 1998; Leonovich and Kozlov, 2013a).

4 Dispersion Relations for the Coupled MHD Modes

We seek the solution of problems 6 and 7 with boundary conditions 9 and 10 as an expansion by harmonics $\Phi_{N}$ and $\Theta_{N}$ in the form

$$\begin{gathered} \Phi= \sum_{N=1}^{\infty} a_{N} \Phi_{N}, \end{gathered}$$

(21)

$$\begin{gathered} \Theta= b_{0} \Theta_{0}+ \sum _{N=1}^{\infty} \Theta_{N}, \end{gathered}$$

(22)

where $a_{N}$ and $b_{N}$ are the coefficients that are yet to be determined.

After we insert Equation 22 into Equation 7 and integrate over the angle, we have

$$ b_{0}= \frac{2\omega}{r} \frac{V_{\mathrm{S}}}{V_{\mathrm{A}}} \frac {V_{\mathrm{C}}^{2}}{V_{\mathrm{S}}^{2}} \frac{ \langle\Theta_{0} \Phi \rangle}{\omega^{2}} , $$

(23)

$$ b_{N}= \frac{2\omega}{r} \frac{V_{\mathrm{S}}}{V_{\mathrm{A}}} \frac {V_{\mathrm{C}}^{2}}{V_{\mathrm{S}}^{2}} \frac{ \langle\Theta_{N} \Phi \rangle}{\omega^{2}-\Omega_{\mathrm{C}N}^{2}} . $$

(24)

Then we substitute Equation 22 into Equation 6, which yields

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \biggl( \frac{\partial^{2}}{\partial\varphi ^{2}} + \frac{\omega^{2} r^{2}}{V_{\mathrm{A}}^{2}} \biggr) \Phi- \beta \kappa r \Phi= 4 \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}} \Biggl[ \langle\Theta_{0} \Phi \rangle+ \sum_{N=1} ^{\infty}\frac{\omega^{2} \Theta_{N}}{\omega^{2}-\Omega _{\mathrm{C}N}^{2}} \langle\Theta_{N} \Phi \rangle \Biggr] . $$

(25)

The symmetric and antisymmetric (with respect to the arcade apex ($\varphi=\pi/2$)) functions $\Phi$ must be considered separately. In this paper, the convolution product $\langle\Theta_{N} \Phi_{N'} \rangle$ is considered as non-negligible only for the lowest relevant $N$ and $N'$ numbers.

4.1 Alfvén Mode Eigenfunctions Symmetric with Respect to $\varphi=\pi/2$

In this case, the only harmonics that considerably contribute to the dispersion relation are $\Theta_{0}$, $\Theta_{2}$, and $\Phi_{1}$. Then Equation 25 is reduced to the form

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \biggl( \frac{\partial^{2}}{\partial\varphi ^{2}} + \frac{\omega^{2} r^{2}}{V_{\mathrm{A}}^{2}} \biggr) \Phi_{1} - \beta \kappa r \Phi_{1} = 4 \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}} \sqrt{\frac{2}{\pi}} \biggl[ \frac{2}{\pi} - \frac{4}{3 \pi} \frac{\omega^{2}}{\omega^{2}-\Omega _{\mathrm{C2}}^{2}} \cos{2\varphi} \biggr] . $$

(26)

After we multiply this expression by $\Phi_{1}$ and integrate over the angle, we have the dispersion relation

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \bigl( \omega^{2}- \Omega_{\mathrm{A1}}^{2} \bigr) - \beta\frac{\kappa V_{\mathrm{A}}^{2}}{r} = \frac{32}{\pi^{2}} \frac{V_{\mathrm{C}}^{2}}{r^{2}} \biggl(1 + \frac{2}{9} \frac{\omega^{2}}{\omega^{2}-\Omega_{\mathrm{C2}}^{2}} \biggr) , $$

(27)

where expressions 15 and 20 were used with the corresponding values of the integer $N$.

The case $k_{r} \to\infty$ corresponds to the Alfvén and slow-mode resonances that occur at the cylindrical surfaces where the wave frequencies are equal to $\Omega_{\mathrm{A1}}$ and $\Omega_{\mathrm{C2}}$, respectively. The opposite case, $k_{r} \to0$, corresponds to the cut-offs (e.g. Cheremnykh, Klimushkin, and Kostarev, 2014). The cut-off surfaces are determined by the equation

$$ \omega= \Omega_{\pm}(r), $$

where $\Omega_{\pm}$ is a solution of biquadratic Equation 27 with $k_{\perp}^{2}/k_{y}^{2}=1$:

$$ \Omega^{2}_{\pm}= \frac{1}{2} \bigl[ \bigl( \Omega_{\mathrm{A1}}^{2}+\Omega_{\mathrm{C2}}^{2}+H \bigr) \pm\sqrt{ D } \bigr], $$

(28)

with

$$ H=\beta\frac{\kappa V_{\mathrm{A}}^{2}}{r}+\frac{32}{\pi^{2}} \frac {11}{9} \frac{V_{\mathrm{C}}^{2}}{r^{2}} $$

(29)

and

$$ D=\bigl(\Omega_{\mathrm{A1}}^{2}-\Omega_{\mathrm{C2}}^{2}+H \bigr)^{2} + \biggl( \frac{16}{3\pi} \biggr)^{2} \frac{V_{\mathrm{C}}^{2}}{r^{2}} \Omega_{\mathrm{C2}}^{2}. $$

(30)

The value of $D$ is always positive.

An instability ($\Omega^{2}_{-}<0$) can develop on the lower frequency oscillation branch, when the root of the discriminant $D$ is larger than the first term in brackets in Equation 28:

$$ \bigl(\Omega_{\mathrm{A1}}^{2}+\Omega_{\mathrm{C2}}^{2}+H \bigr) - \sqrt{ D }< 0, $$

which gives the instability threshold:

$$ \beta\kappa r= -1 - \frac{32}{\pi^{2}} \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}}. $$

(31)

Thus the arcade is unstable when

$$ \beta\kappa r< -1 - \frac{32}{\pi^{2}} \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}}. $$

(32)

The instability growth rate is

$$ \Gamma= \frac{1}{\sqrt{2}} \bigl[\sqrt{ D } - \bigl(\Omega_{\mathrm{A1}}^{2}+\Omega_{\mathrm{C2}}^{2}+H\bigr) \bigr]^{1/2}. $$

(33)

The instability criterion 32 qualitatively agrees with the results of Burdo, Cheremnykh, and Verkhoglyadova (2000) that were obtained for the dipole field. Equation 32 should be considered an approximate threshold of the instability. The exact threshold can be found from Equation 25 with $\omega=0$ and $k_{\perp}^{2}/k_{y}^{2}=1$ and boundary conditions 9,

$$ \frac{\partial^{2}}{\partial\varphi^{2}} \Phi- \beta\kappa r \Phi= 4 \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}} \langle \Theta_{0} \Phi \rangle. $$

(34)

Let a solution of Equation 34 be

$$ \Phi= \sum_{m=1}^{\infty} a_{m} \Phi_{2m-1}, $$

(35)

where $\Phi_{2m-1}$ are odd eigenfunctions $\Phi_{N}$ given by Equation 14. In this case, we find the instability condition

$$ \biggl(\frac{2}{\pi\sqrt{-\beta\kappa r}}\tan{\frac{\pi\sqrt {-\beta\kappa r}}{2}}-1 \biggr)\frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}}- \frac{\beta \kappa r}{4}=0. $$

(36)

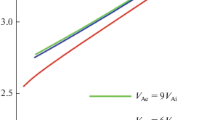
The exact solution of this equation corresponding to the minimum value of $-\beta\kappa r$ is compared with approximate solution 31 in Figure 2. The approximate threshold of the instability, given by Equation 31, differs only slightly from the exact threshold, especially for ${V_{\mathrm{C}}^{2}}/{V_{\mathrm{A}}^{2}}\ll 1$, i.e. for the small $\beta$ typical for coronal arcades.

Figure 2

Exact (solid line) and approximate (dashed line) instability thresholds for the symmetric function $\Phi$.

4.2 Alfvén Mode Eigenfunctions Antisymmetric with Respect to $\varphi=\pi/2$

The principal, antisymmetric with respect to the apex harmonic of the Alfvén mode, is $\Phi_{2}$. Thus, the convolution $\langle \Theta_{N} \Phi_{2} \rangle$ is not zero only for the odd slow-mode harmonics $\Theta_{N}$ (with $N$ being an odd integer). We only take into account the principal odd harmonic, $\Theta _{1}$. Then Equation 25 becomes

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \biggl( \frac{\partial^{2}}{\partial\varphi ^{2}} + \frac{\omega^{2} r^{2}}{V_{\mathrm{A}}^{2}} \biggr) \Phi_{2} - \beta \kappa r \Phi_{2} = 4 \frac{V_{\mathrm{C}}^{2}}{V_{\mathrm{A}}^{2}} \frac{\omega^{2}}{\omega^{2}-\Omega_{\mathrm{C1}}^{2}} \langle\Theta_{1} \Phi_{2} \rangle. $$

(37)

Multiplying this expression by $\Phi_{2}$, and integrating over the angle, we obtain the dispersion relation

$$ \frac{k_{\perp}^{2}}{k_{y}^{2}} \bigl( \omega^{2}- \Omega_{\mathrm{A2}}^{2} \bigr) - \beta\frac{\kappa V_{\mathrm{A}}^{2}}{r} = 4 \frac{V_{\mathrm{C}}^{2}}{r^{2}} \frac{\omega^{2}}{\omega^{2}-\Omega _{\mathrm{C1}}^{2}} \biggl(\frac{8}{3\pi} \biggr)^{2}. $$

(38)

The Alfvén and slow-mode resonances correspond to the case $k_{r} \to \infty$ and occur at the frequencies $\Omega_{\mathrm{A2}}$ and $\Omega_{\mathrm{C1}}$, respectively. The cut-off frequencies, determined by the condition $k_{r} \to0$, are in this case determined as

$$ \Omega^{2}_{\pm}= \frac{1}{2} \bigl[ \bigl( \Omega_{\mathrm{A2}}^{2}+\Omega_{\mathrm{C1}}^{2}+H \bigr) \pm\sqrt{ D } \bigr], $$

(39)

with

$$ H=\beta\frac{\kappa V_{\mathrm{A}}^{2}}{r}+\frac{4 V_{\mathrm{C}}^{2}}{r^{2}} \biggl(\frac{8}{3\pi} \biggr)^{2}, $$

(40)

and

$$ D=\bigl(\Omega_{\mathrm{A2}}^{2}-\Omega_{\mathrm{C1}}^{2}+H \bigr)^{2} + \frac {V_{\mathrm{C}}^{2}}{r^{2}} \biggl(\frac{32}{3\pi} \biggr)^{2} \Omega _{\mathrm{C1}}^{2}. $$

(41)

The instability can develop on the lower-frequency branch given by the solution of Equation 39 denoted as ‘‘−’’ when the condition

$$ \bigl(\Omega_{\mathrm{A2}}^{2}+\Omega_{\mathrm{C1}}^{2}+H \bigr) - \sqrt{ D }< 0 $$

is satisfied. The corresponding instability threshold is

$$ \beta\kappa r< -4, $$

(42)

in complete agreement with the results of Burdo, Cheremnykh, and Verkhoglyadova (2000). The instability growth rate is

$$ \Gamma= \frac{1}{\sqrt{2}} \bigl[\sqrt{ D } - \bigl(\Omega_{\mathrm{A2}}^{2}+\Omega_{\mathrm{C1}}^{2}+H\bigr) \bigr]^{1/2}. $$

(43)

As in the symmetric case, the exact instability threshold can be found from Equation 34, while now $\Phi=\Phi_{2m}$, where $m=1,2,\ldots$ and $\Phi_{2m}$ are even eigenfunctions given by Equation 14. Thus the instability condition is

$$ -\beta\kappa r=(2m)^{2}. $$

(44)

Here $-\beta\kappa r$ is minimum when $m=1$, so in the antisymmetric case, the exact instability threshold coincides with the approximate threshold 42.

4.3 General Properties of the Solutions for Symmetric and Antisymmetric Alfvén Modes

In both symmetric and antisymmetric cases, the discriminant $D$ is a positive value, thus the squares of the cut-off frequencies have real values. This agrees with the well-known MHD theorem that is a consequence of the energetic principle, stating that the wave frequency squared of linear perturbations in ideal MHD is always real (Frieman and Rotenberg, 1960; Kadomtsev, 1966). Hence, no over-stabilities can occur in the considered case.

With the decrease in $\beta$, the lower cut-off frequency $\Omega_{-}$ in both cases tends to the slow-mode resonance frequency ($\Omega _{\mathrm{C2}}$ or $\Omega_{\mathrm{C1}}$), while the higher cut-off frequency $\Omega_{+}$ tends to the Alfvénic resonant frequency ($\Omega_{\mathrm{A1}}$ or $\Omega_{\mathrm{A2}}$). Thus, we can conclude that the frequencies $\Omega_{-}$ and $\Omega_{\mathrm{C}}$ characterise the slow-mode oscillation branch, and $\Omega_{+}$ and $\Omega_{\mathrm{A}}$ characterise the Alfvénic oscillation branch. The instability can develop only on the slow-mode branch. This is in accordance with the results of earlier papers (Mazur, Fedorov, and Pilipenko, 2012; Kozlov et al., 2014; Cheremnykh, Klimushkin, and Kostarev, 2014). However, the instability threshold depends on the symmetry properties of the Alfvén mode. Clearly, for low and moderate $\beta$ values, the instability threshold is lower for the symmetric Alfvén mode than for the antisymmetric mode.

Then, Equations 28 and 39 easily show that the inequalities $\Omega_{-} < \Omega_{\mathrm{C}} < \Omega_{+}$ are satisfied. However, the frequency $\Omega_{+}$ can be either higher or lower than the Alfvénic resonant frequency $\Omega_{\mathrm{A}}$, depending on the profiles $\beta(r)$, $\kappa(r)$, and $B (r)$. Following Cheremnykh, Klimushkin, and Kostarev (2014), for the arbitrary ratio $k_{r}/k_{y}$, the solution of Equations 27 and 38 can be expressed in terms of two pairs of the characteristic frequencies as

$$ k_{r}^{2}(r,\omega) = -k_{y}^{2} \biggl( \frac{\omega^{2}-\Omega^{2}_{-}(r)}{\omega^{2} - \Omega_{\mathrm{C}}^{2}(r)} \biggr) \biggl( \frac{\omega^{2}-\Omega^{2}_{+}(r)}{\omega^{2} - \Omega_{\mathrm{A}}^{2}(r)} \biggr). $$

(45)

In the symmetric case, $\Omega_{\mathrm{C}}$ means $\Omega_{\mathrm{C2}}$, and $\Omega_{\mathrm{A}}$ means $\Omega_{\mathrm{A1}}$. In the antisymmetric case, $\Omega_{\mathrm{C}}$ means $\Omega_{\mathrm{C1}}$, and $\Omega_{\mathrm{A}}$ means $\Omega_{\mathrm{A2}}$. The dependence of the equilibrium parameters on the radial coordinate shows that there are regions of different signs of $k_{r}^{2}$ in the radial direction. The regions where $k_{r}^{2}(r)>0$ can be called the mode localisation regions. In these regions, MHD perturbations have an oscillatory radial structure, cf. the body modes, see Edwin and Roberts (1983), or the leaky modes (e.g. Verwichte, Foullon, and Nakariakov, 2006). Outside these regions, the modes have exponential radial dependences. The cut-off frequencies $\Omega_{\pm}$ prescribe the cylindrical surfaces where the behaviour of the perturbation changes from oscillatory to evanescent in the radial direction. Equation 45 shows that there are mode localisation regions of two kinds. One of them is bounded by the Alfvénic resonance surface where $\omega =\Omega_{\mathrm{A}}(r)$ and the higher cut-off shell where $\omega =\Omega_{+}(r)$. In the following, this region is referred to as the Alfvénic mode localisation region. The other region is bounded by the surface of the cusp resonance where $\omega=\Omega_{\mathrm{C}}(r)$ and the lower cut-off shell where $\omega=\Omega_{-}(r)$. This is the slow-mode localisation region. Because of the inequality $\Omega _{-}<\Omega_{\mathrm{A}}<\Omega_{+}$, these regions do not overlap with each other.

The spatial structure of the perturbation in the mode localisation regions in the considered geometry was studied by Klimushkin (1997) and Cheremnykh, Klimushkin, and Mager (2016). In both Alfvénic and slow-mode localisation regions, the wave was found to have an oscillatory structure across the magnetic shells in the radial direction in the annulus between the cut-off shell and the resonant shell. In such an annulus, the local radial component of the wave vector changes from zero to infinity. On the resonant magnetic surface, the mode is absorbed through mode coupling and subsequent dissipation. Outside these regions, the mode is evanescent. However, this structure corresponds to a stable plasma configuration when all the cut-off and resonant frequencies have real values. However, the lower cut-off frequency $\Omega_{-}$ can take imaginary values. This case corresponds to the corrugation instability.

5 Radial Structure of the Unstable Modes

The instability takes place when $\omega^{2}<0$ for a given $k_{r}^{2}$ value. At the resonances, $k_{r}^{2} \to\infty$, and the modes of the considered plasma configuration are always stable since the resonant frequencies squared are always positive. At the cut-off frequencies, the situation is different. Equations 28 and 39 show that the Alfvénic (the higher) cut-off frequency squared $\Omega_{+}^{2}$ is always positive, while the slow-mode (the lower) cut-off frequency squared $\Omega_{-}^{2}$ can be negative, provided that either condition 32 or 42 is fulfilled. This is the instability condition. Only the slow-mode oscillation branch can be unstable, in agreement with Mazur, Fedorov, and Pilipenko (2012).

In the low-$\beta$ case, the characteristic Alfvénic frequencies $\Omega_{\mathrm{A}}$, $\Omega_{+}$ are much higher than the slow-mode characteristic frequencies $\Omega_{-}$, $\Omega_{\mathrm{C}}$. Then, in the low-$\beta$ limit, in the slow-mode localisation region Equation 45 can be simplified to

$$ k_{r}^{2}(r,\omega) = -K^{2} \frac{\omega^{2}-\Omega^{2}_{-}(r)}{\omega^{2} - \Omega_{\mathrm{C}}^{2}(r)}, $$

(46)

where $K= (\Omega_{+} /\Omega_{\mathrm{A}})k_{y}$. As the values of $\Omega_{+}$ and $\Omega_{\mathrm{A}}$ are close to each other, the value of $K$ is of the same order of magnitude as $k_{y}$.

As the instability can develop at low (moreover, negative) values of $\Omega_{-}^{2}(r)$, we assume that the function $\Omega_{-}^{2}(r)$ has a minimum at some value of $r=r_{\mathrm{min}}$ (Figure 3). Near the magnetic surface $r=r_{\mathrm{min}}$, the function $\Omega _{-}^{2}(r)$ can be approximated with the use of the Taylor expansion as

$$ \Omega_{-}^{2} \approx- \Gamma^{2} \biggl( 1- \frac{x^{2}}{l^{2}} \biggr), $$

(47)

where $x=r - r_{\mathrm{min}}$, $\Gamma^{2} = - \Omega_{-}^{2}(r_{\mathrm{min}})$, and $l$ is a constant linked with the characteristic scale $L$ of the radial non-uniformity (see Figure 3). The region where $\Omega_{-}^{2}<0$ is referred to as an unstable region. Equation 47 shows that the width of this region is approximately $2l$.

Figure 3

Behaviour of the function $\Omega_{-}^{2}(r)$ in the vicinity of its minimum.

The value $\Gamma$ is the characteristic growth rate of the instability. It can be estimated from Equations 28 and 39 as

$$ \Gamma\approx\frac{V_{\mathrm{S}}}{\sqrt{r_{\mathrm{min}}l} }, $$

(48)

where it was taken that the field line curvature radius at $r=r_{\mathrm{min}}$ is $r_{\mathrm{min}}$.

As in the unstable case the wave frequency is imaginary, so we can put $\omega^{2}=-\gamma^{2}$, where $\gamma^{2}>0$. Then Equation 46 can be rewritten as

$$ k_{r}^{2}(r,\gamma) \approx\frac{K^{2}}{\gamma^{2} + \Omega_{\mathrm{C}}^{2}} \biggl( \Gamma^{2}-\gamma^{2} - \Gamma^{2} \frac{x^{2}}{l^{2}} \biggr). $$

(49)

We introduce

$$ \Delta^{2} = l^{2} \frac{\Gamma^{2}-\gamma^{2}}{\Gamma^{2}} $$

(50)

(note that $\Delta$ is a function of the growth rate $\gamma$). Then Equation 49 becomes

$$ k_{r}(r,\gamma) \approx\frac{K}{l}\frac{\Gamma}{\sqrt{\gamma^{2} + \Omega_{\mathrm{C}}^{2}}} \sqrt{ \Delta^{2}-x^{2}}. $$

(51)

This expression shows that $\Delta$ is the radial coordinate of the cut-off magnetic shell. That is, the mode is trapped in the radial direction in the region bounded between the magnetic surfaces with $r_{\pm} =r_{\mathrm{min}} \pm\Delta$ (cut-off points). As we are interested mainly in the order of magnitude estimations, the variation of the $\Omega_{\mathrm{C}}$ across the trapping region can be neglected.

In the cavity (i.e. the wave-trapping region) formed by the radial non-uniformity of the equilibrium parameters, the radial component of the wave vector must satisfy the Bohr–Sommerfeld quantisation condition

$$ \int\limits _{r_{-}} ^{r_{+}} k_{r}(r,\gamma) \mathrm{d}r = \pi \biggl( n+ \frac{1}{2} \biggr), $$

(52)

where $n$ is an integer corresponding to the radial harmonic number. Substituting $k_{r}$ from Equation 51 into Equation 52 and evaluating the integral, we obtain after some rearrangement

$$ \frac{1}{\Gamma} \frac{\Gamma^{2}-\gamma_{n}^{2}}{ \sqrt{\gamma_{n}^{2} + \Omega_{\mathrm{C}}^{2}} } = \frac{2n+1}{Kl}, $$

(53)

where $\gamma_{n}$ is the growth rate of the $n$-th radial harmonic. The solution to this equation has the form

$$ \gamma_{n}^{2} = \Gamma^{2} \biggl( 1 + \frac{1}{2} \zeta^{2} - \sqrt{D_{1}} \biggr), $$

(54)

where

$$ \zeta=\frac{2n+1}{Kl}, \quad \text{and}\quad D_{1}= \biggl(1 + \frac{1}{2} \zeta^{2} \biggr)^{2} - 1+ \frac{\Omega _{\mathrm{C}}^{2}}{\Gamma^{2}} \zeta^{2}. $$

The dependence of the growth rate on the parameter $\zeta$ is illustrated in Figure 4. Note that the discriminant $D_{1}$ is always positive. The figure shows that the perturbations with short wavelengths in the $y$-direction, along the axis of the arcade, are most unstable, while the perturbations with long wavelengths along the axis of the cylinder are stable.

Figure 4

Dependence of the normalised growth rate squared on the parameter $\zeta=(2n+1)/(Kl)$ for the values $\Omega_{\mathrm{C}}^{2}/\Gamma^{2}=0.5$, 1, and 2.

In the unstable regime, for

$$ Kl \gg1, $$

(55)

corresponding to the perturbations with very short wavelengths along the axis of the arcade and small $n$, the solution to Equation 53 can be approximated as

$$ \gamma_{n}^{2} \approx\Gamma^{2} \biggl( 1- \frac{2n+1}{Kl} \sqrt{1 + \frac{\Omega_{\mathrm{C}}^{2}}{\Gamma^{2}}} \biggr). $$

(56)

Thus, for low radial harmonics ($n \approx1$) and $Kl \gg1$, the quantity $\gamma_{n}^{2}$ has the same (positive) sign as $\Gamma^{2}$, and the instability occurs. Therefore, the set of inequalities 32 or 42 and 55 constitutes the corrugation instability condition. In this instability, the wavelength of the unstable perturbation along the arcade is much shorter than its radius, as the unstable perturbations have a ‘‘corrugated’’ spatial structure, see Figure 5. However, there is yet another condition for the instability.

Figure 5

Sketch of an arcade experiencing a corrugation instability. The arrows show the unstable magnetic flux tubes – the ‘‘tongues’’.

Different radial harmonics have different growth rates. By the order of magnitude, the difference between the increments of two neighbouring harmonics with small $n$ is

$$ \Delta\gamma_{n} \approx\frac{\Gamma}{Kl} \approx\frac{V_{\mathrm{S}}}{Kl \sqrt{Rl} }, $$

where $R$ is the radius of the arcade. For larger radial harmonic numbers $n$, however, the value $\gamma _{n}^{2}$ becomes negative and the perturbations become stable. Thus, the instability conditions 32 or 42 and 55 must be complemented by the inequality

$$ n< n_{\mathrm{cr}}, $$

(57)

where $n_{\mathrm{cr}}$ is the critical value of the radial harmonic number, which can be estimated from Equation 54 as

$$ n_{\mathrm{cr}} = \frac{1}{2} \biggl( Kl \frac{\Gamma}{\Omega _{\mathrm{C}}} -1 \biggr) \approx\frac{1}{2} Kl \frac{\Gamma }{\Omega_{\mathrm{C}}}. $$

(58)

This stability condition has a rather simple meaning.

First, Equation 50 shows that in the unstable case $\gamma _{n}^{2}>0$, the inequality $\Delta< l$ holds. As follows from Equation 47, this regime occurs when the cut-off shells are situated in the region where the slow-mode cut-off frequency squared is negative, $\Omega_{-}^{2}<0$. Vice versa, the stable regime, with $\gamma _{n}^{2}<0$, occurs when the cut-off shells are situated outside the unstable region with $\Omega_{-}^{2}<0$. That is, in the radial direction, only the central part of the resonator is situated inside the unstable region: $\Delta> l$.

Second, the characteristic value of the radial component of the wave vector for the critical radial number $n_{\mathrm{cr}}$ can be estimated as $k_{r} \approx n_{\mathrm{cr}}/l$. From Equation 58, we can estimate the ratio of the radial and longitudinal components,

$$ \frac{k_{r} }{k_{y}} \approx \frac{1}{2} \frac{|\Omega_{-}|}{\Omega_{\mathrm{C}}}\frac{\Omega_{+}}{\Omega_{\mathrm{A}}}. $$

(59)

Since both $\Gamma\approx\Omega_{\mathrm{C}}$ and $\Omega_{+} \approx \Omega_{\mathrm{A}}$, for the stable modes with $n \gg n_{cr}$ we have $k_{r} \gg k_{y}$. This allows us to estimate the ratio of transverse components of the magnetic field perturbations in this regime, $|b_{r}/b_{y}| \approx k_{y} /k_{r}$. Then, in the stable case, the field lines oscillate mainly in the direction along the axis of the arcade, $b_{r} \ll b_{y}$, while in the unstable case, they are displaced mainly in the radial direction, $b_{r} \gg b_{y}$. This agrees with results obtained in earlier publications (Agapitov, Cheremnykh, and Parnowski, 2008; Mazur, Fedorov, and Pilipenko, 2012). Thus, the corrugation instability of an arcade distorts its boundary in the radial, i.e. vertical direction. The unstable region has a small size in the direction of the arcade axis, while it includes the whole magnetic flux tube between the footpoints, see Figure 5. A perturbation of this kind could be called a ‘‘tongue’’.

6 Discussion and Conclusions

Waves guided by various plasma non-uniformities are often considered as a superposition of eigenmodes of certain spatially localised resonators where the perturbations have an oscillatory structure between some reflecting or refractive walls and are evanescent outside (e.g. Nakariakov et al., 2016; Cheremnykh, Klimushkin, and Mager, 2016). In this paper, this approach was applied to the study of unstable small-scale corrugation (or ballooning) perturbations of a plasma arcade filled in with a radially non-uniform plasma of finite temperature. This allowed us to understand the influence of the radial wave structure on the instability of an arcade.

We considered an arcade as a half-cylinder with line-tying boundary conditions at the bottom of the corona. The effects of the magnetic shear were neglected, while the dependence of the perturbation along the axis of the arcade was taken into account. We focused on perturbations with wavelengths along the arcade much smaller than the radius of the arcade. We found that this plasma configuration may be unstable to the corrugated perturbations of the slow magnetoacoustic nature, which is mainly characterised by the radial displacement of the plasma. The arcade is most unstable to the perturbations with low radial harmonic numbers, $n \approx1$, and very short longitudinal (along the cylinder) wavelengths, in comparison with the radius of the rope. In the azimuthal direction, along the magnetic field lines, the wavelength is of the order of the field line length. Thus, the unstable perturbations cause displacements of the plasma in the radial direction, and have an almost circularly corrugated structure in the direction along the neutral line. The discussed instability is most effective in hot arcades with non-negligible values of the plasma parameter $\beta$.

The characteristic time of the instability was determined approximately by the ratio of the arcade radius and the sound speed (see Equation 48), i.e. the acoustic travel time across the arcade. For example, in an arcade of radius 50 Mm and filled with the plasma of the temperature of 1 MK, the characteristic time of the instability is estimated as about one minute. For hotter arcades, this time would be shorter, e.g. about twenty seconds, if the temperature were 10 MK. We should stress that the term ‘‘corrugated’’ highlights the ring-like localised (in the longitudinal direction) perturbations of the arcade. In an arcade, these perturbations are of an interchange nature, and hence could be considered to be similar to the fluting, or ballooning, perturbations of a plasma cylinder with the magnetic field along its axis (e.g. considered in Edwin and Roberts, 1983).

With the increase in the radial harmonic number, the ratio of the radial and longitudinal (along the neutral line) components of the magnetic field decreases, as does the instability growth rate. When this ratio approaches unity, the instability ceases. The full set of the instability conditions is determined by inequalities 55 and 57, which prescribe the field-aligned (azimuthal), longitudinal, and radial structure of the unstable corrugated mode.

As in the unstable modes the magnetic field and plasma are displaced mainly in the radial direction, the instability may lead to the formation of tongues that are highly localised in the direction along the arcade, displacing practically a whole line-tied magnetic flux tube in the radial direction. The magnetic field frozen into a plasma tongue pushed by the instability in the radial direction could reconnect with the overlying magnetic field, leading to the heating of the unstable flux tube. The instability can also act as a trigger to a flare or eruption if the host active region is in a subcritical equilibrium state. If the radial profiles of the equilibrium plasma parameters vary slowly along the arcade, the conditions for the corrugation instability could be fulfilled in only certain segments of the arcade, leading to the formation of a non-regular corrugated pattern. This resembles the pronounced irregular variation of the brightness of individual loops, i.e. the circularly corrugated rippling of the arcade in the longitudinal direction that is typical of post-flare arcades.

A sequence of the tongue emergences occurring at different locations along the arcade could induce a sequence of secondary flares in the host active region. In particular, this scenario could lead to the chaotic displacements of hard X-ray sources observed by Kuznetsov et al. (2016). We would like to stress that as the theory developed in this work considers perturbations with the small scales along the arcade, it is applicable to the short (in the longitudinal direction) arcades as well. Thus, the corrugation instability of plasma arcades may be responsible for several dynamical phenomena that are observed in the solar corona, which justifies the need for a better understanding of this effect.