Polarization Calibration of the Chromospheric Lyman-Alpha SpectroPolarimeter for a 0.1 % Polarization Sensitivity in the VUV Range. Part I: Pre-flight Calibration

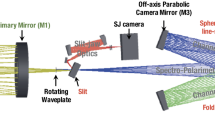
Abstract

The Chromospheric Lyman-Alpha SpectroPolarimeter (CLASP) is a sounding rocket experiment designed to measure for the first time the linear polarization of the hydrogen Lyman-${\alpha}$ line (121.6 nm) and requires a $0.1~\%$ polarization sensitivity, which is unprecedented for a spectropolarimeter in the vacuum UV (VUV) spectral range.

A unique polarization calibration experiment was conducted under vacuum conditions to estimate the response matrix of the instrument. For this purpose, a custom-made light source was designed to inject Lyman-${\alpha}$ light with a known linear polarization state into the spectropolarimeter. Two methods were employed to change the orientation of the linear polarization input: one by rotating the light-source itself (direct method), the other by rotating a half-waveplate located after the light-source’s polarizers (waveplate method). The spurious polarization, scale factor, and azimuth error terms of the response matrix were successfully estimated from the polarization calibration measurements. However, it was found that the direct method could not provide an accuracy better than $0.1~\%$ on the spurious polarization terms, whereas their required tolerance was ${<}\,0.017~\%$. On the other hand, the waveplate method determined these terms with only a ${\sim}\,0.04~\%$ accuracy due to residual cross-talk between polarization and intensity. Nevertheless, the polarization calibration confirmed the very low spurious polarization level of the instrument, which will also be confirmed with the flight data. The resulting response matrix deviated from an ideal one, and possible causes of the deviation are discussed by considering the polarization properties of the optical components.

Appendices

Appendix A: Light-Source Performances

The performances of the high-reflectivity coating applied on the light-source polarizers and spectropolarimeter polarization analyzers were measured at a synchrotron facility. The dependence of the S-polarization and P-polarization reflectivity (Rs and Rp) as a function of the angle of incidence is presented in Figure 18. More details on the coatings used for CLASP are given in Narukage et al. (2016).

Figure 18

Reflectivities Rs (left) and Rp (right) as a function of angle of incidence (AOI) at the Lyman-$\alpha$ wavelength for the $\mathrm{SiO}_{2}+\mathrm{MgF}_{2}$ multilayer coating, measured from six witness samples.

The Rs and Rp performances of the polarizers are important for estimating the polarization degree of the light-source output. Considering the converging beam created by the light-source ($\mathrm{F}/9.66$), the angle of incidence on the polarizers is different for various rays across the aperture, as shown in Figure 19.

Figure 19

Close-up of the converging beam double-reflection by the two polarizers of the light-source. The angle $\alpha$ is the Brewster angle ($68^{\circ}$) and $\beta$ is F number angle ($2.96^{\circ}$).

In this configuration, marginal rays can be defined as the meridional rays (YZ plan) and the sagital rays (XZ plan). The meridional rays are contained in the same YZ plane as the chief-ray, but have different angles of incidence on the polarizers because of the converging beam F number. Therefore, these meridional rays have a different Rs and Rp compared to the chief-ray and a gradient of polarization forms in the plane defined by these rays and the polarizer normal. On the other hand, the angles of incidence of the sagital rays are inclined with respect to the polarizer surface in a way that rotates the s–p axes, resulting in a rotated polarization direction with respect to the polarizer orientation.

The result at the pupil can be calculated by creating a map of the polarization after the reflection by the second polarizer for the ray’s passing through the center of the slit, as shown in Figure 20. The aperture mask placed on the lens was considered in the calculation, but the small spider-holder of the central obscuration was neglected. We note that the polarization gradient in the Y direction is very small as a result of the double reflection by the polarizers.

Figure 20

Stokes $Q/I$ and $U/I$ calculated across the light-source pupil after the reflection by the second polarizer.

In an ideal case with perfect optics, the spot created by the light-source is expected to be point-like, and the polarization of the spot is the averaged polarization over the pupil. In this situation, the $U/I$ (minor term in this configuration) created by the sagital rays is canceled out. In reality, the light-source spot is more complicated than that since the lamp electrode is not a point-like source and optical aberrations from the lens also affect the image. Fully understanding how the optics affect the distribution of polarization across the spot is hard, but the polarization at the pupil indicates that the average polarization amplitude is ${>}\, 99.85~\%$. The $1.5 \times10^{-3}$ difference from the perfectly polarized state could affect the scale factor measurements and was taken into account in the final error estimation. On the other hand, the polarization angle is mostly canceled out as the spot averages the polarization across the pupil, but a residual gradient along the spot might still remain.

In addition, although the polarization might be quite uniform across the center of the spot, the inclination angle of the light rays is affected by the light-source optics: rays illuminating the top or bottom of the spot should have a different inclination angle compared to rays illuminating the center of the spot.

The previous calculations of the polarization at the pupil are valid only if both polarizers are exactly parallel with each other, which was controlled using theodolite measurements, as shown in Figure 21. The reference was set using a small mirror bond onto the light-source interface plate. The angle $\theta$ and $\chi$ from Figure 21 around the X and Y axes were measured as

$$ \begin{aligned} & \theta_{X}' = 68^{\circ}00'29'' \quad \chi_{X}' = 67^{\circ}59'52'' \\ & \theta_{Y}' = 00^{\circ}11'19'' \quad\chi_{Y}' = 00^{\circ}12'48'' \end{aligned} . $$

(8)

Figure 21

Angle measurement with theodolite (dotted lines with arrows) on the light-source polarizers with respect to the light-source interface plate.

The relative tilt between the two polarizers was very small: only $37''$ around the X-axis. The tilt difference around the Y-axis was measured at $1'29''$, but the Y-axis of the polarizers was tilted from the Y-axis of the light-source reference mirror in this measurement. Additional measurements were performed to estimate the tilt of the polarizers around their Y-axis, hereafter $\mathrm{Y}'$, since such a tilt could induce azimuthal error in the calibration. An alignment cube (i.e. small cube with precise $90^{\circ}$ angles and reflecting surfaces) was positioned on the light-source baseplate at the base of each polarizer, and the theodolite was used to measure the angle between each polarizers with respect to the baseplate, giving an information about the tilt around the $\mathrm{Y}'$-axis of the polarizers: $\theta_{Y'} = +1'22''$ and $\chi_{Y'} = +1'13''$. The measured tilt of the polarizers was introduced in the opto-polarimetric calculation, and the resulting influence on both major and minor term was confirmed to be negligible.

An auto-collimator was used to measure the alignment of the light-source polarizers to the interface plate. The auto-collimator was positioned on the left side of the light-source in Figure 21 and created a collimated beam in the $+Z$ direction, which was used to illuminate a flat mirror placed on the interface plate. Part of the collimated beam illuminated the flat mirror after going through the two polarizers, whereas the remaining part of the collimated beam was directly reflected by the flat mirror. Images of the two reflected beams were imaged onto the auto-collimator display, and the angle between the polarizer and the flat mirror could be deduced from the distance between the two spots. The alignment of the two polarizers to the interface plate was measured at $-1'1''$ around the X-axis and $+4'10''$ around Y-axis. These X and Y tilts of the polarizer alignment represent a slight change in the chief-ray angle onto the slit, and their effect on the polarization input of the light-source is negligible.

Finally, the mechanical accuracy of the pins used to align the light-source with the CLASP spectropolarimeter includes an additional ${\pm}\,{\sim}2'$ error on the Z-tilt of the polarizers when attached to the spectropolarimeter. This possible misalignment of the light-source can only create a minor term of $\sin{\pm 2'}= \pm5 \times10^{-4}$ for the input.

Appendix B: Polarization Gradient Along the Slit

Figure 8 revealed a polarization gradient along the slit. These trends were consistently observed for the four orientations of the light-source performed during the waveplate method measurements at the center of the slit and are summarized in Figure 22.

Figure 22

Polarization profile along the slit (X-axis in pixel) for the waveplate method measurements, with illumination at the center of the slit. The light-source orientation is shown by color: blue for $+Q_{0^{\circ}}$, green for $+U_{45^{\circ}}$, orange for $-Q_{90^{\circ}}$, and red for $-U_{315^{\circ}}$.

The quantitative shape of this polarization gradient can be reproduced by considering that the rays forming the light-source spot on the slit have a different average incidence angle depending on their location along the slit, which is due to the light-source optics. These incidence angles are then transferred to the spectropolarimeter polarization analyzers and create a polarization gradient. This effect is similar to the discussion in Appendix A: since the slit is perpendicular to the orientation of the analyzer for channel 1, only a change of AOI occurs and a polarization gradient is formed by the Rs and Rp dependency (Figure 18). For channel 2, the ray angles are rotating the s–p coordinate system on the analyzer, creating a different gradient of polarization.

The observed polarization profiles along the slit were calculated (Figure 23) by considering a $+Q$ input beam, assuming an illumination at the center of the slit and a ray angle distribution along the slit with ${\pm}\,2.9^{\circ}$ (i.e. corresponding to the F number of the light-source), zero being the center of illumination.

Figure 23

Polarization profile simulated along the slit for the two channels for a perfect $+Q$ input beam (along the slit). The dashed line shows the position of the center of illumination.

The shape of the major term gradient for the two channels can be reproduced by these calculations, with the major term maximum in channel 1 being shifted from the position of the maximum intensity (i.e. here the center of the slit). The gradient in the minor term of channel 2 can also be reproduced with a similar order of amplitude (${\sim}\,10~\%$) considering this distribution of ray angle along the slit. The calculation could not reproduce the small minor term gradient observed in channel 1, which can be a residual minor term gradient created by the light-source along the polarizer axis (see Appendix A) because the sign seems to change depending on the light-source orientation. The polarization in the tails of the spot illumination could not be properly reproduced, indicating that another effect might operate, possibly a vignetting of the pupil by the grating clear-aperture for these off-axis positions.

The assumption of a ray angle distribution along the spot created by the lens F number is a simplification of reality, where the extended source of the deuterium lamp and spherical aberration of the lens also play a role. Nevertheless, this simple model quantitatively indicates that the observed polarization gradient is an artifact of the light-source rays on the spectropolarimeter analyzers.

A tilt of all the rays including the chief-ray is introduced when moving the light-source spot to the edge of the slit. The amplitude of this tilt is ${\pm}\,0.27^{\circ}$, considering the focal length of the light-source $\mathrm{MgF}_{2}$ lens ($f=248.5~\mbox{mm}$, located at 535 mm from the slit) and the slit length ($l=5~\mbox{mm}$). The effect of this tilt in the rays on the light-source polarization is small because the dual reflection by the polarizers reduces the polarization error introduced by the off-axis incidence. But this tilt does have an effect on the polarization analyzer inside the spectropolarimeter. Channel 1 is not affected because of its orientation, since the tilt of the rays is contained in the plan perpendicular to the analyzer orientation (meridional rays), which results only in a negligible change of the major term. On the other hand, the tilt of the ray angle is in the plane parallel to the analyzer for channel 2 and creates a non-zero minor term at the illumination center that is due to the rotating the s–p coordinate. This effect was calculated as a ${\pm}\,{\sim}\,0.5^{\circ}$ shift of the polarization angle at the center of illumination, directly translating into a ${\pm}\,{\sim}\,1~\%$ shift in the channel 2 minor term when moving the light-source at the edge of the field of view. This was observed in Figure 8 and indicates that the gradient of the azimuth error terms in channel 2 from Figure 15 is an artifact of the configuration used during the calibration. This is not expected to occur when the telescope feeds the spectropolarimeter in the flight configuration because the off-axis angles of the telescope are much smaller (${\pm}\,200''$ compared to ${\pm}\, 0.27^{\circ}$).

Appendix C: Determination of the LS Half-Waveplate Retardance

A deviation from the perfect retardance of the LS half-waveplate ($\delta=180^{\circ}$) could affect the estimation of the spurious polarization terms depending on the position of the light-source and on the LS half-waveplate orientation. The reason is that the spurious polarization terms are derived from the ($q'_{+Q}, q'_{-Q}$) pair of measurements for the $x_{01}$ term and from the ($u'_{+U},u'_{-U}$) pairs of measurements for the $x_{02}$ term. In a configuration with the light-source at $+Q_{0^{\circ}}$, the LS half-waveplate affects the inputs in different ways depending on the position of its principal axis: $+Q$ input is not affected by the LS half-waveplate because the principal axis is aligned with the polarization direction, i.e. full transmission. On the other hand, $q'_{-Q}$ is multiplied by $\cos{\delta}$ because of the angle between the LS half-waveplate principal axis and the polarization direction of the light-source (${\pm}\, 45^{\circ}$). Finally, the angle between the half-waveplate principal axis and the polarization direction is the same for both $u'_{+U}$ and $u'_{-U}$ positions (${\pm}\,22.5^{\circ}$), and therefore the factor affecting both of them has the same amplitude: ${\pm}\,(1-\cos{\delta })/2$, and the $x_{02}$ terms is not be affected by the LS half-waveplate retardance because the same factor affecting both measurements canceled out. However, $x_{01}$ is affected, as the retardance of the waveplate affects the $q'_{+Q}$ and $q'_{-Q}$ measurements differently.

The retardance of the LS half-waveplate was estimated by performing the least-squares fitting described in Section 3.2.2 for various values of the retardance and in this way changing the input polarization of the fitting. This was performed for each light-source position: $+Q_{0^{\circ}}$, $+U_{45^{\circ}}$, $-Q_{90^{\circ}}$ and $-U_{315^{\circ}}$. The spurious intensity, scale factor, and azimuth error terms were observed to be almost insensitive to the change of the input polarization. On the other hand, the spurious polarization terms were affected depending on the light-source position, as explained previously. Figure 24 shows an example for channel 1 in the $+Q_{0^{\circ}}$ and $+U_{45^{\circ}}$ inputs of the light-source: the $x_{02}$ term appears to be almost insensitive to the LS half-waveplate retardance in the $+Q_{0^{\circ}}$ input, whereas the $x_{01}$ term is highly dependent. The opposite effect can be seen for the $+U_{45^{\circ}}$ input. In this example, the LS half-waveplate retardance was estimated by reporting the value of the $x_{01}$ term for the $+U_{45^{\circ}}$ orientation (i.e. insensitive to the half-waveplate effect) onto the curve of the $x_{01}$ term at $+Q_{0^{\circ}}$ (i.e. sensitive to the half-waveplate effect) and reading the corresponding retardance on the X-axis. Performing this for all four light-source orientations on the $x_{01}$ and the $x_{02}$ terms and for the two channels provided an estimate of $\delta$ around $184.4^{\circ}\pm 0.7^{\circ}$.

Figure 24

Resulting spurious polarization terms after fitting when the input polarization varied by changing the retardance of the LS half-waveplate. Light-source positions were $+Q_{0^{\circ}}$ and $+U_{45^{\circ}}$. Red solid lines indicate when the matrix elements are determined independently of the half-waveplate retardance, with the dashed line indicating their values on the corresponding matrix elements dependent on the half-waveplate retardance.

Appendix D: Mueller Equations from CLASP

The Mueller matrix links the incoming Stokes vector to the measured Stokes vector and can be calculated for CLASP as $M_{\mathit{CLASP}}(\alpha,\beta ,\delta) = L(\alpha)R(\beta,\delta)$, where $L(\alpha)$ is the expression for a linear polarizer with orientation $\alpha$ and $R(\beta ,\delta)$ is the expression for a linear retarder with retardance $\delta$ and a fast-axis angle $\beta$ (see Del Toro Iniesta, 2003).

Although the expression for the Mueller matrix $M_{\mathit{CLASP}}(\alpha,\beta ,\delta)$ is quite complicated, only the intensity can be measured by the cameras. Hence, only the first row of $M_{\mathit{CLASP}}(\alpha,\beta,\delta )$ is important, and the general expression of the intensity (i.e. referred as $D$ to avoid confusion with Stokes $I$) as a function of $\alpha$, $\beta$, and $\delta$ is

$$\begin{aligned} D_{\alpha,\beta,\delta} =& \frac{1}{2} \biggl[ I + \frac{1}{2} (Q\cos{2\alpha}+U\sin{2\alpha} ) (1+\cos {\delta} ) + \sin{ \delta}\sin{(2\alpha-2\beta)}V \\ &{}+ \frac{1}{2}(1-\cos{\delta}) \bigl[(Q\cos{2\alpha}-U\sin{2\alpha}) \cos {4\beta} \\ &{}+ (Q\sin{2\alpha}+U\cos{2\alpha})\sin{4\beta} \bigr] \biggr]. \end{aligned}$$

(9)

The expression of the intensity is simplified by taking $\alpha =90^{\circ}$ for channel 1 and $\alpha=0^{\circ}$ for channel 2. The expression also has to be integrated on $\beta$ to account for the continuous motion of the PMU half-waveplate. This is shown in Equations (10) and (11) with $\beta_{i}$ the initial angle of the half-waveplate and $\beta_{f}$ its final angle for any possible angular position. The factor in front of the integral is a normalization for the angular movement.

$$\begin{aligned} \int_{\beta_{i}}^{\beta_{f}} D_{\beta,\delta,\mathit{ Channel} 1} d\beta =& \frac{1}{2} \biggl[ \biggl[I - \frac{Q}{2}(1+\cos{\delta}) \biggr] \\ &{}-\frac{1}{(\beta_{f}-\beta_{i})}\frac{1}{2}\sin{\delta}V [\cos{2\beta _{f}} - \cos{2\beta_{i}}] \\ &{}+\frac{1}{(\beta_{f}-\beta_{i})}\frac{1}{8}(1-\cos{\delta}) \bigl[-Q[\sin{4 \beta_{f}} - \sin{4\beta_{i}}] \\ &{}+ U[\cos{4\beta_{f}} - \cos{4\beta_{i}}] \bigr] \biggr]. \end{aligned}$$

(10)

$$\begin{aligned} \int_{\beta_{i}}^{\beta_{f}} D_{\beta,\delta, \mathit{Channel} 2} d\beta =& \frac{1}{2} \biggl[ \biggl[I + \frac{Q}{2}(1+\cos{\delta}) \biggr] \\ &{}+\frac{1}{(\beta_{f}-\beta_{i})}\frac{1}{2}\sin{\delta}V [\cos{2\beta _{f}} - \cos{2\beta_{i}}] \\ &{}+\frac{1}{(\beta_{f}-\beta_{i})}\frac{1}{8}(1-\cos{\delta}) \bigl[Q[\sin {4 \beta_{f}} - \sin{4\beta_{i}}] \\ &{}- U[\cos{4\beta_{f}} - \cos{4\beta_{i}}] \bigr] \biggr]. \end{aligned}$$

(11)

Assuming a perfect half-waveplate with retardance $\delta=180^{\circ}$, the expression of the measured intensity for four consecutive exposures taken every $22.5^{\circ}$ can be derived as

$$ \begin{aligned} & D_{1, \mathit{Channel} 1} = \frac{1}{2} \biggl[ I +\frac{2}{\pi}[-Q - U] \biggr] \quad D_{1, \mathit{Channel} 2} = \frac{1}{2} \biggl[ I +\frac{2}{\pi}[+Q + U] \biggr] \\ & D_{2, \mathit{Channel} 1} = \frac{1}{2} \biggl[ I +\frac{2}{\pi}[+Q - U] \biggr] \quad D_{2, \mathit{Channel} 2} = \frac{1}{2} \biggl[ I + \frac{2}{\pi}[-Q + U] \biggr] \\ & D_{3, \mathit{Channel} 1} = \frac{1}{2} \biggl[ I +\frac{2}{\pi}[+Q + U] \biggr] \quad D_{3, \mathit{Channel} 2} = \frac{1}{2} \biggl[ I + \frac{2}{\pi}[-Q - U] \biggr] \\ & D_{4, \mathit{Channel} 1} = \frac{1}{2} \biggl[ I +\frac{2}{\pi}[-Q + U] \biggr] \quad D_{4, \mathit{Channel} 2} = \frac{1}{2} \biggl[ I + \frac{2}{\pi}[+Q - U] \biggr]. \end{aligned} $$

(12)

The measured Stokes $Q'/I'$ and $U'/I'$ shown in Equation (1) can be retrieved with a linear combination of the measured intensity from Equation (12). We note that Equation (1) is multiplied by a $\pi/2$ factor to cancel the $2/\pi$ factor coming out of Equation (12) as a result of the continuous rotation of the PMU half-waveplate.

Appendix E: Estimation of the Azimuth Error Terms

A misalignment of the PMU half-waveplate principal axis with respect to the $+Q$ direction can be represented as a small angle shift $\Delta$ added to the angle $\beta$ from Equation (9). Considering the retardance of the PMU half-waveplate $\delta$ as $180^{\circ}$, the Stokes $Q$ and $U$ can be obtained from the Mueller equations after normalization as

$$ \begin{aligned} &Q' = Q\cos{4\Delta} + U \sin{4\Delta} \\ &U' = -Q\sin{4\Delta} + U\cos{4\Delta}. \end{aligned} $$

(13)

Cross-talk between Stokes $Q$ and $U$ is introduced by the angle shift $\Delta$. The residual error angle of the PMU half-waveplate principal axis after alignment to the $+Q$ direction was measured experimentally at $\Delta=+0.08 \pm0.05^{\circ}$. Considering a perfect polarized input as $(I,Q,U,V)^{\top}= (1,1,0,0)^{\top}$ to the spectropolarimeter, the measured $q'$ would be proportional to $\cos{4\Delta}\sim1$ and $u'$ to $-\sin{4\Delta} \sim-0.006$, which is comparable to the measured $U'/I'$ for a $+Q$ input. When this effect is calculated for other inputs, the sign of the minor term can be seen to nicely match the sign of the observation.

Appendix F: Determining the Modulation Error

The rotation speed of the PMU is expected to be constant. However, systematic fluctuations were recorded by the PMU driver, which produced systematic error on the half-waveplate angle at each exposure, as shown in Figure 25. This angle error on each exposure can be taken into account when integrating the Mueller equation from the initial angle of the half-waveplate (i.e. including the corresponding angle error) $\beta_{i}$ to the final angle $\beta_{f}$ (see Equations (10) and (11)), and results in different scaling factors on the modulated $Q$ and $U$ of each exposure. The demodulated polarization signal was calculated for the mean angle error using a given PMU rotation (i.e. 16 images) taken with the light-source with $+Q_{0^{\circ}}$ input. Similar calculations were also conducted for a PMU rotation with a $+U_{45^{\circ}}$ input. The results were slightly different than from the simple demodulation scheme presented in Equation (1), but this error is already included in the elements of the response matrix. However, possible uncertainty of the angle error on each exposure (i.e. error bar in Figure 25) can produce an additional error on the estimated polarization signal. This error might be important and is represented by $\sigma_{\mathit{modulation}}$.

Figure 25

Average angle error on the PMU half-waveplate due to the non-uniform rotation speed, per full PMU rotation. Data from the PMU driver were recorded for 180 PMU rotation and are shown by the gray curves, and the error bars are shown the standard deviation of the angle error at each point.

The $\sigma_{\mathit{modulation}}$ was estimated using a Monte Carlo (MC) method: the polarization signal was demodulated by varying the angle error on each exposure for multiple trials. The angle error on each exposure was taken from the PMU driver data: assuming random fluctuation of the angle error is incorrect because the consecutive angle errors are correlated (i.e. within the timescale of the PMU feed-back loop). Hence, the angle error of 16 consecutive exposures was selected randomly along the 160 PMU rotations considered from the PMU driver data, effectively increasing the number of possibilities from 160 (i.e. PMU rotation only starting at $D_{1}$) to more than 2700 while keeping the correlation between the different angle errors. The polarization signal was demodulated for each of these 2700 possibilities (i.e. $N=2700$).

The final $\sigma_{\mathit{modulation}}$ was calculated as the standard deviation out of the $N$ polarization signals obtained with the MC method. The results per PMU rotation are dependent on the measured $q'$ and $u'$ and are shown in Figure 26. The $\sigma_{\mathit{modulation}}$ decreases as the square root of the number of PMU rotations stacked when demodulating, as the angular error of the PMU tends toward the mean angle error. In case of the polarization calibration, although the $\sigma_{\mathit{modulation}}$ for a fully polarized signal is close to $1.5~\%$, 180 PMU rotations were summed for each waveplate method measurement, decreasing the $\sigma_{\mathit{modulation}}$ to around $0.1~\%$. In addition, since 16 measurements were taken at each of the four different light-source orientations, the residual effect of the $\sigma_{\mathit{modulation}}$ is already included in the error from the fitting (see Table 3) and might be a contributor to the large error on the spurious polarization. This error might explain the $0.1~\%$ dependence of the input polarization amplitude on the light-source orientation. This error is expected to be of limited importance during the flight, where the input polarization is weakly polarized (${<}\,5~\%$), although it might have to be considered when using a limited number of PMU rotations.

Figure 26

Estimated $\sigma_{\mathit{modulation}}$ per PMU full rotation, as a function of the measured $Q/I$ and $U/I$. The two contour lines show where the $\sigma_{\mathit{modulation}}$ is $0.1~\%$ (outer) and $0.01~\%$ (inner).

Appendix G: Case Study when the Spurious Intensity is Neglected

The results when the effects of $x_{10}$ and $x_{20}$ are neglected are shown in Table 7. Although the scale factor and azimuth error terms are almost unaffected, the spurious polarization becomes significantly larger. The reason is the similar effect of the spurious polarization and the spurious intensity on the measured polarization. It is interesting to note that the accuracy achieved on the spurious polarization improved because the spurious intensity did not compete with the spurious polarization and the spurious polarization was determined only using the major term.

Table 7 Response matrix elements at the center of the slit derived from the waveplate method measurements when the $x_{10}$ and $x_{20}$ terms were neglected. The top table shows channel 1 and the bottom table channel 2. The error was derived as the maximum difference from the average value, with errors larger than the tolerance marked in bold. LS refers to the light-source.