1 Introduction

The understanding of propagating magneto-hydrodynamic (MHD) waves, whilst just one facet of the investigation into the nature of the multitude of observed activity within the solar atmosphere, is an important tool for the description of energy transfer within solar environments and other astrophysical plasmas. The study of MHD waves has, for the most part, been restricted to the study of trapped waves, where the wave propagation is considered to be confined to the interior of the magnetic structure under consideration; for a full review of this theoretical work see e.g. Roberts (2000). Such an analysis is performed in this manner for good reason, the magnetic structures found in the chromosphere or the corona are unlikely to leak significant quantities of energy through the process as investigated and presented in this article. The wave propagation within such non-leaky structures is well described by the series of works by Roberts (1981) through to Edwin and Roberts (1983). Many other studies have expanded upon this framework, and reviews of MHD wave propagation in the context of solar magneto-seismology (SMS) are given by Ruderman and Erdélyi (2009), Wang (2011) and Mathioudakis, Jess, and Erdélyi (2013) for transverse, longitudinal, and Alfvén waves, respectively.

The introductory work, by e.g. Defouw (1976) or Roberts (1981), on MHD wave propagation laid the foundations for the analysis of propagating waves and is widely used in their current format. Most of these early works restricted themselves to models with purely real wave frequency, \(\omega\), representing a conservation of energy within the magnetic structure. Complex frequencies, to account for damping of these MHD waves, were considered by Wilson (1979) for a magnetic field-free environment, whilst Spruit (1982) and Cally (1986) made some of the first rigorous investigations into damping as a result of energy losses into the surrounding magnetic atmosphere. Later works have expanded upon the results found therein; perhaps the most relevant to this article were the efforts made of combining the damping through energy leakage and resonant absorption as investigated by Goossens and Hollweg (1993), Stenuit et al. (1999), and Goossens et al. (2009). For a review of the resonant absorption as discussed in these works, see e.g. Goossens, Erdélyi, and Ruderman (2011).

Time-dependent background plasmas are a growing area of study within the solar physics community. A number of recent studies (e.g., Morton and Erdélyi, 2009, 2010; Morton, Hood, and Erdélyi, 2010; Erdélyi, Al-Ghafri and Morton, 2011) have made a series of investigations into dynamic plasmas and the standing wave modes found therein, whilst the first two works in this series, Williamson and Erdélyi (2014a, 2014b; Paper I and Paper II hereafter, respectively) discussed time-dependent propagating waves in coronal environments, showing that both the fast kink and the slow sausage wave modes are amplified exponentially in time for a temporally decreasing background density. However, both works assumed evanescent wave propagation. This assumption is now relaxed in the first part of this work, allowing for energy leakage into the magnetised atmosphere and allowing for a more generalised description of MHD wave propagation in astrophysical plasmas.

The work performed earlier in this series was carried out under the assumption of a coronal environment, i.e. the over-dense loop and the low plasma-beta assumptions (Papers I and II, respectively). Whilst such work is useful in describing the plentiful wave propagation in the solar atmosphere, it is less applicable in describing wave activity in the photosphere or other regions with a density ratio close to, or greater than, one. We here aim to generalise the study of MHD waves in time-dependent plasmas, allowing for the concept of energy leakage to be taken into account. Energy leakage is of primary concern in under-dense structures, such as coronal holes or sunspots, but will be present in most of the flux tubes found in solar structures.

2 Governing Equations

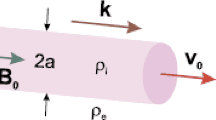
Here, we constructed a magnetic flux tube in a magnetised atmosphere of constant density, to which we, again, applied the zero plasma-\(\beta\) approximation. Therefore, we required that neither the interior nor the exterior region of the waveguide have a finite plasma pressure, i.e. \(p_{\mathrm{i}}=p_{\mathrm{e}}\approx0\). In both regions, the unperturbed magnetic field (\(B_{0z}\)) is constant and vertical. Neglecting the plasma pressure directly implies that the magnetic fields are identical inside and outside the waveguide. In this work, however, we considered an exterior plasma density that is greater than or equal in magnitude to the initial interior density, \(\rho_{\mathrm{i}0}\) allowing for the propagation of leaky MHD waves. We considered such solutions as are appropriate in the analysis of e.g. coronal holes and sunspots. The main emphasis of this analysis is on the time-dependent background density, where the density is assumed to have the form

$$\rho_{\mathrm{i}0}\exp[-At]. $$

Here \(A\) is a small, positive constant. The temporal variation in density necessitates a bulk flow with the form \(V_{0z}=Az\). All other background parameters are assumed to be constant.

Given these constraints, we now attempted to construct two governing equations under the assumption of ideal, linearised MHD for the radial displacement (\(\xi_{r}\)) and perturbed total pressure (\(P\)). In terms of methodology, this analysis closely follows that performed in Paper I and, as such, we merely state the two governing equations after the application of the WKB approximation to leading order. For further details on deriving the governing equations and the WKB approximation used see Paper I. The application of the WKB approximation gives an undetermined wave phase, \(\theta\), the derivatives of which are represented by \(\Omega\), \(K\), and \(\varpi\). The quantities are the dynamic frequency, wavenumber, and Doppler-shifted frequency, respectively,

$$\Omega=-\frac{\partial\theta}{\partial t},\qquad K=\frac{\partial\theta }{\partial z},\qquad\varpi= \Omega-V_{0z}K. $$

In what follows, \(V_{\mathrm{A}}\) is the Alfvén speed and \(\varpi_{\mathrm{A}}\) is the Alfvén frequency. All these quantities are defined in the same manner as in Papers I and II, that is,

$$V_{\mathrm{A}}^{2}=\frac{B_{0}^{2}}{\mu_{0}\rho_{0}},\qquad\varpi_{\mathrm{A}}^{2}=V_{\mathrm{A}}^{2}K^{2}, \qquad\varpi=\Omega-V_{0z}K. $$

The two governing equations are

$$ \rho_{0}\bigl(\varpi^{2}-\varpi_{\mathrm{A}}^{2} \bigr)\frac{1}{r}\frac{\partial(r\xi _{r})}{\partial r}=- \biggl[\varpi^{2}-V_{\mathrm{A}}^{2} \biggl(K^{2}+\frac {m^{2}}{r^{2}} \biggr) \biggr]P, $$
(1)

and

$$ \frac{\partial P}{\partial r}=\rho_{0}\bigl(\varpi^{2}- \varpi_{\mathrm{A}}^{2}\bigr)\xi_{r}. $$
(2)

We note here that with the exclusion of the temporal dependance, the two governing equations reduce to their counterparts in previous studies (see e.g. Hain and Lüst, 1958). At this point we can, once again, solve the two governing equations for the perturbed total pressure and the radial displacement. The differential equation for the perturbed total pressure can therefore be written as

$$ \frac{\partial^{2}P}{\partial r^{2}}+\frac{1}{r}\frac{\partial P}{\partial r}+ \biggl[\frac{\varpi_{\mathrm{i},\mathrm{e}}^{2}-\varpi_{\mathrm{Ai},\mathrm{e}}^{2}}{V_{\mathrm{Ai},\mathrm{e}}^{2}} -\frac{m^{2}}{r^{2}} \biggr]P=0, $$
(3)

where subscripts i and e indicate background variables in either the interior or exterior regions, respectively. The interior counterpart of Equation (3) can be solved in an analogous fashion to that carried out previously in Paper I. However, given the relaxation of the evanescent condition here, the exterior solution will now take a very different form.

3 Dispersion Relation, Frequency, and Wavenumber

At this point, we no longer required that the exterior wave propagation be evanescent. Indeed, in the current regime of an under-dense flux tube, it is far more likely that the wave solution applicable to the exterior region will carry energy away from the flux tube and into the surrounding magnetised atmosphere. Upon the relaxation of this assumption, we find that the mathematical solution to Equation (3) now has more physical applications and, therefore, the perturbed total pressure for body waves can now be written as

$$ Q_{\mathrm{Pi}}=A_{\mathrm{i}}J_{m}(M_{\mathrm{i}}r),\qquad Q_{\mathrm{Pe}}=A_{\mathrm{e}}H_{m}^{(1)}(M_{\mathrm{e}}r), $$
(4)

where \(J_{m}\) and \(H_{m}^{(1)}\) are the Bessel and Hankel functions of the first kind of order \(m\). The quantities \(M_{\mathrm{i}}\) and \(M_{\mathrm{e}}\) are the radial wavenumber in the interior and exterior regions, respectively, and are given by

$$ M_{\mathrm{i}}=\frac{\varpi^{2}-\varpi_{\mathrm{A}}^{2}}{V_{\mathrm{A}}^{2}},\qquad M_{\mathrm{e}}= \frac{(\Omega^{2}-V_{\mathrm{Ae}}^{2}K^{2})}{V_{\mathrm{Ae}}^{2}}. $$
(5)

We note that the \(J_{m}\) function may be replaced by the modified Bessel function of the first kind, \(I_{\mathrm{m}}\). The modified Bessel function solution represents the surface wave mode and is not the focus of this work. We discarded the Hankel function of the second kind because this represents an incoming fast MHD wave, and this scenario would be beyond the scope of this work. Using Equations (2) and (4), we can therefore write the expression for the radial displacement as

$$ \xi_{\mathrm{ri}}=\frac{A_{\mathrm{i}}}{\rho_{\mathrm{i}}(\varpi^{2}-\varpi_{\mathrm{A}}^{2})} \frac{\partial J_{m}(M_{\mathrm{i}}r)}{\partial r},\qquad \xi_{\mathrm{re}} =\frac{A_{\mathrm{e}}}{\rho_{\mathrm{e}}(\Omega^{2}-\varpi_{\mathrm{Ae}}^{2})}\frac {\partial H_{m}^{(1)}(M_{\mathrm{e}}r)}{\partial r}. $$
(6)

By applying continuity in both the perturbed quantities, i.e. the radial displacement and the total pressure perturbation, across the discontinuity in the magnetic field, we can now express the dispersion relation for leaky waves in a steady temporally evolving, time-dependent flux tube as

$$\begin{aligned} &\rho_{\mathrm{i}}\bigl(\varpi^{2}-\varpi_{\mathrm{A}}^{2} \bigr)J_{m}(M_{\mathrm{i}}R)H_{m}^{(1)'}(M_{\mathrm{e}}R)M_{\mathrm{e}} \\ &\quad{}=\rho_{\mathrm{e}}\bigl(\Omega^{2}-\varpi_{\mathrm{Ae}}^{2} \bigr)J_{m}'(M_{\mathrm{i}}R)H_{m}^{(1)}(M_{\mathrm{e}}R)M_{\mathrm{i}}. \end{aligned}$$
(7)

It is worth reiterating at this point that Equation (7) is a partial differential equation for the wave-phase, \(\theta\), with respect to time and height. The complicated nature of this equation necessitates a further approximation to progress analytically with this problem. The approximation chosen is the thin-tube (TT) approximation, as this represents the easiest to way to approach the problem without sacrificing physical application. For the purposes of this work, the thin-tube approximation was taken to be the limit where \(M_{\mathrm{e}}R, M_{\mathrm{i}}R\rightarrow0\) as \(kR\rightarrow 0\). The imaginary component of the Hankel function now represents the damping of the propagating fast wave. Equation (7) can be reduced to

$$ \rho_{\mathrm{i}}\bigl(\varpi^{2}-\varpi_{\mathrm{A}}^{2} \bigr)+\rho_{\mathrm{e}}\bigl(\Omega^{2}-\varpi _{\mathrm{A}}^{2} \bigr)={\mathrm{i}}\frac{\pi}{2}(M_{\mathrm{e}}R)^{2} \rho_{\mathrm{i}}\bigl(\varpi ^{2}-\varpi_{\mathrm{A}}^{2} \bigr). $$
(8)

Whilst at this point other works have performed further analytical simplification to understand this result, we instead determined the explicit forms of the real parts of the frequency and the wavenumber to explore the evolution of the damping in time. The coronal approximation made in Papers I and II is now no longer applicable because the density ratio is unity or greater, therefore, a new method of approximation must be used. By making assuming moderate activity (i.e. \(V_{0z}\ll V_{\mathrm{A}}\)), we can reduce the real part of the dispersion relation from

$$\Omega=\frac{V_{0z}K}{1+\chi}+\frac{\sqrt{2V_{\mathrm{A}}^{2}(1+\chi)-\chi V_{0z}^{2}}}{1+\chi}K $$

to

$$ \frac{\partial\theta}{\partial t}+ \biggl[\frac{V_{0z}}{1+\chi}+\frac {\sqrt{2}V_{\mathrm{A}}}{\sqrt{1+\chi}} \biggr]\frac{\partial\theta}{\partial z}=0. $$
(9)

Equation (9) can be solved using the method of characteristics to give an expression for the wave phase, \(\theta\), in terms of an arbitrary function, \(F\). Then \(\theta\) can be written as

$$\begin{aligned} \theta =&F \biggl[\frac{V_{0z}}{A}(1+\chi)\exp[-At]+\frac{2\sqrt{2}V_{\mathrm{A}0}}{A} \biggl( \sqrt{\exp[-At]+\chi_{0}} \\ &{}-\sqrt{\chi_{0}}\textrm{arctanh} \biggl[\frac{\sqrt{\chi _{0}+\exp[-At]}}{\sqrt{\chi_{0}}} \biggr] \biggr) \biggr], \end{aligned}$$
(10)

for a density ratio, \(\chi=\rho_{\mathrm{e}}/\rho_{\mathrm{i}}\) and an initial density ratio, \(\chi_{0}=\rho_{\mathrm{e}}/\rho_{\mathrm{i}0}\). This expression is unwieldy and without further approximation difficult to apply boundary conditions to. A Taylor-series expansion of the arctanh function is ruled out by physical constraints and, hence, this approach is of little practical use. To make analytical progress, we therefore returned to Equation (9) and approximated the characteristic lines. We now required that the density ratio, \(\chi\), must fulfil the condition \(\chi>1\). We can, then, approximate the characteristic lines, using the binomial expansion, as

$$\begin{aligned} C =&\frac{V_{0z}(1+\chi)}{A}\exp[-At]-\sqrt{2}V_{\mathrm{A}0}\int\sqrt{1+\chi } \exp[-At/2]\,dt \\ =&\frac{V_{0z}(1+\chi)}{A}\exp[-At]-\sqrt{2\chi_{0}}V_{\mathrm{A}0}\int \biggl(\sqrt{1+\frac{1}{\chi}} \biggr)\,dt \\ \approx&\frac{V_{0z}(1+\chi)}{A}\exp[-At]-\sqrt{2\chi_{0}}V_{\mathrm{A}0} \int \biggl(1+\frac{1}{2\chi} \biggr)\,dt. \end{aligned}$$

The general solution to Equation (9) can then be shown to be given by the arbitrary function

$$ \theta=F(g)=F \biggl[\frac{V_{0z}(1+\chi)}{A}\exp[-At]-2\sqrt{2\chi _{0}}V_{\mathrm{A}0} \biggl(t-\frac{1}{2A\chi} \biggr) \biggr]. $$
(11)

After applying the constant-driver condition, i.e. \(\theta (0,t)=-\omega t\), Equation (8) becomes

$$ \theta=\frac{\omega}{A} \biggl[\frac{A}{2\sqrt{2\chi_{0}}V_{\mathrm{A}0}}g-W \biggl(\frac{1}{2\chi_{0}} \exp \biggl[\frac{Ag}{2\sqrt{2\chi_{0}}V_{\mathrm{A}0}} \biggr] \biggr) \biggr], $$
(12)

where \(W\) is the Lambert function defined as

$$W(x)\exp\bigl[W(x)\bigr]=x. $$

For further details on the Lambert function see e.g. Corless et al. (1996).

From Equation (12) we can now find the explicit forms of the dynamic frequency and wavenumber. The dynamic frequency, \(\Omega\), is given by

$$ \Omega=\frac{\omega}{2\sqrt{2\chi_{0}}V_{\mathrm{A}0}}\frac{V_{0z}\exp [-At]+2\sqrt{2}V_{\mathrm{A}0}(1+(2\chi)^{-1})}{(1+W)}, $$
(13)

and the dynamic wavenumber is given by

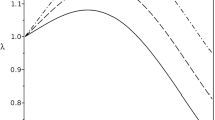
$$ K=\frac{\omega}{2\sqrt{2\chi_{0}}V_{\mathrm{A}0}}\frac{1+\chi}{(1+W)}\exp[-At]. $$
(14)

\(\Omega\) evolves in the manner shown in Figure 1 when plotted for the characteristic density change (\(t/\tau_{\rho}\)) and characteristic flow (\(V_{0z}/V_{\mathrm{A}0}\)). The dynamic frequency can be shown to be decreasing in a manner analogous to that found in the first two papers in this series. The point at which the frequency becomes approximately constant, i.e. past the point of rapid decrease, can be compared to the point at which the interior of the flux tube is largely evacuated of density and, hence, the change in frequency past that point is negligible. A similar property can be derived for the dynamic wavenumber in that there is the initial rapid decrease, before tending to a settled limit after the point where the tube has been effectively evacuated of plasma, see Figure 2.

Figure 1
figure 1

Dynamic frequency of propagating leaky waves plotted for characteristic change periods (\(t/\tau_{\rho}\)) against characteristic flow speeds (\(V_{0z}/V_{\mathrm{A}0}\)).

Full size image
Figure 2
figure 2

Dynamic wavenumber of propagating leaky waves plotted for characteristic change periods (\(t/\tau_{\rho}\)) against characteristic flow speeds (\(V_{0z}/V_{\mathrm{A}0}\)).

Full size image

Now that the dispersion relation has been solved for the real values of the dynamic frequency and wavenumber, the various wave modes can be explored. For MHD wave propagation inside the flux tube we return to Equation (5). Using the explicit forms of \(\Omega\) and \(K\), we plot the amplitude of the radial perturbation for the \(m\geq1\) wave modes. Results for \(m=\)1, also known as the kink wave mode, are shown in Figure 3. The plot has a similar initial amplification to that found in the over-dense loop approximation in Paper I. In this model, however, there exists no such restriction upon the time for which the wave can propagate and, hence, the wave can be amplified in this manner until the density within the flux tube is approximately zero and the governing equations are no longer applicable. The higher-order (i.e. flute) wave modes, \(m\geq\)2, have the same manner of evolution as their counterparts in the over-dense loop and, hence, we can conclude that all the wave modes, \(m\geq3\) will be damped without the need for the energy losses into the magnetic atmosphere. The amplitude of the \(m=\)2 wave mode is plotted in Figure 4 for comparison with the \(m=\)1 mode.

Figure 3
figure 3

Relative amplitude of the propagating \(m=\)1 body wave.

Full size image
Figure 4
figure 4

Relative amplitude of the propagating \(m=\)2 body wave.

Full size image

4 Damping Coefficient

To determine the damping rate and the evolution of the damping rate, we chose to follow one of two methods. In both cases, we assumed that the damping can be written as \(\Omega=\Omega_{\mathrm{r}}+{\mathrm{i}}\gamma\), where \(\Omega_{\mathrm{r}}\) is the real part of the frequency as obtained in the previous section. We also assumed that \(\Omega_{\mathrm{r}}\gg\gamma\) i.e. that the damping rate is low. An algebraic approach would see us solve Equation (8) for the damping coefficient \(\gamma\), ignoring terms of order \(\gamma^{2}\). However, for this work we used the following differential approach, as detailed in e.g. Krall and Trivelpiece (1973). In what follows, only the \(m=1\) wave mode is considered; this is a result of the increasingly insignificant levels of damping known to exist in the higher-order wave modes, i.e. the damping is of the order of \((M_{\mathrm{e}}R)^{m}\). The quantity \(\gamma\) can be written as

$$ \gamma=-\frac{D_{\mathrm{i}}}{\partial D_{\mathrm{r}}/\partial\Omega} \bigg|_{\Omega =\Omega_{\mathrm{r}}=\Omega_{k}}=-\frac{\pi}{4}(M_{\mathrm{e}}R)^{2} \rho_{\mathrm{i}}\frac{\varpi ^{2}-\varpi_{\mathrm{A}}^{2}}{\rho_{\mathrm{i}}\varpi+\rho_{\mathrm{e}}\Omega} \bigg|_{\Omega=\Omega_{k}}. $$
(15)

With the explicit forms of the frequency and wavenumber determined, we now make analytical progress with determining the evolution of the damping coefficient, \(\gamma\). Substituting explicit forms of the dynamic frequency and wavenumber into Equation (15) gives an expression from which it is difficult to clearly see the temporal changes as a result of the decreasing density in time. Hence, we plot the evolution of the damping coefficient with respect to time and height above the driving point.

Figure 5 shows that the level of damping decreases approximately exponentially in time to a negligible level. Given the amplification of the \(m=1\) kink mode, this result would appear to defy the current theory of wave damping through leaky waves. Whilst the dynamic result does seem to contradict the results derived for static and stationary systems, the energy flux, as a result of the damping, is yet to be investigated and may allow for a full unification of these not completely inconsistent ideas.

Figure 5
figure 5

Damping coefficient due to energy leakage, plotted for characteristic change periods (\(t/\tau_{\rho}\)) against characteristic flow speeds (\(V_{0z}/V_{\mathrm{A}0}\)).

Full size image

As a result of the moderate-activity approximation, the analysis with regard to the height above the driving point is potentially inaccurate, therefore, different ratios of the initial Alfvén speed and the background flow can change the initial evolution of the quantities discussed above. However, all the cases tend to the same limit and, therefore, we can consider them to be consistent.

Now, it is convenient to compare the damping within this dynamic system to the damping found in stationary systems. The damping coefficient in stationary systems has previously been found to be

$$ \gamma=-\frac{\pi}{8}\frac{(\rho_{\mathrm{i}}-\rho_{\mathrm{e}})^{2}}{(\rho_{\mathrm{i}}+\rho_{\mathrm{e}})^{2}}(k_{z}R)^{2} \omega_{k}. $$
(16)

For details see e.g. Equation (66) in Goossens et al. (2009). By rewriting Equation (16) in terms of the density ratio, \(\chi\), it is possible to write

$$ \gamma=-\frac{\pi}{8}\frac{(\chi-1)^{2}}{(\chi+1)^{2}}\sqrt{\frac{2B_{0}^{2}\chi }{\rho_{\mathrm{e}}\mu_{0}(1+\chi)}}(k_{z}R)^{2}. $$
(17)

Under the assumption of a constant exterior density, plotting \(\gamma\) in terms of the density ratio gives Figure 6. The plot clearly indicates an increase to a saturation point in the damping as a result of energy leakage; this directly contradicts the results found in the dynamic case. However, it must be noted that Figure 6 was made for a fixed wavenumber. The vertical dependency in the dynamic model ensures that the wavenumber varies significantly in time and is directly related to the change in interior density. A comparable change in the stationary wavenumber would lead to widely varying phase speeds between the two fast MHD waves.

Figure 6
figure 6

Damping coefficient due to leaky waves in a stationary atmosphere.

Full size image

5 Conclusions

We here relaxed the assumption of evanescent wave propagation in the magnetised atmosphere for temporally evolving MHD waveguides. The algebraic form of both the interior and the exterior wave propagation, as well as the damping coefficient were determined and their evolution in time and height explored. The moderate-activity approximation was applied to find the real part of the frequency and the wavenumber. Using the expressions for the dynamic frequency and wavenumber, the full evolution of the propagating wave modes can be simply shown. The various wave modes all follow the same manner of propagation as found in Paper I for the over-dense loop approximation. The \(m=\)1 kink wave is amplified in an approximately exponential manner. This amplification continues without any limiting factor, as was suggested in the case of the over-dense loop, beyond the possibility of wave propagation in an empty flux tube. The \(m=2\) flute wave mode is amplified to a constant level after a few characteristic density change periods. The higher order, \(\geq3\), wave modes are damped after small number of characteristic time periods of density change, with the damping rate increased for higher values of the azimuthal wavenumber, \(m\).

The main focus of this work was on the damping coefficient \(\gamma\) and its evolution in time for time-dependant waveguides. The damping coefficient \(\gamma\) was shown to decrease exponentially in time as the flux tube evacuates. The damping as a result of leaky waves can therefore be considered to be negligible after a small number of characteristic density change periods. By varying several characteristic parameters, it was possible to obtain results that matched the stationary case in their evolution, including an initial increase in the damping rate before the exponential decrease. Analytical attempts to further determine a critical value for this turning point have yet to yield results and as such require further investigation.

Comparison of these results to those found in a stationary system showed a distinct difference between the damping in the case of a stationary plasma and a dynamic plasma. This difference can be mainly attributed to the constant vertical wavenumber in the stationary model, whereas in this dynamic model the temporal evolution of the wavenumber results in a decrease of the damping coefficient.

Further investigations to expand these findings are required, e.g., inclusion of a finite plasma pressure and relaxing of the thin tube approximation, in order to make this an even more useful tool for investigating the magneto-seismology of photospheric structures.