Modeling Gender Life Expectancy Ratio in a Multi-population Framework

Abstract

This paper aims to assess whether the male-to-female ratio in life expectancy is driven by cross-national long-period common trends. If a common trend is detected across a group of countries, then a model taking it into account should provide a more reliable description of the process in scope. We model the gender life expectancy ratio of a set of countries as a multivariate time series. Since our study includes data from 25 countries that are characterized by different longevity patterns, we preliminarily aggregate populations in clusters. Once we verify that all these series are non-stationary, we apply Johansen’s cointegration rank test to each cluster. The idea behind this methodology is to detect any stationary linear combination out of nonstationary variables, which implies that the series share some underlying long-period equilibrium relationships. If the cointegration rank test provides evidence for any cointegrating relationship, we further check whether estimated linear combinations of the single series - namely the error correction terms - are stationary. Finally, we measure forecasting errors with respect to the 10-year testing set. At least for two clusters over six, we find enough evidence to outline some cointegrating relationships in the male-to-female life expectancy ratio. This result leads us to assume that an underlying long-period equilibrium in life expectancy gender differentials does exist among the single countries included in these clusters.

1 Introduction

The evolution of longevity is of crucial importance for researchers who want to develop more accurate forecasting mortality models. Mortality data are used to estimate life expectancy, which is a key indicator of population health and development. Since 1840 several countries have been the record holders of female life expectancy at birth (Nigri et al., 2022a, b), showing an exceptional linear rise (Oeppen and Vaupel, 2002), and this trend has continued until the present. Thereby, demographers have studied disparities for decades, and the gender gap in life expectancy has captured the most attention (Zarulli et al., 2018, 2020, 2021). The gender gap has biological roots that are mitigated by social, behavioral, and environmental effects. Despite biological differences suggesting favoring female life expectancy, several studies attributed the gap in life expectancy to nonbiological factors (Luy and Wegner-Siegmundt, 2015; Oksuzyan et al., 2008), with higher mortality risk among men due to alcohol consumption, smoking behavior, and working-related risks (see, e.g., Loef and Walach, 2012). Females live longer than males in industrialized societies, and females also outlive males in most developing countries today (Austad, 2006; Barford et al., 2006; Glei and Horiuchi, 2007; Zarulli et al., 2018). Nevertheless, since the ’70 s, female and male life expectancies have converged in most developed countries where the gender gap in mortality has started to decrease, compared to the period prior the WWII. Indeed, literature provides evidence of similar health-related behavior between genders, as tobacco consumption decreased for males, but increased for females (see, e.g., Lindahl-Jacobsen et al., 2016). Forecasting mortality of multiple populations separately tends to increase their differences (Li and Lee, 2005). As a result, when forecasting life expectancy at birth, longevity trends by gender should be jointly forecasted taking into account their dependency. Therefore, we suggest directly focusing on the gender life expectancy ratio and expanding the analysis in a multi-population framework. Exogenous factors such as social norms and contexts permit behavioral and environmental differences that affect health. As a result, the evolution of gender differentials in longevity is attributable to common factors for groups of countries that share similar macro-level features, such as socioeconomic factors, and shared improvements in public health.

This scenario encourages investigating and thus forecasting gender life expectancy ratios of a group of countries jointly. Therefore, it seems appropriate to identify clusters of countries having common characteristics detected by the gender life expectancy ratio before developing the forecast with a multi-population model.

Moving from these considerations, we analyze the gender life expectancy at birth ratio patterns by identifying different longevity phases and transitions that allow us to group countries in line with their longevity dynamics through cluster analysis. In the spirit of the framework proposed by (Levantesi et al., 2022, 2023), this work exploits the combination of a functional clustering approach, which enables us to analyze curves rather than scalar data, with econometric modeling. Indeed, once the clusters have been identified, our framework investigates the presence of any long-run equilibrium relations between the series of gender life expectancy ratios included in the cluster to gain insights into their potential dependence.

The input data are the male-to-female life expectancy ratios. We consider 25 countries in the period 1970-2018. The data set is taken from the Human Mortality Database. We have partitioned the data into a training set and a testing set, where the first one includes data over the period 1970-2008, and the second one the data from 2009 to 2018. Our analysis suggests that some clusters enclosed cointegrated series leading to the postulate that an underlying long-period equilibrium does exist for these clusters; this evidence is weaker or does not hold for other clusters.

Our analysis of gender differentials in life expectancy at birth over time and across populations opens a window for research on the lifespan of men and women. To better target health policy, a deeper understanding of the intricate interplay of physiology and culture in determining male–female differences is needed.

2 Social and Sustainability Aspects in Studying Gender Gap in Longevity

An aging society focuses on changes in the age structure of the population, indeed, understanding how these longevity improvements evolve differently among males and females is crucial in identifying tailored sustainable public policies for nations and societies showing different phases and transitions in the gender gap in longevity. Indeed, a larger gap may imply wider disparities, in terms of social conditions, opportunity, services, and long-term sustainability goals. Gender differences in longevity evolution pose crucial challenges for the decades to come. Longer lives imply a need for longer working lives with an increased proportion of people that remain in the labor force after the age of 65, and this aspect needs to be reframed between genders. However, longer working lives will require substantial accompanying changes, such as education, health, and so on, but in almost all countries, the retirement age is not significant between males and females with respect to their differences in longevity. Extending employment at older ages, resulting in a longer tenure, will be one of the most likely effects of longevity. Governments will need to focus policy on certain groups, and gender difference is the most urgent. To reduce the risk of widening inequities, governments will need to target health, education, and employment gender-specific policies to face the future longevity scenario.

3 A Framework for Modeling Multivariate Time Series of Longevity Indicators

This section describes the framework we propose for modeling multivariate time series of the gender life expectancy ratios.

We use the female and male life expectancy at birth in the study period from the Human Mortality Database Human Mortality Database (2022). Formally, life expectancy $e_{x, t}$, at age x and time t, is defined as follows:

$$\begin{aligned} e_{x, t}=\frac{\int _x^{\infty } S(y, t) \textrm{d} y}{S(x, t)} \end{aligned}$$

where $S(x, t)=\exp \left( -\int _0^x \mu (a, t) \textrm{d} a\right)$ is the survival function, and $\mu (a, t)$ is the force of mortality at age a and time t.

The first step relates clustering populations according to their gender life expectancy ratio temporal dynamics. The second step is devoted to the cointegration analysis for investigating the presence of any long-run equilibrium relationships. The third step considers the simultaneous forecasting of the gender life expectancy ratios of the countries within each cluster using vector error correction models where the series are cointegrated or ARIMA if there are not.

The target variable is the ratio between male and female life expectancy at birth measured at an annual pace, and defined as:

$$\begin{aligned} y_{i,t}:=\frac{e_{i,0}^{M}}{e_{i,0}^{F}} \end{aligned}$$

for the i-th population in the t-th year, with $t \in [1, T]$, $i \in [1, p]$.

To find a compromise between the observation period length and the number of populations, we have chosen countries whose data are available between 1970 and 2018. As a second selection criterion, we have considered only populations of more than one million. As a result, the input dataset consists of 49 observations in 25 variables. The training and the testing sets include observations in the years 1970-2008 and 2009-2018, respectively. To work with a homogeneous sample, we split populations into clusters before developing the cointegration analysis.

3.1 Functional Data Clustering

To group populations having common characteristics of the gender life expectancy ratio, we use functional clustering (Jacques and Preda, 2014) that allows for considering curves rather than scalar data. We first reconstruct the functional form of the data-generating process using a B-spline basis expansion. It is assumed that the $Y_{i}$ function underlying the observed male-to-female life expectancy ratio is observed at each j point.

Continuous functional data are arranged in a finite set of knots. We denote by m the number of knots and by L the number of basis functions. Defining an $m \times L$ matrix $\Theta$ of known basis functions $\lbrace \varphi _{b} (t_j) \rbrace , \, b \in [1,L]$ and an $L \times 1$ set of unknown parameters $\lbrace \alpha _{j} \rbrace$ which may be estimated using the least squares method, the basis expansion of Y can be written as:

$$\begin{aligned} Y_{i}(t) = \sum _{b=1}^{L} \alpha _{ib}\varphi _{b}(t) \end{aligned}$$

And the coefficients are estimated as:

$$\begin{aligned} {\hat{\alpha }}_{i} = \left( \Theta ' \Theta \right) ^{-1}\Theta 'y_{i} \end{aligned}$$

Being:

$$\begin{aligned} \Theta\,=\, & {} \left( \begin{array}{cccc} \varphi _{1}(t_{1}) &{} \varphi _{2}(t_{1}) &{}... &{} \varphi _{L}(t_{1})\\ \varphi _{1}(t_{2}) &{} \varphi _{2}(t_{2}) &{}... &{} \varphi _{L}(t_{2})\\ \vdots &{} \vdots &{}\ddots &{}\vdots \\ \varphi _{1}(t_{m}) &{} \varphi _{2}(t_{m}) &{} \ldots &{} \varphi _{L}(t_{m}) \end{array} \right) ;\\ y_{i}'\,=\, & {} (y_{i1}, y_{i2},\ldots , = y_{im}). \end{aligned}$$

The second step consists in applying the k-means algorithm (Hartigan and Wong, 1979) to the fitted basis coefficients of all the functional curves to group the populations. The number of clusters and of K initial centroids (which represent the seeds of the procedure) is given as input. Then, the following steps are iterated:

• 1. Given the K centroids, single observations are assigned to the nearest centroid; the distance function is the Euclidean distance, namely: $d(y_{i},{\bar{y}}_{c}) = \sqrt{\sum _{j=1}^{m} (y_{ij} - {\bar{y}}_{jc})^2}$, being ${\bar{y}}_{c}$ the c-th cluster centroid and $y_i$ the i-th variable of the data set. In practice, minimizing the Euclidean distance equals minimizing the within-group deviance or within the sum of squares. If at least one instance has been moved from one cluster to another, the next step must be performed. Otherwise, the algorithm has converged.

• 2. Given the K clusters, each centroid is calculated. Step 1 is repeated.

A well-known method to determine the optimal number of clusters is the elbow method, which is based on how increasing the number of clusters reduces the total within the sum of squares, $WSS = \sum _{c=1}^{K} \sum _{j=1}^{p_c} \sum _{i=1}^{T} ( x_{tjc} - {\bar{x}}_{jc} )^2$, where $p_c$ is the number of variables in the c-th cluster, and T is the number of observations. This method suggests an optimal number of clusters equal to 3 (Fig. 1). Nevertheless, the choice of three clusters appears to be not consistent with the framework of longevity evolution. Specifically, for any K smaller or equal to 5, we obtain some groups of more than 10 populations that do not allow us to clearly deepen the phenomenon.

Fig. 1

Relationship between the total WSS and the selected number of clusters determined via the K-means algorithm

The length of the observation period is $T=49$ (from 1970 to 2018), and the number of populations is $p=25$. The time set is defined at a two-year pace and the selected B-splines order is 5, so that $m=25$ (number of knots), $L=28$ (number of basis functions). Finally, we set $K=6$ (initial centroids). The following clusters have been obtained at the second iteration of the algorithm.

• Cluster 1: Czechia (CZE), Finland (FIN), France (FRA), Portugal (PRT).

• Cluster 2: Hungary (HUN), Poland (POL), Slovakia (SVK).

• Cluster 3: Belarus (BLR), Estonia (EST), Lithuania (LTU), Latvia (LVA).

• Cluster 4: Spain (ESP), Japan (JPN).

• Cluster 5: Australia (AUS), Austria (AUT), Belgium (BEL), Canada (CAN), Italy (ITA), USA (USA).

• Cluster 6: Switzerland (CHE), Denmark (DNK), Great Britain (GBR), Netherlands (NLD), Norway (NOR), Sweden (SWE).

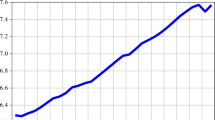
The values of $y_{i,t}$ in the years 1970-2018 for the populations in clusters $i=1,2,\ldots ,6$ are illustrated in Figs. 2, 3, 4, 5, 6 and 7, respectively. All these figures provide evidence that the female life expectancy has been higher than male life expectancy during the observed period (the values of $y_{i,t}$ are always less than 1) but also that the male–female life expectancy gap has narrowed over time for most of the countries included in our analysis.

However, it is generally possible to outline two different patterns based on the different onset of the convergence between male and female life expectancy, one for Eastern European countries (clusters 2 and 3) and the other for Western European and westernized countries (clusters 1, 5, and 6) except the Czech Republic (belonging to cluster 1). While Spain and Japan are apart from these patterns (both constitute cluster 4) and deserve a separate comment. One explanation for this difference relies on different age and cause-of-death mortality dynamics as highlighted by Feraldi and Zarulli (2022) and Nigri et al. (2022c) for Italy. An important driver of men’s relative gain in longevity is given by the reduction in cardiovascular mortality before old age in Western Europe, while in Eastern Europe accidental deaths have played a central role in the difference between female and male life expectancy.

Looking at the ratio between male and female life expectancy at birth of the populations in cluster 1 (Fig. 2), we generally observe a stable trend until around 1990 and an increasing trend in the following years. The average value of $y_{1,t}$ is about 0.93 in 2018.

Differently from cluster 1, cluster 2 includes three neighboring countries, located in Eastern Europe (Fig. 3). In this case, we note a strong decrease of $y_{2,t}$ until 1991 highlighting an increase in the male–female life expectancy gap in the years 1970–1990. After 1991, Hungary, Poland, and Slovakia experienced a rising trend in the male-to-female life expectancy ratio that, on average, reaches the value of about 0.91 in 2018.

The countries in cluster 3 are geographically neighboring as well, and until 1991 they were part of the Soviet Union. We first observe an improvement in the male-to-female life expectancy ratio in the 1980 s, and a dramatic fall in the early 1990 s (Fig. 4). The following decade is characterized by an appreciable heterogeneity of the $y_{3,t}$ trend: an initial period of stagnation in Belarus, a moderate improvement period in Estonia and Latvia, and a short improvement (1994–2000) followed by a declining phase (2000–2007) in Lithuania. In the last decade, $y_{3,t}$ has increased. Overall, in former socialist countries, the gap is larger than in the other European countries (the male-to-female life expectancy ratio, on average, is about 0.88 in 2018, which is the lowest value).

In cluster 4 (Fig. 5) we find only two countries, Spain and Japan, which share an evident initial decline in the gender life expectancy ratio (Spain until around 1990 and Japan until around 2000) and then an increase in this ratio in the following years. The value of $y_{4,t}$ reaches, on average, about 0.94 in 2018. Cluster 5 includes three Western European countries, two North-American countries, namely Canada and the USA, and Australia. The male-to-female life expectancy ratio of these countries shows a rather linear trend from the 1990 s (except for the USA) and the onset of convergence between male and female life expectancy generally from 1980 (Fig. 6). Finally, cluster 6 collects four Northern European countries, Switzerland and Great Britain. From the 1990 s, the trend of the gender life expectancy ratio is similar to the countries in cluster 5, as well as the longevity patterns (Fig. 7). The main difference with the previous cluster is the onset of convergence which is in this case delayed (between 1980 and 1990). The value of $y_{6,t}$ reaches, on average, about 0.96 in 2018, slightly higher than the value for cluster 5 which is about 0.95.

Fig. 2

Values of $y_{i,t}$ for the populations in cluster $i=1$. Years 1970-2018

Fig. 3

Values of $y_{i,t}$ for the populations in cluster $i=2$. Years 1970-2018

Fig. 4

Values of $y_{i,t}$ for the populations in cluster $i=3$. Years 1970-2018

Fig. 5

Values of $y_{i,t}$ for the populations in cluster $i=4$. Years 1970-2018

Fig. 6

Values of $y_{i,t}$ for the populations in cluster $i=5$. Years 1970-2018

Fig. 7

Values of $y_{i,t}$ for the populations in cluster $i=6$. Years 1970-2018

3.2 Cointegration Analysis

Following the definition provided by Engle and Granger (1987), the components of a multivariate time series are said to be cointegrated if they have an integration order equal to or higher than 1, and it is possible to arrange at least one linear combination out of them whose integration order is smaller than input series. By intuition, we may think about the case of a multivariate stochastic process integrated of order 1 (denoted I(1), such as data in scope) whose variables follow the same stochastic trend: then, at least one linear combination of these variables should be stationary. Let us define a p-dimensional VAR(k) process based on k lags of the variable:

$$\begin{aligned} {\textbf{y}}_t = {\varvec{\mu }} + \varvec{\Phi }_1 {\textbf{y}}_{t-1} +\cdots + \varvec{\Phi }_k {\textbf{y}}_{t-k} + {\varepsilon }_t, \end{aligned}$$

(1)

under the following conditions regarding the innovations $\varepsilon _t$: $E \left[ {\varepsilon }_{t} \right] = 0$, $E \left[ {\varepsilon }_{t} {\varepsilon }_{t}' \right] = \varvec{\Sigma }$ and $E \left[ {\varepsilon }_{t} {\varepsilon }_{t-\ell }' \right] = 0$, for any integer $\ell$ greater than zero. VAR models are suitable for stationary variables. If the process is I(1), the non-stationarity can be removed by differentiating the variables in absence of cointegration. If the variables are cointegrated the appropriate model must remove the nonstationarity by taking into account the cointegrating relationships. The vector error correction model (VECM) has been developed to address this issue. From Eq. (1), we can derive the $VECM(k-1)$ under this formulation:

$$\begin{aligned} \Delta {\textbf{y}}_t = {\varvec{\mu }} + \varvec{\Gamma }_1 \Delta {\textbf{y}}_{t-1} + \cdots + \varvec{\Gamma }_{k-1} \Delta {\textbf{y}}_{t-k+1} + \varvec{\Pi y}_{t-k} + \varvec{\varepsilon }_t \end{aligned}$$

(2)

Where $\varvec{\Gamma }_{i} = - {I}+ \varvec{\Phi }_1 + \cdots + \varvec{\Phi }_{i}$ and $\varvec{\Pi } = - {I}+ {\Phi }_1 + \cdots + {\Phi }_{k}$. In this study, we have ${y}_t \sim I(1)$, hence both $\Delta {\textbf{y}}_t$ and $\varepsilon _t$ are stationary, so that ${\Pi y}_{t-k}$ shall be stationary as well. This condition is possible if the $\varvec{\Pi }$ matrix is singular. If the rank of $\varvec{\Pi }$ - henceforth, r - is different from zero, the process is considered to be cointegrated, and the number of cointegrating relationships is equal to r. With $r=0$ instead the ${\textbf{y}}_{i,t}$ processes are devoid of cointegrating relationships.

Another representation of the model that is rather frequent in literature includes ${\textbf{y}}_{t-1}$ in the error correction term:

$$\begin{aligned} \Delta {\textbf{y}}_t = {\varvec{\mu }} + \varvec{\Pi y}_{t-1} + \varvec{\Gamma }_1^{(1)} \Delta {\textbf{y}}_{t-1} + \cdots + \varvec{\Gamma }_{k-1}^{(1)} \Delta {\textbf{y}}_{t-k+1} + \varvec{\varepsilon }_t \end{aligned}$$

(3)

being $\varvec{\Gamma }_{i}^{(1)} = - \varvec{\Phi }_{i+1} - \cdots - \varvec{\Phi }_{k}$.

The former model is presently referred to as the long-run representation, while the latter is called the transitory representation, depending on the lag of the level series multiplied by $\varvec{\Pi }$.

If we use the long-run representation, we may introduce the following notation: $\varvec{\Gamma }:= \left( {\varvec{\Gamma }}_1 \, {\varvec{\Gamma }}_2 \,... \, {\varvec{\Gamma }}_{k-1} \, \, \varvec{\mu } \right)$, $\mathbf {Z'}_{1,t}:= (\varvec{\Delta {y}}_{t-1} \, \, \hdots \, \, \varvec{\Delta {y}}_{t-k+1} \, \,{\textbf{1}})$, and ${\textbf{Z}}_{k,t}:= {\textbf{y}}_{t-k}$, while for the transitory representation we define instead $\varvec{\Gamma }:= \left( {\varvec{\Gamma }}_1^{(1)} \, {\varvec{\Gamma }}_2^{(1)} \,... \, {\varvec{\Gamma }}_{k-1}^{(1)} \, \, \varvec{\mu } \right)$ and ${\textbf{Z}}_{k,t}:= {\textbf{y}}_{t-1}$, and the ${\textbf{Z}}_{1,t}$ matrix is the same under both representations. We can thus rewrite equations 2 and 3 as:

$$\begin{aligned} \varvec{\Delta {y}}_t - \varvec{\Pi Z}_{k,t} = {\varvec{\Gamma } Z_{1,t}} + \varepsilon _t \end{aligned}$$

By regressing $(\Delta {\textbf{y}}_t - \varvec{\Pi Z}_{k,t} )$ on ${\textbf{Z}}_1$, we are able both to estimate the $\varvec{\Gamma }$ parameters matrix and to obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta \hat{{\textbf{y}}}_{t} = \sum _{t=1}^{T} \Delta {\textbf{y}}_{t} {\textbf{Z}}_{1,t}' \left( \sum _{t=1}^{T} {\textbf{Z}}_{1,t} {\textbf{Z}}_{1,t}'\right) ^{-1} {\textbf{Z}}_{1,t} \\ \hat{{\textbf{Z}}}_{k,t} = \sum _{t=1}^{T} {\textbf{Z}}_{k,t} {\textbf{Z}}_{1,t}' \left( \sum _{t=1}^{T} {\textbf{Z}}_{1,t} {\textbf{Z}}_{1,t}'\right) ^{-1} {\textbf{Z}}_{1,t} \end{array} \right. \end{aligned}$$

Hence, we can calculate the residuals ${\textbf{R}}_{0,t}:= \Delta {\textbf{y}}_{t} - \Delta \hat{{\textbf{y}}}_{t}$ and ${\textbf{R}}_{k,t}:= {\textbf{Z}}_{k,t} - \hat{{\textbf{Z}}}_{k,t}$, which we have assumed to follow a Normal distribution. Then, we define the following matrices:

$$\begin{aligned} S_{ij}:= \frac{1}{T}\sum _{t=k}^{T-k} {\textbf{R}}_{i,t} {\textbf{R}}'_{j,t} \quad \quad i,j \in \{0,1,k \} \end{aligned}$$

We define the eigenvalue-eigenvector matrices $\varvec{\Lambda }$ and ${\textbf{V}}$. The former is a diagonal matrix including the ordered eigenvalues ( $\lambda _1> \lambda _2>... >\lambda _p$ ) that are solutions to the equation

$$\begin{aligned} |\lambda S_{kk} - {\textbf{S}}_{k0} {\textbf{S}}_{00}^{-1} {\textbf{S}}_{0k}|=0 \end{aligned}$$

Correspondingly, we have

$$\begin{aligned} {\textbf{V}}: \, \mathbf {S_{kk}} \mathbf {V \Lambda } - \mathbf {S_{k0}} \mathbf {S_{00}}^{-1} \mathbf {S_{0k}} {\textbf{V}} = 0 \quad \text {and} \quad \mathbf { V S_{kk} V} = {\textbf{I}}_p \end{aligned}$$

For any $r \in \left[ 0;p \right)$, the first hypothesis of the VECM is:

$$\begin{aligned} H_1: {\Pi }= {\alpha } {\beta }' \end{aligned}$$

being ${\alpha }$ and ${\beta }$ two matrices of dimensions $p \times r$. The $r \times 1$ vector $\beta ' {\textbf{Z}}_{k,t}$ represents the error correction term (ECT), and the $\beta$ matrix consists of the r cointegrating vectors. It should be noticed that $\alpha$ and $\beta$ are not an unique pair in that for any $r \times r$ invertible matrix, say ${\textbf{C}}$, we could represent the same VECM with ${\bar{\alpha }} = \alpha {\textbf{C}}$ and ${\bar{\beta }} = \beta \mathbf {C'}^{-1}$. Hence, our concern is not the estimate of $\beta$ but only the estimate of the space spanned by it. By doing so, the ECT is treated as a stand-alone variable, and the parameter we need to estimate is $\alpha.$ The hypothesis to test in order to determine the cointegration rank is that no more than r cointegrating relationships are featured in the process, i.e.

$$\begin{aligned} H_2: rk( \varvec{\Pi }) \le r \quad \text {versus} \quad rk( \varvec{\Pi })>r. \end{aligned}$$

The Likelihood Ratio (LR) test statistic for this hypothesis is (see Johansen 1988; Johansen and Juselius 1990):

$$\begin{aligned} LR(r) = 2ln \left[ \ell ^*(\varvec{\Pi },\varvec{\Sigma },r) \right] - 2ln \left[ \ell ^*(\varvec{\Pi }, \varvec{\Sigma }) \right] =-T\sum _{i=r+1}^{p}ln(1-\lambda _i) \end{aligned}$$

(4)

Alternatively, Johansen and Juselius (1990) suggested a test for $H_2(r)$ into $H_2(r+1)$:

$$\begin{aligned} 2ln \left[ \ell ^*(\varvec{\Pi },\varvec{\Sigma },r) \right] - 2ln \left[ \ell ^*(\varvec{\Pi }, \varvec{\Sigma }, r+1) \right] =-Tln(1-\lambda _{r+1}) \end{aligned}$$

(5)

Based on the theorem about the convergence of these statistics (Johansen and Juselius, 1990), they are respectively referred to as the trace and the maximum eigenvalue statistics.

In addition to the estimation of the space spanned by the cointegrating vectors, Johansen and Juselius (1990) provided a test for the hypothesis of the absence of a linear trend in level series, which is an augmented version of $H_2$, say $H_2^{(1)}$. Under this hypothesis, if ${\textbf{Y}}_t$ is I(1), then the lagged differences must be zero-mean stationary processes. We take the long-run representation as an example. Taking expectations of equation 2$H_{2}^{(1)}$, implies that $\mu = -\alpha {\mathbb {E}} [\beta ' {\textbf{y}}_{t-k}]$. Since it holds that $\alpha \beta ' {\textbf{y}}_{t-k} + \mu = \alpha \beta ' {\textbf{y}}_{t-k} -\alpha {\mathbb {E}} [\beta ' {\textbf{y}}_{t-k}]$, it is possible to define

$$\begin{aligned} \beta '^{(1)}:= \left( \beta ' \, \, \right) -{\mathbb {E}} [\beta ' {\textbf{y}}_{t-k}]; \quad {\textbf{Z}}_{k,t}^{(1)} = \left( \begin{array}{ll} {\textbf{y}}_{t-k} \\ 1 \end{array} \right) \end{aligned}$$

Consequently, ${\textbf{Z}}_{1,k}^{(1)}$ only contains the stacked lagged differences, and the model does not include any deterministic regressor, which is intuitively consistent with the absence of linear trends. To test this restricted model versus the unrestricted one, we employ the following LR test:

$$\begin{aligned} LR(H_2^{(1)}|H_2) =-2ln(Q,H_{2}^{(1)}(r)|H_2(r)) = -T ln \left( \frac{|\mathbf {S_{00}}^{(1)}|\sum _{i=r+1}^{p} (1-\lambda _{i}^{(1)})}{|\mathbf {S_{00}}|\sum _{i=r+1}^{p}(1-\lambda _{i})} \right) \end{aligned}$$

Given that the $\mathbf {S_{00}}$ matrix is the same under both the augmented hypothesis and the unrestricted model, the LR is simply:

$$\begin{aligned} LR(H_2^{(1)}|H_2) = -T \sum _{i=r+1}^{p}ln(1-\lambda _{i}^{(1)})-ln(1-\lambda _{i}), \end{aligned}$$

(6)

and follows a $\chi ^2$ distribution with $(p-r)$ degrees of freedom.

Given the number of cointegrating relationships, it is possible to define the VECM. By defining $\varvec{\Lambda }$ as the diagonal matrix of ordered eigenvectors (i.e. $\lambda _1> \lambda _2>... >\lambda _p$ ), and ${\textbf{V}}$ as the corresponding eigenvector matrix, such that $\mathbf {S_{kk}} \mathbf {V \Lambda } - \mathbf {S_{k0}} \mathbf {S_{00}}^{-1} \mathbf {S_{0k}} {\textbf{V}} = 0$ and $\mathbf { V S_{kk} V} = {\textbf{I}}_p$, we define $\beta$ as the first r columns of ${\textbf{V}}$ (see Johansen, 1988).

Once the number of cointegrating relationships is known, we may think of equations (2) and (3]) as $VARX(k-1)$ models with ECT considered as an exogenous variable. Conditioned on r (i.e. on the space spanned by the $\beta$ matrix), we derive the $\alpha$ and $\varvec{\Sigma }$ parameters as well. Then, the autoregressive model on the level series as defined in equation (1) is implemented based on the VECM estimated $\varvec{\Pi }$ and $\varvec{\Gamma }$ parameters. If the cointegration rank test results in the rejection of $r\le 1$ instead we implement the traditional VAR model on differences. Each time we find evidence to reject $r=0$ we compare the forecasting results of the VECM(k-1) to the unrestricted ARIMA (k-1,1,0).

3.3 Model Choice

We limit the analysis to linear time series due to the finite length of observations. We choose the prediction model according to the following methodology, which is illustrated in the workflow in Fig. 8:

• We first test the stationarity of the time series through the Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) unit root tests, and the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test. Given the number of observed items, we limit our analysis to lag-2 and lag-3 models.

• For nonstationary series, we perform the Johansen cointegration rank test employing both the trace and the maximum eigenvalue tests (Johansen, 1988; Johansen and Juselius, 1990).

• Given the number of cointegrating relationships, we test the presence of a linear trend; the result of this test determines the presence of a deterministic term in the corresponding model representation.

• We test the stationarity of ECT. Even though the matrix $\varvec{\Pi }$ is the same both under long-run and transitory model specifications, and stationarity testing results on $\varvec{\Pi } {\textbf{y}}_{t-k}$ and $\varvec{\Pi } {\textbf{y}}_{t-1}$ should be resulting in the same statistics, still stationarity test is performed under both formulations due to the length of the sample. If the estimated ECT has no stationarity evidence, the rejection of the hypothesis of no more than r cointegrating relationships is disregarded and the estimated value for r is reduced by one. For all the tests mentioned above, we chose a significance level of 5% for hypothesis rejection.

Fig. 8

Workflow for the model choice

The intermediate outputs of this procedure are reported in the Appendix, while the final results are summarized in Table 1. We find that clusters 3 and 6 have strong evidence of including a cointegrating relationship whereas the remaining clusters do not show enough evidence of cointegration, and a traditional ARIMA(k-1,1,0) is chosen to describe them.

Table 1 Presence of linear trend and cointegrating relationships within each cluster

4 Models’ Performance and Validation

4.1 Models’ Performance

Table 2 shows the root mean square error (RMSE) values by population and averaged on the cluster in the testing period 2009-2018 for the ARIMA models and VECMs alongside with the coverage indicator of prediction intervals. For cointegrated models, we compare forecasting errors with those from the ARIMA(k-1,1,0). In clusters 3 and 6, which display strong cointegration evidence, VECM has a slightly better overall performance than ARIMA. The coverage indicator refers to the number of forecasted values lying within prediction intervals (see, e.g., Marino et al., 2022, which derived the prediction intervals for future mortality rates and their coverage probability). It is defined on 95% prediction intervals, which are in turn based on the assumption that the residuals follow a Normal distribution. Namely, for $H=10, \, h \in [1,H]$, $\alpha =0.05$, and $z_{\alpha /2}$ indicating the $\alpha /2$-th quantile of the standard Normal distribution, we calculate:

• the lower bound as: ${\hat{y}}_{i,t}^{L}(h) = {\hat{y}}_{i, t}(h)+ z_{\alpha /2} \sqrt{VAR_t[y_{i, t+h} - {\hat{y}}_{i,t}(h)]}$,

• the upper bound as: ${\hat{y}}_{i,t}^{U}(h) = {\hat{y}}_{i,t}(h) + z_{1-\alpha /2} \sqrt{VAR_t[y_{i, t+h} - {\hat{y}}_{i, t}(h)]}$,

with ${\hat{y}}_{i, t}(h)={\mathbb {E}}_t[y_{i, t+h}]$. Therefore, the Prediction Interval Coverage (PIC) for the i-th population is defined as:

$$\begin{aligned} \frac{1}{H} \sum _{h=1}^{H} {\mathbb {I}} \{ y_{i, t+h} \in [{\hat{y}}_{i,t}^{L}(h), \, \, {\hat{y}}_{i,t}^{U}(h) ] \} \end{aligned}$$

In Appendix 8.2, we report the RMSE and the mean absolute error (MAE) for all the tested models.

Table 2 RMSE values and PIC by population and averaged on the cluster. Years 2009-2018

4.2 Model Validation

To validate the model, we inspect the residuals of the model and check the absence of autocorrelation using the Portmanteau test (null hypothesis: no autocorrelation). We employ a modified version of the test specifically suited for small samples. Defining $G_j$ as the residual autocovariance matrix with lag $j \in \left[ 0, \ell \right]$ for a given truncation lag parameter $\ell$, the asymptotic Portmanteau test is defined as:

$$\begin{aligned} T \sum _{j=1}^{\ell } tr \left( \hat{G_j}'\hat{G_0}^{-1}\hat{G_j}\hat{G_0}^{-1} \right) \end{aligned}$$

and follows a $\chi ^2(\ell p^2 - kp^2 +p)$ distribution. The modified version we use is based on the following test statistic:

$$\begin{aligned} T^2 \sum _{j=1}^{\ell } \frac{1}{T-j} tr \left( \hat{G_j}'\hat{G_0}^{-1}\hat{G_j}\hat{G_0}^{-1} \right) \end{aligned}$$

and follows a $\chi ^2(\ell p^2 - kp^2 +p)$ distribution. This test is implemented by setting $\ell =16$ and $\ell =20$.

In Table 3, we show the p-values of the autocorrelation test. We find that, at a confidence level of 5% with a truncation lag parameter equal to 16, VECM is sufficient to capture the residual autocorrelation in clusters 3 and 6, while with a truncation lag parameter of 20 the p-values fall in the rejection region for cluster 6. However, we consider these results sufficient to validate the VECM for these two clusters, thus confirming the results of cointegration rank testing shown in Appendix 1 for clusters 3 and 6, while the estimated VECM formulation for cluster 1 turns out to be inadequate. This result in particular leads us to choose the ARIMA(2,1,0) formulation instead of the VECM.

Table 3 p-values of the autocorrelation test with truncation lag parameters equal to 16 and 20; null hypothesis: no autocorrelation

5 Out-of-Sample Results

Figures 9, 10, 11, 12, 13 and  14 illustrate the prediction of the gender life expectancy ratio for all the populations within each cluster. Predicted values (in blue) are compared with the observed value (in black) and 5%-95% prediction intervals (in grey).

Fig. 9

Prediction of $y_{i,t}$ for the populations in cluster $i=1$ with the ARIMA(2,1,0) model including a drift. Years 2009-2018 (1970-2008). In brackets is the training period

Fig. 10

Prediction of $y_{i,t}$ for the populations in cluster $i=2$ with the ARIMA(1,1,0) model. Years 2009-2018 (1970-2008). In brackets is the training period

Fig. 11

Prediction of $y_{i,t}$ for the populations in cluster $i=3$ with the VECM(1) and $r=1$. Years 2009-2018 (1970-2008). In brackets is the training period

Fig. 12

Prediction of $y_{i,t}$ for the populations in cluster $i=4$ with the ARIMA(2,1,0) model. Years 2009–2018 (1970-2008). In brackets is the training period

Fig. 13

Prediction of $y_{i,t}$ for the populations in cluster $i=5$ with the ARIMA(1,1,0) model including a drift. Years 2009-2018 (1970–2008). In brackets is the training period

Fig. 14

Prediction of $y_{i,t}$ for the populations in cluster $i=6$ with the VECM(1) including a drift (series have been detrended to estimate parameters) and $r=1$. Years 2009–2018 (1970–2008). In brackets is the training period

6 A Sustainable Society from a Longevity Perspective

A sustainable society necessarily goes through the number of years that its members are likely to spend contributing to social actions. Therefore, the concept of lifespan or longevity is intrinsically crucial to consider in evaluating and planning future sustainability policies, both in the short and long term. In this regard, socio-political decision-makers can benefit from long-term estimates by implementing forecasting procedures far in the future. Planning and programming tailor-made sustainable policies require further efforts, however. Indeed, longevity is a heterogeneous phenomenon that may change dramatically over time and between countries. Heterogeneous issues are known also inside the countries and the fundamental dimension refers to the gender difference in longevity. Modeling and forecasting the gender gap in life expectancy is essential to developing adequate sustainability policies, especially for public health, social security, and welfare. Indeed, gender-specific mortality forecasting is more reliable when using a sex-ratio approach (Bergeron-Boucher et al., 2018) or taking into account the gender gap in life expectancy in a country (Pascariu et al., 2018). Moreover, when concerning defined contribution pension schemes, the initial benefit depends on the remaining life expectancy of the pensioner, and the knowledge of longevity gender differential is essential to guarantee the intertemporal equilibrium of the system. The choice of retirement age should be also consistent with longevity forecasts, as well as being socially acceptable (see, e.g., the work of Coppola et al., 2019, which considers a pension indexing mechanism based on the expected residual life for adjusting the retirement age and discuss the implications of the gender gap in life expectancy).

However, gender differentials in life expectancy are not frequently discussed in the sustainability literature. Our proposal aims to exploit a global vision by working directly on gender inequality in longevity using a multivariate time series approach (a similar approach has been followed by Ntamjokouen et al. (2014) and Levantesi et al. (2022) for modeling life expectancy).

7 Discussion and Concluding Remarks

The social sustainability of any scheme of intertemporal resource allocation requires policymakers to understand the dynamics of mortality and longevity under a systematic perspective. Thus, we deem that a multivariate stochastic framework to model forecast life expectancy may be useful for an all-encompassing view. If policymakers involve several countries in their decisions, demographic forecasting must consider multiple populations and evaluate the possible long-term common tendencies. Alongside cross-country longevity convergence, this work is specifically concerned with the coherence of gender-specific forecasting; indeed we find some evidence that also female and male life expectancies are heading towards long-term leveling, at least in developed countries.

Our analysis allows outlining two general situations. In clusters 1, 2, 4, and 5, the cointegration rank tests provide evidence that the gender life expectancy ratio follows a common pattern (presence of cointegrating relationships) but this evidence is weakened by the ECT stationarity test, by the residual autocorrelation test, or both. Hence, we describe these series through ARIMA models. For clusters 3 and 6 instead, we find evidence that the gender life expectancy ratio evolves according to the same pattern across countries, therefore the use of a cointegrated model is fully justified.

Our study also has some limitations. The employed methodology is placed in the field of econometric literature, which focuses on more extended series. In contrast, we have a small number of observations and many parameters. To address these issues, we limited our analysis to models with a lag order of 2 or 3 in level series, by setting lag of order 2 as the default choice. We selected a lag of order 3 in the level series only when we obtained more accurate forecasting.

Considering the nature of the target variable and the difficulty to provide adequate forecasting, our speculation may need further evidence and more data. Indeed, the gender gap behavior may significantly change across countries and periods, then affecting the accuracy of predictions.

Appendix

1.1 Model Choice Process

1.1.1 Stationarity Testing and Linear Trend Testing Results

In the following, we report the intermediate outputs of the model choice process. In Table 4 we show the p-values of the stationarity testing applied to level series and differences. For level series, the KPSS test is applied either under the hypothesis of a linear trend or in absence of deterministic terms. Hypothesis rejection occurs at a $5 \%$ significance level.

Table 4 p-values of the stationarity testing (PP, ADF, KPSS). For PP and ADF test $H_{0}$: nonstationary; for KPSS,$H_{0}$: stationary

Table 5 shows the p-values of the linear trend test both with 1 and 2 cointegrating relationships (Tables 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27).

Table 5 p-values of the linear trend test. Null hypothesis: the process has no linear trend

1.1.2 Cointegration Rank Testing

Cluster 1. If a lag-2 formulation is chosen, the resulting model would have no deterministic regressors and lead to poor forecasting. Given the number of parameters, a lag-3 representation is a reasonable choice. The cointegration rank test provides the following outputs:

Table 6 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 1

Based on this result, at a 5$\%$ significance level, we should find two cointegrating relationships. Then, we test the stationarity and obtain the following results:

Table 7 Unit root testing (ADF, PP, KPSS) for cluster 1 with $r=2$

Stationarity holds only for one linear combination. Lowering r would provide these p-values instead:

Table 8 Unit root testing (ADF, PP, KPSS) for cluster 1 with $r=1$

Both unit root tests and KPSS test fall in the rejection region (except for the ADF test applied to $\beta ' {\textbf{y}}_{t-k}$). Nevertheless, this model has a weakness element since model validation provides unsatisfactory results (a cointegrated lag-3 model would fail in capturing residual autocorrelation). Based on this result the evidence to employ a VECM(2) to describe this process is considered too weak and a non-cointegrated ARIMA (2,1,0) model is chosen instead.

Cluster 2. Differently from the previous cluster, there is no evidence for a linear trend, and cointegration rank is consequently tested through the restricted formulation leading to these results:

Table 9 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 2

ECT stationarity testing would provide these results:

Table 10 Unit root testing (ADF, PP, KPSS) for cluster 2 with $r=1$. Asterisk rating system: *** rejection at a 1% significance level; ** rejection at a 2.5% significance level; * rejection at a 5% significance level

The result of the cointegration rank test is not confirmed by the estimated cointegrating relationships and this evidence is not deemed sufficient to employ a VECM instead of an ARIMA.

Cluster 3. As in the previous cluster, given the evidence of no deterministic regressor in level series the Johansen procedure is applied to a restricted model with the following results:

Table 11 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 3

ECT stationarity testing would provide these results:

Table 12 Unit root testing (ADF, PP, KPSS) for cluster 3 with $r=1$. Asterisk rating system: *** rejection at a 1% significance level; ** rejection at a 2.5% significance level; * rejection at a 5% significance level

There is strong stationarity evidence and the conclusion that series are cointegrated is fully justified. Hence, we model this series through a VEC(1) representation with $r=1$.

Cluster 4. As in clusters 3 and 4, there is no evidence for a linear trend, and cointegration rank is tested via the restricted formulation leading to these results:

Table 13 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 4

Based on these results, the $r\le 1$ hypothesis should be rejected at a 5$\%$ significance level. If $\varvec{\Pi }$ were a non-singular matrix, however, the stationary process should be $y_t$ itself, which is in contradiction with stationarity tests on level series. ECT stationarity testing provides these results:

Table 14 Unit root testing (ADF, PP, KPSS) for cluster 4 with $r=1$. Asterisk rating system: *** rejection at a 1% significance level; ** rejection at a 2.5% significance level; * rejection at a 5% significance level

All tests are in the acceptance region; On the basis of the cointegration rank test and ECT stationarity test, evidence for cointegration is not deemed sufficient and we choose to describe this series with an ARIMA(2,1,0) model.

Cluster 5. This cluster has evidence for a linear trend, hence the cointegration rank test is performed on an unrestricted model. The cointegration rank test provides these outcomes:

Table 15 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 5

ECT stationarity testing would provide these results:

Table 16 Unit root testing (ADF, PP, KPSS) for cluster 5 with $r=1$. Asterisk rating system: *** rejection at a 1% significance level; ** rejection at a 2.5% significance level; * rejection at a 5% significance level

ECTs are nonstationary; if the series were detrended, $r=0$ should have been accepted directly. There is not enough evidence to assess that this process is cointegrated and we choose an ARIMA(1,1,0) model with a drift to describe it.

Cluster 6. In the same way as the previous cluster, there is evidence for a linear trend that justifies testing the cointegration rank on the unrestricted model. At the price of a loss in forecasting accuracy, series are detrended in order to obtain an actually stationary ECT. The cointegration rank test would have led to the same outcome:

Table 17 Trace test and Maximal eigenvalue test used to determine the cointegration rank for cluster 6

ECT stationarity testing provides these results:

Table 18 Unit root testing (ADF, PP, KPSS) for cluster 6 with $r=1$. Asterisk rating system: *** rejection at a 1% significance level; ** rejection at a 2.5% significance level; * rejection at a 5% significance level

As for cluster 3, there is enough evidence to assess that the process is cointegrated.

1.2 Out-of-Sample Errors

In the following, we show the forecasting errors (MAE and RMSE) for all the tested models by cluster. We include models for which the Johansen procedure suggests rejecting the hypothesis of $r=0$, regardless of the stationarity check performed on the estimated error correction terms. The only case in which this hypothesis has been accepted is for the detrended version of cluster 5. Tested VECMs have 1 cointegrating relationship (i.e. $r=1$)

Cluster 1.

Table 19 Cluster 1 with lag order = 2. Models do not include a drift

Table 20 Cluster 1 with lag order = 3. Models include a drift

Cluster 2.

Table 21 Cluster 2. Models do not include a drift

Cluster 3.

Table 22 Cluster 3. Models do not include a drift

Cluster 4.

Table 23 Cluster 4. Models do not include a drift

Cluster 5.

Table 24 Cluster 5 with lag order = 2. Models include a drift

Table 25 Cluster 5 with lag order = 3. Models include a drift

Cluster 6.

Table 26 Cluster 6 with lag order = 2. Models include a drift

Table 27 Cluster 6 with lag order = 3. Models include a drift