1 Introduction

In multiple contexts, composite indicators have been shown to be valuable instruments for the representation of complex phenomena, by highlighting any existing inequalities, helping to generate attention and analysis, and enabling the progress to be monitored. A variety of entities have considered this instrument in their own way, in order to synthesise information and to ultimately generate internationally comparable measures.

A composite indicator should verify certain basic features. Firstly, it must include a solid foundation in theory that supports the aggregation of individual measures and the adequate representation of the target pursued by the composite indicator. The proposed indicator must also be operationally viable and easily replicable. Finally, the comparison across the entities should be guaranteed, depending on the context, whether it be across regions, entities, etc.

The connection of education and composite indicators would require a wide review of the literature. An exhaustive literature review of this topic is beyond the purpose of this study. It is interesting to highlight that education performance has been considered traditionally integrated into composite indicators that propose the measure of development or inequalities in comparative studies across countries (e.g., Ferrara & Nisticò, 2013; Mitrovic et al., 2016; Monte & Schoier, 2022). But composite indicators have also been shown to be a valuable tool in the analysis of education performance. Hence, several studies have proposed comparative analysis of educational systems across countries (e.g., Stumbriene et al., 2020; Jovanovic-Gavrilovic & Radivojevic, 2017; Villar, 2017; Dominguez et al., 2021) or an analysis of particular aspects like higher education. In this line, most of the rankings existing nowadays have developed and used composite indicators to provide rankings of HE institutions or countries (among others, the Times Higher Education World University Ranking, the World University Ranking or the one developed by Torres-Salinas et al. (2011)). In a similar sense, the proposal of constructing composite indicators in order to analyse the quality of universities can be found in, among others Murias et al. (2007), El Gibari et al. (2018) (for the Spanish public university system), Benito and Romera (2011), Gnaldi and Ranalli (2016), Docampo and Cram (2017) and Bas and Carot (2020).

The proposal of comparable indicators with a gender perspective has received increasing attention in recent decades. The objective of a gender indicator involves the measurement of gender-related changes over time or across entities. According to Moser (2007), gender indicators can refer to quantitative indicators based on sex disaggregated statistical data, which provides separate measures for men and women, but can also capture qualitative changes. Measurements of gender equality might address changes in the relations between men and women, the outcomes of a particular policy, programme, or activity for women and men, or changes in the status or situation of men and women.

In the field of education, the inclusion of gender indicators plays a significant role. A number of indicators have been proposed to measure the literacy gap between men and women, and male and female enrolment rates in primary, secondary and tertiary education, among others. Traditionally, the consideration of gender perspective in education has focused on inequality of access for female students, the relevance of the curriculum in teaching gender perspective and the obstacles to the inclusion of such a perspective.

The interest in the inclusion of gender-indicators in education has largely been related with the study of development, how gender inequalities in education can hinder development, or, equivalently, how the promotion of equality in education can break the poverty cycle by reducing economic inequalities and promoting gender equality. In this regard, The Sustainable Development Goals (United Nations, 2020), include, as one of their targets, “to ensure inclusive and equitable quality education and promote lifelong learning opportunities for all by 2030, and eliminate gender disparities and ensure equal access to all levels of education and vocational training for the vulnerable, including persons with disabilities, indigenous peoples and children in vulnerable situations”. In a similar aim, The Incheon Declaration recognises “the importance of gender equality in achieving the right to education for all… supporting gender-sensitive policies, planning and learning environments; mainstreaming gender issues in teacher training and curricula; and eliminating gender-based discrimination and violence in schools” (UNESCO, 2015). This report includes the target of gender equality for the 2030 Agenda in a central position. In most studies that propose the use of composite indicators, the inclusion of education and gender is justified either as a part of a complex index to measure inequalities (e.g., Bericat & Sanchez-Bermejo, 2016; Ferrant, 2014; Bericat, 2012), to analyse the connection between education performance (e.g., Hadjar & Buchmann, 2016; Blossfeld et al., 2016; Arcos et al., 2007) or as a contextual aspect to make comparisons among the results (e.g., INES project from (OECD, 2021b)).

Defining gender inequality and gender equality in schooling entails more than a description of the numbers of girls and boys enrolled in and progressing through stages of instruction. The definition of inequality derived from Sen (1999) points to the existence of limits and constraints on opportunities.

In this paper we do not propose an analysis from a gender-perspective in the aforementioned sense, nor do we try to measure the gender-inequalities by computing the limitation in the access, the differences in the contents of the classes, or the discrimination in the classrooms. We strive to ascertain whether the evaluation of the outcomes from national educational systems presents differences when the evaluation is carried out on girls and boys separately, that is, whether the performance in academic results and in the social-transforming role of the systems differs for boys and girls. To this end, a methodology for the construction of composite indicators is proposed, and the evaluation of the educational systems for the OECD countries is carried out. By comparing the results of male and female students, considered as two separate subgroups of the same population, we strive to shed light on the matter and evaluate whether significant differences appear between genders, when the outcomes of education, as a broad concept, are evaluated.

Hence, the main target of the paper is to present a case study. To that end, we have considered an ad hoc methodology obtained as an adaptation of an existing procedure, that could be extended to other contexts which similar characteristics. With the proposed methodology, we ensure that all the objectives of the study are achieved. Firstly, to determine a composite indicator with an objective set of weights. Secondly, we propose a composite indicator developed under an aggregation scheme that places special emphasis on those aspects in which the unit under evaluation presents a poor indicator.

One unit with unbalanced values in the sub-indicators would opt for a compensatory aggregation scheme (like the additive aggregation) since such schemes allow a perfect substitutability among indicators. On the contrary, the geometric aggregation scheme inhibits this perfect transference of values from the highest indicators to the lowest ones. This characteristic leads the decision-makers to concentrate their effort on those measures that will have a greater impact on the improvement of the aspect most undervalued. It is important to bear in mind that the marginal increase of the global evaluation derived from an improvement in the lowest-valued indicators is larger than that which would be obtained from an increase in a better-valued indicator.

In addition, the geometric nature of the indicator will permit comparing the results for separate subgroups and identifying the main sources of comparative advantage from one unit to another or from one subgroup to the other for the same unit. This information about the performance of the units will be also helpful in the decision-making process. As will be discussed later, the nature of the proposed indicator permits insulating the sources of advantages (or disadvantages) of one unit with respect to others or from one subgroup with respect to the other. We can determine the individual effects generated from the comparison of the individual observed values, the weighting schemes and the benchmark considered as a basis on the aggregated value obtained for each unit when a comparative analysis is performed. In the light of these results, the decision-maker can detect if the weakness of the unit (or the group) is derived from their own observed values (in such cases, actions should be addressed to improve those values) or, in contrast, from the benchmarks or the weighting schemes. In those cases, the effort should be directed to improving the complete set of sub-indicators.

The rest of the paper is organised as follows. Section 2 summarises the methodological procedure for the construction of the composite indicator. Section 3 incorporates the application of the proposed methodology into the evaluation of the educational systems in the OECD countries. Finally, Sect. 4 is devoted to the main concluding remarks and political implications.

2 A Geometric Composite Indicator Under the Benefit-of-the-Doubt Principle

From a methodological point of view, a composite indicator (CI) is a mathematical aggregation of a set of individual indicators (often referred to as subindicators), for the measurement of multidimensional concepts that cannot be captured by only one single indicator (OECD, 2008). The process of generating a composite indicator implies several successive decisions (OECD, 2008): selection of initial indicators, the way in which they are conceptually grouped (generating dimensions which cluster individual indicators), the decision on the data normalisation method, and the choice of the method to weight and aggregate sub-indicators. A complete revision of the concepts related with the construction of CIs can be seen, among others, in Nardo et al. (2005a), Nardo et al. (2005b).

The weighting and aggregation phases are two of the most determinants phases in this process (Esty et al., 2005; Saisana & Tarantola, 2002). In this section, a methodology based on a geometric aggregation scheme is proposed, in which the weighting factors are freely determined. The so-called Benefit of the Doubt (BoD) principle is taken as reference Cherchye et al. (2003), Cherchye et al. (2007), Murias et al. (2007) to determine the weighting scheme. As will be discussed later, Data Envelopment Analysis (DEA) is considered as a tool to determine weighting profiles for composite indicators.

In order to introduce the proposed methodology, let us consider a generic set of \(n\) units of alternatives that are to be evaluated by means of a CI. Let us also suppose that a set of \(m\) individual indicators have been collected. The individual indicator \(r\) with respect to the alternative \(i\) is denoted as \({I}_{ri}\), with \(i=\mathrm{1,2},\dots ,n\) and \(r=1,\dots ,m\). The composite indicator for the alternative \(i\) is denoted as \(C{I}_{i}\). For the sake of simplicity, we assume that all the individual indicators \({I}_{ri}\) have been treated in such a way that the higher the value, the better the alternative.

In order to determine the \(C{I}_{i}\) values, a multiplicative aggregation scheme is proposed such that:

$$C{I}_{i}=\prod_{r=1}^{m}{I}_{ri}^{{\omega }_{r}}, {\omega }_{r}\ge 0, \sum_{r=1}^{m}{\omega }_{r}=1,$$
(1)

where \({\omega }_{r}\) denotes the normalised weighting factor associated to the \(r\)th individual indicator.

Several authors have studied the advantages of geometric aggregation over the classical additive scheme. In Ebert and Welsch (2004) and Zhou et al. (2010), the authors point out several desirable properties, such as the scale-invariance and a lower degree of compensation between individual indicators. The latter supposes that this aggregation function penalises those alternatives with lower values in certain individual indicators (Yoon & Hwang, 1995). Consequently, a modification in an originally low-value indicator, would cause a greater variation in the CI than in high-value indicators. That is to say, the alternatives are encouraged to improve their weaknesses rather than reinforce those aspects in which they are top performers. Other authors, see Zhou et al. (2006, 2010) among others, found that geometric aggregation implies a lower information loss.

The selection of the weighting scheme is inspired from the Benefit of the doubt (BoD) principle Cherchye et al. (2007), which is based on DEA methodology (Banker et al., 1984; Charnes et al., 1978). This family of procedures permits each alternative to select its own vector of weights. The underlying idea is to allow each alternative to maximise its composite value, under a set of common constraints in order to guarantee that all the values are limited. This free selection of weights enables each unit to use its own weight set Murias et al. (2007). Two major benefits are derived from these models. First, since the weighting values are adapted to unit measures of the sub-indicators, the application of a normalisation method is not necessary. Secondly, the CIs are computed with an objectively determined vector of weights and are not derived from a set of subjective decisions of the analyst. Several recent procedures, which combine both multiplicative aggregation and BoD, can be consulted in Blancas et al. (2012), Giambona and Vassallo (2014), Zhou et al. (2010), Van Puyenbroeck and Rogge (2017), Verbunt and Rogge (2018) and Dominguez et al. (2021), among others.

In this paper, a procedure based on the indirect CI-framework is developed as proposed in Van Puyenbroeck and Rogge (2017). The authors propose the construction of a CI with geometric aggregation using the weights derived from a DEA-inspired model. Hence, the procedure implies a number of successive steps. Firstly, the weighting scheme is determined using a BoD model. The sub-indicators are subsequently aggregated using these weighting factors in a multiplicative scheme.

As a first step, a max–min normalisation process is applied to guarantee the comparison between sub-indicators, thereby determining \({I}_{ir}^{N}\in [\mathrm{1,2}]\). To determine the weights associated to sub-indicator \(r\), the revisited optimistic/pessimistic DEA model is considered, as developed in Contreras and Hinojosa (2020). In this proposal, the maximum and minimum aggregated values are computed for each alternative.

For each unit \(o\) \((o=1,\dots ,n)\), the optimistic \(C{I}_{o}^{+}\) and pessimistic \(C{I}_{o}^{-}\) evaluations are computed as follows

$$\begin{array}{llll}C{I}_{o}^{+}/C{I}_{o}^{-}=& max/min& \sum_{r=1}^{m}{w}_{ro}^{+}\cdot {I}_{ro}^{N}& \\ & s.t.& \sum_{i=1}^{n}\sum_{r=1}^{m}{w}_{ro}^{+}\cdot {I}_{ri}^{N}=1& \\ & & {L}_{r}\le \frac{{w}_{or}^{+}\cdot {I}_{ro}^{N}}{\sum_{r=1}^{m}{w}_{ro}^{+}\cdot {I}_{ro}^{N}}\le {U}_{r},& \forall r\\ & & {w}_{ro}^{+}\ge 0,& \forall r,i;\end{array}$$
(2)

where \({L}_{r}\) and \({U}_{r}\) are the lower and upper bounds respectively imposed for the determination of the optimal values of \({w}_{ro}^{+}\) and \({w}_{ro}^{-}\). The outcome from the models (2) is a pair of optimal weighting vectors for each unit (one in the optimistic perspective and a vector for the pessimistic perspective).

To mitigate the effect of outliers and/or the existence of errors, both models are robustified using the concepts proposed in Cazals et al. (2002). DEA models (like other non-parametric models) are highly influenced by the existence of observations with extreme values or by outliers. It is important to bear in mind that the optimal evaluation of each unit is affected not only by its own observation but also by the observations of the remaining units. The procedure proposed in Cazals et al. (2002), suggests computing a number or rounds (2000 in our case) of each model with a sub-sample of randomly selected units and comparing the results to detect the existence of extreme values.

It is important to remark that an alternative DEA-inspired model is proposed in order to determine the optimal values for \({w}_{ri}^{+}\) and \({w}_{ri}^{-}\). In contrast with classic DEA models, not only is the unit under evaluation considered for the construction of the normalisation constraint. In this proposal, the complete set of alternatives participates in the construction of the normalisation condition. The main benefit of this new proposal is derived from the uniqueness of the solution (see Khodabakhshi and Aryavash (2012) for a detailed explanation).

Following the ideas proposed by Van Puyenbroeck and Rogge (2017) and Verbunt and Rogge (2018), we proceed to determine the normalised optimistic and pessimistic weights, denoted respectively by \({\omega }_{ri}^{+}\) and \({\omega }_{ri}^{-}\). These values are obtained as:

$${\omega }_{ri}^{+}=\frac{{w}_{ri}^{+}{I}_{ri}^{N}}{\sum_{r=1}^{m}{w}_{ri}^{+}{I}_{ri}^{N}}; {\omega }_{ri}^{-}=\frac{{w}_{ri}^{-}{I}_{ri}^{N}}{\sum_{r=1}^{m}{w}_{ri}^{-}{I}_{ri}^{N}}.$$
(3)

This last step involves the construction of the optimistic and pessimistic geometric indicators. To this end, the original values of the sub-indicators are retrieved. In this phase, a benchmark value or baseline sub-indicator value \({I}_{rB}\) is considered for each sub-indicator \(r\) (\(r=1,\dots ,m\)). In this study, the averages of the observed values have been considered as the baseline.

For each alternative, \(C{I}_{i}^{+}\) and \(C{I}_{i}^{-}\) are computed as

$$C{I}_{i}^{+}=\prod_{r=1}^{m}{\left(\frac{{I}_{ri}}{{I}_{rB}}\right)}^{{\omega }_{ri}^{+}}, C{I}_{i}^{-}=\prod_{r=1}^{m}{\left(\frac{{I}_{ri}}{{I}_{rB}}\right)}^{{\omega }_{ri}^{-}}.$$
(4)

It is interesting to note that, in (4), values \({\omega }_{ri}^{+}\) and \({\omega }_{ri}^{-}\) correspond to the relative contribution of sub-indicator \(r\) to the aggregated values \(C{I}_{i}^{+}\) and \(C{I}_{i}^{-}\). That is, these values represent the percentage variation in the \(CI\)-value as a result of a \(1\mathrm{\%}\) increase in \(\frac{{I}_{ri}}{{I}_{rB}}\).

Once the optimistic and pessimistic geometric measures (\(C{I}_{i}^{+}\) and \(C{I}_{i}^{-}\)) are computed, both measures can be added to determine a single indicator such that

$$C{I}_{i}=\sqrt{C{I}_{i}^{+}\times C{I}_{i}^{-}}=\prod_{r=1}^{m}{\left(\frac{{I}_{ri}}{{I}_{rB}}\right)}^{{w}_{ri}^{*}}$$
(5)

where \({\omega }_{ri}^{*}=\frac{{\omega }_{ri}^{+}+{\omega }_{ri}^{-}}{2}\).

2.1 Comparing two Subsets of Alternatives

The form of geometric composite indicator proposed above enables the analysis of subsets of indicators, alternatives, or even a dynamic analysis to be carried out. In Verbunt and Rogge (2018), an analysis of the temporal decomposition of the geometric indicator is proposed. In this work, a comparison between two separate subgroups is realised which, enables a comparative analysis of male (M) and female (F) results. The set of all the alternatives is denoted as \(C=\{\mathrm{1,2},\dots ,n\}\), and consider that the \(n\) alternatives are distributed into two separate groups \(M\) and \(F\), that is, sets \(M\) and \(F\) are such that \(M\cup F=C\) and \(M\cap F=\mathrm{\varnothing }\).

In order to perform the comparison, the notation of all the relevant variables should to be extended accordingly in order to include the sub-group reference. Hence the values of the sub-indicators are denoted by \({I}_{ri}^{M}\) and \({I}_{ri}^{F}\), by \({I}_{rB}^{M}\) and \({I}_{rB}^{F}\) the baseline values are denoted, and the relative importance of the sub-indicators are denoted by by \({\omega }_{ri,M}^{*}\) and \({\omega }_{ri,F}^{*}\), in all the cases, for subgroups \(M\) and \(F\) respectively.

If the results of both sub-groups are evaluated separately, then a measure of the performance change for unit \(i\) denoted by \(P{C}_{i}\), can be measured as follows:

$$P{C}_{i}=\frac{\prod_{r=1}^{m}{\left(\frac{{I}_{ri}^{F}}{{I}_{rB}^{F}}\right)}^{{\omega }_{ri,F}^{*}}}{\prod_{r=1}^{m}{\left(\frac{{I}_{ri}^{M}}{{I}_{rB}^{M}}\right)}^{{\omega }_{ri,M}^{*}}}.$$
(6)

The interpretation of \(P{C}_{i}\) is straightforward. A value of \(P{C}_{i}\) greater (less) than the unity indicates that unit \(i\) has a better (worse) evaluation for subgroup \(F\) than for sub-group \(M\). Note that this interpretation could be carried out separately, by considering optimal weights from optimistic and pessimistic evaluations and the conjoin evaluation.

In Verbunt and Rogge (2018), a tripartite decomposition of \(P{C}_{i}\) is proposed for the comparison of two successive periods. This decomposition can be extended for the comparison of subgroups such that

$$P{C}_{i}=\Delta OW{N}_{i}\times\Delta B{P}_{i}\times\Delta {W}_{i}^{*}.$$
(7)

The component \(\Delta OW{N}_{i}\) measures the changes derived from the variations in the sub-indicators of unit \(i\).

$$\Delta OW{N}_{i}=\prod_{r=1}^{m}{\left(\frac{{I}_{ri}^{F}}{{I}_{ri}^{M}}\right)}^{\frac{{\omega }_{ri,F}^{*}+{\omega }_{ri,M}^{*}}{2}}.$$
(8)

A value greater (less) than the unity represents an improvement (deterioration) in the performance of the individual indicators in subgroup \(F\) with respect to \(M\). That is, a value greater (less) than 1 indicates that the valuation of the indicators \({I}_{ri}\), with the corresponding weighting vectors, is greater (less) in \(F\) than in \(M\).

With \(\Delta B{P}_{i}\), the changes derived from the variation of the base-line of \(F\) over \(M\) are measured.

$$\Delta B{P}_{i}=\prod_{r=1}^{m}{\left(\frac{{I}_{rB}^{M}}{{I}_{rB}^{F}}\right)}^{\frac{{\omega }_{ri,F}^{*}+{\omega }_{ri,M}^{*}}{2}}.$$
(9)

Here, a value greater than the unity indicates that the composite value of the baseline of \(M\) is lower than the corresponding value of subgroup \(F\). Note that, since the sub-indicators are computed in relative terms with respect to the baseline (\(\frac{{I}_{ri}}{{I}_{rB}}\)), a lower value of the baseline value implies an indirect gain to the evaluation.

Finally, the value of \(\Delta {W}_{i}^{*}\) evaluates the impact of the weighting scheme (comparing whether the evaluation is carried out in the first or the second subgroup).

$$\Delta {W}_{i}^{*}=\frac{\prod_{r=1}^{m}{\left(\sqrt{\frac{{I}_{ri}^{M}}{{I}_{rB}^{M}}\cdot \frac{{I}_{ri}^{F}}{{I}_{rB}^{F}}}\right)}^{{\omega }_{ri,F}^{*}}}{\prod_{r=1}^{m}{\left(\sqrt{\frac{{I}_{ri}^{M}}{{I}_{rB}^{M}}\cdot \frac{{I}_{ri}^{F}}{{I}_{rB}^{F}}}\right)}^{{\omega }_{ri,M}^{*}}}$$
(10)

A value \(\Delta {W}_{i}^{*}\) greater (less) than the unity indicates that the weighting scheme has been selected in such a way that it represents an advantage (disadvantage) for sub-group \(F\). That is to say, a value greater (less) than the unity indicates a positive (negative) impact derived from the selection of weights in the construction of the composite indicator in subgroup \(F\) with respect to \(M\).

3 Case study: Evaluation of the Educational Systems of OECD Countries

The aim of this section is to construct a composite indicator to evaluate the educational system in OECD countries. The proposal involves the application of the methodology described in the previous section to the values included in the Programme for International Student Assessment (PISA) report for 2018 (OECD, 2021a). The PISA report, initially launched in 2000, offers triennial statistics on the structure and performance of educational systems. The PISA database constitutes a major source of information for the development of comparative analysis across economies. The number of participating schools and countries has risen in every edition of the report, currently standing at about 500,000 students from 80 countries (in the edition of 2018).

Even though the main target of the study is to evaluate the skills and knowledge of 15-year-old students in Mathematics, Science, and Reading skills and, since 2012, financial literacy has also been included as an option, the database includes a large amount of interesting data related to academic achievements (results from standardised test scores), the students’ households, and on the schools they attend. Furthermore, it contains synthetic indices created by OECD experts of some interesting aspects (see OECD (2021a) for a detailed discussion).

The results for the complete set of students are obtained for every country (the complete set denoted by C in the previous section) as are the separate results for female and male students (denoted by F and M, respectively), in order to carry out a comparison of these two subgroups. The multiplicative nature of the proposed methodology permits the results of these comparative results to be separated into three effects, and the contribution of each considered dimension can therefore be determined.

3.1 Panel of Indicators

In this paper, we include a proposal of a panel of individual indicators for the comprehensive evaluation of educational systems that extends beyond the simple computation of academic outcomes. An expansion of the concept of the objective of a educational system is proposed. We consider that, although the main objective to achieve is the optimal transfer of skills to the students, a transforming role in a social context must also constitute one of the desirable goals of the systems. In other words, the educational function should be broadly interpreted by including social features and the well-being of the students during their scholar stage.

Therefore, in the evaluation of the performance and outcomes from the educational systems, not only are the academic results taken into account.

We classify the sub-indicators into three main areas or dimensions in order to cover the entire set of valuable elements: academic outcomes, social equity, and the students’ perception of the system. The following scheme summarises the main concepts studied in each dimension and the selected subindicators (in italics).

  1. (a)

    Academic outcomes. In the first dimension, we propose the inclusion of the academic results obtained by the students. It is clear that the better the academic results, measured by results from normalised test scores, the higher the standard of the educational system. On the basis of the quantification of the education received by an individual this is not an easy task, due to its inherent intangibility and the necessity of considering a long period. However, there is certain consensus in the consideration of standardised test results as one of the main educational outcomes. In Morrison (2011), a complete review of the main aspect related with standardised tests in the OECD context can be seen, including the implication for the students in their future academic outcomes.

    This dimension includes a total of five indicators.

    1. (a.1)

      Academic average performance. With the academic average performance, the overall achievement of the students is measured. The average student learning outcome is considered through the average of the standardised test scores in the main disciplines included in PISA: Mathematics (MATH), Science (SCI), and Reading (READ) in order to compute the average outcomes of education as a production process.

    2. (a.2)

      Excellence of the educational system. A high-quality education is desirable in any modern society. In order to take this aspect into account, the students’ proficiency levels published in PISA reports have been examined. The results from PISA tests are represented by means of six levels of educational proficiency, built from the test scores (a detailed explanation is given in OECD (2017)). PISA reports establish that an educational system achieves the minimum objectives if the students achieve at least the second level of proficiency. Students who reach levels equal to or greater than 5, are considered to present high performance. In order to take into account the excellence of the educational system, an indicator (EXCE) is considered that computes the percentage of students who obtain a level equal to or greater than 5 in any of the three main subjects measured in PISA.

    3. (a.3)

      Academic inclusion. One of the desirable objectives of educational systems is that all students reach at least a minimum level of knowledge (defined as a baseline level of skills). We consider an indicator (INCL) that measures the percentage of students who reach at least second proficiency level in the three referred subjects. It is reasonable to assume that one of the goals of the system is to guarantee that all the students reach at least a baseline level of skills in all subjects.

  2. (b)

    Equity of the educational system. The second aspect to be studied in this multidimensional indicator involves the equity derived from the performance of the educational system. The transforming role of the educational system is evaluated when access to learning goes beyond the socio-economic background of the student so that the required mechanisms can guarantee that every interested student has the opportunity to attain his/her academic achievements. Equity in education constitutes a specific target of the Sustainable Development Goals set by the United Nations in 2015. Equity does not mean that all students will have the same results in education, but that their results will not be conditioned by their circumstances (Downey & Condron, 2016; Roemer & Trannoy, 2015).

    Several meta-analyses related to socioeconomic status and students’ academic performance can be found in the literature (e.g., Liu et al., 2019; Selvitopu & Kaya, 2021; Sirin, 2005; White, 1982). The main results pointed out that the relation between socio-economic status and academic performance is, in general, positive but depends on the particular measurement considered to represent socio-economic achievement. In this paper, two approaches to this concept are considered: social equity and socioeconomic incidence.

    1. (b.1)

      Resilient students. Ideally individuals should be able to obtain excellent academic results depending on only their individual abilities, no matter how adverse the conditions in their environment may be. The percentage of resilient students is included as an indicator (RESI). In PISA, a student is classified as resilient if he or she is placed in the bottom quarter of the PISA index of Economic, Social and Cultural Status (ESCS) and placed in the top quarter of students regarding academic results. At this point, the definition given by Agasisti et al. (2018) has been borne in mind.

    2. (b.2)

      Socio-economic incidence. The equity in an educational system can also be measured by the existence of a favourable context that permits all the students to develop their talent, and to overcome the limitations derived from their economic and social circumstances. It is clear that the quantification of this idea is not straightforward. We try to approximate this point through the percentage of variation in the scores of the main subjects that cannot be explained by a student’s socio-economic status. Three different indicators have been considered to measure the incidence in Science (INCS), Mathematics (INCM) and Reading (INCR).

      The idea here is to measure the capacity of a system in minimising the influence of socio-economic background on the academic achievements of the students. It is interesting to note the main differences between the two groups of indicators included in this dimension. Note that the concept of resilient students only considers those students that are placed in the bottom quarter of the ESCS. In contrast, the former indicator takes into account the complete set of students.

  3. (c)

    Students’ self-perceptions. One of the main characteristics of the education function Mancebon and Bandres (1999) is, among others, that the educational process is carried out by the customers themselves. This justifies the incorporation of the self-evaluation of the student into the complete evaluation of the educational system. Hence, a third dimension is included in an effort to measure the students’ well-being during their scholar stage. Although the desirability of excellent academic results is paramount, this target should not be achieved at a cost to the students’ well-being. Hence, we propose the inclusion of a group of indicators that reflect the self-perceptions of the students during their scholar stage.

    Previous studies suggested that the school environment is a key aspect to understand the degree of satisfaction of the students with teachers, classmates... (e.g., Casas et al., 2013; Rees & Main, 2015). In Berkowitz et al. (2017) there is a comprehensive literature review of those studies that examined if a positive climate at the school has a positive influence on academic outcomes and can mitigate the association between socio-economic status and academic achievements. From the different results, the direction and relations between socio-economic status, school climate, and academic performance is not unique and conclusive.

    Some previous proposals (see, for instance, Rothstein, 2000) suggested a composite index of school performance that included aspects such as students’ security at school, the adult attention the students receive and the role of teachers in addition to academic results.

    We strive measure these self-perceptions with respect to the environment of the educational institutions, their wellness, the teachers’ performance, and the added value of the scholar ages for their future working lives.

    1. (c.1)

      Sense-of belonging. Firstly, we include one of the composite indices developed by PISA as a proxy of the overall well-being of the students at school: the Sense of Belonging index. This indicator (BELO) attempts to measure how accepted, respected, and supported students feel in their social context at school (Goodenow & Grady, 1993). Previous studies have shown a positive association of this variable with other, such as positive disciplinary climate, participating in extracurricular activities, family support, and positive teacher-student relations.

    2. (c.2)

      Bullying exposure. A second aspect of interest is that of the prevention of bullying behaviour. This aspect is currently one a growing scourge in almost all countries. The composite indicator developed by PISA, Index of Exposure to Bullying, is included, which quantifies the exposure to bullying with respect to average student across countries (BULL).

    3. (c.3)

      Motivation in teaching goals. A third relevant aspect for the students involves the motivation in their day-to-day activities. This is considered to be a positive aspect of an educational system if the environment of the schools and the motivation of the students are such that the students’ goal of their daily activity is to learn as much as possible or to understand the content of the classes. We have included the composite index proposed by PISA to measure the ambition towards the Learning Goals with respect to the average (GOAL).

    4. (c.4)

      Valuation of the teachers’ activity. It is clear that one of the most determining elements in the education process is that of the role of teachers. We propose the inclusion of the students’ evaluations regarding the teachers’ attitude (TEACH). We have included the index of Teacher Support proposed in PISA, which strives to measure the interest level of the teachers in the learning process or the extent to which the teachers help.

    5. (c.5)

      Valuation of the scholar stage. Finally, the inclusion of the index Value of School proposed in PISA strives to measure how the students quantify the added value that schools incorporate into their subsequent scholar stages and their future working lives. This index (V ALU) is developed by including the answers to a set of questions such as whether trying hard at school will help towards entering a good university and/or to get a good job in the future.

To summarise, a list of fourteen indicators, separated into the aforementioned three dimensions, is considered. Table 1 outlines the main descriptive statistics for the set of indicators.

Table 2 summarises the results of independent samples t-test and proportion test for comparison of the proposed indicators with respect to gender both globally and segmented by each of the 37 OECD countries included in this work. Note that only eleven of the fourteen variables have been tested, since the three variables extracted from the incidence of ESCS index could not be compared with the respect to the average values. In those cases in which the variables are constructed from plausible values, a separate analysis of the variables has been carried out, taking into account each plausible value. In all the cases, the results have been weighted with the size of the sample. For each country, the normalised weights are used. In this way, comparisons between countries can be performed, thereby obtaining robust estimations.

Significant differences between men and women are found in all the studied variables, except TEACH and SCI. Regarding average scores in Mathematics, the performance by men is better than that of women, the opposite being the case in Reading. It is interesting to point out that the differences in the latter case (READ) are greater. Similarly, men have a higher average value in the index of BELO and women in BULL (note that this indicator must be modified so that a higher value indicates a better situation).

The highest number of differences are found in Finland, Norway (with differences in all the variables but one, index TEACH), Canada (in which all the differences appear in the same direction of global evaluation), and Israel (in which no differences exist with respect to EXCE). In contrast, USA is the country in which a minimum number of differences are found between men and women. The only differences arise in MATH and BELO, in favour to men, and in READ, GOAL, and VALU; in which women perform better than men.

With respect to each individual indicator, women perform better than men with respect to variables READ, VALU, and GOAL. The opposite situations appear in BELO, in which the higher performance corresponds to the group of men. It is interesting to highlight the case of RESI. Significant differences appear in favour of men in the case of Chile, Colombia, Spain, and Mexico. The case of Spain may be justified since the information for Reading is not available, in which women have generally better results than men.

It is interesting to highlight how the third dimension presents a negative or statistically non-significant correlation with the other indicators. Concerning this point authors such as Mikk et al. (2016) and Ma et al. (2021) have shown how the effect of student-perceived teacher support on reading literacy is not significant at the school level, but it is at the student level. In addition, the correlation between teacher-students relations and the academic outcome shows a weak positive relationship at the student level, a positive correlation at the school level but a negative correlation at the country level.

3.2 Discussion of the Results

The results obtained for the composite indicator are summarised in Table 3. The table includes the results obtained for each country in three cases: global (considering all the students), male and female (considering separately the results of each subgroup of students). In addition, the ranking induced by these values has been also included. Note that in this order, the first position is assigned to the top-performing country and 37th position to the worst-rated country, and that each ranking is constructed by considering solely the values of the corresponding subgroup, since this indicator, as seen in the section of methodology, must be analysed with respect to the set of alternatives under consideration in each evaluation.

For illustrative purposes, the results of a weighted additive aggregation have been also included in Table 3. It is important to note that this aggregation scheme permits a complete compensation between the indicators. Although the majority of the results are similar, some units take advantage of this feature. That is the case of Slovenia, which is ranked in the 30th position in the geometric indicator and in the 25th in the additive aggregation. This unit presents really good values in three indicators (READ, INCL and RESI) but poor values in the remaining ones. This circumstance, an unbalanced vector of observations, is reflected in a poor evaluation when a geometric aggregation is considered. But the full compensation between sub-indicators is allowed (additive aggregation) having as a consequence a better evaluation for the unit.

It is important to bear in mind that each indicator has been constructed with an individual vector of weights and that an upper bound of 0.15 and a lower bound of 0.03 have been included in the relative importance of the weights. These vectors are computed taking into account the observed values of the remaining units of the subset (and not the global evaluation of both subgroups). That is, for the determination of the values of male indicators, only the values of the sub-indicators of this subgroup were considered for the unit under evaluation and for the remaining units. By way of example, Tables 4 and 5 (see Annex) include the normalised weights for the global data in the optimistic and pessimistic evaluation, respectively. In is interesting to bear in mind that the model which determines optimal weights proposes a relative evaluation of the units. That is to say, in the optimistic evaluations, the optimal weights will be selected to identify which variables the unit presents a comparative advantage with regarding the remaining ones (by giving higher values). In contrast, in the pessimistic evaluations, those in which the composite evaluation of each unit is minimised, comparative disadvantages are identified by assigning higher values.

The results of the rankings are represented for comparison purposes in Fig. 1. For each country, the positions occupied in the orders induced in the global evaluation and the evaluations of each subgroup (male and female students) are represented. When the rankings coincide, the markers are overlapped. Otherwise, the vertical distance between points measures the difference between the position in each order. In general terms, there are no large differences between the three orders, with two exceptions in which differences between rankings attain seven units: ESP, with a better performance of the male subgroup, and ISL, where the worst evaluation corresponds to male students. The rank position induced in global and male evaluations coincide in 15 times, and the order position in the global ranking and in the female ranking is the same 28 times.

Fig. 1
figure 1

Induced rankings. Comparative results

Full size image

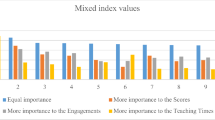
The multiplicative nature of the CI permits enables the identification of the individual contribution of each of the three dimensions considered. In Table 6 (see the Appendix), the values of the indicator separated by subgroups and each dimension are included. Figure 2 presents the contribution of each dimension to the global case (similar figures could be constructed for male and female evaluations). The solid bars represent the value of the weighted indicator for each dimension (academic, equity, and students’ self-perceptions). The height of the non-filled box represents the value of the CI. This graph permits to detect, the strengths and weakness of each country to be detected (aggregated by the three referred dimensions).

Fig. 2
figure 2

Contribution of each dimension to the composite index

Full size image

It is interesting to see how, due to the multiplicative nature of the composite indicator, those units with a “well-balanced” situation are rewarded with a greater value of the composite indicator, especially if the value of the components is greater than the unit (the individual indicator is over the average). These are the cases of the best-valued countries: Korea, Japan, Sweden, and Finland.

In the opposite situation, we found countries with a low value in one (or more than one) dimension. The geometric aggregation does not permit compensation between parts and penalises the existence of low values in one of its parts. This is the situation of Mexico and Colombia, where the poor performance in the academic dimension drops the global result even lower. This situation would force the units to focus their efforts on the improvements of those aspects in which the observed values are lowest. A marginal progress in the academic dimension would have a major effect for these countries, much more than if the same improvement occurred in any of the other dimensions. That is to say, the geometric aggregation implies a penalisation factor that captures the unbalance from the observed values. This aggregation scheme in some way permits evaluating more appropriately a complex phenomenon, since all the valuable attributes or aspects are jointly considered.

A correlation analysis (Spearman’s Rho) enables us to see that the global evaluation, together with the academic and equity dimensions, present similar values, with positive and statistically significant correlation coefficients. This situation appears when two of these sets of values are compared for an individual evaluation (total, male, and female) as well as for an individual dimension (global, academic, and equity).Conversely, the third dimension (students’ self-perceptions) presents negative or statistically non-significant correlation coefficients when they are compared with the other three values in both cases: they are compared with different evaluations as well as with respect to the other three values of the same group of students.

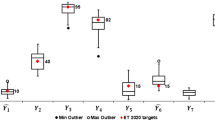
Figure 3 enables the comparison between countries considering the subgroups’ evaluations. Each point represents the values of the composite indicator for males (abscissa axis) and for females (ordinate axis). Those units located at a distance from the origin represent the countries with a better evaluation in both subgroups (Korea and Japan). Conversely, those countries closer to the origin represent the worst performers (Colombia, Mexico, and Chile).

Fig. 3
figure 3

Global Indicator. Comparative male vs. female

Full size image

The distance from the origin to the right (upwards) indicates a better valued unit in the male (female) indicator. A continuous line that represents the bisector has also been incorporated. Those units located above this line are those in which the index in the female subgroup is greater than the value in the male index. The units located below the line present the inverse situation. If the indicator had coincided for the two subgroups, then the unit would be located on the bisector. Note that the larger the difference of angle with respect to 45°, the greater the differences of the evaluation of both subsets.

It is interesting to see that, 17 times, the numeric value of CI is greater for the female evaluation (and, conversely, in 20 countries the value of CI is greater for the male subgroup). The greatest differences in favour of the male subgroup are found in Japan and Colombia. The greatest differences where the CI of the female subgroup is higher correspond to Poland and Finland.

Finally, Table 7 (see Appendix) summarises the decomposition of the values PCi, which enables the identification of the main causes that explain a greater value of CIi for one of the subgroups.

In a similar way to that in the Fig. 4, the filled bars represent the value of the individual effects (own performance, base, and weighting vectors)

Fig. 4
figure 4

Decomposition of the comparison between female and male results

Full size image

while the height of the non-filled box represents the value of PCi which compares the composite indicator for females over the corresponding value for males. In this way, a value of PCi greater than the unity implies that, for this country, the value of the CI is greater for the female students than for the male students.

The values of OWN represent the contribution (positive or negative) of the observed sub-indicator. Values greater than the unity represent a better result in the country derived exclusively from a better performance in the individual indicators. All the countries except two (Colombia and Hungary) present values greater than the unity in this component, with special mention to Finland and Lithuania, which present the largest differences in favour of the female subgroup.

The BP values quantify the influence of the variation of the baseline in the composite indicator. Here, the comparison of the baseline of male over female is measured. Note that, in this case, greater values of the bases would have a negative influence on the composite indicator since the value of the indicator is included through \(\left(\frac{{I}_{ri}}{{I}_{rB}}\right)\). That is, a lower value of the baseline exerts an indirect positive effect on the composite indicator. Values lower than the unity (common in all countries) reflect that the baseline for the female subgroup is greater than the corresponding values for the male subgroup.

Finally, W enables the incidence of the weighting vectors over PCi to be measured. A value greater (less) than the unity indicates that the selection of the weighting factor in female induces an improvement (deterioration) in values of this subgroup with respect to those of the male subgroup. In this case, the results vary although they remain favourable for female students, since the effect of the selection of optimal weights is positive for the evaluation of this subgroup (values greater than the unity) in 24 countries).

4 Concluding Remarks

Composite indicators have proved in the past to be suitable for the evaluation of complex phenomena. In this work, we propose a methodology for the construction of composite indicators based on the multiplicative aggregation and free selection of weights. In brief, a two-step procedure based on Data Envelopment Analysis in the determination of the weighting profiles has been described in order to construct a composite indicator. The main objective is to develop a valuable tool for the comparison of the performance of educational systems. We are interested in providing a global measure that yields a global evaluation for each country, which enables the strengths and weakness of the evaluations to be identified, and comparisons to be performed between the results obtained by male and female students separately. The main contribution is the development of an aggregation scheme that permits identifying the sources of relative advantages or disadvantages of one unit or subgroup with respect to the others.

A geometric aggregation of the sub-indicators in order to avoid the compensation between individual aspects has been considered. This family of indicators reward those alternatives with a well-balanced situation (above average values of all the indicators) over those alternatives with a higher value in one or two of the aspects, but very low results in one of the remaining aspects. Furthermore, the multiplicative nature of the indicator enables the easy identification of the contribution of each dimension to the global value. It was observed that the worst-ranked countries correspond to those with a very low values in any of the referred dimensions (academic, such as Colombia and Mexico, or students’ self-perceptions, such as Slovenia and Latvia) that cannot be compensated by good results in the other aspects. This feature of the indicators based on geometric aggregation provides information the countries as to which aspects must be improved, since improvements in worst-valued aspects will have a greater impact on the composite indicator. To certain extent, this provides a first approach to the general outlines for political measures. On the other hand, if the sources of the low values are the weighting schemes or the basis considered as a benchmark, the aim of the political measures should be a global improvement of the observations.

Herein, the results of male and female students have been compared separately. Considering them as two independent populations, we computed the composite indicators for both subgroups and compared the results. It is important to point out that this analysis implies computing all the results for the two subgroups separately. That is to say, the set of individual sub-indicators, the baseline that provides a basis for the normalisation phase, and the optimal weighting profiles are different for the first evaluation (which includes all the observations), to those for the other two computations.

It is interesting to bear in mind that the aim of this paper is not to perform a gender-perspective study like those found in the literature on this topic. Our intention is not to measure the gender-gap, to identify the sources of the differences between the values, or to propose political measures to mitigate these differences. Instead, our approach strives to measure the performance of national educational systems by considering a global view, and to evaluate separately the two groups of students in an effort to point out those cases (countries) where the results are significantly different. These results can be seen as a starting point for a posterior gender perspective analysis, in order to identify the causes of these differences and to propose measures for the mitigation of these gaps.

A first approach to the individual sub-indicators gave a first comparison between female and male results. Clearly, the male results in Mathematics and Sense of Belonging are better than the female results; the opposite occurs in Reading and certain indicators included in the third dimension (Motivation in teaching goals). When all these individual values are gathered together as the components of the composite indicators, the results indicate that there are no significant differences in the global indicator or in any of the dimensions regarding gender (results that are confirmed through Mann–Whitney tests).

When the aggregated evaluations are analysed, a similar performance for male and female results can be observed. In fact, a high correlation exists between the results of the two subgroups and between the results of two of the three dimensions. Only the third dimension, that which measures the self-perception of the students, presents a different performance with respect to the global or individual evaluation.

The proposed methodology permits to analyse main sources of the differences between male and female results. The proposed model enables the identification of whether a better result of one of the subgroups (male or female) is derived from its own observations, the impact of the baseline, or the optimal weighting profiles. On this point, it is interesting to see how the higher value of the average in the female subgroup exerts, in general terms, a negative impact on the evaluation since a higher value of the observed sub-indicators is required to lead the normalised value to be greater than the unity.

It would also be of interest to analyse the results with respect to the main economic variables traditionally associated with education. In particular, we consider GNP and accumulative educational expenditure per student. The correlation between these two variables is high (0.881) and the values of the composite indicator are statistically significant. Likewise, when the ranges in these variables and in the global indicators are considered, it can be observed that the correlations between the global indicators, those of dimension 1 (academic) and 2 (equity) (both globally and segmented by gender), are statistically significant. Nevertheless, the results for third dimension (students’ self-perceptions) do not depend on either the academic or the social part. In this case, the correlation is negative or non-significant, that is, countries with a low value for GNP and accumulative educational expenditure can achieve good results in this third dimension, perhaps due to the work of heads teachers and teachers, which overcome the difficulties derived from a lack of resources.

This work was supported by grant from the Spanish Ministry of Economy and Competitiveness PGC2018 095,786-B-IOO, and from the Ministry of Economy, Knowledge, Business and University, of the Andalusian Government, within the frameworkof the FEDER Andalusia 2014–2020 operational program. Specific objective 1.2.3. «Promotion and generation of frontier knowledge and knowledge oriented to the challenges of society, development of emerging technologies») within the framework of the reference research project (UPO-1380624). FEDER co-financing percentage 80%.

Funding for open access publishing: Universidad Pablo de Olavide/CBUA.

The authors are also thankful to two anonymous reviewers whose constructive comments and suggestions have helped to improve the paper.