Skip to main content

Advertisement

SpringerLink
Log in

Comparing the Performance of National Educational Systems: Inequality Versus Achievement?

  • Published:
Social Indicators Research Aims and scope Submit manuscript

Abstract

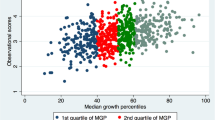
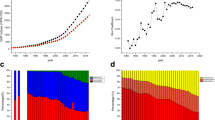
We measure performance change for the educational systems of 28 countries which participated in the Trends in International Mathematics and Science Study in years 2007 and 2011 for eighth grade basic education students. We consider simultaneously variables related to academic achievement and inequality in the discipline of mathematics. From a methodological point of view, we use the global Malmquist–Luenberger productivity index due to the presence of bad outputs. To the best of our knowledge, this methodology had not been applied previously in the field of education despite these desirable which are particularly useful in this field. Results indicate that the countries participating in the study not only chose different paths to improve their educational performance but, in addition, results varied remarkably among them. They also suggest that, on average, educational performance deteriorated between 2007 and 2011, although we also found (successful) efforts in several countries to improve equality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. Among the international studies we may find the Programme for International Student Assessment (PISA), the Teaching and Learning International Survey (TALIS), the Third Regional Comparative and Explanatory Study (TERCE), the International Computer and Information Literacy Study (ICILS), the Progress in International Reading Literacy Study (PIRLS), the Trends in International Mathematics and Science Study (TIMSS) and the International Civic and Citizenship Study (ICCS).

  2. We refer to inequality in terms of academic performance. As we will show throughout the paper we model inequality as a bad output in the context of frontier estimation and directional distance functions.

  3. Education provision is considered to be efficient if its producers make the best possible use of available inputs.

  4. A good output is a result variable (produced simultaneously with good outputs) that, when its value increases, has a positive impact on the process under evaluation and, therefore, is a desirable result. In the context of education, examples of good outputs could be students’ academic achievement, the percentage of students who obtain the maximum qualification, or the achievement of certain competences. In contrast, a bad output is a result variable that, when its value increases, negatively impacts on the process under evaluation and, therefore, is a non-desirable result. In the context of education a bad output could be dispersion in the academic results obtained or the percentage of students not reaching a minimum threshold of qualification. A typical example of a bad output in environmental economics would be pollution.

  5. If we were explicitly interested in conducting a dynamic analysis in the context of Data Envelopment Analysis, we could consider approaches such as those by Nemoto and Goto (1999, 2003), Chen and Dalen (2010) and Kao (2013). We thank an anonymous reviewer for this comment.

  6. Readers interested in a more detailed mathematical formulation, or a graphic illustration of this methodology may refer to Oh (2010, p. 186).

  7. For an extensive review of their use in the literature, see Emrouznejad et al. (2008) and, more recently, Emrouznejad and Yang (2017). We are grateful to an anonymous reviewer for this comment.

  8. These directions should be selected exogenously from the model in order to characterize the desirability of the movements in a specific direction according, for instance, to their specific prices or the statement of strategic goals. A good example of different possible directions can be found in Picazo-Tadeo et al. (2012).

  9. The literature on efficiency identifies mainly two types of technologies for these cases. First, strong disposability, which implies that the bad output may be reduced while maintaining the level of good outputs. In the context of education, this could imply reducing inequality without affecting the best perfomers’ level of learning. Second, weak disposability involves a more restrictive technology, for which reducing the bad output implies accepting reductions in the good output. In the context of education, this would imply that inequality cannot be reduced without eroding the best performers’ average learning levels.

  10. See also the recent relevant contribution by Dakpo et al. (2016) and Epure and Lafuente (2015).

  11. See http://www.un.org/millenniumgoals/education.shtml, accessed November 2nd, 2017.

  12. Software alternatives are freely available to estimate both global and local bandwidths. In the case of global bandwidth, the KernSmooth package for R considers the dpik function for the direct plug-in; for the local bandwidths, we considered R’s locfit package and the locfit function.

References

  • Agasisti, T. (2014). The efficiency of public spending on education: An empirical comparison of EU countries. European Journal of Education, 49(4), 543–557.

    Article  Google Scholar 

  • Balk, B. M. (2001). Scale efficiency and productivity change. Journal of Productivity Analysis, 15(3), 159–183.

    Article  Google Scholar 

  • Barro, R. J. (1997). Determinants of economic growth: A cross-country empirical study. Cambridge, MA: MIT Press.

    Google Scholar 

  • Carlson, D. (2001). Focusing state educational accountability systems: Four methods for judging school quality and progress. Center for Assessment (NCIEA), Dover, NH: Technical report.

  • Caves, D. W., Christensen, L. R., & Diewert, W. E. (1982). The economic theory of index numbers and the measurement of input, output, and productivity. Econometrica, 50(6), 1393–1414.

    Article  Google Scholar 

  • Chang, C.-H., & Pascua, L. (2017). The curriculum of climate change education: A case for Singapore. The Journal of Environmental Education (forthcoming).

  • Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444.

    Article  Google Scholar 

  • Chen, C.-M., & van Dalen, J. (2010). Measuring dynamic efficiency: Theories and an integrated methodology. European Journal of Operational Research, 203(3), 749–760.

    Article  Google Scholar 

  • Chung, Y. H., Färe, R., & Grosskopf, S. (1997). Productivity and undesirable outputs: A directional distance function approach. Journal of Environmental Management, 51, 229–240.

    Article  Google Scholar 

  • Dakpo, K. H., Jeanneaux, P., & Latruffe, L. (2016). Modelling pollution-generating technologies in performance benchmarking: Recent developments, limits and future prospects in the nonparametric framework. European Journal of Operational Research, 250(2), 347–359.

    Article  Google Scholar 

  • De Witte, K., & López-Torres, L. (2017). Efficiency in education: A review of literature and a way forward. Journal of the Operational Research Society (forthcoming).

  • Deng, Z., & Gopinathan, S. (2016). PISA and high-performing education systems: Explaining Singapore’s education success. Comparative Education, 52(4), 449–472.

    Article  Google Scholar 

  • Dufrechou, P. A. (2016). The efficiency of public education spending in Latin America: A comparison to high-income countries. International Journal of Educational Development, 49, 188–203.

    Article  Google Scholar 

  • Emrouznejad, A., Parker, B. R., & Tavares, G. (2008). Evaluation of research in efficiency and productivity: A survey and analysis of the first 30 years of scholarly literature in DEA. Socio-Economic Planning Sciences, 42(3), 151–157.

    Article  Google Scholar 

  • Emrouznejad, A., Parker, B. R., & Tavares, G. (2010). Evaluation of research in efficiency and productivity: A survey and analysis of the first 30 years of scholarly literature in DEA. Socio-economic Planning Sciences, 42(3), 151–157.

    Article  Google Scholar 

  • Emrouznejad, A., & Yang, G. (2017). A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Economic Planning Sciences, 61(2018), 4–8.

  • Epure, M., & Lafuente, E. (2015). Monitoring bank performance in the presence of risk. Journal of Productivity Analysis, 44(3), 265–281.

    Article  Google Scholar 

  • Färe, R., & Grosskopf, S. (2004). Modeling undesirable factors in efficiency evaluation: Comment. European Journal of Operational Research, 157(1), 242–245.

    Article  Google Scholar 

  • Färe, R., & Grosskopf, S. (2009). A comment on weak disposability in nonparametric production analysis. American Journal of Agricultural Economics, 91(2), 535–538.

    Article  Google Scholar 

  • Färe, R., Grosskopf, S., Lovell, C. A. K., & Pasurka, C. (1989). Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. The Review of Economics and Statistics, 71(1), 90–98.

    Article  Google Scholar 

  • Färe, R., Grosskopf, S., Noh, D.-W., & Weber, W. W. (2005). Characteristics of a polluting technology: Theory and practice. Journal of Econometrics, 126(2), 469–492.

    Article  Google Scholar 

  • Färe, R., Grosskopf, S., & Pasurka, C. A, Jr. (2007). Environmental production functions and environmental directional distance functions. Energy, 32(7), 1055–1066.

    Article  Google Scholar 

  • Färe, R., Grosskopf, S., Norris, M., & Zhang, Z. (1994). Productivity growth, technical progress, and efficiency change in industrialized countries. American Economic Review, 84(1), 66–83.

    Google Scholar 

  • García, M. J., & Arechavaleta, C. (2011). Cuáles son las razones subyacentes al éxito educativo de Corea del Sur? Revista Española de Educación Comparada, 18, 203–224.

    Article  Google Scholar 

  • Giménez, V., Thieme, C., Prior, D., & Tortosa-Ausina, E. (2017). An international comparison of educational systems: A temporal analysis in presence of bad outputs. Journal of Productivity Analysis, 47(1), 83–101.

    Article  Google Scholar 

  • Golany, B., & Roll, Y. (1989). An application procedure for DEA. Omega, 17(3), 237–250.

    Article  Google Scholar 

  • Grosskopf, S., Hayes, K. J., & Taylor, L. L. (2014). Efficiency in education: Research and implications. Applied Economic Perspectives and Policy, 36(2), 175–210.

    Article  Google Scholar 

  • Hailu, A., & Veeman, T. S. (2001). Non-parametric productivity analysis with undesirable outputs: An application to the Canadian pulp and paper industry. American Journal of Agricultural Economics, 83(3), 605–616.

    Article  Google Scholar 

  • Hairon, S., & Tan, C. (2017). Professional learning communities in Singapore and Shanghai: implications for teacher collaboration. Compare: A Journal of Comparative and International Education (forthcoming).

  • Hanushek, E. A., & Kimko, D. D. (2000). Schooling, labour force quality, and the growth of the nations. American Economic Review, 90, 1184–1208.

    Article  Google Scholar 

  • Hanushek, E. A., & Luque, J. A. (2003). Efficiency and equity in schools around the world. Economics of Education Review, 22(5), 481–502.

    Article  Google Scholar 

  • Heng, M. A., & Atencio, M. (2017). “I assume they don’t think!”: Teachers’ perceptions of Normal Technical students in Singapore. The Curriculum Journal, 28(2), 212–230.

    Article  Google Scholar 

  • Johnes, J. (2015). Operational research in education. European Journal of Operational Research, 243(3), 683–696.

    Article  Google Scholar 

  • Kao, C. (2013). Dynamic data envelopment analysis: A relational analysis. European Journal of Operational Research, 227(2), 325–330.

    Article  Google Scholar 

  • Krueger, A., & Lindahl, M. (2001). Education for growth: Why and for whom? Journal of Economic Literature, 39, 1101–1136.

    Article  Google Scholar 

  • Kumar, S., & Russell, R. R. (2002). Technological change, technological catch-up, and capital deepening: Relative contributions to growth and convergence. American Economic Review, 92(3), 527–548.

    Article  Google Scholar 

  • Kuosmanen, T. (2005). Weak disposability in nonparametric production analysis with undesirable outputs. American Journal of Agricultural Economics, 87, 1077–1082.

    Article  Google Scholar 

  • Kuosmanen, T., & Podinovski, V. V. (2009). Weak disposability in nonparametric production analysis: Reply to Färe and Grosskopf. American Journal of Agricultural Economics, 91, 539–545.

    Article  Google Scholar 

  • Loader, C. R. (1996). Local likelihood density estimation. The Annals of Statistics, 24(4), 1602–1618.

    Article  Google Scholar 

  • Luenberger, D. (1992). New optimality principles for economic efficiency and equilibrium. Journal of Optimization Theory and Applications, 75(2), 221–264.

    Article  Google Scholar 

  • Mandal, S. K., & Madheswaran, S. (2010). Environmental efficiency of the Indian cement industry: An interstate analysis. Energy Policy, 38(2), 1108–1118.

    Article  Google Scholar 

  • Nemoto, J., & Goto, M. (1999). Dynamic data envelopment analysis: Modeling intertemporal behavior of a firm in the presence of productive inefficiencies. Economics Letters, 64(1), 51–56.

    Article  Google Scholar 

  • Nemoto, J., & Goto, M. (2003). Measurement of dynamic efficiency in production: An application of data envelopment analysis to Japanese electric utilities. Journal of Productivity Analysis, 19(2–3), 191–210.

    Article  Google Scholar 

  • Oh, D. (2010). A global Malmquist–Luenberger productivity index. Journal of Productivity Analysis, 34(3), 183–197.

    Article  Google Scholar 

  • Pastor, J. T., & Lovell, C. A. K. (2005). A global Malmquist productivity index. Economics Letters, 88(2), 266–271.

    Article  Google Scholar 

  • Patron, R., & Vaillant, M. (2012). Can education policy address the wage gap? A note on public skill formation in developing countries. Journal of International Development, 24, 369–378.

    Article  Google Scholar 

  • Picazo-Tadeo, A. J., Beltrán-Esteve, M., & Gómez-Limón, J. A. (2012). Assessing eco-efficiency with directional distance functions. European Journal of Operational Research, 220(3), 798–809.

    Article  Google Scholar 

  • Picazo-Tadeo, A. J., Castillo-Giménez, J., & Beltrán-Esteve, M. (2014). An intertemporal approach to measuring environmental performance with directional distance functions: Greenhouse gas emissions in the European Union. Ecological Economics, 100, 173–182.

    Article  Google Scholar 

  • Picazo-Tadeo, A. J., & Prior, D. (2009). Environmental externalities and efficiency measurement. Journal of Environmental Management, 90(11), 3332–3339.

    Article  Google Scholar 

  • Reinhard, S., Lovell, C. A. K., & Thijssen, G. J. (2002). Analysis of environmental efficiency variation. American Journal of Agricultural Economics, 84, 1054–1065.

    Article  Google Scholar 

  • Seiford, L. M., & Zhu, J. (2002). Modeling undesirable factors in efficiency evaluation. European Journal of Operational Research, 142(1), 16–20.

    Article  Google Scholar 

  • Sheather, S. J., & Jones, M. C. (1991). A reliable data-based bandwidth selection method for kernel density estimation. Journal of the Royal Statistical Society, Series B, 53(3), 683–690.

    Google Scholar 

  • So, K., & Kang, J. (2014). Curriculum reform in Korea: Issues and challenges for twenty-first century learning. Asia-Pacific Education Researcher, 23(4), 795–803.

    Article  Google Scholar 

  • Sueyoshi, T., & Goto, M. (2011). Measurement of returns to scale and damages to scale for dea-based operational and environmental assessment: How to manage desirable (good) and undesirable (bad) outputs? European Journal of Operational Research, 211(1), 76–89.

    Article  Google Scholar 

  • Teddlie, C., & Reynolds, D. (2000). The international handbook of school effectiveness research. London: Routledge.

    Google Scholar 

  • Tsai, S., Smith, L., & Hauser, R. (2017). Families, schools, and student achievement inequality. Sociology of Education, 90(1), 64–88.

    Article  Google Scholar 

  • Watanabe, M., & Tanaka, K. (2007). Efficiency analysis of Chinese industry: A directional distance function approach. Energy Policy, 35(12), 6323–6331.

    Article  Google Scholar 

  • Xue, M., & Harker, P. T. (2002). Note: Ranking DMUs with infeasible super-efficiency DEA models. Management Science, 48(5), 705–710.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Business, Universitat Autònoma de Barcelona, Barcelona, Spain

    Víctor Giménez & Diego Prior

  2. Facultad de Economía y Empresa, Universidad Diego Portales, Santiago de Chile, Chile

    Claudio Thieme

  3. Departament d’Economia, Universitat Jaume I, Campus del Riu Sec, 12071, Castelló de la Plana, Spain

    Emili Tortosa-Ausina

Authors
  1. Víctor Giménez
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claudio Thieme
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Diego Prior
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Emili Tortosa-Ausina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emili Tortosa-Ausina.

Additional information

We are grateful to four anonymous reviewers whose comments have greatly contributed to improving the quality of the paper. Claudio Thieme and Emili Tortosa-Ausina thank FONDECYT (National Fund of Scientific and Technological Development, Grants #1121164 and #1151313) for generous financial support. Víctor Giménez, Diego Prior and Emili Tortosa-Ausina acknowledge the financial support of the Spanish Ministerio de Economía y Competitividad (ECO2013-46954-C3-2-R, ECO2013-44115-P and ECO2014-55221-P). Emili Tortosa-Ausina also acknowledges the financial support of Generalitat Valenciana (PROMETEOII/2014/046) and Universitat Jaume I (P1.1B2014-17). The usual disclaimer applies.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Giménez, V., Thieme, C., Prior, D. et al. Comparing the Performance of National Educational Systems: Inequality Versus Achievement?. Soc Indic Res 141, 581–609 (2019). https://doi.org/10.1007/s11205-018-1855-x

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11205-018-1855-x

Keywords

JEL Classification

Search

Navigation