The h-index as an almost-exact function of some basic statistics

Abstract

As is known, the h-index, h, is an exact function of the citation pattern. At the same time, and more generally, it is recognized that h is “loosely” related to the values of some basic statistics, such as the number of publications and the number of citations. In the present study we introduce a formula that expresses the h-index as an almost-exact function of some (four) basic statistics. On the basis of an empirical study—in which we consider citation data obtained from two different lists of journals from two quite different scientific fields—we provide evidence that our ready-to-use formula is able to predict the h-index very accurately (at least for practical purposes). For comparative reasons, alternative estimators of the h-index have been considered and their performance evaluated by drawing on the same dataset. We conclude that, in addition to its own interest, as an effective proxy representation of the h-index, the formula introduced may provide new insights into “factors” determining the value of the h-index, and how they interact with each other.

Introduction

The purpose of this paper is to present a formula with which to determine (estimate) the h-index, h, under incomplete information conditions (IIC). By IIC we mean the situation in which, for different kinds of reasons, we do not know the whole set of citation data, the entire citation profile that would allow us to obtain the actual exact value of the h-index. This is the case, for example, when only few “basic” citation statistics (other than the h-index) are published, or known to us.

To be concrete, we will refer to simple citation indicators—to use the words of Hirsch (2005), “single-number criteria commonly used to evaluate scientific output”—as:

• 1. total number of citations $C$;

• 2. total number of citations for the $t$ ($t \in \left\{ {1,2,3, \ldots } \right\}$) most-cited publications, $C_{t}$; thus, $C_{t} = \sum\nolimits_{i = 1}^{t} {c\left( i \right)}$, where $c\left( i \right)$ represents the number of citations to publication i, and where publications are ranked in decreasing order of the number of citations: $c\left( 1 \right) \ge c\left( 2 \right) \ge \cdots \ge c\left( T \right)$.

• 3. total number of publications $T$;

• 4. total number of “significant” publications, that is, those with at least a predetermined number of citations $k$ each ($k \in \left\{ {1,2,3, \ldots } \right\}$), $T_{k}$.

In this paper we focus on these indicators in their simplest versions, that is: $C$, $C_{1}$, $T$ and $T_{1}$. The purpose of the analysis is twofold: to estimate the h-index (when it cannot be determined directly from the data) and hence at the same time to identify the main factors which influence the level of the h-index. A crucial question is therefore the extent to which the h-index can be satisfactorily predicted from knowledge of only the above basic statistics—i.e. under IIC.

More formally, we are searching for a formula

$$\hat{h} = \hat{h}\left( {S_{1} , \ldots ,S_{r} } \right),$$

(1)

$1 \le r \le 4$, $S_{j} \in {\mathcal{S}}$, $1 \le j \le r$, where ${\mathcal{S}} = \left\{ {C,C_{1} ,T,T_{1} } \right\}$. To be noted is that the formula $\hat{h}$ can be interpreted as a genuine estimator of the h-index, $h$, i.e. $\hat{h} \cong h$, because it does not depend on values of unknown parameters.

Possible estimators under IIC of the h-index can be found in the literature:

• A very simple proxy for the h-index is given by $h_{H} = \sqrt {C/a}$. This model, which can be traced back to Hirsch (2005), is not a genuine estimator of the h-index because $h_{H}$ is still a function of an unknown parameter, $a$, and it is not specified (by the formula itself) how to estimate this parameter in terms of the above basic statistics. Nevertheless, an estimator for the h-index can be obtained by substituting the unknown parameter $a$ with a fixed constant (Hirsch found “empirically” that $a$ lay between 3 and 5). Redner (2010) found that “$\sqrt C$ is essentially equivalent to the h-index, up to an overall factor that is close to 2” (put otherwise, he found that the distribution ratio $\sqrt C /2h$ has an empirical distribution “sharply peaked about 1”). This suggests the approximating formula

  $$\hat{h} = h_{R} = \sqrt C /2$$

  (2)

  with $r = 1$, ${\mathcal{S}} = \left\{ C \right\}$, which we could then call the Redner formula—probably the simplest estimator of the h-index, under IIC.

• While $h_{R}$ is a model-free proxy for the h-index, more elaborate solutions has been attempted in the literature by assuming specific probabilistic distributions for the citation rate. For example, a formula that follows model (1), with $r = 4$, has been recently introduced by Bertoli-Barsotti and Lando (2017),

  $$\hat{h} = \tilde{h}_{W}^{\left(1 \right)} = \frac{- 1}{{\log \left({1 - \tilde{m}_{1}^{- 1}} \right)}} \cdot W\left({\frac{{T_{1}}}{{1 - \tilde{m}_{1}^{- 1}}} \cdot \log \left({1 - \tilde{m}_{1}^{- 1}} \right)} \right),$$

  (3)

  where $\tilde{m}_{1} = \left( {C - C_{1} } \right)/\left( {T_{1} - 1} \right)$ is nothing but a “trimmed” version of the simple sample mean $C/T_{1}$, and where $W\left( \cdot \right)$ represents the so-called Lambert-W function (Corless and Jeffrey 2015). The Lambert-W function is the function $W\left( z \right)$ satisfying $z = W\left( z \right){\text{e}}^{W\left( z \right)}$, and can be currently computed using mathematical software, for example the Mathematica^® software package (Wolfram Research, Inc. 2014), or the R statistical computing environment (R Development Core Team 2012). The use of a “trimmed” version of the sample mean is a simple technique with which to make the sample mean more robust with respect to a single outlier—a single highly-cited paper that could substantially inflate the mean, as is well known.

Formula $\tilde{h}_{W}^{\left( 1 \right)}$ $(r=4,\,{\mathcal{S}} = \left\{ {C,C_{1} ,T,T_{1} } \right\})$ is based on the assumption that the citation rate of papers (cited at least once) follows a shifted-geometric distribution (SGD) with parameter $Q(Q>1)$ with probability function $p\left( y \right) = Q^{ - y} \left( {Q - 1} \right)^{y - 1}$, $y = 1,2, \ldots$; $p\left( y \right)$ represents the probability of observing the number of citations $y$ of a paper (cited at least once), while $Q$ represents the expectation of the SGD. Then, $\hat{n}\left( y \right) = Tp\left( y \right)$ expresses the “expected”/estimated number of articles with $y$ citations.

• As an alternative approach, an important class of models is the one defined by the formula

  $$\hat{h} = \gamma_{0} C^{2/3} T^{ - 1/3}$$

  (4)

  where $\gamma_{0}$ is a fixed and known positive constant (Schubert and Glänzel 2007). From model (4), specific ready-to-use formulas are obtained by taking, in particular: (a) $\gamma_{0} = 4^{ - 1/3}$ (Iglesias and Pecharroman 2007; see also Ionescu and Chopard 2013; Panaretos and Malesios 2009; Vinkler 2009, 2013), (b) $\gamma_{0} = 0.75$ (Schubert and Glänzel 2007), (c) $\gamma_{0} = 1$ Prathap (2010a, b). Following the notation of Bertoli-Barsotti and Lando (2017), let $h_{SG} \left( {\gamma_{0} } \right) = \gamma_{0} C^{2/3} T^{ - 1/3}$. Note that these formulas are functions of the data only through two out of the four basic statistics ($r = 2$, ${\mathcal{S}} = \left\{ {C,T} \right\}$), and they are based on the assumption of a continuous-type distribution. The formula $h_{SG} \left( 1 \right)$ is also known as the “p-index” (Prathap 2010a, b).

• Another approach which deserves mention for completeness, even if it does not yield a ready-to-use formula, is that proposed by Iglesias and Pecharroman (2007). Adopting a different perspective, i.e. the rank-size formulation, and starting from the assumption that the number $c\left( k \right)$ of citations of the paper of rank $k$, is approximately distributed following a stretched exponential type PDF

  $$f\left( {k;\eta ,\beta } \right) = C\eta^{1/\beta } {{\varGamma }}\left( {1 + \beta^{ - 1} } \right)^{ - 1} \exp \left\{ { - \eta k^{\beta } } \right\},\quad k > 0,$$

  (5)

  (not to be confused with a Weibull PDF, see below), Iglesias and Pecharroman suggest deriving a formula for the h-index as the solution of the equation

  $$f\left( {x;\eta ,\beta } \right) = x.$$

  (6)

  Interestingly, the solution may be derived in closed form (even if authors did not realize this) by means of the Lambert-W function. Unfortunately, this solution still depends on the value of an unknown free parameter, specifically $\beta$ [see their Eqs. (16) and (17)]. Hence, their formula could become a genuine estimator of the h-index—of the form $\hat{h} = \hat{h}\left( {C,T,T_{1} } \right)$, $r = 3$—only by constraining the unknown parameter $\beta$ to assume a fixed (but arbitrary) value $\beta_{0}$.

A new formula for the h-index under the Weibull assumption

Let $N\left( y \right)$ be the empirical citation distribution function, i.e. the function giving the number of papers which have been cited $y$ times at most. Then, in particular, $n\left( y \right) = N\left( y \right) - N\left( {y - 1} \right)$, for $y = 1,2, \ldots$, $n\left( 0 \right) = N\left( 0 \right)$, is the number of papers that have been cited exactly y times. We assume that the citation rate of a paper is a random variable $X$ that is distributed as a two-parameter Weibull distribution, with CDF $F\left( {x;a,\beta } \right) = 1 - { \exp }\left\{ { - ax^{\beta } } \right\}$, $x > 0$, and 0 otherwise, where $a > 0$ and $\beta > 0$. The probability density function is then

$$f\left( {x;a,\beta } \right) = a\beta x^{\beta - 1} \exp \left\{ { - ax^{\beta } } \right\},$$

(7)

for $x > 0$, and 0 otherwise. The Weibull distribution is a rather flexible model: the PDF is reverse J-shaped for $\beta \le 1$ and bell-shaped otherwise.

Since our assumption involves a continuous distribution, a suitable discretization rule is needed. In particular, for every $y$, $y = 0,1,2, \ldots$, let $T\exp \left\{ { - ay^{\beta } } \right\}$ express the “expected” number of articles with at least $y$ citations. Hence, $\hat{n}\left( y \right) = T\int_{y}^{y + 1} {f\left( {x;a,\beta } \right){\text{d}}x = T \cdot \left( {F\left( {y + 1;a,\beta } \right) - F\left( {y;a,\beta } \right)} \right)}$ represents the expected number of articles with $y$ citations exactly, and $\hat{N}\left( y \right) = TF\left( {y + 1;a,\beta } \right)$ the expected number of papers which have been cited $y$ times at most. As a special case,

$$F\left( {1;a,\beta } \right) - F\left( {0;a,\beta } \right) = 1 - e^{ - a}$$

(8)

can be interpreted as a model for the so-called uncitedness factor, $\frac{{T - T_{1} }}{T} = \frac{n\left( 0 \right)}{T}$ (Hsu and Huang 2012; see also Egghe 2013; Burrell 2013). A Weibull model for the h-index is then yielded by the solution of the equation

$$T { \exp }\left\{ { - ax^{\beta } } \right\} = x,\quad x \in {\Re }\text{.}$$

(9)

Replacing $ax^{\beta }$ with $t$ in the equation, we have

$$te^{\beta t} = aT^{\beta } .$$

(10)

Thus, replacing $\beta t$ with $s$, we obtain the equivalent equation

$$se^{s} = a\beta T^{\beta } .$$

(11)

Hence, by definition of the above mentioned Lambert-W function, we find the solution $s = W\left( {a\beta T^{\beta } } \right)$ and, since $x = \left( {\frac{s}{a\beta }} \right)^{1/\beta }$, we finally arrive at the formula

$$x = \left( {\frac{{W\left( {a\beta T^{\beta } } \right)}}{a\beta }} \right)^{1/\beta } .$$

(12)

An empirical counterpart of the above theoretical model for the h index may now be obtained by substituting the parameters $a$ and $\beta$ with estimates, $a^{*}$ and $\beta^{*}$, based on suitable functions of the citation data only through the basic statistics $C,C_{1} ,T$ and $T_{1}$. This can be done firstly by using the uncitedness factor to derive the equation $1 - e^{ - a} = \frac{{T - T_{1} }}{T}$, that can be solved (under the assumption $0 < T_{1} < T$) for the variable $a$ as

$$a^{*} = \log \left( {\frac{T}{{T_{1} }}} \right),$$

(13)

as an estimate of parameter $a$, and secondly, by using the trimmed sample citation rate,

$$m^{*} = \frac{{C - C_{1} }}{T - 1} + 0.5,$$

(14)

as an estimate of the expectation of X, that is $E\left( X \right) = g\left( {a,\beta } \right) = a^{ - 1/\beta } {{\varGamma }}\left( {1 + \frac{1}{\beta }} \right) > 0$. Note that, by construction, our approximation slightly overestimates the true average number of citations, so that a correction for continuity by one-half is needed. We then find $\beta^{*}$ as the solution (method of moments) of the equation

$$m^{*} = g\left( {a^{*} ,\beta } \right),$$

(15)

that can be solved numerically. It should be noted that the existence and uniqueness of the solution of Eq. (15) are not always warranted a priori. Indeed, it can be proved that the necessary and sufficient condition for existence and uniqueness of the solution is $m^{*} > 1$ (see "Appendix"). We should then consider “out of range” the cases where $m^{*} \le 1$, and exclude them from the analysis.

With $a$ and $\beta$ replaced by $a^{*} = a^{*} \left( {T, T_{1} } \right)$ and $\beta^{*} = \beta^{*} \left( {C,C_{1} ,T} \right)$ in formula (12) one finally obtains ($r = 4$, ${\mathcal{S}} = \left\{ {C,C_{1} ,T,T_{1} } \right\}$)

$$\hat{h} = h_{WW} = \left( {\frac{{W\left( {a^{*} \beta^{*} T^{{\beta^{*} }} } \right)}}{{a^{*} \beta^{*} }}} \right)^{{1/\beta^{*} }} ,$$

(16)

where the suffix WW is motivated by the fact that the formula is based on a Weibull distribution and on the Lambert-W function.

Analysis

Two datasets

This section empirically investigates the effectiveness of formula $h_{WW}^{{}}$ as an estimate of the actual value of the h-index, $h$. We will compare estimates derived from $h_{WW}^{{}}$ with the real values of the h-index. In order to facilitate possible comparisons with other formulas (see below), we choose to use the same two datasets as in Bertoli-Barsotti and Lando (2017), where the authors present an empirical study based on citation data obtained from two different sets of journals belonging to two different scientific fields: (1) the S&MM list and (2) the EE&F list.

• 1. S&MM list The former dataset includes the 231 journals as selected from a former list of 568 journals identified as important (in the opinion of a group of experts) in the area “Statistics and Mathematical Methods” (S&MM). Overall, the S&MM dataset included 485,628 citations of 99,409 publications from these journals (for details see Bertoli-Barsotti and Lando 2017). For each journal, the actual value $h$ of the h-index was computed—on the basis of citations retrieved from the Scopus database in last week of December 2015—as the largest number of papers published in the journal between 2010 and 2014 and which obtained at least $h$ citations each, from the time of publication until December 2015. Thus, citation data referred to a 6-year citation window, 2010–2015, and a 5-year publication window, 2010–2014. The four basic statistics $C$, $C_{1}$, $T$ and $T_{1}$ were derived as well. The list of the 231 journals in the S&MM dataset is reported in Table 1.

  Table 1 Basic statistics for the S&MM list of journals and the approximation of the Hirsch h-index calculated by means of the $h_{WW}$ formula (rounded values). The value $h_{WW}$ is not uniquely defined (N/D) for the first journal on the list (because of a too small average number of citations per paper).

• 2. EE&F list The second dataset included the 100 journals (with a minimum number of 50 publications) top ranked according to the Scopus Impact per Publication (IPP; the IPP is defined as the ratio of citations in a year to papers published in the three previous years divided by the number of papers published in those same years) in 2014, within the Scopus subject area of “Economics, Econometrics and Finance” (EE&F). The citation data of all 100 journals in the EE&F list were retrieved during the last week of April 2016. The dataset obtained included 19,889 publications receiving a total of 74,096 citations. In this case, differently from the above dataset, in order to obtain citation and publication windows as similar as possible to those employed for the computation of the IPP 2014 by Scopus, the citations used were those received during 2014 of papers published within the previous 3 years 2011–2013 (for further details see Bertoli-Barsotti and Lando 2017). For each journal the actual value $h$ of the h-index was then computed as the largest number of papers published in the journal between 2011 and 2013 and which obtained at least $h$ citations each in the year 2014. The list of the journals in the EE&F dataset is reported in Table 2.

  Table 2 Basic statistics for the EE&F list of journals and the approximation of the Hirsch h-index calculated by means of the $h_{WW}$ formula (rounded values)

Estimation of the h-index with the formula $h_{WW}^{{}}$

Table 1 for the S&MM list and Table 2 for the EE&F list report, for each journal, identified by its ISSN code, the four basic statistics, $C$, $C_{1}$, $T$ and $T_{1}$, the h-index, $h$, as computed using the above procedure, and the value provided by the formula $h_{WW}^{{}}$ in its rounded-off version $\left\langle {h_{WW} } \right\rangle$, that is, in symbols,

$$\left\langle {h_{WW} } \right\rangle = \lfloor h_{WW} + 0.5\rfloor,$$

(17)

where $\left\lfloor { \cdot } \right\rfloor$ is the floor function (recall that the floor function of $x$ gives the greatest integer less than or equal to $x$). Note that, from an operational point of view, all estimating formulas (1) generate real numbers. However, for estimation purposes, these numbers should be rounded-off to the nearest integer, not only in order to produce numbers in the same range of values as the h-index but also to avoid “false precision”. (Hicks et al. 2015).

To give an example illustrating the calculation of this estimate, let us consider the case of the Journal of the American Statistical Association (ISSN 0162-1459, from the S&MM list). We have $C = 5231,C_{1} = 156,T = 663$ and $T_{1} = 519$. Hence

$$a^{*} = \log \left( {\frac{T}{{T_{1} }}} \right) = {\text{log }}\left( {663} \right) - {\text{log }}\left( {519} \right) = 0.2449$$

(18)

$$m^{*} = \frac{{C - C_{1} }}{T - 1} + 0.5 = \frac{5231 - 156}{663 - 1} + 0.5 = 8.166$$

(19)

Then, substituting $a^{*}$ and $m^{*}$ into the Eq. (15) we find

$$8.166 = \left( {0.2449} \right)^{ - 1/\beta } \varGamma \left( {1 + \frac{1}{\beta }} \right),$$

(20)

which yields the solution $\beta^{*} = 0.7365$. Thus, since

$$W\left( {0.2449 \cdot 0.7365 \cdot 663^{0.7365} } \right) = 2.26,$$

(21)

we finally conclude that

$$h_{WW} = \left( {\frac{{W\left( {a^{*} \beta^{*} T^{{\beta^{*} }} } \right)}}{{a^{*} \beta^{*} }}} \right)^{{1/\beta^{*} }} = \left( {\frac{2.26}{0.2449 \cdot 0.7365}} \right)^{1/0.7365} = 30.9,$$

(22)

so that the rounded-off version of $h_{WW}^{{}}$ in this case exactly coincides with the actual h-index, $h = 31.$

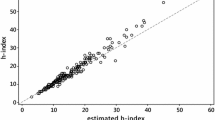
In Figs. 1 and 2 we plot for each journal, respectively for the S&MM list and the EE&F list, the empirical value of the h-index h versus its predicted value by $h_{WW}^{{}}$.

Fig. 1

Scatterplot of the empirical value of the h-index h versus its predicted value by $h_{WW}^{{}}$, for the S&MM list of journals. The dashed line is identity, so ideally all the points should overlie this line

Fig. 2

Scatterplot of the empirical value of the h-index h versus its predicted value by $h_{WW}^{{}}$, for the EE&F list of journals. The dashed line is identity, so ideally all the points should overlie this line

A comparative analysis of the accuracy

To verify the accuracy of formula $h_{WW}^{{}}$, comparatively, we considered, among several possible ready-to-use formulas, the following ones among those defined above: $\tilde{h}_{W}^{\left( 1 \right)}$, $h_{SG} \left( {0.63} \right)$, $h_{SG} \left( {.75} \right)$, $h_{SG} \left( 1 \right)$, $h_{R}$, which have been viewed as important or promising alternatives to the $h_{WW}^{{}}$ formula—due to an empirically recognized high correlation with the h-index [see Bertoli-Barsotti and Lando (2017) for formula $\tilde{h}_{W}^{\left( 1 \right)}$, Glänzel (2006), Malesios (2015), Schreiber et al. (2012) and Schubert and Glänzel (2007) for formulas $h_{SG}$, and Redner (2010), for formula $h_{R}$]. To measure the magnitude of the observed accuracy, for each of the six estimation formulas respectively numbered as: (1) $h_{WW}^{{}}$, (2) $\tilde{h}_{W}^{\left( 1 \right)}$, (3) $h_{SG} \left( {0.63} \right)$, (4) $h_{SG} \left( {0.75} \right)$, (5) $h_{SG} \left( 1 \right)$, (6) $h_{R}$,

• (a) we calculated the absolute relative error (ARE) of the estimator $\left\langle {\hat{h}_{j} \left( i \right)} \right\rangle$ of the actual h-index, $h_{j}$, for each journal $j$, $j = 1, \ldots ,J$,

  $${\text{ARE}}_{j} \left( i \right) = \frac{{\left| {\left\langle {\hat{h}_{j} \left( i \right)} \right\rangle - h_{j} } \right|}}{{h_{j} }},$$

  (23)

  where $\left\langle {\hat{h}_{j} \left( i \right)} \right\rangle = \lfloor\hat{h}_{j} \left( i \right) + 0.5 \rfloor$ is the rounded-off version of formula $i$, $i = 1,2, \ldots ,6$, then,

• (b) as a criterion with which to assess the overall quality of the formula, we computed the mean absolute relative error (MARE),

  $${\text{MARE}}\left( {\hat{h}\left( i \right)} \right) = \mathop \sum \limits_{j = 1}^{J} {\text{ARE}}_{j} \left( i \right)/J .$$

  (24)

The results are summarized in Table 3.

Table 3 Relative accuracy, computed in terms of MARE, of different estimators of the h-index; r represents the number of basic metrics on which the estimation formula is based for each dataset, the smallest error is indicated by a boldface number

Conclusion

This paper has addressed the need to gain better understanding of how simple citation metrics are related to the h-index, or rather, to a “good” proxy representation of the h index. This also responds to the more basic requirement of “building bridges” between different types of known and available measures of impact/impact indicators—under IIC.

Differently from other studies (that consider the problem of defining a “model” of the h-index), our concern has not been to estimate the parameters (sometimes even considered at the unit level, i.e. single journal, or single scientist; see e.g. Petersen et al. 2011) of a parametric model for the h-index under the assumption of knowing the entire citation pattern; rather, we addressed the quite different and more practical problem of finding a proxy representation of $h$ through a universal formula that only depends on few summary statistics of the data. The formula $h_{WW}^{{}}$ is “universal” in the sense that it gives a proxy representation of h that holds for any given journal and any dataset.

The issue of determining an indicator under IIC is closely related to the search for a solution of the problem of recovering and comparing impact indicators from different databases. As a simple but significant example of this issue, we may cite the specific problem of determining/estimating the IF for journals using the Google Scholar-based h-index as a predictor (Bertocchi et al. 2015).

As confirmed in our case study analysis, the h-index can be viewed as an almost-exact function of $C,C_{1} ,T$ and $T_{1}$, through $h_{WW}^{{}}$, i.e. that the basic statistics $C,C_{1} ,T$ and $T_{1}$ provide salient information for the evaluation of the h-index with high precision. In practice, while computation of the h-index h requires knowledge of the entire citation profile (or at least large part of it, e.g. the so-called h-core), formula $h_{WW}^{{}}$ requires knowledge of only a few elementary summary statistics, but reproduces the actual value of h quite well. In truth, in our computations we found that the estimates yielded by $h_{WW}^{{}}$ were slightly biased downwards for quite high values of the h-index but, as can be seen from Table 3, overall the formula $h_{WW}^{{}}$ yields very accurate approximations to the empirical value of the h-index, with values of the MARE ranging around 5–6%, not too dissimilar from those obtained by formula $\tilde{h}_{W}^{\left( 1 \right)}$ (Bertoli-Barsotti and Lando 2017). Both formulas $\tilde{h}_{W}^{\left( 1 \right)}$ and $h_{WW}^{{}}$ exhibit comparable levels of accuracy (the advantages of the formula $\tilde{h}_{W}^{\left( 1 \right)}$, as compared to formula $h_{WW}^{{}}$, may be that: (i) it yields an explicit expression of the basic indicators $C,C_{1} ,T$ and $T_{1}$, while the latter not, and (ii) it is based on a simpler probabilistic model). Even though the Pearson correlation, $\rho$, is not an adequate measure of the accuracy of the estimation and should not be used to compare the effectiveness of the different estimators considered (and this is the reason why this concept has been banished from this study), for the sake of completeness we point out that: (1) for the S&MM dataset (230 journals), we found $\rho \left( {h,h_{WW}^{{}} } \right) = 0.99$, $\rho \left( {h,\tilde{h}_{W}^{\left( 1 \right)} } \right) = 0.98$, $\rho \left( {h,h_{SG} } \right) = 0.98$ and $\rho \left( {h,h_{R} } \right) = 0.96$; (2) for the EE&F dataset we found $\rho \left( {h,h_{WW}^{{}} } \right) = 0.97$, $\rho \left( {h,\tilde{h}_{W}^{\left( 1 \right)} } \right) = 0.98$, $\rho \left( {h,h_{SG} } \right) = 0.97$ and $\rho \left( {h,h_{R} } \right) = 0.90$. Ultimately, despite the differences between the datasets considered—in terms of scientific areas, time windows for publication and citation, types of “citable” documents considered, mean level of the basic indicators $C,C_{1} ,T$ and $T_{1}$ (with values of respectively 2111, 95, 432 and 312 for the S&MM dataset and 741, 33, 199 and 159 for the EE&F dataset)—we may conclude that, on the whole, $h_{WW}^{{}}$ provides fairly accurate approximations to the real value of the h-index, at least for not too large values of T (e.g. $T < 2000$), m (e.g. $m < 20$) and h (e.g. h < 40), such as those considered in this study.

Appendix

Conditions for existence and uniqueness of a solution of Eq. (15)

For every fixed $a = a^{*} > 0$, $g\left( {a^{*} ,\beta } \right) \to + \infty$ as $\beta \to 0$ and $g\left( {a^{*} ,\beta } \right) \to 1$ as $\beta \to + \infty$. Moreover, since

$$\frac{\partial }{\partial \beta }g\left( {a^{*} ,\beta } \right) = \frac{{g\left( {a^{*} , \beta } \right)}}{{\beta^{2} }}\left( {\log a^{*} - \psi \left( {1 + \frac{1}{\beta }} \right)} \right),$$

(25)

where $\psi$ is the digamma function, i.e. the function defined by $\psi \left( z \right) = \frac{\text{d}}{{{\text{d}}z}}\log \varGamma \left( z \right) = \varGamma '\left( z \right)/\varGamma \left( z \right)$ (see Johnson et al. 2005, pp. 8–9), we find that the inequality

$$\frac{\partial }{\partial \beta }g\left( {a^{*} ,\beta } \right) < 0$$

(26)

holds if and only if it holds

$$\log a^{*} - \psi \left( {1 + \frac{1}{\beta }} \right) < 0.$$

(27)

Now, the function $\psi \left( {1 + \frac{1}{\beta }} \right)$ is (convex and) strictly decreasing from $+ \infty$ at 0 to

$$\mathop {\text{lim}}\limits_{\beta \to \infty } \psi \left( {1 + \frac{1}{\beta }} \right) = \psi \left( 1 \right) = \varGamma^{\prime}\left( 1 \right) = - \gamma ,$$

(28)

where $\gamma$ is the Euler–Mascheroni constant ($\gamma = - {{\varGamma^{\prime}}}\left( 1 \right) \cong 0.5772$), at $+ \infty$.

Hence $\psi \left( {1 + \frac{1}{\beta }} \right) > - \gamma > \log a^{*}$ for every $\beta > 0$ if and only if $0 < a^{*} \le \exp \left( { - \gamma } \right) \cong 0.561$.

Thus the following two cases are possible.

• (a) If $0 < a^{*} \le \exp \left( { - \gamma } \right)$, the inequality (26) holds. In this case the function $g\left( {a^{*} ,\beta } \right)$ is strictly decreasing from $+ \infty$ at 0 to 1 at $+ \infty$, with a limit approached from above. We conclude that, in this case, Eq. (15) has a unique solution if and only if $m^{*} > 1$; otherwise, if $m^{*} \le 1$, Eq. (15) has no solution.

• (b) On the other hand, if $a^{*} > \exp \left( { - \gamma } \right)$, the derivative function $\frac{\partial }{\partial \beta }g\left( {a^{*} ,\beta } \right)$ changes its sign from negative to positive at $\beta = \beta_{0}$, for some $\beta_{0} > 0$; hence $g\left( {a^{*} ,\beta } \right)$ is strictly decreasing for every $0 < \beta < \beta_{0}$, and strictly increasing for every $\beta > \beta_{0}$, and the point $\beta_{0}$ is a global minimum for $g\left( {a^{*} ,\beta } \right)$. Moreover since, as seen before, $\mathop {\lim }\limits_{\beta \to \infty } g\left( {a^{*} ,\beta } \right) = 1$, then $0 < g\left( {a^{*} ,\beta_{0} } \right) < 1$, and the limit at infinity is approached from below. We conclude that, in this case too, Eq. (15) has a unique solution if and only if $m^{*} > 1$; conversely, if $m^{*} \le 1$ Eq. (15) may have two solutions, or no solution at all.

In both cases (a) and (b), Eq. (15) has one and only one solution if and only if $m^{*} > 1$.