1 Introduction

Braess showed that adding resources to transportation networks can hurt the performance of the system [1]. Many authors have been interested in investigating the existence of such a paradox in several contexts related to queueing networks (see for instance [2,3,4,5,6]). In this work, we analyze whether such a phenomenon exists in dynamic matching models where the compatibility graph is non-bipartite.

In our previous work [7], we analyzed the performance of the stochastic First Come First Match (FCFM) matching model with a general compatibility graph, when the flexibility increases, i.e., when an edge is added to the compatibility graph. We showed that, when there is a unique bottleneck in the system, increasing the flexibility can decrease the overall performance of the system, which is reminiscent of the Braess paradox. The existence of such a performance paradox leads to many questions:

  • First, is it only due to the FCFM discipline? Are other disciplines like Match the Longest or Random also prone to this phenomenon? In this article, we develop some theoretical techniques to transfer the existence of a paradox from FCFM discipline to any greedy discipline (i.e., to any discipline where an arriving item must be assigned to a compatible item immediately if there is one). Most of the disciplines considered in the literature are shown to be greedy with the notable exception of the threshold disciplines studied in [8] and [9]. We first prove that all greedy disciplines exhibit the performance paradox for quasi-complete compatibility graphs. The results are proved using strong aggregation of Markov chains. Intuitively we prove that all the greedy disciplines are equivalent for quasi-complete compatibility graphs when we are interested in the total number of items. We then introduce two operations on compatibility graphs, the JOIN and the UNION. We show that if compatibility graph G associated with a greedy discipline satisfies the conditions for the existence a performance paradox, then the compatibility graph \(G \bowtie IN_n\) (\(IN_n\) being a set of n independent nodes) associated with the same discipline also satisfies these conditions and thus also exhibits a performance paradox.

  • Is the paradox related to the size or the number of edges of the compatibility graph? An important conclusion of our work is that there exists a performance paradox for a compatibility graph with \(n>3\) nodes and \(4n-11\) edges. Therefore, the paradox can be obtained for any number of nodes or any number of edges.

  • Does the paradox only appear when we have only one bottleneck in the system? Is this condition only technical or is it mandatory? In Sect. 2.4, we provide an example with two bottlenecks where the performance paradox exists. Therefore, the assumption on the uniqueness of the bottleneck is only a technical condition required to prove our previous result about the existence of the performance paradox.

1.1 Related work

The model we consider in this work was introduced in [10], where it is called general stochastic matching model to emphasize that the compatibility graph is non-bipartite, and further studied in [11]. The works [10] and [11] present interesting properties of this model such as that the policies Match the Longest, in which the incoming item is matched with an item of the compatible class with the longest queue size, and FCFM disciplines have a maximal stability region. Recently, Comte shows that this matching model with the FCFM discipline is related to the order-independent loss queueing networks [12]. An extension of FCFM stochastic matching model to multigraphs with self-loops has been studied in [13].

A related model to ours is the bipartite dynamic matching model. In this model, the graph that determines compatibilities between items is bipartite and, thus, the nodes can be separated in two disjoint sets: server nodes and customer nodes. To the best of our knowledge, Kaplan [14] was the first analyzing the fully dynamic setting of matching model, i.e., all the items arrive to the system according to a random process. He analyzed the problem of how to assign public houses to tenants. In that work, it is considered that an available public house is assigned to the longest waiting family among those that expressed their interest for that house. The First Come First Served infinite bipartite matching model, proposed by Caldentey et al. [15], considers an infinite sequence of server nodes, independent and identically distributed according to a probability distribution on the server classes, and an independent infinite sequence of job items, independent and identically distributed according to a probability distribution on the job classes. Busic et al. [16] study the stability of the system for different matching policies, whereas in [17] Gardner and Righter study, the relation between the bipartite matching model under FCFM and the order-independent queues is observed. Optimal matching policies of bipartite matching models have been studied in an asymptotic regime in [8] and for the N-shaped model in [9]. Weiss in [18] studies a bipartite matching model, in which jobs and servers are assigned according to the First Come First Served policy, but jobs are immediately lost if they do not find an available server upon arrival.

Adan and Weiss in [19] show that, under the heavy-traffic assumption on the arrivals, the First Come First Served infinite bipartite matching model has the same stationary distribution as the First Come First Served-Assign the Longest Idle Server queueing model. Furthermore, Adan et al. in [20] show that the First Come First Served-Assign the Longest Idle Server model has the same stationary distribution as the redundancy service model. In the context of redundancy networks, the work of [21] shows that providing more flexibility to a class leads to a performance improvement of this class but it might not be beneficial for the other classes (the work of [22] shows that the Least Redundant First scheduling policy that is optimal with respect to overall system response time, can be unfair in that it can hurt the jobs that become redundant). Therefore, from the aforementioned works, one might conclude that the performance paradox existence analysis in dynamic matching models has been already carried out. However, we would like to remark that these works assume a bipartite compatibility graph (whereas in our work we consider non-bipartite matching dynamic models) and strongly depend on the product form result for First Come First Served discipline so they cannot be generalized to any greedy discipline.

1.2 Organization

The rest of the article is organized as follows. In Sect. 2, we present the model we study as well as the previous results on the existence of the performance paradox for FCFM. In Sect. 3, we focus on the greedy policies and we study the existence of the performance paradox for quasi-complete graphs. In Sect. 4, we consider the join operation on compatibility graphs and analyze the performance paradox for this instance. In Sect. 5, we present the main conclusions of our work as well as the future work.

2 Matching model and performance paradox

We consider a queueing system with n classes of items. Items of different classes arrive to the system according to independent Poisson processes, with rates \(\lambda _i>0, \; i=1, \dots , n\). The compatibilities between item classes are described by a connected non-bipartite compatibility graph \(G=(V,\mathcal {E})\), where \(V=\{1,\dots ,n\}\) is the set of item classes and \(\mathcal {E}\) is the set of allowed compatible pairs: items of classes i and j are compatible if and only if \((i,j)\in \mathcal {E}\). If an incoming item is incompatible with all items present in the system, it is placed at the end of the queue of unassigned items. If it is compatible, and if policies are not restricted to be greedy, the controller has the option of not matching it to one of the compatible items, in which case it is also added to the end of the queue. If a compatible item is matched (or assigned) to the incoming item, both items disappear.

For a class \(i \in V\), we denote by \(\Gamma (i)= \{j \in V: (i,j) \in \mathcal {E}\}\) the set of all the neighbors of the node i in the compatibility graph G, i.e., if \(j\in \Gamma (i)\) items of class i are compatible with items of class j. For any subset of item classes \(V_1 \subseteq V\), let \(\Gamma (V_1)=\bigcup _ {i\in V_1} \Gamma (i)\), and \( \lambda _{V_1} =\sum _{i \in V_1} \lambda _i\). A subset of nodes \(\mathcal {I}\subseteq V\) is called an independent set if there is no edge between any two nodes in \(\mathcal {I}\), i.e., for any \(i,j \in \mathcal {I}, \; (i,j) \notin \mathcal {E}\).

2.1 Markov representation for greedy policies

Let \(\mathcal{{V}}^*\) be the set of finite words over the alphabet V and we denote the empty word by \(\emptyset \). Let

$$\begin{aligned} \mathbb {W}=\{w=w_1 \cdots w_q\in \mathcal{{V}}^*: \forall (i,j)\in [1,q]^2,\; i\ne j,\; (w_i,w_j)\notin \mathcal {E}\} \end{aligned}$$

be the subset of words without a compatible pair of letters, i.e., the set of ordered independent sets of G. For any \(w\in \mathbb {W}\) and any \(x \in V\), let \(\vert w \vert _x\) be the number of occurrences of letter x in word w. Let \( \vert w \vert \) be the length of w (i.e., the number of letters of the word w). A word containing only letters i will be denoted by \(i^*.\)

In a greedy policy, a unique compatible item is matched with the incoming one and both disappear (a formal definition of greedy policies will be presented in Sect. 3). Under a greedy policy, a state of the system right after the new arrival (if any) has been assigned or placed in the queue of unassigned items can be described by a word \(w\in \mathbb {W}\). Each letter \(w_i \in V\) represents the class of an unassigned item waiting in the system and the order of the letters represents their order of arrival.

Let us present some notation that we will use throughout the paper. Let \(M(G,\lambda ,D)\) be the continuous-time Markov chain associated with compatibility graph G, matching discipline D and arrival rates of letters \(\lambda \). Let \(\mathbb {E}[M(G,\lambda ,D)]\) be the expectation of the total number of letters for this Markov chain in steady state. Let \(K_n\) be a complete graph with n nodes and \(IN_n\) be a set with n independent nodes (i.e., n nodes without edges). Similarly, \(G-(a,b) \) denotes the subgraph of G where edge (a,b) has been deleted. Let \(K_n -(a,b)\) denote the complete graph with n nodes without edge (a, b): it is called a quasi-complete graph in this paper.

After applying standard uniformization technique, with a uniformization constant \(\Lambda > \sum _{i=1}^n \lambda _i\), we obtain a matching model in discrete time. In each time slot \(t \in N\), one item arrives to the system with probability \(1-\alpha _0\), and there are no arrivals with probability

$$\begin{aligned} \alpha _0 = 1 - \frac{\Vert \lambda \Vert _1}{\Lambda } > 0. \end{aligned}$$

Thus, each item belongs to a class within the set of item classes sampled from a conditional probability distribution over V given the event that there is an arrival: \(\alpha =(\alpha _1,\cdots ,\alpha _n)\), with \(\alpha _i = \frac{\lambda _i}{\Vert \lambda \Vert _1}, \; \forall 1 \le i \le n\). It follows that \(\alpha _i > 0, \; \forall i\).

\(\mathbb {E}[M(G,\alpha ,D)]\) will denote the expectation of the total number of letters for this discrete-time Markov chain with arrival probabilities \(\alpha \).

Let \(\mathbb {I}\) be the set of independent sets of G. We assume that

$$\begin{aligned} \alpha _{\mathcal {I}} < \alpha _{\Gamma (\mathcal {I})},\quad \forall \mathcal {I}\in \mathbb {I}. \end{aligned}$$
(1)

According to [10, Proposition 2], the above condition is a necessary condition for any matching policy to be stable. As a consequence, if the compatibility graph is bipartite, the system is not stable, see [10]. Therefore, throughout the paper, we assume that the compatibility graph is not bipartite, even if we consider bipartite graphs as subgraphs. We also assume the compatibility graph has at least four nodes, to eliminate trivial cases.

For any \(\mathcal {I}\in \mathbb {I}\), let \(\Delta _{\mathcal {I}} =\alpha _{\Gamma (\mathcal {I})}- \alpha _{\mathcal {I}}\) be the stability gap of independent set \(\mathcal {I}\).

We summarize the notation of this work in Table 1.

Table 1 A summary of the main notation
Full size table

2.2 Performance paradox analysis of [7]

We say that there exists a performance paradox for compatibility graph G and discipline D if there exists an edge (a, b) such that

$$\begin{aligned} \mathbb {E}[M(G,\alpha ,D)] > \mathbb {E}[M(G-(a,b),\alpha ,D)] \end{aligned}$$
(2)

that is, if the mean number of items increases by adding an edge to the compatibility graph.

Let us now recall our previous results [7]. We first present some notation to understand the main result of this section.

Definition 1

(Bottleneck) A set \(\mathcal {I}\in \text {argmin}_{\mathcal {I}\in \mathbb {I}}\Delta _{\mathcal {I}}\) will be called a bottleneck set in the sense that it has the smallest maximal draining speed.

Let

$$\begin{aligned} {\bar{\delta }}=\min _{\mathcal {I}\in \mathbb {I}} \Delta _{\mathcal {I}} = \min _{\mathcal {I}\in \mathbb {I}} (\alpha _{\Gamma (\mathcal {I})} - \alpha _{\mathcal {I}} ). \end{aligned}$$
(3)

We have \({\bar{\delta }} >0\) as we assume that \(\alpha \) satisfies (1). We select a bottleneck set (or saturated independent set) \({\hat{\mathcal {I}}}\in \text {argmin}_{\mathcal {I}\in \mathbb {I}}\Delta _{\mathcal {I}}\) with the highest cardinality, i.e.,

$$\begin{aligned} \vert {\hat{\mathcal {I}}} \vert = \max _{\mathcal {I}\in \mathbb {I}\text { s.t. } \Delta _{\mathcal {I}} = {\bar{\delta }}} \vert \mathcal {I}\vert . \end{aligned}$$
(4)

We are interested in how the performance of the system evolves by adding an edge when \(\Delta _{{\hat{\mathcal {I}}}}\) tends toward 0. First, we define a parameterized family of item class distributions:

$$\begin{aligned} \alpha ^{\delta }_i=\left\{ \begin{array}{ll} \alpha _i + \frac{{\bar{\delta }}}{2}\frac{\alpha _i}{\vert \alpha _{{\hat{\mathcal {I}}}}\vert } - \frac{\delta }{2}\frac{\alpha _i}{\vert \alpha _{{\hat{\mathcal {I}}}}\vert }, &{} \text {if } i\in {\hat{\mathcal {I}}}, \\ \alpha _i - \frac{{\bar{\delta }}}{2}\frac{\alpha _i}{\vert \alpha _{\Gamma ({\hat{\mathcal {I}}})}\vert } + \frac{\delta }{2}\frac{\alpha _i}{\vert \alpha _{\Gamma ({\hat{\mathcal {I}}})}\vert }, &{} \text {if } i\in \Gamma ({\hat{\mathcal {I}}}), \\ \alpha _i, &{} \text {otherwise}, \end{array}\right. \end{aligned}$$

for all \(0<\delta \le {\bar{\delta }}\), where \({\bar{\delta }}\) is defined in (3) and \({\hat{\mathcal {I}}}\) in (4). It is clear that \(\alpha ^{{\bar{\delta }}}=\alpha \). By definition of \(\alpha ^\delta \),

$$\begin{aligned} \alpha _{\Gamma ({\hat{\mathcal {I}}})}^\delta -\alpha _{{\hat{\mathcal {I}}}}^\delta = \alpha _{\Gamma ({\hat{\mathcal {I}}})}-\frac{{\bar{\delta }}}{2}+\frac{\delta }{2}-\alpha _{{\hat{\mathcal {I}}}}-\frac{{\bar{\delta }}}{2}+\frac{\delta }{2}={\bar{\delta }}-{\bar{\delta }}+\delta =\delta , \end{aligned}$$

which tends to 0 when \(\delta \) tends to 0.

We now consider the expectations of the total number of items for the models both with and without edge as a function of \(\delta \) and analyze their difference when \(\delta \) tends to 0.

Definition 2

(Saturated Independent Set) An independent set \(\mathcal {I}\) is called saturated if \(\Delta ^{\delta }_{\mathcal {I}} = \alpha ^{\delta }_{\Gamma (\mathcal {I})}-\alpha ^{\delta }_{\mathcal {I}} \) tends to 0 when \(\delta \) tends to 0.

In our previous work [7], we assume there is only one saturated independent set \({\hat{\mathcal {I}}}\).

Theorem 1

[Adapted from Theorem 2 of [7]] If \({\hat{\mathcal {I}}}\) is uniquely defined for graph G, and if \({\hat{\mathcal {I}}}\) has both a and b as neighbors, then there exists a performance paradox for adding the edge (a, b) to G for \(\delta \) sufficiently small.

We would like to emphasize that the assumption about the uniqueness of the saturated independent set is a technical condition required to prove the existence of a performance paradox. As we will see in Sect. 2.4, the performance paradox also occurs when this assumption does not hold.

2.3 An example of performance paradox

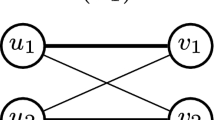
In the following, we provide an example in which we can establish the exact value of \(\delta \) for the performance paradox to occur. The example is based on a matching model formed by a quasi-complete graph with four nodes (denoted as \(K_4 - (3,4)\)) (see Fig. 1). We also consider the graph where we add edge (3, 4) (i.e., complete graph \(K_4\)). Therefore, each node different from 3 and 4 is an independent set that is connected to these nodes.

Fig. 1
figure 1

Quasi-complete compatibility graph with 4 nodes: \(K_4-(3,4)\)

Full size image

We consider the following conditional probability distribution of arrivals: \(\alpha _1=0.45\), \(\alpha _2=0.11\) and \(\alpha _3=\alpha _4=0.22\). For this instance, the saturated independent set is \({\hat{\mathcal {I}}}=\{1\}\) with \({\bar{\delta }}= \alpha _{\{2,3,4\}} - \alpha _1 =0.1\). We define a new collection of conditional probability distributions \(\alpha ^\delta \) for all \(0<\delta \le 0.1\), i.e \(\alpha ^\delta _1=0.5 - \frac{\delta }{2}\), \(\alpha ^\delta _2=0.1 + \frac{\delta }{10}\) and \(\alpha ^\delta _3=\alpha ^\delta _4=0.2 + \frac{\delta }{5}\). Since the saturated independent set has the nodes that connect the missing edge as neighbors (i.e., the node 1 is a neighbor of node 3 and node 4), we know from Theorem 1 that there exists a performance paradox for \(\delta \) sufficiently small.

We study the exact value of the saturation threshold, i.e., the maximum \(\delta \) value for the existence of the paradox under the FCFM policy. According to Lemma 1 and Lemma 4 (which are presented in the next section as they are proved for any greedy policy), we can conclude that, for FCFM policy, for the matching model under consideration here, the performance paradox exists if and only if \(\delta <0.0818369\). All the details of the computations as well as a plot representing the mean number of items of both matching models when \(\delta \) varies are presented in Appendix A.2.

2.4 An example with multiple saturated independent sets

The definition of the parametrized \(\alpha ^\delta \) implies that the unique saturated independent set is \({{\hat{\mathcal {I}}}}\). We now discuss the situation where there are multiple saturated independent sets. This means that multiple independent sets have their stability gaps that tend to 0 as \(\delta \) tends to 0. In that case, the conditions of Theorem 1 in [7] are not satisfied. However, in this section, we present an example with two saturated independent sets where the performance paradox exists.

Now we consider compatibility graph \(K_4\) and \(K_4 - (1,2)\). Let us define the conditional probability distribution of the arrivals as \(\alpha _1=\alpha _2=0.15\), \(\alpha _3=0.4\) and \(\alpha _4=0.3\). We choose the saturated independent sets to be \(\{3\}\) and \(\{1,2\}\). We define a new parametrized family of conditional probability distributions \(\alpha ^\delta \), for all \(0<\delta \le 0.1\), as \(\alpha ^\delta _1=\alpha ^\delta _2=0.25 - \delta \), \(\alpha ^\delta _3=0.5 - \delta \) and \(\alpha ^\delta _4=3\delta \). In the following result, we prove that there exists a performance paradox and compute exactly for which value of \(\delta \) it appears. Its proof is available in Appendix B.1.

Proposition 1

For the dynamic matching model under consideration, there exists a performance paradox if and only if \(\delta \in (0,0.0563)\).

A plot representing the number of items of the matching models under study as a function of \(\delta \) is represented in Appendix B.2. In the following result, we show that the difference \(\mathbb {E}[M(K_4,\alpha ^\delta ,FCFM)]-\mathbb {E}[M(K_4-(1,2),\alpha ^\delta ,FCFM)]\) is unbounded as \(\delta \) tends to 0 and we quantify its growth rate. Its proof is available in Appendix B.3.

Proposition 2

When \(\delta \) tends to 0,

$$\begin{aligned} \delta (\mathbb {E}[M(K_4,\alpha ^\delta ,FCFM)]-\mathbb {E}[M(K_4-(1,2),\alpha ^\delta ,FCFM)]) \rightarrow \frac{1}{24}. \end{aligned}$$

Remark 1

This example shows that the existence of the paradox is not related to the uniqueness of a saturated independent set. This was only a technical condition used to prove Theorem 1 in [7].

3 Greedy matching disciplines

In the following, we denote by \(\Gamma (w) = \cup _{x \in w} \Gamma (x)\) for any word w and by S the set of words. Let us first present some definitions.

Definition 3

(Compatibility) Let w be a state of the system and x a letter which arrives in the system. We say that x is compatible with w if \(x \in \Gamma (w)\).

Remember that a subsequence of a word (or a sequence of letters) w is derived from w by deleting some or no letters without changing the order. Subsequences can contain consecutive letters which were not consecutive in the original word. Thus, subsequences are not necessarily substrings.

Definition 4

(Effect of a compatibility) Let w be a state of the system and x a letter which arrives in the system. If x is not compatible with w, it is appended at the end of word w. Otherwise, if x is compatible with w, the transition is described by the matching discipline.

Definition 5

(Matching discipline) Let \(x \in \Gamma (w)\). A matching discipline D is a function from \(S \times V\) which returns a non-empty subset of states \(N_D(w,x)\) and a discrete distribution of probability \(\psi _{N_D(w,x)}\) on this subset such that:

  1. 1.

    All the words in \(N_D(w,x)\) are possibly subsequences of the word w concatenated with letter x.

  2. 2.

    The distribution gives the probability to make a transition to any state in \(N_D(w,x)\): \(\psi _{N_D(w,x)} (p)\) is the probability to jump from state w to any state p in \(N_D(w,x)\), due to the arrival of an item of class x. Obviously:

    $$\begin{aligned} \sum _{p \in N_D(w,x)} \psi _{N_D(w,x)} (p) = 1, \end{aligned}$$

    and if the set \(N_D(w,x)\) is a singleton, the probability distribution is a Dirac.

Remark 2

This definition allows us to model disciplines where \(N_D(w,x) = \{ w \} \) (i.e., the matching has no effect on word w even when x is compatible with a letter in w). It is also possible to represent disciplines where the effect of a matching is to remove all the letters in w which are compatible with letter x. We now introduce the notion of greedy matching discipline.

Definition 6

(Greedy matching discipline) A matching discipline GD is greedy if, given state w and arriving compatible letter x, for all states p in \(N_{GD} (w,x)\), we have \(\vert p \vert = \vert w \vert -1\) and \(x \notin p\).

Example 1

Clearly, FCFM is a greedy discipline such that the set \( N_D (w,x) \) is a singleton for all words w and letters x that are compatible with w. Match the Longest with random drawing of tie breaking is a greedy discipline but the set \( N_D (w,x) \) may contain several words.

Definition 7

(RANDOM discipline) Assuming that a letter is compatible with a word, we delete one compatible letter in the word, where this letter is chosen with a uniform distribution among the compatible letters.

Example 2

(RANDOM) Consider a state \(w=abcaba\). Suppose that a letter t arrives and that t is compatible with both a and b but it is not compatible with with c.

$$\begin{aligned} N_D(w,t) = \{ bcaba, acaba, abcba,abcaa,abcab \} \end{aligned}$$

Under the RANDOM discipline, each of these words has a probability of 1/5 to be selected.

Remark 3

RANDOM is a greedy discipline.

Proposition 3

If the compatibility graph is such that the degree of every node is positive, the arrival rates of all items are positive and the discipline is greedy, then the Markov chain contains a state with 0 items which is reachable from any state.

Proof

Indeed all items can be deleted due to a succession of arrivals of compatible classes. \(\square \)

Now we establish some relations between the FCFM discipline and any greedy discipline (GD).

3.1 Complete graphs and greedy disciplines

The performance paradox analysis consists of comparing the mean number of items for a quasi-complete graph and a complete graph. In the main result of this section, we provide an explicit expression for the mean number of items of a complete graph with an arbitrary greedy matching policy.

The following result characterizes the Markov chain associated with \(K_n\) and any greedy matching policy as well as its expected value.

Lemma 1

For a greedy matching discipline GD, the states of the Markov chain associated with \(K_n\) are words which are associated with the independent sets of the compatibility graph, i.e., the following words: \(\emptyset , 1^*, 2^*,\ldots , n^*\). In fact, the Markov chain consists of n birth and death processes which are connected through the empty word; when the state is \(x^*\), with probability \(\alpha _x\) the number of letters increases by one and with probability \(1-\alpha _x\) decreases by one. Assuming \(\alpha _i<0.5\) for all \(i=1,\dots ,n\), the mean number of items is

$$\begin{aligned} \left( 1+\sum _{i=1}^n\frac{\alpha _i(1-\alpha _i)}{1-2\alpha _i}\right) ^{-1} \left( \sum _{i=1}^n\frac{\alpha _i(1-\alpha _i)}{(1-2\alpha _i)^2}\right) . \end{aligned}$$
(5)

Proof

We assume that the initial state is the empty word. The first arrival (say a class x item) triggers a transition to word x. If the next arrival is again a class x item (with probability \(\alpha _x\)), the next state is xx, otherwise the arriving letter (say y) matches with the x as the compatibility graph is a complete graph. For any greedy matching discipline, this matching causes the destruction of both y and x and a transition to the empty word. Such an event occurs with probability \(\alpha _y\). Thus, by induction on the transitions, we only obtain words with only one class of item or the empty word. As the valid states only contain one class of items, the discipline does not matter as soon as it is greedy and exactly one letter is deleted in the word. Furthermore, for this compatibility graph, the transition rates of the chain do not depend on the matching discipline (note that this is not true for sparser compatibility graphs). The derived Markov chain may be described as a collection of n birth and death processes connected through state \(\emptyset \). When the state is \(x^*\), the birth-probability is \(\alpha _x\) and the death-probability \(1-\alpha _x.\) It is easy to check that the mean number of items is (5). \(\square \)

Remark 4

From the above result, we conclude that the mean number of items associated with compatibility graph \(K_n\) and disciplines GD and FCFM are equal, i.e.,

$$\begin{aligned} \mathbb {E}[M(K_n,{\lambda },GD)] = \mathbb {E}[M(K_n,{\lambda },FCFM)]. \end{aligned}$$
(6)

The above result provides an explicit expression for the expectation of the total number of items if the matching is a complete graph. In the next section, we give a similar result when the compatibility graph is a quasi-complete graph.

3.2 Quasi-complete graphs and greedy disciplines

Let us now study the expectation of the number of items for compatibility graph \(K_n\) with a deleted edge (which is denoted by \(K_n - (n-1,n)\)). We first show how to derive two compatibility graphs which have the same expected size of words in steady state. This construction is based on the exact aggregation of Markov chains and the strong lumpability property (see [23] for the initial definition of aggregation for finite state space chains, and [24] for a recent description of this subject for denumerable ones). The following presentation follows [24].

Let W be a Markov chain on set of states \(\mathbb {W}\). Let \((B_1,..,B_k)\) be a partition of \(\mathbb {W}\). We define a new process Y as follows:

$$\begin{aligned} Y_n = m \leftrightarrow W_n \in B_m. \end{aligned}$$

The question is to find conditions such that Y is also a Markov chain. Under these conditions, Y will be denoted as an exact aggregation of W for partition \((B_1,..,B_k)\). The strong lumpability condition (defined in the following) implies such a result (see [24] for the proof).

Definition 8

(Strong Lumpability) W is strongly lumpable for partition \((B_1,..,B_k)\) of its state space if for all subset indices i and j and for all states \(m_1\) and \(m_2\) in \(B_i\), we have

$$\begin{aligned} Pr(W_{n+1} \in B_j \vert W_n = m_1) = Pr(W_{n+1} \in B_j \vert W_n = m_2). \end{aligned}$$

\(B_i\) will be denoted as macro-state i in the following.

We first consider an arbitrary compatibility graph and an arbitrary node x. Let us denote by \(G_x\) this graph. Let \(W_x=M(G_x,\lambda ,GD)\), i.e., \(W_x\) is the Markov chain associated with matching \(G_x\) and an arbitrary greedy matching policy GD.

Definition 9

(Decomposition matching and Aggregated matching) We define a new matching by a decomposition of x into two nodes y and z. The decomposition is defined by:

  • \(\Gamma (y) = \Gamma (z) = \Gamma (x) \)

  • \(\alpha _y >0\)

  • \(\alpha _z >0\)

  • \(\alpha _y + \alpha _z = \alpha _x\).

Let \(G_{yz}\) be a new compatibility graph where x is decomposed into y and z. \(G_{yz}\) will be denoted as the decomposition compatibility graph while \(G_{x}\) is called the aggregated compatibility graph. Let \(W_{yz}=M(G_{xy},\lambda ,GD)\). i.e., \(W_{yz}\) is the Markov chain associated with \(G_{yz}\) and an arbitrary greedy matching policy GD.

For instance, we consider an aggregated matching in Fig. 2c. Node x is decomposed into nodes n and \(n-1\) to build the decomposition compatibility graph (see Fig. 2b).

Fig. 2
figure 2

Compatibility graphs: \(K_n\) (a), \(K_n - (n-1,n) \) (b), \(K_{n-1}\) (c). The triple edge represents that the node (\(n-1\) and n for a, b, and x for c) is connected to all the nodes in \(K_{n-2}\)

Full size image

Proposition 4

If the aggregated matching is associated with a stable Markov chain, so is the decomposition matching.

Note that by construction \(y \notin \Gamma (z) \) and \(z \notin \Gamma (y)\).

Lemma 2

We consider the continuous-time Markov chain associated with compatibility graph \(K_n - (n-1,n)\), arrival rates \({\lambda }\) and a greedy discipline GD: \(M(K_n - (n-1,n), {\lambda }, GD)\). The states of the chain are the words \(\emptyset \), \(1^*\),\(2^*\), \(3^*\),.., \((n-2)^*\) and words written with letters \(n-1\) and n. The chain is lumpable according to the following partition.

  • Each of the states represented by \(i^*\) remain as individual states, for \(i>0\), as does state \(\emptyset \).

  • All the states w, formed only by letters n and n-1 and such that \(\vert w\vert =l>0\), are gathered into a macro-state called \(C_l\).

Proof

We consider the uniformized version of the chain with uniformization rate \(\Lambda \) as mentioned formerly to get \( M(K_n - (n-1,n), {\alpha }, GD)\). Let \(P_{GD} \) denote the transition probability matrix of this DTMC. First, we will prove that this chain is lumpable for the partition. Let S be its state space. We have to prove the following equality for all macro-states \(C_l\). Let i and j be macro-state indices

$$\begin{aligned} \sum _{k \in C_i} P_{GD} [k,m] = \sum _{k \in C_i} P_{GD} [k,n] ~~ \forall ~ m,n \in C_j. \end{aligned}$$

If such a condition holds, we note \( P_{GD} (C_i, C_j) = \sum _{k \in C_i} P_{GD} [k,m] \) where m is any state in \(C_j\).

Since all the words in \(C_l\) have length equal to l, we have to consider all the events:

  • Arrival of a class n item. A class n item is not compatible with any letter in word w (remember that w only contains letters n and \(n-1\)). Thus, letter n is appended to word w and the state becomes \((w \vert n)\). This state is in macro-state \(C_{l+1}\), and the probability of this transition is \(\alpha _n\). Thus from any state in \(C_l\), we have a single transition with probability \(\alpha _n\) to a state in \(C_{l+1}\).

  • Arrival of a class \(n-1\) item: same property, from any state in \(C_l\), we have a transition with probability \(\alpha _{n-1}\) to a state in \(C_{l+1}\).

  • Arrival of a class k item (with \(k<n-1\)): such an arrival deletes a class n or class \(n-1\) item. In the chain, we have a transition from state w to all the states p in set \(N_{GD}(w,k)\) with probability \(\alpha _k \psi _{N_D(w,x)}(p)\). As the discipline is greedy, set \(N_{GD}(w,k)\) is not empty. And all the states in \(N_{GD}(w,k)\) have a length equal to \(l-1\). Thus, they are all included into macro-state \(C_{l-1}\). As

    $$\begin{aligned} \sum _{p \in N_D(w,x)} \psi _{N_D(w,x)}(p) = 1, \end{aligned}$$

    we clearly have

    $$\begin{aligned} P (C_l, C_{l-1}) = \sum _{p \in N_D(w,x)} \alpha _k \psi _{N_D(w,x)}(p) = \alpha _k. \end{aligned}$$

    Thus, we have one transition with probability \(\alpha _k\) from any state in \(C_l\), to a state in \(C_{l-1}\). \(\square \)

Let Y be the lumped Markov chain presented in the above result. Note that both the arrival rates and the discipline have been modified when we switch from the decomposition compatibility graph to the aggregated one. Let \(\lambda \) be the arrival rate vector in the model before aggregation of nodes n and \(n-1\), we define the rates \(\mu \) in the aggregated model as follows: \(\mu _i = \lambda _i\) for all \(i<n-1\) and \(\mu _{n-1} = \lambda _n + \lambda _{n-1}\). For the matching discipline, as we change y and z into x, we modify the sets \(N_D\) and the distributions of probability for the aggregated model. However, it is not necessary to describe them precisely. We just remark that the discipline is still greedy in the aggregated model and we emphasize that the discipline may change in general by changing its name to \(GD'\) in the equation. From the above result, we directly obtain the following.

Proposition 5

Y can be identified with the Markov chain associated with compatibility graph \(K_{n-1}\), arrival rate vector \(\mu \) and matching discipline \(GD'\). Therefore,

$$\begin{aligned} \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,GD) ] = \mathbb {E}[M(K_{n-1},\mu ,GD') ]. \end{aligned}$$
(7)

Remark 5

In some cases, it is possible to easily obtain the matching discipline in the aggregated model. For instance, if the original model uses FCFM discipline for the decomposition model, then the matching discipline after aggregation is also FCFM. Therefore,

$$\begin{aligned} \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,FCFM) ] = \mathbb {E}[M(K_{n-1},\mu ,FCFM) ]. \end{aligned}$$
(8)

We now present the following result that proves, for a quasi-complete graph, that the expected total number of items coincides for all greedy disciplines.

Lemma 3

For compatibility graph \(K_n-(n-1,n)\), all greedy disciplines provide the same expectation for the total number of items. More precisely,

$$\begin{aligned} \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,GD) ] = \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,FCFM) ]. \end{aligned}$$

Proof

: Let GD be an arbitrary greedy discipline. From Proposition 5, we have

$$\begin{aligned} \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,GD) ] = \mathbb {E}[M(K_{n-1},\mu ,GD') ]. \end{aligned}$$

And according to Remark 4, we have for any greedy discipline \(GD'\),

$$\begin{aligned} \mathbb {E}[M(K_{n-1},\mu ,GD') ] = \mathbb {E}[M(K_{n-1},\mu ,FCFM) ]. \end{aligned}$$

Remark 5 allows to conclude as:

$$\begin{aligned} \mathbb {E}[M(K_{n}-(n,n-1),\lambda ,FCFM) ] = \mathbb {E}[M(K_{n-1},\mu ,FCFM) ]. \end{aligned}$$
(9)

\(\square \)

Thus, one can obtain from  (5) the expected number of items with a simple modification of the arrival rates for all greedy disciplines.

Lemma 4

Assume \(\alpha _i<0.5\) for all \(i=1,\dots ,n-2\) and \(\alpha _{n-1}+\alpha _n<0.5\). For any greedy matching policy, the mean number of items in a quasi-complete graph with n nodes and edge \((n,n-1)\) missing, is

$$\begin{aligned}{} & {} \left( 1+\sum _{i=1}^{n-2}\frac{\alpha _i}{1-2\alpha _i}+\frac{\alpha _{n-1}+\alpha _n}{1-2(\alpha _{n-1}+\alpha _n)}\right) ^{-1}\nonumber \\{} & {} \left( \sum _{i=1}^{n-2}\frac{\alpha _i(1-\alpha _i)}{(1-2\alpha _i)^2}+\frac{(\alpha _{n-1}+\alpha _n)(1-\alpha _{n-1}-\alpha _n)}{(1-\alpha _{n-1}-\alpha _n)^2}\right) . \end{aligned}$$
(10)

3.3 Existence of a performance paradox for any greedy discipline for \(K_n - (n-1,n)\) compatibility graph

From the above results, we conclude that, if a paradox occurs for graphs \(K_n\) and \(K_n - (n-1,n)\) under FCFM discipline, it also occurs for any greedy discipline.

Theorem 2

Combining previous lemmas, we get that:

  • if a paradox exists for compatibility graph \(K_n - (n-1,n)\) and discipline FCFM, it also exists for any greedy discipline GD with the same arrival rates

  • a paradox exists for \((K_4-(3,4))\) for any greedy discipline GD

Proving the existence of a performance paradox for the complete graph with arbitrary size n and discipline FCFM will need first that we present some results about the modular construction of compatibility graphs. This is the aim of the next section.

4 Modular construction of matching models

In this section, we aim to analyze operations on the compatibility graph that preserve the performance paradox. We present a modular construction of matching models by defining operations on compatibility graphs, on arrival processes and on the matching disciplines. For this purpose, we restrict ourselves to consistent matching policies, which are a subset of greedy matching policies.

Definition 10

A discipline is consistent if for any word w, if two letters x and y have the same neighborhood within w, they also have the same subset of states \(N_D(w,x)\) and the same discrete distribution of probability \(\psi _{N_D(w,x)}\) on this subset. More formally,

$$\begin{aligned} \text {if }~ w \cap \Gamma (x) = w \cap \Gamma (y), ~~then~~ N_D(w,x) = N_D(w,y)~~and~~\psi _{N_D(w,x)} = \psi _{N_D(w,y)}. \end{aligned}$$

Definition 11

We define the compatibility index of a letter x in word w as the binary vector \(IC_{w,x} \) with size \(\vert w \vert \) such that, for all i between 1 and \( \vert w \vert \), \(IC_{w,x} [i] = 1 \) if \(w[i] \in \Gamma (x) \) and 0 otherwise.

Definition 12

A position-based discipline is a policy which uniquely uses the compatibility index \(IC_{w,x} \) to build set \(N_D (w,x) \) and probability distribution \(\psi _{N_D (w,x) }\).

The following proposition follows directly from the definitions.

Proposition 6

Position-based disciplines are consistent.

Remark 6

 

  1. (a)

    FCFM, Last Come First Match and Random are position-based disciplines while Match the Longest and Priority are not.

  2. (b)

    Match the Longest is not position-based but it is consistent.

  3. (c)

    We remark that Priority is not a consistent discipline. For instance, consider the word \(w=abc\) and two items x and y such that

    $$\begin{aligned} \Gamma (x) \cap w = \{ a,c \} = \Gamma (y) \cap w. \end{aligned}$$

    One can design a discipline D such that \(N_D(w,x) = \{bc\}\) and \(N_D(w,y) = \{ab\}\). The greedy assumption is satisfied for this word and these items and the discipline is not consistent.

In the following, we assume that the matching disciplines are greedy and consistent. We would like to remark that this assumption excludes matching disciplines that make use of item class information, such as priorities. We now consider the following operations to build compatibility graphs: the JOIN operation and the UNION operation. These two operations allow to have a modular presentation of compatibility graphs and how to combine them.

Definition 13

[\(\cup \) operation] We consider two arbitrary disjoint graphs \(G_1= (V_1,\mathcal {E}_1)\) and \(G_2 = (V_2,\mathcal {E}_2)\). The UNION of \(G_1\) and \(G_2\) is graph \(G=(V,\mathcal {E})\) defined as follows:

  • Nodes: \(V= V_1 \cup V_2\),

  • Edges: \(\mathcal {E}= \mathcal {E}_1 \cup \mathcal {E}_2\).

Definition 14

(JOIN operation) We consider two arbitrary disjoint graphs \(G_1= (V_1,\mathcal {E}_1)\) and \(G_2 = (V_2,\mathcal {E}_2)\). The JOIN of \(G_1\) and \(G_2\) is graph \(G=(V,\mathcal {E})\) defined as follows:

  • Nodes: \(V= V_1 \cup V_2\),

  • Edges: \(\mathcal {E}= \mathcal {E}_1 \cup \mathcal {E}_2 \cup \{ (x,y), x \in V_1, y \in V_2 \}\).

In words, we keep all nodes and edges of \(G_1\) and \(G_2\) and we add all the edges between nodes in \(V_1\) and \(V_2\). The JOIN operation will be denoted by \(\bowtie \).

We depict in Fig. 3 the JOIN of a graph with 4 isolated nodes (nodes 4 to 7) and a complete graph with 3 nodes (nodes 1 to 3).

Fig. 3
figure 3

Graph \(IN_4 \bowtie K_3\)

Full size image

Remark 7

If \(\mathcal {E}_1=\mathcal {E}_2 = \emptyset \), then G, which is the join of \(G_1\) and \(G_2\), is a complete bipartite graph. Remember that we do not study model associated with bipartite compatibility graphs as their associated Markov chains are not ergodic (Fig. 4).

Fig. 4
figure 4

Graph \(G_1 \bowtie G_2\)

Full size image

As a matching model is a triple with a compatibility graph, a collection of arrival processes and a matching discipline, we also have to explain how we associate the last two parts of the model to both modular constructions of compatibility graphs. For the arrival processes, we consider the union of the sets of Poisson processes associated with \(G_1\) and \(G_2\). This is easier in continuous time thanks to the race condition which is already well known for the modular construction of stochastic models. For a composition of two compatibility graphs \(G_1\) and \(G_2\) associated with transition rates vectors \(\lambda \) and \(\mu \), we denote as \((\lambda , \mu )\) the rate vector associated with the composition of \(G_1\) and \(G_2\).

For the matching disciplines, we first have to find the state space of the models as they are defined as sets of states and probability distributions on these sets.

State Space for UNION

Let \(G_1\) and \(G_2\) be two disjoint compatibility graphs. Consider the compatibility graph G which is the UNION of graphs \(G_1\) and \(G_2\). Then, the state space of the continuous-time Markov chain associated with G is the Cartesian product of the state spaces of the two Markov chains associated with \(G_1\) and \(G_2\).

State Space for JOIN

Remark 8

Consider a compatibility graph G which is the JOIN of graphs \(G_1\) and \(G_2\). Remember that \(G_1\) and \(G_2\) are disjoint. Let \(M_1\) (resp. \(M_2\)) be the continuous-time Markov chain associated with \(G_1\) (resp. \(G_2\)) and vectors of arrival rates \(\lambda \) (resp. \(\mu \)). Both chains have an empty state because the discipline is greedy. Then, the continuous-time Markov chain associated with G has the following states which are a couple of words:

  • The states associated with \(M_1\) (no items of \(G_2\) are in the system) denoted by \((w1,\emptyset )\) where w1 is a state of \(M_1\) (i.e., a word). This set of states will be denoted by \(S_1\).

  • The states associated with \(M_2\) (no items of \(G_1\) are in the system) denoted by \((\emptyset ,w2)\) where w2 is a state of \(M_2\). Similarly, we denote as \(S_2\) this set of states.

  • Both chains are connected through their empty states which are merged.

The proof is trivial as it is not possible to reach a state (w1, w2) with both \(w1 \ne \emptyset \) and \(w2 \ne \emptyset \) due to the edges between \(G_1\) and \(G_2\) after the JOIN under a greedy policy. See Fig. 5 for an example.

Finally, we explain how we build a matching discipline on these constructions of compatibility graphs. Again we have to give separate statements. To be more precise for these definitions, we add a superscript to the name of the sets to know from which compatibility graphs they come.

Discipline for UNION

Let (w1, w2) a state of the chain associated with \(G_1 \cup G_2\). We have to consider two types of arrival: a letter x in \(V(G_1) \) or a letter y in \(V(G_2) \). We define the discipline on the UNION as follows:

$$\begin{aligned} N^{G_1 \cup G_2}_D ((w1,w2),x) = N^{G_1}_D (w1,x), \end{aligned}$$
(11)

and

$$\begin{aligned} N^{G_1 \cup G_2}_D ((w1,w2),y) = N^{G_2}_D (w2,y). \end{aligned}$$
(12)

The probability distributions are also defined similarly.

Thus, due to this discipline and the race condition between the arrival processes, the transition matrix of the Markov chain is the Kronecker sum of the transition matrices associated with \(G_1\) and \(G_2\) (see Plateau [25] for such a result for stochastic automata networks).

Discipline for JOIN

We consider an arbitrary non-empty set \((w1, \emptyset )\). Indeed there is no need for a matching discipline for the empty state and states \((\emptyset , w2)\) play a symmetrical role. We have two cases, according to the arriving letter (say x):

  • If \(x \in V(G_1)\), if there is compatibility with w1, then we keep the same discipline

    $$\begin{aligned} N^{G_1 \bowtie G_2}_D ((w1,\emptyset ),x) = N^{G_1}_D (w1,x), \end{aligned}$$
    (13)

    and the distribution of probability does not change.

  • \(x \in V(G_2)\). Because of the JOIN between \(G_1\) and \(G_2\), all the letters in w1 match with x. We take as a discipline in that case (i.e., \(N^{G_1 \bowtie G_2}_D ((w1,\emptyset ),x) \)), any consistent discipline. Indeed in the next section, we will aggregate all the letters x into only one letter, thus we need that the discipline does not depend on x in that case.

The transitions are the same as in the Markov chains associated with \(G_1\) or \(G_2\). More precisely: we have a transition from \((x_1,\emptyset )\) to \((x_2,\emptyset )\) if there is a transition from \(x_1\) to \(x_2\) in \(M_1\). Similarly, there is a transition from \((\emptyset ,y_1)\) to \((\emptyset ,y_2)\) if there is a transition from \(y_1\) to \(y_2\) in \(M_2\). Thus, the set of states of the chain is \(S_1 \cup S_2\). Let E be the empty state: \(E=(\emptyset ,\emptyset )\).

We are now able to study the models based on these modular decompositions.

Fig. 5
figure 5

Markov chain of the compatibility graph \(IN_2 \bowtie K_2\) for RANDOM discipline. The chain is truncated to words smaller than 4 letters. The labels (except E) and the rates are omitted for the sake of readability

Full size image

4.1 Compatibility graphs \(G_1 \bowtie G_2\)

We first consider graphs \(G_1\) and \(G_2\) which both contain at least 2 nodes and one edge (formally \(K_2 \subset G_1 \) and \(K_2 \subset G_2\)). The case where one of these graphs is a set of isolated nodes is studied in Sect. 4.2. We consider any greedy and consistent discipline D built as in the previous section. We assume that all the chains we define are ergodic.

Remark 9

Let \(\lambda \) be the vector of arrival rates for compatibility graph \(G_1\) and let \(\mu \) be the vector of rates for items in \(G_2\). After uniformization with rate \(\Lambda = 2(\Vert \lambda \Vert _1+ \Vert \mu \Vert _1)\), the transition probability matrix of discrete-time Markov chain associated with \(G_1 \bowtie G_2\) and vector of arrivals rates \((\lambda , \mu )\) has the following block decomposition associated with the partition of the states \((\{E\},S_1 \setminus \{E\},S_2 \setminus \{E\})\):

$$\begin{aligned} M = \left( \begin{array} {c|c|c} 1/2&{}L_1&{} L_2 \\ \hline C_1 &{} P_1 &{} 0 \\ \hline C_2 &{} 0 &{} P_2 \\ \end{array} \right) , \end{aligned}$$

where \(L_1\) and \(L_2\) are row vectors such that \(\Vert L_1 \Vert _1 = \frac{\Vert \lambda \Vert _1 }{\Lambda }\) and \(\Vert L_2 \Vert _1 = \frac{\Vert \mu \Vert _1 }{\Lambda }\), \(C_1\) and \(C_2\) are column vectors and \(P_1\) and \(P_2\) are sub-stochastic matrices. Similarly, we decompose the steady-state distribution \(\pi ^M \) as \((\pi _0^{M},\pi _{S_1}^{M}, \pi _{S_2}^{M})\). Note that we only need that \(\Lambda > \Vert \lambda \Vert _1+ \Vert \mu \Vert _1\) for uniformization. This value of \(\Lambda \) has been chosen to improve the readability of the matrices.

We now prove that the steady-state distribution of the chain associated with G has a closed form solution based on the steady-state solutions of chains associated with compatibility graphs we now describe. We call this solution a separable solution for the steady-state distribution. Let us begin with the description of the sub-models.

Fig. 6
figure 6

\(G'_2\): New compatibility graph for the first sub-model

Full size image

We build a simpler compatibility graph as follows: we replace \(G_1\) by a single node \(s_1\), we add a loop on \(s_1\) due to the edges in \(G_1\), we keep \(G_2\) unchanged, and we add the edges between \(s_1\) and all the nodes in \(G_2\) (see Fig. 6). Compatibility graphs with self-loops were recently introduced by Moyal et al. in [13] and independently in [26]. Let \(G'_2\) be this compatibility graph. The arrival rates associated with this compatibility graph are \((\Vert \lambda \Vert _1, \mu )\). The discipline associated with \(G'_2\) is derived from D. As D is consistent, all the letters of \(G_1\) provoke the same transitions on a word \((\emptyset , m2) \) and we use this set of nodes and this distribution to define the discipline.

Let \(M_2\) be the transition probability matrix after uniformization with rate \(\Lambda \) and let \(\pi ^{M_2}\) be its steady-state distribution. The state space of the Markov chain associated with \(G'_2\) is the following (see Fig. 7):

  • The state \((1,\emptyset ) \) with one item of class \(s_1\) and no items of \(G_2\). Note that this is the only state with a positive number of items of class \(s_1\) as \(G'_2\) contains a loop on \(s_1\).

  • The state \((0,\emptyset )=E \) which represents an empty system.

  • The states associated with items of \(G_2\) (no \(s_1\) items are present in the system): the states will be denoted as (0, y) where y is a node of \(G_2\). Clearly, there is a one-to-one mapping between states (0, y) in Markov chain \(M_2\) and states \( (\emptyset ,y)\) in Markov chain P. Therefore, we also denote as \(S_2\) this set of states.

Fig. 7
figure 7

Markov chain for \(G'_1\) for \(G_1 = K_2\) and Random discipline

Full size image

Proposition 7

\(M_2\) has the following block decomposition associated with the partition of the states \((\{(1,\emptyset )\}, \{E\}, S_2 {\setminus } \{E\})\).

$$\begin{aligned} M_2 = \left( \begin{array} {c|c|c} 1/2 &{} 1/2 &{} \textbf{0} \\ \hline c_2 &{} 1/2&{} L_2 \\ \hline 0&{}C_2 &{} P_2 \\ \end{array} \right) , \end{aligned}$$

where blocks \(L_2\), \(C_2\) and \(P_2\) have already been obtained in the decomposition of matrix M and \(c_2=\frac{\Vert \lambda \Vert _1}{\Lambda }\).

The proof of the above result is provided in Appendix C.1. We also consider a decomposition of the steady-state distribution of \(M_2\): \((\pi _1^{M_2},\pi _0^{M_2},\pi _{S_1}^{M_2})\).

We do a similar construction for \(G'_1\) which is depicted in Fig. 8 by aggregation all the nodes of \(G_2\) into a single node \(s_2\) and adding a self-loop on \(s_2\), with similar definitions for \(M_1\). For this case, we have a block decomposition for \(M_1\) based on this partition:

$$\begin{aligned} M_1 = \left( \begin{array} {c|c|c} 1/2&{} 1/2 &{} \textbf{0} \\ \hline c_1&{} 1/2 &{} L_1 \\ \hline 0 &{} C_1 &{} P_1\\ \end{array} \right) , \end{aligned}$$

with \(c_1 = \frac{ \Vert \mu \Vert _1}{\Lambda }.\)

Fig. 8
figure 8

\(G'_1\): New compatibility graph for the other sub-model

Full size image

We can now show the relation between the steady-state distributions associated with these three models. Let G be the JOIN of graph \(G_1\) and \(G_2\), and M the discrete-time Markov chain associated with G and arrival probabilities \((\alpha ,\beta )\). These probabilities have been derived by uniformization of rates \((\lambda ,\mu )\) by rate \(\Lambda \). Assume that M, \(M_1\) and \(M_2\) are ergodic discrete-time Markov chains. Let \(\pi _M\) be the steady state distribution of the chain associated with M. We decompose this distribution into three parts: the probability of the empty state, the probability of the states of \(S_1\) and the probability of the states of \(S_2\).

$$\begin{aligned} \pi _M = (\pi _{0}^M, \pi _{S_1}^M, \pi _{S_2}^M), \end{aligned}$$

where these elements are obtained through the steps detailed in the following. The steady-state distribution of \(M_1\) is:

$$\begin{aligned} \pi _{M_1} = (\pi _{1}^{M_1},\pi _{0}^{M_1}, \pi _{S_1}^{M_1}), \end{aligned}$$

with an abuse of notation here. Indeed \(S_1\) is the set of states of M (not of \(M_1\)), but there is a one-to-one mapping between the set of nonzero states of \(M_1\) and \(S_1\). Therefore, we use the same index for the decomposition of the probability vector. Similarly, we denote:

$$\begin{aligned} \pi _{M_2} = (\pi _{1}^{M_2},\pi _{0}^{M_2}, \pi _{S_2}^{M_2}). \end{aligned}$$

Theorem 3

Consider the former construction. We have:

$$\begin{aligned} \pi _{S_1}^M = \pi _{S_1}^{M_1} \frac{\pi _0^M}{\pi _0^{M_1}}, \end{aligned}$$

and

$$\begin{aligned} \pi _{S_2}^M = \pi _{S_2}^{M_2} \frac{\pi _0^M}{\pi _0^{M_2}}, \end{aligned}$$

and finally

$$\begin{aligned} \pi _{0}^M = \left( \frac{1}{\pi _0^{M_1} } + \frac{1}{\pi _0^{M_2}} -2 \right) ^{-1}. \end{aligned}$$

Furthermore, the expectation of the total number of items is:

$$\begin{aligned} \mathbb {E}[M((G_1 \bowtie G_2), (\lambda ,\mu ),D) = \frac{\pi _0^M}{\pi _0^{M_1}} \mathbb {E}[M(G'_1, \lambda ,D_1)] + \frac{\pi _0^M}{\pi _0^{M_2}} \mathbb {E}[M(G'_2,\mu ,D_2)] - 1, \end{aligned}$$

where \(D_1\) and \(D_2\) are the disciplines derived from D.

The proof of the above result is provided in Appendix C.2. It is important to remark that the Markov chain associated with \(G'_1\) is not a lumped version of the DTMC associated with G. In general this Markov chain is not lumpable due to the possible matching between the items of \(G_2\). In the next subsection, we study a simpler case where we have a strong aggregation of the DTMC and this leads to a lifting theorem for the paradox.

4.2 Compatibility graphs \(IN_{n1} \bowtie K_{n2}\)

We consider a compatibility graph \(G= IN_{n1} \bowtie K_{n2} \) with \(n1 \ge 1 \) and \(n2 \ge 2\), the JOIN of a set of n1 isolated nodes and a complete graph with size n2. We assume that the matching discipline is greedy and consistent. Let us first mention some results from graph theory. First, we have that, if \(n2 \ge 2\), then G is not bipartite; indeed, the graph contains at least one triangle. Furthermore, we also have that

$$\begin{aligned} IN_{1} \bowtie K_{n} = K_{n+1}. \end{aligned}$$
(14)

One can easily show that the latter result also holds for quasi-complete graphs, i.e.,

$$\begin{aligned} IN_{1} \bowtie (K_{n}-(a,b)) = K_{n+1}-(a,b). \end{aligned}$$
(15)

We begin with a result even more general for the state space of \(IN_{n1} \bowtie G_{n2} \) where \(G_{n2} \) is an arbitrary graph with size n2.

Theorem 4

Consider a compatibility graph \(G= IN_{n1} \bowtie G_{n2} \), arrival rates of letters \((\lambda , \mu )\) and an arbitrary consistent and greedy discipline D as defined in Sect. 4. Assume that \(n1>1\) and \(K_2 \subset G_{n2}\). We have uniformized the continuous-time Markov chain with rate \(\Lambda > \Vert \lambda \Vert _1 + \Vert \mu \Vert _1 \) to obtain a discrete-time model. This DTMC is lumpable for the following partition:

  1. 1.

    State E remains unchanged

  2. 2.

    States \((\emptyset ,Y)\) remain unchanged.

  3. 3.

    States \((X,\emptyset )\) are aggregated into macro-state \((\vert X \vert , \emptyset )\).

We aggregate all the nodes of the independent set into one macro-state which is the length of the word. Let \(\alpha _y = \lambda _y/\Lambda \) be the probability of an arrival of letters y for the letters in the set of isolated nodes. z will denote the aggregated letters of this set. The arrival probability of letter z is \(\alpha _z = \sum _{y=1}^{n1} \alpha _y \). The lumped Markov chain is associated with the compatibility graph \(IN_{1} \bowtie G_{n2}\) and discipline \(D'\) which is derived from D as in Sect. 3.

Proof

As states E and \((\emptyset ,Y)\) for every word Y remain unchanged, we just have to consider the macro-states which contain the states \((X,\emptyset )\). Consider two arbitrary states \((X_1,\emptyset )\) and \((X_2,\emptyset )\) such that \(\vert X_1 \vert = \vert X_2 \vert = k\). They are members of the same macro-state \((k, \emptyset )\). We have two cases: arrival of a letter in \(V(IN_{n1})\) or in \(V(G_2)\).

  • Consider the arrival of an arbitrary letter in \(V(IN_{n1})\). The letter does not match with \(X_1 \) or \(X_2\) as this part of the compatibility graph does not contain any edges. Therefore, it provokes a transition to a state which is aggregated into macro-state \((k+1, \emptyset )\) and the matching discipline is irrelevant here as no matching occurs.

  • Assume now an arrival of an arbitrary letter in \(V(G_2)\). A matching takes place and as the discipline is greedy and consistent, exactly one letter is deleted among the letters of \(X_1\) or \(X_2\). Therefore, both states belong to macro-state \((k-1, \emptyset )\).

Thus, the lumpability conditions hold. \(\square \)

As usual, both chains give the same expectation for the total number of letters.

Corollary 1

Consider an arbitrary greedy and consistent discipline D. We have the same expectation for the total number of items for model \(IN_{1} \bowtie G_{n2}\) and model \(IN_{n1} \bowtie G_{n2}\) assuming that \(\beta _z = \sum _y \alpha _y \) for the arrivals of letters z in \(IN_{1}\) and \(\beta _y = \alpha _y\) for y in \(G_{n2}\) for a discipline \(D'\) derived from D.

$$\begin{aligned} \mathbb {E}[M(IN_{n1} \bowtie G_{n2}, \alpha , D)] = \mathbb {E}[M((IN_{1} \bowtie G_{n2}, \beta , D')]. \end{aligned}$$

In general, we are not able to analyze chain \(M((IN_{1} \bowtie G_{n2}, \beta , D')\). However, we focus on some simple cases. First, we consider \(G_2=K_{n2}\), using Corollary 1 and (14), we obtain the following result.

Corollary 2

Using the same transformation of arrival rates and matching disciplines, we get:

$$\begin{aligned} \mathbb {E}[M(IN_{n1} \bowtie K_{n2}, \alpha , D)] = \mathbb {E}[M(K_{n2+1}, \beta , D')]. \end{aligned}$$

We now consider \(G_2=K_{n2}\), using Corollary 1 and (15), we obtain:

Corollary 3

We use the same transformation of arrival rates and matching disciplines and we obtain the same expectation for the total number of items for model \(K_{n2+1} -(a,b) \) and model \(IN_{n1} \bowtie (K_{n2}-(a,b))\).

$$\begin{aligned} \mathbb {E}[M(IN_{n1} \bowtie K_{n2}-(a,b), \alpha , D)] = \mathbb {E}[M(K_{n2+1}-(a,b), \beta , D')]. \end{aligned}$$

And the existence of a paradox follows:

Theorem 5

If there exists a paradox between compatibility graph \(K_{n2+1}\) and \(K_{n2+1}-(a,b)\) for a greedy and consistent discipline, the same (i.e., we keep the same arrival rates for letters in \(K_{n2}\)) paradox exists between \(IN_{n1} \bowtie K_{n2}\) and \(IN_{n1} \bowtie (K_{n2}-(a,b))\).

Proof

Corollary 2 proves that \(K_{n2+1}\) and \(IN_{n1} \bowtie K_{n2}\) have the same expectation for total number of items, while Corollary 3 establishes the same relation for chains associated with compatibility graphs \(K_{n2+1}-(a,b)\) and \(IN_{n1} \bowtie (K_{n2}-(a,b))\). Thus, if a paradox exists between \(K_{n2+1}\) and \(K_{n2+1}-(a,b)\), it also exists between \(K_{n2+1}-(a,b)\) and \(IN_{n1} \bowtie (K_{n2}-(a,b))\). \(\square \)

Corollary 4

For all \(n\ge 4\), there exists a compatibility graph with size n which exhibits a paradox for any discipline D.

Proof

For \(n=4\), we give the example for FCFM discipline for compatibility graph \(K_4-(3,4)\) in Sect. 2.2 and we generalize to in Sect. 3 to any discipline D. For larger n, we consider compatibility graph \(IN_{n-4} \bowtie (K_4 - (3,4))\) and Theorem 5 proves the claim with the previous results on \(K_4 -(3,4)\). \(\square \)

Remark 10

Note that the number of edges in graph \(K_{n1} \bowtie (K_4 -(3,4)) \) is only \(4 n_1 + 5\). With \(n=n_1+4\), we have a compatibility graph for all n with a graph with \(n>3\) nodes and \(4 n -11 \) edges. Thus, the average degree is asymptotically 4.

Lemma 5

If compatibility graph G with discipline FCFM satisfies the assumption of Theorem 1, then matching graph \(G \bowtie IN_1\) with discipline FCFM also satisfies the same assumptions when the arrival probability of the letter in \(IN_1\) is sufficiently small. Therefore, compatibility graph \(G \bowtie IN_1\) also exhibits a performance paradox.

Proof

Let x be the letter of \(IN_1\). And \(\alpha ^\delta \) the arrival probabilities for graph G. We have to prove that the assumptions of Theorem 1 on the saturated independent sets are still valid for \(G \bowtie \{x\}\). First, the independent sets of \(G \bowtie IN_1\) are the independent sets of G and \(\{x\}\). Let us consider the following arrival probabilities for graph \(G \bowtie \{x\} \):

$$\begin{aligned} \beta _0^\delta = \alpha ^\delta _0 (1-\delta ), ~~\beta _x^\delta = \alpha ^\delta _0 \delta , ~~ \beta _y^\delta = \alpha _y^\delta ~~\forall y \in V(G). \end{aligned}$$

As \(\alpha ^\delta \) is a probability distribution, \(\beta ^\delta \) is also a probability distribution when \(\delta <1\). Now we have to compute the stability gap for all independent sets of \(G \bowtie \{x\}\). We slightly change the notation about the stability gap as follows: \(\Delta _{G} (\mathcal {I})\) will denote the stability gap of independent set \(\mathcal {I}\) in graph G. Let us begin with \( \{x\}\). All the nodes of G are neighbors of x. Thus:

$$\begin{aligned} \Delta ^{G \bowtie \{x\}}_{\{x\}} = \sum _{y \in V(G)} \beta _y ~-~ \beta _x = \sum _{y \in V(G)} \alpha _y ~-~ \alpha _0 \delta = 1 - \alpha _0 - \alpha _0 \delta . \end{aligned}$$

Therefore, \(\{x\}\) is not a saturated independent set. Now consider any independent set \(\mathcal {I}\) of \(G \bowtie \{x\}\) which is also an independent set of G. \(\mathcal {I}\) does not contain x, unlike \(\Gamma (\mathcal {I})\). Therefore, due to the arrival probabilities we considered:

$$\begin{aligned} \Delta ^{G \bowtie \{x\}}_{\mathcal {I}}= \Delta ^{G}_{\mathcal {I}} + \alpha _0 \delta . \end{aligned}$$

Clearly, as the transformation of the gaps keep unchanged the saturated independent set and if we have only one saturated independent set in G, we have only one saturated independent set in \(G \bowtie \{x\}\). Therefore, the assumptions of Theorem 1 are still valid for the graph we have designed. \(\square \)

Corollary 5

Using existence of a paradox for discipline FCFM and compatibility graph \(K_4 - (3,4)\), Lemma 5 implies that a performance paradox exists for compatibility graph \( K_n-(n-1,n)\) and discipline FCFM for any n.

Proof

The proof is an induction on n based on Lemma 5 and Eq. 14 and 15 to build the graphs adding one node at each step of the induction. \(\square \)

Then combining this last corollary with Theorem 2, we prove that a performance paradox exists for compatibility graph \(K_n-(n-1,n)\) for all greedy disciplines and size n.

Corollary 6

If a discipline does not exhibit such a paradox for graph \(K_n\)-(n-1,n), for some \(\lambda \), then this discipline is not greedy.

4.3 Compatibility graph \(IN_{n1} \bowtie (G_2 \cup G_1)\)

Assume now the following decomposition for the compatibility graph into three subgraphs:

$$\begin{aligned} G = IN_{n1} \bowtie (G_1 \cup G_2), \end{aligned}$$

where \(G_1\) and \(G_2\) are distinct and non-empty. We now establish that G may have some paradox if one of the sub-models exhibits a performance paradox. Again we assume that all the Markov chains considered in this section are ergodic (Fig. 9).

Fig. 9
figure 9

Graph \(G= IN_1 \bowtie (K_2 \cup IN_3 )\), \(IN_1\) contains node 4. We note that G is connected while the subgraphs \(IN_1\) and \(IN_3\) are not

Full size image

Proposition 8

Consider an arbitrary greedy and consistent matching discipline D. Assume that the compatibility graph G is the UNION of \(G_1\) and \(G_2\). Let \(\lambda \) and \(\mu \) be, respectively, the arrival rates associated with \(G_1\) and \(G_2\). Then:

$$\begin{aligned} M(G_1 \cup G_2, (\lambda ,\mu ), D) = M(G_1, \lambda , D) \oplus M(G_2, \mu , D), \end{aligned}$$

where \(\oplus \) is the tensor (or Kronecker sum).

Proof

As the items in \(G_1\) and \(G_2\) do not interact, we have built two independent continuous-time Markov chains. And it is well known (see, for instance, the literature on stochastic automata networks, for example, [25] and references therein) that the resulting Markov chains is the Kronecker sum of the components. \(\square \)

Corollary 7

Because of the independence of the Markov chains associated with \(G_1\) and \(G_2\), we clearly have:

$$\begin{aligned} \mathbb {E}[M(G_1 \cup G_2), (\lambda ,\mu ),D )] = \mathbb {E}[M(G_1,\lambda ,D)] + \mathbb {E}[M(G_2,\mu ,D)]. \end{aligned}$$

Therefore if a paradox exist for compatibility graph \(G_1\) and discipline D, it also exists for compatibility graph \(G_1 \cup G_2\) and discipline D.

Lemma 6

Assume that \(G_1\) with FCFM matching discipline satisfies the assumptions of Theorem 1 for vector of arrival rates \(\mu \). Assume also that \(G_2\) with vector of arrival rates \(\lambda \) does not contain any saturated independent set for FCFM matching discipline. Then, \(G_1 \cup G_2\) with FCFM discipline and vector of arrivals \((\mu , \lambda )\) satisfies the assumptions of Theorem 1.

Proof

The independent sets of \(G_1 \cup G_2\) are:

  • the independent sets of \(G_1\),

  • the independent sets of \(G_2\),

  • all the sets which are the union of an independent set of \(G_1\) and an independent set of \(G_2\).

Therefore, the saturated independent set of \(G_1\) is also a saturated independent set of \(G_1 \cup G_2\). We now have to check that \(G_1 \cup G_2\) contains only one saturated independent set. As \(G_2\) does not have a saturated independent set, there exists \(\Delta >0\) such that all the stability gaps of independent sets of \(G_2\) are larger than \(\Delta \). Let \(\mathcal {I}_1\) be an independent set of \(G_1\) and \(\mathcal {I}_2\) an independent set of \(G_2\). \(\mathcal {I}_2\) is not saturated by assumption and clearly, due to the UNION operation:

$$\begin{aligned} \Delta ^{G_1 \bowtie G_2}_{ \mathcal {I}_1 \cup \mathcal {I}_2 } = \Delta ^{G_1}_{ \mathcal {I}_1} + \Delta ^{G_2}_{\mathcal {I}_2}. \end{aligned}$$

Therefore as \(\Delta ^{G_2}_{\mathcal {I}_2} \ge \Delta \), \(\mathcal {I}_1 \cup \mathcal {I}_2\) cannot be saturated. Thus, the saturated independent set of \(G_1\) is the saturated independent set of \(G_1 \cup G_2\). \(\square \)

Remember that \(G_1 \cup G_2\) is not connected. However, we can build connected compatibility graphs with UNION and JOIN operations. The following result is a simple corollary of Remark 8.

Lemma 7

(State Space) Let \(G_3 \bowtie (G_1 \cup G_2)\), then the states of the Markov chain associated with G are

  • State E,

  • states \((X,\emptyset ,\emptyset )\) where X is a state of the chain associated with \(G_3\),

  • states \((\emptyset ,Y,Z)\) where Y (resp. Z) is a state of the chain associated with \(G_1\) (resp. \(G_2\)),

Theorem 6

We assume the FCFM matching discipline and that compatibility graph \(G_1\) satisfies the assumptions of Theorem 1. Let \(\mu \) be the vector of arrival rates associated with this paradox for \(G_1\). Then, we also have a performance paradox for compatibility graph \( IN_{n1} \bowtie (G_1 \cup G_2)\) associated with arrival rate vector \((\lambda ,\mu ,\nu )\) and FCFM discipline.

Proof

We first aggregate all the nodes of \(IN_{n1}\) into one single node because the associated chain is lumpable. According to Theorem 4, using discipline FCFM

$$\begin{aligned}{} & {} \mathbb {E}[M((IN_{n1} \bowtie (G_1 \cup G_2)), (\lambda ,\mu ,\nu ), FCFM)] \\{} & {} \quad = \mathbb {E}[M((IN_1 \bowtie (G_1 \cup G_2)), \beta , FCFM)], \end{aligned}$$

with \( \beta = (\lambda ,\mu ,\nu )\). Lemma 6 shows that as soon as the assumptions of Theorem 1 hold for \(G_1\), \(G_1 \cup G_2\) also satisfies the same assumptions and the compatibility graph \(IN_1 \bowtie (G_1 \cup G_2)\) also exhibits a paradox for FCFM discipline according to Lemma 5. \(\square \)

5 Conclusions

We consider the dynamic matching model with a non-bipartite matching graph and we analyze the existence of a performance degradation when the flexibility increases, i.e., when we add an edge to the matching graph. This analysis can be seen as analogous to the Braess paradox. In our previous work, we focused on the FCFM discipline and an arbitrary matching graph and we provided sufficient conditions on the existence of a performance paradox. In this work, the performance paradox existence study is extended to greedy disciplines, which is a large family of matching disciplines that includes, not only FCFM, but also other popular disciplines such as Match the Longest and Random. We provide constructions for families of graphs with performance paradox.

As future work, we are interested in exploring the existence of a performance paradox for other compatibility graphs. We also plan to study the existence of a performance paradox for greedy policies for the related bipartite stochastic matching model.