Skip to main content
SpringerLink
Log in

Entanglement witness and linear entropy in an open system influenced by FG noise

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

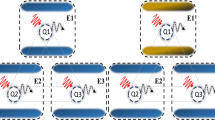
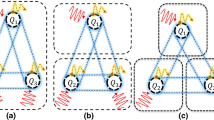
We investigate the behavior of tripartite entanglement and entropy disorder in three non-interacting qubits that are first prepared in a mixture state containing Greenberger–Horne–Zeilinger (GHZ) and Werner (W) states, and then exposed to classical transmitting channels influenced by fractional Gaussian (FG) noise. To investigate the coupling of the three non-interacting qubits, single, double, and triple local channel configurations are used. We address the question of how GHZ and W states can have different capacities to protect entanglement while avoiding entropy disorder in different qubit-channel couplings. Using entanglement witness and linear entropy functions, we find that GHZ state is more resourceful when coupled with a single channel, whereas W state remains more resourceful when exposed to more than one local channel. The statistical ensemble states that are initially designed, as well as the designs of the medium to which they are exposed, have a strong influence on the initial state entanglement retention in quantum systems. Moreover, we realize that FG noise is more harmful than frequently found local noises, resulting in faster entropy disorder generation and, as a result, the destruction of tripartite quantum correlations. However, the tripartite correlations can be preserved by increasing the FG noise parameter known as the Hurst exponent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in this paper.

References

  1. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2010)

    MATH  Google Scholar 

  2. Gruska, J.: Quantum computing challenges. In: Engquist, B., Schmid, W. (eds.) Mathematics Unlimited and Beyond, vol. 529. Springer, Berlin (2001)

    Google Scholar 

  3. Ge, R.C., Gong, M., Li, C.F., Xu, J.S., Guo, G.C.: Quantum correlation and classical correlation dynamics in the spin-boson model. Phys. Rev. A 81, 064103 (2010)

    Article  ADS  Google Scholar 

  4. Schrödinger, E.: Die gegenwärtige situation in der quantenmechanik. Naturwissenschaften 23, 807 (1935)

    Article  ADS  MATH  Google Scholar 

  5. Einstien, A., Podolsky, B., Rosen, N.: Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 47, 777 (1935)

    Article  ADS  MATH  Google Scholar 

  6. Kenfack, L.T., Tchoffo, M., Fouokeng, G.C., Fai, L.C.: Dynamical evolution of entanglement of a three-qubit system driven by a classical environmental colored noise. Quantum Inf. Process. 17, 76 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Bennett, C.H., Di Vincenzo, D.P.: Quantum information and computation. Nature 404, 247 (2000)

    Article  ADS  MATH  Google Scholar 

  8. Terhal, B.M.: Quantum dense coding. In: Kao, M.Y. (ed.) Encyclopedia of Algorithms. Springer, New York (2016)

    Google Scholar 

  9. Takano, T., Fuyama, M., Namiki, R., Takahashi, Y.: Continuous-variable quantum swapping gate between light and atoms. Phys. Rev. A. 78, 010307 (2008)

    Article  ADS  Google Scholar 

  10. Scarani, V., Iblisdir, S., Gisin, N., Acín, A.: Quantum cloning. Rev. Mod. Phys. 77, 1225 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Richter, T., Vogel, W.: Nonclassical characteristic functions for highly sensitive measurements. Phy. Rev. A 76, 053835 (2012)

    Article  ADS  Google Scholar 

  12. Benenti, G., Casati, G., Strini, G.: Principles of Quantum Computation and Information; Basic Tools and Special Topics. World Scientific Publishing, Singapore (2007)

    Book  MATH  Google Scholar 

  13. Hu, M.L., Hu, X., Wang, J., Peng, Y., Zhang, Y.R., Fan, H.: Quantum coherence and geometric quantum discord. Phys. Rep. 762, 1 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  14. Xu, X.X., Hu, M.L.: Maximal steered coherence and its conversion to entanglement in multiple bosonic reservoirs. Ann. Phys. (Berlin) 534, 2100412 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  15. Hu, M.L., Zhang, Y.H., Fan, H.: Nonlocal advantage of quantum coherence in a dephasing channel with memory. Chin. Phys. B 30, 030308 (2021)

    Article  ADS  Google Scholar 

  16. Hu, M.L., Zhou, W.: Enhancing two-qubit quantum coherence in a correlated dephasing channel. Laser Phys. Lett. 16, 045201 (2019)

    Article  ADS  Google Scholar 

  17. Hu, M.L., Fan, H.: Evolution equation for quantum coherence. Sci. Rep. 6, 29260 (2016)

    Article  ADS  Google Scholar 

  18. Hu, M.L., Fan, H.: Relative quantum coherence, incompatibility, and quantum correlations of states. Phys. Rev. A 95, 052106 (2017)

    Article  ADS  Google Scholar 

  19. Hu, M.L., Fan, H.: Quantum coherence of multiqubit states in correlated noisy channels. Sci. China Phys. Mech. Astron. 63, 230322 (2020)

    Article  ADS  Google Scholar 

  20. Benabdallah, F., Haddadi, S., Arian Zad, H., Pourkarimi, M.R., Daoud, M., Ananikian, N.: Pairwise quantum criteria and teleportation in a spin square complex. Sci. Rep. 12, 6406 (2022)

    Article  ADS  Google Scholar 

  21. Haddadi, S., Pourkarimi, M.R., Haseli, S.: Relationship between quantum coherence and uncertainty bound in an arbitrary two-qubit X-state. Opt. Quantum Electron. 53, 529 (2021)

    Article  Google Scholar 

  22. Zhao, F., Wang, D., Ye, L.: Relationship between entanglement and coherence in some two-qubit states. Int. J. Theor. Phys. 61, 10 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mohamed, A.B.A., Khedr, A.N., Haddadi, S., Rahman, A.U., Tammam, M., Pourkarimi, M.R.: Intrinsic decoherence effects on nonclassical correlations in a symmetric spin-orbit model. Results Phys. 39, 105693 (2022)

    Article  Google Scholar 

  24. Liu, B.H., Li, L., Huang, Y.F., Li, C.F., Guo, G.C., Laine, E.M., Piilo, J.: Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 7, 931 (2011)

    Article  Google Scholar 

  25. Peters, N.A., Toliver, P., Chapuran, T.E., Runser, R.J., McNown, S.R., Peterson, C.G., Rosenberg, D., Dallmann, N., Hughes, R.J., McCabe, K.P., Nordholt, J.E., Tyagi, K.T.: Dense wavelength multiplexing of 1550 nm QKD with strong classical channels in reconfigurable networking environments. New J. Phys. 11, 045012 (2009)

    Article  ADS  Google Scholar 

  26. Pirandola, S., Lupo, C., Giovannetti, V., Mancini, S., Braunstein, S.L.: Quantum reading capacity. New J. Phys. 13, 113012 (2011)

    Article  ADS  MATH  Google Scholar 

  27. Wengerowsky, S., Joshi, S.K., Steinlechner, F., Hübel, H., Ursin, R.: An entanglement-based wavelength-multiplexed quantum communication network. Nature 564, 225 (2018)

    Article  ADS  Google Scholar 

  28. Xu, S., et al.: Universal low-temperature Ohmic contacts for quantum transport in transition metal dichalcogenides. 2D Mater. 3, 021007 (2016)

    Article  Google Scholar 

  29. Fei, F., Zhang, S., Zhang, M., Shah, S.A., Song, F., Wang, X., Wang, B.: The material efforts for quantized Hall devices based on topological insulators. Adv. Mater. 32, 1904593 (2020)

    Google Scholar 

  30. Benedetti, C., Buscemi, F., Bordone, P., Paris, M.G.A.: Effects of classical environmental noise on entanglement and quantum discord dynamics. Int. J. Quantum Inf. 10, 1241005 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  31. Rahman, A.U., Haddadi, S., Pourkarimi, M.R.: Tripartite quantum correlations under power-law and random telegraph noises: collective effects of Markovian and non-Markovian classical fields. Ann. Phys. (Berlin) 534, 2100584 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  32. Rahman, A.U., Ji, Z.X., Zhang, H.G.: Demonstration of entanglement and coherence in GHZ-like state when exposed to classical environments with power-law noise. Eur. Phys. J. Plus 137, 440 (2022)

    Article  Google Scholar 

  33. Rahman, A.U., Javed, M., Ji, Z., Ullah, A.: Probing multipartite entanglement, coherence and quantum information preservation under classical Ornstein–Uhlenbeck noise. J. Phys. A Math. Theor. 55, 025305 (2021)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Rahman, A.U., Noman, M., Javed, M., Ullah, A.: Dynamics of bipartite quantum correlations and coherence in classical environments described by pure and mixed Gaussian noises. Eur. Phys. J. Plus 136, 846 (2021)

    Article  Google Scholar 

  35. Mandelbrot, B.B., Van Ness, J.W.: Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422 (1968)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Zunino, L., Zanin, M., Tabak, B.M., Pérez, D.G., Rosso, O.A.: Forbidden patterns, permutation entropy and stock market inefficiency. Physica A 388, 2854 (2009)

    Article  ADS  Google Scholar 

  37. Bae, J., Chruściński, D., Hiesmayr, B.C.: Mirrored entanglement witnesses. npj Quantum Inf. 6, 15 (2020)

    Article  ADS  Google Scholar 

  38. Bourennane, M., Eibl, M., Kurtsiefer, C., Gaertner, S., Weinfurter, H., Gühne, O., Sanpera, A.: Experimental detection of multipartite entanglement using witness operators. Phys. Rev. Lett. 92, 087902 (2004)

    Article  ADS  Google Scholar 

  39. Acín, A., Bruß, D., Lewenstein, M., Sanpera, A.: Classification of mixed three-qubit states. Phys. Rev. Lett. 87, 040401 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  40. Gühne, O., Tóth, G.: Entanglement detection. Phys. Rep. 474, 1 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  41. Weinstein, Y.S.: Tripartite entanglement witnesses and entanglement sudden death. Phys. Rev. A 79, 012318 (2009)

    Article  ADS  Google Scholar 

  42. Acín, A., Andrianov, A., Costa, L., Jané, E., Latorre, J.I., Tarrach, R.: Generalized Schmidt decomposition and classification of three-quantum-bit states. Phys. Rev. Lett. 85, 1560 (2000)

    Article  ADS  Google Scholar 

  43. Ming, F., Song, X.K., Ling, J., Ye, L., Wang, D.: Quantification of quantumness in neutrino oscillations. Eur. Phys. J. C 80, 275 (2020)

    Article  ADS  Google Scholar 

  44. Li, L.J., Ming, F., Song, X.K., Ye, L., Wang, D.: Characterizing entanglement and measurement’s uncertainty in neutrino oscillations. Eur. Phys. J. C 81, 728 (2021)

    Article  ADS  Google Scholar 

  45. Ming, F., Wang, D., Li, L.J., Fan, X.G., Song, X.K., Ye, L., Chen, J.L.: Tradeoff relations in quantum resource theory. Adv. Quantum Technol. 4, 2100036 (2021)

    Article  Google Scholar 

  46. Yang, Y.Y., Sun, W.Y., Shi, W.N., Ming, F., Wang, D., Ye, L.: Dynamical characteristic of measurement uncertainty under Heisenberg spin models with Dzyaloshinskii–Moriya interactions. Front. Phys. 14, 31601 (2019)

    Article  ADS  Google Scholar 

  47. Haddadi, S., Hu, M.L., Khedif, Y., Dolatkhah, H., Pourkarimi, M.R., Daoud, M.: Measurement uncertainty and dense coding in a two-qubit system: combined effects of bosonic reservoir and dipole–dipole interaction. Results Phys. 32, 105041 (2022)

    Article  Google Scholar 

  48. Hashem, M., Mohamed, A.B.A., Haddadi, S., Khedif, Y., Pourkarimi, M.R., Daoud, M.: Bell nonlocality, entanglement, and entropic uncertainty in a Heisenberg model under intrinsic decoherence: DM and KSEA interplay effects. Appl. Phys. B 128, 87 (2022)

    Article  ADS  Google Scholar 

  49. Rahman, A.U., Abd-Rabbou, M.Y., Zangi, S., Javed, M.: Entropic uncertainty and quantum correlations dynamics in a system of two qutrits exposed to local noisy channels. Phys. Scr. 97, 105101 (2022)

    Article  ADS  Google Scholar 

  50. Pan, J.W., Zeilinger, A.: Greenberger–Horne–Zeilinger-state analyzer. Phys. Rev. A 57, 2208 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  51. Zheng, S.B.: Splitting quantum information via W states. Phys. Rev. A 74, 054303 (2006)

    Article  ADS  Google Scholar 

  52. Ganguly, N., Adhikari, S., Majumdar, A.S., Chatterjee, J.: Entanglement witness operator for quantum teleportation. Phy. Rev. Lett. 107, 270501 (2011)

    Article  Google Scholar 

  53. Islam, R., Preiss, P.M., Tai, M.E., Lukin, A., Rispoli, M., Greiner, M.: Measuring entanglement entropy in a quantum many-body system. Nature 528, 77 (2015)

    Article  ADS  Google Scholar 

  54. Rahman, A.U., Noman, M., Javed, M., Luo, M.X., Ullah, A.: Quantum correlations of tripartite entangled states under Gaussian noise. Quantum Inf. Process. 20, 290 (2021)

    Article  MathSciNet  Google Scholar 

  55. Buscemi, F., Bordone, P.: Time evolution of tripartite quantum discord and entanglement under local and nonlocal random telegraph noise. Phys. Rev. A 87, 042310 (2013)

    Article  ADS  Google Scholar 

  56. Tchoffo, M., Kenfack, L.T., Fouokeng, G.C., Fai, L.C.: Quantum correlations dynamics and decoherence of a three-qubit system subject to classical environmental noise. Eur. Phys. J. Plus 131, 380 (2016)

    Article  Google Scholar 

  57. Sun, J., Sheng, H.: A hybrid detrending method for fractional Gaussian noise. Physica A 390, 2995 (2011)

    Article  ADS  Google Scholar 

  58. Erramilli, A., Narayan, O., Willinger, W.: Experimental queueing analysis with long-range dependent packet traffic. IEEE/ACM Trans. Netw. 4, 209 (1996)

    Article  Google Scholar 

  59. Kaplan, L.M., Kuo, C.C.: Extending self-similarity for fractional Brownian motion. IEEE Trans. Signal Process. 42, 3526 (1994)

    Article  ADS  Google Scholar 

  60. Zunino, L., Pérez, D.G., Kowalski, A., Martín, M.T., Garavaglia, M., Plastino, A., Rosso, O.A.: Fractional Brownian motion, fractional Gaussian noise, and Tsallis permutation entropy. Physica A 387, 6057 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  61. Taqqu, M.S., Teverovsky, V.: On estimating the intensity of long-range dependence in finite and infinite variance time series. In: A Practical Guide to Heavy Tails: Statistical Techniques and Applications, vol. 177 (1998)

  62. Mollaei, S., Darooneh, A.H., Karimi, S.: Multi-scale entropy analysis and Hurst exponent. Physica A 528, 121292 (2019)

    Article  Google Scholar 

  63. Gamble, J.K., Lindner, J.F.: Demystifying decoherence and the master equation of quantum Brownian motion. Am. J. Phys. 77, 244 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  64. Wanqing, S., Chen, X., Cattani, C., Zio, E.: Multifractional Brownian motion and quantum-behaved partial swarm optimization for bearing degradation forecasting. Complexity 2020, 8543131 (2020)

    Article  Google Scholar 

  65. Maniscalco, S., Piilo, J., Intravaia, F., Petruccione, F., Messina, A.: Simulating quantum Brownian motion with single trapped ions. Phys. Rev. A 69, 052101 (2004)

    Article  ADS  MATH  Google Scholar 

  66. Bauer, M., Bernard, D., Tilloy, A.: The open quantum Brownian motions. J. Stat. Mech. 2014, P09001 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  67. Benedetti, C., Paris, M.G.A.: Characterization of classical Gaussian processes using quantum probes. Phys. Lett. A 378, 2495 (2014)

    Article  ADS  MATH  Google Scholar 

  68. Rossi, M.A.C., Benedetti, C., Paris, M.G.A.: Engineering decoherence for two-qubit systems interacting with a classical environment. Int. J. Quantum Inf. 12, 1560003 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  69. Rossi, M.A.C., Paris, M.G.A.: Entangled quantum probes for dynamical environmental noise. Phys. Rev. A 92, 010302(R) (2015)

    Article  ADS  Google Scholar 

  70. Lionel, T.K., Martin, T., Collince, F.G., Fai, L.C.: Effects of static noise on the dynamics of quantum correlations for a system of three qubits. Int. J. Mod. Phys. B 31, 1750046 (2017)

    Article  ADS  MATH  Google Scholar 

  71. Haddadi, S., Pourkarimi, M.R., Wang, D.: Tripartite entropic uncertainty in an open system under classical environmental noise. J. Opt. Soc. Am. B 38, 2620 (2021)

    Article  ADS  Google Scholar 

  72. Benabdallah, F., Rahman, A.U., Haddadi, S., Daoud, M.: Long-time protection of thermal correlations in a hybrid-spin system under random telegraph noise. Phys. Rev. E 106, 034122 (2022)

    Article  ADS  Google Scholar 

  73. Cai, X.: Quantum dephasing induced by non-Markovian random telegraph noise. Sci. Rep. 10, 88 (2020)

    Article  ADS  Google Scholar 

  74. Zhou, D., Lang, A., Joynt, R.: Disentanglement and decoherence from classical non-Markovian noise: random telegraph noise. Quantum Inf. Process. 9, 727 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  75. Gorman, D.J., Young, K.C., Whaley, K.B.: Overcoming dephasing noise with robust optimal control. Phys. Rev. A 86, 012317 (2012)

    Article  ADS  Google Scholar 

  76. Li, J.Q., Liang, J.Q.: Quantum and classical correlations in a classical dephasing environment. Phys. Lett. A 375, 1496 (2011)

    Article  ADS  MATH  Google Scholar 

  77. Benabdallah, F., Daoud, M.: Dynamics of quantum discord based on linear entropy and negativity of qutrit-qubit system under classical dephasing environments. Eur. Phys. J. D 75, 3 (2021)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Physics, University of Chinese Academy of Science, Yuquan Road 19A, Beijing 100049, China

    Atta Ur Rahman

  2. Faculty of Physics, Semnan University, P.O. Box 35195-363, Semnan, Iran

    Saeed Haddadi

  3. Saeed’s Quantum Information Group, P.O. Box 19395-0560, Tehran, Iran

    Saeed Haddadi

  4. Quantum Optics and Information Research Team, Department of Physics, University of Malakand, Dir(L) Chakdara, KPK, Pakistan

    Muhammad Javed & Arif Ullah

  5. Research Unit of Condensed Matter, Electronic and Signal Processing, Department of Physics, Dschang School of Sciences and Technology, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Lionel Tenemeza Kenfack

Authors
  1. Atta Ur Rahman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Saeed Haddadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Muhammad Javed
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lionel Tenemeza Kenfack
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Arif Ullah
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saeed Haddadi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

A Appendix

A Appendix

Here, we present the explicit form of statistical ensembles of final density matrices of SQC, DQC and TQC configurations. For three non-interacting qubits initially prepared in the state \(\rho (0)\) given in Eq. (3) when considered in SQC configuration under FG noise, Eq. (11), the corresponding density matrix takes the form

$$\begin{aligned} \rho _{\textrm{SQC}}(t)=\left[ \begin{array}{cccccccc} \mathcal {A}_{1} &{} \mathcal {A}_{2} &{} \mathcal {A}_{2} &{} \mathcal {A}_{3} &{} \mathcal {A}_{2} &{} \mathcal {A}_{3} &{} \mathcal {A}_{3} &{} \mathcal {A}_{4} \\ \mathcal {A}_{2} &{} \mathcal {A}_{5} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{7} \\ \mathcal {A}_{2} &{} \mathcal {A}_{5} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{7} \\ \mathcal {A}_{3} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{8} &{} \mathcal {A}_{2} \\ \mathcal {A}_{2} &{} \mathcal {A}_{5} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{5} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{7} \\ \mathcal {A}_{3} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{8} &{} \mathcal {A}_{2} \\ \mathcal {A}_{3} &{} \mathcal {A}_{6} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{6} &{} \mathcal {A}_{8} &{} \mathcal {A}_{8} &{} \mathcal {A}_{2} \\ \mathcal {A}_{4} &{} \mathcal {A}_{7} &{} \mathcal {A}_{7} &{} \mathcal {A}_{2} &{} \mathcal {A}_{7} &{} \mathcal {A}_{2} &{} \mathcal {A}_{2} &{} \mathcal {A}_{9} \\ \end{array} \right] \end{aligned}$$
(A.1)

where

$$\begin{aligned} \mathcal {A}_{1}&=\frac{1}{32} e^{-18 \beta (t) } \left[ -3 e^{16 \beta (t) } (r-1)+6 e^{10 \beta (t) } (2 r-1)+e^{18 \beta (t) } (4 r+6)+3 (r-1)\right] ,\\ \mathcal {A}_{2}&=\frac{1}{16} \left( e^{-8 \beta (t) }-1\right) r,\\ \mathcal {A}_{3}&=-\frac{1}{32} e^{-18 \beta (t) } \left( e^{8 \beta (t) }-1\right) \left[ 3 e^{8 \beta (t) } (r-1)+e^{10 \beta (t) } (4 r-2)+3 (r-1)\right] ,\\ \mathcal {A}_4&=\frac{1}{16} \left( 3 e^{-8 \beta (t) }+5\right) r,\\ \mathcal {A}_{5}&=\frac{1}{96} e^{-18 \beta (t) } \left[ -7 e^{16 \beta (t) } (r-1)+e^{18 \beta (t) } (10-4 r)+e^{10 \beta (t) } (6-12 r)-9(r-1)\right] ,\\ \mathcal {A}_{6}&=\frac{1}{16} \left( 1-e^{-8 \beta (t) }\right) r,\\ \mathcal {A}_{7}&=-\frac{1}{32} e^{-18 \beta (t) } \left( e^{8 \beta (t) }-1\right) \left[ -3 e^{8 \beta (t) } (r-1)+e^{10 \beta (t) } (4 r-2)-3(r-1)\right] ,\\ \mathcal {A}_{8}&=\frac{1}{96} e^{-18 \beta (t) } \left[ 7 e^{16 \beta (t) } (r-1)+e^{18 \beta (t) } (10-4 r)+e^{10 \beta (t) } (6-12 r)+9 (r-1)\right] ,\\ \mathcal {A}_{9}&=\frac{1}{32} e^{-18 \beta (t) } \left[ 3 e^{16 \beta (t) } (r-1)+6 e^{10 \beta (t) } (2 r-1)+e^{18 \beta (t) } (4 r+6)-3(r-1)\right] .&\end{aligned}$$

The final density matrix for the case of DQC configuration driven by FG noise, Eq. (12), has the following form

$$\begin{aligned} \rho _{\textrm{DQC}}(t)=\left[ \begin{array}{cccccccc} \mathcal {B}_{1} &{}\mathcal {B}_{2} &{}\mathcal {B}_{3} &{}\mathcal {B}_{4} &{}\mathcal {B}_{3} &{}\mathcal {B}_{4} &{} \mathcal {B}_{5} &{} \mathcal {B}_{6} \\ \mathcal {B}_{7} &{} \mathcal {B}_{8} &{} \mathcal {B}_{9} &{} \mathcal {B}_{10} &{} \mathcal {B}_{9} &{} \mathcal {B}_{10} &{} \mathcal {B}_{11} &{} \mathcal {B}_{12} \\ \mathcal {B}_{10} &{} \mathcal {B}_{9} &{} \mathcal {B}_{13} &{} \mathcal {B}_{14} &{} \mathcal {B}_{13} &{} \mathcal {B}_{14} &{} \mathcal {B}_{10} &{} \mathcal {B}_{15} \\ \mathcal {B}_{4} &{}\mathcal {B}_{3} &{} \mathcal {B}_{16} &{} \mathcal {B}_{17} &{} \mathcal {B}_{16} &{} \mathcal {B}_{17} &{} \mathcal {B}_{18} &{}\mathcal {B}_{3} \\ \mathcal {B}_{10} &{} \mathcal {B}_{9} &{} \mathcal {B}_{13} &{} \mathcal {B}_{14} &{} \mathcal {B}_{13} &{} \mathcal {B}_{14} &{} \mathcal {B}_{10} &{} \mathcal {B}_{15} \\ \mathcal {B}_{4} &{}\mathcal {B}_{3} &{} \mathcal {B}_{16} &{} \mathcal {B}_{17} &{} \mathcal {B}_{16} &{} \mathcal {B}_{17} &{} \mathcal {B}_{18} &{}\mathcal {B}_{3} \\ \mathcal {B}_{5} &{} \mathcal {B}_{19} &{}\mathcal {B}_{3} &{} \mathcal {B}_{18} &{}\mathcal {B}_{3} &{} \mathcal {B}_{18} &{} \mathcal {B}_{20} &{}\mathcal {B}_{2} \\ \mathcal {B}_{21}&{} \mathcal {B}_{12} &{} \mathcal {B}_{15} &{} \mathcal {B}_{10} &{} \mathcal {B}_{15} &{} \mathcal {B}_{10} &{} \mathcal {B}_{7} &{} \mathcal {B}_{22} \\ \end{array} \right] \end{aligned}$$
(A.2)

where

$$\begin{aligned} \mathcal {B}_{1}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -20 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)+4 e^{10 \beta (t) } (2 r+7)\right. \\&\left. \quad +\, e^{6 \beta (t) } (65 r-17)+19 (r-1)\right] ,\\ \mathcal {B}_{2}&=\frac{1}{192} e^{-10 \beta (t) } \left[ e^{6 \beta (t) } (r-1)+12 e^{2 \beta (t) } r-12 e^{10 \beta (t) } r-r+1\right] ,\\ \mathcal {B}_{3}&=-\frac{1}{192} e^{-10 \beta (t) } \left( e^{6 \beta (t) }-1\right) (r-1),\\ \mathcal {B}_{4}&=-\frac{1}{192} e^{-10 \beta (t) } \left[ -15 e^{6 \beta (t) }+16 e^{8 \beta (t) }+16 e^{10 \beta (t) }-17\right] (r-1),\\ \mathcal {B}_{5}&=\frac{1}{192} e^{-10 \beta (t) } \left[ e^{6 \beta (t) } (r-1)-20 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)\right. \\&\left. \quad +\, e^{10 \beta (t) } (12-24 r)+19 (r-1)\right] ,\\ \mathcal {B}_{6}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 12 e^{2 \beta (t) } r+36 e^{10 \beta (t) } r+e^{6 \beta (t) } (49 r-1)-r+1\right] ,\\ \mathcal {B}_{7}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -e^{6 \beta (t) } (r-1)+12 e^{2 \beta (t) } r-12 e^{10 \beta (t) } r+r-1\right] ,\\ \mathcal {B}_{8}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -12 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)+4 e^{10 \beta (t) } (2 r+7)\right. \\&\left. \quad +\, e^{6 \beta (t) } (17-65 r)-19 (r-1)\right] ,\\ \mathcal {B}_{9}&=-\frac{1}{192} e^{-10 \beta (t) } \left[ 15 e^{6 \beta (t) }+16 e^{8 \beta (t) }+16 e^{10 \beta (t) }+17\right] (r-1),\\ \mathcal {B}_{10}&=\frac{1}{192} e^{-10 \beta (t) } \left( e^{6 \beta (t) }-1\right) (r-1),\\ \mathcal {B}_{11}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 12 e^{2 \beta (t) } r+36 e^{10 \beta (t) } r+e^{6 \beta (t) } (1-49 r)+r-1\right] ,\\ \mathcal {B}_{12}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -e^{6 \beta (t) } (r-1)+20 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)\right. \\&\left. \quad +\, e^{10 \beta (t) } (12-24 r)-19 (r-1)\right] ,\\ \mathcal {B}_{13}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -e^{6 \beta (t) } (r-1)-12 e^{8 \beta (t) } (r-1)+e^{10 \beta (t) } (20-8 r)\right. \\&\left. \quad +\, e^{2 \beta (t) } (12-24 r)-19 (r-1)\right] ,\\ \mathcal {B}_{14}&=\frac{1}{192} e^{-10 \beta (t) } \left[ -e^{6 \beta (t) } (r-1)-12 e^{2 \beta (t) } r+12 e^{10 \beta (t) } r+r-1\right] ,\\ \mathcal {B}_{15}&=-\frac{1}{192} e^{-10 \beta (t) } \left[ -17 e^{6 \beta (t) }-16 e^{8 \beta (t) }+16 e^{10 \beta (t) }+17\right] (r-1),\\ \mathcal {B}_{16}&=\frac{1}{192} e^{-10 \beta (t) } \left[ e^{6 \beta (t) } (r-1)-12 e^{2 \beta (t) } r+12 e^{10 \beta (t) } r-r+1\right] ,\\ \mathcal {B}_{17}&=\frac{1}{192} e^{-10 \beta (t) } \left[ e^{6 \beta (t) } (r-1)+12 e^{8 \beta (t) } (r-1)+e^{10 \beta (t) } (20-8 r)\right. \\&\left. \quad + \, e^{2 \beta (t) } (12-24 r)+19 (r-1)\right] ,\\ \mathcal {B}_{18}&=-\frac{1}{192} e^{-10 \beta (t) } \left[ 17 e^{6 \beta (t) }-16 e^{8 \beta (t) }+16 e^{10 \beta (t) }-17\right] (r-1),\\ \mathcal {B}_{19}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 12 e^{2 \beta (t) } r+36 e^{10 \beta (t) } r-e^{6 \beta (t) } (47 r+1)-r+1\right] ,\\ \mathcal {B}_{20}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 12 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)+4 e^{10 \beta (t) } (2 r+7)\right. \\&\left. \quad +\, e^{6 \beta (t) } (15-63 r)+19 (r-1)\right] ,\\ \mathcal {B}_{21}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 12 e^{2 \beta (t) } r+36 e^{10 \beta (t) } r+e^{6 \beta (t) } (47 r+1)+r-1\right] ,\\ \mathcal {B}_{22}&=\frac{1}{192} e^{-10 \beta (t) } \left[ 20 e^{8 \beta (t) } (r-1)+12 e^{2 \beta (t) } (2 r-1)+4 e^{10 \beta (t) } (2 r+7)\right. \\&\left. \quad +\, 3 e^{6 \beta (t) } (21 r-5)-19 (r-1)\right] . \end{aligned}$$

Finally, using Eq. (13), the density matrix for TQC configuration of three qubits under FG noise can be written as

$$\begin{aligned} \rho _{\textrm{TQC}}(t)=\left[ \begin{array}{cccccccc} \mathcal {C}_{1} &{} 0 &{} 0 &{}\mathcal {C}_{2} &{} 0 &{}\mathcal {C}_{2} &{}\mathcal {C}_{2} &{}\mathcal {C}_{3} \\ 0 &{}\mathcal {C}_{4} &{}\mathcal {C}_{5} &{} 0 &{}\mathcal {C}_{5} &{} 0 &{}\mathcal {C}_{6} &{}\mathcal {C}_{7} \\ 0 &{}\mathcal {C}_{5} &{}\mathcal {C}_{4} &{} 0 &{}\mathcal {C}_{5} &{}\mathcal {C}_{6} &{} 0 &{}\mathcal {C}_{7} \\ \mathcal {C}_{2} &{} 0 &{} 0 &{}\mathcal {C}_{8} &{}\mathcal {C}_{6} &{}\mathcal {C}_{9} &{}\mathcal {C}_{9} &{} 0 \\ 0 &{}\mathcal {C}_{5} &{}\mathcal {C}_{5} &{}\mathcal {C}_{6} &{}\mathcal {C}_{4} &{} 0 &{} 0 &{}\mathcal {C}_{7} \\ \mathcal {C}_{2} &{} 0 &{}\mathcal {C}_{6} &{}\mathcal {C}_{9} &{} 0 &{}\mathcal {C}_{8} &{}\mathcal {C}_{9} &{} 0 \\ \mathcal {C}_{2} &{}\mathcal {C}_{6} &{} 0 &{}\mathcal {C}_{9} &{} 0 &{}\mathcal {C}_{9} &{}\mathcal {C}_{8} &{} 0 \\ \mathcal {C}_{3} &{}\mathcal {C}_{7} &{}\mathcal {C}_{7} &{} 0 &{}\mathcal {C}_{7} &{} 0 &{} 0 &{} \mathcal {C}_{10} \\ \end{array} \right] \end{aligned}$$
(A.3)

where

$$\begin{aligned} \mathcal {C}_{1}&=\frac{1}{8} e^{-6 \beta (t) } \left[ e^{6 \beta (t) }-e^{4 \beta (t) } (r-1)+e^{2 \beta (t) } (4 r-1)+r-1\right] ,\\ \mathcal {C}_{2}&=-\frac{1}{12} e^{-6 \beta (t) } \left( e^{2 \beta (t) }-1\right) \left( e^{2 \beta (t) }+1\right) ^2 (r-1),\\ \mathcal {C}_{3}&=\frac{1}{8} \left( 3 e^{-4 \beta (t) }+1\right) r,\\ \mathcal {C}_{4}&=\frac{1}{24} e^{-6 \beta (t) } \left( e^{2 \beta (t) }+1\right) \left[ 3 e^{4 \beta (t) }-e^{2 \beta (t) } (r+2)-3 r+3\right] ,\\ \mathcal {C}_{5}&=-\frac{1}{12} e^{-6 \beta (t) } \left[ e^{2 \beta (t) }+e^{4 \beta (t) }+e^{6 \beta (t) }+1\right] (r-1),\\ \mathcal {C}_{6}&=\frac{1}{8} \left( 1-e^{-4 \beta (t) }\right) ,\\ \mathcal {C}_{7}&=-\frac{1}{12} e^{-6 \beta (t) } \left( e^{2 \beta (t) }-1\right) ^2 \left( e^{2 \beta (t) }+1\right) (r-1),\\ \mathcal {C}_{8}&=\frac{1}{24} e^{-6 \beta (t) } \left( e^{2 \beta (t) }-1\right) \left[ 3 e^{4 \beta (t) }+e^{2 \beta (t) } (r+2)-3 r+3\right] ,\\ \mathcal {C}_{9}&=-\frac{1}{12} e^{-6 \beta (t) } \left[ e^{2 \beta (t) }-e^{4 \beta (t) }+e^{6 \beta (t) }-1\right] (r-1),\\ \mathcal {C}_{10}&=\frac{1}{8} e^{-6 \beta (t) } \left[ e^{6 \beta (t) }+e^{4 \beta (t) } (r-1)+e^{2 \beta (t) } (4 r-1)-r+1\right] . \end{aligned}$$

Now, we provide the analytical results for entanglement witness and linear entropy for the dynamics of the physical model described in the above density matrices. For three non-interacting qubits initially created in a mixture state and assumed in SQC, DQC, and TQC couplings given in Eqs. (A.1), (A.2), and (A.3) under the impact of FG noise, we use Eqs. (1) and (2) to analyze entanglement witness and linear entropy. The analytical expressions are given as

$$\begin{aligned} E[\rho _{\textrm{SQC}}(t)]&=\frac{1}{32} e^{-18 \beta (t) } \left[ 6 e^{10 \beta (t) } \left( 5 r^2-4 r+1\right) \right. \nonumber \\&\left. \quad +\, 2 e^{18 \beta (t) } \left( 9 r^2-4 r-3\right) +7 e^{16 \beta (t) } (r-1)^2+9 (r-1)^2\right] , \end{aligned}$$
(A.4)
$$\begin{aligned} L[\rho _{\textrm{SQC}}(t)]&=1-\left\{ \frac{1}{32} e^{-36 \beta (t) } \left[ 7 e^{32 \beta (t) } (r-1)^2+6 e^{20 \beta (t) } (r (5 r-4)+1)\right. \right. \nonumber \\&\left. \left. \quad +\, 2 e^{36 \beta (t) } (r (9 r-4)+5)+9 (r-1)^2\right] \right\} , \end{aligned}$$
(A.5)

For the DQC configurations, the entanglement witness and linear entropy results are

$$\begin{aligned} E[\rho _{\textrm{DQC}}(t)]&=\frac{1}{576} e^{-10 \beta (t) } \left[ a+b+36 e^{2 \beta (t) } \left( 5 r^2-4 r+1\right) \right. \nonumber \\&\left. \quad +\, 124 e^{8 \beta (t) } (r-1)^2+163 (r-1)^2\right] , \end{aligned}$$
(A.6)
$$\begin{aligned} L[\rho _{\textrm{DQC}}(t)]&=1-\left\{ \frac{1}{576} e^{-20 \beta (t)} \left[ 124 e^{16 \beta (t) } (r-1)^2\right. \right. \nonumber \\&\left. \left. \quad +\, 36 e^{4 \beta (t) } (r (5 r-4)+1)+163 (r-1)^2+c + d\right] \right\} , \end{aligned}$$
(A.7)

where

$$\begin{aligned} a&=4 e^{10 \beta (t) } (55 r^2-44 r-29),&b&=3 e^{6 \beta (t) } (155 r^2-86 r+27),\\ c&=4 e^{20 \beta (t) } (55 r^2-44 r+43),&d&=3 e^{12 \beta (t) } (155 r^2-86 r+27). \end{aligned}$$

Similarly, for the TQC configurations, the analytical expressions of entanglement witness and linear entropy are as follows

$$\begin{aligned} E[\rho _{\textrm{TQC}}(t)]&=\frac{1}{24} e^{-6 \beta (t) } \left[ 5 e^{4 \beta (t) } (r-1)^2+e^{6 \beta (t) } (r (7 r-8)-5)\right. \nonumber \\&\left. \quad +\, e^{2\beta (t) } (r (29 r-16)+5)+7 (r-1)^2\right] , \end{aligned}$$
(A.8)
$$\begin{aligned} L[\rho _{\textrm{TQC}}(t)]&=1-\left\{ \frac{1}{24} e^{-12 \beta (t) } \left[ 5 e^{8 \beta (t) } (r-1)^2+e^{12 \beta (t) } (r (7 r-8)+7)\right. \right. \nonumber \\&\left. \left. \quad +\, e^{4 \beta (t) } (r (29 r-16)+5)+7 (r-1)^2\right] \right\} . \end{aligned}$$
(A.9)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahman, A.U., Haddadi, S., Javed, M. et al. Entanglement witness and linear entropy in an open system influenced by FG noise. Quantum Inf Process 21, 368 (2022). https://doi.org/10.1007/s11128-022-03720-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-022-03720-5

Keywords

Search

Navigation