Measurement-induced geometric measures of correlations based on the trace distance for two-qubit X states

Abstract

We apply the modified Brodutch and Modi method of constructing geometric measures of correlations to obtain analytical expressions for measurement-induced geometric classical and quantum correlations based on the trace distance for two-qubit X states. Moreover, we study continuity of the classical and quantum correlations for these states. In particular, we show that these correlations may not be continuous.

1 Introduction

In quantum information science, the problem of classification and quantification of correlations present in quantum systems has been extensively studied over the past few decades [1,2,3,4,5]. In this regard, the most substantial progress was achieved in the case of bipartite systems that have been studied initially in the entanglement-separability paradigm, formalized by Werner [6]. Under this paradigm, the correlations can be classified as either classical or quantum, where the latter ones are identified with entanglement that can be quantified by different entanglement measures [1].

However, due to the discovery that some quantum information processing tasks can be performed without entanglement [7,8,9,10,11,12,13,14], it has become clear that some separable states can have quantum correlations, other than entanglement, and therefore the entanglement-separability paradigm should be replaced by a new one.

The paradigm shift was triggered independently by Ollivier and Zurek [15] who introduced quantum discord as an information-theoretic measure of quantum correlations present in bipartite quantum systems and by Henderson and Vedral [16] who studied the problem of separation of classical and quantum correlations in such systems from an information-theoretic perspective. Under the information-theoretic paradigm, the problem of classification and quantification of correlations has been extensively studied [2, 4, 5], due to the discovery [17] that quantum discord may be the key resource in the deterministic quantum computation with one qubit (DQC1) [7]. It is worth emphasizing that both quantum entanglement and quantum discord have been also investigated in the framework of special and general relativity as well as quantum field theory [1, 2, 18] (for recent advances see, e.g., [19,20,21,22]).

Since quantum discord cannot be computed analytically even for arbitrary two-qubit states [2, 4, 5], an alternative information-theoretic approach to the problem of quantification of different types of correlations was proposed [23]. This approach is based on the idea that a distance from a given state to the closest state without the desired property is a measure of that property. The first measure of quantum correlations in which this idea has been implemented was geometric quantum discord [24], where the Schatten 2-norm was applied as the distance measure between a given state and the closest zero discord state. Since geometric quantum discord can be computed analytically for arbitrary two-qubit states [24], it has attracted considerable attention [2,3,4,5]. However, it was shown that geometric quantum discord based on the Schatten 2-norm cannot be regarded as a bona fide measure of quantum correlations [25] because of the lack of contractivity of this norm under trace-preserving quantum channels [26]. Moreover, it turned out that among all geometric quantum discords based on the Schatten p-norms [27] only the one based on the Schatten 1-norm is a bona fide measure of quantum correlations [26].

The problem with geometric quantum discord based on the Schatten 2-norm has emphasized the need for a general method of constructing bona fide measures of correlations under the information-theoretic paradigm.

Recently, Brodutch and Modi [28] proposed a method based on the idea that a measurement performed on one subsystem of a multipartite system in a given state, in general, may disturb the state of the system and this disturbance can be used to quantify correlations present in the system. According to this method, quantum correlations are quantified by a distance between a given state and the classical-quantum state emerging from a measurement performed on the considered state, where the measurement is chosen according to a specific strategy. Moreover, classical correlations are quantified by a distance between the classical-quantum state and the completely separable state resulting from the same measurement performed on the tensor product of the states of the individual subsystems. Furthermore, Brodutch and Modi [28] identified two strategies that provide bona fide measures of classical and quantum correlations that satisfy the following conditions: (i) product states have no correlations, (ii) all correlations are invariant under local unitary operations, (iii) all correlations are non-negative, and (iv) classical states have no quantum correlations. Moreover, Brodutch and Modi showed that the first strategy always provides continuous measures of quantum correlations, while the second one always provides continuous measures of classical correlations. An open problem, interesting from both theoretical and experimental points of view, is the continuity of measures of classical and quantum correlations provided by the first and the second strategy, respectively [28]. The lack of the continuity of measures of correlations would imply that probing these correlations in the laboratory would be extremely misleading, because a small uncertainty of the state of the system could cause a big difference in the amount of the correlations present in this system, as measured by these measures of correlations.

More recently, it was shown that the Brodutch and Modi method should be modified as in the case of measurement-induced geometric classical and quantum correlations based on the trace distance for two-qubit Bell diagonal states¹ one of two possible strategies results in the non-uniqueness of classical correlations [29]. Moreover, the modification of the Brodutch and Modi method was proposed to avoid the problem of non-unique results in the general case [29].

The purpose of this paper is twofold. First, we apply the modified Brodutch and Modi method to obtain measurement-induced geometric classical and quantum correlations based on the trace distance for two-qubit X states using two possible strategies of constructing bona fide measures of correlations. Second, we solve the open problem of continuity of measures of classical and quantum correlations provided by the first and the second strategy, respectively.

2 Measurement-induced geometric measures of correlations based on the trace distance and their continuity

In the framework of the modified Brodutch and Modi method, measurement-induced geometric classical and quantum correlations present in a multipartite state $\rho$ are quantified by:

$$\begin{aligned}&C(\rho ) = K[M(\rho ), M(\pi _{\rho })], \end{aligned}$$

(1)

$$\begin{aligned}&Q(\rho ) = K[\rho , M(\rho )], \end{aligned}$$

(2)

where $K[\eta , \tau ]$ is a non-negative real-valued function of states $\eta$ and $\tau$ that vanishes for $\eta = \tau$, $M(\rho )$ is the classical-quantum state emerging from a measurement M performed on $\rho$, $M(\pi _{\rho })$ is the completely separable state resulting from the same measurement M performed on $\pi _{\rho }$ being the tensor product of the states of the individual subsystems, and the measurement M is chosen according to one of the following strategies:

• M is a non-selective rank-1 projective measurement performed on one subsystem of the multipartite system in a state $\rho$, and M minimizes the quantum correlations $Q(\rho )$ [28], but if the classical correlations $C(\rho )$ are not uniquely determined by the minimization procedure, then the classical correlations $C(\rho )$ are additionally maximized over the all measurements M that minimize the quantum correlations $Q(\rho )$ [29],

• M is a non-selective rank-1 projective measurement performed on one subsystem of the multipartite system in a state $\rho$, and M maximizes the classical correlations $C(\rho )$ [28], but if the quantum correlations $Q(\rho )$ are not uniquely determined by the maximization procedure, then the quantum correlations $Q(\rho )$ are additionally minimized over the all measurements M that maximize the classical correlations $C(\rho )$ [29].

In the framework of this method, measurement-induced geometric classical and quantum correlations based on the trace distance are quantified by:

$$\begin{aligned}&C(\rho ) = d_{T}[M(\rho ), M(\pi _{\rho })],\end{aligned}$$

(3)

$$\begin{aligned}&Q(\rho ) = d_{T}[\rho , M(\rho )], \end{aligned}$$

(4)

with $d_{T}[\eta , \tau ] = || \eta - \tau ||_{1} = \text {Tr}[\sqrt{(\eta - \tau )^{\dagger }(\eta - \tau )}]$ being the trace distance between states $\eta$ and $\tau$ [30], adopted as a function $K[\eta , \tau ]$, and the measurement M is chosen according to one of the above-mentioned strategies.

In the computational basis $\{ |00\rangle , |01\rangle , |10\rangle , |11\rangle \}$, the density matrix of a two-qubit X state has the following form [31]:

$$\begin{aligned} \rho = \left( \begin{array}{cccc} \rho _{11} &{} 0 &{} 0 &{} \rho _{14} \\ 0 &{} \rho _{22} &{} \rho _{23} &{} 0 \\ 0 &{} \rho _{23}^{*} &{} \rho _{33} &{} 0 \\ \rho _{14}^{*} &{} 0 &{} 0 &{} \rho _{44} \end{array} \right) , \end{aligned}$$

(5)

where the normalization and the positive semidefiniteness of $\rho$ require $\sum _{i=1}^{4} \rho _{ii} = 1$ and $\rho _{11} \rho _{44} \ge |\rho _{14}|^{2}$, $\rho _{22} \rho _{33} \ge |\rho _{23}|^{2}$, respectively [32, 33]. Let us note that the antidiagonal elements of the density matrix (5) can always be brought into real non-negative numbers by local unitary transformations [32, 33], which preserve the correlations (3) and (4) [28]. Therefore, a two-qubit X state can be represented by [32]:

$$\begin{aligned} \rho = \dfrac{1}{4} \left( I \otimes I + \sum _{i = 1}^{3} c_{i}\, \sigma _{i} \otimes \sigma _{i} + c_{4}\, I \otimes \sigma _{3} + c_{5}\, \sigma _{3} \otimes I\right) , \end{aligned}$$

(6)

where I is the identity matrix, $\sigma _{i}$ are the Pauli matrices, and

$$\begin{aligned}&c_{1} = \text {Tr}[(\sigma _{1} \otimes \sigma _{1})\rho ] = 2 (\rho _{23} + \rho _{14}), \end{aligned}$$

(7a)

$$\begin{aligned}&c_{2} = \text {Tr}[(\sigma _{2} \otimes \sigma _{2})\rho ] = 2 (\rho _{23} - \rho _{14}), \end{aligned}$$

(7b)

$$\begin{aligned}&c_{3} = \text {Tr}[(\sigma _{3} \otimes \sigma _{3})\rho ] = 1 - 2 (\rho _{22} + \rho _{33}), \end{aligned}$$

(7c)

$$\begin{aligned}&c_{4} = \text {Tr}[(I \otimes \sigma _{3})\rho ] = 2 (\rho _{11} + \rho _{33}) - 1, \end{aligned}$$

(7d)

$$\begin{aligned}&c_{5} = \text {Tr}[(\sigma _{3} \otimes I)\rho ] = 2 (\rho _{11} + \rho _{22}) - 1. \end{aligned}$$

(7e)

In the Fano–Bloch representation (6), the positive semidefiniteness of $\rho$ requires [32]

$$\begin{aligned}&(1 + c_{3})^{2} \ge (c_{1} - c_{2})^{2} + (c_{4} + c_{5})^{2}, \end{aligned}$$

(8a)

$$\begin{aligned}&(1 - c_{3})^{2} \ge (c_{1} + c_{2})^{2} + (c_{4} - c_{5})^{2}, \end{aligned}$$

(8b)

with the coefficients (7) taking values in the interval $[-1, 1]$. The above inequalities describe a region of $\mathbb {R}^{5}$. Thus, there is a one-to-one correspondence between two-qubit X states and points within region (8).

It is worth mentioning here that two-qubit X states contain a few important classes of states, such as Bell diagonal states [34], maximally nonlocal mixed states [35] and maximally entangled mixed states [36].

Let us note that if the measurement M, described by a complete set of one-dimensional orthogonal projectors $\{ \Pi _{\pm } \}$, is performed on the first qubit of the two-qubit system in a X state, then the classical-quantum state $M(\rho )$ and the completely separable state $M(\pi _{\rho })$ have the form:

$$\begin{aligned}&M(\rho ) = \sum _{m = +, -} (\Pi _{m} \otimes I) \rho (\Pi _{m} \otimes I), \end{aligned}$$

(9)

$$\begin{aligned}&M(\pi _{\rho }) = \sum _{m = +, -} (\Pi _{m} \otimes I) (\rho _{A} \otimes \rho _{B}) (\Pi _{m} \otimes I), \end{aligned}$$

(10)

where $\Pi _{\pm } = \frac{1}{2} (I \pm \mathbf {n} \cdot \varvec{\sigma })$, $\mathbf {n} = (n_{1}, n_{2}, n_{3})$ is a real three-dimensional unit vector and $\varvec{\sigma } = (\sigma _{1}, \sigma _{2}, \sigma _{3})$.

In order to compute the correlations (3) and (4) for two-qubit X states, we first need to find the trace distance between states $M(\rho )$ and $M(\pi _{\rho })$ and then the trace distance between states $\rho$ and $M(\rho )$. One can show that in the case of two-qubit X states and the measurement M described by $\{ \Pi _{\pm } \}$ the trace distance between states $M(\rho )$ and $M(\pi _{\rho })$ is given by:

$$\begin{aligned} ||M(\rho ) - M(\pi _{\rho })||_{1} = \left( c_{1}^{2} n_{1}^{2} + c_{2}^{2} n_{2}^{2} + \left( c_{3} - c_{4} c_{5}\right) ^{2} n_{3}^{2}\right) ^{\frac{1}{2}}, \end{aligned}$$

(11)

while the trace distance between states $\rho$ and $M(\rho )$ is given by:

$$\begin{aligned} ||\rho - M(\rho )||_{1}&= \dfrac{1}{2} \left( c_{1}^{2} + c_{2}^{2} + c_{3}^{2} + c_{5}^{2} - c_{1}^{2} n_{1}^{2} - c_{2}^{2} n_{2}^{2} - c_{3}^{2} n_{3}^{2} - c_{5}^{2} n_{3}^{2}\right. \nonumber \\&\quad -\, 2 \left( c_{3}^{2} c_{5}^{2} + c_{2}^{2} c_{3}^{2} n_{1}^{2} + c_{1}^{2} c_{3}^{2} n_{2}^{2} + c_{1}^{2} c_{2}^{2} n_{3}^{2}\right. \nonumber \\&\quad \left. \left. -\, 2 c_{3}^{2} c_{5}^{2} n_{3}^{2} + c_{1}^{2} c_{5}^{2} n_{1}^{2} n_{3}^{2} + c_{2}^{2} c_{5}^{2} n_{2}^{2} n_{3}^{2} + c_{3}^{2} c_{5}^{2} n_{3}^{4}\right) ^{\frac{1}{2}}\right) ^{\frac{1}{2}} \nonumber \\&\quad +\, \dfrac{1}{2} \left( c_{1}^{2} + c_{2}^{2} + c_{3}^{2} + c_{5}^{2} - c_{1}^{2} n_{1}^{2} - c_{2}^{2} n_{2}^{2} - c_{3}^{2} n_{3}^{2} - c_{5}^{2} n_{3}^{2}\right. \nonumber \\&\quad +\, 2 \left( c_{3}^{2} c_{5}^{2} + c_{2}^{2} c_{3}^{2} n_{1}^{2} + c_{1}^{2} c_{3}^{2} n_{2}^{2} + c_{1}^{2} c_{2}^{2} n_{3}^{2}\right. \nonumber \\&\quad \left. \left. -\, 2 c_{3}^{2} c_{5}^{2} n_{3}^{2} + c_{1}^{2} c_{5}^{2} n_{1}^{2} n_{3}^{2} + c_{2}^{2} c_{5}^{2} n_{2}^{2} n_{3}^{2} + c_{3}^{2} c_{5}^{2} n_{3}^{4}\right) ^{\frac{1}{2}}\right) ^{\frac{1}{2}}. \end{aligned}$$

(12)

The analytical expressions for $||M(\rho ) - M(\pi _{\rho })||_{1}$ and $||\rho - M(\rho )||_{1}$ make it possible to obtain measurement-induced geometric classical and quantum correlations based on the trace distance for two-qubit X states under the two possible strategies of choosing the measurement M. In what follows, it is assumed without loss of generality that $c_{1}^{2} \ge c_{2}^{2}$ since the sign of $\rho _{14}$ in the density matrix (5) can always be changed by a local unitary transformation [32].

2.1 Strategy 1

In the framework of the first strategy, for a given two-qubit X state (6) we first identify all measurements M that minimize the quantum correlations (4) and then we use these measurements to compute the classical correlations (3). However, if the classical correlations are not uniquely determined by the minimization procedure, then they are additionally maximized over the all measurements that minimize the quantum correlations.² In other words, for a given point $(c_{1}, c_{2}, c_{3}, c_{4}, c_{5})$ of region (8) we first identify all unit vectors $(n_{1}, n_{2}, n_{3})$ that minimize $||\rho - M(\rho )||_{1}$ given by Eq. (12) and then we use these vectors to compute $||M(\rho ) - M(\pi _{\rho })||_{1}$ given by Eq. (11). However, if (11) is not uniquely determined by the minimization procedure, then it is additionally maximized over the all unit vectors that minimize (12).

It can be shown that under this strategy the following cases occur:

• 1. If $c_{1}^{2} = c_{2}^{2}$ and $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} < 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = |c_{3} - c_{4} c_{5}|, \end{aligned}$$

  (13a)
  $$\begin{aligned}&Q(\rho ) = |c_{1}|. \end{aligned}$$

  (13b)

• 2. If $c_{1}^{2} = c_{2}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} \ge 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 3. If $c_{1}^{2} = c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$ and $c_{5}^{2} = 0$, then all measurements M minimize (12) and uniquely determine (11). Therefore, in this case all measurements M are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 4. If $c_{1}^{2} = c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$ and $c_{5}^{2} = 0$, then all measurements M minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with $n_{1}^{2} + n_{2}^{2} = 1$ and $n_{3}^{2} = 0$ maximize (11). Therefore, in this case only measurements M with $n_{1}^{2} + n_{2}^{2} = 1$ and $n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = |c_{1}|,\end{aligned}$$

  (14a)
  $$\begin{aligned}&Q(\rho ) = |c_{1}|. \end{aligned}$$

  (14b)

• 5. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} < 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 6. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} < c_{3}^{2}$ and $c_{5}^{2} = 0$, then only measurements M with $n_{1}^{2} = 0$, $0 \le n_{2}^{2} \le (c_{2}^{2} - c_{1}^{2})/(c_{2}^{2} - c_{3}^{2} + c_{5}^{2})$ and $n_{3}^{2} = 1 - n_{2}^{2}$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ maximize (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 7. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} = 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 8. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$ and $c_{5}^{2} = 0$, then all measurements M minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ maximize (11). Therefore, in this case only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 9. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} < 0$, then only measurements M with $(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})/(c_{1}^{2} - c_{2}^{2}) \le n_{1}^{2} \le 1$, $n_{2}^{2} = 1 - n_{1}^{2}$ and $n_{3}^{2} = 0$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = |c_{1}|, \end{aligned}$$

  (15a)
  $$\begin{aligned}&Q(\rho ) = |c_{3}|. \end{aligned}$$

  (15b)

• 10. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} < 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ or $(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})/(c_{1}^{2} - c_{2}^{2}) \le n_{1}^{2} \le 1$, $n_{2}^{2} = 1 - n_{1}^{2}$ and $n_{3}^{2} = 0$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with:

  • $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ maximize (11) if $c_{1}^{2} < (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ maximize (11) if $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11) if $c_{1}^{2} > (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (14).

• 11. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} < c_{3}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} > 0$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} < 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 12. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} = 0$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (15).

• 13. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} = 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with:

  • $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ maximize (11) if $c_{1}^{2} < (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ maximize (11) if $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11) if $c_{1}^{2} > (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (14).

• 14. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} < c_{3}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} > 0$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} = 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$, $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$, $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 15. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{2}^{2} > c_{3}^{2}$ and $c_{5}^{2} = 0$, then only measurements M with $(c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2}) \le n_{1}^{2} \le 1$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = |c_{1}|, \end{aligned}$$

  (16a)
  $$\begin{aligned}&Q(\rho ) = |c_{2}|. \end{aligned}$$

  (16b)

• 16. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = \sqrt{ \frac{c_{1}^{2} \left( c_{1}^{2} - c_{2}^{2}\right) + \left( c_{3} - c_{4} c_{5}\right) ^{2} \left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) }{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}}, \end{aligned}$$

  (17a)
  $$\begin{aligned}&Q(\rho ) = \sqrt{\frac{c_{1}^{2} \left( c_{2}^{2} + c_{5}^{2}\right) - c_{2}^{2} c_{3}^{2}}{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}}. \end{aligned}$$

  (17b)

• 17. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$ and $c_{5}^{2} > 0$, then only measurements M with $0 \le n_{1}^{2} \le (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ minimize (12), but they do not uniquely determine (11). Thus, the additional maximization procedure is required. It turns out that among the all measurements M that minimize (12) only those with:

  • $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ maximize (11) if $c_{1}^{2} < (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $0 \le n_{1}^{2} \le (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ maximize (11) if $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $0 \le n_{1}^{2} \le (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ maximize (11) if $c_{1}^{2} > (c_{3} - c_{4} c_{5})^{2}$; therefore, in this case only measurements M with $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ are optimal, and the classical and quantum correlations are given by Eqs. (17).

• 18. If $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} < c_{3}^{2}$, $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} > 0$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$ and $c_{5}^{2} > 0$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) and uniquely determine (11). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

Let us note that the classical and quantum correlations are uniquely determined under the first strategy, despite the fact that for a wide class of two-qubit X states there is more than one optimal measurement M, which means that for those states the classical-quantum state $M(\rho )$ cannot be uniquely determined.

The above results regarding to measurement-induced geometric quantum correlations based on the trace distance for two-qubit X states can be summarized as follows:

• if $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, then

  $$\begin{aligned} Q(\rho ) = H\left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) \sqrt{\frac{c_{1}^{2} \left( c_{2}^{2} + c_{5}^{2}\right) - c_{2}^{2} c_{3}^{2}}{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}} + H\left( -\left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) \right) |c_{3}|, \end{aligned}$$

  (18a)

• and otherwise

  $$\begin{aligned} Q(\rho ) = |c_{1}|, \end{aligned}$$

  (18b)

where H(x) is the Heaviside step function with the half-maximum convention. This result coincides with that obtained in [37], where the trace distance geometric quantum discord for two-qubit X states was considered.³ Recently, measurement-induced geometric quantum correlations based on the trace distance were computed analytically for some specific classes of two-qudit states [39].

Moreover, the above results regarding to measurement-induced geometric classical correlations based on the trace distance for two-qubit X states can be summarized as follows:

• if $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{5}^{2} > 0$ or $c_{1}^{2} > c_{2}^{2}$, $c_{1}^{2} = c_{3}^{2}$, $c_{1}^{2} > (c_{3} - c_{4} c_{5})^{2}$, $c_{5}^{2} > 0$, then

  $$\begin{aligned} C(\rho )&= H\left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) \sqrt{\frac{c_{1}^{2} \left( c_{1}^{2} - c_{2}^{2}\right) + \left( c_{3} - c_{4} c_{5}\right) ^{2} \left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) }{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}} \nonumber \\&\quad +\, H\left( -\left( c_{2}^{2} - c_{3}^{2} + c_{5}^{2}\right) \right) |c_{1}|, \end{aligned}$$

  (19a)

• if $c_{1}^{2} \ge c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{5}^{2} = 0$, then

  $$\begin{aligned} C(\rho ) = |c_{1}|, \end{aligned}$$

  (19b)

• and otherwise

  $$\begin{aligned} C(\rho ) = |c_{3} - c_{4} c_{5}|. \end{aligned}$$

  (19c)

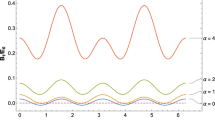
Let us note that the quantum correlations given by Eqs. (18) are continuous because the first strategy always provides continuous measures of quantum correlations [28]. Remarkably, it is not the case for the classical correlations given by Eqs. (19). As an illustrative example, let us consider two-qubit X states with $c_{1} = 1/3$, $c_{2} = 1/3$, $c_{3} = 1/4$, $c_{4} = 0$ and $-\sqrt{17}/12 \le c_{5} \le \sqrt{17}/12$. For this one-parameter class of X states the following cases occur:

• if $c_{5}^{2} = 0$, then only measurements M with $n_{1}^{2} + n_{2}^{2} = 1$ and $n_{3}^{2} = 0$ are optimal (see Case 4), and the classical correlations are given by Eq. (19b) (see Fig. 1),

• if $0 < c_{5}^{2} \le 17/144$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal (see Case 2), and the classical correlations are given by Eq. (19c) (see Fig. 1).

Thus, we see that the classical correlations cannot change continuously because the optimal measurements M do not change in a continuous way. Therefore, we have shown that, in general, measures of classical correlations provided by the modified Brodutch and Modi method under the first strategy may not be continuous. It is worth emphasizing that experimental investigation of classical correlations present in quantum systems by employing discontinuous measures of correlations may give misleading results. For example, if quantum state tomography is used to determine the state of the investigated system, then any small uncertainties could cause a big difference between the measured and actual classical correlations present in the system.

Fig. 1

The measurement-induced geometric classical correlations based on the trace distance for two-qubit X states with $c_{1} = 1/3$, $c_{2} = 1/3$, $c_{3} = 1/4$, $c_{4} = 0$ and $-\sqrt{17}/12 \le c_{5} \le \sqrt{17}/12$ (under the first strategy) (Color online)

2.2 Strategy 2

In the framework of the second strategy, for a given two-qubit X state (6) we first identify all measurements M that maximize the classical correlations (3) and then we use these measurements to compute the quantum correlations (4). However, if the quantum correlations are not uniquely determined by the maximization procedure, then they are additionally minimized over the all measurements that maximize the classical correlations. In other words, for a given point $(c_{1}, c_{2}, c_{3}, c_{4}, c_{5})$ of region (8) we first identify all unit vectors $(n_{1}, n_{2}, n_{3})$ that maximize $||M(\rho ) - M(\pi _{\rho })||_{1}$ given by Eq. (11) and then we use these vectors to compute $||\rho - M(\rho )||_{1}$ given by Eq. (12). However, if (12) is not uniquely determined by the maximization procedure, then it is additionally minimized over the all unit vectors that maximize (11).

It can be shown that under this strategy the following cases occur:

• 1. If $c_{1}^{2} = c_{2}^{2} = c_{3}^{2}$ and $c_{5}^{2} = 0$, then all measurements M maximize (11) and uniquely determine (12). Therefore, in this case all measurements M are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 2. If $c_{1}^{2} = c_{2}^{2} = (c_{3} - c_{4} c_{5})^{2}$ and $c_{5}^{2} > 0$, then all measurements M maximize (11), but they do not uniquely determine (12). Thus, the additional minimization procedure is required. It turns out that among the all measurements M that maximize (11) only those with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 3. If $c_{1}^{2} > c_{2}^{2} = (c_{3} - c_{4} c_{5})^{2}$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by:

  $$\begin{aligned}&C(\rho ) = |c_{1}|, \end{aligned}$$

  (20a)
  $$\begin{aligned}&Q(\rho ) = \text {Max}\left[ |c_{3}|, \sqrt{c_{2}^{2} + c_{5}^{2}} \right] . \end{aligned}$$

  (20b)

• 4. If $(c_{3} - c_{4} c_{5})^{2} > c_{1}^{2} = c_{2}^{2}$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 5. If $c_{1}^{2} = c_{2}^{2} > (c_{3} - c_{4} c_{5})^{2}$, then only measurements M with $n_{1}^{2} + n_{2}^{2} = 1$ and $n_{3}^{2} = 0$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} + n_{2}^{2} = 1$ and $n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (20).

• 6. If $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2} > c_{2}^{2}$, then only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ maximize (11), but they do not uniquely determine (12). Thus, the additional minimization procedure is required. It turns out that among the all measurements M that maximize (11) only those with:

  • $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ minimize (12) if (i) $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} \le 0$ and $c_{5}^{2} > 0$ or (ii) $c_{1}^{2} < c_{3}^{2}$ and $c_{1}^{2} - c_{3}^{2} + c_{5}^{2} > 0$; therefore, in these cases only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$ and $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ minimize (12) if (i) $c_{1}^{2} = c_{3}^{2}$ and $c_{5}^{2} = 0$ or (ii) $c_{1}^{2} = c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} \le 0$ and $c_{5}^{2} > 0$; therefore, in these cases only measurements M with $n_{1}^{2} + n_{3}^{2} = 1$ and $n_{2}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (13),

  • $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ minimize (12) if (i) $c_{1}^{2} = c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} = 0$ or (ii) $c_{1}^{2} > c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} < 0$; therefore, in these cases only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (20),

  • $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ minimize (12) if $c_{1}^{2} > c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$; therefore, in this case only measurements M with $n_{1}^{2} = (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ are optimal, and the classical and quantum correlations are given by:

    $$\begin{aligned}&C(\rho ) = |c_{1}|, \end{aligned}$$

    (21a)
    $$\begin{aligned}&Q(\rho ) = \sqrt{\frac{c_{1}^{2} \left( c_{2}^{2} + c_{5}^{2}\right) - c_{2}^{2} c_{3}^{2}}{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}}, \end{aligned}$$

    (21b)

  • $0 \le n_{1}^{2} \le (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ minimize (12) if $c_{1}^{2} = c_{3}^{2}$ and $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$; therefore, in this case only measurements M with $0 \le n_{1}^{2} \le (c_{1}^{2} - c_{2}^{2})/(c_{1}^{2} - c_{3}^{2} + c_{5}^{2})$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 1 - n_{1}^{2}$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

• 7. If $c_{1}^{2}> c_{2}^{2} > (c_{3} - c_{4} c_{5})^{2}$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (20).

• 8. If $c_{1}^{2}> (c_{3} - c_{4} c_{5})^{2} > c_{2}^{2}$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal, and the classical and quantum correlations are given by Eqs. (20).

• 9. If $(c_{3} - c_{4} c_{5})^{2}> c_{1}^{2} > c_{2}^{2}$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$, $n_{3}^{2} = 1$ maximize (11) and uniquely determine (12). Therefore, in this case only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$, $n_{3}^{2} = 1$ are optimal, and the classical and quantum correlations are given by Eqs. (13).

Let us note that the classical and quantum correlations are uniquely determined under the second strategy, despite the fact that for a wide class of two-qubit X states there is more than one optimal measurement M, which means that for those states the classical-quantum state $M(\rho )$ cannot be uniquely determined.

Recently, measurement-induced geometric classical and quantum correlations based on the Bures distance, the trace distance and the Hellinger distance for two-qubit Bell diagonal states⁴ under the two possible strategies of choosing the measurement M were studied [29, 40]. Remarkably, it turns out that for a given two-qubit Bell diagonal state the optimal measurements M are exactly the same for measurement-induced geometric classical and quantum correlations based on the Bures distance, the trace distance and the Hellinger distance under the both strategies of choosing the measurement M.

The above results regarding to measurement-induced geometric quantum correlations based on the trace distance for two-qubit X states can be summarized as follows:

• if $c_{1}^{2} \ge c_{2}^{2} > (c_{3} - c_{4} c_{5})^{2}$ or $c_{1}^{2} > (c_{3} - c_{4} c_{5})^{2} \ge c_{2}^{2}$ or $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} < 0$, then

  $$\begin{aligned} Q(\rho ) = \text {Max}\left[ |c_{3}|, \sqrt{c_{2}^{2} + c_{5}^{2}} \right] , \end{aligned}$$

  (22a)

• if $c_{1}^{2} = (c_{3} - c_{4} c_{5})^{2} > c_{2}^{2}$, $c_{1}^{2} > c_{3}^{2}$, $c_{2}^{2} - c_{3}^{2} + c_{5}^{2} > 0$, then

  $$\begin{aligned} Q(\rho ) = \sqrt{\frac{c_{1}^{2} \left( c_{2}^{2} + c_{5}^{2}\right) - c_{2}^{2} c_{3}^{2}}{c_{1}^{2} - c_{3}^{2} + c_{5}^{2}}}, \end{aligned}$$

  (22b)

• and otherwise

  $$\begin{aligned} Q(\rho ) = |c_{1}|. \end{aligned}$$

  (22c)

Moreover, the above results regarding to measurement-induced geometric classical correlations based on the trace distance for two-qubit X states can be summarized as follows:

$$\begin{aligned} C(\rho ) = \text {Max}\left[ |c_{1}|, |c_{2}|, |c_{3} - c_{4} c_{5}| \right] . \end{aligned}$$

(23)

Fig. 2

The measurement-induced geometric quantum correlations based on the trace distance for two-qubit X states with $c_{1} = 1/5$, $c_{2} = 0$, $c_{3} = 0$, $c_{4} = 3/5$ and $-(2\sqrt{6} - 3)/5 \le c_{5} \le (2\sqrt{6} - 3)/5$ (under the second strategy) (Color online)

Let us note that the classical correlations given by Eq. (23) are continuous because the second strategy always provides continuous measures of quantum correlations [28]. Remarkably, it is not the case for the quantum correlations given by Eqs. (22). As an illustrative example, let us consider two-qubit X states with $c_{1} = 1/5$, $c_{2} = 0$, $c_{3} = 0$, $c_{4} = 3/5$ and $-(2\sqrt{6} - 3)/5 \le c_{5} \le (2\sqrt{6} - 3)/5$. For this one-parameter class of X states the following cases occur:

• if $c_{5}^{2} = 0$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal (see Case 3), and the quantum correlations are given by Eq. (22a) (see Fig. 2),

• if $0< c_{5}^{2} < 1/9$, then only measurements M with $n_{1}^{2} = 1$ and $n_{2}^{2} = n_{3}^{2} = 0$ are optimal (see Case 8), and the quantum correlations are given by Eq. (22a) (see Fig. 2),

• if $c_{5}^{2} = 1/9$, then only measurements M with $n_{1}^{2} = 9/34$, $n_{2}^{2} = 0$ and $n_{3}^{2} = 25/34$ are optimal (see the penultimate item of Case 6), and the quantum correlations are given by Eq. (22b) (see Fig. 2),

• if $1/9 < c_{5}^{2} \le (33 - 12\sqrt{6})/25$, then only measurements M with $n_{1}^{2} = n_{2}^{2} = 0$, $n_{3}^{2} = 1$ are optimal (see Case 9), and the quantum correlations are given by Eq. (22c) (see Fig. 2).

Thus, we see that quantum correlations cannot change continuously because the optimal measurements M do not change in a continuous way. Therefore, we have shown that, in general, measures of quantum correlations provided by the modified Brodutch and Modi method under the second strategy may not be continuous. It is worth emphasizing that experimental investigation of quantum correlations present in quantum systems by employing discontinuous measures of correlations may give misleading results.

3 Conclusion

We have applied the modified Brodutch and Modi method to obtain analytical expressions for measurement-induced geometric classical and quantum correlations based on the trace distance for two-qubit X states using two possible strategies of constructing bona fide measures of correlations. Moreover, we have addressed the problem of continuity of measures of classical and quantum correlations provided by this method under the first and the second strategy, respectively. In particular, we have shown that, in general, these measures of correlations may not be continuous, contrary to measures of quantum and classical correlations provided by the modified Brodutch and Modi method under the first and the second strategy, respectively.