Performance of quantum cloning and deleting machines over coherence

Abstract

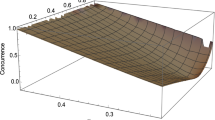
Coherence, being at the heart of interference phenomena, is found to be an useful resource in quantum information theory. Here we want to understand quantum coherence under the combination of two fundamentally dual processes, viz., cloning and deleting. We found the role of quantum cloning and deletion machines with the consumption and generation of quantum coherence. We establish cloning as a cohering process and deletion as a decohering process. Fidelity of the process will be shown to have connection with coherence generation and consumption of the processes.

Appendix A: Explicit expressions

Explicit expression of the coefficients of the cloned state $\rho _{ab}^{\mathrm{clone}}$ given in Eq. (8):

$$\begin{aligned} p_{00,00}= & {} \alpha ^2\hat{a}^2+\beta ^2\tilde{c}^2+\alpha \beta (\hat{a} \tilde{c}^*\langle \tilde{C}|A\rangle +\hat{a}^*\tilde{c}\langle A|\tilde{C}\rangle ) =\langle u_1|u_1\rangle \nonumber \\ p_{01,01}= & {} \alpha ^2b_1^2+\beta ^2\tilde{b_2}^2+\alpha \beta (b_1\tilde{b_2}^* \langle \tilde{B_2}|B_1\rangle +b_1^*\tilde{b_2}\langle B_1|\tilde{B_2}\rangle ) =\langle v_1|v_1\rangle \nonumber \\ p_{10,10}= & {} \alpha ^2b_2^2+\beta ^2\tilde{b_1}^2+\alpha \beta (b_2\tilde{b_1}^* \langle \tilde{B_1}|B_2\rangle +b_2^*\tilde{b_1}\langle B_2|\tilde{B_1}\rangle ) =\langle v_2|v_2\rangle \nonumber \\ p_{11,11}= & {} \alpha ^2c^2+\beta ^2\tilde{\hat{a}}^2+\alpha \beta (c\tilde{\hat{a}}^* \langle \tilde{A}|C\rangle +c^*\tilde{\hat{a}}\langle C|\tilde{A}\rangle ) =\langle u_2|u_2\rangle \nonumber \\ p_{00,01}= & {} p^*_{01,00}=\alpha ^2\hat{a}b_1^*\langle B_1|A\rangle +\beta ^2 \tilde{b_2}^*\tilde{c}\langle \tilde{B_2}|\tilde{C}\rangle +\alpha \beta (\hat{a}\tilde{b_2}^*\langle \tilde{B_2}|A\rangle +b_1^*\tilde{c}\langle B_1 |\tilde{C}\rangle )\nonumber \\= & {} \langle v_1|u_1\rangle \nonumber \\ p_{00,10}= & {} p^*_{10,00}=\alpha ^2\hat{a}b_2^*\langle B_2|A\rangle +\beta ^2 \tilde{b_1}^*\tilde{c}\langle \tilde{B_1}|\tilde{C}\rangle +\alpha \beta (\hat{a}\tilde{b_1}^*\langle \tilde{B_1}|A\rangle +b_2^*\tilde{c}\langle B_2|\tilde{C}\rangle )\nonumber \\= & {} \langle v_2|u_1\rangle \\ p_{00,11}= & {} p^*_{11,00}=\alpha ^2\hat{a}c^*\langle C|A\rangle +\beta ^2\tilde{\hat{a}}^*\tilde{c}\langle \tilde{A}|\tilde{C}\rangle +\alpha \beta (\hat{a}\tilde{\hat{a}}^*\langle \tilde{A}|A\rangle +c^*\tilde{c}\langle C|\tilde{C} \rangle )\nonumber \\= & {} \langle u_2|u_1\rangle \nonumber \\ p_{01,10}= & {} p^*_{10,01}=\alpha ^2b_1b_2^*\langle B_2|B_1\rangle +\beta ^2 \tilde{b_1}^*\tilde{b_2}\langle \tilde{B_1}|\tilde{B_2}\rangle +\alpha \beta (b_1\tilde{b_1}^*\langle \tilde{B_1}|B_1\rangle \nonumber \\&\quad +\,b_2^*\tilde{b_2}\langle B_2|\tilde{B_2} \rangle )=\langle v_2|v_1\rangle \nonumber \\ p_{01,11}= & {} p^*_{11,01}=\alpha ^2b_1c^*\langle C|B_1\rangle +\beta ^2\tilde{\hat{a}}^*\tilde{b_2}\langle \tilde{A}|\tilde{B_2}\rangle +\alpha \beta (b_1 \tilde{\hat{a}}^*\langle \tilde{A}|B_1\rangle \nonumber \\&\quad +\,c^*\tilde{b_2}\langle C|\tilde{B_2} \rangle )=\langle u_2|v_1\rangle \nonumber \\ p_{10,11}= & {} p^*_{11,10}=\alpha ^2b_2c^*\langle C|B_2\rangle +\beta ^2\tilde{\hat{a}}^*\tilde{b_1}\langle \tilde{A}|\tilde{B_1}\rangle +\alpha \beta (b_2 \tilde{\hat{a}}^*\langle \tilde{A}|B_2\rangle \nonumber \\&\quad +\,c^*\tilde{b_1}\langle C|\tilde{B_1} \rangle )=\langle u_2|v_2\rangle \nonumber \end{aligned}$$

(A1)

where $|u_1\rangle =\alpha \hat{a}|A\rangle +\beta \tilde{c}|\tilde{C}\rangle$, $|u_2\rangle =\alpha c|C\rangle +\beta \tilde{\hat{a}}|\tilde{A}\rangle$, $|v_1\rangle =\alpha b_1|B_1\rangle +\beta \tilde{b_2}|\tilde{B_2}\rangle$, $|v_2\rangle =\alpha b_2|B_2\rangle +\beta \tilde{b_1}|\tilde{B_1}\rangle$

Explicit expression of the coefficients of the state $\rho _{ab}^{c\rightarrow d}$ given in Eq. (14):

$$\begin{aligned} \begin{aligned} r_{00,00}&=\alpha ^2\hat{a}^2+\beta ^2\tilde{c}^2+\alpha \beta (\hat{a}\tilde{c}^*\langle A_1|A_0\rangle +\hat{a}^*\tilde{c}\langle A_0|A_1\rangle )\\ r_{01,01}&=\alpha ^2b_1^2+\beta ^2\tilde{b_2}^2+\alpha \beta (b_1 \tilde{b_2}^*\langle \tilde{B_2}|B_1\rangle +b_1^*\tilde{b_2}\langle B_1 |\tilde{B_2}\rangle )\\ r_{10,10}&=\alpha ^2(b_2^2+c^2+b_2c^*\langle A_3|B_2\rangle +b_2^*c\langle B_2|A_3\rangle )+\beta ^2(\tilde{\hat{a}}^2+\tilde{b_1}^2\\&\quad +\,\tilde{\hat{a}}^*\tilde{b_1}\langle A_2|\tilde{B_1}\rangle +\tilde{\hat{a}} \tilde{b_1}^*\langle \tilde{B_1}|A_2\rangle )\\&\quad +\,\alpha \beta (b_2\tilde{\hat{a}}^*\langle A_2|B_2\rangle +b_2^*\tilde{\hat{a}} \langle B_2|A_2\rangle +b_2\tilde{b_1}^*\langle \tilde{B_1}|B_2\rangle +b_2^*\tilde{b_1}\langle B_2|\tilde{B_1}\rangle \\&\quad +\,c^*\tilde{\hat{a}}\langle A_3|A_2\rangle +c\tilde{\hat{a}}^*\langle A_2|A_3\rangle +c^*\tilde{b_1} \langle A_3|\tilde{B_1}\rangle +c\tilde{b_1}^*\langle \tilde{B_1}|A_3\rangle )\\ r_{00,01}&=r^*_{01,00}=\alpha ^2\hat{a}b_1^*\langle B_1|A_0\rangle +\beta ^2 \tilde{b_2}^*\tilde{c}\langle \tilde{B_2}|A_1\rangle +\alpha \beta (\hat{a} \tilde{b_2}^*\langle \tilde{B_2}|A_0\rangle \\&\quad +\,b_1^*\tilde{c}\langle B_1|A_1\rangle )\\ r_{00,10}&=r^*_{10,00}=\alpha ^2(\hat{a}b_2^*\langle B_2|A_0\rangle +\hat{a} c^*\langle A_3|A_0\rangle )+\beta ^2(\tilde{b_1}^*\tilde{c}\langle \tilde{B_1} |A_1\rangle +\tilde{\hat{a}}^*\tilde{c}\langle \tilde{A_2}|A_1\rangle )\\&\quad +\,\alpha \beta (\hat{a}\tilde{\hat{a}}^*\langle A_1|A_0\rangle +\hat{a} \tilde{b_1}^*\langle \tilde{B_1}|A_0\rangle +\hat{a}^*\tilde{c}\langle A_0|A_1 \rangle +b_2^*\tilde{c}\langle B_2|A_1\rangle )\\ r_{01,10}&=r^*_{10,01}=\alpha ^2(b_1b_2^*\langle B_2|B_1\rangle +b_1c^* \langle A_3|B_2\rangle )+\beta ^2(\tilde{b_1}^*\tilde{b_2}\langle \tilde{B_1} |\tilde{B_2}\rangle \\&\quad +\,\tilde{\hat{a}}^*\tilde{b_2}\langle A_2|\tilde{B_2}\rangle )\\&\quad +\,\alpha \beta (b_1\tilde{\hat{a}}^*\langle A_2|B_1\rangle +b_1\tilde{b_1}^* \langle \tilde{B_1}|B_1\rangle +b_2^*\tilde{b_2}\langle B_2|\tilde{B_2}\rangle +c^*\tilde{b_2}\langle A_3|\tilde{B_2}\rangle )\\ \end{aligned} \end{aligned}$$

(A2)

Explicit expression of the coefficients of the state $\rho _{aa'}^{d\rightarrow c}$ given in Eq. (23):

$$\begin{aligned}&m_{00,00}=\alpha ^2\hat{a}^2+\beta ^2\tilde{c}^2\nonumber \\&m_{01,01}=\alpha ^2b_1^2+\beta ^2\tilde{b_2}^2\nonumber \\&m_{10,10}=\alpha ^2b_2^2+\beta ^2\tilde{b_1}^2\nonumber \\&m_{11,11}=\alpha ^2c^2+\beta ^2\tilde{\hat{a}}^2\nonumber \\&m_{00,01}=m^*_{01,00}=\alpha ^2\hat{a}b_1^*\langle B_1|A\rangle +\beta ^2\tilde{b_2}^*\tilde{c}\langle \tilde{B_2}|\tilde{C}\rangle \nonumber \\&m_{00,10}=m^*_{10,00}=\alpha ^2\hat{a}b_2^*\langle B_2|A\rangle +\beta ^2\tilde{b_1}^*\tilde{c}\langle \tilde{B_1}|\tilde{C}\rangle \nonumber \\&m_{00,11}=m^*_{11,00}=\alpha ^2\hat{a}c^*\langle C|A\rangle +\beta ^2\tilde{\hat{a}}^*\tilde{c}\langle \tilde{A}|\tilde{C}\rangle \nonumber \\&m_{01,10}=m^*_{10,01}=\alpha ^2b_1b_2^*\langle B_2|B_1\rangle +\beta ^2 \tilde{b_1}^*\tilde{b_2}\langle \tilde{B_1}|\tilde{B_2}\rangle \nonumber \\&m_{01,11}=m^*_{11,01}=\alpha ^2b_1c^*\langle C|B_1\rangle +\beta ^2 \tilde{\hat{a}}^*\tilde{b_2}\langle \tilde{A}|\tilde{B_2}\rangle \nonumber \\&m_{10,11}=m^*_{11,10}=\alpha ^2b_2c^*\langle C|B_2\rangle +\beta ^2 \tilde{\hat{a}}^*\tilde{b_1}\langle \tilde{A}|\tilde{B_1}\rangle \end{aligned}$$

(A3)

Explicit expression of the coefficients of the state $\rho _{bb'}^{d\rightarrow c}$ given in Eq. (23) are same as $m_i$’s, just replacing $\alpha ^2$ by $1-\alpha ^2\beta ^2$ and $\beta ^2$ by $\alpha ^2\beta ^2$ in Eq. (A3).