Teleportation-based continuous variable quantum cryptography

Abstract

We present a continuous variable (CV) quantum key distribution (QKD) scheme based on the CV quantum teleportation of coherent states that yields a raw secret key made up of discrete variables for both Alice and Bob. This protocol preserves the efficient detection schemes of current CV technology (no single-photon detection techniques) and, at the same time, has efficient error correction and privacy amplification schemes due to the binary modulation of the key. We show that for a certain type of incoherent attack, it is secure for almost any value of the transmittance of the optical line used by Alice to share entangled two-mode squeezed states with Bob (no 3 dB or 50% loss limitation characteristic of beam splitting attacks). The present CVQKD protocol works deterministically (no postselection needed) with efficient direct reconciliation techniques (no reverse reconciliation) in order to generate a secure key and beyond the 50% loss case at the incoherent attack level.

Appendices

Appendix 1: The modified CV teleportation protocol

A key ingredient to the present scheme is the CV teleportation protocol [51,52,53] adapted to the case where Alice and Bob have a complete knowledge of the pool of possible states to be teleported [57]. With such a knowledge, Alice and Bob can greatly improve the fidelity between the teleported state with Bob and Alice’s input by changing certain parameters of the original proposal. Our goal in this section is to review in a self-contained way this modified CV teleportation protocol, following closely the presentation given in [57].

Let $\hat{x}_k=(\hat{a}_k+\hat{a}_k^\dagger )/2$ and $\hat{p}_k=(\hat{a}_k-\hat{a}_k^\dagger )/2i$ be the position and momentum quadratures of mode k, respectively, where $\hat{a}_k$ and $\hat{a}_k^\dagger$ are the annihilation and creation operators with commutation relation $[\hat{a}_k,\hat{a}_k^\dagger ]=1$.

Any input state with Alice can be expressed in the position basis as

$$\begin{aligned} |\varphi \rangle = \int dx_1\varphi (x_1)|x_1\rangle , \end{aligned}$$

(8)

where the integral covers the entire real line and $\varphi (x_1)= \langle x_1 | \varphi \rangle$. The entangled two-mode squeezed state shared between Alice and Bob can also be expressed in the position basis,

$$\begin{aligned} |\psi _r\rangle = \int dx_2 dx_3 \psi _r(x_2, x_3) |x_2, x_3 \rangle , \end{aligned}$$

(9)

with $\psi _r(x_2,x_3)= \langle x_2, x_3 | \psi _r \rangle$ and $|x_2, x_3 \rangle = |x_2\rangle \otimes |x_3 \rangle$. Here the first two modes/kets are with Alice and the third one with Bob. Using Eqs. (8) and (9), the initial state describing all modes before the teleportation is as follows:

$$\begin{aligned} |\varPsi \rangle= & {} |\varphi \rangle \otimes |\psi _r\rangle =\int dx_1 dx_2 dx_3 \varphi (x_1) \psi _r(x_2,x_3)|x_1,x_2,x_3\rangle . \end{aligned}$$

(10)

The teleportation begins sending mode 1 (input state) and mode 2 (Alice’s share of the entangled state) into a BS with transmittance $\cos ^2\theta$ (see Fig. 1). If $\hat{B}_{12}(\cos ^2\theta )$ is the operator representing the action of the BS in the position basis, we have [36, 37]

$$\begin{aligned} \hat{B}_{12}(\cos ^2\theta ) |x_1, x_2 \rangle = |x_1 \sin \theta + x_2 \cos \theta , x_1 \cos \theta - x_2 \sin \theta \rangle . \end{aligned}$$

(11)

Inserting Eq. (11) into (10) and changing variables such that $x_v = x_1 \sin \theta + x_2 \cos \theta$ and $x_u =x_1 \cos \theta - x_2 \sin \theta$, we get

$$\begin{aligned} |\varPsi ' \rangle= & {} \int dx_v dx_u dx_3 \varphi (x_v\sin \theta + x_u\cos \theta )\nonumber \\&\times \psi _r(x_v\cos \theta - x_u\sin \theta ,x_3)|x_v,x_u,x_3\rangle \end{aligned}$$

(12)

for the total state after modes 1 and 2 go through the BS.

In the next step, Alice measures the momentum and position quadratures of modes v and u, respectively. Since Alice will project mode v onto the momentum basis, it is convenient to rewrite Eq. (12) using the Fourier transformation relating the position and momentum basis,

$$\begin{aligned} |x_v \rangle = \frac{1}{\sqrt{\pi }} \int dp_v \hbox {e}^{- 2i x_v p_v} |p_v\rangle . \end{aligned}$$

(13)

This leads to

$$\begin{aligned} |\varPsi ' \rangle= & {} \frac{1}{\sqrt{\pi }}\int dp_v dx_v dx_u dx_3 \varphi (x_v\sin \theta + x_u\cos \theta ) \nonumber \\&\times \psi _r(x_v\cos \theta - x_u\sin \theta ,x_3)\hbox {e}^{- 2i x_v p_v}|p_v,x_u,x_3\rangle . \nonumber \\ \end{aligned}$$

(14)

Let us assume Alice obtains for the momentum of mode v and for the position of mode u the values $\tilde{p}_v$ and $\tilde{x}_u$. Thus, the state after the measurement is

$$\begin{aligned} |\varPsi ''\rangle =\hat{P}_{\tilde{p}_v,\tilde{x}_u}|\varPsi '\rangle / \sqrt{\mathbb {p}(\tilde{p}_v,\tilde{x}_u)}, \end{aligned}$$

where $\hat{P}_{\tilde{p}_v,\tilde{x}_u}= |\tilde{p}_v,\tilde{x}_u\rangle \langle \tilde{p}_v,\tilde{x}_u| \otimes \mathbb {1}_{3}$ is the von Neumann projector describing the measurements. Here $\mathbb {1}_3$ is the identity operator acting on mode 3 and $\mathbb {p}(\tilde{p}_v,\tilde{x}_u)=\mathrm{tr}\; (|\varPsi '\rangle \langle \varPsi '|\hat{P}_{\tilde{p}_v,\tilde{x}_u})$ is the probability of measuring momentum $\tilde{p}_v$ and position $\tilde{x}_u$, with $\mathrm{tr}\;$ denoting the total trace. Specifying to the position basis and using that $\langle p_v|\tilde{p}_v\rangle =\delta (p_v-\tilde{p}_v)$ and $\langle x_u|\tilde{x}_u\rangle =\delta (x_u-\tilde{x}_u)$ we have

$$\begin{aligned} |\varPsi '' \rangle = |\tilde{p}_v,\tilde{x}_u\rangle \otimes |\chi '\rangle , \end{aligned}$$

(15)

where Bob’s state is

$$\begin{aligned} |\chi ' \rangle= & {} \frac{1}{\sqrt{\pi \mathbb {p}(\tilde{p}_v,\tilde{x}_u)}}\int dx_v dx_3 \hbox {e}^{- 2i x_v \tilde{p}_v} \varphi (x_v\sin \theta + \tilde{x}_u\cos \theta ) \nonumber \\&\times \psi _r(x_v\cos \theta - \tilde{x}_u\sin \theta ,x_3) |x_3\rangle . \end{aligned}$$

(16)

Here

$$\begin{aligned} \mathbb {p}(\tilde{p}_v,\tilde{x}_u) = \int dx_3 |\varPsi '(\tilde{p}_v,\tilde{x}_u,x_3)|^2 \end{aligned}$$

(17)

and $\varPsi '(\tilde{p}_v,\tilde{x}_u,x_3)=\langle \tilde{p}_v,\tilde{x}_u,x_3| \varPsi '\rangle$ such that

$$\begin{aligned} \varPsi '(\tilde{p}_v,\tilde{x}_u,x_3)= & {} \frac{1}{\sqrt{\pi }}\int dx_v \varphi (x_v\sin \theta + \tilde{x}_u\cos \theta ) \nonumber \\&\times \psi _r(x_v\cos \theta - \tilde{x}_u\sin \theta ,x_3)\hbox {e}^{- 2i x_v \tilde{p}_v}, \end{aligned}$$

(18)

where Eq. (18) was obtained using (14).

Via a classical channel, Alice sends to Bob her measurement results, allowing Bob to displace his mode quadratures as follows, $x_3 \rightarrow x_3 + g_u\tilde{x}_u$ and $p_3 \rightarrow p_3 + g_v\tilde{p}_v$. Mathematically this corresponds to the application of the displacement operator $\hat{D}(\lambda )=\hbox {e}^{\lambda \hat{a}^\dagger -\lambda ^*\hat{a}}= \hbox {e}^{-2iRe[\lambda ]\hat{p}+2iIm[\lambda ]\hat{x}}$, with $\lambda = g_u\tilde{x}_u + ig_v\tilde{p}_v$ and $\,^*$ denoting the complex conjugation. Since $\hat{x}$ and $\hat{p}$ commute with their commutator Glauber’s formula applies, giving $\hat{D}(\lambda )=\hbox {e}^{iRe[\lambda ]Im[\lambda ]}\hbox {e}^{-2iRe[\lambda ]\hat{p}}\hbox {e}^{2iIm[\lambda ]\hat{x}}$ and finally

$$\begin{aligned} \hat{D}(g_u\tilde{x}_u + ig_v\tilde{p}_v)|x_3\rangle = \hbox {e}^{ig_ug_v\tilde{x}_u\tilde{p}_v}\hbox {e}^{2ig_v\tilde{p}_vx_3} |x_3 + g_u\tilde{x}_u\rangle . \end{aligned}$$

(19)

Bob’s state after the displacement, $|\chi \rangle =\hat{D}(g_u\tilde{x}_u + ig_v\tilde{p}_v)|\chi '\rangle$, can be written as follows if we use Eq. (19) and change variable such that $x_3 \rightarrow x_3 - g_u\tilde{x}_u$,

$$\begin{aligned} |\chi \rangle =\int dx_3 \chi (x_3) |x_3\rangle , \end{aligned}$$

(20)

with

$$\begin{aligned} \chi (x_3)= & {} \frac{\hbox {e}^{-ig_ug_v\tilde{x}_u\tilde{p}_v}}{\sqrt{\pi \mathbb {p}(\tilde{p}_v,\tilde{x}_u)}} \int dx_v\varphi (x_v\sin \theta + \tilde{x}_u\cos \theta ) \nonumber \\&\times \psi _r(x_v\cos \theta - \tilde{x}_u\sin \theta ,x_3-g_u\tilde{x}_u) \hbox {e}^{- 2i (x_v -g_vx_3)\tilde{p}_v}. \end{aligned}$$

(21)

In order to estimate after a single run of the protocol the closeness of Bob’s state, $\hat{\rho }_{\mathrm{B}}=|\chi \rangle \langle \chi |$, with the original one at Alice’s, $\rho _{\mathrm{input}}=|\varphi \rangle \langle \varphi |$, we use the fidelity

$$\begin{aligned} F=\langle \varphi | \hat{\rho }_{\mathrm{B}} | \varphi \rangle = \int dx_3'dx_3 \varphi ^*(x_3')\chi (x_3')\chi ^*(x_3)\varphi (x_3). \end{aligned}$$

(22)

In general, F depends on the input state $|\varphi \rangle$, the measurement outcomes of Alice ($\tilde{x}_u$ and $\tilde{p}_v$), the squeezing r of the entangled two-mode squeezed state, $\theta$, $g_u$, and $g_v$. Also, F achieves its highest value ($F=1$) if we have a flawless teleportation ($\hat{\rho }_{\mathrm{B}} = \hat{\rho }_{\mathrm{input}}$) and its minimal one ($F=0$) if the output is orthogonal to the input.

We will be dealing with input states given by coherent states, $|\varphi \rangle =|\alpha \hbox {e}^{i\xi }\rangle$, with $\alpha$ and $\xi$ reals, and with entangled two-mode squeezed states shared between Alice and Bob $|\psi _r\rangle = \sqrt{1-\tanh ^2r}\sum _{n=0}^{\infty }\tanh ^nr|n\rangle _\mathrm{A}\otimes |n\rangle _{\mathrm{B}}$, where $|n\rangle _{A(B)}$ are Fock number states with Alice (Bob) and r is the squeezing parameter. When $r=0$, we have $|00\rangle$, the vacuum state, and for $r\rightarrow \infty$ the unphysical maximally entangled Einstein–Podolsky–Rosen (EPR) state.

In the position basis, we have [36, 37]

$$\begin{aligned} \varphi (x_1)=\langle x_1 | \alpha \hbox {e}^{i\xi } \rangle = \left( \frac{2}{\pi }\right) ^{1/4}\hbox {e}^{-x_1^2+2\alpha \hbox {e}^{i\xi } x_1 -\alpha ^2/2-\alpha ^2\hbox {e}^{i2\xi }/2} \end{aligned}$$

(23)

and

$$\begin{aligned} \psi _r(x_2,x_3)= \langle x_2,x_3 | \psi _r \rangle = \sqrt{\frac{2}{\pi }}\exp \left[ -\hbox {e}^{-2r}(x_2+x_3)^2/2\right. \left. -\hbox {e}^{2r}(x_2-x_3)^2/2\right] . \end{aligned}$$

(24)

Note that for a two-mode squeezed state, the variance $\Delta _r^2(x_2-x_3)=\langle \psi _r| (x_2-x_3)^2 |\psi _r \rangle -\langle \psi _r| (x_2-x_3) |\psi _r \rangle > ^2=\mathrm{e}^{-2r}/2$, which is employed to measure the squeezing of this state in decibel:

$$\begin{aligned} I_{\mathrm{dB}} = -10 \log _{10}\left[ \frac{\Delta _r^2(x_2-x_3)}{\Delta _0^2(x_2-x_3)}\right] =20r\log _{10}(e). \end{aligned}$$

(25)

Appendix 2: The teleportation-based CVQKD protocol

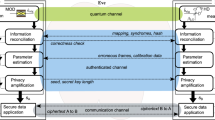
The present CVQKD protocol is based on a binary encoding for the key such that $\{|-\alpha \rangle ,|\alpha \rangle ,|-i\alpha \rangle ,|i\alpha \rangle \}=\{0,1,0,1\}$, with $\alpha$ a real number. These states are to be teleported from Alice to Bob randomly. A step-by-step description of a successful run of the protocol, generating a common random bit between Alice and Bob, is as follows. (1) Alice randomly chooses between the real or imaginary coherent state “basis” and then randomly prepares $|\pm \alpha \rangle$ or $|\pm i\alpha \rangle$, respectively, to teleport to Bob. In Fig. 1, we describe the case where Alice chooses $|\alpha \rangle$ (mode 1 given by the solid/blue line). (2) Alice generates a two-mode squeezed entangled state (modes 2 and 3), whose squeezing parameter r is chosen according to the value of $\alpha$, and sends mode 3 to Bob. (3) Alice adjusts the beam splitter (BS) transmittance according to her choosing the real or imaginary basis and then sends mode 1 to interact with her share of the two-mode squeezed state (mode 2). (4) She measures the position and momentum quadratures of the modes u and v, respectively, that emerge after the BS and classically informs Bob of those results ($\tilde{x}_u$ and $\tilde{p}_v$). (5) Bob randomly chooses $(g_u, g_v)$ from two possible pairs of values and implements a displacement operation on his mode given by $\hat{D}(\lambda )$, where $\lambda = g_u\tilde{x}_u+ig_v\tilde{p}_v$. $g_u$ and $g_v$ are such that the fidelity of Bob’s output state with Alice’s input is greatest if she chooses a real (imaginary) state and he assumes a real (imaginary) state and, at the same time, least if she chooses an imaginary (real) state and he assumes a real (imaginary) state. The optimal pair ($g_u$, $g_v$) depends on the input being a real or imaginary coherent state but not on its sign. (6) Bob implements another displacement on his mode, $\hat{D}(\alpha )$ or $\hat{D}(i\alpha )$, depending on the choice he made for the pair $(g_u, g_v)$. Figure 1 shows the case in which Bob assumes Alice chooses the real basis (solid lines). Had he assumed the wrong basis, which Alice and Bob will discover classically communicating after finishing the whole protocol, they would discard this run of the protocol. (7) Bob measures the intensity of his mode and assigns the bit value 0 if he sees no light (vacuum mode) and the bit 1 otherwise.

1.1 Fidelity analysis

We will explicitly analyze the case where Alice chooses the real basis, namely she teleports either $|-\alpha \rangle$ or $|\alpha \rangle$ to Bob. The calculations for the imaginary basis are similar, and only the final results for this case will be given. Therefore, assuming that we have a real coherent state, Eqs. (20), (23), and (24) when inserted into Eq. (22) give

$$\begin{aligned} F = h_1(r,\theta )\exp [f_1(\tilde{p}_v,\tilde{x}_u,g_v,g_u,r,\theta )+2\alpha \tilde{x}_u f_2(g_u,r,\theta )+\alpha ^2 f_3(r,\theta )], \end{aligned}$$

(26)

where

$$\begin{aligned} h_1(r,\theta )= & {} \sqrt{1-\cos ^2(2 \theta )\tanh ^4r },\\ f_1(\tilde{p}_v,\tilde{x}_u,g_v,g_u,r,\theta )= & {} \left\{ \left[ g_u^2 \tilde{x}_u^2-g_v^2 \tilde{p}_v^2\right] \cos (2 \theta ) \tanh r +4 g_u \tilde{x}_u^2 \sin \theta \right. \\&\left. +4 g_v \tilde{p}_v^2 \cos \theta \right\} \tanh r \\&+\tilde{x}_u^2 \left[ -g_u^2+\frac{2}{\cosh ^2r- \cos (2 \theta )\sinh ^2r}-2\right] \\&+\tilde{p}_v^2 \left[ -g_v^2+\frac{2}{\cosh ^2r+\cos (2 \theta )\sinh ^2r }-2\right] , \\ f_2(g_u,r,\theta )= & {} g_u -\{g_u \cos (2 \theta )\tanh r+2 [1+g_u \cos \theta ]\sin \theta \}\tanh r \nonumber \\&+2 \left( \frac{1}{ \cos (2 \theta )\sinh ^2r-\cosh ^2r}+1\right) \cos \theta , \\ f_3(r,\theta )= & {} -\frac{\{\cosh r- [\tanh r \cos (2 \theta )+\sin (2 \theta )]\sinh r\}^2}{\cosh ^2r- \cos (2 \theta )\sinh ^2r}. \end{aligned}$$

Since we want the optimal F in a way that the optimal settings do not depend on the sign of $\alpha$, we set $f_2(g_u,r,\theta )=0$. This gives the following value for $g_u$,

$$\begin{aligned} g_u(r,\theta ) = \frac{\sinh (2 r) \sin \theta }{\cosh ^2r-\cos (2 \theta )\sinh ^2r }. \end{aligned}$$

(27)

Moreover, since $g_v$ only appears in the exponent and we want the maximum of F, we maximize the exponent as a function of $g_v$. Differentiating the exponent with respect to $g_v$ and equating to zero, we get

$$\begin{aligned} g_v(r,\theta ) = \frac{2 \coth r \cos \theta }{\coth ^2r+\cos (2 \theta )}. \end{aligned}$$

(28)

Inserting $g_u$ and $g_v$ back into F, we finally obtain

$$\begin{aligned} F^{\mathrm{re}}(r,\theta )= & {} \sqrt{1- \cos ^2(2 \theta )\tanh ^4r} \nonumber \\&\times \exp \left\{ \frac{-\alpha ^2 \{\cosh r-\sinh r [ \cos (2 \theta )\tanh r+ \sin (2\theta )]\}^2}{\cosh ^2r-\cos (2 \theta )\sinh ^2r }\right\} , \nonumber \\&\, \end{aligned}$$

(29)

where we use the superscript “re” to remind us that this is the optimal F for real inputs. Also, it is important to note that the optimal expression for F, as well as for $g_u$ and $g_v$, do not depend on the measurement outcomes $\tilde{x}_u$ and $\tilde{p}_v$ obtained by Alice. This is one of the reasons making the present CVQKD scheme yield high key rates without postselecting a subset of all possible measurement outcomes of Alice.

For an imaginary input, namely either $|i\alpha \rangle$ or $|-i\alpha \rangle$, the roles of $g_u$ and $g_v$ are reversed. In order to have a solution for F independent of the sign of the imaginary coherent state, we fix $g_v$. Then, we maximize the exponent of F as a function of $g_u$. The final result is that we obtain the same expressions for $g_u$ and $g_v$ as given before for the real case and the following expression for the fidelity:

$$\begin{aligned} F^{\mathrm{im}}(r,\theta )= & {} \sqrt{1- \cos ^2(2 \theta )\tanh ^4r} \nonumber \\&\times \exp \left\{ \frac{-\alpha ^2 \{\cosh r+\sinh r [ \cos (2 \theta )\tanh r- \sin (2\theta )]\}^2}{\cosh ^2r+ \cos (2 \theta )\sinh ^2r}\right\} . \nonumber \\&\, \end{aligned}$$

(30)

Comparing both expressions for the fidelity, we see that

$$\begin{aligned} F^{\mathrm{re}}(r,\theta ) = F^{\mathrm{im}}(r,\pi /2-\theta ). \end{aligned}$$

(31)

The final calculations needed to determine the optimal r and $\theta$ are as follows. We want r and $\theta$ such that if Alice chooses the real basis and Bob assumes Alice chose the real basis, $F^{\mathrm{re}}$ is maximal and $F^{\mathrm{im}}$ is minimal. This is achieved maximizing the following function:

$$\begin{aligned} \varPi ^{\mathrm{re}}(r,\theta ) = F^{\mathrm{re}}(r,\theta ) [1-F^{\mathrm{im}}(r,\theta )]. \end{aligned}$$

(32)

It is not possible, however, to analytically solve the optimization problem associated with Eq. (32) and get simple closed expressions for the optimal r and $\theta$. Thus, the maximization of Eq. (32) is carried out numerically once the value of $\alpha$ is specified. This is what was done to get the optimal data shown in Fig. 2 of the main text.

The optimal parameters if Alice chooses the imaginary basis and Bob assumes Alice chose the imaginary basis are obtained imposing that $F^{\mathrm{re}}$ be minimal and $F^{\mathrm{im}}$ be maximal. This is obtained maximizing the following function:

$$\begin{aligned} \varPi ^{\mathrm{im}}(r,\theta ) = F^{\mathrm{im}}(r,\theta ) [1-F^{\mathrm{re}}(r,\theta )]=\varPi ^{\mathrm{re}}(r,\pi /2-\theta ). \end{aligned}$$

(33)

It is clear by the last equality that the optimal $\theta$ for the imaginary input is obtained from the optimal one for the real input by subtracting it from $\pi /2$. The relations between the optimal settings for the real and imaginary inputs are as follows:

$$\begin{aligned} \theta ^{\mathrm{re}}= & {} \pi /2 - \theta ^{\mathrm{im}}, \end{aligned}$$

(34)

$$\begin{aligned} g_v^{\mathrm{re}}= & {} g_u^{\mathrm{im}}, \end{aligned}$$

(35)

$$\begin{aligned} g_u^{\mathrm{re}}= & {} g_v^{\mathrm{im}}, \end{aligned}$$

(36)

$$\begin{aligned} r^{\mathrm{re}}= & {} r^{\mathrm{im}}. \end{aligned}$$

(37)

1.2 Key generation analysis

The state with Bob after finishing the teleportation protocol is given by Eq. (20), where he has already implemented either the real or imaginary displacement on his mode. By real and imaginary displacements, we mean that Bob applied the displacement $\hat{D}(\lambda )$, with $\lambda = g_u\tilde{x}_u+ig_v\tilde{p}_v$, using either the real ($g_u^{\mathrm{re}}$ and $g_v^{\mathrm{re}}$) or imaginary ($g_u^{\mathrm{im}}$ and $g_v^{\mathrm{im}}$) optimal parameters.

In the next step of the teleportation-based CVQKD protocol, he implements another displacement, which depends on whether he chose the real or imaginary displacement. For a previously real displaced mode, he now applies the displacement $\hat{D}(\alpha )$, and for a previously imaginary displaced mode, he applies $\hat{D}(i\alpha )$. The goal of these last displacements is to transform states nearly described by $|-\alpha \rangle$ or $|-i\alpha \rangle$ to vacuum states and to push further away from the vacuum the states $|\alpha \rangle$ or $|i\alpha \rangle$. Note that Bob’s state will be very close to one of those four states only if the “matching condition” occurred, i.e., if Alice teleported a real (imaginary) state and Bob used the optimal settings presuming a real (imaginary) input by Alice.

Mathematically, the state after the last displacement is

$$\begin{aligned} |\tilde{\chi }\rangle = \hat{D}(\gamma )|\chi \rangle , \end{aligned}$$

(38)

where $\gamma = \alpha$ or $\gamma = i\alpha$. The probability to detect the vacuum state is

$$\begin{aligned} Q^{\mathrm{B}}_0 = |\langle 0|\tilde{\chi }\rangle |^2=|\langle -\gamma |\chi \rangle |^2 = \left| \int dx_3\varphi ^*_{{-\gamma }}(x_3)\chi (x_3)\right| ^2, \end{aligned}$$

(39)

where we used that $\hat{D}(\gamma )=\hat{D}^\dagger (-\gamma )$ and $\langle 0|\hat{D}(\gamma )=\langle -\gamma |$. In Eq. (39), $\varphi ^*_{{-\gamma }}(x_3)$ is the complex conjugate of (23), with the subscript $-\gamma$ as a reminder to which coherent state the kernel $\varphi (x_3)$ refers to, and $\chi (x_3)$ is given by Eq. (20).

Figure 3 in the main text is a plot of $Q^{\mathrm{B}}_0$ for all possible combinations of input state by Alice and displacement by Bob when a matching condition occurs (the first four curves from top to bottom). The fifth and sixth curves are $Q^{\mathrm{B}}_0$ averaged over all possible measurement outcomes $\tilde{x}_u$ and $\tilde{p}_v$ for Alice, weighted by Alice’s probability to get $\tilde{x}_u$ and $\tilde{p}_v$ [cf. Eq. (17)],

$$\begin{aligned} q^{\mathrm{B}}_0=\int d\tilde{p}_vd\tilde{x}_u \mathbb {p}(\tilde{p}_v,\tilde{x}_u) Q^{\mathrm{B}}_0(\tilde{p}_v,\tilde{x}_u). \end{aligned}$$

(40)

This averaging is needed whenever the matching condition does not occur since $Q^{\mathrm{B}}_0$ depends on $\tilde{x}_u$ and $\tilde{p}_v$ in this case. See Fig. 8 for a reproduction of Fig. 3 of the main text but this time with a different caption, where we employ the notation just developed to describe each one of the plotted curves.

Fig. 8

First curve is $Q^{\mathrm{B}}_0$ computed with the following parameters, $\hbox {Alice's input} = |-\alpha \rangle ,r^{\mathrm{re}},\theta ^{\mathrm{re}},\lambda =g_u^{\mathrm{re}}\tilde{x}_u+ig_v^{\mathrm{re}}\tilde{p}_v,\gamma =\alpha$. The second curve is $Q^{\mathrm{B}}_0$ for $\hbox {Alice's input} = |-i\alpha \rangle ,r^{\mathrm{im}},\theta ^{\mathrm{im}},\lambda =g_u^{\mathrm{im}}\tilde{x}_u+ig_v^{\mathrm{im}}\tilde{p}_v,\gamma =i\alpha$. The third curve is $Q^{\mathrm{B}}_0$ for $\hbox {Alice's input} = |\alpha \rangle ,r^{\mathrm{re}},\theta ^{\mathrm{re}},\lambda =g_u^{\mathrm{re}}\tilde{x}_u+ig_v^{\mathrm{re}}\tilde{p}_v,\gamma =\alpha$. The fourth curve is $Q^{\mathrm{B}}_0$ for $\hbox {Alice's input} = |i\alpha \rangle ,r^{\mathrm{im}},\theta ^{\mathrm{im}},\lambda =g_u^{\mathrm{im}}\tilde{x}_u+ig_v^{\mathrm{im}}\tilde{p}_v,\gamma =i\alpha$. The fifth curve is the averaged $Q^{\mathrm{B}}_0$ for $\hbox {Alice's input} = |\pm \alpha \rangle ,r^{\mathrm{re}},\theta ^{\mathrm{re}},\lambda =g_u^{\mathrm{im}}\tilde{x}_u+ig_v^{\mathrm{im}}\tilde{p}_v,\gamma =i\alpha$. The sixth curve is the averaged $Q^{\mathrm{B}}_0$ for $\hbox {Alice's input} = |\pm i\alpha \rangle ,r^{\mathrm{im}},\theta ^{\mathrm{im}},\lambda =g_u^{\mathrm{re}}\tilde{x}_u+ig_v^{\mathrm{re}}\tilde{p}_v,\gamma =\alpha$

We have also tested the robustness of the optimal settings by randomly and independently changing the optimal parameters about their correct values. As can be seen in Fig. 9, the optimal settings are very robust, supporting fluctuations of $\pm 2\%$ about the optimal values for small and large $\alpha$. For small $\alpha$ fluctuations of $\pm 10\%$ is still tolerable.

Fig. 9

For each value of $\alpha$, we have implemented 100 realizations of random fluctuations about the input state, about the optimal values $r,\theta ,g_v,g_u$, and about $\gamma$. We worked with Alice’s sending a real state and Bob assuming a real state. Similar results are obtained for the imaginary matching condition. The red/square curves connect the maximal and minimal values for $q^{\mathrm{B}}_0$ due to the random fluctuations assuming Alice sent a negative real state. The gray dots between the red/square curves represent the value of $q^{\mathrm{B}}_0$ at each realization. The black/circle curves have the same meaning of the red/square curves but assuming Alice sent a positive real state (Color figure online)

Appendix 3: Security analysis

We want to study how the teleportation-based CVQKD protocol responds to a lossy channel, or equivalently, to the BS attack. This will allow us to determine the level of loss in which a secure key can be extracted via direct reconciliation and no postselection.

1.1 Lossy channel or the presence of Eve

We want to investigate the security of the present scheme to the BS attack. In the BS attack, an eavesdropper (Eve) inserts a BS of transmittance $\eta$, $0\le \eta \le 1$, during the transmission to Bob of his share of the entangled two-mode squeezed state (mode 3 in Fig. 1). In this case, Bob will receive a signal with intensity $\eta$ and Eve the rest. With her share of the signal, $1-\eta$, Eve proceeds as Bob in order to extract information of the key.

The BS is inserted before Bob receives his mode and therefore before he applies the displacements $\hat{D}(\lambda )$ and $\hat{D}(\gamma )$, with $\gamma = \alpha$ or $i\alpha$. Bob’s state before the insertion of the BS is $|\chi '\rangle$ as given in Eq. (16). Hence, the joint state of Bob and Eve before the BS is

$$\begin{aligned} |\varOmega \rangle = |\chi '\rangle |0\rangle = \int dx_3dx_4 \langle x_3|\chi '\rangle \langle x_4|0\rangle |x_3\rangle |x_4\rangle = \int dx_3dx_4 \chi '(x_3) \varphi _0(x_4) |x_3,x_4\rangle , \end{aligned}$$

(41)

with $\varphi _0(x_4)$ given by Eq. (23) with $\alpha =0$. But since

$$\begin{aligned} \hat{B}_{34}(\eta ) |x_3, x_4 \rangle = \left| \sqrt{\eta }x_3 -\sqrt{1-\eta }x_4, \sqrt{1-\eta }x_3 + \sqrt{\eta }x_4\right\rangle \end{aligned}$$

(42)

we have after the BS,

$$\begin{aligned} |\varOmega \rangle= & {} \hat{B}_{34}(\eta )|\chi '\rangle _3|0\rangle _4 \nonumber \\= & {} \int dx_3dx_4 \chi '(x_3) \varphi _0(x_4) \left| \sqrt{\eta }x_3 -\sqrt{1-\eta }x_4, \sqrt{1-\eta }x_3 + \sqrt{\eta }x_4\right\rangle , \nonumber \\= & {} \int dx_3dx_4 \chi '(\sqrt{\eta }x_3+\sqrt{1-\eta }x_4) \varphi _0(\sqrt{\eta }x_4-\sqrt{1-\eta }x_3) |x_3,x_4\rangle .\quad \quad \quad \end{aligned}$$

(43)

The last equality was obtained making the following change in variables, $x_3 \rightarrow \sqrt{\eta }x_3+\sqrt{1-\eta }x_4$ and $x_4 \rightarrow \sqrt{\eta }x_4-\sqrt{1-\eta }x_3$. Bob’s state after the BS is given by the partial trace of the state $\rho _{\mathrm{BE}}=|\varOmega \rangle \langle \varOmega |$ with respect to Eve’s mode, $\rho '_{\mathrm{B}}=\mathrm{tr}\; _E(\rho _{\mathrm{BE}})$. In the position basis, we have

$$\begin{aligned} \rho '_{\mathrm{B}}=\int dx_4\langle x_4 | \rho _{\mathrm{BE}} |x_4\rangle =\int dx_3dx'_3 \rho '_{\mathrm{B}}(x_3,x'_3)|x_3\rangle \langle x'_3| \end{aligned}$$

(44)

where

$$\begin{aligned} \rho '_{\mathrm{B}}(x_3,x'_3)= & {} \int dx_4 \chi '(\sqrt{\eta }x_3+\sqrt{1-\eta }x_4) \chi '^*(\sqrt{\eta }x'_3+\sqrt{1-\eta }x_4) \nonumber \\&\times \varphi _0(\sqrt{\eta }x_4-\sqrt{1-\eta }x_3)\varphi _0^*(\sqrt{\eta }x_4-\sqrt{1-\eta }x'_3). \end{aligned}$$

(45)

Note that Eve’s state is $\rho '_E=\mathrm{tr}\; _{\mathrm{B}}(\rho _{\mathrm{BE}})$, which is simply obtained from Eq. (45) by changing $\eta \rightarrow 1-\eta$.

Using the state $\rho '_{\mathrm{B}}$ ($\rho '_E$), Bob (Eve) proceeds as explained before to finish all the steps of a single run of the teleportation-based CVQKD protocol. Bob displaces his mode by $\lambda$, which depends on whether he assumed Alice teleported a real or imaginary state, finishing the teleportation stage of the protocol. His state at this stage is $\rho _{\mathrm{B}}=\hat{D}(\lambda )\rho '_{\mathrm{B}}\hat{D}^\dagger (\lambda )$. Then he implements the last displacement $\hat{D}(\gamma )$, which depends on his first displacement as explained before, and measures the intensity of his mode. Hence, Bob’s probability to detect the vacuum state (no light) is

$$\begin{aligned} Q^{\mathrm{B}}_0(\tilde{p}_v,\tilde{x}_u)=\mathrm{tr}\; [|0\rangle \langle 0|\, \hat{D}(\gamma )\rho _{\mathrm{B}}\hat{D}^\dagger (\gamma )] = \langle -\lambda -\gamma | \rho '_{\mathrm{B}}|-\lambda -\gamma \rangle , \end{aligned}$$

(46)

where we have made explicit that $Q^{\mathrm{B}}_0$ depends on the measurement outcomes of Alice when $\eta \ne 1$, i.e., when we have a lossy channel. In the position representation, we have

$$\begin{aligned} Q^{\mathrm{B}}_0(\tilde{p}_v,\tilde{x}_u)= \int dx_3dx'_3\varphi ^*_{\,_{-\lambda -\gamma }}(x_3) \rho '_{\mathrm{B}}(x_3,x'_3)\varphi _{\,_{-\lambda -\gamma }}(x'_3). \end{aligned}$$

(47)

As before, we define the unconditional (no postselection) probability as

$$\begin{aligned} q^{\mathrm{B}}_0=\int d\tilde{p}_vd\tilde{x}_u \mathbb {p}(\tilde{p}_v,\tilde{x}_u) Q^{\mathrm{B}}_0(\tilde{p}_v,\tilde{x}_u) \end{aligned}$$

(48)

and in Fig. 10, we show its value for several values of loss.

Fig. 10

Probability $q^{\mathrm{B}}_0$ to detect the vacuum state for several values of loss ($1-\eta$), which increases ($\eta$ decreases) from top to bottom. The other parameters used to compute $q^{\mathrm{B}}_0$, namely, $r, \theta , g_v, g_u$, and $\gamma$, were the optimal ones when the matching condition occurs. The remaining parameter, Alice’s input, was set to $-\alpha$ (solid lines) and $\alpha$ (dashed lines)

1.2 Secure key rates

For direct reconciliation, the secure key rate between Alice and Bob is

$$\begin{aligned} K=\max \{0,\beta I_{\mathrm{AB}} - I_{\mathrm{AE}}\}=\{0,\Delta I\}, \end{aligned}$$

(49)

where $\beta$ is the reconciliation efficiency, $I_{\mathrm{AB}}$ is the mutual information between Alice and Bob, and $I_{\mathrm{AE}}$ is the mutual information between Alice and Eve. In what follows we will prepare the ground for defining and computing those mutual information for our problem. Also, since the present teleportation-based CVQKD protocol is symmetric to both matching conditions, we will work with the one where Alice teleported a real state and Bob implemented the real displacement.

Let X and Y be two binary discrete variables, whose possible values for X are $x=0,1$ and for Y are $y=0,1$. If we associate variable X to Alice and adopt the convention $\{-|\alpha \rangle ,|\alpha \rangle \}=\{0,1\}$, we have

$$\begin{aligned} P_X(0) = P_X(1) = 1/2, \end{aligned}$$

(50)

where $P_X(x)$ is the probability distribution associated with X. This means that Alice randomly chooses between the negative or positive coherent states at each run of the protocol.

If we associate variable Y to Bob, we can define the conditional probability of Bob assigning the value y to his variable if Alice assigned the value x as $P_{Y|X}(y|x)$. For the present protocol, and according to the encoding that Alice and Bob mutually agreed on for the key, the four conditional probabilities are

$$\begin{aligned} P_{Y|X}(0|0)= & {} q_0^{\mathrm{B}}(-\alpha ), \end{aligned}$$

(51)

$$\begin{aligned} P_{Y|X}(1|0)= & {} 1 - q_0^{\mathrm{B}}(-\alpha ), \end{aligned}$$

(52)

$$\begin{aligned} P_{Y|X}(0|1)= & {} q_0^{\mathrm{B}}(\alpha ), \end{aligned}$$

(53)

$$\begin{aligned} P_{Y|X}(1|1)= & {} 1-q_0^{\mathrm{B}}(\alpha ), \end{aligned}$$

(54)

where $q_0^{\mathrm{B}}$, the probability to detect the vacuum state, is given by Eq. (48). If we define

$$\begin{aligned} q_1^{\mathrm{B}}(\alpha )=1 - q_0^{\mathrm{B}}(\alpha ), \end{aligned}$$

(55)

where $q_1^{\mathrm{B}}$ is the probability to detect light, we have

$$\begin{aligned} P_{Y|X}(0|0)= & {} q_0^{\mathrm{B}}(-\alpha ), \end{aligned}$$

(56)

$$\begin{aligned} P_{Y|X}(1|0)= & {} 1 - q_0^{\mathrm{B}}(-\alpha ), \end{aligned}$$

(57)

$$\begin{aligned} P_{Y|X}(0|1)= & {} 1-q_1^{\mathrm{B}}(\alpha ), \end{aligned}$$

(58)

$$\begin{aligned} P_{Y|X}(1|1)= & {} q_1^{\mathrm{B}}(\alpha ). \end{aligned}$$

(59)

Note that we have explicitly written the dependence of $q_j^{\mathrm{B}}$, $j=0,1$, on Alice’s teleported state to remind us that we should compute it using the appropriate sign for $\alpha$.

We can understand the previous conditional probabilities as follows. If Alice teleports the state $|-\alpha \rangle$ (bit 0) and Bob displaces his mode by $\alpha$, for a faithful teleportation he will likely detect the vacuum state after that final displacement and assign correctly the bit 0. The chance for that happening is quantified by $P_{Y|X}(0|0) = q_0^{\mathrm{B}}(-\alpha )$. He will obviously make a mistake, assigning erroneously the bit 1, if he does not detect the vacuum state. For that reason, we have $P_{Y|X}(1|0) = 1 - q_0^{\mathrm{B}}(-\alpha )$. In the same fashion, if Alice teleports the state $|\alpha \rangle$ (bit 1) and Bob displaces his mode by $\alpha$, for a faithful teleportation, he will very likely not detect the vacuum state and will correctly assign the bit 1. This event occurs with probability $1-q_0^{\mathrm{B}}(\alpha )$, which implies $P_{Y|X}(1|1) = 1-q_0^{\mathrm{B}}(\alpha )$. He makes a mistake if he gets the vacuum state and therefore $P_{Y|X}(0|1) = q_0^{\mathrm{B}}(\alpha )$.

Since the conditional probability is related to the joint probability distribution $P_{XY}(x,y)$ by the rule $P_{XY}(x,y)=P_X(x)P_{Y|X}(y|x)$, we have

$$\begin{aligned} P_{XY}(0,0)= & {} q_0^{\mathrm{B}}(-\alpha )/2, \end{aligned}$$

(60)

$$\begin{aligned} P_{XY}(0,1)= & {} [1 - q_0^{\mathrm{B}}(-\alpha )]/2, \end{aligned}$$

(61)

$$\begin{aligned} P_{XY}(1,0)= & {} [1-q_1^{\mathrm{B}}(\alpha )]/2, \end{aligned}$$

(62)

$$\begin{aligned} P_{XY}(1,1)= & {} q_1^{\mathrm{B}}(\alpha )/2. \end{aligned}$$

(63)

If we now use that $P_Y(y)=\sum _{x}P_{XY}(x,y)$, we have

$$\begin{aligned} P_{Y}(0)= & {} [1+q_0^{\mathrm{B}}(-\alpha )-q_1^{\mathrm{B}}(\alpha )]/2, \end{aligned}$$

(64)

$$\begin{aligned} P_{Y}(1)= & {} [1+q_1^{\mathrm{B}}(\alpha )-q_0^{\mathrm{B}}(-\alpha )]/2. \end{aligned}$$

(65)

The mutual information between Alice and Bob is defined as

$$\begin{aligned} I_{\mathrm{AB}} = \sum _{x=0}^1\sum _{y=0}^1P_{XY}(x,y)\log _2\left[ \frac{P_{XY}(x,y)}{P_X(x)P_Y(y)}\right] \end{aligned}$$

(66)

and a direct computation using Eqs. (50) and (60)-(65) gives

$$\begin{aligned} I_{\mathrm{AB}}= & {} 1 +[q_0^{\mathrm{B}}\log _2q_0^{\mathrm{B}}+(1-q_0^{\mathrm{B}})\log _2(1-q_0^{\mathrm{B}}) +q_1^{\mathrm{B}}\log _2q_1^{\mathrm{B}}\nonumber \\&+\,(1-q_1^{\mathrm{B}})\log _2(1-q_1^{\mathrm{B}})]/2 -[(1+q_0^{\mathrm{B}}-q_1^{\mathrm{B}})\log _2(1+q_0^{\mathrm{B}}-q_1^{\mathrm{B}}) \nonumber \\&+\,(1+q_1^{\mathrm{B}}-q_0^{\mathrm{B}})\log _2(1+q_1^{\mathrm{B}}-q_0^{\mathrm{B}})]/2. \end{aligned}$$

(67)

Here we have dropped the $\pm \alpha$ dependence since $q_0^{\mathrm{B}}$ is always computed with $-\alpha$ and $q_1^{\mathrm{B}}$ with $\alpha$. Note that $I_{\mathrm{AB}}$ also depends on $r,\theta , g_v, g_u$, and $\eta$. In order to obtain $I_{\mathrm{AE}}$, we simply replace $\eta$ for $1-\eta$ in the expression for $I_{\mathrm{AB}}$ since $q_j^{\mathrm{B}} \rightarrow q_j^E$ if $\eta \rightarrow 1-\eta$.

Using Eq. (67) and the equivalent one for $I_{\mathrm{AE}}$, we can compute the secret key rate K (Eq. (49)). Figure 4 in the main text was obtained this way, where we employed for each curve a different value for $\eta$ and for all of them the optimal values of $r,\theta , g_v$, and $g_u$ assuming the real matching condition as given in Fig. 2 of the main text.

Note that when the loss is precisely $50\%$, no key can be extracted since Bob’s and Eve’s state are exactly the same, leading to $I_{\mathrm{AB}}=I_{\mathrm{AE}}$ and $K=0$. When the loss is exactly $100\%$, the protocol does not work either. In this case, Bob’s state is the vacuum state $|0\rangle$, i.e., he receives no signal, and Eve can also operate on a vacuum state instead of the intercepted signal. It is clear, thus, that Bob and Eve will have the same mutual information with Alice and obviously $K=0$.

This suggests a possible attack on the present protocol whenever we have high losses. Indeed, Eve can work with a vacuum state instead of her share of the intercepted signal since the former is closer to the state with Bob, whose state in a very lossy environment is nearly the vacuum state. Therefore, we have to improve the security analysis when we have great losses in order to handle the fact that Eve can work with both the intercepted signal and the vacuum state. In this situation, the effective secure key rate that can be achieved between Alice and Bob is

$$\begin{aligned} K_e = \max \{0,\min \{\Delta I,\Delta I_0\}\}, \end{aligned}$$

(68)

where $\Delta I_0 = \beta I_{\mathrm{AB}}-I^0_{\mathrm{AE}}$ and $I^0_{\mathrm{AE}}$ is the mutual information between Alice and Eve assuming Eve’s state is the vacuum. $I^0_{\mathrm{AE}}$ is easily obtained from the general expression for $I_{\mathrm{AE}}$ by setting $\eta =1.0$, the case where Bob receives the whole signal and Eve gets nothing, i.e., she has the vacuum state.

Table I of the main text was obtained maximizing $K_e$ for several values of fixed r, $\eta$, and $\beta$. Equations (27) and (28) were used for $g_u$ and $g_v$ and $\theta$ was determined in such a way that $K_e$ be maximal. As always, we assumed the real matching condition to fix the remaining parameters needed to evaluate $K_e$, namely Alice’s input was either $|-\alpha \rangle$ or $|\alpha \rangle$ and Bob’s final displacement was $\hat{D}(\alpha )$.

Fig. 11

Here both r and $\theta$ are adjusted to get the optimal key rates with $\beta =0.8$. We assume the real matching condition

Appendix 4: Further examples

Assuming squeezing is a cheap resource, we can let r, together with $\theta$, be a free parameter in the maximization of the key rate. In this scenario, we get the results in Figs. 11 and 13 for the effective optimal key rates for several values of loss. The optimal parameters leading to such key rates are given in Figs. 12 and 14.

Fig. 12

Optimal parameters leading to the key rates in Fig. 11. In the maximization process, we have restricted r from 0 to 3 while $\theta$ could assume any value. The optimal $g_u$ and $g_v$ are obtained using these values of $\theta$ and r to evaluate Eqs. (27) and (28)

Fig. 13

Here both r and $\theta$ are adjusted to get the optimal key rates with $\beta =0.8$. We assume the real matching condition

Fig. 14

Optimal parameters leading to the key rates in Fig. 13. In the maximization process, we have restricted r from 0 to 3 while $\theta$ could assume any value. The optimal $g_u$ and $g_v$ are obtained using these values of $\theta$ and r to evaluate Eqs. (27) and (28)

It is interesting to note that whenever we have loss ($\eta \ne 1.0$), the optimal squeezing is not the greatest value possible. For losses lower than $50\%$ ($\eta$ from 1.0 to 0.6), the greater the loss the lower the key rate. Interestingly, the behavior for losses greater than $50\%$ is different. Once you cross the border of $50\%$ loss, more loss means a better key rate. But this trend stops at about $70\%$ loss ($\eta = 0.3$), from which the key rate starts to decrease again with loss. When the exact values of $50\%$ or $100\%$ loss are used, no effective key rate can be achieved since Bob and Eve share the same level of information with Alice. We also remark that in most of the cases, the optimal squeezing is not greater than $r=2.0 (17.4\,\hbox {dB})$.

Finally, it is important to note that for losses lower than $50\%$, i.e., when more than half of the signal sent from Alice reaches Bob, the effective key rate $K_e$ is simply K as given by Eq. (49). However, when we go beyond the level of $50\%$ loss, Eq. (68) starts to be relevant. Depending on the value of $|\alpha |$, either $\Delta I$ or $\Delta I_0$ is the lowest term that defines the key. That is why in the cases with more than $50\%$ loss, the curves for $K_e$ have an abrupt behavior. And for very high loss, $\Delta I_0$ is always the lowest term.