Abstract
In this paper, we study the ‘wrong skewness phenomenon’ in stochastic frontiers (SF), which consists in the observed difference between the expected and estimated sign of the asymmetry of the composite error, and causes the ‘wrong skewness problem’, for which the estimated inefficiency in the whole industry is zero. We propose a more general and flexible specification of the SF model, introducing dependences between the two error components and asymmetry (positive or negative) of the random error. This re-specification allows us to decompose the third moment of the composite error into three components, namely: (i) the asymmetry of the inefficiency term; (ii) the asymmetry of the random error; and (iii) the structure of dependence between the error components. This decomposition suggests that the wrong skewness anomaly is an ill-posed problem, because we cannot establish ex ante the expected sign of the asymmetry of the composite error. We report a relevant special case that allows us to estimate the three components of the asymmetry of the composite error and, consequently, to interpret the estimated sign. We present two empirical applications. In the first dataset, where the classic SF has the wrong skewness, an estimation of our model rejects the dependence hypothesis, but accepts the asymmetry of the random error, thus justifying the sign of the skewness of the composite error. More importantly, we estimate a non-zero inefficiency, thus solving the wrong skewness problem. In the second dataset, where the classic SF does not yield any anomaly, an estimation of our model provides evidence for the presence of dependence. In such situations, we show that there is a remarkable difference in the efficiency distribution between the classic SF and our class of models.



Similar content being viewed by others
Notes
The proof of this statement is available upon request.
Throughout this paper, we will denote this distribution by GL(α v , δ v ).
The general form of a hypergeometric function is given by
\(_2{F_1}\left( {a,b;c;s} \right) = \frac{{{\it{\Gamma }}\left( c \right)}}{{{\it{\Gamma }}\left( {c - b} \right){\it{\Gamma }}\left( b \right)}} {\int}_0^1 {{t^{b - 1}}{{\left( {1 - t} \right)}^{c - b - 1}}{{\left( {1 - st} \right)}^{ - a}}}dt = \mathop {\sum}\limits_{i = 0}^\infty {\frac{{{{\left( a \right)}_i}{{\left( b \right)}_i}}}{{{{\left( c \right)}_i}}}} \frac{{{s^i}}}{{i!}}\ \)
In the region \(\left\{ {x:\left| s \right| < 1} \right\}\), it admits the following representation:
\(_2{F_1}\left( {a,b;c;s} \right) = \mathop {\sum}\limits_{i = 0}^\infty {\frac{{{{\left( a \right)}_i}{{\left( b \right)}_i}}}{{{{\left( c \right)}_i}}}} {\kern 1pt} \frac{{{s^i}}}{{i!}}\)
where \({\it{\Gamma }}(.)\) is the Gamma function and (d) i = d(d+1)…(d+i−1) is the Pochhammer symbol, with (d)0 = 1.
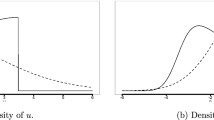
We have analyzed the impact of the dependence structure on the pdf of \({\cal E}\). Smith (2008) demonstrate this effect in the case of symmetric-v. We observe the same results under different conditions of skewness for V (negative or positive). For this reason, we do not show the plots here.
The maximization routine has been developed through the software R-project using the ‘maxLik’ package and then the estimates have been controlled with the algorithm discussed in Appendix 2.
Note, however, that the fact that the association parameter θ in models DS and DA is extremely high suggests that the FGM copula does not account correctly for the dependence. In fact, Kendall’s τ K is probably well above the maximum level which the FGM copula can account for (0.22)
Burnham and Anderson (2004) employ the measure Δ i = AIC i − AIC min and consider that models having Δ i ⩽ 2 are supported with substantial evidence, those for which 4 ⩽ Δ i ⩽ 7 have less support, and those for which Δ i>10 have no support.
Departing from the demonstration of Zenga (1985) for descriptive measures, we obtain the following expression to account for the sign of the skewness:
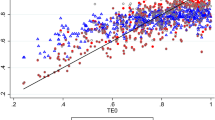
$$E[ {\cal E} - Me( {\cal E} ) ]^3 = \ E[ {\cal E} - E( {\cal E} ) ]^3 + [ E( {\cal E} ) - Me( {\cal E} ) ]^3 + 3[ E( {\cal E} ) \\ - Me( {\cal E} ) ]Var( {\cal E} ).$$(13)The derivation of the \(T{E_\Theta }\) scores is presented in Appendix 3.
We calculate the ICT and R&D investments as percentages of yearly sales. This percentage is from the EFIGE dataset (European Firms in a Global Economy: Internal policies for external competitiveness), which combines measures of firms’ international activities with quantitative and qualitative information, with a focus on R&D and innovation.
The system is over-determined, but possesses a unique solution ω 1,…,ω n .
These are basic concepts in numerical analysis. For more details about orthogonal polynomials and Gaussian quadrature, any textbook in this topic may be consulted. A standard reference for economists is Judd (1998).
References
Aigner D, Lovell C, Schmidt P (1977) Formulation and estimation of stochastic frontier production function models. J Econom 6:21–37
Almanidis P, Sickles RC (2011) The skewness issue in stochastic frontiers models: fact or fiction? In: Van Keilegom I, Wilson PW (eds) Exploring research frontiers in contemporary statistics and econometrics. Springer, Berlin, pp 201–227
Almanidis P, Qian J, Sickles RC (2014) Stochastic frontier models with bounded inefficiency. In: Sickles RC, Horrace WC (eds) Festschrift in honor of Peter Schmidt: econometric methods and applications. Springer, New York, NY, pp 47–81
Amsler C, Prokhorov A, Schmidt P (2014) Using copulas to model time dependence in stochastic frontier models. Econom Rev 33(5–6):497–522
Amsler C, Prokhorov A, Schmidt P (2016) Endogeneity in stochastic frontier models. J Econom 190(2):280–288
Azzalini A (2005) The skew-normal distribution and related multivariate families. Scand J Stat 32(2):159–188
Bădin L, Simar L (2009) A bias-corrected nonparametric envelopment estimator of frontiers. Econometr Theor 25(5):1289–1318
Bartelsman EJ, Gray W (1996) The NBER manufacturing productivity database. NBER technical, Working Paper
Battese GE, Corra GS (1977) Estimation of a production frontier model: with application to the pastoral zone of eastern Autralia. Aus J Agr Resour Econ 21(3):169–179
Berndt ER, Hall BH, Hall RE, Hausman JA (1974) Estimation and inference in nonlinear structural models. Ann Econ Soc Meas 3(4):653–665
Burnham KP, Anderson DR (2004) Multimodel inference. Understanding AIC and BIC in model selection. Socio Meth Res 33(2):261–304
Carree M (2002) Technological inefficiency and the skewness of the error component in stochastic frontier analysis. Econ Lett 77:101–107
Carta A, Steel MFJ (2012) Modelling multi-output stochastic frontiers using copulas. Comput Stat Data Anal 56(11):3757–3773
Coelli TJ, Rao DSP, O’Donnell CJ, Battese GE (2005) An introduction to efficiency and productivity analysis. Springer, New York, NY
Domma F (2004) Kurtosis diagram for the log-dagum distribution. Statistica & Applicazioni 2(2):3–23
Domma F, Perri P (2009) Some developments on the log-dagum distribution. Stat Method Appl 18:205–220
Feng Q, Horrace WC, Wu GL (2015) Wrong skewness and finite sample correction in parametric stochastic frontier models. center for policy research – The Maxwell School, working paper N. 154
Gómez-Déniz E, Pérez-Rodriguez JV (2015) Closed-form solution for a bivariate distribution in stochastic frontier models with dependent errors. J Prod Anal 43(2):215–223
Greene WH (1990) A gamma-distributed stochastic frontier model. J Econom 46(1-2):141–163
Green A, Mayes D (1991) Technical inefficiency in manufacturing industries. The Econ J 101:523–538
Hafner C, Manner H, Simar L (2016) The “wrong skewness” problem in stochastic frontier model: a new approach. Econometr Rev. doi:10.1080/07474938.2016.1140284
Huynh V-N, Kreinovich V, Sriboonchitta S (2014) Modeling dependence in econometrics. Springer, New York, NY
Joe H (1997) Multivariate models and dependence concepts. Chapman & Hall, London; New York
Johnson NL, Kotz S, Balakrishnan N (1995) Continuous univariate distributions, 2nd edn, Vol. 2. Wiley, New York, NY
Judd KL (1998) Numerical methods in economics. The MIT, Cambridge
Kumbhakar SC, Lovell CAK (2000) Stochastic frontier analysis. Cambridge University Press, Cambridge
Lai H, Huang C (2013) Maximum likelihood estimation of seemingly unrelated stochastic frontier regressions. J Prod Anal 40(1):1–14
Lewis RA, McDonald JB (2013) Partially adaptive estimation of the censored regression model. Econometr Rev. doi:10.1080/07474938.2012.690691
Lin J-G, Xie F-C, Wei B-C (2013) Statistical diagnostics for skew-t-normal nonlinear models. Commun Stat-Simul C 38(10):2096–2110
Meeusen W, van den Broek J (1977) Efficiency estimation from Cobb-Douglas production functions with composed error. Int Econ Rev 18(2):435–444
Meyer C (2013) The bivariate normal copula. Commun Stat-Theory Methods 42(13):2402–2422
Nelsen RB (1999) An introduction to Copula. Springer, New York, NY
Pal M, Sengupta A (1999) A model of FPF with correlated error components: an application to Indian agriculture. Sankhyā: The Indian Journal of Statistics, Series B (1960-2002) 61(2):337–350
Qian J, Sickles RC (2009) Stochastic frontiers with bounded inefficiency. Rice University, Working Paper
Shi P, Zhang W (2011) A copula regression model for estimating firm efficiency in the insurance industry. J Appl Stat 38(10):2271–2287
Simar L, Wilson P (2010) Inferences from cross-sectional, stochastic frontier models. Econom Rev 29(1):62–98
Simar L, Wilson P (2011) Estimation and inference in nonparametric frontier models: recent developments and perspectives. Found Trends Econometr 5(3–4):183–337
Smith MD (2008) Stochastic frontier models with dependent error components. Econom J 11:172–192
Stevenson RE (1980) Likelihood functions for generalized stochastic frontier estimation. J Econom 13:57–66
Tran KC, Tsionas EG (2015) Endogeneity in stochastic frontier models: Copula approach without external instruments. Econ Lett 133(C):85–88
Tsionas EG (2007) Efficiency measurement with the Weibull stochastic frontier. Oxf Bull Econ Stat 69(5):693–706
Wu L-C (2013) Variable selection in joint location and scale models of the skew-t-normal distribution. Commun Stat–Simul C 43(3):615–630
Zenga M (1985) Statistica descrittiva. Giappichelli Ed., Torino
Acknowledgements
We would like to thank Francesco Aiello, Antonio Alvarez, Sergio Destefanis, Sabrina Giordano, Luis Orea, Léopold Simar and all participants to LECCEWEPA 2015 held in Lecce.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interests.
Appendices
Appendix 1
1.1 Proof of proposition 1
In order to prove Proposition 1 easily, we report some preliminary results in the following Lemma.
Lemma 1
1. U ~ Exp(δ u ) then
-
r-th moment is \(E\left( {{U^r}} \right) = \delta _u^r{\it{\Gamma }}\left( {r + 1} \right)\). Consequently, we have: E(U) = δ u , \(E\left( {{U^2}} \right) = 2\delta _u^2\) and \(E\left( {{U^3}} \right) = 6\delta _u^3\).
-
Denoted with \(F(u) = 1 - {e^{ - \frac{u}{{{\delta _u}}}}}\) the distribution function of the random variable U, after algebra, we obtain \(E\left[ {{U^r}F\left( U \right)} \right] = E\left( {{U^r}} \right)\left( {1 - \frac{1}{{{2^{r + 1}}}}} \right)\)
-
2.
If V ~ GL(α v ,δ v ), with pdf \({g_V}\left( v \right) = \frac{{{\alpha _v}}}{{{\delta _v}}}{e^{ - \frac{{v + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}{\left( {1 + {e^{ - \frac{{v + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}} \right)^{ - {\alpha _v} - 1}}\) then
-
E(V) = 0;
-
\(E\left( {{V^2}} \right) = Var\left( V \right) = \delta _v^2\left[ {\Psi \prime \left( {{\alpha _v}} \right) + \Psi \prime \left( 1 \right)} \right]\);
-
\(E\left( {{V^3}} \right) = \delta _v^3\left[ {\Psi \prime\prime \left( {{\alpha _v}} \right) - \Psi \prime\prime \left( 1 \right)} \right]\).
-
Denoted with \({G_V}(v) = {\left( {1 + {e^{ - \frac{{v + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}} \right)^{ - {\alpha _v}}}\) the distribution function of the random variable V, it is easy to prove that E[V k G(V)] = (1/2)E{[δ v (Ψ(2α v )−Ψ(α v )) + V]k|2α v ,δ v }, where E[.|2α v ,δ v ] is the expectation with respect to the GL with parameters 2α v and δ v . In particular, for k = 1 and k = 2 we have \(E\left[ {VG\left( V \right)} \right] = \frac{{{\delta _v}}}{2}\left[ {\Psi \left( {2{\alpha _v}} \right) - \Psi \left( {{\alpha _v}} \right)} \right]\) and \(E\left[ {{V^2}G\left( V \right)} \right] = \frac{{\delta _v^2}}{2}\left\{ {{{\left[ {\Psi \left( {2{\alpha _v}} \right) - \Psi \left( {{\alpha _v}} \right)} \right]}^2} + \left[ {\Psi \prime \left( {2{\alpha _v}} \right) - \Psi \prime \left( 1 \right)} \right]} \right\}\hfill\), respectively.
-
3.
if (U,V) ~ f U,V (u,v) = f U (u)g V (v)[1 + θ(1−2F U (u)) (1−2G V (v))] then
Now, we can prove the Proposition 1.
-
1.
The pdf of composite error is \({f_{\cal E}}\left( \epsilon \right) = {\int}_{{\Re ^ + }} {f_{U,V}}\left( {u,\epsilon + u} \right)du \) where f U,V (u,ϵ + u) = f U (u) V (ϵ + u)c(F V (u),G V (ϵ + u)).
Given that c(⋅, ⋅) is a density copula of a FGM copula, we have
$$ {f_{U,V}}\left( {u,\epsilon + u} \right) = \left( {1 + \theta } \right){f_U}\left( u \right){g_V}\left( {\epsilon + u} \right) - 2\theta {f_U}(u)\\ \\ {g_V}\left( {\epsilon + u} \right) {G_V}\left( {\epsilon + u} \right)- 2\theta {f_U}(u){g_V}\left( {\epsilon + u} \right){F_U}\left( u \right)\\ \\ + 4\theta {f_U}(u){g_V}\left( {\epsilon + u} \right){F_U}\left( u \right){G_V}\left( {\epsilon + u} \right)\\ $$(14)Using (14), we have \({f_{\cal E}}\left( \epsilon \right) = \left( {1 + \theta } \right){I_1} - 2\theta \left\{ {{I_2} + {I_3} - 2I} \right\}\), where \(I = {\int}_{{\Re ^ + }} {{f_U}\left( u \right){g_V}\left( {\epsilon + u} \right){F_U}\left( u \right){G_V}\left( {\epsilon + u} \right)du} \), and I i , for i = 1,2,3 are special cases of I.
Now, in order to calculate the integral I, we observe that
$${f_U}\left( u \right){g_V}\left( {\epsilon + u} \right){F_U}\left( u \right){G_V}\left( {\epsilon + u} \right)\kern6pc \\ \\ = \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{{\delta _u}{\delta _v}}}{e^{ - \frac{u}{{{\delta _u}}} - \frac{u}{{{\delta _v}}}}}\left( {1 - {e^{ - \frac{u}{{{\delta _u}}}}}} \right){\left( {1 + {k_1}\left( \epsilon \right){e^{ - \frac{u}{{{\delta _u}}}}}} \right)^{ - 2{\alpha _v} - 1}}\\ $$(15)where \({k_1}\left( \epsilon \right) = {e^{ - \frac{{\epsilon + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}\). After algebra, we can write
$$I = \frac{{\alpha _v}{k_1}(\epsilon )^{-2{\alpha _v}}}{{\delta _u}{\delta _v}}\left\{ {\int\limits_{\Re^+}} ({e^{- u}})^{\frac{1}{\delta _u} + \frac{1}{{\delta _v}}}[ 1 + {k_1}(\epsilon )({e^{- u}})^{\frac{1}{{{\delta _v}}}} ]^{ - 2{\alpha _v} - 1}du - \right.\\ \left. - \mathop {\int}\limits_{\Re ^ + } ({e^{- u}} )^{\frac{2}{\delta _u} + \frac{1}{\delta _v}}[1 + {k_1}( \epsilon )({e^{- u}})^{\frac{1}{\delta _v}}]^{- 2{\alpha _v} - 1}du \right\}$$If before we put y = e −u and then \(t = {y^{\frac{1}{{{\delta _v}}}}}\), after algebra, we obtain
$$I = \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{{\delta _u}}}\left\{ {\mathop {\int}\limits_0^1 {{t^{\frac{{{\delta _v}}}{{{\delta _u}}}}}{{\left( {1 + {k_1}\left( \epsilon \right)t} \right)}^{ - 2{\alpha _v} - 1}}dt} - \mathop {\int}\limits_0^1 {{t^{2\frac{{{\delta _v}}}{{{\delta _u}}}}}{{\left( {1 + {k_1}\left( \epsilon \right)t} \right)}^{ - 2{\alpha _v} - 1}}dt} } \right\}$$Bearing in mind that for hypergeometric function is true the following
$$\frac{{{\it{\Gamma }}\left( {c - b} \right){\it{\Gamma }}\left( b \right)}}{{{\it{\Gamma }}\left( c \right)}}{{}_2}{F_1}\left( {a,\,b;\,c;\,s} \right) = \mathop {\int}\limits_0^1 {{t^{b - 1}}{{\left( {1 - t} \right)}^{c - b - 1}}{{\left( {1 - st} \right)}^{ - a}}dt} $$We obtain
$$\begin{array}{ccccc}\\ I = & \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{{\delta _u}}}\left\{ {\frac{1}{{\frac{{{\delta _v}}}{{{\delta _u}}} + 1}}{\,_2}{F_1}\left( {2{\alpha _v} + 1,\frac{{{\delta _v}}}{{{\delta _u}}} + 1;\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right)} \right.\\ \\ & - \left. {\frac{1}{{2\frac{{{\delta _v}}}{{{\delta _u}}} + 1}}{\,_2}{F_1}\left( {2{\alpha _v} + 1,2\frac{{{\delta _v}}}{{{\delta _u}}} + 1;2\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right)} \right\}\\ \end{array}$$ -
2.
By Lemma 1, we can to verify that
-
E(ϵ) = −E(U) = −δ u
-
\(Var\left( \epsilon \right) = Var\left( U \right) + Var\left( V \right) - 2cov\left( {U,V} \right) = \delta _u^2 + \delta _v^2\left[ {\Psi \prime \left( {{\alpha _v}} \right) + \Psi \prime \left( 1 \right)} \right] - 2cov\left( {U,V} \right)\), where \(cov\left( {U,V} \right) = \frac{\theta }{2}E\left( U \right)E\left[ {V{G_V}\left( V \right)} \right] = \frac{\theta }{4}{\delta _u}{\delta _v}\left[ {\Psi \left( {2{\alpha _v}} \right) - \Psi \left( {{\alpha _v}} \right)} \right].\)
-
Moreover, recalling that for a generic random variable, Z, we have E[Z−E(Z)]3 = E(Z 3)−3E(Z 2)E(Z) + 2[E(Z)]3, after simple algebra, \(E{\left[ {U - E\left( U \right)} \right]^3} = 2\delta _u^3\) and \(E{\left[ {V - E\left( V \right)} \right]^3} = \delta _v^3\left[ {\Psi \prime\prime \left( {{\alpha _v}} \right) - \Psi \prime\prime \left( 1 \right)} \right]\). Moreover, by Lemma, we have:
and
by (2), after algebra, we obtain E[ϵ−E(ϵ)]3 as in Eq. (11).
Appendix 2
1.1 The numerical procedure
The estimation of models like those described in Section 2 requires the ability to compute the density of the composite error. Closed-form expressions for this quantity are available only in some few special cases, such as the noteworthy case addressed by Smith (2008). While in the previous section we provided one more example of a closed-form expression, this section is intended to describe the scheme we use to approximate the likelihood (6) starting from a general joint density f U,V . Our goal is to provide a numerical tool capable of managing different joint distributions for the couple (U,V), thus widening the set of alternatives one can use when defining an SF model.
Our approach is fairly simple. We approximate the convolution of U with V by means of a numerical quadrature. To be more precise, put \({\cal E} = V - U\). Its density function, \({f_{\cal E}}\left( { \cdot ;{{\Theta }}} \right)\), is obtained by the convolution of U with V:
An explicit evaluation of the integral in (16) is in general infeasible, which has kept a potential range of possible joint densities almost unexplored. However, an approximation of (16) by Gauss-Laguerre quadrature has proved to be easy and effective, and is presented below.
Let us first rewrite (16) as
with g x (u) = e u f U,V (u,x + u). Fix an integer m, which we will refer to as the order of quadrature. For h = 1…,m, let: (i) t h be the h-th root of the Laguerre polynomial of order m, L m (u), and (ii) ω h be defined by the following system of linear equationsFootnote 12 , Footnote 13
Then, we can write
Inasmuch as the function g x ( ⋅ ) is Riemann integrable on the interval [0,∞), standard results in numerical analysis ensure the goodness of the approximation.
We can thus approximate the integral appearing in (16) (and its gradient with respect to Θ) by a finite sum, and insert the approximating density function and its gradient into a quasi Newton-like iteration (however, from experience with the normal—half-normal model with the FGM copula, a few initial iterations with the algorithm of Berndt et al. (1974) is highly recommended). As for the order of quadrature, practice with the normal—half-normal case with the FGM copula shows that m = 12 is sufficient to obtain safe approximations. For values of m around 12, computations of the Laguerre nodes and weights require a fraction of a second, and this is needed only once.
Appendix 3
1.1 Calculation of TE scores
Given the Proposition 1, its Proof in Appendix 1 and Eq. (7) in Section 2, we derive the formula to calculate the Technical Efficiency scores TE Θ for our models.
We can write
where f U,V (u,ϵ + u) is derived in Eq. (14).
After algebra, we obtain:
where the H−functions represent hypergeometric functions. In particular, we have:
with \({k_1}\left( \epsilon \right) = {e^{ - \frac{{\epsilon + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}\) and the ω−functions are respectively defined as:
Appendix 4
1.1 Gaussian and Frank copula functions
Gaussian | Frank | |
|---|---|---|
Parameter | θ∈(−1,1) | θ∈(−∞, +∞)\{0} |
Density | \(\frac{1}{{\sqrt {1 - {\theta ^2}} }}exp\left( {\frac{{2\theta {{\it{\Phi }}^{ - 1}}\left[ {F\left( u \right)} \right]{{\it{\Phi }}^{ - 1}}\left[ {G\left( v \right)} \right] - {\theta ^2}\left( {{{\it{\Phi }}^{ - 1}}{{\left[ {F\left( u \right)} \right]}^2} + {{\it{\Phi }}^{ - 1}}{{\left[ {G\left( v \right)} \right]}^2}} \right)}}{{2\left( {1 - {\theta ^2}} \right)}}} \right)\) | \(\frac{{\theta \left( {1 - {e^{ - \theta }}} \right){e^{ - \theta \left( {F\left( u \right) + G\left( v \right)} \right)}}}}{{{{\left[ {\left( {1 - {e^{ - \theta }}} \right) - \left( {1 - {e^{ - \theta F\left( u \right)}}} \right)\left( {1 - {e^{ - \theta G\left( v \right)}}} \right)} \right]}^2}}}\) |
Distribution | Φ(Φ −1[F(u)],Φ −1[G(v)];θ) | \( - {\theta ^{ - 1}}{\rm{ln}}\left[ {1 + \frac{{\left( {{e^{ - \theta F\left( u \right)}} - 1} \right)\left( {{e^{ - \theta G\left( v \right)}} - 1} \right)}}{{\left( {{e^{ - \theta }} - 1} \right)}}} \right]\) |
Legend: Φ is the Standard Normal distribution and Φ −1 is the inverse function.
Rights and permissions
About this article
Cite this article
Bonanno, G., De Giovanni, D. & Domma, F. The ‘wrong skewness’ problem: a re-specification of stochastic frontiers. J Prod Anal 47, 49–64 (2017). https://doi.org/10.1007/s11123-017-0492-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-017-0492-8