Introduction

Quinones can accept two electrons and two protons via the initial protonation of semiquinone, Q·− to QH·, and second protonation of hydroquinone, QH− to QH2. Ubiquinone serves as an electron acceptor at the QA and QB binding sites in reaction centers of purple bacteria (PbRC) from Rhodobacter sphaeroides (Fig. 1). Similarly, menaquinone (vitamin K2) is the acceptor at the QA site in PbRC from Blastochloris viridis, while phylloquinone (vitamin K1) is the active center at the A1A and A1B sites in photosystem I (PSI). In reaction centers of green non-sulfur bacteria from Chloroflexus aurantiacus, menaquinones are also located at both the QA and QB sites (Hale et al. 1983). It should be noted that phylloquinone and menaquinone have the same head-group structure (Fig. 2). Plastoquinone serves as an electron acceptor at the QA and QB sites in photosystem II (PSII) (Fig. 1) (Robinson and Crofts 1984; Rutherford et al. 1984; Okamura et al. 2000; Brettel and Leibl 2001; Wraight 2004). Rhodoquinone is a required cofactor for anaerobic respiration in Rhodospirillum rubrum (Okayama et al. 1968). Because rhodoquinone is assumed to have a higher pK a(Q·−/QH·) than ubiquinone, rhodoquinone-substituted PbRC has been used to investigate the mechanism of proton transfer to QB (e.g., Graige et al. 1999; Maroti et al. 2015).

Fig. 1
figure 1

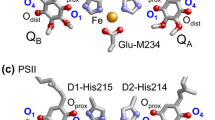
Quinones in photosynthetic reaction centers: a menaquinone as QA and ubiquinone as QB in bacterial photosynthetic reaction centers from Blastochloris viridis (Blc. viridis, PDB ID: 2I5N) (Li et al. 2006); b ubiquinone as QA and QB in bacterial photosynthetic reaction centers from Rhodobacter sphaeroides (Rb. sphaeroides, PDB ID: 3I4D), where the 2-methoxy group of each ubiquinone is red circled; c plastoquinone as QA and QB in PSII (PDB ID: 3ARC) (Umena et al. 2011); and d phylloquinone as A1A and A1B in PSI (PDB ID:1JB0) (Jordan et al. 2001). Red and blue balls indicate O and N atoms, respectively. In PbRC and PSII, Oprox and Odist stand for O atoms of the quinones at the proximal and distal positions with respect to the non-heme Fe complex, respectively. Note that except for QB in PSII, Oprox is O1 and Odist is O4 in PbRC and PSII

Full size image
Fig. 2
figure 2

Molecular structures of a ubiquinone (n = 10), b menaquinone/phylloquinone (n = 3–9), c plastoquinone (n = 6–9), and d rhodoquinone (n = 10), where n is the number of isoprene units

Full size image

In PbRC and PSII, QA/QA ·− acts as a one-electron redox couple and donates an electron to the second quinone QB, without undergoing protonation itself. In contrast, QB reduction involves two consecutive one-electron reduction reactions with a series of associated proton uptake reactions (reviewed in Diner and Rappaport 2002; Renger and Renger 2008; Holzwarth 2008; Cardona et al. 2012; Muh et al. 2012; Petrouleas and Crofts 2005). Both QA and QB are located near the non-heme Fe2+ and the ligands to the Fe2+ (i.e., His-L190 and His-M217 (or M219) in PbRC and D1-His215 and D2-His214 in PSII) donate an H-bond to the carbonyl O atoms of quinones that are nearer to the Fe complex (Oprox) (Fig. 1a–c). The carbonyl O atoms of quinones at the distal position (Odist) also form H-bonds with the proteins. On the other hand, in PSI, the non-heme Fe2+ is absent, but the Fe4S4 cluster FX is located near the two A1 binding sites (Fig. 1d). For many 1,4-quinones, experimentally measured pK a(Q·−/QH·) in aqueous solution were summarized by Swallow (1982) and experimentally measured pK a(QH−/QH2) in aqueous solution were reported by Bishop and Tong (1965).

As far as we are aware, experimentally measured pK a(Q·−/QH·) and pK a(QH−/QH2) for ubiquinone, menaquinone, plastoquinone, and rhodoquinone in aqueous solution have not been reported, because of their insoluble hydrophobic isoprene side-chains (Fig. 2). The pK a(Q·−/QH·) for ubiquinone was roughly estimated to be 4.9 in aqueous solution (Swallow 1982) or measured to be 6.5 in methanol (Land and Swallow 1970; Swallow 1982). In theoretical studies by Cape et al. (2006), pK a(Q·−/QH·) for ubiquinone, plastoquinone, and rhodoquinone were calculated to be 5.35, 4.86, and 5.09, respectively (Cape et al. 2006), although pK a(Q·−/QH·) of rhodoquinone is assumed to be higher than pK a(Q·−/QH·) of ubiquinone (Graige et al. 1999). The pK a(QH−/QH2) for ubiquinone were measured to be 13.3 in 80% ethanol (Morrison et al. 1982). On the other hand, to calculate pK a(QH−/QH2) of QB in PbRC from R. sphaeroides, Zhu and Gunner used a pK a(QH−/QH2) of 10.7 for ubiquinone in aqueous solution in their theoretical studies (Zhu and Gunner 2005). Reliable pK a(Q·−/QH·) and pK a(QH−/QH2) values for ubiquinone, menaquinone, and plastoquinone in aqueous solution are required for understanding the mechanisms of reactions involving quinones in PbRC, PSI, and PSII. Here, we report the pK a(Q·−/QH·) and pK a(QH−/QH2) for ubiquinone, menaquinone, phylloquinone, and plastoquinone in aqueous solution, obtained by adopting a quantum chemical approach.

Computational procedures

In the deprotonation reaction of the protonated state (AH) to deprotonated state (A−) in aqueous solution, pK a is defined as

$$p{K_{\text{a}}}=\frac{{\Delta {G_{{\text{aq}}}}}}{{2.303RT}},$$
(1)

where ΔG aq is the free energy difference between (AH) and (A− + H+) (i.e., ΔG aq = G aq(A−) − G aq(AH) + G aq(H+)), R is the gas constant, and T is the temperature. ΔG aq can also be approximated as

$$\Delta {G_{{\text{aq}}}}={\text{ }}k\Delta {E_{{\text{QM}}/{\text{PCM}}}}+C,$$
(2)

where k is the scaling factor, ΔE QM/PCM is the energy difference between AH and A− in aqueous phase (i.e., ΔE QM/PCM = E QM/PCM(A−) − E QM/PCM(AH)), which can be calculated using a quantum chemical (QM) approach with the polarizable continuum model (PCM) method, and C is the constant [“simple pK a estimation with energy of the optimized geometry scheme” (Matsui et al. 2012)]. If pK a of molecules are obtained at the same temperature, Eq. 1 can be written into Eq. 3 using Eq. 2,

$$p{K_{\text{a}}}=k'\Delta {E_{{\text{QM}}/{\text{PCM}}}}+C',$$
(3)

where k′ is the scaling factor and C′ is constant. To determine k′ and C′, we calculated ΔE QM/PCM for nine 1,4-quinones whose experimentally measured pK a(Q·−/QH·) (Swallow 1982) and pK a(QH−/QH2) (Bishop and Tong 1965) are reported. We employed the unrestricted DFT method with the B3LYP functional and 6-31g++** basis sets, using the Gaussian (Frisch et al. 2004) program code with the PCM method, i.e., water molecules were considered implicitly. This treatment is more appropriate to describe H-bonds between quinones and bulk water molecules, in which the H-bond patterns are not unique. We evaluated all possible conformations of each protonated quinone (i.e., QH· and QH2) regarding the –OH group orientation, and we took the energetically lowest conformation as the relevant structure. In the resulting structures, the –OH group was essentially in the plane of the quinone ring (SI Dataset 1 for atomic coordinates). Because the isoprene units are not composed of conjugated double bonds, the isoprene side-chain length n (Fig. 2) was set to 1 for the calculations of ubiquinone, menaquinone, phylloquinone, and plastoquinone. This could also reduce the number of the possible conformations. In fact, the length of the ubiquinone does not practically affect the energetics of ubiquinones, as demonstrated by the experimentally measured redox potential values of ubiquinone-1 and -10 in dimethylformamide being −611 and −602 mV versus saturated calomel reference electrode, respectively, essentially no difference (Prince et al. 1983).

Results and discussion

Correlation of calculated energies with pK a for 1,4-quinones

The calculated ΔE QM/PCM for deprotonation of QH· to Q·− for nine 1,4-quinones were highly associated with the experimentally measured pK a(Q·−/QH·) ranging from 4.0 to 5.1 (summarized in Swallow 1982), which was best fitted in the following equations (Fig. 3):

Fig. 3
figure 3

Correlation between experimentally measured pK a(Q·−/QH·) and calculated ΔE QM/PCM (coefficient of determination R 2 = 0.99). ΔE QM/PCM can be calculated using a quantum chemical approach with the PCM method. The solid line was drawn according to Eq. 4

Full size image
$$p{K_{\text{a}}}({{\text{Q}}^{ \cdot - }}/{\text{Q}}{{\text{H}}^ \cdot }){\text{ }}=\frac{1}{{4.20}}\left( {\Delta {E_{{\text{QM}}/{\text{PCM}}}} - 268.48\left[ {{\text{kcal}}/{\text{mol}}} \right]} \right).$$
(4)

The term of −268.48 kcal/mol corresponds to the proton solvation energy, which typically ranges from −252.6 to −271.7 kcal/mol [see Schmidt am Busch and Knapp (2004) and references therein]. Using Eq. 4, the calculated pK a(Q·−/QH·) for nine 1,4-quinones are listed in Table 1, which confirms that Eq. 4 can reproduce the experimentally measured pK a(Q·−/QH·). It should be noted that the accuracy of the experimentally measured pK a values is generally considered to be within 0.2 units (Swallow 1982).

Table 1 Calculated pK a(Q·−/QH·) for the first protonation process Q·− to QH· in water, using Eq. 4
Full size table

Symmetrically shaped quinones (e.g., benzoquinone and 2,3-dimethylbenzoquinone) had a single pK a value, whereas asymmetrically shaped quinones (e.g., methylbenzoquinone and 2,6-dimethylbenzoquinone) had two distinguishable pK a values (Table 1). The difference in pK a values is caused by the difference in the chemical environment of the two O sites (O1 and O4). For example, the calculated pK a(Q·−/QH·) of the O4 site in 2,6-dimethylbenzoquinone was larger than the calculated pK a(Q·−/QH·) of the O1 site by 0.46 (Table 1), because the protonation at O1 (i.e., the formation of –OH at O1) increases the steric hindrance with the two methyl groups, which results in a decrease in pK a at O1. Since protonation of Q·− to QH· occurs predominantly at one of the two O sites with a higher pK a(Q·−/QH·), the higher pK a(Q·−/QH·) can be considered to be relevant for asymmetrically shaped quinones and are used to obtain Eq. 4.

The calculated ΔE QM/PCM for deprotonation of QH2 to QH− for nine 1,4-quinones were also highly correlated with the experimentally measured pK a(QH−/QH2) ranging from 9.85 to 11.25 (Bishop and Tong 1965), which was best fitted in the following equations (Fig. 4):

Fig. 4
figure 4

Correlation between experimentally measured pK a(QH−/QH2) and calculated ΔE QM/PCM (coefficient of determination R 2 = 0.96). ΔE QM/PCM can be calculated using a quantum chemical approach with the PCM method. The solid line is drawn according to Eq. 5

Full size image
$$p{K_{\text{a}}}({\text{Q}}{{\text{H}}^ - }/{\text{Q}}{{\text{H}}_2})=\frac{1}{{2.40}}\left( {\Delta {E_{{\text{QM}}/{\text{PCM}}}} - 280.00\left[ {{\text{kcal}}/{\text{mol}}} \right]} \right).$$
(5)

The pK a(QH−/QH2) calculated for nine quinones using Eq. 5 are listed in Table 2, which confirms that Eq. 5 can reproduce the experimentally measured pK a(QH−/QH2) when ΔE QM/PCM can be calculated appropriately.

Table 2 Calculated pK a(QH−/QH2) for the second protonation process QH− to QH2 in water, using Eq. 5
Full size table

pK a(Q·−/QH·) and pK a(QH−/QH2) for ubiquinone, menaquinone, phylloquinone, plastoquinone, and rhodoquinone in aqueous solution

Using Eqs. 4 and 5, we also calculated pK a(Q·−/QH·) and pK a(QH−/QH2) for ubiquinone, menaquinone, phylloquinone, and plastoquinone in aqueous solution, respectively. The calculated pK a(Q·−/QH·) were 5.31 for ubiquinone, 4.92 for menaquinone/phylloquinone, and 5.11 for plastoquinone in aqueous solution (Table 1). pK a(Q·−/QH·) did not significantly differ between O1 and O4 in plastoquinone and ubiquinone (Table 1). This result suggests that which of the two O sites, O1 and O4, serves as the initial (i.e., Q·− to QH·) and second (i.e., QH− to QH2) protonation sites of QB in PbRC and PSII, is predominantly determined by the protein environments.

The calculated pK a(Q·−/QH·) for ubiquinone was closer to the value of 4.9 roughly estimated for aqueous solution (Swallow 1982) than the value of 6.5 measured in methanol (Land and Swallow 1970; Swallow 1982). Because methanol (dielectric constant = 33) is less polar than water (dielectric constant = 80), the negatively charged Q·− state is less stable in methanol than in water; this could explain the high pK a(Q·−/QH·) in methanol with respect to water.

In theoretical studies by Cape et al., the calculated pK a(Q·−/QH·) of 5.09 for rhodoquinone was lower than their calculated pK a(Q·−/QH·) of 5.35 for ubiquinone (Cape et al. 2006). In contrast, in the present study, the calculated pK a(Q·−/QH·) of rhodoquinone was significantly high, 5.78 (Table 1). It should be noted that pK a(Q·−/QH·) of rhodoquinone is assumed to be higher than pK a(Q·−/QH·) of ubiquinone (e.g., Graige et al. 1999), which is consistent with the present result.

The calculated pK a(QH−/QH2) of 10.86 for ubiquinone (Table 2) is very close to pK a(QH−/QH2) of 10.8 measured for trimethylbenzoquinone (Bishop and Tong 1965). Zhu and Gunner considered pK a(QH−/QH2) for trimethylbenzoquinone being more relevant to the pK a(QH−/QH2) for ubiquinone in aqueous solution (Zhu and Gunner 2005) than pK a(QH−/QH2) = 13.3 in 80% ethanol (Morrison et al. 1982). The present study supports their conclusion. The calculated pK a(QH−/QH2) of 10.86 for ubiquinone is also close to the calculated pK a(QH−/QH2) of 10.74 for plastoquinone (Table 2), which might be associated with the similarity in the QB protonation events for PbRC and PSII (Robinson and Crofts 1984; Rutherford et al. 1984; Okamura et al. 2000; Wraight 2004; Ishikita and Knapp 2005).

Influence of the 2-methoxy group orientation in pK a(Q·−/QH·) for ubiquinone

It was proposed that difference in the 2-methoxy orientation of ubiquinone (Fig. 1b) was responsible for (i) the E m difference of more than 160 mV between QA and QB in PbRC (Taguchi et al. 2013) or (ii) the quantum chemically obtained electron affinity difference of more than 170 meV between QA and QB in PbRC (de Almeida et al. 2014). On the other hand, FTIR studies suggested that the QA binding to PbRC (i.e., interaction between QA and the PbRC protein environment) was affected by the H-bond interaction with the protein environment but not by the methoxy orientation (Remy et al. 2003). In the present study, using the crystal structure (PDB: 3I4D; Fig. 1b) whose different 2-methoxy orientations between QA and QB were highlighted in ref. (de Almeida et al. 2014), pK a(Q·−/QH·) were calculated. The calculated pK a(Q·−/QH·) were the same, 5.30 at the O4 site in the QA conformation and 5.31 at the O4 site in the QB conformation in water (Table S1), irrespective of the different 2-methoxy orientations in the quantum chemically optimized quinone structures (SI Dataset 2 for atomic coordinates). In the protonated QH· state, the energetically lowest conformations showed that the –OH group was oriented toward the 2-methoxy O atom (–O–H⋯Omethoxy angle = 116° and –O⋯Omethoxy distance = 2.1 Å in both QA and QB conformations). When the –OH group was oriented away from the 2-methoxy O atom, the calculated pK a(Q·−/QH·) were lowered by ~0.6 to 1 pK a unit from the pK a(Q·−/QH·) value of the energetically lowest conformation (Table S1). In the quantum chemically optimized QA and QB conformations, the 2-methoxy group was out of the quinone ring, as identified in the crystal structure (PDB: 3I4D). These results suggest that pK a(Q·−/QH·) is more affected by the difference in the –OH orientation than the difference in the 2-methoxy orientation. The influence of the 2-methoxy orientation might be more pronounced when calculated in vacuum (i.e., in the absence of the protein environment), where H-bond partners of ubiquinone (e.g., bulk water molecules and protein environments) are absent. In vacuum, alteration in the molecular configuration is the only way to alter the stability of the Q·− and QH· states. It should be noted that the influence of –OH orientation can be ignored when considering E m(Q/Q·−), because –OH is absent in both the Q and Q·− states.

Evolutionary transition of quinones in photosynthetic reaction centers

Among all of the 1,4-quinones investigated here, plastoquinone and ubiquinone employed at QB in PbRC and PSII have the second and third largest pK a(Q·−/QH·) (Table 1). This might be a reason why nature uses these quinones exclusively as the terminal electron acceptor QB in PbRC and PSII. The large pK a(Q·−/QH·) would result in a larger population of QH·. This will then enable it to accept the second electron, leading to the fully protonated QBH2 state. Thus, the large pK a(Q·−/QH·) is advantageous in fixing the two transferred electrons using protonation in the form of QBH2. Remarkably, QA in PbRC from B. viridis and A1A and A1B in PSI, which serve as electron donors (to QB and the Fe4S4 cluster FX, respectively, Fig. 1) without altering the protonation states, are menaquinone/phylloquinone with lower pK a(Q·−/QH·) = 4.9 (Table 1).

Menaquinone is assumed to represent the ancestral type of quinones in bioenergetics systems, whereas ubiquinone and plastoquinone are assumed to represent “more recent” quinones (Schoepp-Cothenet et al. 2009). Intriguingly, E m(Q/Q·−) of the “more recent” quinones are higher [by ~100 mV (Prince et al. 1983)] than E m(Q/Q·−) of the “ancestral” quinone. Reduced menaquinone becomes rapidly oxidized in the presence of O2, whereas ubiquinone and plastoquinone are less sensitive toward oxygen, minimizing loss of the unproductive reduced power (Schoepp-Cothenet et al. 2009); it seems plausible that the difference in E m(Q/Q·−) is associated with rising levels of dioxygen 2.5 billion years ago. In most PbRC, the tightly bound cofactor at the QA site can be either menaquinone or ubiquinone, whereas the cofactor at the terminal electron acceptor QB site is ubiquinone [except for, e.g., PbRC from Halorhodospira halophile, which has menaquinone at both the QA and QB site (Schoepp-Cothenet et al. 2009)]. The higher E m(Q/Q·−) of ubiquinone at the QB site would contribute to the driving force of the electron transfer from QA to QB when menaquinone is the cofactor at the QA site (e.g., B. viridis). The present results show that the “more recent” quinones, ubiquinone and plastoquinone, have larger pK a(Q·−/QH·) and pK a(QH−/QH2) values than the “ancestral” quinone, menaquinone/phylloquinone (Tables 1, 2), which is also consistent with a role of QB, fixation of two electrons and two protons in the form of QBH2.

In photosynthetic reaction centers of the green non-sulfur bacteria (e.g., Chloroflexus aurantiacus), which is assumed to have evolved first as the type-II reaction center (Gupta 2003), menaquinone occupies at both the QA and QB sites (Hale et al. 1983). One of the simplest ways to generate the driving force for electron transfer between the identical menaquinone cofactors would be to alter the solvent accessibility between the QA and QB sites. As the quinone-binding site is more exposed to the bulk water region, it can stabilize the Q·− state with respect to Q state, which results in an increase in E m(Q), i.e., the case for E m(QB), even if the amino acid sequences near the QA and QB binding sites were similar. In addition, the exposure of the quinone-binding site makes (P)bRC easier to hire external quinones. The effort to make the solvent accessibility of the quinone-binding sites different between the two quinone-binding sites in the homodimeric type-I reaction center would lead to formation of the heterodimeric type-II reaction center with E m(QB) > E m(QA) and might also explain why the cofactor can be ubiquinone at the QB site in most PbRC.

Conclusions

Experimentally measured pK a(Q·−/QH·) (Swallow 1982) and pK a(QH−/QH2) (Bishop and Tong 1965) values of nine 1,4-quinones in aqueous solution were highly correlated with the quantum chemically calculated energy differences (ΔE QM/PCM) between the protonated and deprotonated states (Figs. 3, 4). They can be best fitted to Eqs. 4 and 5, respectively. The calculated pK a(Q·−/QH·) values were 5.31 for ubiquinone, 4.92 for menaquinone/phylloquinone, 5.11 for plastoquinone, and 5.78 for rhodoquinone in aqueous solution (Table 1). pK a(Q·−/QH·) for plastoquinone and ubiquinone in aqueous solution are the largest among all of the 1,4-quinones but rhodoquinone listed in Table 1, partially explaining why nature employs these two 1,4-quinones specifically as the terminal electron acceptors QB in PbRC and PSII.

In PbRC and PSII, the initial protonation of Q·− to QH· predominantly occurs at the distal carbonyl site Odist of QB (Fig. 1) (Okamura et al. 2000; Wraight 2004; Saito et al. 2013). The pK a(Q·−/QH·) at the O1 and O4 sites did not differ significantly for each quinone (Table 1), suggesting that the protein environments predominantly determine the initial protonation O site of QB.

The pK a(QH−/QH2) values were calculated to be 10.86 for ubiquinone, 9.16 for menaquinone/phylloquinone, 10.74 for plastoquinone, and 9.81 for rhodoquinone in aqueous solution using Eq. 5 (Table 2). The calculated pK a(QH−/QH2) for ubiquinone was closer to the experimentally measured value of 10.8 for trimethylbenzoquinone (Bishop and Tong 1965) than the experimentally measured pK a(QH−/QH2) of 13.3 for ubiquinone in 80% ethanol (Morrison et al. 1982), as already pointed out (Zhu and Gunner 2005).

The pK a(Q·−/QH·) and pK a(QH−/QH2) for ubiquinone, menaquinone/phylloquinone, and plastoquinone in aqueous solution, which were determined in the present study, will help understand the mechanisms of quinone-mediated reactions in photosynthetic reaction centers, such as formation of QBH2 in PbRC and PSII (Robinson and Crofts 1984; Rutherford et al. 1984; Okamura et al. 2000; Wraight 2004; Saito et al. 2013), formation of QAH2 in PSII (van Mieghem et al. 1995; Noguchi 2002), and evolutionary relationship between the type-I and type-II photosynthetic reaction centers (Gupta 2003; Rutherford and Faller 2003; Schoepp-Cothenet et al. 2009).