Abstract
This paper is devoted to providing a unifying approach to the study of the uniqueness of unconditional bases, up to equivalence and permutation, of infinite direct sums of quasi-Banach spaces. Our new approach to this type of problem permits to show that a wide class of vector-valued sequence spaces have a unique unconditional basis up to a permutation. In particular, solving a problem from Albiac and Leránoz (J Math Anal Appl 374(2):394–401, 2011. https://doi.org/10.1016/j.jmaa.2010.09.048) we show that if \(X\) is quasi-Banach space with a strongly absolute unconditional basis then the infinite direct sum \(\ell _{1}(X)\) has a unique unconditional basis up to a permutation, even without knowing whether \(X\) has a unique unconditional basis or not. Applications to the uniqueness of unconditional structure of infinite direct sums of non-locally convex Orlicz and Lorentz sequence spaces, among other classical spaces, are also obtained as a by-product of our work.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and background
Given a Banach space (or, more generally, a quasi-Banach space) \(X\) with a normalized unconditional basis \(({\varvec{x}}_{n})_{n=1}^{\infty }\), let us write \(X\in {\mathscr {U}}\) if every normalized unconditional basis of \(X\) is equivalent to a permutation \(({\varvec{x}}_{\pi (n)})_{n=1}^{\infty }\) of the basis \(({\varvec{x}}_{n})_{n=1}^{\infty }\). If we impose a stronger uniqueness property, where it is required that \(\pi \) be the identity, we write \(X\in {\mathscr {U}}_S\). Notice that \(X\in {\mathscr {U}}_S\) if and only if X has a symmetric basis and X belongs to \({\mathscr {U}}\). In the context of Banach spaces it is well known that \(X\in {\mathscr {U}}_S\) if and only if \(X\) is isomorphic to one of the spaces from the set \({\mathscr {S}}=\{c_0,\ell _1,\ell _2\}\) ([29, 31]). However, for quasi-Banach spaces which are not Banach spaces the situation is quite different since there is a wide class of non-locally convex Orlicz sequence spaces, including the spaces \(\ell _p\) for \(0<p<1\), which belong to \({\mathscr {U}}_S\) ( [22]).
Bourgain et al. studied in [14] the class \({\mathscr {Z}}\) of those Banach spaces which can be obtained by taking the infinite direct sum of a space from \({\mathscr {S}}\) in the sense of a space also in \({\mathscr {S}}\), and gave a complete description of the class \({\mathscr {Z}}\cap {\mathscr {U}}\) by proving that the spaces \(c_{0}(\ell _{1})\), \(\ell _{1}(c_{0})\), \(c_{0}(\ell _{2})\) and \(\ell _{1}(\ell _{2})\) belong to \({\mathscr {U}}\), while \(\ell _{2}(\ell _{1})\) and \(\ell _{2}(c_{0})\) do not. Many of the questions the authors formulated in their 1985 Memoir remain open as of today. They conjectured that if a Banach space \(X\) belongs to \({\mathscr {U}}\) then so does the iterated copy of \(X\) in the sense of one of the spaces from \({\mathscr {S}}\). This conjecture was disproved in the general case in 1999 by Casazza and Kalton, who showed that Tsirelson’s space \({\mathcal {T}}\in {\mathscr {U}}\) whereas \(c_{0}({\mathcal {T}})\notin {\mathscr {U}}\) ( [17]). Casazza and Kalton’s work gave thus continuity to a research topic that was central in Banach space theory in the 1960’s and 1970’s, but that was interrupted after the Memoir. Perhaps the researchers felt discouraged to put effort into a subject that required the discovery of novel tools in order to make headway, with little hope for attaining a satisfactory classification of the Banach spaces belonging to \({\mathscr {U}}\).
At the same time, the positive results on uniqueness of unconditional basis obtained in the context of non-locally convex quasi-Banach spaces motivated further study with a number of authors contributing to the development of a coherent theory. An important advance was the paper [25] by Kalton et al. followed by the work of Leránoz [28], who proved that \(c_{0}(\ell _{p})\in {\mathscr {U}}\) for all \(0<p<1\), and Wojtaszczyk [37], who proved that the Hardy space \(H_{p}({\mathbb {T}})\) also belongs to the class \({\mathscr {U}}\) for \(0<p<1\). Subsequently, it was proved that \(\ell _{p}(\ell _{2})\), \(\ell _{p}(\ell _{1})\), and \(\ell _{1}(\ell _{p})\) also belong to \({\mathscr {U}}\) for all \(0<p<1\) ([7, 8]), and the question arose of what can be said about infinite direct sums of other quasi-Banach spaces. Our aim in this paper is to fill this gap in the literature. To that end, we develop a new set of techniques which combined with reinterpretations of the already existing methods permit to obtain a myriad of new additions to the list of spaces with a unique unconditional basis.
The article is structured in five more sections. Section 2 gathers the terminology and the notation that are more heavily used. Section 3 is preparatory but becomes instrumental in what follows. We survey the techniques developed by the specialists in their study of the uniqueness of unconditional structure which will be of interest for us, and give them a quantitative twist. In particular we further the study of strongly absolute bases. Section 4 addresses the uniqueness of unconditional basis of infinite direct sums of quasi-Banach spaces in the sense of an atomic quasi-Banach lattice whose unit vector system is strongly absolute, while in Sects. 5 and 6 we concentrate on \(c_0\)-sums and \(\ell _1\)-sums of quasi-Banach spaces with a strongly absolute basis. A brief digression could help the reader to understand better our approach in these theoretical sections. An infinite direct sum \(X=(\bigoplus _{j=1}^{\infty } X_{j})_{{{\mathcal {L}}}}\) of quasi-Banach spaces \((X_{j})_{j=1}^{\infty }\) in the sense of some quasi-Banach lattice \({{\mathcal {L}}}\) may be regarded as an infinite matrix whose jth row is occupied by the vectors in \(X_{j}\). Since the spaces \(X_{j}\) come with a basis \({\mathcal {X}}_{j}\), the vectors in \(X_{j}\) are sequences of scalars (relative to the basis \({\mathcal {X}}_{j}\)). Understanding the geometry of \(X\) often requires working simultaneously with several (or even all) rows of \(X\) and in doing so, we need to count on estimates for the bases \({\mathcal {X}}_{j}\) and the spaces \(X_{j}\) that do not depend on the specific row(s) we are looking at. This compels us to introduce the quantitative versions of the notions we will use and to keep track of the constants involved in our arguments. Finally, Sect. 7 is devoted to applying our theoretical schemes to practical cases. Among the vast amount of novel examples that we can tailor, we exhibit a selection of important new examples of spaces that belong to \({\mathscr {U}}\) and which involve Lebesgue sequence spaces, Lorentz sequence spaces, Orlicz sequence spaces, Bourgin–Nakano spaces, Hardy spaces, and Tsirelson’s space.
2 Terminology
We use standard terminology and notation in Banach space theory as can be found, e.g., in [6]. Most of our results, however, will be established in the general setting of quasi-Banach spaces; the unfamiliar reader will find general information about quasi-Banach spaces in [26]. In keeping with current usage we will write \(c_{00}({\mathcal {J}})\) for the set of all \((a_j)_{j\in {\mathcal {J}}}\in {\mathbb {F}}^{{\mathcal {J}}}\) such that \(|\{j\in {\mathcal {J}}:a_j\not =0\}|<\infty \), where \({\mathbb {F}}\) can be the real or complex scalar field. The convex hull of a subset Z of a vector space will be denoted by \({\text {co}}(Z)\). A quasi-norm on a vector space \(X\) over \({\mathbb {F}}\) is a map \(\Vert \cdot \Vert :X\rightarrow [0,\infty )\) satisfying \(\Vert f\Vert >0\) when \(f\not =0\), \(\Vert t\, f\Vert =|t| \, \Vert f\Vert \) for all \(t\in {\mathbb {F}}\) and all \(f\in X\), and
for some constant \(\kappa \ge 1\). The optimal constant such that (2.1) holds will be called the modulus of concavity of \(X\). If \(\Vert \cdot \Vert \) verifies
for some \(0<p\le 1\), the quasi-norm \(\Vert \cdot \Vert \) is said to be a p-norm. Note that a p-norm is a quasi-norm with modulus of concavity at most \(2^{1/p-1}\). If \(X\) is complete with the metric topology induced by the quasi-norm, \((X,\Vert \cdot \Vert )\) is said to be a quasi-Banach space. A p-Banach space will be a quasi-Banach space equipped with a p-norm. The closed unit ball of a quasi-Banach space \(X\) will be denoted by \(B_X\) and the closed linear span of a subset Z of \(X\) will be denoted by [Z].
We will frequently index unconditional bases and basic sequences by an unordered countable index set \({\mathcal {N}}\) which needs not be the set \(\mathbb N\) of natural numbers. A countable family \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) in \(X\) is an unconditional basic sequence if for every \(f\in [{\varvec{x}}_n :n \in {\mathcal {N}}]\) there is a unique family \((a_n)_{n \in {\mathcal {N}}}\) in \({\mathbb {F}}\) such that the series \(\sum _{n \in {\mathcal {N}}} a_n \, {\varvec{x}}_n\) converges unconditionally to f. If \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) is an unconditional basic sequence, there is a constant \(K\ge 1\) such that
for all finitely non-zero sequence of scalars \((a_n)_{n\in {\mathcal {N}}}\) with \(|a_n|\le |b_n|\) for all \(n\in {\mathcal {N}}\) (see [3, Theorem 1.10]). If this condition is satisfied some \(K\ge 1\) we say that \({\mathcal {X}}\) is K-unconditional and if, additionally, \([{\varvec{x}}_n :n \in {\mathcal {N}}]=X\) then \({\mathcal {X}}\) is said to be an unconditional basis of \(X\). An unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) in \(X\) becomes 1-unconditional under the renorming
Thus, we will in general take the viewpoint that an unconditional basis in a quasi-Banach space \(X\) confers the structure of an atomic quasi-Banach lattice on \(X\).
If \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) is an unconditional basis of \(X\) with biorthogonal functionals \(({\varvec{x}}_n^*)_{n \in {\mathcal {N}}}\), the map \({\mathcal {F}}:X\rightarrow {\mathbb {F}}^{\mathcal {N}}\) given by
will be called the coefficient transform with respect to \({\mathcal {X}}\). The support of \(f\in X\) with respect to \({\mathcal {X}}\) is the set
and the support of a functional \(f^*\in X^*\) with respect to \({\mathcal {X}}\) is the set
Given \(A\subseteq {\mathcal {N}}\), we denote by \(S_A:X\rightarrow X\) the coordinate projection associated to the basis \({\mathcal {X}}\) onto the subspace \([{\varvec{x}}_{n}:n\in A]\),
If \({\mathcal {J}}\) is a countable set, we write \({\mathcal {E}}_{{\mathcal {J}}}:=({\varvec{e}}_j)_{j\in {\mathcal {J}}}\) for the canonical unit vector system of \({\mathbb {F}}^{{\mathcal {J}}}\), i.e., \({\varvec{e}}_j=(\delta _{j,k})_{k\in {\mathcal {J}}}\) for each \(j\in {\mathcal {J}}\), where \(\delta _{j,k}=1\) if \(j=k\) and \(\delta _{j,k}=0\) otherwise. A sequence space on \({\mathcal {J}}\) will be a quasi-Banach lattice \({{\mathcal {L}}}\subseteq {\mathbb {F}}^{{\mathcal {J}}}\) for which the 1-unconditional basic sequence \({\mathcal {E}}_{{\mathcal {J}}}\) is normalized. If \(c_{00}\) is dense in \({{\mathcal {L}}}\), so that \({\mathcal {E}}_{{\mathcal {J}}}\) is a normalized 1-unconditional basis of \({{\mathcal {L}}}\), we say that \({{\mathcal {L}}}\) is a minimal sequence space. The most important examples of minimal sequence spaces \({{\mathcal {L}}}\) on a set \({\mathcal {J}}\) are the classical Lebesgue sequence spaces \(\ell _p({\mathcal {J}})\) for \(0<p<\infty \), and \(c_0({\mathcal {J}})\). As is customary, \(\ell _p\) will stand for the space \(\ell _p({\mathbb {N}})\) and \(\ell _p^s\) will denote the space \(\ell _p(\{n\in {\mathbb {N}}:n\le s\})\) for \(s\in {\mathbb {N}}\).
We will refer to a sequence space \({{\mathcal {L}}}\) on \({\mathbb {N}}\) as being subsymmetric if for each increasing function \(\phi :{\mathbb {N}}\rightarrow {\mathbb {N}}\), the operator \(S_\phi :{{\mathcal {L}}}\rightarrow {{\mathcal {L}}}\) defined by
is an isometric embedding. If \(S_\phi \) is an isometry for every one-to-one map \(\phi \), \({{\mathcal {L}}}\) will be said to be symmetric.
Given a sequence space \({{\mathcal {L}}}\) on \({\mathcal {J}}\), and a family \((X_j, \Vert \cdot \Vert _{X_{j}})_{j\in {\mathcal {J}}}\) of (possibly repeated) quasi-Banach spaces with moduli of concavity uniformly bounded, the space
is a quasi-Banach space with the quasi-norm
Let \((Y_j)_{j\in {\mathcal {J}}}\) be another collection of (possibly repeated) quasi-Banach spaces. If for each \(j\in {\mathcal {J}}\), the map \(T_j:X_j\rightarrow Y_j\) is a bounded linear operator and \(M:=\sup _{j\in {\mathcal {J}}} \Vert T_j\Vert <\infty \), then the linear operator
is bounded with \(\Vert T\Vert \le M\).
The dual space \({{\mathcal {L}}}^*\) of a minimal sequence space on \({\mathcal {J}}\) can be isometrically identified with a sequence space on \({\mathcal {J}}\). Thus, the dual space of \(\left( \bigoplus _{j\in {\mathcal {J}}} X_j\right) _{{\mathcal {L}}}\) can be isometrically identified with \(\left( \bigoplus _{j\in {\mathcal {J}}} X_j^*\right) _{{{\mathcal {L}}}^*}\).
For each \(k\in {\mathcal {J}}\) let \(L_k:X_k \rightarrow (\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) be the canonical embedding. If there is a constant K such that, for each \(j\in {\mathcal {J}}\), \({\mathcal {X}}_j=({\varvec{x}}_{j,n})_{n\in {\mathcal {N}}_j}\) is a K-unconditional basic sequence, then the sequence
is a K-unconditional basic sequence of \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\). If \({\mathcal {X}}_j\) is normalized for all \(j\in {\mathcal {J}}\), so is \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{\mathcal {L}}}\). If \({\mathcal {X}}_j\) is a basis of \(X_j\) for all \(j\in {\mathcal {J}}\) and \({{\mathcal {L}}}\) is minimal, then \(\left( \bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j\right) _{{\mathcal {L}}}\) is a basis of \(X=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) whose dual basis is \(\left( \bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j^*\right) _{{{\mathcal {L}}}^*}\) via the aforementioned identification between \(X^*\) and \(\left( \bigoplus _{j\in {\mathcal {J}}} X_j^*\right) _{{{\mathcal {L}}}^*}\).
If \({\mathcal {J}}\) is finite and \({{\mathcal {L}}}=\ell _\infty ({\mathcal {J}})\) we set \(\bigoplus _{j\in {\mathcal {J}}} X_j =(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) and \(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j )_{{\mathcal {L}}}\). If \(X_j=X\) for all \(j\in {\mathcal {J}}\), we set \({{\mathcal {L}}}(X)=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\). Similarly, if \({\mathcal {X}}_j={\mathcal {X}}\) for all \(j\in {\mathcal {J}}\), we set \({{\mathcal {L}}}({\mathcal {X}}) =(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\). Finally, given \(s\in {\mathbb {N}}\), we put \(X^s=\ell _\infty ^s(X)\) and \({\mathcal {X}}^s=\ell _\infty ^s({\mathcal {X}})\).
Suppose that \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) and \({\mathcal {Y}}=({\varvec{y}}_n)_{n \in {\mathcal {N}}}\) are families of vectors in quasi-Banach spaces \(X\) and \(Y\), respectively. Let \(C\in (0,\infty )\). We say that \({\mathcal {X}}\) C-dominates \({\mathcal {Y}}\) if there is a linear map T from \([{\mathcal {X}}]\) into \(Y\) with \(T({\varvec{x}}_n)={\varvec{y}}_n\) for all \(n \in {\mathcal {N}}\) and \(\Vert T\Vert \le C\). If T is an isomorphic embedding with \(\max \{\Vert T\Vert , \Vert T^{-1}\Vert \} \le C\in [1,\infty )\), \({\mathcal {X}}\) and \({\mathcal {Y}}\) are said to be C-equivalent. We say that \({\mathcal {X}}\) is permutatively C-equivalent to a family \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) in \(Y\), and we write \({\mathcal {X}}\sim _C{\mathcal {Y}}\), if there is a bijection \(\pi :{\mathcal {N}}\rightarrow {\mathcal {M}}\) such that \({\mathcal {X}}\) and \(({\varvec{y}}_{\pi (n)})_{n \in {\mathcal {N}}}\) are C-equivalent. A subbasis of an unconditional basis \(({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) is a family \(({\varvec{x}}_n)_{n\in {\mathcal {M}}}\) for some subset \({\mathcal {M}}\) of \({\mathcal {N}}\).
The symbol  will mean that the unconditional basic sequence \({\mathcal {Y}}\) is C-equivalent to a permutation of a subbasis of the unconditional basis \({\mathcal {X}}\). In all the above cases, if the precise constants are irrelevant, we simply drop them from the notation.
will mean that the unconditional basic sequence \({\mathcal {Y}}\) is C-equivalent to a permutation of a subbasis of the unconditional basis \({\mathcal {X}}\). In all the above cases, if the precise constants are irrelevant, we simply drop them from the notation.
A sequence \(({\varvec{x}}_{n})_{n\in {\mathcal {N}}}\) in a quasi-Banach space \(X\) said to be semi-normalized if
If \(a=b=1\) we say that \(({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) is normalized.
Given an unconditional basic sequence \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) and non-zero scalars \((a_n)_{n\in {\mathcal {N}}}\), the rescaled basic sequence \((a_n \, {\varvec{x}}_n)_{n\in {\mathcal {N}}}\) is equivalent to \({\mathcal {X}}\) if and only if \((a_n)_{n\in {\mathcal {N}}}\) is semi-normalized. Thus, the properties related to the uniqueness of unconditional bases in quasi-Banach spaces must be stated in terms of normalized (or, equivalently, semi-normalized) basic sequences. We say that a quasi-Banach space \(X\) has a unique unconditional basis up to equivalence and permutation (UTAP unconditional basis for short) if it has a normalized unconditional basis \({\mathcal {X}}\) and any other normalized unconditional basis is permutatively equivalent to \({\mathcal {X}}\). Other more specific terminology will be introduced in context when needed.
3 Preliminary results
Our approach to the uniqueness of unconditional basis problem in infinite direct sums of quasi-Banach spaces will rely on an amalgamation of a set of techniques, most of which are specific to the non-locally convex case. In this preparatory section we present the properties and the different methods that will be used in the proofs of our main results in Sects. 4, 5, and 6.
The earliest applications of combinatorial methods to the uniqueness of unconditional basis problem can be found in the work of Mitjagin in the early 1970’s [32, 33], but it was Wójtowicz who gave in 1988 a precise formulation of the so-called Schröder–Bernstein principle for unconditional bases (see [38, Corollary 1]).
Theorem 3.1
(Schröder–Bernstein principle for unconditional bases) Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be unconditional bases of quasi-Banach spaces \(X\) and \(Y\), respectively. Suppose that  and
and  . Then \({\mathcal {X}}\sim {\mathcal {Y}}\).
. Then \({\mathcal {X}}\sim {\mathcal {Y}}\).
Wojtaszczyk rediscovered independently ten years later, in 1997, the idea of using a combinatorial argument in his study of the uniqueness of unconditional basis of \(H_{p}({\mathbb {T}})\) for \(0<p<1\) and reproved Theorem 3.1 (see [37, Proposition 2.11]). He added to the previous arguments the following refinement of the Marriage Lemma. Notice that the case \(N=1\) in Theorem 3.2 is the Marriage Lemma as stated by Hall (see [20, Theorem 1]).
Theorem 3.2
Let \({\mathcal {N}}\) be a set and \(({\mathcal {N}}_i)_{i\in I}\) be a family of finite subsets of \({\mathcal {N}}\). Suppose \(N\in {\mathbb {N}}\) is such that
for all \(F\subseteq I\) finite. Then there exist a partition \((I_j)_{j=1}^N\) of I, and one-to-one maps \(\phi _j:I_j\rightarrow {\mathcal {N}}\) with \(\phi _j(i)\in {\mathcal {N}}_i\) for all \(i\in I_j\) and all \(j=1, \ldots , N\).
We next enunciate a simple lemma, whose straightforward proof we omit.
Lemma 3.3
Let \({{\mathcal {L}}}\) be a sequence space on a countable set \({\mathcal {J}}\), and for \(j\in {\mathcal {J}}\) let \(X_j\) and \(Y_j\) be quasi-Banach spaces with moduli of concavity uniformly bounded by \(\kappa \). Suppose that for each \(j\in {\mathcal {J}}\), \({\mathcal {X}}_j\) is a normalized K-unconditional basic sequence of \(X_j\) and that \({\mathcal {Y}}_j\) is an unconditional basic sequence of \(Y_j\) which is C-equivalent to \({\mathcal {X}}_j\), where K and C are constants independent of j.Then the semi-normalized unconditional basic sequence \( (\oplus _{j\in {\mathcal {J}}}{\mathcal {Y}}_j)_{{{\mathcal {L}}}}\) of \( (\oplus _{j\in {\mathcal {J}}}Y_j)_{{{\mathcal {L}}}}\) is C-equivalent to the normalized unconditional basic sequence \((\bigoplus _{j\in {\mathcal {J}}}{\mathcal {X}}_j)_{{\mathcal {L}}}\) of \((\bigoplus _{j\in {\mathcal {J}}}X_j)_{{\mathcal {L}}}\).
Our first result provides sufficient conditions for an infinite direct sum of unconditional bases to be equivalent to its square.
Lemma 3.4
Let \({{\mathcal {L}}}\) be a sequence space on a countable set \({\mathcal {J}}\). For each \(j\in {\mathcal {J}}\) let \({\mathcal {X}}_j\) be a normalized K-unconditional basis of a quasi-Banach space \(X_j\) with modulus of concavity bounded above by \(\kappa \), where \(\kappa \) and K are constants independent of j. Suppose that one the the following conditions holds:
-
(a)
There is a constant C such that \({\mathcal {X}}_j^2\sim _C{\mathcal {X}}_j\) for all \(j\in {\mathcal {J}}\).
-
(b)
\({{\mathcal {L}}}^2\) is lattice isomorphic to \({{\mathcal {L}}}\), and \({\mathcal {X}}_j={\mathcal {Y}}\) for all \(j\in {\mathcal {J}}\) and some unconditional basis \({\mathcal {Y}}\).
-
(c)
\({{\mathcal {L}}}\) is subsymmetric, and there is constant C such that, for each \(j\in {\mathcal {J}}\),
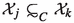 for infinitely many values of \(k\in {\mathcal {J}}={\mathbb {N}}\).
for infinitely many values of \(k\in {\mathcal {J}}={\mathbb {N}}\).
Then the basis \({\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{\mathcal {L}}}\) is equivalent to a permutation of its square.
Proof
The unconditional basis \({\mathcal {X}}^2\) is equivalent to a permutation of \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j^2)_{{\mathcal {L}}}\). Thus, if (a) holds, applying Lemma 3.3 yields \({\mathcal {X}}^2\sim {\mathcal {X}}\).
The basis \({\mathcal {X}}^2\) is also equivalent to a permutation of \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{{\mathcal {L}}}^2}\). Therefore, in the cases (b) and (c), since \({{\mathcal {L}}}^2\) is lattice isomorphic to \({{\mathcal {L}}}\), \({\mathcal {X}}^2\) is equivalent to a permutation of \({\mathcal {X}}':=(\bigoplus _{j\in {\mathcal {N}}}{\mathcal {X}}_{\phi (j)})_{{\mathcal {L}}}\) for some map \(\phi :{\mathcal {N}}\rightarrow {\mathcal {N}}\). If (b) holds, \( {\mathcal {X}}_{\phi (j)} ={\mathcal {X}}_j\) for all \(j\in {\mathcal {N}}\) so that \({\mathcal {X}}'={\mathcal {X}}\). Finally, assume that (c) holds. Then, we recursively construct an increasing map \(\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}\) such that  . By Lemma 3.3,
. By Lemma 3.3,  . By subsymmetry, \({\mathcal {X}}''\) is isometrically equivalent to a subbasis of \({\mathcal {X}}\). Hence, by Theorem 3.1, \({\mathcal {X}}^2\sim {\mathcal {X}}\). \(\square \)
. By subsymmetry, \({\mathcal {X}}''\) is isometrically equivalent to a subbasis of \({\mathcal {X}}\). Hence, by Theorem 3.1, \({\mathcal {X}}^2\sim {\mathcal {X}}\). \(\square \)
3.1 The Cassaza–Kalton paradigm extended
In a couple of papers of classical elegance (see [16, 17]), Casazza and Kalton crucially used the lattice structure induced by an unconditional basis on a Banach space to provide a much shorter proof than the original one of the uniqueness of unconditional basis (UTAP) of \(c_{0}(\ell _{1})\). Of course, these techniques were not yet available when Bourgain et al. wrote their AMS Memoir [14], otherwise the proofs of their aforementioned results would have been considerably simpler.
Cassaza and Kalton’s methods were transferred to the setting of quasi-Banach lattices and put into practice in [7] to obtain the uniqueness of unconditional basis (UTAP) in the spaces \(\ell _{1}(\ell _{p})\) and \(\ell _{p}(\ell _{1})\) for \(0<p<1\), and in [10] to give a much shorter proof than the original one of the uniqueness of unconditional basis of \(\ell _{p}(c_{0})\) for \(0<p<1\) (cf. [8]). The extension to quasi-Banach lattices required the notions of L-convexity and anti-Euclidean spaces, which we recall next for the convenience of the reader.
A quasi-Banach lattice \(X\) is said to be L-convex if there is \(0<\varepsilon <1\) so that
whenever f and \((f_i)_{i=1}^k\) in \(X\) satisfy \((1-\varepsilon )kf\ge \sum _{i=1}^k f_i\) and \(0\le f_i\le f\) for every \(i=1, \ldots , k\). We say that a family \((X_j)_{j\in {\mathcal {J}}}\) of quasi-Banach lattices is L-convex if there is \(\varepsilon >0\) such each lattice \(X_j\) is L-convex with constant \(\varepsilon \) for every \(j\in {\mathcal {J}}\). Kalton [23] showed that a quasi-Banach lattice \(X\) is L-convex if and only if it is p-convex for some \(p>0\), that is, for some constant C and all \(f_{1},\ldots , f_{k}\) in \(X\) we have
The element \((\sum _{i=1}^k \vert f_i\vert ^p)^{1/p}\) of \(X\) is defined via the procedure outlined in [30, pp. 40-41]. The optimal constant in (3.1) will be denoted by \(M_p(X)\).
Quantitatively, if \(X\) is L-convex with constant \(\varepsilon \), there exists \(r>0\) and constants \((C_p)_{0<p<r}\) depending only on \(\varepsilon \) and the modulus of concavity of \(X\), such that \(M_p(X)\le C_p\) for all \(0<p<r\). Conversely, if \(X\) is a p-convex quasi-Banach lattice with \(M_p(X)\le C\), there exist \(\kappa \) and \(\varepsilon \) depending only on p and C such that \(X\) is at once an L-convex lattice with constant \(\varepsilon \) and a quasi-Banach space with modulus of concavity at most \(\kappa \). This quantitative approach is perhaps the easiest way to see that if \({{\mathcal {L}}}\) is an L-convex sequence space on a set \({\mathcal {J}}\) and \((X_j)_{j\in {\mathcal {J}}}\) is a family of L-convex quasi-Banach lattices, then \(X:=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) is an L-convex lattice. In fact, if \(p>0\) and \(C\ge 1\) are such that \(M_p({{\mathcal {L}}})\le C\) and \(M_p(X_j)\le C\) for all \(j\in {\mathcal {J}}\), then \(M_p(X)\le C^2\).
A quasi-Banach space \(X\) is then called natural if it is isomorphic to a subspace of an L-convex quasi-Banach lattice. Most quasi-Banach spaces arising in analysis are natural. However, it should be pointed out that there are non-natural spaces with an unconditional basis [24]. It is known [23] that any lattice structure on a natural quasi-Banach space is L-convex. Thus, once we make sure that a quasi-Banach space \(X\) has a lattice structure, the notions of L-convexity and naturality become equivalent.
Our results will apply to those natural spaces where the lattice structure is induced by an unconditional basis. In such spaces any unconditional basis induces an L-convex lattice structure; then many of the standard techniques of Banach lattice theory can be employed in this setting. For most applications it is easy to verify that a certain space X is natural either by showing that it is p-convex for some \(p>0\) with the lattice structure induced by some unconditional basis, or by identifying X as a subspace of an L-convex lattice.
Definition 3.5
A family \(({\mathcal {X}}_j)_{j\in {\mathcal {J}}}\) of unconditional bases of quasi-Banach spaces \((X_j)_{j\in {\mathcal {J}}}\) is said to be L-convex if there are constants \(K\ge 1\) and \(0<\varepsilon <1\) such that \({\mathcal {X}}_j\) is K-unconditional and it induces an L-convex lattice structure on \(X_j\) with constant \(\varepsilon \) for all \(j\in {\mathcal {J}}\).
Notice that if \(({\mathcal {X}}_j)_{j\in {\mathcal {J}}}\) is an L-convex family of unconditional bases of quasi-Banach spaces \((X_j)_{j\in {\mathcal {J}}}\), then the modulus of concavity of the space \(X_j\) is uniformly bounded. Moreover, if \({{\mathcal {L}}}\) is an L-convex sequence space over \({\mathcal {J}}\), then \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{\mathcal {L}}}\) is an unconditional basis of the quasi-Banach space \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) which induces a structure of L-convex lattice.
A Banach space \(X\) is said to be anti-Euclidean if it does not contain uniformly complemented copies of finite-dimensional Hilbert spaces. As for L-convexity, to deal with families of quasi-Banach spaces we need a more quantitative definition.
Definition 3.6
A family \((X_j)_{j\in {\mathcal {J}}}\) of Banach spaces is said to be anti-Euclidean if for every \(R\in (0,\infty )\) there is \(k\in {\mathbb {N}}\) such that \(\Vert S\Vert \, \Vert T\Vert \ge R\) whenever \(j\in {\mathcal {J}}\) and \(S:\ell _2^k\rightarrow X_j\), \(T:X_j\rightarrow \ell _2^k\) are linear operators with \(T\circ S=\mathrm {Id}_{\ell _2^k}\).
By the principle of local reflexivity, a family \((X_j)_{j\in {\mathcal {J}}}\) of Banach spaces is anti-Euclidean if and only if \((X_j^*)_{j\in {\mathcal {J}}}\) is. The most natural and important examples of anti-Euclidean spaces are \(c_0\) and \(\ell _1\). Let us bring up a result by Casazza and Kalton.
Theorem 3.7
[17, Proposition 2.4] Suppose that the countable family \((X_j)_{j\in {\mathcal {J}}}\) of Banach spaces is anti-Euclidean. Then the Banach space \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{\ell _1}\) is anti-Euclidean.
Note that, although Definition 3.6 makes sense for quasi-Banach spaces, as a matter of fact we only state it (and will use it) for the “closest” Banach spaces to the quasi-Banach spaces we study, i.e., their Banach envelopes. Formally speaking, the Banach envelope of a quasi-Banach space \(X\) consists of a Banach space \({\widehat{X}}\) together with a linear contraction \(E_X:X\rightarrow {\widehat{X}}\), called the envelope map of \(X\), satisfying the following universal property: for every Banach space \(Y\) and every linear contraction \(T:X\rightarrow Y\) there is a unique linear contraction \({\widehat{T}}:{\widehat{X}}\rightarrow Y\) such that \({\widehat{T}}\circ E_X=T\). The Banach envelope of a quasi-Banach space can be effectively constructed from the Minkowski functional of \({\text {co}}(B_X)\). This construction shows that \(E_X({\text {co}}(B_X))\) is a dense subset of \(B_{{\widehat{X}}}\). We say that a Banach space \(Y\) is the Banach envelope of \(X\) via the map \(J:X\rightarrow Y\) if the associated map \({\widehat{J}}:{\widehat{X}}\rightarrow Y\) is an isomorphism.
The Banach envelope of a minimal sequence space is isometrically isomorphic to a minimal sequence space via the inclusion map (see [3, Proposition 10.9]). We will need the following result.
Proposition 3.8
Let \({{\mathcal {L}}}\) be a minimal sequence space on \({\mathcal {J}}\). Suppose that \(X_j\) is a quasi-Banach space with modulus of concavity bounded by a uniform constant \(\kappa \) for all \(j\in {\mathcal {J}}\). Then the Banach envelope of \(X=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) is isometrically isomorphic to \(Y=(\bigoplus _{j\in {\mathcal {J}}} \widehat{X_j})_{{\widehat{{{\mathcal {L}}}}}}\) via the map
Proof
Since J defines a linear contraction from \(X\) into \(Y\), it suffices to prove that \(J({\text {co}}(B_X))\) is a dense subset of \(B_Y\). Let \(f=(f_j)_{j\in {\mathcal {J}}}\in B_Y\) and \(\varepsilon >0\). For each \(j\in {\mathcal {J}}\) set \(g_j=f_j/\Vert f_j\Vert \) if \(f_j\not =0\) and \(g_j=0\) otherwise. Since \(g_j\in B_{\widehat{X_j}}\), for each \(j\in {\mathcal {J}}\) there is \(h_j\in {\text {co}}(B_{X_j})\) such that \(\Vert g_j-E_{X_j}(h_j)\Vert \le \varepsilon /2\). Put \(\Gamma =(\gamma _j)_{j\in {\mathcal {J}}}\), where \(\gamma _j=\Vert f_j\Vert \) for \(j\in {\mathcal {J}}\). Since \(\Gamma \in B_{{\widehat{{{\mathcal {L}}}}}}\), there is \(\Lambda \in {\text {co}}(B_{{\mathcal {L}}})\) such that \(\Vert \Gamma -\Lambda \Vert _{{\widehat{{{\mathcal {L}}}}}}\le \varepsilon /2\). Moreover, passing to a suitable projection, we can choose \(\Lambda \) to be finitely supported. Then, if we denote \(\Lambda =(\lambda _j)_{j\in {\mathcal {J}}}\), we have that \(h:=(\lambda _j h_j)_{j\in {\mathcal {J}}}\in {\text {co}}(B_X)\). Therefore, if \(g=(\lambda _j g_j)_{j\in {\mathcal {J}}}\),
\(\square \)
In most cases, the proof of the uniqueness of unconditional basis in a given Banach (or quasi-Banach) space also sheds light onto the unconditional structure of its complemented subspaces with an unconditional basis. A sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) in a quasi-Banach space \(X\) is said to be complemented if its closed linear span \(Y= [{\mathcal {Y}}]\) is a complemented subspace of \(X\), i.e., there is a bounded linear map \(P:X\rightarrow Y\) with \(P|_{Y}=\mathrm {Id}_Y\). An unconditional basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) is complemented in \(X\) if and only if there exists a sequence \({\mathcal {Y}}^*=({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\) in \(X^*\) such that \({\varvec{y}}_m^*({\varvec{y}}_n)=\delta _{m,n}\) for all \((m,n)\in {\mathcal {M}}^2\) and there is a bounded linear map \(P:X\rightarrow X\) given by
in which case
We will refer to \({\mathcal {Y}}^*\) as a sequence of projecting functionals for \({\mathcal {Y}}\).
To understand the simplifications derived from taking into account the lattice structure induced by an unconditional basis \({\mathcal {X}}\) on the entire space \(X\), we must look at the supports of \({\mathcal {Y}}\) and \({\mathcal {Y}}^*\) with respect to \({\mathcal {X}}\).
Definition 3.9
Let \(X\) be a quasi-Banach space with an unconditional basis \({\mathcal {X}}\). We say that an unconditional basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) is well complemented in \(X\) if it is complemented in \(X\) and there is a sequence \({\mathcal {Y}}^*=({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\) of projecting functionals for \({\mathcal {Y}}\) such that:
-
(i)
\({\text {supp}}({\varvec{y}}_m^*)\subseteq {\text {supp}}({\varvec{y}}_m)\) for all \(m\in {\mathcal {M}}\), and
-
(ii)
\(({\text {supp}}({\varvec{y}}_m))_{m\in {\mathcal {M}}}\) is a pairwise disjoint family consisting of finite sets.
In this case, we say that \({\mathcal {Y}}^*\) is a sequence of good projecting functionals for \({\mathcal {Y}}\). If \(\Gamma {[{\mathcal {Y}},{\mathcal {Y}}^*]} \le C\) we will say that \({\mathcal {Y}}\) is well C-complemented and that \({\mathcal {Y}}^*\) are good C-projecting functionals.
Remark 3.10
Note that a subbasis of a well C-complemented basic sequence \(({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) is a a well C-complemented basic sequence. In particular, if \(({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\) are good C-projecting functionals, \(\Vert {\varvec{y}}_m\Vert \, \Vert {\varvec{y}}_m^*\Vert \le C\) for all \(m\in {\mathcal {M}}\).
The following definition identifies and gives relevance to an unstated feature shared by some unconditional bases. Examples of such bases can be found, e.g., in [9, 16, 22], where the property naturally arises in connection with the problem of uniqueness of unconditional basis.
Definition 3.11
A normalized unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) of a quasi-Banach space will be said to be universal for well complemented block basic sequences if for every normalized well complemented basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) of \({\mathcal {X}}\) there is a map \(\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}\) such that \(\pi (m)\in {\text {supp}}({\varvec{y}}_m)\) for every \(m\in {\mathcal {M}}\), and \({\mathcal {Y}}\) is equivalent to the rearranged subbasis \(({\varvec{x}}_{\pi (m)})_{m\in {\mathcal {M}}}\) of \({\mathcal {X}}\). In the case when there is a function \(\eta :[1,\infty )\rightarrow [1,\infty )\) such that \({\mathcal {Y}}\) is \(\eta (C)\)-equivalent to \(({\varvec{x}}_{\pi (m)})_{m\in {\mathcal {M}}}\) of \({\mathcal {X}}\) whenever \({\mathcal {Y}}\) is well C-complemented, we say that \({\mathcal {X}}\) is uniformly universal for well complemented block basic sequences (with function \(\eta \)).
Thus, the following theorem summarizes what can be rightfully called the “Casazza-Kalton paradigm” to tackle the uniqueness of unconditional basis problem extended to quasi-Banach lattices. To be able to prove it in this optimal form (even for locally convex spaces) has required the very recent solution in the positive of the “canceling squares” problem (see [1]).
Theorem 3.12
(see [1, Theorem 3.9]) Let \(X\) be a quasi-Banach space with a normalized unconditional basis \({\mathcal {X}}\). Suppose that:
-
(i)
The lattice structure induced by \({\mathcal {X}}\) in \(X\) is L-convex;
-
(ii)
The Banach envelope of \(X\) is anti-Euclidean;
-
(iii)
\({\mathcal {X}}\) is universal for well complemented block basic sequences; and
-
(iv)
\({\mathcal {X}}\sim {\mathcal {X}}^2\).
Then \(X\) has a (UTAP) unconditional basis.
3.2 The peaking property
Another technique that has become crucial to determine the uniqueness of unconditional basis in quasi-Banach spaces is the “large coefficient technique.” It was introduced by Kalton in [22] to prove the uniqueness of unconditional basis in nonlocally convex Orlicz sequence spaces \(\ell _{F}\). Kalton called a complemented basic sequence \(({\varvec{y}}_{n})\) in \(\ell _{F}\) inessential if
and proved that if \(({\varvec{y}}_{n})\) is inessential then it is equivalent to the canonical basis \(({\varvec{x}}_{k})\) of \(\ell _{F}\).
Kalton’s ideas were extended to the general framework of quasi-Banach lattices in [25]. Here we reformulate this property and regard it as a feature of the unconditional basis \(({\varvec{x}}_n)\) of the space instead of the complemented basic sequence \(({\varvec{y}}_{n})\).
Definition 3.13
An unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) of a quasi-Banach space \(X\) will be said to have the peaking property if for every well complemented basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) with respect to \({\mathcal {X}}\) there is a sequence \(({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\) of good projecting functionals such that
In the case when there is a function \(\gamma :[1,\infty )\rightarrow [1,\infty )\) such that \( \gamma (C)\ge 1/c\) whenever \({\mathcal {Y}}\) is well C-complemented, we say that \({\mathcal {X}}\) has the uniform peaking property (with function \(\gamma \)).
The proof of Proposition 3.15 below relies on the following reduction lemma which will be used as well in Sect. 4.
Lemma 3.14
(cf. [2, Lemma 3.1]) Let \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) be a well complemented basic sequence with respect to an unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) of a quasi-Banach space \(X\), and let \(({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\) be a sequence of good projecting functionals for \({\mathcal {Y}}\). Suppose \({\mathcal {U}}=({\varvec{u}}_m)_{m\in {\mathcal {M}}}\) and \(({\varvec{u}}_m^*)_{m\in {\mathcal {M}}}\) are sequences in \(X\) and \(X^{*}\) respectively such that:
-
(i)
\(|{\varvec{x}}_n^*({\varvec{u}}_m)| \le D_1 |{\varvec{x}}_n^*({\varvec{y}}_m)|\) for all \((n,m)\in {\mathcal {N}}\times {\mathcal {M}}\),
-
(ii)
\(|{\varvec{u}}_m^*({\varvec{x}}_n)| \le D_2 |{\varvec{y}}_m^*({\varvec{x}}_n)|\) for all \((n,m)\in {\mathcal {N}}\times {\mathcal {M}}\), and
-
(iii)
\(|{\varvec{u}}_m^*({\varvec{u}}_m)|\ge {1}/{D_3}\) for all \(m\in {\mathcal {M}}\),
for some positive constants \(D_1\), \(D_2\) and \(D_3\). Then \({\mathcal {U}}\) is a well complemented basic sequence equivalent to \({\mathcal {Y}}\). Quantitatively, if \({\mathcal {Y}}\) is well C-complemented, and \({\mathcal {X}}\) is K-unconditional, then:
-
(i)
The sequence \({\mathcal {U}}\) is well B-complemented with good B-projecting functionals \((\lambda _m\, {\varvec{u}}_m^{*})_{m\in {\mathcal {M}}}\), where \(B=C D_1 D_2 D_3 K^2\) and \(\lambda _{m}=1/{\varvec{u}}_m^{*}(u_{m})\); and
-
(ii)
The basic sequence \({\mathcal {Y}}\) (\(CD_1K\))-dominates \({\mathcal {U}}\); and
-
(iii)
the basic sequence \({\mathcal {U}}\) (\(CD_2D_3K\))-dominates \({\mathcal {Y}}\).
Proof
The proof follows the steps of the proof of [2, Lemma 3.1], keeping track of the constants involved. \(\square \)
Proposition 3.15
(cf. [1, Proposition 3.3]) Let \(X\) be a quasi-Banach space with a normalized unconditional basis \({\mathcal {X}}\). If \({\mathcal {X}}\) has the peaking property, then \({\mathcal {X}}\) is universal for well complemented block basic sequences. Moreover, if \({\mathcal {X}}\) is K-unconditional and has the uniform peaking property with function \(\gamma \), then \({\mathcal {X}}\) is uniformly universal for well-complemented block basic sequences with function \(C\mapsto K C\gamma (C)\).
Proof
Go through the proof of [1, Proposition 3.3] with Lemma 3.14 in mind, paying attention to the constants involved. \(\square \)
The following lemma relies on Lemma 3.14. Given a family \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) in a quasi-Banach space \(X\) and \(A\subseteq {\mathcal {N}}\) finite, we will use the notation
Lemma 3.16
(cf. [7, Lemma 4.1]) Suppose \({\mathcal {X}}\) is a normalized K-unconditional basis of a quasi-Banach space \(X\) with dual basis \({\mathcal {X}}^*\). Assume that \({\mathcal {X}}\) D-dominates the unit vector system of \(\ell _1\). If \(B=4C^2DK^2\), then for every normalized C-complemented basic sequence \({\mathcal {U}}\) in \(X\) there is a well B-complemented basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) in \(X\) such that:
-
(i)
\({\text {supp}}({\varvec{y}}_m)\subseteq {\text {supp}}({\varvec{u}}_m)\) for all \(m\in {\mathcal {M}}\);
-
(ii)
\({\mathcal {Y}}\) is E-equivalent to \({\mathcal {U}}\), where \(E=2CK\max \{C,D\}\); and
-
(iii)
\((\mathbb {1}_{{\text {supp}}({\varvec{y}}_m)}[{\mathcal {X}}^*])_{m\in {\mathcal {M}}}\) is a family of good B-projecting functionals for \({\mathcal {Y}}\).
Proof
Just go over the lines of the proof of [1, Lemma 3.6] paying attention to the constants involved. \(\square \)
3.3 Strongly absolute bases
Strong absoluteness was identified by Kalton, Leránoz, and Wojtaszczyk in [25] as the crucial differentiating feature of unconditional bases in quasi-Banach spaces in their investigation of the uniqueness of unconditional bases. One could say that strongly absolute bases are “purely nonlocally convex” bases, in the sense that if a quasi-Banach space \(X\) has a strongly absolute basis, then its unit ball is far from being a convex set and so \(X\) is far from being a Banach space. Although the term strongly absolute for a basis was coined in [25], here we work with a slightly different but equivalent definition.
Definition 3.17
An unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) of a quasi-Banach space \(X\) is strongly absolute if for every constant \(R>0\) there is a constant \(C>0\) such that
If \(\alpha :(0,\infty )\rightarrow (0,\infty )\) is such that (3.4) holds with \(C= \alpha (R)\) for every \(0<R<\infty \), we say that \({\mathcal {X}}\) is strongly absolute with function \(\alpha \).
Note that if we rescale a strongly absolute basis we obtain a strongly absolute basis with the same function. Note also that a normalized unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) is strongly absolute with function \(\alpha \) if and only if
If \({\mathcal {X}}=({\varvec{x}}_n)_{n \in {\mathcal {N}}}\) is a strongly absolute basis with function \(\alpha \) of a quasi-Banach space \(X\), the normalized basis \(({\varvec{x}}_n/\Vert {\varvec{x}}_n\Vert )_{n\in {\mathcal {N}}}\) D-dominates the unit vector basis of \(\ell _1({\mathcal {N}})\), where
Roughly speaking a normalized (or semi-normalized) unconditional basis is strongly absolute if and only if it dominates the unit vector basis of \(\ell _1\), and whenever the \(\ell _1\)-norm and the quasi-norm of a vector are comparable then so are the \(\ell _{\infty }\)-norm and the \(\ell _1\)-norm of its coordinates.
Adding combinatorial arguments to the methods from [25] enabled Wojtaszczyk to prove the following criterion for spaces with a strongly absolute basis. Needless to say, he could not count on the Casazza-Kalton paradigm since it had not been discovered yet.
Theorem 3.18
(See [37, Theorem 2.12]) Let \(X\) be a natural quasi-Banach space with a strongly absolute unconditional basis \(({\varvec{x}}_{n})_{n\in {\mathcal {N}}}\). Assume also that \(X\) is isomorphic to some of its cartesian powers \(X^{s}\), \(s\ge 2\). Then all normalized unconditional bases of \(X\) are permutatively equivalent.
For further reference, we record an elementary lemma.
Lemma 3.19
Let \({\mathcal {X}}\) and \({\mathcal {Y}}\) be normalized unconditional bases of quasi-Banach spaces \(X\) and \(Y\) respectively. Suppose that \({\mathcal {X}}\) is strongly absolute with function \(\alpha \) and that \({\mathcal {Y}}\) D-dominates \({\mathcal {X}}\). Then \({\mathcal {Y}}\) is strongly absolute with function \(D\alpha \).
The following proposition guarantees the strongly absoluteness of infinite direct sums of strongly absolute bases. Some applications in Sect. 7 will rely on it as we shall see.
Proposition 3.20
Let \({{\mathcal {L}}}\) be a sequence space on a set \({\mathcal {J}}\). Suppose the canonical basis of \(\mathcal L\) is absolute basis. For each \(j\in {\mathcal {J}}\) let \({\mathcal {X}}_j\) be a K-unconditional basis of a quasi-Banach space with modulus of concavity at most \(\kappa \), where \(\kappa \) and K are constants independent of j. Suppose that there is \(\alpha \) such that \({\mathcal {X}}_j\) is strongly absolute with function \(\alpha \) for all \(j\in {\mathcal {J}}\). Then \({\mathcal {X}}:=(\bigoplus _{j\in {\mathcal {N}}} {\mathcal {X}}_j)_{{\mathcal {L}}}\) is a strongly absolute unconditional basis of \(X:=(\bigoplus _{j\in {\mathcal {N}}} X_j)_{{\mathcal {L}}}\). Moreover, if \(\beta \) is a strongly absolute function for the unit vector system of \({{\mathcal {L}}}\), then the map
is a strongly absolute function for \({\mathcal {X}}\).
Proof
Without lost of generality we assume that \({\mathcal {X}}_j\) is normalized for all \(j\in {\mathcal {J}}\) so that \({\mathcal {X}}\) is normalized too. For each \(j\in {\mathcal {J}}\) let \({\mathcal {F}}_j\) be the coefficient transform with respect to \({\mathcal {X}}_j\). Let \(\beta \) be a strongly absolute function for \({{\mathcal {L}}}\). Pick \(f=(f_j)_{j\in {\mathcal {J}}} \in X\) and \(R\in (0,\infty )\) such that
Since, by unconditionality,
we obtain
Let \(k\in {\mathcal {J}}\) be such that \(\Vert {\mathcal {F}}_k(f_k)\Vert _1=\sup _{j\in {\mathcal {J}}} \Vert {\mathcal {F}}_j(f_j)\Vert _1\). By unconditionality,
so that,
Since \(\Vert {\mathcal {F}}(f)\Vert _\infty =\sup _j \Vert {\mathcal {F}}_j(f_j) \Vert _\infty \), we obtain
\(\square \)
4 Infinite \({{\mathcal {L}}}\)-sums of quasi-Banach spaces, where \({{\mathcal {L}}}\) is a sequence space with a strongly absolute basis
Our first theorem in this section uses the previous ingredients and the language introduced in Sect. 3 to provide, in particular, an extension of [7, Theorem 4.5], which established the uniqueness of unconditional basis (UTAP) in the spaces \(\ell _{p}(\ell _{1})\) for \(0<p<1\).
Theorem 4.1
Let \({{\mathcal {L}}}\) be a sequence space on a set \({\mathcal {J}}\). Suppose the canonical basis of \(\mathcal L\) is absolute basis. For each \(j\in {\mathcal {J}}\), let \({\mathcal {X}}_j\) be a normalized K-unconditional basis of quasi-Banach space \(X_j\) with modulus of concavity at most \(\kappa \), where K and \(\kappa \) are independent of j. Suppose that there is a function \(\eta :[1,\infty )\rightarrow [1,\infty )\) such that \({\mathcal {X}}_j\) is uniformly universal for well complemented block basic sequences with function \(\eta \) for all \(j\in {\mathcal {J}}\). Then the unconditional basis \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{{\mathcal {L}}}}\) of the infinite direct sum \(X:=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{{\mathcal {L}}}}\) is uniformly universal for well complemented block basic sequences.
Proof
We isometrically identify \(X^*\) with \({\mathbb {V}}:=(\oplus _{j\in {\mathcal {J}}} X_j^*)_{{{\mathcal {L}}}^*}\) via the natural dual pairing \(\langle \cdot ,\cdot \rangle :{\mathbb {V}}\times X\rightarrow {\mathbb {F}}\). For each \(j\in {\mathcal {J}}\), let \(L_j:X_j\rightarrow X\) and \(L_j':X_j^*\rightarrow {\mathbb {V}}\) be the natural ‘inclusion’ maps, and let \(T_j:X\rightarrow X_j\) be the natural projection. Set \({\mathcal {X}}_j=({\varvec{x}}_{j,n})_{n\in {\mathcal {N}}_j}\). Let \(C\in [1,\infty )\) and let \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) be a normalized well C-complemented basic sequence with good C-projecting functionals \({\mathcal {Y}}^*=({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\). Let \(({\varvec{v}}_m)_{m\in {\mathcal {M}}}\) the corresponding sequence in \({\mathbb {V}}\) via the above described dual mapping. Set \({\varvec{y}}_m=({\varvec{y}}_{j,m})_{j\in {\mathcal {J}}}\) and \({\varvec{v}}_m=({\varvec{y}}^*_{j,m})_{j\in {\mathcal {J}}}\) for each \(m\in {\mathcal {M}}\). Set also
For \(m\in {\mathcal {M}}\), we have
and
Hence, if the unit vector system of \({{\mathcal {L}}}\) is strongly absolute with function \(\alpha \), we have
Therefore, there is a map \(\phi :{\mathcal {M}}\rightarrow {\mathcal {J}}\) such that
for all \(m\in {\mathcal {M}}\). By Lemma 3.14, the sequence \((L_{\phi (m)}({\varvec{y}}_{\phi (m),m}) )_{m\in {\mathcal {M}}}\) is E-equivalent to \({\mathcal {Y}}\), where \(E=\alpha (C) CK\). We have, in particular,
Set \(B=E^2CK^2\) and \(E'=ECK\). Applying again Lemma 3.14 gives that
is a normalized well B-complemented basic sequence \(E'\)-equivalent to \({\mathcal {Y}}\). For each \(j\in {\mathcal {J}}\) put
Composing the projections from \(X\) onto \(X\) associated to the well complemented basic sequence \(({\varvec{u}}_m)_{m\in {\mathcal {M}}_j}\) with the maps \(L_j\) and \(T_j\) we obtain that
is well B-complemented in \(X_j\). By assumption, for each \(j\in {\mathcal {J}}\) there is a map \(\nu _j:{\mathcal {M}}_j\rightarrow {\mathcal {N}}_j\) such that \(\nu _j(m)\in {\text {supp}}({\varvec{y}}_{j,m})\) for all \(m\in {\mathcal {M}}_j\) and \({\mathcal {Y}}_j\) is \(\eta (B)\)-equivalent to \(({\varvec{x}}_{j,\nu _{j}(m)})_{m\in {\mathcal {M}}_j}\). By Lemma 3.3, \({\mathcal {U}}\) is \(\eta (B)\)-equivalent to \((L_{\phi (m)}({\varvec{x}}_{\phi (m),\nu _{\phi (m)}(m)}))_{m\in {\mathcal {M}}}\). \(\square \)
We are now ready to obtain the main theoretical result of the section.
Theorem 4.2
Let \({{\mathcal {L}}}\) be an L-convex sequence space on a countable set \({\mathcal {J}}\). Let \(({\mathcal {X}}_j)_{j\in {\mathcal {J}}}\) be an L-convex family of normalized unconditional bases of quasi-Banach spaces \((X_j)_{j\in {\mathcal {J}}}\). Suppose that:
-
(i)
\({\mathcal {X}}_j\) is uniformly universal for well-complemented block basic sequences with function \(\eta \) for all \(j\in {\mathcal {J}}\);
-
(ii)
the family of Banach envelopes \(\left( \widehat{X_j}\right) _{j\in J}\) is anti-Euclidean;
-
(iii)
The unit vector system of \({{\mathcal {L}}}\) is strongly absolute; and
-
(iv)
one the the following conditions holds:
-
(a)
there is a constant C such that \({\mathcal {X}}_j^2\sim _C{\mathcal {X}}_j\) for all \(j\in {\mathcal {J}}\).
-
(b)
\({{\mathcal {L}}}^2\) is lattice isomorphic to \({{\mathcal {L}}}\), and \({\mathcal {X}}_j={\mathcal {Y}}\) for all \(j\in {\mathcal {J}}\) and some unconditional basis \({\mathcal {Y}}\).
-
(c)
\({{\mathcal {L}}}\) is subsymmetric, and there is a constant C such that, for each \(j\in {\mathcal {J}}\),
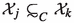 for infinitely many values of \(k\in {\mathcal {J}}\).
for infinitely many values of \(k\in {\mathcal {J}}\).
-
(a)
Then \(X=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{{\mathcal {L}}}\) has a (UTAP) unconditional basis.
Proof
Since the unit vector system of \({{\mathcal {L}}}\) is strongly absolute, its Banach envelope is lattice isomorphic to \(\ell _1\). By Proposition 3.8, the Banach envelope of \(X\) is isomorphic to \( \left( \bigoplus _{j\in {\mathcal {J}}} \widehat{X_j}\right) _{\ell _1}, \) which is anti-Euclidean by Theorem 3.7. By Theorem 4.1, \({\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{\mathcal {L}}}\) is (uniformly) universal for well complemented block basic sequences. By Lemma 3.4, \({\mathcal {X}}^2\sim {\mathcal {X}}\). Applying Theorem 3.12 puts an end to the proof. \(\square \)
Remark 4.3
A variation of the argument used to prove Theorem 4.1 gives that, if we replace the hypothesis “\({\mathcal {X}}_j\) is uniformly universal for well-complemented block basic sequences with function \(\eta \) for all \(j\in {\mathcal {J}}\)” with “there is a function \(\gamma :[1,\infty )\rightarrow [1,\infty )\) such that \({\mathcal {X}}_j\) has the uniform peaking property with function \(\gamma \)”, we obtain that the unconditional basis \((\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{{{\mathcal {L}}}}\) of \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{{{\mathcal {L}}}}\) has the uniform peaking property. In particular, any strongly absolute unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n\in {\mathcal {N}}}\) of any quasi-Banach space \(X\) has the uniform peaking property. Let us see a more direct proof of this result. For any \(f\in X\) and \(f^*\in X^*\) we have
and, if \({\mathcal {X}}\) is K-unconditional and normalized,
Because of this, if \(C\in (0,\infty )\) is such that \(\Vert f^*\Vert \, \Vert f\Vert \le C |f^*(f)|\), we obtain
where \(\alpha \) is the strongly absolute function of \({\mathcal {X}}\). Hence, if \(({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) is a well-complemented basic sequence with good C-projecting functionals \(({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\),
We conclude that \({\mathcal {X}}\) has the uniform peaking property with function \(C\mapsto \alpha (CK)\).
5 Infinite \(c_0\)-sums of spaces with strongly absolute bases
The uniqueness of unconditional basis of \(c_0(X)\) where \(X\) is a quasi-Banach space with a strongly absolute basis was proved in [12]. Here we show that the canonical basis of \(c_0(X)\) has the additional property of being uniformly universal for well complemented basic sequences. This fact will be crucial to deduce in Sect. 7 the uniqueness of unconditional basis of direct sums of infinitely many copies of the space \(c_0(X)\).
Theorem 5.1
For each \(j\in {\mathcal {J}}\), let \({\mathcal {X}}_j\) be a normalized K-unconditional basis of a quasi-Banach space \(X_j\) with modulus of concavity at most \(\kappa \), where \(\kappa \) and K are constants independent of j. Suppose that \({\mathcal {X}}_j\) is a normalized strongly absolute with the same function \(\alpha \) for all \(j\in {\mathcal {J}}\). Then the unconditional basis \({\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{c_0}\) of \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{c_0}\) is uniformly universal for well complemented basic sequences.
Proof
For each \(D\in [1,\infty )\), let \(\kappa _D\in [1,\infty )\) be such that
Let \({\mathcal {Y}}= ({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) be a normalized well C-complemented basic sequence with good C-projecting functionals \(({\varvec{y}}_m^*)_{m\in {\mathcal {M}}}\). Set \(R=2CK\) and, with the same terminology as in Lemma 6.2, for \(m\in {\mathcal {M}}\) put
and
Since \(B_m\subseteq {\text {supp}}({\varvec{y}}_m)\) for all \(m\in {\mathcal {M}}\), \((B_m)_{m\in {\mathcal {M}}}\) is a family of pairwise disjoint finite subsets of \({\mathcal {N}}\). If for each \(j\in {\mathcal {J}}\), we let \(A_{m,j}\) denote the jth-section of \(A_m\) we have
Hence,
A first consequence of (5.1) is that \(B_m\not =\emptyset \) for all \(m\in {\mathcal {M}}\) and so
In light of Lemma 3.14, inequality (5.1) also gives that \((S_{B_m}({\varvec{y}}_m))_{m\in {\mathcal {M}}}\) 2CK-dominates \({\mathcal {Y}}\). Moreover, since \(\vert \overline{{\varvec{x}}}_{j,n}^*({\varvec{y}}_m)\vert \le K\) for all \(m\in {\mathcal {M}}\) and \((j,n)\in {\mathcal {N}}\),
Let \(B_{m,j}\) denote the jth section of \(B_m\). Since \(\sum _{n\in {\mathcal {N}}_j} |\overline{{\varvec{x}}}_{j,n}^*({\varvec{y}}_m)|\le D(\alpha )\),
Choose an integer N larger than \(S:=\alpha ( 4 R \alpha (R) C K^2 \kappa _D )\), and consider the partition \(({\mathcal {M}}_0,{\mathcal {M}}_c)\) of \({\mathcal {M}}\) given by
and \({\mathcal {M}}_0={\mathcal {M}}{\setminus }{\mathcal {M}}_c\). Pick a map \(\pi _0:{\mathcal {M}}_0\rightarrow {\mathcal {N}}\) such that \(\pi _0(m)\in B_m\), and \(|{\varvec{y}}_{m}^*({\varvec{x}}_{\pi _0(m)})| >1/(4K DN)\) for all \(m\in {\mathcal {M}}_0\). Notice that, given \(n\in {\mathcal {N}}\) and \(m\in {\mathcal {M}}_0\),
and, if \(n=\pi _0(m)\),
Therefore, by Lemma 3.14, \(({\varvec{y}}_m)_{m\in {\mathcal {M}}_0}\) is \(E_0\)-equivalent to \((\overline{{\varvec{x}}}_{\pi _0(m)})_{m\in {\mathcal {M}}_0}\), where
Set \({\mathcal {B}}_j=\cup _{m\in {\mathcal {M}}_c} B_{m,j}\) and assume by contradiction that there is \(j\in {\mathcal {J}}\) such that \(|{\mathcal {B}}_j|\ge N\). Then, there is \(M\subseteq {\mathcal {M}}_c\) with \(L:=|M|\le N\) such that the cardinality of \(A=\cup _{m\in M} B_{m,j}\) is at least N. By unconditionality,
where \({{\tilde{{\mathcal {Y}}}}}= ({{\tilde{{\varvec{y}}}}}_m)_{m\in {\mathcal {M}}}\) is the basis defined by \({\varvec{x}}_n^*({{\tilde{{\varvec{y}}}}}_m)=|{\varvec{x}}_n^*({\varvec{y}}_m)|\) for all \(n\in {\mathcal {N}}\) and \(m\in {\mathcal {M}}\). Notice that, by (5.4),
and, by (5.3),
Let \((m_i)_{i=1}^L\) be an enumeration of M. Combining inequalities (5.6) and (5.7) allows to recursively construct subsets \((J_i)_{i=1}^L\) of \({\mathcal {J}}\) such that
and
for \( i=1,\ldots , L\).
Set \(J_m=J_{i}\) if \(m=m_i\), so that \((J_m)_{m\in M}\) are disjoint subsets of \({\mathcal {J}}\). Pick signs \((\varepsilon _{j,n})_{(j,n)\in {\mathcal {N}}}\) such that \(\varepsilon _{j,n} {\varvec{y}}_m^*(\overline{{\varvec{x}}}_{j,n})=|{\varvec{y}}_m^*(\overline{{\varvec{x}}}_{j,n})|\) for all \((j,n)\in {\mathcal {N}}\) and \(m\in {\mathcal {M}}\). The vector
satisfies
and, by (5.4), \(|{\text {supp}}(f_j)|\le D\) for all \(j\in {\mathcal {J}}\). Therefore,
Combining (5.5) with (5.8) and using that \(\alpha \) is a strongly absolute function for \({\mathcal {X}}_j\) yields \(N\le S\). This absurdity proves that \(|{\mathcal {B}}_j|\le N-1\) for all \(j\in {\mathcal {J}}\). Therefore, the elementary relation
where \({\mathcal {J}}_m=\{ j\in {\mathcal {J}}:B_{m,j} \not =\emptyset \}\), gives
Notice that \({\mathcal {J}}_m\) is finite for all \(m\in {\mathcal {M}}\). Hence, combining (5.2) with (5.9) permits to apply Theorem 3.2 to obtain a partition \(({\mathcal {M}}_i)_{i=1}^{N-1}\) of \({\mathcal {M}}_c\) and one-to-one maps \(\eta _i:{\mathcal {M}}_i\rightarrow {\mathcal {J}}\) such that \(\eta _i(m)\in {\mathcal {J}}_m\) for all \(i=1, \ldots , N-1\) and all \(m\in {\mathcal {M}}_i\). Pick, for each \(i=1, \ldots , N-1\), a map \(\pi _i:{\mathcal {M}}_i\rightarrow {\mathcal {N}}\) whose first coordinate is \(\eta _i\) such that \(\pi _i(m) \in B_m\) for all \(m\in {\mathcal {M}}_i\). We infer that \((\overline{{\varvec{x}}}_{\pi _i(m)})_{m\in {\mathcal {M}}_i}\) is isometrically equivalent to the unit vector system of \(c_0\).
It is clear that \(({\varvec{y}}_m)_{m\in {\mathcal {M}}_c}\) C-dominates the the unit vector system of \(c_0({\mathcal {M}})\). And the other way around,
for all \((a_m)_{m\in {\mathcal {M}}_c} \in c_{00}({\mathcal {M}}_c)\). Summing up, \(({\varvec{y}}_m)_{m\in {\mathcal {M}}_i}\) is \(E_1\)-equivalent to \((\overline{{\varvec{x}}}_{\pi _i(m)})_{m\in {\mathcal {M}}_i}\) for all \(i=1, \ldots , N-1\), where
This way, the function \(\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}\) obtained by glueing the functions \((\pi _i)_{i=0}^{N-1}\) shows that \({\mathcal {Y}}\) is uniformly equivalent to a subbasis of \({\mathcal {X}}\) as desired. \(\square \)
6 Infinite \(\ell _1\)-sums of spaces with strongly absolute bases
In this section, we generalize the main result from [11] and solve an explicit problem raised ten years ago in [11, Remark 3.6]. In hindsight, and in light of Theorem 3.18, it also sets right [11, Corollary 3.4], whose validity seemed to rely on a wrong set of hypotheses.
Theorem 6.1
For each \(j\in {\mathcal {J}}\), let \({\mathcal {X}}_j\) be a normalized K-unconditional basis of a quasi-Banach space \(X_j\) with modulus of concavity at most \(\kappa \). Suppose that there is \(\alpha \) such that \({\mathcal {X}}_j\) is strongly absolute with function \(\alpha \) for all \(j\in {\mathcal {J}}\). Then the unconditional basis \({\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{\ell _1}\) of \((\bigoplus _{j\in {\mathcal {J}}} X_j)_{\ell _1}\) is uniformly universal for well-complemented block basic sequences.
The proof of Theorem 6.1 will be shortened considerably after taking care of the following lemma.
Lemma 6.2
For each \(j\in {\mathcal {J}}\), let \({\mathcal {X}}_j=({\varvec{x}}_{j,n})_{n\in {\mathcal {N}}_j}\) be a normalized K-unconditional basis of a quasi-Banach space \(X_j\) with modulus of concavity at most \(\kappa \) and let \(L_j:X_j\rightarrow X:=(\oplus _{j\in {\mathcal {J}}} X_j)_{\ell _1}\) be the canonical embedding. For \((j,n)\in {\mathcal {N}}:=\cup _{j\in {\mathcal {J}}} \{j\}\times {\mathcal {N}}_j\) denote \(\overline{{\varvec{x}}}_{j,n}=L_j({\varvec{x}}_{j,n})\), so that \({\mathcal {X}}:=(\oplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{\ell _1}=(\overline{{\varvec{x}}}_{j,n})_{(j,n)\in {\mathcal {N}}}\). For each \(j\in {\mathcal {J}}\), let \({\mathcal {X}}_j^{*}=({\varvec{x}}_{j,n}^*)_{n\in {\mathcal {N}}_j}\) denote the dual basis of \({\mathcal {X}}_j\), and let \({\mathcal {X}}^*=(\overline{{\varvec{x}}}_{j,n}^{*})_{(j,n)\in {\mathcal {N}}}\) be the dual basis of \({\mathcal {X}}\). Suppose \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) is a normalized well C-complemented basic sequence with respect to the normalized unconditional basis \({\mathcal {X}}\) of \(X\) for which \( ({\varvec{y}}_m^*)_{m\in {\mathcal {M}}} = (\mathbb {1}_{{\text {supp}}({\varvec{y}}_m)}[{\mathcal {X}}^*]) _{m\in {\mathcal {M}}} \) is a family of good C-projecting functionals. Put \({\varvec{y}}_m=({\varvec{y}}_{j,m})_{j\in {\mathcal {J}}}\) and set
Then:
-
(a)
If \({\mathcal {X}}_j\) D-dominates the unit vector system of \(\ell _1\) for all \(j\in {\mathcal {J}}\), \(({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) D-dominates the unit vector system of \(\ell _1({\mathcal {M}})\).
-
(b)
If \(|M|\le |\cup _{m\in M} J_m|\) for every \(M\subseteq {\mathcal {M}}\) finite, there is a one-to-one map \(\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}\) such that the rearranged subbasis \((\overline{{\varvec{x}}}_{\pi (m)})_{m\in {\mathcal {M}}}\) of \({\mathcal {X}}\) is isometrically equivalent to the unit vector system of \(\ell _1\) and C-dominates \({\mathcal {Y}}\).
-
(c)
If
-
(i)
\({\mathcal {X}}_j\) is strongly absolute with function \(\alpha \) for every \(j\in {\mathcal {J}}\), and
-
(ii)
there is \(M\subseteq {\mathcal {M}}\) finite and nonempty such that \(|\cup _{m\in M} J_m| < |M|\),
for every \(R\in (0,\infty )\) we have
$$\begin{aligned} \Delta :=\sup \left\{ |{\varvec{x}}_{j,n}^*({\varvec{y}}_{j,m})| :m \in {\mathcal {M}},\, j\in {\mathcal {J}}, \, n\in {\mathcal {N}}_j\right\} \ge \frac{R-C}{R\, \alpha (R)}. \end{aligned}$$ -
(i)
Proof
(a) The basis \({\mathcal {X}}\) D-dominates the unit vector system of \(\ell _1({\mathcal {N}})\). That is,
For \((a_m)_{m\in {\mathcal {M}}}\in c_{00}({\mathcal {M}})\), write \(f=\sum _{m\in {\mathcal {M}}} a_m\, {\varvec{y}}_m\). Then,
(b) By Theorem 3.2, there is a one-to-one map \(\phi :{\mathcal {M}}\rightarrow {\mathcal {J}}\) such that \({\varvec{y}}_{\phi (m),m}\not =0\) for all \(m\in {\mathcal {M}}\). Thus, there is \(\nu :{\mathcal {M}}\rightarrow \cup _{j\in {\mathcal {J}}} {\mathcal {N}}_j\) such that \(\nu (m)\in {\mathcal {N}}_{\phi (m)}\) for all \(m\in {\mathcal {M}}\) and such that \(\overline{{\varvec{x}}}^*_{\phi (m),\nu (m)}({\varvec{y}}_m)\not =0\). Define \(\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}\) by \(\pi (m)=(\phi (m),\nu (m))\) for all \(m\in {\mathcal {M}}\). Let \(T_j\) be the canonical projection of \(X\) onto \(X_j\). Since, given \(m\in {\mathcal {M}}\), \(T_j(\overline{{\varvec{x}}}_{\pi (m)})\not =0\) for at most one \(j\in {\mathcal {J}}\), for every \((a_m)_{m\in {\mathcal {M}}}\in c_{00}({\mathcal {M}})\) we have
Let \(P=P[{\mathcal {Y}},{\mathcal {Y}}^*]\) be the projection defined in (3.2). If \((j,n)\in \sup ({\varvec{y}}_m)\) for some \(m\in {\mathcal {M}}\),
Hence, if \(f=\sum _{m\in {\mathcal {M}}} a_m\, {\varvec{y}}_m\),
(c) Note that \({\mathcal {X}}_j\) \(D(\alpha )\)-dominates the unit vector system of \(\ell _1({\mathcal {N}}_j)\) for all \(j\in {\mathcal {J}}\). Pick \({\mathcal {M}}_0\) minimal with \(|\cup _{m\in {\mathcal {M}}_0} J_m|<|{\mathcal {M}}_0|<\infty \). Since \(J_m\not =\emptyset \) for all \(m\in {\mathcal {M}}\) we have \(|{\mathcal {M}}_0|\ge 2\). Pick \(m_0\in {\mathcal {M}}_0\) arbitrary and set \(M={\mathcal {M}}_0{\setminus }\{m_0\}\). By Lemma 6.2 (b), the unit vector system of \(\ell _1(M)\) C-dominates the finite basis \(({\varvec{y}}_m)_{m\in M}\). If we set \(J=\cup _{m\in M} J_m\),
Since
we are done. \(\square \)
Proof of Theorem 6.1
Let \(C\in [1,\infty )\). Pick \(R> B:=4C^2D(\alpha ) K^2\), \(E>R \alpha (R)/(R-C)\) and \(E'=2CK\max \{C,D(\alpha )\}\). Let \({\mathcal {U}}\) be a well C-complemented basic sequence in \({\mathcal {X}}\). By Lemma 3.16, there is a well B-complemented basic sequence \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) in \({\mathcal {X}}\) with good B-projecting functionals
which is \(E'\)-equivalent to \({\mathcal {U}}\). With the terminology of Lemma 6.2, put
By Lemma 6.2 there is \(\pi _0:{\mathcal {M}}_0 \rightarrow {\mathcal {N}}\) such that \(\pi _0(m)\in {\text {supp}}({\varvec{y}}_m)\) for all \(m\in {\mathcal {M}}_0\) and \(({\varvec{y}}_m)_{m\in {\mathcal {M}}_0}\) \(D(\alpha )\)-dominates and it is B-dominated by \((\overline{{\varvec{x}}}_{\pi _0(m)})_{m\in {\mathcal {M}}_0}\). In turn, there is \(\pi _1:{\mathcal {M}}_1\rightarrow {\mathcal {N}}\) such that
Hence, by Lemma 3.14, \(({\varvec{y}}_m)_{m\in {\mathcal {M}}_1}\) BK-dominates and it is BKE-dominated by \((\overline{{\varvec{x}}}_{\pi _1(m)})_{m\in {\mathcal {M}}_1}\). We infer that if
and \(\pi :{\mathcal {M}}\rightarrow {\mathcal {N}}\) is obtained by glueing the functions \(\pi _0\) and \(\pi _1\), \({\mathcal {U}}\) \(D_1\)-dominates and it is \(D_2\)-dominated by \((\overline{{\varvec{x}}}_{\pi (m)})_{m\in {\mathcal {M}}}\). \(\square \)
Because of its applicability to examples, we shall put an end to this section by making explicit a uniqueness theorem that is obtained by combining the results on \(\ell _1\)-sums and \(c_0\)-sums with the Casaza-Kalton paradigm.
Theorem 6.3
Let \(({\mathcal {X}}_j)_{j\in {\mathcal {J}}}\) be an L-convex family of normalized unconditional bases of quasi-Banach spaces \((X_j)_{j\in {\mathcal {J}}}\). Suppose that:
-
(a)
\({\mathcal {X}}_j\) is strongly absolute with the same function \(\alpha \) for all \(j\in {\mathcal {J}}\); and
-
(b)
Either:
-
(i)
There is a constant C such that \({\mathcal {X}}_j^2\sim _C{\mathcal {X}}_j\) for all \(j\in {\mathcal {J}}\), or
-
(ii)
There is a constant C such that, for each \(j\in {\mathcal {J}}\),
 for infinitely many values of \(k\in {\mathcal {N}}\).
for infinitely many values of \(k\in {\mathcal {N}}\).
-
(i)
Then, the spaces \(X=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{\ell _1}\) and \(Y=(\bigoplus _{j\in {\mathcal {J}}} X_j)_{c_0}\) have a (UTAP) unconditional basis.
Proof
Since \({\mathcal {X}}_j\) \(D(\alpha )\)-dominates the unit vector system of \(\ell _1({\mathcal {N}}_j)\) for all \(j\in {\mathcal {J}}\), the normalized basis \({\mathcal {X}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{\ell _1}\) of \(X\) \(D(\alpha )\)-dominates the unit vector system of \(\ell _1({\mathcal {N}})\). Hence the Banach envelope of \(X\) is isomorphic to the anti-Euclidean space \(\ell _1({\mathcal {N}})\). Similarly, the Banach envelope of \(Y\) is isomorphic to the anti-Euclidean space \(c_0(\ell _1)\) (see [17]). By Theorem 6.1, Theorem 5.1, and Remark 4.3, \({\mathcal {X}}\) and \({\mathcal {Y}}=(\bigoplus _{j\in {\mathcal {J}}} {\mathcal {X}}_j)_{c_0}\) are (uniformly) universal for well complemented block basic sequences. By Lemma 3.4, \({\mathcal {X}}^2\sim {\mathcal {X}}\) and \({\mathcal {Y}}^2\sim {\mathcal {Y}}\), and so applying Theorem 3.12 concludes the proof. \(\square \)
7 Applications and examples
Theorems 4.2 and 6.3, combined with Proposition 3.20, yield a myriad of new examples of quasi-Banach spaces with a (UTAP) unconditional bases. In this section we highlight applications only to a sampler of infinite direct sums involving classical spaces, but the reader is encouraged to create their favourite infinite direct sums and use our previous results to check that they enjoy the property of uniqueness (UTAP) of unconditional basis. The possibilities for new examples are endless.
7.1 Lorentz sequence spaces
Let \({\varvec{w}}=(w_n)_{n=1}^\infty \) be a sequence of non-negative scalars with \(w_1>0\) and \((s_n)_{n=1}^\infty \) be the primitive weight of \({\varvec{w}}\), defined by
Given \(0<p<\infty \) and \(0<q\le \infty \), the Lorentz sequence space \(d_{p,q}({\varvec{w}})\) consists of all \(f\in c_0\) whose non-increasing rearrangement \((a_n)_{n=1}^\infty \) satisfies
with the usual modification if \(q=\infty \). If \((s_n)_{n=1}^\infty \) is doubling, i.e., \(\sup _m s_{m}/s_{\lceil m/2\rceil }<\infty \), then \(\Vert \cdot \Vert _{p,q,{\varvec{w}}}\) is a quasi-norm. In this case, \(d_{p,q}({\varvec{w}})\) is a symmetric sequence space. Moreover, if \(q<\infty \), \(d_{p,q}({\varvec{w}})\) is minimal.
In our notation, the Lorentz space \(d_{p,p}({\varvec{w}})\) coincides with the Lorentz space denoted \(d({\varvec{w}}, p)\) by Altshuler in [13] (see also [1, 9, 15]). We emphasize that Altshuler only considered non-increasing weights \({\varvec{w}}\in c_0{\setminus }\ell _1\), but this restriction is unnecessary here.
The space \(d_{p,\infty }({\varvec{w}})\) coincides with the weak Lorentz space denoted \(d^\infty ({\varvec{w}}, p)\) in [15]. We will denote by \(d^{\,0}_{p,\infty }({\varvec{w}})\) the separable part of \(d_{p,\infty }({\varvec{w}})\), i.e., the closed linear span of \(c_{00}\) in \(d_{p,\infty }({\varvec{w}})\).
If \(0<q<r\le \infty \), we have
and for all \(A\subset {\mathbb {N}}\) with \(|A|=m\),
Thus, it could be said that for fixed p and \({\varvec{w}}\), the spaces \(d_{p,q}({\varvec{w}})\) are close to each other in the sense that all of them share (essentially) the fundamental function of the canonical basis. This is important to be taken into account when considering embeddings (see below).
We point out that if \(0<p,q<\infty \) and the primitive weight of \({\varvec{w}}'\) is \((s_n^{q/p})_{n=1}^\infty \), then
up to an equivalent norm. Similarly, if \({\varvec{w}}'=(w_n')_{n=1}^\infty \) denotes the weight whose primitive weight is \((s_n^{1/p})_{n=1}^\infty \),
Thus, every sequence Lorentz space \(d_{p,q}({\varvec{w}})\) can be identified, up to an equivalent quasi-norm, with a Lorentz sequence space \(d_{1,q}({\varvec{w}}')\) for a suitable weight \({\varvec{w}}'\). The advantages of establishing results concerning sequence Lorentz spaces in terms of the scale of spaces \(d_{1,q}({\varvec{w}})\), \(0<q\le \infty \), must be understood in light of (7.1) and (7.2). For a concise introduction to Lorentz sequence spaces we refer to [3, §9.2]. Next we focus on the features of these spaces that are of interest for the purposes of this paper.
We next include a proof of the fact that all Lorentz sequence spaces are L-convex. To that end we need to introduce the following concept.
We say that a sequence \((\Phi (m))_{m=1}^\infty \) of positive scalars has the upper regularity property (URP for short) if there is \(r\in {\mathbb {N}}\) such that
If \((\Phi (m))_{m=1}^\infty \) has the URP, then there are \(0<\alpha <1\) and \(0<C<\infty \) such that
(see [19, §4]). This implies that
for some constant \(C'\).
Given \(r\in (0,\infty )\), the r-convexification of a sequence space \({{\mathcal {L}}}\) on a countable set \({\mathcal {J}}\) is the sequence space consisting of all \(f:{\mathcal {J}}\rightarrow {\mathbb {F}}\) such that \(|f|^r\in {{\mathcal {L}}}\). By definition, \({{\mathcal {L}}}\) is lattice p-convex if and only its r-convexification is (pr)-convex. Note that the r-convexification of \(d_{p,q}({\varvec{w}})\) is \(d_{pr,qr}({\varvec{w}})\).
Theorem 7.1
(cf. [27, Theorem 8] and [21, Proposition 1]) Let \({\varvec{w}}\) be a weight whose primitive weight \((s_n)_{n=1}^\infty \) is doubling. Then \(d_{1,q}({\varvec{w}})\) is L-convex for all \(0< q \le \infty \).
Proof
We will show that \(d_{1,q}({\varvec{w}})\) is r-convex for some \(r>0\). Let \(C\in [1,\infty )\) be such that \(s_{2n} \le C s_n\) for all \(n\in {\mathbb {N}}\). Pick \(\alpha _0\in (0,1)\) and \(k\in {\mathbb {N}}\) such that \( C^{\alpha _0} \le 2^{1-1/k} \). Then, if \(r=2^k\),
That is, \((s_n^\alpha )_{n=1}^\infty \) has the URP and, then, satisfies inequality (7.4) for all \(0<\alpha <\alpha _0\).
We shall prove that \(d_{1,q}({\varvec{w}})\) is lattice r-convex for all \(0<r<\min \{\alpha _0,q\}\). Set \(p=1/r\). In the case when \(q<\infty \), an application of [15, Theorem 2.5.10] gives that \(d_{pq,pq}({\varvec{w}}_{q})\) is locally convex, where \({\varvec{w}}_q\) is the weight whose primitive weight is \((s_n^q)_{n=1}^\infty \). Hence, by (7.3), \(d_{p,pq}({\varvec{w}})\) is locally convex. In the case when \(q=\infty \), by [15, Theorem 2.5.11] this result still holds. Taking into account that local convexity is equivalent to lattice 1-convexity, we infer that \(d_{1,q}({\varvec{w}})\) is lattice r-convex. \(\square \)
Next we tackle the strong absoluteness of the canonical basis of Lorentz sequence spaces.
Proposition 7.2
Suppose that the primitive weight \((s_n)_{n=1}^\infty \) of \({\varvec{w}}=(w_n)_{n=1}^\infty \) is doubling.
-
(a)
The following are equivalent:
-
(i)
\(d_{1,\infty }({\varvec{w}})\) is continuously included in \(\ell _1\).
-
(ii)
\(\sum _{n=1}^\infty 1/s_n <\infty \).
-
(iii)
The unit vector system is a strongly absolute basis of \(d^{\,0}_{1,\infty }({\varvec{w}})\).
-
(i)
-
(b)
Let \(1<q<\infty \) and let \(q'\) be its conjugate exponent. Suppose that \(\sum _{n=1}^\infty w_n^{-q'+1} s_n^{-1} <\infty \). Then the unit vector system is a strongly absolute basis of \(d_{1,q}({\varvec{w}})\).
-
(c)
Let \(0<q\le 1\).
-
(i)
\(d_{1,q}({\varvec{w}})\) is continuously included in \(\ell _1\) if and only if \(\inf _n s_n/n>0\). Moreover.
-
(ii)
if \(\lim _n s_n/n=\infty \), then the unit vector system is a strongly absolute basis of \(d_{1,q}({\varvec{w}})\).
-
(iii)
if \(\inf _n s_n/n>0\) and \(q<1\), the unit vector system of \(d_{1,q}({\varvec{w}})\) is uniformly universal for well complemented block basic sequences.
-
(i)
Proof
The implication (iii) \(\Rightarrow \) (i) in (a) is obvious. If \(f=(1/s_n)_{n=1}^\infty \), we have \(\Vert f \Vert _{1,\infty ,{\varvec{w}}}=1\). This yields (i) \(\Rightarrow \) (ii). To prove (b) and the implication (ii) \(\Rightarrow \) (iii) in (a) we pick \(1<q\le \infty \) and \(0<R<\infty \). Choose \(m=m(R)\in {\mathbb {N}}\) such that
Let \(f\in {\mathbb {F}}^{\mathbb {N}}\) and denote by \((a_n)_{n=1}^\infty \) its non-increasing rearrangement. By Holder’s inequality,
Thus, if \(\Vert f\Vert _{1,q,{\varvec{w}}}\le R \Vert f\Vert _1\), we obtain \(\Vert f\Vert _1\le 2m a_1=2m\Vert f\Vert _\infty \).
As far as (c) is concerned, the “only if” part in (i) is clear. By (7.1), to prove the converse it suffices to consider the case \(q=1\). If \({\varvec{w}}'=(w'_{n})_{n=1}^\infty \) is the weight defined by \(w'_n=1\) for all \(n\in {\mathbb {N}}\), then \(d_{1,1}({\varvec{w}})\subseteq d_{1,1}({\varvec{w}}')\). Since \(d_{1,1}({\varvec{w}}')=\ell _1\) we are done.
(ii) is essentially known (see [34, Lemma 4] and [25, Theorem 2.6]). However, as an explicit proof is not available in the literature, we next include one for the sake of completeness. Again, by Lemma 3.19, it suffices to consider the case \(q=1\). Let \(R\in (0,\infty )\). Choose \(m\in {\mathbb {N}}\) such that \(s_n\ge 2R n\) for all \(n\ge m+1\). If \((a_n)_{n=1}^\infty \) is the non-increasing rearrangement of f, by Abel’s summation formula,
Therefore, \(\Vert f\Vert _1 \le 2m\) whenever \( \Vert f\Vert _{1,1,{\varvec{w}}}\le R \Vert f\Vert _1\).
In regards to (iii), we point out that it was proved in [1, Proposition4.2] that \(d_{1,q}({\varvec{w}})\) has the peaking property. A close look at the proof of this result reveals that, in fact, it has the uniform peaking property. Essentially, this is due to the validity of a constructive version of the proof of [35, Lemma 3.1]. Specifically, there is a function \(\zeta :(0,\infty )\rightarrow (0,\infty )\) depending on p and \({\varvec{w}}\) such that every normalized disjointly supported sequence \(({\varvec{y}}_m)_{m=1}^\infty \) with respect to \(({\varvec{e}}_{n})_{n=1}^{\infty }\) with \(\liminf _m \Vert {\varvec{y}}_m \Vert _\infty < \zeta (\varepsilon )\) has a subsequence that \((1+\varepsilon )\)-dominates the unit vector system of \(\ell _p\). By Proposition 3.15, \(({\varvec{e}}_{n})_{n=1}^{\infty }\) is uniformly universal for block basic sequences. \(\square \)
To complement the theoretical contents of this section we shall introduce lattice concavity and a quantitative tool from approximation theory that serves in particular to measure how far an unconditional basis is from the canonical \(\ell _{1}\)-basis. The main idea is to use embeddings into Lorentz sequence spaces to deduce that certain bases are strongly absolute.
Given a (semi-normalized) unconditional basis \({\mathcal {X}}\) of a quasi-Banach space \(X\) we define its lower democracy function as
If \({{\mathcal {L}}}\) is a sequence space, \(\varphi _l[{{\mathcal {L}}}]\) will denote the lower democracy function of its unit vector system. The quasi-Banach lattice \({{\mathcal {L}}}\) is said to be q-concave, \(0<q\le \infty \), if there is a nonnegative constant C such that
Any quasi-Banach lattice is trivially \(\infty \)-concave.
Theorem 7.3
Let \(X\) be a quasi-Banach space with a normalized unconditional basis \({\mathcal {X}}=({\varvec{x}}_n)_{n=1}^\infty \). Suppose that \({\mathcal {X}}\) induces a q-concave lattice structure on \(X\) for some \(0<q\le \infty \). Let \({\varvec{w}}=(w_n)_{n=1}^\infty \) be a weight with
Then \({\mathcal {X}}\) dominates the unit vector system of \(d_{1,q}({\varvec{w}})\), i.e., \(X\) continuously embeds into \(d_{1,q}({\varvec{w}})\) via \({\mathcal {X}}\).
Proof
If \(q=\infty \) the result is known (see [4, Lemma 6.1]). Suppose that \(q<\infty \). Put \({\varvec{w}}'=(w_n')_{n=1}^\infty \), where \(w'_n=s_n^q-s_{n-1}^q\) with the convention that \(s_0=0\). Let \((a_n)_{n=1}^\infty \in c_{00}\) such that \((|a_n|)_{n=1}^\infty \) is non-increasing. Put \(t=|a_1|\) and for each \(k\in {\mathbb {N}}\) consider the set
Notice that \((J_k)_{k=1}^\infty \) is a partition of \(\{n\in {\mathbb {N}}:a_n\not =0\}\). Set \(m_0=0\) and for \(j\in {\mathbb {N}}\) put \(m_j=\sum _{k=1}^j |J_k|\), so that \(J_j=\{n\in {\mathbb {N}}:m_{j-1}+1\le n \le m_j\}\) for all \(j\in {\mathbb {N}}\). Define
By Abel’s summation formula,
Therefore, if C is the q-concavity constant of \({\mathcal {X}}\) and K is its unconditionality basis constant,
Using (7.3), and taking into account that the concavity constants and the unconditionality constants of \(({\varvec{x}}_{\pi (n)})_{n=1}^\infty \) are still C and K for any permutation \(\pi \) of \({\mathbb {N}}\), we are done. \(\square \)
We also need the dual property of URP. A sequence \((\Phi (m))_{m=1}^\infty \) of positive scalars is said to have the lower regularity property (LRP for short) if there is \(r\in {\mathbb {N}}\) such that
\((\Phi (m))_{m=1}^\infty \) has the LRP if and only if \((m/\Phi (m))_{m=1}^\infty \) has the URP. Hence a dual inequality of (7.4) holds, i.e., for any sequence \((\Phi (m))_{m=1}^\infty \) with the LRP there is a constant C such that
Lemma 7.4
Suppose that a sequence space \({{\mathcal {L}}}\) on a set \({\mathcal {J}}\) is q-concave for some \(0<q<\infty \). Then \(\varphi _l[{{\mathcal {L}}}]\) has the LRP.
Proof
Let r, \(m\in {\mathbb {N}}\), and \(A\subseteq {\mathcal {J}}\) with \(|A|=rm\). Pick a partition \((A_j)_{j=1}^r\) of A with \(|A_j|=m\) for all \(j=1, \ldots , r\). If C is the q-concavity constant of \({{\mathcal {L}}}\),
Hence, if we pick \(r \ge (2C)^q\) we get \(\varphi _l[{{\mathcal {L}}}](rm)\ge 2 \varphi _l[{{\mathcal {L}}}](m)\). \(\square \)
Even without having any information on the concavity of the space X, Proposition 7.5 below provides an improvement of [1, Proposition 5.6]. In addition to that, it shows that imposing some nontrivial concavity to the lattice structure allows to weaken the assumption on the lower democracy function.
Proposition 7.5
Let \(X\) be a quasi-Banach space with a normalized unconditional basis \({\mathcal {X}}\). Suppose that \({\mathcal {X}}\) induces a q-concave lattice structure, \(1\le q\le \infty \). Denote by \(q'\) the conjugate exponent of q, and put \(s_{m}= \varphi _l[{\mathcal {X}}](m)\) for all \(m\in {\mathbb {N}}\). Suppose that either \(q=1\) and
or \(q>1\) and
Then \({\mathcal {X}}\) is strongly absolute.
Proof
If \(1\le q<\infty \), applying Lemma 7.4 gives a constant C such that
Set \({\varvec{w}}=(s_n/n)_{n=1}^\infty \) if \(1<q<\infty \), and let \({\varvec{w}}\) be the weight whose primitive weight is \((s_m)_{m=1}^\infty \) if \(q\in \{1,\infty \}\). Notice that \((s_{m})_{m=1}^{\infty }\) is doubling (see [3, p. 40]). By Proposition 7.2, the unit vector system of \(d_{1,q}({\varvec{w}})\) is strongly absolute. Then, the result follows from combining Theorem 7.3 with Lemma 3.19. \(\square \)
Example 7.6
Let \({\varvec{w}}=(w_n)_{n=1}^\infty \) be a weight whose primitive weight \((s_n)_{n=1}^\infty \) is doubling.
-
(i)
If \(\sum _{n=1}^\infty 1/s_n <\infty \), the spaces
$$\begin{aligned} \ell _{p}(d^{\,0}_{1,\infty }({\varvec{w}}))&=(d^{\,0}_{1,\infty }({\varvec{w}})\oplus \cdots \oplus d^{\,0}_{1,\infty }({\varvec{w}})\oplus \cdots )_{\ell _p},\\ d^{\,0}_{1,\infty }({\varvec{w}})(\ell _{p})&=(\ell _{p}\oplus \cdots \oplus \ell _{p}\oplus \cdots )_{d^{\,0}_{1,\infty }({\varvec{w}})} \end{aligned}$$have a (UTAP) unconditional basis for all \(0<p<1\).
-
(ii)
Let \(1<q<\infty \) and denote by \(q'\) its conjugate exponent. Suppose that \(\sum _{n=1}^\infty w_n^{-q'+1} s_n^{-1} <\infty \). Then the spaces
$$\begin{aligned} \ell _{p}(d_{1,q}({\varvec{w}}))&=(d_{1,q}({\varvec{w}})\oplus \cdots \oplus d_{1,q}({\varvec{w}})\oplus \cdots )_{\ell _p},\\ d_{1,q}({\varvec{w}})(\ell _{p})&=(\ell _{p}\oplus \cdots \oplus \ell _{p}\oplus \cdots )_{d_{1,q}({\varvec{w}})} \end{aligned}$$have a (UTAP) unconditional basis for all \(0<p<1\).
-
(iii)
If \(\inf _m s_n/n>0\), then the space
$$\begin{aligned} \ell _{p}(d_{1,q}({\varvec{w}}))=(d_{1,q}({\varvec{w}})\oplus \cdots \oplus d_{1,q}({\varvec{w}})\oplus \cdots )_{\ell _{p}} \end{aligned}$$has a (UTAP) unconditional basis for all \(0<p<1\) and \(0<q<1\). Recall that \(d_{1,q}({\varvec{w}})\) is, for a different weight \({\varvec{w}}'\), the classical space \(d(q,{\varvec{w}}')\), considered in [9] (see 7.1).
-
(iv)
Let \(0<q\le 1\) and suppose that \(\lim _n s_n/n=\infty \). Then the spaces \(\ell _{p}(d_{1,q}({\varvec{w}}))\) and \( d_{1,q}({\varvec{w}})(\ell _{p})\) have a (UTAP) unconditional basis for all \(0<p\le 1\).
7.2 Orlicz sequence spaces
A normalized Orlicz function is a right-continuous increasing function \(F:[0,\infty )\rightarrow [0,\infty )\) such \(F(0)=0\) and \(F(1)=1\). The topological vector space built from the modular
is the Orlicz sequence space usually denoted by \(\ell _F\). The space \(\ell _F\) is locally bounded if and only if there is \(p>0\) such that
(see [22, Proposition 4.2]), in which case \(\ell _F\) is complete, i.e., \(\ell _F\) is a quasi-Banach space equipped with the quasi-norm
Moreover, if (7.5) holds for a given p, then the unit vector system induces a p-convex lattice structure on \(\ell _F\).
Let G be the “dual” function of F, defined by \(G(t)=t/F(t)\) for \(0<t<\infty \). A standard argument gives that (7.5) holds for some p if and only if G is doubling near the origin, i.e., there is a constant C such that
Summing up, if G is doubling near the origin, then \(\ell _F\) is an L-convex (symmetric) sequence space. The sequence space \(\ell _F\) is minimal if and only F is doubling near the origin. Moreover \(\ell _F\) is contained in \(\ell _1\) if and only if \(\inf _{0\le t \le 1} F(t)/t>0\).
Given a normalized Orlicz such F we define its inverse by
If the dual function G is doubling near the origin, then \(\ell _F\) is a symmetric sequence space.
In order to apply Theorems 4.1 and 6.1 to Orlicz squence spaces it is convenient to have a criterion that guarantees that the unit vector system of \(\ell _F\) is strongly absolute, which will imply that it is uniformly universal for well complemented block basic sequences. In some particular cases, the strong absoluteness of the unit vector system of \(\ell _F\) can be derived from Proposition 7.5. However, using specific techniques for this type of spaces allows to obtain better results. For instance, we will next show that the unit vector system of most Orlicz sequence spaces contained in \(\ell _1\) is strongly absolute.
Proposition 7.7
Let F be a normalized Orlicz function and set \(G(t)=t/F(t)\), \(0<t<\infty \). Suppose that G is doubling near the origin, essentially increasing, and satisfies \(\lim _{t\rightarrow 0^+}G(t)=0\). Then F is doubling near the origin, the Orlicz sequence space \(\ell _F\) is minimal, and the canonical basis is strongly absolute.
Proof
Let \(C\in [1,\infty )\) be such that \( G(s)\le CG(t) \) for all \(0<s\le t\le 1\). Since
F is doubling near the origin.
Fix \(R<\infty \) and pick \(\delta >0\) such that \(G(t)\le 1/(RC)\) for every \(0<t\le \delta \). Given \(f=(a_n)_{n=1}^\infty \in \ell _F\), set \(u=\Vert f \Vert _\infty \) and \(v=\Vert f \Vert _{\ell _F}\). Then
In the case when \(u/v\le \delta \) we have \(w\le v/R\). Otherwise,
Hence, \(\ell _F\) is strongly absolute with function \(\alpha \) given by
\(\square \)
Let us mention that Kalton [22] (implicitly) proved that if F and its dual function G are doubling near the origin, G is bounded near the origin, and
then the unit vector system of the minimal sequence space \(\ell _F\) has the peaking property. It is unclear whether these assumptions imply that \(\ell _F\) has the uniform peaking property.
Example 7.8
Let F be a normalized Orlicz function and for \(t>0\) let \(G(t)=t/F(t)\). Assume that F and G are doubling near the origin, that G is essentially increasing, and that \(\lim _{t\rightarrow 0^+} G(t)=0\). Then the following spaces have a (UTAP) unconditional basis:
-
(i)
\(\ell _{1}(\ell _{F})=(\ell _{F}\oplus \ell _{F}\oplus \cdots \oplus \ell _{F}\oplus \cdots )_{1}\);
-
(ii)
\((\bigoplus _{n=1}^\infty \ell _q^n)_{\ell _F}=( \ell _{q}^{1}\oplus \ell _{q}^{2}\oplus \cdots \oplus \ell _{q}^{n}\oplus \cdots )_{\ell _{F}}\) for all \(0<q\le 1\);
-
(iii)
\(\ell _{F}(c_{0})=(c_{0}\oplus c_{0}\oplus \cdots \oplus c_{0}\oplus \cdots )_{\ell _{F}}\);
-
(iv)
\(\ell _{F}(d^{\,0}_{1,\infty }({\varvec{w}}))=(d^{\,0}_{1,\infty }({\varvec{w}})\oplus d^{\,0}_{1,\infty }({\varvec{w}})\oplus \cdots d^{\,0}_{1,\infty }({\varvec{w}})\dots )_{\ell _{F}}\), \(d^{\,0}_{1,\infty }({\varvec{w}})(\ell _{F})=(\ell _{F}\oplus \ell _{F}\oplus \cdots \ell _{F}\ldots )_{d^{\,0}_{1,\infty }({\varvec{w}})}\), and \(\ell _F(c_0(d^{\,0}_{1,\infty }({\varvec{w}})))\), where \({\varvec{w}}\) is as in Example 7.6 (i).
-
(v)
\(\ell _{F}(d_{1,q}({\varvec{w}}))=(d_{1,q}({\varvec{w}})\oplus d_{1,q}({\varvec{w}})\oplus \cdots d_{1,q}({\varvec{w}})\ldots )_{\ell _{F}}\) and \(d_{1,q}({\varvec{w}})(\ell _{F})=(\ell _{F}\oplus \ell _{F}\oplus \cdots \ell _{F}\ldots )_{d_{1,q}({\varvec{w}})}\), where \({\varvec{w}}\) and q are as in Example 7.6 (ii) and (iv).
For instance, the uniqueness of unconditional basis in \(\ell _{1}(\ell _{F})\) is an application of Theorem 6.3. To see (ii) when \(0<q<1\), we just need to apply Theorem 3.18 since condition (c) in Lemma 3.4 is fulfiled. Then by Proposition 3.20, the canonical basis of \(\ell _{F}(\ell _{q})\) is strongly absolute and equivalent to its square. To show the case when \(q=1\) in part (ii) and part (iii) however, we need to appeal to Theorem 4.2 and take into account that the unit vector basis of \(\ell _{1}\) and \(c_{0}\) is perfectly homogeneous, hence uniformly universal for well complemented block basic sequences with function \(C\mapsto 1\). To obtain the uniqueness of unconditional basis of the third space in (iv) we must combine Theorem 5.1 with Theorem 4.2. The verification of the corresponding hypotheses leading to the uniqueness property in the remaining cases is totally straightforward, and so we leave it for the reader.
7.3 Bourgin–Nakano spaces
A Bourgin–Nakano index is a family \((p_n)_{n \in {\mathbb {N}}}\) in \((0,\infty )\) with \(p=\inf _n p_n>0\). The Bourgin–Nakano space \(\ell (p_{n})\) is the quasi-Banach space built from the modular
If we endow \(\ell (p_{n})\) with the natural ordering, it becomes a p-convex quasi-Banach lattice. The separable part \(h(p_{n})=[{\varvec{e}}_n :n \in {\mathcal {N}}]\) of \(\ell (p_{n})\) is a minimal sequence space. We have \(\ell (p_{n})=h(p_{n})\) if and only if \(\sup _n p_n<\infty \).
The unit vector system \(({\varvec{e}}_{n})_{n=1}^{\infty }\) of \(\ell (p_{n})\) is a 1-unconditional basis which is universal for well complemented block basic sequences ( [1, Proposition 4.7]), and which is strongly absolute if and only if \(q:=\limsup p_{n}< 1\). Indeed, this condition implies that the space embeds naturally into \(\ell _{q}\) and so we can apply Lemma 3.19. Moreover, the Banach envelope of \(\ell (p_{n})\) is anti-Euclidean if and only if \(\limsup p_{n}\le 1\) (see [1, Proposition 4.5 and Corollary 4.6]). Combining [1, Lemma 4.3] with Lemma 3.14 gives that the unit vector system of any Bourgin–Nakano space is uniformly universal for well-complemented block basic sequences with function \(C\mapsto 4C^2\).
Example 7.9
The following spaces have a (UTAP) unconditional basis:
-
(i)
\(\ell (p_{n})(\ell _{1})=\{(z_{n})_{n=1}^{\infty }:z_{n}\in \ell _{1} \;\text {and}\; \sum _{n=1}^{\infty }\Vert z_{n}\Vert _{1}^{p_{n}}<\infty \}\), where \(\limsup p_{n}<1\).
-
(ii)
\(\ell _{F}(\ell (p_{n}))=(\ell (p_{n})\oplus \ell (p_{n})\oplus \cdots \oplus \ell (p_{n})\oplus \cdots )_{\ell _{F}}\), where F is an Orlicz function as in Example 7.8 and \(\limsup p_{n}\le 1\).
-
(iii)
\(\ell _{1}(\ell (p_{n}))=(\ell (p_{n})\oplus \ell (p_{n})\oplus \cdots \oplus \ell (p_{n})\oplus \cdots )_{\ell _q}\), where \(\lim p_{n}< 1\).
Indeed, the uniqueness of unconditional basis in the first example follows from a direct application of Theorem 4.2, where we use that the canonical basis of \(\ell _{1}\) is equivalent to its square (condition (iv) (a)). In the second example we use also Theorem 4.2, but now we employ condition (iv) (b) since, while \(\ell (p_{n})\) needs not be lattice isomorphic to its square, \(\ell _F\) is. The last case is just a direct application of Theorem 6.3, since the hypothesis ensures that the canonical basis of \(\ell (p_{n})\) is strongly absolute. Note that in the cases (ii) and (iii), the uniqueness of unconditional basis in the direct sum is obtained without knowing whether the space \(\ell (p_{n})\) has a unique unconditional basis or not!
7.4 Hardy spaces
Because of their importance in Analysis, we single out as well some examples involving Hardy spaces. For the convenience of the reader we will next state a few known facts about the spaces \(H_p({\mathbb {T}}^d)\) that we will need in order to apply Theorems 4.2 and 6.3.
The first unconditional bases in \(H_p({\mathbb {T}})\) for \(0<p<1\) were constructed in [36]. It is remarkable that thanks to them we obtain a manageable expression for the norm in terms of the coefficients relative to the basis. Namely, if \({\mathcal {H}}= ({\varvec{x}}_n)_{n=0}^\infty \) is such a normalized basis then
where \((h_n)_{n=0}^\infty \) is the classical Haar system on [0, 1] normalized with respect to the norm in \(L_p([0,1])\). In addition, those bases permit to construct unconditional bases in \(H_p({\mathbb {T}}^d)\) for \(d\in {\mathbb {N}}\) by means of tensor products which satisfy an equivalence analogous to (7.6). Using those tensored bases, Kalton et al. [25] showed that the spaces \(H_p({\mathbb {T}}^d) \) and \(H_p({\mathbb {T}}^{d'})\) with \(0<p<1\) and d, \(d'\in {\mathbb {N}}\), are isomorphic if and only if \(d=d'\). Then it was proved in [37] that all the spaces \(H_p({\mathbb {T}}^d)\) for \(0<p<1\) and \(d\in {\mathbb {N}}\) have a (UTAP) unconditional basis.
The canonical basis \({\mathcal {H}}\) of the Hardy spaces \(H_p({\mathbb {T}}^d)\), \(0<p<1\), induces a p-convex lattice structure and satisfies the estimate
Hence, Proposition 7.5 implies that \({\mathcal {H}}\) is strongly absolute. This way we can use Hardy spaces (or more generally subspaces of Hardy spaces generated by subbases of the Haar system) to build examples of spaces with a (UTAP) unconditional basis. Given a (finite or infinite) nonempty subset \({{\varvec{n}}}\subseteq {\mathbb {N}}\), \(H_p^{{\varvec{n}}}({\mathbb {T}})\) denotes the subspace of \(H_p({\mathbb {T}})\) generated by Haar functions belonging to layers in \({{\varvec{n}}}\).
Example 7.10
The following spaces have a (UTAP) unconditional basis:
-
(i)
The space \(H_{p}({\mathbb {T}},d_{1,q}({\varvec{w}}))=d_{1,q} \oplus d_{1,q}({\varvec{w}})\oplus \cdots \oplus d_{1,q}({\varvec{w}})\oplus \cdots )_{H_{p}}\), consisting of all sequences \(({\varvec{z}}_{n})_{n=1}^{\infty }\) such that \({\varvec{z}}_{n}\in d_{1,q}({\varvec{w}})\) for all \(n\in {\mathbb {N}}\) and
$$\begin{aligned} \left( \int _0^1\left( \sum _{n=0}^\infty \Vert {\varvec{z}}_n\Vert ^2 h_n^2(t)\right) ^{p/2}dt\right) ^{1/p}<\infty , \end{aligned}$$where \(p<1\), \(0<q< 1\) and the primitive weight \((s_m)_{m=1}^\infty \) of \({\varvec{w}}\) satisfies \(\inf _m s_m/m>0\).
-
(ii)
\(\ell _{F}(H_{p}({\mathbb {T}}))=(H_{p}({\mathbb {T}})\oplus H_{p}({\mathbb {T}})\oplus \cdots \oplus H_{p}({\mathbb {T}})\oplus \cdots )_{\ell _{F}}\), where F is as in Proposition 7.7.
-
(iii)
\((\bigoplus _{k=1}^\infty H_p^{{{\varvec{n}}}_k}({\mathbb {T}}))_{\ell _1}=(H_{p}^{{{\varvec{n}}}_1}({\mathbb {T}})\oplus H_{p}^{{{\varvec{n}}}_2}({\mathbb {T}})\oplus \cdots \oplus H_{p}^{{{\varvec{n}}}_k}({\mathbb {T}})\oplus \cdots )_{\ell _1}\), where \(0<p<1\) and \(({{\varvec{n}}}_k)_{k=1}^\infty \) is an increasing sequence of subsets of \({\mathbb {N}}\).
Note that in the last example, since there are sets of layers \({{\varvec{n}}}\subseteq {\mathbb {N}}\) for which \(H_p^{{{\varvec{n}}}}({\mathbb {T}})\) is not isomorphic to its square (see [37]), we must use condition (b) (ii) in order for all the hypotheses of Theorem 6.3 to be satisfied. As a matter of fact, it is unknown whether \(H_p^{{{\varvec{n}}}}({\mathbb {T}})\) has a (UTAP) unconditional basis in the case when it is not isomorphic to its square (see Theorem 3.18).
7.5 Tsirelson’s space
Casazza and Kalton established in [16] the uniqueness of unconditional basis up to permutation of Tsirelson’s space \({\mathcal {T}}\) and its complemented subspaces with unconditional basis as a byproduct of their study of complemented basic sequences in lattice anti-Euclidean Banach spaces. Their result answered a question by Bourgain et al. ([14]), who had proved the uniqueness of unconditional basis up to permutation of the 2-convexifyed Tsirelson’s space \({\mathcal {T}}^{(2)}\). Unlike \({\mathcal {T}}^{(2)}\), which is “highly” Euclidean, the space \({\mathcal {T}}\) is anti-Euclidean. To see the latter requires the notion of dominance, introduced in [16].
Let \({\mathcal {X}}=({\varvec{x}}_n)_{n=1}^\infty \) be a (normalized) unconditional basis of a quasi-Banach space \(X\). Given f, \(g\in X\), we write \(f\prec g\) if \(m<n\) for all \(m\in {\text {supp}}(f)\) and \(n\in {\text {supp}}(g)\). Given \(D\ge 1\), the basis \({\mathcal {X}}\) is said to be left (resp. right) D-dominant if whenever \((f_i)_{i=1}^n\) and \((g_i)_{i=1}^n\) are disjointly supported families with \(f_i\prec g_i\) (resp. \(g_i\prec f_i\)) and \(\Vert f_i\Vert \le \Vert g_i\Vert \) for all \(i=1, \ldots , n\), then \(\Vert \sum _{i=1}^n f_i\Vert \le D \Vert \sum _{i=1}^n g_i\Vert \). As is customary, if the constant D is irrelevant, we just drop it from the notation. If \(X\) is a Banach space with a left (resp. right) dominant semi-normalized unconditional basis \({\mathcal {X}}\) there is a unique \(r=r({\mathcal {X}})\in [1,\infty ]\) such that \(\ell _r\) is finitely block representable in \(X\). In the case when \(r({\mathcal {X}})\in \{1,\infty \}\), \(X\) is anti-Euclidean (see [16, Proposition 5.3]).
The canonical basis of the Tsirelson space \({\mathcal {T}}\) is (normalized, 1-unconditional and) right–dominant (see [16, Proposition 5.12]) with \(r({\mathcal {T}})=1\). In turn, by [16, Lemma 5.1], the canonical basis of the original Tsirelson’s space \({\mathcal {T}}^{*}\) is left-dominant.
Moreover, by [16, Proposition 5.5] and [18, page 14], the canonical bases of \({\mathcal {T}}\) and \({\mathcal {T}}^{*}\) (as well as each of their subases) are equivalent to their square. In our language, [16, Theorem 5.6] says that every left (resp. right) dominant unconditional basis is universal for well complemented block basic sequences. Combining the arguments used in its proof with Lemma 3.14 yields the following quantitative result.
Theorem 7.11
Let \({\mathcal {X}}=({\varvec{x}}_k)_{k=1}^\infty \) be a left (or right) D-dominant normalized K-unconditional basis of a quasi-Banach space \(X\) with modulus of concavity at most \(\kappa \). Then \({\mathcal {X}}\) is uniformly universal for well complemented block basic sequences with function depending on D, K and \(\kappa \).
Proof
Let us just do the right-dominant case since the left-dominant case is similar. For that, we first show that there are constants \(D_1\) and \(D_2\) (depending only on D), \(\kappa \) and K such that any semi-normalized disjointly supported basic sequence \({\mathcal {U}}=({\varvec{u}}_m)_{m\in {\mathcal {M}}}\) \(D_2\)-dominates \((a\,{\varvec{x}}_{k_m})_{m\in {\mathcal {M}}}\) and it is \(D_1\)-dominated by \((b\, {\varvec{x}}_{j_m})_{m\in {\mathcal {M}}}\), where \(a=\inf _m\Vert {\varvec{u}}_m\Vert \), \(b=\sup _{m} \Vert {\varvec{u}}_m\Vert \), \(j_m=\min ({\text {supp}}({\varvec{y}}_m))\), and \(k_m=\max ({\text {supp}}({\varvec{y}}_m))\).
Indeed, if \(A_m={\text {supp}}({\varvec{u}}_m){\setminus }\{ j_m\}\), and \((a_m)_{m\in {\mathcal {M}}}\in c_{00}({\mathcal {M}})\),
In turn, if \(F_m={\text {supp}}({\varvec{u}}_m){\setminus }\{ k_m\}\), there are \((\lambda _m)_{m\in {\mathcal {M}}}\) and \((\gamma _m)_{m\in {\mathcal {M}}}\) such that \(a=\kappa (\lambda _m+\gamma _m)\), \(0\le \lambda _m\le \Vert S_{F_m}({\varvec{u}}_m)\Vert \), and \(0\le \gamma _m\le |{\varvec{x}}_{k_m}^*({\varvec{u}}_m)|\) for all \(m\in {\mathcal {M}}\). Hence,
Pick \(0<\lambda <1\). Let \({\mathcal {Y}}=({\varvec{y}}_m)_{m\in {\mathcal {M}}}\) be a well complemented normalized basic sequence with good C-projecting functionals \({\mathcal {Y}}=({\varvec{y}}^*_m)_{m\in {\mathcal {M}}}\). For each \(m\in {\mathcal {M}}\) there is \(k_m\in {\text {supp}}({\varvec{y}}_m)\) such that, if \(A^{l}_m={\text {supp}}({\varvec{y}}_m)\cap [1,k_m]\) and \(A^{r}_m={\text {supp}}({\varvec{y}}_m)\cap [k_m,\infty )\),
By Lemma 3.14, \({\mathcal {Y}}^r:=(S_{A^r_m}({\varvec{y}}_m))_{m\in {\mathcal {M}}}\) \((CK/(1-\lambda ))\)-dominates \({\mathcal {Y}}\), and \({\mathcal {Y}}\) (CK)-dominates \({\mathcal {Y}}^l:=(S_{A^l_m}({\varvec{y}}_m))_{m\in {\mathcal {M}}}\). Moreover \({\mathcal {Y}}^l\) \((CK/\lambda )\)-dominates \({\mathcal {Y}}\), whence
Therefore, \({\mathcal {Y}}^l\) \((CKD_2/\lambda )\)-dominates \(({\varvec{x}}_{k_m})_{m\in {\mathcal {M}}}\). Since \(\Vert S_{A^r_m}({\varvec{y}}_m)\Vert \le K\) for all \(m\in {\mathcal {M}}\), \(({\varvec{x}}_{k_m})_{m\in {\mathcal {M}}}\) \((KD_1)\)-dominates \({\mathcal {Y}}^r\). Summing up, choosing \(\lambda =1/(1+\kappa C K)\) we infer that \({\mathcal {X}}\) is uniformly universal for well complemented basic sequences with function
\(\square \)
Finally, since they are locally convex, both \({\mathcal {T}}\) and \({\mathcal {T}}^{*}\) are trivially L-convex lattices.
Combining the above background information with our main results we show a couple of examples:
Example 7.12
For \(0<p<1\) and F an Orlicz function as in Proposition 7.7, the spaces
-
(i)
\(\ell _{p}({\mathcal {T}})=({\mathcal {T}}\oplus {\mathcal {T}}\oplus \cdots \oplus {\mathcal {T}}\oplus \cdots )_{\ell _p}\) and
-
(ii)
\(\ell _{F}({\mathcal {T}}^{*})=({\mathcal {T}}^{*}\oplus {\mathcal {T}}^{*}\oplus \cdots \oplus {\mathcal {T}}^{*}\oplus \cdots )_{\ell _{F}}\)
have a (UTAP) unconditional basis.
7.6 Mixed-norm Lebesgue sequence spaces
We close with applications to finite and infinite direct sums of mixed-norm Lebesgue sequence spaces.
Example 7.13
Suppose \((p_j)_{j=1}^n\) is a sequence of indexes in (0, 1] with \(p_j=1\) for at most one j. We consider the space
of recursive direct sums of a finite number of (possibly repeated) sequence spaces \(\ell _{p_{j}}\). \(X\) is a p-Banach space for \(p=\min _{j} p_{j}\), and its canonical basis \({\mathcal {X}}\) is unconditional and equivalent to its square. Moreover, \({\mathcal {X}}\) induces on \(X\) a p-convex lattice structure, and it dominates the unit vector system of \(\ell _q\), where \(q:=\max _j p_j\). Thus, in the case when \(q<1\), Lemma 3.19 implies that \({\mathcal {X}}\) is also strongly absolute. Therefore, by Theorem 3.18, \(X\) has a (UTAP) unconditional basis. If we let one (and only one) of the indexes \(p_{j}\) be 1, we need to distinguish two cases. Suppose first that \(p_{1}=1\) and \(0<p_{j}<1\) for \(1<j\le n\). Then, as before, the canonical basis of \(\ell _{p_2}(\ell _{p_3}(\cdots \ell _{p_i}(\cdots (\ell _{p_n})))\) is strongly absolute and so the uniqueness of unconditional basis of \(\ell _{1}(\ell _{p_2}(\cdots \ell _{p_i}(\cdots (\ell _{p_n})))\) follows from Theorem 6.3. Now, suppose that an index other than \(p_{1}\), say \(p_{3}\), is equal to 1. On one hand, the canonical basis of \(\ell _{p_4}(\ell _{p_5}(\cdots \ell _{p_i}(\cdots (\ell _{p_n})))\) is strongly absolute, so that by Theorem 6.1, the canonical basis of \(\ell _{p_{3}}(\ell _{p_4}(\ell _{p_5}(\cdots \ell _{p_i}(\cdots (\ell _{p_n})))\) is uniformly universal for well-complemented block basic sequences. On the other hand, since the canonical basis of \(\ell _{p_{1}}(\ell _{p_{2}})\) is strongly absolute, we just need to apply Theorem 4.2.
Remark 7.14
In Example 7.13, the hypothesis that at most one \(p_{j}=1\) is important for the validity of the uniqueness result. For instance, we don’t known whether \(\ell _1(\ell _p(\ell _1)))\) has a (UTAP) unconditional bases.
Example 7.15
Suppose \((p_j)_{j=1}^n\) is a sequence of indexes in (0, 1), and let \(k\in [0,n]\cap {\mathbb {Z}}\). Then
has a (UTAP) unconditional basis.
Example 7.16
Let \((p_n)_{n=1}^\infty \) be a one-to-one sequence in (0, 1] with \(s:=\inf _n p_n>0\), and let \(q\in (0,1]\). Consider now the space
Note that since \(\ell _p(\ell _p)=\ell _p\) isometrically for all \(p>0\), there is no real restriction in assuming that the indices \(p_j\) are not repeated.
The unit vector system \({\mathcal {E}}_p\) of \(\ell _p\) is \(2^{1/p}\)-equivalent to its square. Moreover, \({\mathcal {E}}_p\) is perfectly homogeneous, thus uniformly universal for well complemented block basic sequences with function \(C\mapsto 1\). Finally, \({\mathcal {E}}_p\) is 1-unconditional and, if we consider on \(\ell _p\) the lattice structure induced by \({\mathcal {E}}_p\), \(M_r(\ell _p)=1\) for all \(r\le p\). Hence, in the case when \(q<1\), the uniqueness of unconditional basis of \(X\) is an application of Theorem 4.2, where the hypothesis (iv) is fulfilled with condition (a).
Suppose now that \(q=1\) and \(t:=\sup _n p_n<1\). The important detail here is that the canonical basis of \(\ell _{p_{n}}\) is strongly absolute with the same function \(\alpha \). In fact, by [5, Lemma 3.2], we can choose
Hence, applying Theorem 6.3 gives that \(X\) has a (UTAP) unconditional basis.
Remark 7.17
In Example 7.16, we do not know whether \(X\) has a (UTAP) unconditional basis in the case when \(q=1\) and \(\lim _n p_n=1\). Similarly, in Example 7.15 we do not know whether \(X\) has a (UTAP) unconditional basis in the case when some of the indices \(p_j\) are equal to 1.
References
Albiac, F., Ansorena, J.L.: On the permutative equivalence of squares of unconditional bases. arXiv e-prints arXiv2002.09010 (2020)
Albiac, F., Ansorena, J.L.: Projections and unconditional bases in direct sums of \(\ell _p\) spaces, \(0<p\le \infty \). Math. Nachr. 294(11), 2052–2062 (2021). https://doi.org/10.1002/mana.201900537
Albiac, F., Ansorena, J.L., Berná, P.M., Wojtaszczyk, P.: Greedy approximation for biorthogonal systems in quasi-Banach spaces. Dissertationes Math. (Rozprawy Mat.) 560, 1–88 (2021). https://doi.org/10.48550/arXiv.1903.11651
Albiac, F., Ansorena, J.L., Dilworth, S.J., Kutzarova, D.: Banach spaces with a unique greedy basis. J. Approx. Theory 210, 80–102 (2016). https://doi.org/10.1016/j.jat.2016.06.005
Albiac, F., Ansorena, J.L., Wojtaszczyk, P.: Quasi-greedy bases in \(\ell _ p\)\((0<p<1)\) are democratic. J. Funct. Anal. 280(7), 108871 (2021). https://doi.org/10.1016/j.jfa.2020.108871
Albiac, F., Kalton, N.J.: Topics in Banach Space Theory, 2nd edn. Graduate Texts in Mathematics, 233. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31557-7 (With a foreword by Gilles Godefroy)
Albiac, F., Kalton, N.J., Leránoz, C.: Uniqueness of the unconditional basis of \(l_1(l_p)\) and \(l_p(l_1)\), \(0<p<1\), Positivity 8(4), 443–454 (2004)
Albiac, F., Leránoz, C.: Uniqueness of unconditional basis of \(l_p(c_0)\) and \(l_p(l_2),\ 0<p<1\). Studia Math. 150(1), 35–52 (2002). https://doi.org/10.4064/sm150-1-4
Albiac, F., Leránoz, C.: Uniqueness of unconditional basis in Lorentz sequence spaces. Proc. Am. Math. Soc. 136(5), 1643–1647 (2008). https://doi.org/10.1090/S0002-9939-08-09222-8
Albiac, F., Leránoz, C.: An alternative approach to the uniqueness of unconditional basis of \(\ell _p(c_0)\) for \(0<p<1\). Expo. Math. 28(4), 379–384 (2010). https://doi.org/10.1016/j.exmath.2010.03.004
Albiac, F., Leránoz, C.: Uniqueness of unconditional bases in nonlocally convex \(\ell _1\)-products. J. Math. Anal. Appl. 374(2), 394–401 (2011). https://doi.org/10.1016/j.jmaa.2010.09.048
Albiac, F., Leránoz, C.: Uniqueness of unconditional bases in nonlocally convex \(\mathbf{c_0}\)-products. Isr. J. Math. 184, 79–91 (2011). https://doi.org/10.1007/s11856-011-0060-2
Altshuler, Z.: Uniform convexity in Lorentz sequence spaces. Isr. J. Math. 20(3–4), 260–274 (1975). https://doi.org/10.1007/BF02760331
Bourgain, J., Casazza, P.G., Lindenstrauss, J., Tzafriri, L.: Banach spaces with a unique unconditional basis, up to permutation. Mem. Am. Math. Soc. 54, 322 (1985). https://doi.org/10.1090/memo/0322
Carro, M.J., Raposo, J.A., Soria, J.: Recent developments in the theory of Lorentz spaces and weighted inequalities. Mem. Am. Math. Soc. 187, 877 (2007). https://doi.org/10.1090/memo/0877
Casazza, P.G., Kalton, N.J.: Uniqueness of unconditional bases in Banach spaces. Isr. J. Math. 103, 141–175 (1998). https://doi.org/10.1007/BF02762272
Casazza, P.G., Kalton, N.J.: Uniqueness of unconditional bases in \(c_0\)-products. Studia Math. 133(3), 275–294 (1999)
Casazza, P.G., Shura, T.J.: Tsirelson’s Space, Lecture Notes in Mathematics, 1363. Springer, Berlin (1989). https://doi.org/10.1007/BFb0085267 (With an appendix by J. Baker, O. Slotterbeck and R. Aron)
Dilworth, S.J., Kalton, N.J., Kutzarova, D., Temlyakov, V.N.: The thresholding greedy algorithm, greedy bases, and duality. Approx. Constr 19(4), 575–597 (2003). https://doi.org/10.1007/s00365-002-0525-y
Hall, M., Jr.: Distinct representatives of subsets. Bull. Am. Math. Soc. 54, 922–926 (1948). https://doi.org/10.1090/S0002-9904-1948-09098-X
Jameson, G.J.O.: The \(q\)-concavity constants of Lorentz sequence spaces and related inequalities. Math. Z. 227(1), 129–142 (1998). https://doi.org/10.1007/PL00004364
Kalton, N.J.: Orlicz sequence spaces without local convexity. Math. Proc. Cambr. Philos. Soc. 81(2), 253–277 (1977). https://doi.org/10.1017/S0305004100053342
Kalton, N.J.: Convexity conditions for nonlocally convex lattices. Glasg. Math. J. 25(2), 141–152 (1984). https://doi.org/10.1017/S0017089500005553
Kalton, N.J.: Banach envelopes of nonlocally convex spaces Can. J. Math. 38(1), 65–86 (1986). https://doi.org/10.4153/CJM-1986-004-2
Kalton, N.J., Leránoz, C., Wojtaszczyk, P.: Uniqueness of unconditional bases in quasi-Banach spaces with applications to Hardy spaces, 1990. Isr. J. Math. 72(3), 299–311 (1991). https://doi.org/10.1007/BF02773786
Kalton, N.J., Peck, N.T., Roberts, J.W.: An \(F\)-Space Sampler, London Mathematical Society Lecture Note Series, 89. Cambridge University Press, Cambridge (1984). https://doi.org/10.1017/CBO9780511662447
Kamińska, A., Parrish, A.M.: Convexity and concavity constants in Lorentz and Marcinkiewicz spaces. J. Math. Anal. Appl., 343(1), 337–351 (2008). https://doi.org/10.1016/j.jmaa.2008.01.034
Leránoz, C.: Uniqueness of unconditional bases of \(c_0(l_p),\;0<p<1\). Studia Math. 102(3), 193–207 (1992)
Lindenstrauss, J., Pełczyński, A.: Absolutely summing operators in \(L_{p}\)-spaces and their applications. Studia Math. 29, 275–326 (1968). https://doi.org/10.4064/sm-29-3-275-326
Lindenstrauss, J., Tzafriri, L.: Classical Banach Spaces. II—Function Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas], 97. Springer, Berlin (1979)
Lindenstrauss, J., Zippin, M.: Banach spaces with a unique unconditional basis. J. Funct. Anal. 3, 115–125 (1969)
Mitjagin, B.: Fréchet spaces with a unique unconditional basis. Studia Math. 38, 23–34 (1970). https://doi.org/10.4064/sm-38-1-23-34
Mitjagin, B.S.: Equivalence of bases in Hilbert scales. Studia Math. 37, 111–137 (1970/71)
Nawrocki, M., Ortyński, A., Mackey, T.: Topology and complemented subspaces of Lorentz sequence spaces \(d(w, p)\) for \(0<p<1\). Trans. Am. Math. Soc. 287(2), 713–722 (1985). https://doi.org/10.2307/1999672
Popa, N.: Basic sequences and subspaces in Lorentz sequence spaces without local convexity. Trans. Am. Math. Soc. 263(2), 431–456 (1981). https://doi.org/10.2307/1998360
Wojtaszczyk, P.: \(H_{p}\)-spaces, \(p\le 1\), and spline systems. Studia Math. 77(3), 289–320 (1984). https://doi.org/10.4064/sm-77-3-289-320
Wojtaszczyk, P.: Uniqueness of unconditional bases in quasi-Banach spaces with applications to Hardy spaces. II. Isr. J. Math. 97, 253–280 (1997). https://doi.org/10.1007/BF02774040
Wójtowicz, M.: On the permutative equivalence of unconditional bases in \(F\)-spaces. Approx. Comment. Math. Funct. 16, 51–54 (1988)
Funding
Open Access funding provided by Universidad Pública de Navarra.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
F. Albiac acknowledges the support of the Spanish Ministry for Science and Innovation under Grant PID2019-107701GB-I00 for Operators, lattices, and structure of Banach spaces. F. Albiac and J. L. Ansorena acknowledge the support of the Spanish Ministry for Science, Innovation, and Universities under Grant PGC2018-095366-B-I00 for Análisis Vectorial, Multilineal y Aproximación.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Albiac, F., Ansorena, J.L. Uniqueness of unconditional basis of infinite direct sums of quasi-Banach spaces. Positivity 26, 35 (2022). https://doi.org/10.1007/s11117-022-00905-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11117-022-00905-1



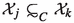 for infinitely many values of
for infinitely many values of 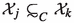 for infinitely many values of
for infinitely many values of  for infinitely many values of
for infinitely many values of