Introduction

Despite the long-lasting political negotiations on the global level for reducing greenhouse gas emissions and achievements in some sectors such as electricity generation in developed countries, the transportation sector is still not showing a downward trend in most countries—not to mention the global level (Lamb et al. 2021; Intergovernmental Panel on Climate Change (IPCC) 2022). This is especially true for aviation and road transport. Road transport, in particular, is still highly dependent on fossil oil and contributes the lions’ share of the total emissions stemming from the sector. Hence, it seems that cutting down greenhouse gas emissions in transportation is still a challenging task [Creutzig et al. (2015)] even though there is a comprehensive stream of literature on potential policy instruments [e.g., Kok et al. (2011); Stepp et al. (2009); Haasz et al. (2018); Whitehead et al. (2021)]. Many of these policy instruments, such as energy or carbon taxes, target at increasing fuel prices, which should decrease miles travelled (VMT) – depending on the fuel price elasticity. This is well documented in the literature [e.g., Dahl and Sterner (1991)]. We use the term "fuel price elasticity” to refer to a change in vehicle miles travelled due to fuel price changes. Thus, the term "price elasticity of passenger car usage” would be more specific. However, in the literature, the term "fuel price elasticity” is used more often, so we use this terminology in our paper.

However, most of the econometric estimation of fuel price elasticities either consider only linear effects or if non-linear effects are considered, they are based on an approach which has been found questionable in the literature [see Brambor et al. (2006)]. Hence, the objective of this paper is to find statistical evidence of heterogeneous effects, i.e., differences in fuel price elasticity among vehicle users across different socio-economic, demographic and spatial variables.

Some studies [e.g., Alberini et al. (2022)] have investigated the issue of heterogeneity in elasticities regarding variables like income, rural vs. urban regions, employment of members in the household etc. They followed the split-sample approach to investigate the issue and found evidence that there is heterogeneity in elasticities among German residents. This methodological approach, however, is fraught with challenges: First, dividing the sample across the moderating variable and running separate regression equations do indeed provide us with elasticities for those different subsamples; however, it doesn’t provide any evidence if the elasticity estimates significantly differ from each other. To gain such knowledge, one needs to conduct separate statistical tests (for instance, that suggested by Cohen (1983) and Clogg et al. (1995), which have not been conducted and reported by any study so far). Second, splitting the sample across a moderating variable forces one to dichotomize a continuous variable (e.g., income). This leads to the loss of variance and valuable information, which may otherwise be interesting to study.

We, therefore, follow the approach suggested by Brambor et al. (2006) and apply it to the representative mobility data set for German passenger car travel [Karlsruhe Institute of Technology (KIT) (2022)]. We analyse changes in mileage among private households as a reaction to changes in fuel prices. Herein, we also consider if these reactions differ across different car- and household-specific characteristics.

The research questions that we investigate are the following:

  • What are the factors influencing the price elasticity of passenger car usage in Germany?

  • Whether and how do these elasticities vary according to the car-specific and household-specific characteristics?

The results obtained are highly relevant for policymakers to design greenhouse gas mitigation policies more effectively and provide suitable compensation methods for socially disadvantaged private households which are sometimes highly dependent on cars. These households might be existence-threateningly affected if heterogeneity is not considered by policymakers. Furthermore, other modellers can also benefit from our results, as they may integrate our insights into their economic models such as general equilibrium models [cf. Mayer et al. (2021)]. Herewith, these models can improve their consideration of equity issues, which supports policymakers for designing suitable and effective policy instruments.

In the following sections, we start by providing an overview of the current literature (“Literature review” section) before we introduce our econometric model in “Methodology” section. This is followed by a results (“Empirical results” section) and discussion (“Conclusion” section). Finally, our conclusions provide corresponding policy recommendations.

Literature review

There is large literature on price elasticities in road passenger transport [e.g. Dahl and Sterner (1991); Goodwin et al. (2004); De Jong and Gunn (2001); Graham and Glaister (2004); Basso and Oum (2007); Sterner and Dahl (1992); Dahl (1995); Graham and Glaister (2002b, 2002a)]. Many of these studies differ regarding the time horizon of the effect. While short-term effects focus on the reduction of mileage by car (i.e. mainly avoidance of trips or short-term modal shifts), the long-term effects might even include the substitution of cars by more efficient cars or long-term modal shifts [cf. Blum et al. (1988); Drollas (1984); Oum et al. (1992)]. Therefore, the long-term elasticities have been found to be somewhat higher (e.g. − 0.8) compared to the short-term elasticities [e.g. − 0.3) Graham and Glaister (2004)]. The literature has also analysed if fuel price elasticities vary over time [e.g. Espey (1998)] and with the level of fuel prices [cf. Rouwendal and de Vries (1999)].

Core insights into this issue were mainly gained during the sharp increases in fuel prices [cf. Rouwendal and de Vries (1999)]. Rouwendal and de Vries (1999) estimated a random effects panel model for the Netherlands, which distinguished the effects across trip purposes and other variables. They conducted their analysis across the two years, 1986 and 1991, during which the national petroleum tax was increased. They focussed on private road transport and found price elasticities to be between − 0.44 and − 0.65. The German specific literature, which focuses on private road transport, has also found the elasticities to be lying in the same range [e.g. Frondel et al. (2008); Frondel and Vance (2010); Frondel et al. (2012); Matiaske et al. (2012); Frondel and Vance (2014)].

Another research stream which is aligned to fuel price elasticities is the literature on rebound effects [cf. Goodwin et al. (2004); Sorrell (2007); Matiaske et al. (2012); Linn (2016)]. Most studies in the literature have identified the rebound effect almost exclusively via fuel price elasticities. These studies have relied on the assumption that both rebound and price effects are simply two sides of the same coin: decreasing unit costs of energy services such as car travelling leads to its more extensive usage.

Some studies in the literature argue that fuel price elasticities are not constant across all groups of the population. Instead, they vary across the different socio-economic and geographical dynamics [e.g. Wadud et al. (2010a); Wadud et al. (2010b); Tilov and Weber (2020); Frondel et al. (2017); Archibald and Gillingham (1980, 1981); Greening et al. (1995); Kayser (2000); Nicol (2003); West and Williams III (2004)]. These studies suggest that, for instance, car users in rural areas respond less to a price change as compared to those located in the urban areas. The argument is that in the rural areas, the availability of alternate modes of transportation is relatively lower [e.g. Wadud et al. (2009); Santos and Catchesides (2005)]. However, there is also contradictory evidence which suggests that car users in rural areas could, in fact, be more price elastic than those in urban areas (Spiller et al. 2017)

One core focus in the literature is to understand the heterogeneity in fuel price elasticity across income. It is argued that lower income households would have higher fuel price elasticities as compared to higher income households (e.g. West and Williams III 2004). However, as pointed out by Kayser (2000), it is also possible for lower income households to be rather price inelastic. The rationale provided for this is that lower income households may already be driving as little as possible because of their budget constraints and, hence, may find it difficult to further reduce their level of driving (Kayser 2000). Moreover, it could be possible for higher income households to have higher price elasticities – as they may have more options to reduce their driving given that much of their travel could be discretionary (e.g. for leisure trips) (Kayser 2000). In addition, they may find it easier to switch to other modes of transport (e.g. air travel for holidays).

All these factors suggest that one can expect considerable heterogeneity in elasticities across location and income. Moreover, in addition to these variables, one can expect the household’s response to a price change to vary regarding the household’s size, number of children, number of car users, vehicle type, vehicle usage, quality of public transportation etc.

In context to Germany, some studies empirically investigated the possibility of heterogeneity in fuel price elasticities among German households [e.g. Frondel and Vance (2018, 2014)]. However, they, in contrast to the wider understanding, found out that the fuel price elasticities for Germany are rather homogeneous and don’t vary with regard to income and other household characteristics. These studies, to identify and analyse heterogeneity, employed interaction models, wherein they interacted fuel prices with income and other variables of interest.

In employing and analysing interaction models, however, they failed to consider the econometric insights brought about by the seminal work of Brambor et al. (2006). Brambor et al. point out the common mistakes that are being made while using and interpreting the results of the interaction model. They also provide the guidelines and methodological steps that one must follow while using these models. Given this, the question arises whether the contradictory results obtained for Germany reflect the true empirical phenomenon, or are they just the artefact of the methodological approaches used, and the limitations associated with it. The objective of this paper is to throw light on this issue.

The results suggest that when we use interaction models and follow all methodological steps as recommended by Brambor et al., we do uncover significant heterogeneity in fuel price responses among German households. These results have an important bearing on the policy; they could help policymakers in coming out with targeted instruments to accelerate modal shifts in the sustainable direction for the different groups in the society.

Methodology

Data and data manipulation

For the modelling, we used the German Mobility Panel (MOP), a longitudinal survey that collects detailed data about German mobility behaviour (Ecke et al. 2021). The data is available from 1994 onward and has been used extensively for estimating fuel price elasticities for Germany in the past.

MOP has a rotating sample, that is, households stay in the panel for three consecutive years, and then are replaced by a new set of households. It consists of different survey modules. For this analysis, we draw on the module ’refuelling diary’ (‘Tankbuch’) which provides detailed data on car mileage, fuel consumption, fuel prices and car-specific characteristics. The data is generated by a survey that happens every year for eight weeks during April and June. As part of the survey, the households are required to maintain a travel diary and record all their refuelling activities, odometer reading, fuel consumption, fuel prices, mileage etc. We merge the ‘Tankbuch’ module with the general survey that provides information about demographic, socio-economic and spatial characteristics of the households.

Following the literature [e.g. Frondel et al. (2007); Frondel and Vance (2014, 2018)], we restrict our analysis to single car-owning households. This is done to abstract from complexities associated with the substitution between cars in multiple vehicle households. Past studies suggest that such substitution can substantially bias the results (see De Borger et al. 2016).Footnote 1 In Germany, the share of single-car (car-less) households equals about 53% (22%) (Nobis and Kuhnimhof 2018). The average number of cars per household in Germany is 1.1 (or 1.4 neglecting the car-less households).

Our final sample consists of 4166 households which were analysed during the period 2002–2020. 19% of the households participated in only one period, 63% in two consecutive years and 18% of the households participated for three years. Although the MOP dataset provides data from 1994 onward, 2002 is the starting year of our analysis as some variables (e.g. income classes) are available only from 2002 onward.

Modelling approach and baseline model

For the modelling, we explored the use of different panel data estimation techniques: pooled OLS method, fixed effects (FE) method, and random effects (RE) method. The latter two methods yield consistent and efficient estimates only when certain conditions are satisfied. For instance, RE model requires that the household-specific effects are randomly distributed and are uncorrelated with explanatory variables. We test for the fulfilment of these conditions by conducting the Hausman test. The test rejected the use of the RE models in favour of FE models. The use of FE models is, however, not appropriate for our analysis, as in our dataset the households stay in the panel for a short period of maximum 3 years, leading to a rather small t. The use of FE in this case can lead to misleading inferences (Wadud et al. 2009). We therefore use a pooled OLS model, as it is the most suitable given our data and variables.

To estimate fuel price elasticities, we use the following baseline model:

$$\begin{aligned} VMT_{i,t} = \alpha _1 +\alpha _2\cdot FP_{i,t} + \alpha _3\cdot Z_{i,t}' + e_{i,t} \end{aligned}$$
(1)

where:

  • \({VMT}_{i,t}\) is the log of vehicle miles travelled (in kilometres) by household i at the time t,

  • \(\alpha _1\) is the intercept,

  • \(\alpha _2\) gives the fuel price elasticity,

  • \(FP_{i,t}\) is the log of real fuel price per litre of household i at the time t,

  • Z is the vector of control variables, and

  • \(e_{i,t}\) the error term.

The dependent variable, VMT, is obtained by summing the total kilometres driven over the period of eight weeks and converting this sum into a monthly figure (total kilometres/number of days \(\cdot\) 30). The real fuel price variable is derived by first taking an average of the fuel price per litre as reported on every visit to the gas station. The nominal fuel prices are then converted to real fuel prices by dividing them by the consumer price index (CPI), obtained from Germany’s Federal Statistical Office (2022).

Across various price elasticity studies, the major issue of concern is the endogeneity of prices in the regression. We believe that at the macro level, fuel prices could be endogenous to the demand for travel. However, at the micro level, from the perspective of individual households, they are generally treated as exogenous [see, for instance, Frondel et al. (2012); Frondel and Vance (2018); Alberini et al. (2022)]. In other words, there is a lower possibility of endogeneity due to reserve causality between VMT and fuel prices.

Following the literature, we control for the diesel dummy, horsepower (as a proxy for the power of the engine), age of car, size of household, and income. Descriptive statistics for these and other variables used in the model can be found in Table 8 in the Appendix.Footnote 2 We also control for year dummies to account for all changes that happen over time and that affect the households in the sample.

To address the problem of heteroscedasticity and autocorrelation, we use cluster-robust standard errors (cf. White (1984), pp. 134–142) which allow for correlation of errors within households.

Heterogeneity

To test for heterogeneity in fuel price elasticities, we modify the model given in Eq. (1). The model used for analysing heterogeneity is given as follows:

$$\begin{aligned} VMT_{i,t}= \alpha _1 +\alpha _2\cdot FP_{i,t}+ \alpha _3\cdot X_{i,t} + \alpha _4\cdot (FP_{i,t} \cdot X_{i,t}) + \alpha _5\cdot Z_{i,t}' + e_{i,t} \end{aligned}$$
(2)

Where X is the moderating variable, the variable across which we are interested in testing for heterogeneity. This could be a continuous variable or a dummy variable. Z’ now represents the vector of other control variables included in the model. Fuel price elasticity is now given by Eq. (3).

$$\begin{aligned} \frac{\partial {VMT}}{\partial FP} = \alpha _2 + \alpha _4\cdot X_{i_t} \end{aligned}$$
(3)

While testing for heterogeneity in fuel price elasticities, many of the existing studies in the literature have used interaction models, similar to the one given in Eq. (2). The existing approach looks at the significance of the interaction term – that is, the \(\alpha _4\) coefficient – to form conclusions whether there is heterogeneity or not. When the interaction term is insignificant, it is concluded that there is no heterogeneity regarding the moderating variable, X [e.g. Frondel et al. (2012)].

However, this approach has been criticized by the seminal work of Brambor et al. (2006). According to Brambor et al., just looking at the significance of the interaction term and forming conclusions about heterogeneity could lead us to draw erroneous conclusions. They emphasize that while interpreting the results of an interaction model, one must first estimate the standard errors, given in Eq. (4). These standard errors do not get automatically reported by the standard software packages, but need to be estimated separately.

$$\begin{aligned} SE = \sqrt{Var(\alpha _2)+ X_{i,t}^2 \cdot Var(\alpha _4)+ 2\cdot X_{i,t}\cdot {Cov(\alpha _2,\alpha _4)}} \end{aligned}$$
(4)

To the best of our knowledge, there has not been a single study in the fuel price elasticity literature that has reported these standard errors, or drawn inferences based on that. Owing to this, it is difficult to trust the conclusions formed in the literature.

Moreover, according to Brambor et al., just estimating the standard errors as given in Eq. (4), perhaps at some average or representative value of the moderating variable, is not enough. It is important to calculate and report the marginal effects and standard errors across all values of the moderating variable. Brambor et al. show, using examples, that the results and statistical significance could differ across the different values of the moderating variable. From the policy perspective, it is important to move beyond the aggregated/average picture, and calculate and analyse the effects across all possible values that the moderating variable can take.

We therefore follow the rules and guidelines prescribed by Brambor et al. to test for heterogeneity in fuel price elasticities.

Empirical results

Baseline model elasticities

We start with a parsimonious model, where we include only fuel prices and year dummies as independent variables. The results, as shown in Column 1 of Table 1, suggest that a 1% increase in fuel prices leads to a 1.5% decrease in VMT. We now sequentially add other variables in the model. The results are presented in Column 2 to 7. On adding the other variables, the absolute value of the fuel price coefficient reduces in magnitude, but it remains significant at the 1% level of significance. The full model (cf. Column 7) suggests that 1% increase in fuel prices leads to 0.5% decrease in VMT.

Regarding the control variables, the results are as expected and in line with the literature on short-term fuel price elasticitiesFootnote 3. The coefficient of diesel dummy is significantly positive. The results suggest that driving a diesel car leads to around 33% more travel as compared to a non-diesel car (see Column 7). The coefficient of horsepower is also significantly positive, suggesting that 1% increase in horsepower leads to 0.2% increase in VMT.

The age of a car, on the other hand, has a significantly negative effect on VMT. As the age of a car increases by one year, VMT decreases by 2%. Regarding socio-economic variables, the size of household as well as income have significantly positive effects on VMT; as the household size and income increase by one unit (i.e. adding a household member or switching to a higher income class), VMT increases by 8% and 3% respectively. Regarding regional variables, the full model suggests that living in a medium-sized city leads to 5% more travel as compared to living in a large city. Living in the countryside leads to 16% more travel.

In the next section, we conduct different checks to test for the robustness of our results.

Table 1 Baseline model: fuel price elasticities and control variables
Full size table

Robustness checks

First, we test for the possibility of high multicollinearity among variables, which could lead to inefficient estimations. To do so, we construct a correlation matrix (cf. Table 9). The matrix suggests the presence of low correlation among variables. The estimated variance inflation factors (VIF) for each variable (cf. Table 10) further confirms that the model is not subject to the problem of high multicollinearity.Footnote 4

Further, we test for the robustness by removing outliers using the DFITS index (cf. Column 1 of Table 11). The fuel price elasticity coefficient is \(-\)0.48. We also used an alternative method of removing outliers (i.e. Cooks’ D test). The results, available upon request, suggest the fuel price elasticity coefficient to be in the order of −0.5. The magnitudes of other coefficients vary a bit but remain consistent in terms of both economic and statistical significance.

We also use alternative measures of fuel prices, as have been commonly used in the literature (e.g. Frondel and Vance 2018). We calculate nominal fuel prices by dividing the total expenditure for fuel over the survey period by the total litres purchased. This nominal value was then converted to real values by using the consumer price index for Germany (CPI). The results, as presented in Column 2 of Table 11, show the fuel price elasticity coefficient to be −0.57. We also calculate the nominal fuel prices by dividing the expenditure for fuel by the total litres purchased, as reported on the first visit to the petrol station (cf. Column 3 of Table 11). The real values were then used in the model. The corresponding fuel price elasticity coefficient is estimated to be around \(-\)0.6.

We also control for events that may have happened during the survey period and may have disrupted the normal pattern of travel – for instance, relocation, vacations, sickness, and car damage. The results, as presented in Table 12 in the Appendix, suggest that the fuel price coefficient remains significantly negative, with its magnitude lying in the range of −0.47 to −0.57.

In sum, the fuel price elasticity coefficients, across all the different models and specifications, lie in the range of 0.5 and −0.6, suggesting that 1% increase in real fuel prices leads to 0.5–0.6% decrease in VMT. These results for elasticities are consistent with those obtained in the literature (see Frondel et al. 2017, 2012, 2008; Frondel and Vance 2014, 2010, 2009). In the next section, we test for whether the fuel price elasticities vary according to the different household and car-specific characteristics.

Do fuel price elasticities vary according to the households’ characteristics?

We first focus on socio-economic characteristics such as number of car users, number of people in the household, number of children, and income. As a first step, we use an interaction model and interact each of these variables with the fuel price variable. The results are presented in Table 2. Column 1 presents the results of the interaction of fuel prices by number of car users. The interaction term is insignificant. However, as suggested by Brambor et al., we calculate marginal effects and standard errors across all the values of the moderating variable—which in this case is the number of people in the household using the car (cf. Fig. 4a).Footnote 5

Table 2 Heterogeneity across socio-economic characteristics of households: results of interaction models
Full size table

We also see from Table 2 that the interaction terms of size of household, number of children, and income in Columns 2, 3, and 4 are significant, too. Correspondingly, Figs. 1a, b, and 4b present the marginal effects and their significance across all values of the moderating variable. The results suggest that fuel price elasticities vary across all the three moderating variables.

Fig. 1
figure 1

Marginal effects graph: Fuel price elasticities across different socio-economic variables (a number of household members and b income classes)

Full size image

In these Figures the solid sloping line gives the fuel price elasticities. The moderating variable is given on the horizontal axis. The dotted lines give the 90% confidence intervals. The elasticities are statistically significant whenever the upper and lower bounds of the confidence interval are both above (or below) zero.

The elasticities are higher, for instance, for the smaller households, and decrease as the size of household increases (see Fig. 1a). Interestingly, the results are not significant across the entire range of the household size; they are significant only up to the household size of five. If we had only looked at the significance of the interaction term given in Table 2, we would have concluded that the size of households affects elasticities, overlooking the fact that it affects elasticities only in a certain range. Notably and as expected, most of the observations in our sample have the household size of less than four members.

Similarily, for the considered income groups, Fig. 1b shows that elasticities vary across the different groups. They are the highest for households with less than €500 net income per month, but decrease as the income level increases. The elasticities are the lowest for the households with greater than €3500 income. These results stand in contrast with the findings of Frondel et al. (2012) which conclude that there is no heterogeneity regarding income for German households. The results reinforce the argument that higher income households react to fuel price changes not by reducing VMT, but rather by increasing their mobility budgets (cf. Zumkeller et al. 2005)—a luxury that lower income households cannot afford. Lower income households are forced to switch modes, resulting in a higher than average price elasticity (Wadud 2007; Wadud et al. 2010a).

We also tested if the elasticities vary according to the usage of cars – that is, whether they are used for private purposes or business purposes. This is an important variable, as in Germany, the usage of business cars is quite widespread. About 62% of new cars are sold and used for business purposes. Most of these cars can also be used for private purpose; however, herein the vehicle users don’t directly pay for the fuel (Kraftfahrt-Bundesamt (KBA) 2022b). We, therefore, expected a lower price elasticity for such cars as compared to the cars which are private cars and used solely for private purposes. Our sample shows a share of business cars in the fleet of about 14%, which is a slight over-representation compared to the average German fleet [where the share is about 10%, Kraftfahrt-Bundesamt (KBA) (2022a)]. In Column 1 of Table 3, we interact fuel prices with private car. The other category—that is, business car—is the reference category. The interaction term is insignificant. However, when we estimate the marginal effects and correct standard errors (see Table 4), we find that the elasticities are statistically significant: when a car is used only for private purposes, the elasticity is −0.55, but when it is also used for business purposes, the elasticity is −0.49, and therewith lower.

In Fig. 4a, we see that the fuel price elasticities vary according to the number of car users. When there are not many people in the household using a car, elasticities are higher, but as the number of car users increases, the elasticities decrease. We also see that the elasticities are not significant across all the values given on the horizontal axis. We see statistically significant effects up to the number of car users being four. To put the results in perspective, we follow Berry et al. (2012) and superimpose a histogram over the marginal effects graph. The histogram shows the number of observations that fall under each value of the moderating variable. The histogram suggests that most of the cases observed in the data set fall within the significant range, indicating the importance of results from the policy perspective. Had we just looked at the significance of the interaction term and not followed the other recommended methodological steps, we would have ended up drawing the erroneous conclusion that the extent of car dependency has no effect on fuel price elasticities. Households without children have higher elasticities compared to those having 1–2 children (the effects are insignificant thereafter, cf. Fig. 4b).

Table 3 Heterogeneity across the usage type and other characteristics of a car: results of interaction models
Full size table

We also test if the elasticities differ according to the habits and characteristics of households, in the sense of whether they are ‘car-lovers’ or not [cf. Jochem et al. (2021)]. To test for this, we look at the kind of car a household drives. The hypothesis is that if a household drives a premium car, it most likely is a ‘car-loving’ household, and may not be as responsive to changes in fuel prices. 31% of the households in our sample own a premium car, while the rest own a non-premium car. We also look at whether a household owns a diesel car. Normally, people who extensively rely on cars for their travel tend to buy diesel cars owing to the higher fuel efficiency and lower price in Germany (Frondel and Vance 2014). 23% of the households in our sample own a diesel car.

Table 4 Marginal effects: fuel price elasticities across the usage type and other characteristics of a car
Full size table

The results, as presented in Table 3 (Columns 2 and 3), show that the interaction terms are insignificant. However, Table 4, which presents the marginal effects and significance level based on the corrected standard errors, suggests that the elasticities are significantly different from zero. These results support the argument that mobility is not only seen as a means to get from one destination to another, but also as a measure of esteem and lifestyle positioning in the society Jensen (1999); Aarts and Dijksterhuis (2000); Gärling and Schuitema (2007); Jochem (2009).

Although we have restricted our attention to single-car owning households, we also test if the presence of multiple cars affects how people respond to fuel price changes. The results are presented in Table 3 (Column 4) and Table 4. Although the interaction effect is insignificant, Table 4 suggests that the elasticities for the two groups are significantly different from zero. These results contrast the findings of Frondel et al. (2012) who concluded that there is no heterogeneity across multiple versus single car owning households. Our results indicate that multiple car-owning households have lower responsiveness compared to single car-owning households. This could be because households with multiple cars can choose among the most efficient cars, thereby maintaining their travel. Furthermore, possession of multiple cars can be seen as an indicator of wealth, suggesting that multiple-car households have lower elasticities as they can more easily transfer their non-travel budget for travel purposes.

It is quite possible that the elasticities vary according to the local and regional characteristics of where households reside. To test for this, we start by investigating whether the elasticities differ according to where the households are located – that is, whether in and around a large city, in and around a medium city or in rural areas and the countryside. Table 5 (Column 1) presents the results of the interaction model. The interaction terms are insignificant. We calculate the marginal effects and significance levels based on the corrected standard errors. These results are presented in Table 6.

The results suggest that the elasticities differ across the three regions, with rural dwellers might even be more price elastic. As our dependent variable is the VMT and people in rural areas need to drive longer distances, every trip is more costly and consequently the optimization of trips is very meaningful and leads to a mileage reduction.

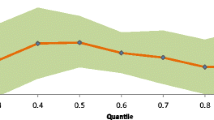
To further check our results, we calculated the marginal effects for the other spatial variables in the MOP data set (Table 13). For further plausibility, we bootstrapped our model to investigate the distribution of our estimated parameters and validated the differences between the parameters with a T-test. The results highlight the robustness and significance of our findings (Fig. 3).

We also look at whether the ease or difficulty of parking, and the roads that the households typically travel on, affect the elasticities. The results of the interaction model are presented in Table 5 (Column 2 and 3). Although the interaction terms are insignificant, we see from the Table 6 that the elasticities are lower when the parking is relatively difficult. Furthermore, households travelling mostly on the inner-city roads react the most to fuel price changes (with the elasticity coefficient being \(-\)0.55) followed by the households travelling on country roads (\(-\)0.45). The elasticity coefficient for the households mostly driving on highways is insignificant.

Next, the distance that people need to travel for meeting their daily needs or for leisure and whether that affects households’ responsiveness to fuel price changes is considered. Column 4 and 5 of Table 5 present the results from the interaction. The marginal effects and the corrected significance levels are presented in Fig. 2. The results suggest that the elasticities reduce as the travelling distance increases; however, the effect is not significant across the entire range. For daily needs, the effects are significant until around 8 kms, and for leisure, the effects are significant until around 18 kms. These results support the argument that the distance to amenities is an important indicator of the household’s ability to refrain from car usage Kingham et al. (2001); Graham and Glaister (2002b).

Table 5 Heterogeneity across the regional and locational characteristics: Results of interaction models
Full size table
Table 6 Marginal effects: fuel price elasticities across the regional and locational characteristics
Full size table
Fig. 2
figure 2

Fuel price elasticities across distance to travel for daily needs and leisure activities

Full size image

We also tested for whether the elasticities vary according to the quality of public transportation. To do so, we use walking time (in minutes) to different transportation modes as a proxy measure for the quality of public transportation. Lower walking time indicates the presence of a better quality of transportation. The results are presented in Table 7 and Fig. 5. Although the interactions terms in most specifications are insignificant (see Table 7), the results presented in Fig. 5 show that the elasticities vary according to the quality of public transportation (which is measured by walking distance to the next access point). The elasticities are higher when the walking time to different transportation modes is not as high. But as the walking time increases, the elasticities reduce and become insignificant. This supports the argument that the households are influenced by the infrastructure improvements that make public transit more convenient Kingham et al. (2001); Bamberg and Rölle (2003). Only in the case of railway station, we see elasticities to be mostly the same irrespective of the walking time (cf. Fig. 5e). This is intuitive as railway stations are mostly used for infrequent longer duration travels rather than day to day travel and are approached by different means of transport. This insight supports our hypothesis that heterogeneity effects are decisive when considering fuel price elasticities.

Table 7 Heterogeneity across the quality of public transportation (Walking time to different transportation modes): results of interaction models
Full size table

In sum, the overall results contrast the existing literature that there is not much heterogeneity in the fuel price elasticities among German households. The results in this study suggest that the elasticities, in fact, vary according to the different socio-economic and spatial characteristics. More explicitly, the results of the study lead to the following insights:

  • Heterogeneity in the number of household members The results support the hypothesis that the more the number of members in a household, the lower are the price elasticities.

  • Heterogeneity in income The insignificant effect of income, as found in the German literature, has been disproved. The results show a significantly negative effect of income – that is, the higher the income, the lower is the fuel price elasticity.

  • Heterogeneity in the quality of service by public transportation The effect of the quality of public transportation, which is associated with mixed evidence in the literature, is significantly positive – that is, the closer the access to public transportation, the higher is the fuel price elasticity).

  • Heterogeneity in regional characteristics The results confirm the recent evidence by Spiller et al. (2017) that car users in rural areas have higher price elasticities than those in the urban areas.

These insights can be used for improving the consideration of fuel-price changes and their impact on car mileage of traffic participants in transport models. Correspondingly, policymakers can develop more effective and fair policy measures of increased fuel prices for reducing car mileage. Nevertheless, while during the period of investigation no disproportionate price change occurred, our results should be handled with care for price changes above 20%.

Conclusion

Fuel price elasticities have been widely analysed during the last decades. They are a decisive factor in determining the socio-economic effects of policy instruments in the transportation sector, particularly the instruments that cause an increase in fuel prices. This paper contributes to the literature by analysing heterogeneity in fuel price elasticities for Germany. The paper uses an interaction model and follows all methodological steps as recommended by Brambor et al. (2006). The results contrast the existing literature and show that fuel price elasticities are not constant for the entire German population. Instead, they vary depending upon the socio-economic and spatial characteristics of German households.

While most results such as the influence of the number of household members, income, and quality of public transportation are consistent with our expectation, the results on regional variables are rather surprising. They show that passenger car use is more price elastic in rural than in urban areas. This might illustrate that the economic burdens on rural dwellers are already high and that higher fuel prices cannot be compensated for but lead directly to a significant reduction in mileage.

Our results help transport modellers and policymakers identify the differentiated effects on households as a result of higher fuel prices. This in turn could help in the formulation of targeted policies and prevent the households from undergoing unacceptable and unfair burdens (e.g. by implementing a compensation via the annual income tax for highly car-dependent but low-income households).

Our statistical results say little about causal mechanisms, which could be an interesting domain for researchers to explore in the future research. Moreover, our data set does not allow identifying avoidance strategies of high prices by individuals (i.e. refueling at lower-price gas stations or refueling at other day times). Finally, while this study focuses on household-level characteristics, it will be interesting to study the differences across individual-level variables such as age, gender, nature, and form of employment etc. This is an important area for future research.