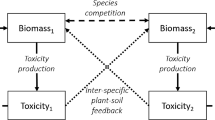
Abstract
Theory and experiments have demonstrated that negative plant-soil feedback (PSF) promotes coexistence between plant species. Plants and soils, however, face the challenge of an increasingly unpredictable environment due to multiple global change factors. Environmental stochasticity induces fluctuations that increase the variability and unpredictability of population dynamics, plant associations in the community and thus properties such as overall productivity. In this paper, we formulate a stochastic version of a classic PSF deterministic model, which describes the outcome of plant species competition in the presence of soil feedback. Especially when the soil feedback is negative, the deterministic expectation is that pulse perturbations to the system (e.g. a drought episode) cause plants and soil to move away from their equilibrium and then return to it. Environmental stochasticity alters this expectation: the system can either settle into a fluctuation regime around the deterministic expectation, or plant species may go extinct. Probability of extinction predictably increases with environmental stochasticity but the more negative the PSF, the more it can counteract the increase in extinction probability caused by increased environmental stochasticity. We stress that in nature the actual impact of PSF will depend on the interactions that link different types of soil organisms to plant species. We conclude that theory shows that plant communities with strong negative PSF are best placed to withstand the risk posed by increased environmental stochasticity but also that we still need more experimental evidence to validate theory and develop applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Very many factors structure plant communities (Tilman 1998; Rees et al. 2001; Hille Ris Lambers et al. 2002; Adler 2007; HilleRisLambers et al. 2012) but in the last three decades the so called plant-soil feedback (PSF) has been increasingly investigated at multiple levels, from theory and in silico modelling studies (Bever 2003; Bonanomi et al. 2005; Bever et al. 2010) to glasshouse experiments, combined experimental and field studies, and metanalysis (Crawford et al. 2019; in’t Zandt et al. 2021). In very general terms, PSF can be defined as the reciprocal effects the soil and plants exert on each other at the population and community level (Bever et al. 1997). The effects can be either negative or positive and can ultimately determine whether competing plant species will coexist or not. In more specific terms, soil can affect the plant growth rate, with major consequence on the population dynamic processes that determine how different plant species come together to form communities. The plant species, too, exert effects on the soil community, hence the term “feedback”.
The simplest possible case to analyse PSF is when two plant species (A and B) compete, and we ask about the conditions for these two species to coexist (Bever 2003). In the presence of competition, the classic condition for coexistence (Case 2000) is intraspecific competition be larger than interspecific competition. Intraspecific competition is larger than interspecific competition when individuals of one plant species compete more strongly between themselves than with individuals of the other species. The product of the competition coefficients (cA and cB) that describe the negative effects of one species on the other, should be smaller than 1 for the two species to coexist, which will generally imply the superior competitors will not lead inferior ones to extinction. But there is also another way for plant A and B to coexist, and which is not mutually exclusive with the classic way: a net negative PSF. We define the net negative PSF more formally in the next paragraphs but in the simple case of two competing species the net PSF is negative if the summed effects of soil on plants add up to a negative term. If that is the case, plants can coexist even under levels of strong interspecific competition that would normally lead to one species outcompeting the other species (Bever et al. 1997, 2010; Bever 2003). That happens because PSF can reduce the negative effects of the superior competitor by either increasing the growth rate of the inferior competitor or decreasing the one of the superior competitor, or both.
In the simple case of two competing plant species, it is customary to conceptualise the entire soil biota as a variable or “soil axis”, which is an extremely simplistic caricature of the tremendous diversity that soil biota actually encompass. As such, the soil axis is not a biologically realistic description of soil biodiversity and the multiple effects that soil biota exerts on plants. The axis is, however, very useful in mathematical models, where it has been shown to represent well the overall soil community in terms of how this community collectively affects plant population dynamics (Bever et al. 2010). That soil axis may range from an arbitrary value, say SA, which represents the soil community characteristic of plant A, to another value, say SB, which represents the soil community characteristic of plant B. The simplification used by ecological modellers when describing the entire soil biota as a numerically standardised soil axis is analogous to the so called “characteristic” soil community, which the experimentalists define as the soil biota associated with two generations of a plant monoculture grown on the same soil. In other words that is the so called “home” soil (Brinkman et al. 2010). The definition of “home” soil is also based on the effect of the entire soil community on plants. In that sense, there is an analogy between the simplification of classic PSF mathematical models and the simplification of PSF experiments. That analogy makes the interpretation of in silico computational results relevant to experimental results.
In mathematical models, the soil axis is typically standardised to vary between 0 and 1. That helps with a formal mathematical definition of the net PSF. In general terms, the net PSF is the total sum of the effects of soil on plants. If there are two plants, A and B, we can describe the impact of soil on them in terms of the impact that the soil community SA typical of A (“home soil of A”) has on plant A (αA) as well as the impact that the same soil has on the other plant B (αB). We also need to quantify the impact that the soil community typical of B (SB = 1—SA) has on its own plant B (βB) as well as on plant A (βA). Using these definitions, the PSF can be defined with the metric Is = αA—αB—βA+βB. Previous theoretical works have shown that when two species compete, the space for coexistence is greatly expanded for Is < 1, even if the product of the competition coefficient cA and cB is bigger than 1 (Fig. 3 of Bever 2003). To be more accurate, it is possible to define a relationship that links Isto cA x cB and determines the conditions under which a certain combination of Is(PSF) and competition associates with coexistence of A and B. In general, coexistence greatly increases with negative Is, which can support the growth rate of the inferior competitor and reduce the one of the superior competitor. Under weak competition, coexistence is even possible for positive Is but the parameter space for coexistence is much reduced. It is important to note that the four terms that quantitatively describe the PSF in terms of the metric Is can each be either positive or negative. That is very useful because it allows describing multiple types of combined positive, negative, direct and indirect effects of soil on plants. All these effects ultimately, although indirectly, describe the multiple and contrasting (i.e. mixture of positive and negative effects) impact of soil pathogens, mutualists and also saprotrophs on plants.
How does the population dynamics of competing plant species change in the presence of PSF? PSF cause systematic and predictable fluctuations around the equilibrium of the system (Bever 2003), and can greatly expand the space for coexistence between plants that would otherwise coexist under a very limited range of conditions, or not even coexist at all (Bever 2003; Bever et al. 2010). There are also many other implications of PSF dynamics, which have been analysed extensively in the last 10 years (Van der Putten et al. 2013, 2016) but the classic theoretical approaches to PSF are mostly based on deterministic models. It has, however, clearly been suggested that plant-soil community interactions vary spatially and temporally, which implies a degree of stochasticity (Kardol et al. 2006, 2007). Also, natural systems are facing increasingly more unpredictable environments, especially in relation to multiple, interacting global change factors (Rillig et al. 2019). In the conservation biology literature, models that embrace stochasticity are the norm: time series of any natural population are, in fact, characterised by fluctuations that can, at least at first, appear erratic but that result from the interaction of many unknown events, which are best modelled using probability distributions (Lande et al. 2003). The main impact of stochasticity on deterministic dynamic is that coexistence may no longer be guaranteed even when the expectation (e.g. average outcome) is coexistence (May 1973a). This is important for plant ecologists because models and experiments that have formalised and investigated the impact of soil biota on plant populations show that negative PSF is a major determinant of plant species coexistence (Bever 2003). We, thus, investigated how a general model that incorporates environmental stochasticity modifies the classic expectation of PSF theory. The idea that plant assembly processes mediated by PSF can take multiple paths is, indeed, not new. For example, the intensity and quality of PSF can be spatially and temporally variable. (Kardol et al. 2006, 2007; Mangan et al. 2010; Suding et al. 2013; Bauer et al. 2015) and we here explore that idea with a general stochastic model.
In this paper, we thus offer an expansion of the classic analytical models by incorporating environmental stochasticity and reformulating the most classic expectation of PSF models in a stochastic framework. That means that we reframe the classic expectations of PSF theory in terms of probability of extinction and coexistence or, more generally, the probability distribution of species relative abundances (Lande et al. 2003; Allen 2010). In general, increasing levels of stochasticity decreases long term population growth rates (Lande et al. 2003; Tuljapurkar 2013) and may decrease the space for coexistence even when the average (i.e. deterministic) dynamics implies coexistence (May 1973b; Gravel et al. 2011). We here explore the tension between the not very well explored destabilising force of stochasticity and the well-known stabilising effect of negative PSF. We also explore how the balance between different types (positive and negative) of plant-soil interactions affects the final impact of PSF on plant stochastic dynamics. We introduce a simple general stochastic model for PSF dynamics, we numerically explore some aspects of the model to formulate expectations on probability of coexistence and extinction, and how the PSF affects this probability, and finally discuss the implications of our analysis for future model extensions and experiments.
Methods
The deterministic model
We start from the classic Bever deterministic model (Bever 2003) that couples the population dynamics of two competing plant species, A and B, to their soil, SA and SB = 1—SA. The system of coupled ordinary differential equations (ODE) that describes this model is (eqs. 1):
where A and B are the population size of species A and B, and SA is the soil axis variable that reaches the maximum value when the soil communities equals the one associated to a monoculture of plant A. The parameter r and m are the intrinsic growth rate and logistic term of the classic logistic population model, and the terms “c” are the competition coefficients. Note that the parameters αA, αB, βAand βBare either positive or negative. The two alphas parameters (αA and αB) describe the net effect of soil of A on plant A and B, while the beta parameters (βAand βB) describe the net effect of the soil of B on plant A and B. The soil state variable thus can fluctuate between the soil typical of A and that typical of B. Finally, the parameter v describes the impact of B on the soil of A. The behaviour of this model is well known (Bever, 2003), and in the supplementary materials (RScript_Bever_Model_Stochastic.R) we provide an R script that reproduces the behaviour of the model with an example based on the same parameters originally presented by Bever (2003). If the system starts away from the equilibrium values, and the combination of parameters is such that the system allows plant coexistence, the trajectories of the system will be characterised by sinusoidal oscillations that quickly dampen until the system reaches the equilibrium, which is stable (Fig. 1a). Note that a multivariate extension of these models to include more plant species as well a more complex description of the soil biota are possible (Bonanomi et al. 2005; de Castro et al. 2021). Also note that we implement the model with no assumption on competitive equivalence between species.
In panel a), numerical solution to the deterministic plant-soil feedback (PSF) model of Bever (2003). The parameters are the same as in Bever (2003) but with equal carrying capacity for the two plants (set to 100), and starting initial conditions set at 50 (0.5 for soil, which ranges from zero to 1). The numerical solution has been derived from applying the Euler-Maruyana algorithm to our system of stochastic differential equations (SDEs) but with variance and correlation set to zero (which collapses our system of SDEs to Bever’s ODEs model). In panel b, ten trajectories or paths (each colour correspond to one simulation for the coupled equations of the three populations) for plant A, Soil and plant B from ten independent simulations of our system of SDEs. Environmental stochasticity puts the system into a series of periodic fluctuations around the expectation for the deterministic equilibrium. The 10 trajectories represent a system over a period of time for which a quasi-equilibrium is reached. For high level of stochasticity, the system may exit this quasi-equilibrium state to become unfeasible
Stochastic model: formulation
We introduce environmental stochasticity to the ODE system of eqs.1 through the Itô calculus formalism for continuous stochastic differential equations (SDE). SDEs for interacting populations are constructed by combining the deterministic component (the ODE of eqs. 1 for us), which represents the “drift” term, and either a continuous time Markov chain describing probabilistic transitions within the population due demographic stochasticity (Allen 2010) or an external source of random variability due to environmental fluctuations (Allen 2010; Dobrow 2016), or a combination of both demographic and environmental stochasticity (Lande et al. 2003). Here, we are mostly interested in broad scale population dynamics, where the impact of demographic stochasticity is likely to be minor given the size of the population under consideration and considering that, typically, demographic stochasticity scales as the inverse of population size (Lande et al. 2003). We thus consider a general model with environmental stochasticity only, which can in the future be expanded to include also demographic stochasticity. The general SDE model then is:
where the bold notation indicates vectors, and so N is a vector with population sizes A, B and the soil state variable, dW is a vector of independent Wiener processes (often referred to as white noise in ecology), which we use as the source of environmental stochasticity (Lande et al. 2003; Dobrow 2016), and the matrix Σ is the diffusion matrix, which quantifies the intensity of stochasticity for each state variable. The drift term μ, which is a function of population size, corresponds to the deterministic structure of our ODEs, that is the classic Bever model (Bever 2003). Note that there is no limit to how many equations, and thus plant and soil species, can make up our SDE system, but in this introductory paper we keep the system as simple as possible (two plant species, one soil axis) both for the purpose of illustration and the complexity involved in introducing stochasticity into actual experiments. If plant A, B and soil were affected by independent environmental stochasticity, the diffusion matrix would simply be
And the corresponding SDEs would then be
This model can be made more realistic by introducing correlations in the source of environmental stochasticity, and so to the responses of plants and soil to environmental fluctuations. For example, a flood event will modify water availability, but also produce physical disturbance and anoxic conditions, at the same time. The individual effects of all these factors on the different plants and soil may differ, but the resulting responses of the state variables might be correlated. The more general model should thus account for possible correlations in the three stochastic terms via a covariance matrix
where the variance terms σ2 for plant A and B and soil S reflects the strength of environmental stochasticity, and the terms ρ are the correlations. Note that this matrix is symmetric, simply because the covariance between variable i and j is the same as the covariance between j and i. We used Cholesky factorization (Allen 2010; Kloeden et al. 2012) of the covariance matrix Kij to define the diffusion matrix that account for correlated environmental fluctuations in our matrix. The diffusion matrix now becomes:
Note that if the correlation terms ρ are set to zero, the matrix returns to the special case of independent Wiener processes, with variance terms in the diagonal equal to the three σ terms for A, B and S and all the off-diagonal elements equal to zero. Extensions to more than three equations are straightforward in terms of Cholesky factorization (Allen 2010; Kloeden et al. 2012) and numerical simulations.
Computation
The key goal of the analysis of a stochastic process is the characterization of the probability distribution that describes how the population changes with time (Karlin and Taylor 1975). The variation of the population is not deterministic, meaning that given the same initial conditions, the population can take many different paths or trajectories. The population of size N is thus best described by a probability distribution P(N, t) that quantifies the key features of the collective behaviour of the paths. The mean and variance of N over time t are some of these key features. Another important feature is the probability that the population goes below a certain value, for example below zero (i.e. extinction). Or also, the probability for the population to be at a certain value (for example two times the initial population size, or zero) after a certain amount of time (i.e. hitting time). For simple processes, the probability distribution P(N, t) has an analytically close form that can be derived by the Fokker–Planck equation corresponding to the Itô SDE. Our system, however, has a complex form, and we could not resolve it analytically. We thus simulated it numerically, using the Euler–Maruyama method (Allen 2010; Dobrow 2016), and we provide the full R script that implemented this method for our system (RScript_Bever_Model_Stochastic.R). The script we offer can be extended to multiple plant species and more soil components.
We analysed multiple scenarios, starting from the same parameters as in Bever (2003), apart from equating the carrying capacity of the two plant species (which we did just for convenience, and with no effect on the final results). First, we compared a scenario in which the stochastic components of the process are not correlated with a scenario in which they are correlated and, within each of these two scenarios, we also compared a scenario where the variances of plant A and B were relatively high with a scenario in which the variances where low (results in Fig. 2). Also, we compared a scenario in which only the variance of A was high (or low) with the opposite scenario (results in Fig. 3). Finally, we also investigated how variance controls the probability of extinction at different level of soil feedback Is (results of Fig. 4). We replicated the simulation of each scenario 1000 times, and estimated the probability of a certain outcome (e.g. unfeasible system, that is at least one species goes extinct) as the frequency of that outcome over 1000 independent replicates of the same process. In the scenarios in which we changed the soil feedback Is = αA—αB—βA+ βB, we set to negative the PSF by keeping three parameters (αB, βA,βB) and decreasing the other parameters (αA). But PSF being the same, we expected that the probability of extinction changed with different combination of parameters. We thus also explored scenarios in which we kept the PSF positive, constant, and compatible with coexistence at low level of variance, and then progressively increased the difference between parameters αB and βA.
Frequency distribution (histograms, y-axis) of the ratio (x-axis) between the population size of plant A and plant B. The vertical blue line (just after 0.8 on the x-axis) shows the ratio for the deterministic model (and for the parameters used in Bever (2003), which are the same as in Fig. 1a). In general, stochasticity shifts the ratio to the right (that is > 0.8) and correlation seems not to affect this shift. The shift is particularly pronounced (> 95% of stochastic path have a ratio > 0.8) for scenarios with high variance in both species A and B, meaning that, for this combination of parameters, stochasticity tends to favour the inferior competitor (species A). Each distribution is calculated from 1000 simulations of the system
Same as Fig. 2, but with variance in A either higher (panel a and b) or lower (panel c and d) than variance in B. This time, in all cases stochasticity markedly shift the ratio to the right of the deterministic expectation, regardless of which species is affected by the highest level of stochasticity
Relationship between variance (i.e. strength of stochasticity, x-axis) and the probability of extinction (y-axis) estimated as the number of unfeasible configurations over 1000 simulations of the same system. Each data point thus corresponds to 1000 simulations. Both in panels a) and b), eleven levels of variance, ranging from 0.5 to 10 were considered. For each level, the 1000 simulations of panel a) were run for each of the 5 different levels of plant soil feedback (PSF), marked with the different colours and symbols. In panel a), the scenario in orange, with the diamond symbol, corresponds to a PSF of + 0.15, that quickly leads to extinction for moderately high level of stochasticity. But all the scenarios in figure a) keep the impact of soil A on plant B, that of soil B on plant A, and that of soil B on plant B constant, and negativizes PSF by making the impact of soil A on plant A more and more negative. In panel b), instead, we kept PSF constant (at 0.15) and also kept the impact of plant A on soil A and that of plant B on soil B constant. The scenarios in panel b) differ in the difference between the impact of soil A on plant B and that of soil B on plant A. As this difference increases, higher variance is required to lead the system to extinction
Results
First, we verified that the Euler–Maruyama method of our SDEs with zero variance and zero correlation returned an accurate approximation of the trajectory expected under the deterministic model, which was the case (Fig. 1a). To explore the behaviour of the model qualitatively, we plotted 10 paths of two parameterizations of our SDE: one with no correlation, and the other one with correlation (Fig. 1b, we report just the one with correlation). As qualitatively visible across the 10 trajectories plotted in Fig. 1b, the system rapidly converges towards the deterministic equilibrium but it then keeps fluctuating indefinitely around the equilibrium, with plant A and B out of phase, and with the soil variable with a phase intermediate between that of plant A and B. A key metric to describe the asymptotic behaviour of the system is the long-term value of the ratio between plant A and plant B population size. For the parameters of the deterministic model based on Bever (2003) this ratio is 0.8, and the two plants coexist although plant B is the superior competitor. Stochasticity alters this expectation in two ways: first, depending on the variance level, a fraction of the simulations returned unfeasible configurations, which we defined as those where one of the plant populations went either extinct or to infinity. Second, when the system could settle into a feasible configuration for the time span analysed in our simulation, the distribution of plant A to plant B ratio slightly shifted to the right, that is above 0.8, and so in favour of plant A (Figs. 2 and 3).
When plotting probability of extinction (defined has the fraction of trajectories that returned an unfeasible system, with one of the two plants going extinct) as a function of environmental stochasticity (with the variance terms of both plant A and B ranging from 0.5 to 10) and five different levels of PSF (ranging from slightly positive to slightly and more decisively negative) we observed a clear stabilising effect of PSF (Fig. 4a): the more negative the PSF the higher the level of variance needed to increase probability of extinction. to The details of these results, however, depend on the combination of parameters used in the simulation scenarios, in which we changed the soil feedback Is = αA—αB—βA+βB by keeping three parameters (αB, βA,βB) constant while decreasing the parameters αA. But there are also combinations for which, PSF being the same, probability of extinction varies depending on the ratios between the 4 parameters. We give an example (among the infinite number of possibilities) in Fig. 4b, where PSF is initially positive, constant, and compatible with coexistence at low level of variance. We then progressively increased the difference between parameters αB and βA while keeping the PSF at the same level. This set of simulations shows how the details of the PSF parameters matter in determining probability of extinctions and the response of this probability to increased levels of stochasticity.
Discussion
New predictions, limitations and possible extensions
Much experimental evidence on species coexistence theories come from plant communities (Vellend 2010; Gravel et al. 2011; HilleRisLambers et al. 2012) and is rooted in classic ecological theory based on the niche concept (Tilman 1982; Chase and Leibold 2003). Stochastic versions of the classic niche framework were formulated already early in the history of ecology (May 1973b), and have been reframed more recently following input from stochastic theories of community assembly (Tilman 2004; Adler 2007; Vellend 2010). Our model applies that general theory of stochastic population dynamics to a general PSF model and shows that, differently from the deterministic classic case, stochastic PSF dynamics may result in a fraction of trajectories along which one plant species goes extinct. That generally means a reduction of the space for coexistence, and it is not surprising. Stochastic models account for the realistic fact that in nature, especially under the influence of temporally dynamic and multiple global change factors (Rillig et al. 2019), there are sources of environmental variance that are difficult to predict and that are thus best modelled stochastically (Lande et al. 2003; Allen 2010). Under global change, the impact of environmental variance on soil biota, for example in the form of unpredictable weather events, is expected to increase (Bardgett and Caruso 2020), which implies fluctuations in community dynamics that involve PSF (Kardol et al. 2006, 2007).
Our key result, however, goes beyond the plain verification of the fact that stochasticity may reduce the space for coexistence (Lande et al. 2003): our simulations collectively show that, despite an overall reduction of the space for coexistence, the more negative the PSF the higher stochasticity needs to be to generate a sizeable probability of extinction. Negative PSF, which reduces the negative effects on the inferior competitors and positive effects on the superior competitor, counteracts the extinction risk brought about by stochasticity. Our theoretical model thus generalises the key expectation from the classical PSF model: PSF buffers plant-soil systems from the negative impact that environmental stochasticity has on the risk of plant species extinction (for local population). It is, however, important to clarify a crucial point: the impact of an increasingly more negative PSF on the probability of extinction can be evaluated when conditions are fully controlled. Controlled conditions are, in our simulations, represented by keeping three (out of four) PSF parameters constant, and varying PSF by decreasing/increasing the fourth parameter. For example, consider the following two combinations of parameters for Is = αA—αB—βA + βB: i) αA = 0.35, αB = 0.2, βA=0.2, and βB = 0.2; and ii) αA = 0.35, αB = 0.3, βA=0.1, and βB = 0.2. In both cases, the total PSF equals 0.15. But in case 1, which is the same as in Fig. 4a (i.e. see that figure for PSF = 0.15), the system rapidly becomes unfeasible for moderate levels of environmental variance, while in case 2 probability of extinction is comparable to some of the negative PSF explored in Fig. 4a. The implication is that PSF being the same, the nature and intensity of the interaction between soil and the plant species matters. In practice, a net positive (or negative) PSF exerted through, say, just positive mutualistic interactions can impact probability of extinction very differently from the same net positive (or negative) PSF but exerted through negative or a mixture of negative and positive interactions. The biology of the system does matter. The compound metrics used to quantify the net PSF helps, but those metrics are not sufficient to predict how environmental variance may impact the probability of extinction in local systems and in the real world.
Also, we stress that the current presentation of our model is based on two species only, and a single “soil axis” representing the overall soil community and so its impact on plants. But in nature, multiple plant species interact with an enormous amount of different soil organisms, and it is nowadays textbook knowledge that the nature of the interactions vary enormously spatially and temporally. These basic facts of nature do not invalidate our theoretical results but directly call for a multivariate extension of the form of the model presented here, which should in the future include at least two more elements: first, more plant species (one more equation per plant species), and second a decomposition of the “soil axis” into the different components that make up the soil community (de Castro et al. 2021; Potapov 2022), at least in terms of major microbial groups (e.g. fungi and bacteria; (de Vries et al. 2018; Müller and Bahn 2022)) and animals (e.g. micro vs. meso vs. macro fauna). We expect this multivariate extension and explicit consideration of spatial scales to make the relationship between PSF and extinction probability more articulated and dependent on the multidimensional nature of the relationship that link plant species to each other as well as plants to soil, and plants and soil to degree of disturbance and environmental unpredictability experienced by the entire ecological community (Kardol et al. 2006, 2007; Suding et al. 2013; Crawford et al. 2019).
Experimental tests
Some of our predictions can in principle be tested experimentally using classic PSF experiments (Van der Putten et al. 2013; Crawford et al. 2019) on pairs of plant species but with the addition of an experimental regime that should incorporate environmental variance (Benedetti-Cecchi et al. 2006). The environmental variables to consider for manipulation should be any that have an impact on the growth rate of the plants involved in the experiment. At a mechanistic level, the growth rate is the key focus here because it reflects the speed at which the processes connecting plants and soil take place. Key environmental variable to introduce a stochastic regime in the environment could be temperature, or a physical disturbance imposed on the system (drought, flood). The variance regime should be a factor in the experiment (Benedetti-Cecchi et al. 2006), ranging from low to high variance, as per the x-axis of Fig. 4. This “variance factor” can be either continuous or categorical. The variance factor would have been effective if it could be shown to alter the probability that the two species coexist. This may require pilot studies to identify the amount of environmental variance that can trigger a shift in the regime of the system, as in Fig. 4, where there is a range of variances for which the system rapidly goes from relatively low levels of extinction to the certainty that the plants cannot coexist. An advantage of the stochastic approach is that the prediction is probabilistic and so the result of the experiment can be recorded in terms of number of experimental units for which a certain outcome is observed. That means that the key observation is not a time series of the plant population, but rather the frequency at which coexistence or extinction are observed over a relatively long but well-defined period of time. Standard measurements of PSF (Brinkman et al. 2010) can also be taken to validate the expectation that the PSF controls the relationship between environmental variance and probability of extinction of plant species.
General implication of stochasticity for plant-soil feedback
Negative PSF can predict the relative abundance of species in tropical forests (Mangan et al. 2010) and has recently be shown to be linked to fluctuations in the relative abundance of plant species in diverse mountain meadows (in’t Zandt et al. 2021). In these very species rich system, PSF is hypothesised to be a key factor maintaining species diversity. Through its link to plant coexistence, PSF could also control the biodiversity-productivity relationship (Forero et al. 2021). If time series are available (e.g. in’t Zandt et al. 2021), they can be modelled as stochastic processes (Brouste et al. 2014; Iacus and Yoshida 2018). Our current model presentation is limited in that for the purpose of a first illustration we limited our analysis to a two species system. But, our system of equations can easily be extended to multiple equations and then be fitted to plant time series using the formalism of SDEs through the R package Yuima (Brouste et al. 2014; Iacus and Yoshida 2018). Fitting a stochastic model to an actual time series of plant populations may help quantify the degree of stochasticity, population trends, and extinction risks.
There currently remains a major limitation when it comes to actual applications of the type of models we presented here. Ideally, one wishes to control for the negative implications of stochasticity on plant population dynamics. Models suggest that one way of controlling negative effects (e.g. increase of extinction risk) is controlling the PSF through the type of biotic interactions that determine the PSF, for example mutualistic vs. pathogenic effects. In principle, one could harness the soil community to control the PSF in a manner that boosts the ability of plants to resist to or recover from the perturbation regime continuously created by environmental stochasticity. Controlling the PSF would, however, require a mechanistic knowledge of the biological interactions that underpin the total PSF (van der Putten et al. 2016), and these interactions are at least of two kinds, positive and negative, and notoriously very challenging to harness. But our models currently collapse the total collective impact of the soil community, and so all the complexity of soil biodiversity, into just one simplistic variable and a few parameters controlling for the impact of this variable on the plant population. While this approach is powerful at the phenomenological level (i.e., description of dynamics under the assumption of certain population processes: Bever et al. 2010; Eppinga et al. 2018), it does not itself shed light on the actual biological and ecological mechanisms that cause PSF. Only manipulative experiments can achieve that level of understanding of PSF, which is needed for a future harnessing of PSF via soil biota. At that empirical level, the first operation will be a decomposition of the model soil axis into the actual major groups of soil organisms that affect plant dynamics.
An alternative to harness the PSF is the plant community itself, because the PSF depends on the mutual interaction that links plant to soil biota, and different pairs of plants will thus be associated with different types of PSF. Current models and syntheses, including our own model presented here, suggest that, all else being the same, plant communities with strong negative PSF are resilient to environmental stochasticity (e.g. Kardol et al. 2007; Mangan et al. 2010; Suding et al. 2013). There are studies that have investigated and quantified the effect of PSF at the entire multispecies plant community level (Eppinga et al. 2018). And yet, a still unresolved, major challenge is identifying the management actions that can harness the entire plant community to increase negative PSF and so counteract the impact of an increasingly more unpredictable environment.
Change history
11 December 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11104-022-05834-2
References
Adler PB (2007) A niche for neutrality. Ecol Lett 10:95–104. https://doi.org/10.1111/j.1461-0248.2006.00996.x
Allen LJ (2010) An introduction to stochastic processes with applications to biology. Chapman & Hall, Taylor & Francis group, NY
Bardgett RD, Caruso T (2020) Soil microbial community responses to climate extremes: resistance, resilience and transitions to alternative states. Philos Trans R Soc B Biol Sci 375:20190112. https://doi.org/10.1098/rstb.2019.0112
Bauer JT, Mack KML, Bever JD (2015) Plant-soil feedbacks as drivers of succession: evidence from remnant and restored tallgrass prairies. Ecosphere 6:158. https://doi.org/10.1890/ES14-00480.1
Benedetti-Cecchi L, Bertocci I, Vaselli S, Maggi E (2006) Temporal variance reverses the impact of high mean intensity of stress in climate change experiments. Ecology 87:2489–2499. https://doi.org/10.1890/0012-9658(2006)87[2489:TVRTIO]2.0.CO;2
Bever JD (2003) Soil community feedback and the coexistence of competitors: conceptual frameworks and empirical tests. New Phytol 157:465–473. https://doi.org/10.1046/j.1469-8137.2003.00714.x
Bever JD, Dickie IA, Facelli E et al (2010) Rooting theories of plant community ecology in microbial interactions. Trends Ecol Evol 25:468–478. https://doi.org/10.1016/j.tree.2010.05.004
Bever JD, Westover KM, Antonovics J (1997) Incorporating the Soil Community into Plant Population Dynamics: The Utility of the Feedback Approach. J Ecol 85:561–573
Bonanomi G, Giannino F, Mazzoleni S (2005) Negative plant–soil feedback and species coexistence. Oikos 111:311–321
Brinkman PE, Van der Putten WH, Bakker E, Verhoeven KJ (2010) Plant–soil feedback: experimental approaches, statistical analyses and ecological interpretations. J Ecol 98:1063–1073
Brouste A, Fukasawa M, Hino H et al (2014) The yuima project: A computational framework for simulation and inference of stochastic differential equations. J Stat Softw 57:1–51
Case TJ (2000) An illustrated Guide to Theoretical Ecology. Oxford University Press, New York
Chase JM, Leibold MA (2003) Ecological Niches: Linking Classical and Contemporary Approaches. Chicago University Press, Chicago, IL
Crawford KM, Bauer JT, Comita LS et al (2019) When and where plant-soil feedback may promote plant coexistence: a meta-analysis. Ecol Lett 22:1274–1284
de Castro F, Adl SM, Allesina S et al (2021) Local stability properties of complex, species-rich soil food webs with functional block structure. Ecol Evol 11:16070–16081
de Vries FT, Griffiths RI, Bailey M et al (2018) Soil bacterial networks are less stable under drought than fungal networks. Nat Commun 9:3033
Dobrow RP (2016) Introduction to stochastic processes with R. John Wiley & Sons
Eppinga MB, Baudena M, Johnson DJ et al (2018) Frequency-dependent feedback constrains plant community coexistence. Nat Ecol Evol 2:1403–1407. https://doi.org/10.1038/s41559-018-0622-3
Forero LE, Kulmatiski A, Grenzer J, Norton JM (2021) Plant-soil feedbacks help explain biodiversity-productivity relationships. Commun Biol 4:1–8
Gravel D, Guichard F, Hochberg ME (2011) Species coexistence in a variable world. Ecol Lett 14:828–839
HilleRisLambers J, Clark JS, Beckage B (2002) Density-dependent mortality and the latitudinal gradient in species diversity. Nature 417:732–735. https://doi.org/10.1038/nature00809
HilleRisLambers J, Adler PB, Harpole W et al (2012) Rethinking community assembly through the lens of coexistence theory. Annu Rev Ecol Evol Syst 43:227–248
Iacus NM, Yoshida N (2018) Simulation and inference for stochastic processes with YUIMA. UseR series, Springer, Cham Switzerland, A comprehensive R framework for SDEs and other stochastic processes. https://doi.org/10.1007/978-3-319-55569-0
in’t Zandt D, Herben T, van den Brink A, et al. (2021) Species abundance fluctuations over 31 years are associated with plant–soil feedback in a species-rich mountain meadow. J Ecol 109:1511–1523
Kardol P, Cornips NJ, van Kempen MML et al (2007) Microbe-mediated plant–soil feedback causes historical contingency effects in plant community assembly. Ecol Monogr 77:147–162. https://doi.org/10.1890/06-0502
Kardol P, Martijn Bezemer T, Van Der Putten WH (2006) Temporal variation in plant–soil feedback controls succession. Ecol Lett 9:1080–1088
Karlin S, Taylor HM (1975) A first course in stochastic processes. Academic Press, San Diego
Kloeden PE, Platen E, Schurz H (2012) Numerical solution of SDE through computer experiments. Springer-Verlag, Berlin Heidelberg. https://doi.org/10.1007/978-3-642-57913-4
Lande R, Engen S, Saether B-E (2003) Stochastic population dynamics in ecology and conservation. Oxford Series in Ecology and Evolution Oxford. https://doi.org/10.1093/acprof:oso/9780198525257.001.0001
Mangan SA, Schnitzer SA, Herre EA et al (2010) Negative plant–soil feedback predicts tree-species relative abundance in a tropical forest. Nature 466:752–755
May RM (1973a) Stability and complexity in model ecosystems. Princeton University Press, Princeton
May RM (1973b) Stability in randomly fluctuating versus deterministic environments. Am Nat 107:621–650
Müller LM, Bahn M (2022) Drought legacies and ecosystem responses to subsequent drought. Glob Change Biol. https://doi.org/10.1111/gcb.16270
Potapov A (2022) Multifunctionality of belowground food webs: resource, size and spatial energy channels. Biol Rev 97:1691–1711. https://doi.org/10.1111/brv.12857
Rees M, Condit R, Crawley M et al (2001) Long term studies of vegetation dynamics. Science 293:650–655
Rillig MC, Ryo M, Lehmann A et al (2019) The role of multiple global change factors in driving soil functions and microbial biodiversity. Science 366:886. https://doi.org/10.1126/science.aay2832
Suding KN, Stanley Harpole W, Fukami T et al (2013) Consequences of plant–soil feedbacks in invasion. J Ecol 101:298–308. https://doi.org/10.1111/1365-2745.12057
Tilman D (1998) Plant Strategies and the Dynamics and Structure of Plant Communities
Tilman, D (1992) Resource Competition and Community Structure. Princeton University Press, Princeton, NJ
Tilman D (2004) Niche tradeoffs, neutrality, and community structure: A stochastic theory of resource competition, invasion, and community assembly. Proc Natl Acad Sci U S A 101:10854–10861. https://doi.org/10.1073/pnas.0403458101
Tuljapurkar, (2013) Population dynamics in variable environments. Springer-Verlag, Berlin Heidelberg. https://doi.org/10.1007/978-3-642-51652-8
Van der Putten WH, Bardgett RD, Bever JD et al (2013) Plant–soil feedbacks: the past, the present and future challenges. J Ecol 101:265–276
van der Putten WH, Bradford MA, Brinkman PE et al (2016) Where, when and how plant–soil feedback matters in a changing world. Funct Ecol 30:1109–1121
Vellend M (2010) Conceptual synthesis in community ecology. Q Rev Biol 85:183–206
Acknowledgements
This study was supported by the Science Foundation of Ireland, grant 20/FFP-P/8584 and by the Department of Agriculture, Food and the Marine (Ireland) grant 2021EJPSOILEN303. We wish to thank the handling editor and three anonymous reviewers for their very constructive comments on an earlier version of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Johannes Heinze.
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Caruso, T., Rillig, M.C. A general stochastic model shows that plant-soil feedbacks can buffer plant species from extinction risks in unpredictable environments. Plant Soil 485, 45–56 (2023). https://doi.org/10.1007/s11104-022-05698-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11104-022-05698-6