Abstract
This paper provides a sorely-needed evaluation of the view that mathematical explanations in science explain by unifying. Illustrating with some novel examples, I argue that the view is misguided. For believers in mathematical explanations in science, my discussion rules out one way of spelling out how they work, bringing us one step closer to the right way. For non-believers, it contributes to a divide-and-conquer strategy for showing that there are no such explanations in science. My discussion also undermines the appeal to unifying power in support of the enhanced indispensability argument.
Similar content being viewed by others
1 Introduction
Call any explanation of a physical phenomenon that turns on a pure mathematical fact a mathematical explanation. There is a debate over whether there are mathematical explanations in science (see Baker 2005, 2009, 2017; Baker and Colyvan 2011; Bangu 2008; Baron 2014; Colyvan 2001, 2002, 2010, 2013; Daly and Langford 2009; Knowles and Saatsi 2019; Leng 2010: 241–252; Lyon 2012; Melia 2000; Pincock 2007, 2015; Saatsi 2011, 2016; Yablo 2013). Another debate begins with the assumption that there are and asks how they work (see Baron 2016, 2019, 2020; Baron et al. 2017; Barrantes 2020; Craver and Povich 2017; Lange 2013, 2017; Leng 2012; Povich 2019, 2020). This paper contributes to both. Assuming that there are mathematical explanations in science, I argue against the view that they explain by unifying. Call this view m-unificationism.
M-unificationism has intrinsic interest. We need a theory of how mathematical explanations work, and m-unificationism appears to enjoy some antecedent support, as an application of the intuitively-appealing view that the essence of scientific explanation is unification (unificationism). (Friedman 1974 pioneered unificationism; Bangu 2017; Bartelborth 2002; Jones 1995a, b, 2012; Kitcher 1981, 1989; Schurz 1999; Schurz and Lambert 1994; and Weber 1999 provide alternative elaborations and defences.) M-unificationism also has extrinsic interest. The enhanced indispensability argument for mathematical platonism includes the premise that mathematics plays an indispensable explanatory role in science. Some have appealed to the unifying power of mathematics in support of this premise, presupposing that increasing mathematical unification increases explanatory power (see Baker 2009: 621, 2017: 199; Baker and Colyvan 2011: 331; Colyvan 2002: 71–72).
Despite its importance, there is no detailed discussion of m-unificationism in the literature. Sam Baron (2020) offers a worked-out articulation of the view, but with little accompanying discussion of the justification for and consequences of his appeal to unification. The central importance of this paper is its provision of a sorely-needed, in-depth discussion and evaluation of m-unificationism. I am guided by four questions:
-
(1)
Does the intuitive case for unificationism provide antecedent support for m-unificationism?
-
(2)
What does it mean to say that mathematical explanations explain by unifying?
-
(3)
Is unifying power proportional to explanatory power?
-
(4)
Can we distinguish explanatory from non-explanatory applications of mathematics in terms of their capacity to unify?
In §2, I answer (1) in the negative: the intuitive case for unificationism tells against rather than in favour of m-unificationism. In §3, I provide some novel examples of mathematical explanation, and use them to shed light on (2). In §4, I answer (3) in the negative: increased unification can help us find better explanations, but there is reason to doubt that the improved explanations are better because they unify further. In §5, I answer (4) in the negative: Baron (2020) divides explanatory from non-explanatory applications of mathematics in terms of unification; but my examples from §3 are counterexamples, and explaining them away raises a serious epistemological problem that any articulation of m-unificationism aspiring to empirical adequacy will court. In §6, I consider an alternative form of m-unificationism that appears able to avoid the difficulties raised in §§4–5, and offer reasons to think this appearance is misleading.
In §7, I conclude that m-unificationism is misguided, and draw out lessons from my discussion. For those who believe in mathematical explanations in science, it takes us one step closer to the right theory of them by process of elimination, and provides a guiding principle to help with the search. For non-believers, it contributes to a divide-and-conquer strategy for showing that there are no mathematical explanations in science. Finally, it undermines the appeal to unifying power in support of the enhanced indispensability argument.
2 Unification and understanding
In this section, I determine whether the intuitive case for unificationism provides antecedent support for m-unificationism. Ex hypothesi, mathematical explanations are scientific explanations, so we should expect them to share core features with other kinds of scientific explanation. Intuitive support for unificationism should therefore translate to intuitive support for m-unificationism. Unfortunately, this is not so.
Many would consider the following a truism about scientific explanation:
- EU:
Good scientific explanations increase our understanding.
The intuitive case for unificationism is that it flows directly from EU, modulo a particular conception of explanatory understanding (cf. Bangu 2017: 103–105; Friedman 1974: 18; Kitcher 1989: 430; Schurz 1999: 97–100; Schurz and Lambert 1994: 65–99). We begin by stipulating that explanatory understanding is increased when the overall number of mysteries (i.e. brute assumptions) about the world is reduced. But reducing the number of mysteries about the world just is unification, since unification is the reduction of the number of brute assumptions. It follows that unification is the essence of scientific explanation.
The move from EU to unificationism assumes that explanatory understanding is a global matter, whose object is the entire world, and whose vehicle is entire theories. This is a substantial assumption that can be challenged. We can agree that global understanding is a noble aim of science; but that alone does not imply that it is the goal of scientific explanation. Intuitively, explanatory understanding is a local matter, whose object is particular phenomena, and whose vehicle is particular explanations. When we seek an explanation of something, we seek understanding of that thing, not the entire world.
The intuition can be bolstered by considerations about scientific practice. When scientists develop, appraise, and contrast rival explanations, they are guided by judgements about how explanatory they are (i.e. how much explanatory understanding they offer). It is implausible that individual scientists routinely and explicitly contrast rival derivations of phenomena in terms of their capacity to effect global theoretical simplicity (see Woodward 2019: §5.6 for more on the epistemology of unification). Indeed, some explanatory judgements cannot be arrived at this way. For example, scientists can appreciate the explanatory value of novel explanations whose premises conflict with scientific orthodoxy, despite their inability to effect global understanding (Gijsbers 2007: 499). Consider also causal explanatory judgements based directly on experience (Woodward 2019: §5.6).
While all of this is far from conclusive, it threatens the intuitive case for unificationism. It suggests that EU is only intuitively appealing when interpreted in terms of the local conception of explanatory understanding, and so provides no intuitive support for unificationism after all.
If our interest were simply defending unificationism, we could respond by looking elsewhere for support. We could concede that individual explanatory judgements do not track the provision of global understanding, but downplay the significance of such judgements as confused or led by pragmatic factors that should be ignored. We could then argue that we stand to gain a lot by adopting the global conception of explanatory understanding. Global understanding is objective, distinguishing it from the mere psychological ‘Ah-ha!’ feeling. It is scientifically valuable, as illustrated by countless examples from the history of science, such as Newton’s unification of terrestrial and celestial motion, or Maxwell’s unification of electricity and magnetism. The view that good scientific explanation yields global understanding connects scientific explanation to other epistemic goals that we independently value, and so promises an account of the value of scientific explanation (see Woodward 2019: §7.2 for further discussion).
This means of defending unificationism should be explored, but not here. It is not compatible with the debate over how mathematical explanations work, which is case-driven. Certain applications of mathematics seem explanatory; others do not. The aim is to develop a theory that classifies cases in accordance with our explanatory judgements, while offering insight into how mathematical facts can explain physical phenomena. Consider the following examples:
Strawbs: Someone tries to share out their strawberries among their 3 children and repeatedly fails. Why? Because they have 23 strawberries and there is no \(n = \frac{23}{3}\).
Trains: Train T arrives at station \(S_2\) at 3:00 pm, after leaving station \(S_1\) at 2:00 pm. Why? Because \(S_1\) and \(S_2\) are 10 km apart, T travels at 10 kph, and \(\frac{10}{10} = 1\).
Intuitively, the mathematical fact cited in Trains merely facilitates calculation, while the mathematical fact cited in Strawbs explains. (Lange 2013: 488 introduced Strawbs. Baron 2016: 459–460 used Trains as a point of contrast. Both have been widely discussed since.) Judgements like these are elicited in the literature to demarcate the phenomenon of mathematical explanation, and motivate the need for a theory of how it works. Mathematical explanation is supposed to be whatever answers to these judgements. Accordingly, a desideratum of a theory is to divide cases in accordance with our judgements, which are presumed to be mainly accurate. Of course, we sometimes get things wrong; but a theory should not imply that we are radically mistaken, lest we lose our grip on the very target of our theorising (Baron 2019: 686–686, 2020: 536–538).
Abandoning the intuitive case for unificationism precludes the phenomenon of mathematical explanation. It may turn out that, in defending unificationism elsewhere, we end up classifying certain applications of mathematics as explanatory. By some coincidence, there may even be broad overlap between this classification and the classification induced by our explanatory judgements. But this would not amount to a theory of mathematical explanation. Mathematical explanation is that which answers to a particular class of explanatory judgements. One cannot provide a theory of it while simultaneously denying the significance of those judgements. To secure antecedent support for m-unificationism, we must therefore salvage the intuitive case for unificationism, by arguing that our individual explanatory judgements track the provision of global understanding.
It would be implausible to suggest that our explanatory judgements are a direct recognition of the provision of global understanding, especially in relation to mathematical explanation. Examples such as Strawbs and Trains are never presented alongside any information that might be relevant to judging whether they provide global understanding, and we cannot tell just from considering Strawbs and Trains in isolation which of them facilitates a simpler theory of the world. Our judgements about such cases are therefore not directly sensitive to the provision of global understanding, and the practice of eliciting them does not presume that they are. Our judgements instead appear to be sensitive to the provision of local understanding.
In light of this, we are forced to argue that local understanding and global understanding are related, such that our reliable judgements about the former effect convergence on explanations that offer the latter. It is difficult to evaluate this approach independently of particular accounts of the relationship between global and local understanding. Thankfully, we can draw lessons from two recent defences of unificationism, which aim to show that local understanding and global understanding are the two faces unification.
Gerhard Schurz and Karel Lambert argue that providing local understanding involves taking something more in need of explanation (i.e. less integrated into our background theory), and showing that it follows from something less in need of explanation (i.e. more integrated into our background theory) (Schurz 1999; Schurz and Lambert 1994). It follows that local understanding guarantees global understanding. However, for any mathematical derivation of a contingent physical phenomenon, the mathematical fact(s) will be more integrated into our background theory than the physical phenomenon. So, on the present view, any mathematical derivation of a physical phenomenon provides local understanding, and our discerning explanatory judgements fail to track a meaningful distinction.
Sorin Bangu (2017) argues that explanatory unification brings together phenomena under a common ontological reduction. This ontological reduction provides an improved re-conceptualisation of the unified phenomena, providing local understanding of them. Again, local understanding guarantees global understanding. However, such ontological reduction is only ever the result of large-scale theoretical unification, such as the aforementioned Newtonian reduction of celestial and terrestrial phenomena. As Bangu notes, this renders the provision of local understanding an ‘epochal intellectual achievement’ (2017: 122). I submit that applications of mathematics that plausibly provide an ontological reduction are even more elusive, if they exist at all. Again, our explanatory judgements fail to track a meaningful distinction.
Of the above accounts, one seems to trivialise mathematical explanation, while the other rules it out. These are different symptoms of a common dysfunction. The explanatory judgements that demarcate mathematical explanations are fine-grained, distinguishing between superficially similar derivations couched in the same mathematical theories. In contrast, the provision of global understanding is a coarse-grained affair. If one application of a given mathematical theory provides global understanding, by connecting a contingent physical phenomenon to our background beliefs in a certain way, then we should expect any superficially similar application of that mathematical theory to do the same. Given this, it is no wonder that attempts to link our explanatory judgements to the provision of global understanding seem to either trivialise or rule out explanatory applications of mathematics.
The intuitive case for unificationism tells against, rather than in favour, of m-unificationism. So, we have no antecedent reason for accepting m-unificationism. However, it may turn out that m-unificationism does a good job of accounting for particular examples of mathematical explanation. In §4 and §5 I argue that it does not. But first, I introduce some novel examples of mathematical explanation, and use them to shed some light on our second guiding question: What does it mean to say that mathematical explanations explain by unifying?
3 Group theory for housework
Consider a regular rectangle. Assigning the numbers 1 to 4 to the four corners, we can represent its symmetries as permutations of the sequence (1, 2, 3, 4), as follows:

Here, e represents the identity symmetry, b the rotation through \(180^\circ \), r the vertical reflection, and t the horizontal reflection. The set of these operations, closed under function composition, forms the group  .
.  is non-cyclical: none of its elements can generate all of the others via self-composition. This fact has explanatory import. For example:
is non-cyclical: none of its elements can generate all of the others via self-composition. This fact has explanatory import. For example:
Mattress
: To minimise uneven sagging, rectangular spring mattresses must be regularly flipped. I care for my mattress by repeating the same flipping action. There is uneven sagging on my mattress. Why? Because
is non-cyclical.
The fact that  is non-cyclical explains the uneven sagging on my mattress because it means that no single flipping action will rotate my mattress through all of its possible orientations on the bed frame. Assuming I tend to sleep in the same position, my use of a single flipping action means that some areas of my mattress will regularly support my weight and eventually sag, while others will not. For example, suppose I use the action associated with b only, regularly rotating my mattress through \(180^\circ \) while keeping the same face up. Sagging would occur on the two sides of the mattress on the top face, but no sagging would occur on the two sides of the mattress on the bottom face. Over time, my mattress would exhibit uneven sagging.
is non-cyclical explains the uneven sagging on my mattress because it means that no single flipping action will rotate my mattress through all of its possible orientations on the bed frame. Assuming I tend to sleep in the same position, my use of a single flipping action means that some areas of my mattress will regularly support my weight and eventually sag, while others will not. For example, suppose I use the action associated with b only, regularly rotating my mattress through \(180^\circ \) while keeping the same face up. Sagging would occur on the two sides of the mattress on the top face, but no sagging would occur on the two sides of the mattress on the bottom face. Over time, my mattress would exhibit uneven sagging.
I submit that Mattress is a case of mathematical explanation. The contribution of the group theory exhibits the hallmarks highlighted by theorists. The mathematics seems to run the explanation at an appropriate level of generality: the fact that
is a case of mathematical explanation. The contribution of the group theory exhibits the hallmarks highlighted by theorists. The mathematics seems to run the explanation at an appropriate level of generality: the fact that  is non-cyclical reveals that uneven sagging would have emerged no matter which action I chose to repeat, and no matter the nature of the underlying physical processes involved. (For generality as a feature of mathematical explanation, see Baker 2017; Baker and Colyvan 2011; Pincock 2007: 253–275; Leng 2012; Lyon 2012; Knowles and Saatsi 2019). The mathematics also seems to capture the inevitability of the explanandum, given the general structure of the situation. (For modal strength as a feature, see Leng 2012; Lange 2013, 2017; Povich 2019, 2020). Beyond this theoretical appraisal, the mathematics in Mattress
is non-cyclical reveals that uneven sagging would have emerged no matter which action I chose to repeat, and no matter the nature of the underlying physical processes involved. (For generality as a feature of mathematical explanation, see Baker 2017; Baker and Colyvan 2011; Pincock 2007: 253–275; Leng 2012; Lyon 2012; Knowles and Saatsi 2019). The mathematics also seems to capture the inevitability of the explanandum, given the general structure of the situation. (For modal strength as a feature, see Leng 2012; Lange 2013, 2017; Povich 2019, 2020). Beyond this theoretical appraisal, the mathematics in Mattress just seems explanatory.
just seems explanatory.
What does it mean to say that the mathematical fact that  is non-cyclical explains the uneven sagging on my mattress by unifying it with other physical phenomena? That depends on what kind of unification we have in mind. There are two degrees of freedom: the range of distinct physical phenomena we appeal to; and what unifying them amounts to. Regarding the former, we can distinguish two ranges: the range of physically similar phenomena, and the range of physically dissimilar phenomena.
is non-cyclical explains the uneven sagging on my mattress by unifying it with other physical phenomena? That depends on what kind of unification we have in mind. There are two degrees of freedom: the range of distinct physical phenomena we appeal to; and what unifying them amounts to. Regarding the former, we can distinguish two ranges: the range of physically similar phenomena, and the range of physically dissimilar phenomena.
The range of physically similar phenomena covers those arising as a result of the same kinds of physical processes. These can be thought of as physical systems of the same kind (relative to the explanatory context), but with certain parameters taking different values. For Mattress, the range will cover uneven sagging on spring mattresses of any regular polygonal shape. (As a courtesy, count regular rectangles as regular polygons.) In each case, the same kinds of physical processes produce the sagging: those relevant to the compression of fabrics and the fatigue of coil springs. Let us assume for the sake of argument that there are spring mattresses of different regular polygonal shapes currently being used in ways that give rise to relevant sagging phenomena. Then explanations such as the following will be available:
Mattress
: To minimise uneven sagging, hexagonal spring mattresses must be regularly flipped. Tilly owns a hexagonal mattress, and she cares for her mattress by repeating the same flipping action. There is uneven sagging on Tilly’s mattress. Why? Because
is non-cyclical.
While a different mathematical fact (involving a different symmetry group) is invoked in Mattress , the group theory unifies its explanandum with that of Mattress
, the group theory unifies its explanandum with that of Mattress via the same mathematical property: non-cyclicality. In this way, the mathematical property non-cyclicality can explain, and so unify, a range of distinct but physically similar phenomena.
via the same mathematical property: non-cyclicality. In this way, the mathematical property non-cyclicality can explain, and so unify, a range of distinct but physically similar phenomena.
The range of physically dissimilar phenomena covers those arising as a result of different kinds of physical processes. Take the following for example:
Rug
: The rectangular rug on my living room floor gets direct sunlight on one side during the day, causing its colours to fade in that area. To minimise uneven fading, the rug should be regularly flipped. I care for my rug by repeating a single flipping action. There is uneven fading on my rug. Why? Because
is non-cyclical.
The uneven fading on my rug is a result of the physical chemistry of photodegradation, which bears no resemblance to the processes of spring fatigue and fabric compression underlying Mattress . Thus, the fact that
. Thus, the fact that  is non-cyclical can explain, and so unify, physically dissimilar phenomena.
is non-cyclical can explain, and so unify, physically dissimilar phenomena.
The other degree of freedom concerns what unifying a range of phenomena amounts to. Featuring as a premise in the derivation of each phenomenon in the range will be part of it; but to distinguish explanatory from non-explanatory applications of mathematics, explanatory unification must involve something more. Baron (2020) draws on a particular articulation of unificationism (Kitcher 1981, 1989) to spell out the extra ingredient (see §5). But one could draw on other articulations of unificationism (e.g. Bangu 2017 or Schurz 1999; Schurz and Lambert 1994), or develop novel apparatus for the mathematical case. For now, we can remain neutral about the details of this extra ingredient.
4 Unification and explanatory power
With some examples on the table, and a better understanding of what it means to say that mathematical explanations explain by unifying, we can begin to evaluate what m-unificationism says about its targets. In this section, I answer our third guiding question: Is unifying power proportional to explanatory power? On the plausible and widely-accepted assumption that explanatory power comes in degrees, m-unificationism suggests a positive answer. I show that, notwithstanding some initially compelling examples, we have reason to answer in the negative.
The question at hand can be specified in terms of the unification of physically similar or physical dissimilar phenomena. Let us consider the latter first. Does increasing the number of physically dissimilar phenomena unified by a given mathematical explanation increase its explanatory power? (Baron 2020: 549 answers in the affirmative.) Mattress and Rug
and Rug provide relevant examples. The explananda of these are physically dissimilar, and yet they are explained in terms of the very same fact. It is hard to deny the effect of recognising this. We are struck with the feeling that we have uncovered an explanatory joint so deep that it runs across entirely different physical subject matters. And this feeling may convince us that unification of physically dissimilar phenomena is a good-making feature of mathematical explanation.
provide relevant examples. The explananda of these are physically dissimilar, and yet they are explained in terms of the very same fact. It is hard to deny the effect of recognising this. We are struck with the feeling that we have uncovered an explanatory joint so deep that it runs across entirely different physical subject matters. And this feeling may convince us that unification of physically dissimilar phenomena is a good-making feature of mathematical explanation.
But we should be careful not to get carried away. Take a moment to think precisely about what we recognise, what we feel in response, and what we ought to be convinced of in light of this. We recognise that the two physical phenomena that there is uneven sagging on my mattress and that there is uneven fading on my rug hold for the same mathematical reason. We are struck with the feeling that we have uncovered a deep explanatory joint. But what exactly does this mean? We can distinguish the following two feelings.
On the one hand, there is the feeling of realising that two phenomena previously considered unconnected are in fact importantly related: the feeling of a collection of seemingly disparate phenomena suddenly hanging together in a satisfying way. I do not deny the potency of this feeling, nor the importance of its object. Unification and global understanding are scientifically valuable (see §2). But we can concede this while denying that the feeling is connected to the explanatory power of individual explanations. Recognising and valuing that Mattress and Rug
and Rug share an explanatory core by no means forces us to accept that their unity makes these explanations better than they would be without it.
share an explanatory core by no means forces us to accept that their unity makes these explanations better than they would be without it.
On the other hand, there is the feeling that we are vindicated in our explanatory hypothesis, with respect to the initial explanandum. Imagine I independently recognise that my mattress is sagging unevenly and my rug is fading unevenly. After some sustained thought and relevant reading, I land on Mattress  as an explanation of the first phenomenon. This may strike me as perfectly explanatory, but I may still have my reservations. Perhaps I’m concerned that I’ve been led astray by a peculiarity of the physical situation. On recognising that the same mathematics allows me to explain the second phenomenon, these reservations may diminish. However, this would not provide any information regarding how the mathematics in Mattress
as an explanation of the first phenomenon. This may strike me as perfectly explanatory, but I may still have my reservations. Perhaps I’m concerned that I’ve been led astray by a peculiarity of the physical situation. On recognising that the same mathematics allows me to explain the second phenomenon, these reservations may diminish. However, this would not provide any information regarding how the mathematics in Mattress and Rug
and Rug explains.
explains.
I submit that the feeling we get when confronted with striking cases of unification of physically dissimilar phenomena is some combination of the above. These feelings can clearly play an important epistemic role in our search for better explanations. Moreover, explanations that unify in this way may provide prima facie evidence for the existence of mathematical explanations in science. If we are convinced via mathematical unification that two physical phenomena share a common explanatory joint, and we can point to no physical similarity between the situations in which the phenomena arise, it seems they share a common mathematical joint. This implies that there are at least two mathematical explanations. (See Colyvan 2013: 1041–1042 for this argument.) However, neither this argument, nor the above feelings, force on us any particular view about how mathematical explanation works.
In fact, there is reason to deny that explanatory power is proportional to unification of dissimilar phenomena. Consider a possible world in which the laws of nature are different, such that photodegradation does not occur. In this world, my rug does not fade, so the fact that  is non-cyclical does not unify the fact that there is uneven sagging on my mattress with the fact that there is uneven fading on my rug. Yet Mattress
is non-cyclical does not unify the fact that there is uneven sagging on my mattress with the fact that there is uneven fading on my rug. Yet Mattress seems just as good an explanation in this world as it is in actuality. Moving from this possible world to the actual world, we get an increase in unification of physically dissimilar phenomena with no increase in explanatory power.
seems just as good an explanation in this world as it is in actuality. Moving from this possible world to the actual world, we get an increase in unification of physically dissimilar phenomena with no increase in explanatory power.
Let us turn to the second specification of our guiding question. Does increasing the number of physically similar phenomena unified by a given mathematical explanation increase its explanatory power? Mattress and Mattress
and Mattress are relevant examples. Recognising that the same mathematical property is relevant in every case involving a regular polygonal shape provides an opportunity to gain a deeper understanding of the situation, by revealing a new phenomenon that cries out for explanation. For a mattress of any regular polygonal shape whatsoever, repeated use of a single flipping action will fail to minimise uneven sagging. Why is that? The answer that all of the associated symmetry groups are non-cyclical is unsatisfying: we could just as well ask why all symmetry groups associated with regular polygonal mattresses are non-cyclical.
are relevant examples. Recognising that the same mathematical property is relevant in every case involving a regular polygonal shape provides an opportunity to gain a deeper understanding of the situation, by revealing a new phenomenon that cries out for explanation. For a mattress of any regular polygonal shape whatsoever, repeated use of a single flipping action will fail to minimise uneven sagging. Why is that? The answer that all of the associated symmetry groups are non-cyclical is unsatisfying: we could just as well ask why all symmetry groups associated with regular polygonal mattresses are non-cyclical.
The answer is that the symmetry groups of regular polygons are dihedral: their elements include rotations and reflections. This guarantees that they are non-cyclical because a rotation always maintains the orientation of the elements it operates on, while a reflection always changes the orientation. We can see this in the group  . The permutation \(b = (1,2,3,4) \rightarrow (3,4,1,2)\) represents a rotation through \(180^\circ \). If we imagine cycling through the sequences over and over, we see that b doesn’t change the orientation of the numbers. In contrast, the permutation \(r = (1,2,3,4) \rightarrow (4,3,2,1)\) reverses the orientation. So self-composition of b can never equal r, and self-composition of r can never equal b. The same holds of any reflection and rotation pair, so all dihedral groups (and thus all symmetry groups associated with regular polygonal mattresses) are non-cyclical.
. The permutation \(b = (1,2,3,4) \rightarrow (3,4,1,2)\) represents a rotation through \(180^\circ \). If we imagine cycling through the sequences over and over, we see that b doesn’t change the orientation of the numbers. In contrast, the permutation \(r = (1,2,3,4) \rightarrow (4,3,2,1)\) reverses the orientation. So self-composition of b can never equal r, and self-composition of r can never equal b. The same holds of any reflection and rotation pair, so all dihedral groups (and thus all symmetry groups associated with regular polygonal mattresses) are non-cyclical.
We can now formulate a better explanation of our original explanandum. Why is there uneven sagging on my mattress? Because  is dihedral. The original explanation provided some understanding by showing that the explanandum has something to do with the symmetries of the mattress. Our improved explanation goes further by identifying precisely what it is about the symmetries of the mattress that results in the explanandum. In this sense, the new explanation is deeper than the original. (Baker 2017: 199 highlights mathematics’ provision of deeper explanations through unification of physically similar phenomena. See also Baron et al. 2017: 17.)
is dihedral. The original explanation provided some understanding by showing that the explanandum has something to do with the symmetries of the mattress. Our improved explanation goes further by identifying precisely what it is about the symmetries of the mattress that results in the explanandum. In this sense, the new explanation is deeper than the original. (Baker 2017: 199 highlights mathematics’ provision of deeper explanations through unification of physically similar phenomena. See also Baron et al. 2017: 17.)
Associated with this process is another constellation of feelings that are apt to mislead. Unification plays an important role in uncovering the better explanation. By recognising that the same property, non-cyclicality, applies in all cases in which the mattress has a regular polygonal shape, we begin to feel dissatisfied with our original explanation, and so suspect that there is a deeper explanation in the offing. Considering the range of applicability of the property shows us that the rectangular shape of my mattress is not special. There is a distinctive class of spring mattresses that have non-cyclical symmetry groups, and our original explanation does not equip us with the means of predicting which mattresses are in it. (Our original explanation does not come with a ‘condition of application’ (Baker 2017: 199).) We are convinced that, while we know that  rules out my flipping regime as an optimum strategy, we don’t really understand why.
rules out my flipping regime as an optimum strategy, we don’t really understand why.
This may invite the feeling that we have provided a better explanation by increasing unification. But that is not right. The better explanation we ended up with and the worse explanation we started with unify to the same degree. We have the same range of physically similar explananda, and both explanations show that they follow from a single mathematical fact. Yet one of them provides a more satisfying explanation. So, it appears we have an increase in explanatory power without an increase in unification. Far from supporting it, this speaks against a positive answer to our guiding question.
One might object as follows. Granted, the above process of moving from a worse to a better explanation is not a case of increasing the range of unification; but it could be understood as ‘tightening’ unification, so to speak, by revealing what the phenomena have in common in virtue of which they are in the range of unification. This response fails to appreciate that the process of tightening unification, and the improved explanation of our original explanandum suggested by this process, are not the same explanatory effort. The first involves explaining why all symmetry groups of regular polygons are non-cyclical, by appealing to the fact that all such symmetry groups are dihedral. The second involves explaining why there is uneven sagging on my mattress, by appealing to the fact that the symmetry group of my mattress is dihedral. These are different explanations of different phenomena.
The first explanation is of a universal generalisation. We can agree that revealing the similarities between the instances of the generalisation, in virtue of which they are its instances, is a mark of success for such an explanation. By contrast, the second explanation is not of a universal generalisation, so we should not expect it to explain in the same way or be good for the same reasons. We can accept that the tightening of unification is a good thing because it provides a good new explanation of a new explanandum, while also playing a heuristic role in guiding us towards the improved explanation of our original explanandum. But there is no reason here to accept that the improved explanation is better because unification has been tightened.
On both specifications of our guiding question, we have reason to answer in the negative. Since m-unificationism implies a positive answer, there is good reason to doubt m-unificationism. In the following section, I answer our final guiding question: Can we distinguish explanatory from non-explanatory applications of mathematics in terms of their capacity to unify? Again, I argue that we have good reason to answer in the negative.
5 Unification and empirical adequacy
If a particular articulation of m-unificationism divides cases of explanatory and non-explanatory applications of mathematics in accordance with our explanatory judgements, that counts in its favour. It is empirically adequate. Baron develops a particular articulation with the explicit aim of achieving empirical adequacy (2020: 537). Baron’s theory is presented as an elaboration of the counterfactual approach to scientific explanation. Its central claim is stated as follows:
A mathematical fact M explains a physical fact P just when the counterfactual ‘if M had not been the case, P would not have been the case’ is explanatory.
But Baron spells out what makes a counterfactual explanatory in terms of unification (drawing on Kitcher 1981, 1989). In fact, the counterfactual element of Baron’s theory can be stripped away with no effect. This is a serious problem for Baron, who claims that the complexity of his theory is a cost ‘worth paying’ because ‘a counterfactual approach to [mathematical explanation] opens up the enticing possibility of developing a theory of scientific explanation that is fully general’ (2020: 560). Baron is appealing to the success of the counterfactual approach to scientific explanation in other areas. (In particular, Woodward’s (2003) interventionist account of causal explanation.) The superficiality of the counterfactual element of his theory undermines this appeal.
But this problem is good news for our discussion. Our purpose is to evaluate the ability of Baron’s theory to achieve empirical adequacy by appeal to unification. The fact that the counterfactual element can be cleanly stripped away makes this easier. Without its counterfactual window-dressing, Baron’s central thesis can be stated as follows:
A mathematical fact M explains a physical fact P just when there is a derivation of P from M that unifies in an explanatory way.
Spelling out explanatory unification requires new terminology. A scheme is composed of three things. First, a schematised argument, obtained from an ordinary argument by replacing some or all of its non-logical expressions with dummy letters. Second, filling instructions, detailing how instances of the scheme can be obtained by filling in the dummy letters of the schematised argument. Third, a classification, specifying the logical structure of the obtained arguments. A mathematical scheme is one whose filling instructions ensure that all of its instances have a physical conclusion and at least one mathematical premise. A physical scheme ensures all of its instances have a physical conclusion and only physical premises. Nomically distinct arguments appeal to physical laws from distinct domains of inquiry. We can now state Baron’s account of explanatory unification.
A mathematical derivation A of a physical phenomenon unifies in an explanatory way iff:
-
(1)
A is an instance of a mathematical scheme S such that:
-
(i)
All of the instances of S are sound.
-
(ii)
At least two instances of S are nomically distinct.
-
(i)
-
(2)
There is no physical scheme \(S^\prime \) such that:
-
(i)
All of the instances of \(S^\prime \) are sound.
-
(ii)
For each instance of S with conclusion \(P_1, ..., P_n\), there is a true instance of \(S^\prime \) with exactly that conclusion.
-
(iii)
Each instance of S is sound because the mathematical facts appealed to in those instances represent the physical facts responsible for the unifying power of \(S^\prime \).
-
(i)
Let us test this theory against our examples from §3. The following is a mathematical scheme of which suitably regimented versions of Mattress and Rug
and Rug are instances:
are instances:
Schematised argument
-
A1.
X has been regularly rotated by repeated application of just one from among \(a_1, ..., a_n\).
-
A2.
Uneven distribution of Q in X, subject to \(L_1, ... L_n\), has been minimised only if X has been regularly and systematically cycled through all possible orientations of X permitted by any combination of \(a_1, ..., a_n\).
-
A3.
If [A1], then X has been regularly and systematically cycled through all possible orientations of X permitted by any combination of \(a_1, ..., a_n\) only if S(X) is cyclical.
-
A4.
X has been regularly and systematically cycled through all possible orientations of X permitted by any combination of \(a_1, ..., a_n\) only if S(X) is cyclical.
-
A5.
S(X) is non-cyclical.
-
A6.
X has not been regularly and systematically cycled through all possible orientations of X permitted by any combination of \(a_1, ..., a_n\).
-
A7.
Uneven distribution of Q in X has not been minimised.
Filling instructions
-
1.
X is a physical object that, relative to the explanatory context, can be modelled as a regular polygon.
-
2.
\(a_1, ..., a_n\) are all of the symmetry-preserving operations on X.
-
3.
Q is a property that increasingly manifests in X as a result of normal use, and manifests in different parts of X for each possible orientation of X.
-
4.
\(L_1, ... L_n\) are the physical laws relevant to Q.
-
5.
S(X) is the symmetry group of X formed of elements \(a_1, ..., a_n\) closed under function composition.
Classification
-
1.
A4 follows from A1 and A3 via Modus Ponens.
-
2.
A6 follows from A4 and A5 via Modus Tollens.
-
3.
A7 follows from A6 and A2 via Modus Tollens.
The classification and filling instructions secure the soundness of any instances, and our examples Mattress and Rug
and Rug correspond to two nomically distinct instances of the scheme. So, Mattress
correspond to two nomically distinct instances of the scheme. So, Mattress and Rug
and Rug meet condition (1). Unfortunately, they do not meet condition (2), since there is a physical correlate of the operative mathematical property. Let X be a physical object, and let \(a_1, ..., a_n\) be the operations on X that preserve symmetry, where \(a_1\) is the ‘null’ operation of doing nothing to X. Let \(o_1, ..., o_n\) be the orientations of X, such that each \(o_i\) is the result of applying \(a_i\) to X in its starting orientation \(o_1\). Then X is non-cyclical iff there is no \(a_i\) such that its repeated application cycles X systematically through each of \(o_1, ..., o_n\). This schematic definition can be spelled out in purely physical terms.
meet condition (1). Unfortunately, they do not meet condition (2), since there is a physical correlate of the operative mathematical property. Let X be a physical object, and let \(a_1, ..., a_n\) be the operations on X that preserve symmetry, where \(a_1\) is the ‘null’ operation of doing nothing to X. Let \(o_1, ..., o_n\) be the orientations of X, such that each \(o_i\) is the result of applying \(a_i\) to X in its starting orientation \(o_1\). Then X is non-cyclical iff there is no \(a_i\) such that its repeated application cycles X systematically through each of \(o_1, ..., o_n\). This schematic definition can be spelled out in purely physical terms.
By replacing the dummy letter ‘S(X)’ with ‘X’ in A3, A4, and A5, and deleting entry 6 of the filling instructions, we form a physical scheme with only sound instances that matches the unifying power of the mathematical scheme. Two sound arguments exploiting our physical correlate of non-cyclicality can be obtained from the physical scheme, whose conclusions are the explananda of Mattress and Rug
and Rug . Moreover, each instance of the mathematical scheme is sound because the mathematical fact corresponding to A6 in the mathematical scheme represents the physical fact corresponding to A6 in the physical scheme, which is responsible for the unifying power of the physical scheme.
. Moreover, each instance of the mathematical scheme is sound because the mathematical fact corresponding to A6 in the mathematical scheme represents the physical fact corresponding to A6 in the physical scheme, which is responsible for the unifying power of the physical scheme.
So, on Baron’s theory, the mathematical fact that  is non-cyclical does not explain why there is uneven sagging on my mattress, nor why there is uneven fading on my rug. Our explanatory judgements say otherwise, so Mattress
is non-cyclical does not explain why there is uneven sagging on my mattress, nor why there is uneven fading on my rug. Our explanatory judgements say otherwise, so Mattress and Rug
and Rug are counter-examples to Baron’s theory. The existence of a counter-example or two does not refute a theory like Baron’s (§2; Baron 2019: 686, 2020: 536–538). But it does generate certain obligations. In cases where his theory seems to yield the wrong results, Baron must explain why our explanatory judgements are mistaken.
are counter-examples to Baron’s theory. The existence of a counter-example or two does not refute a theory like Baron’s (§2; Baron 2019: 686, 2020: 536–538). But it does generate certain obligations. In cases where his theory seems to yield the wrong results, Baron must explain why our explanatory judgements are mistaken.
Suppose we come across Mattress and judge the mathematics in it to be explanatory, while unaware of the existence of Rug
and judge the mathematics in it to be explanatory, while unaware of the existence of Rug or any other nomically distinct explanation turning on the same mathematics. On Baron’s theory, our mistake is twofold. First, we fail to notice that the mathematical fact that
or any other nomically distinct explanation turning on the same mathematics. On Baron’s theory, our mistake is twofold. First, we fail to notice that the mathematical fact that  is non-cyclical has a physical correlate in this situation. Second, we fail to realise that, across all the nomically distinct explanations turning on the same mathematical fact, the same physical correlate is present.
is non-cyclical has a physical correlate in this situation. Second, we fail to realise that, across all the nomically distinct explanations turning on the same mathematical fact, the same physical correlate is present.
Both mistakes are more than understandable. Regarding the first, one of the key benefits mathematics brings to scientific explanation is increased generality and abstractness. But this brings with it an epistemic risk. As we move further away from the physical particularities, we risk losing track of which parts of the mathematical representation we end up with retain physical significance. Thus, as we move from a particular description of the forces that contribute to wear on my mattress and the details of my mattress care regime, to a representation of the symmetries of a rectangle in terms of permutations of positive integers, we understandably lose track of the fact that certain properties of these permutations retain physical significance. The second mistake is even more understandable. We cannot glean from Mattress alone whether there are nomically distinct explanations turning on the same mathematics, let alone which physical features are likely to be instantiated across them.
alone whether there are nomically distinct explanations turning on the same mathematics, let alone which physical features are likely to be instantiated across them.
It looks as though Baron is well-equipped to deal with the odd counter-example. The problem is, the explanation of our error is a little too plausible. So much so that the general reliability of our explanatory judgements is undermined. To reliably detect mathematical explanation on Baron’s account, our explanatory judgements must be sensitive to both the existence of nomically distinct explanations turning on the same mathematical fact, and the absence of a physical correlate instantiated across them. We must after all be able to reliably detect when the conditions for both (1) and (2) are satisfied. But that is completely implausible.
When we judge that a mathematical fact explains a physical phenomenon, we do not go looking for nomically distinct explanations turning on the same mathematical fact before we make our mind up, and we can’t glean from considering an explanation in isolation whether there exist such further explanations. So our explanatory judgements are not sensitive to the conditions for the satisfaction of (1). It is perhaps more plausible that we can sometimes recognise whether a given mathematical fact has a physical correlate in a given explanation. But without also being able to recognise whether there are nomically distinct explanations turning on the same mathematics, and whether the same physical correlate is present or absent across them, this would not be enough. Our explanatory judgements are not sensitive to the conditions for the satisfaction of (2).
So, our explanatory judgements are not sensitive to the what on Baron’s theory is constitutive of mathematical explanation. This raises a serious epistemological problem for Baron. Because the theory carves cases along joints to which our explanatory judgements are not sensitive, in the absence of a case-by-case demonstration that Baron’s theory is empirically adequate, there is little reason to think that it will be. And even if it turns out that Baron’s theory is empirically adequate, it seems in principle unable to explain how we are capable of recognising mathematical explanation when we see it. This renders our success in developing and recognising cases of mathematical explanation a mystery.
I can anticipate two broad strategies of response. The first is to tackle the problem head-on. The second is to downplay its significance. Tackling the problem head-on involves arguing that explanatory unification tends to co-occur with features to which our explanatory judgements are plausibly sensitive, at least enough of the time to explain why our explanatory judgements are often correct. I do not have space to exhaust the options here. It will suffice to discuss a representative one, and show that it fails for reasons that permit generalisation.
One feature of mathematical explanations that we could plausibly recognise is the topic generality of the mathematics they employ: the mathematical facts they invoke make no particular demands on the physical processes underlying their explananda. (See Baker 2017 and Knowles and Saatsi 2019 for more on the topic generality.) Topic generality is surely a necessary condition for explanatory unification. But, unfortunately, being a necessary condition for something does not guarantee co-occurrence with it.
Consider Mattress , for example. The fact that
, for example. The fact that  is non-cyclical is neutral with respect to the underlying physical processes of spring fatigue and fabric compression. Does this alone provide reason for thinking that condition (1) is satisfied? We can concede that it renders the mathematics apt to be applicable in nomically distinct domains; but it doesn’t provide any assurance that there are situations in nomically distinct domains amenable to the same mathematical analysis, and, if there are, no reason whatsoever for thinking they satisfy condition (2). Topic generality at best suggests aptness for explanatory unification; it cannot reliably indicate it. The reasons here are general. No features of individual explanations to which our explanatory judgements could plausibly be sensitive could ever reliably indicate explanatory unification, as Baron’s theory characterises it.
is non-cyclical is neutral with respect to the underlying physical processes of spring fatigue and fabric compression. Does this alone provide reason for thinking that condition (1) is satisfied? We can concede that it renders the mathematics apt to be applicable in nomically distinct domains; but it doesn’t provide any assurance that there are situations in nomically distinct domains amenable to the same mathematical analysis, and, if there are, no reason whatsoever for thinking they satisfy condition (2). Topic generality at best suggests aptness for explanatory unification; it cannot reliably indicate it. The reasons here are general. No features of individual explanations to which our explanatory judgements could plausibly be sensitive could ever reliably indicate explanatory unification, as Baron’s theory characterises it.
In light of this, Baron might instead downplay the significance of the problem. He could argue that, while a theory is obliged to explain away counterexamples, it is under no obligation to explain the success of our intuitions when they are vindicated by it. Why? One suggestion is that, while our intuitions provide us with our initial grip on the target phenomenon, it is doubtful that their content is clear enough to delineate the features to which they are sensitive pre-theoretically. Given this, if a theory is in accord with most of our intuitions, that is in itself a reason to think that the features the theory identifies as constitutive of the target phenomenon are those to which our intuitions are (through a glass, darkly) sensitive.
While this is plausible enough, it does not address the problem. The problem is not just that, on Baron’s theory, the features constitutive of mathematical explanation are not the features our explanatory judgements track. Nor is it just that, thus far, no explanation, compatible with Baron’s theory, of the correctness of our explanatory judgements has been provided. It is that Baron’s theory rules out the provision of any such explanation, by locating the features that constitute the target phenomenon well beyond that to which our explanatory judgements could plausibly be sensitive. Even if Baron’s theory accorded with all of our explanatory judgements, we could not conclude that the features identified as constitutive of the target phenomenon are those to which our intuitions are sensitive, however dark the proverbial glass.
The problem does not stem from the methodological principle that, whenever a theory accords with our intuitions, it should be accompanied with an explanation of the correctness of those intuitions. I agree that this sets an unacceptably high standard. Rather, it stems from a far weaker, and far more plausible principle: a theory should not rule out the provision of such explanations. Or: a theory should not make a mystery of the correctness of our intuitions. My objection to Baron’s theory is that it makes a mystery of the correctness of the judgements that guide us in developing and recognising mathematical explanations. This is a serious problem.
The epistemological problem I have raised here is not just a result of the peculiarities of Baron’s theory. There is reason to think that any articulation of m-unificationism that aspires to empirically adequacy will court the same problem. As noted in §2, the explanatory judgements that demarcate mathematical explanation are fine-grained, while unification is a coarse-grained affair. Any given mathematical fact will feature in countless derivations of distinct physical phenomena, so, for a given articulation of m-unificationism to be empirically adequate, it must place further conditions on what counts as explanatory mathematical unification (see the close of §3). Such conditions will rule out some applications of the same mathematics as explanatory, and rule in others.
But that means, whether a given mathematical derivation of a physical phenomenon is explanatory will partly be a function of what kinds of other physical phenomena there are. It is not plausible that we can glean this kind of information from consideration of a single derivation in isolation. But considering derivations in isolation is precisely how our explanatory judgements arise. So, any articulation of m-unificationism aspiring to empirically adequacy runs the risk of placing the conditions for mathematical explanation beyond that to which our explanatory judgements can plausibly be sensitive. While this argument is not conclusive, it provides a strong presumption against m-unificationism.
6 The potential to unify
In §4, I argued that unifying power is not proportional to explanatory power. In §5, I argued that we cannot recognise explanatory unification in a putative mathematical explanation by considering that explanation alone. These arguments tell against the thesis that mathematical explanations explain by unifying actual phenomena. Might one instead claim that mathematical explanations explain by exhibiting the potential to unify? On this view, unifying power would be proportional to the number of possible phenomena an explanation can unify.
For example, Mattress( ) has the potential to unify a wide range of physically similar phenomena. There could be spring mattresses of a wide range of different regular polygonal shapes used in ways that give rise to uneven sagging phenomena. For each hypothetical case, the same mathematical property (non-cyclicality) explains the uneven sagging. This is a function of the level of generality exhibited by Mattress(
) has the potential to unify a wide range of physically similar phenomena. There could be spring mattresses of a wide range of different regular polygonal shapes used in ways that give rise to uneven sagging phenomena. For each hypothetical case, the same mathematical property (non-cyclicality) explains the uneven sagging. This is a function of the level of generality exhibited by Mattress( ): the explanatory relationship between non-cyclicality and uneven sagging is robust under a wide range of changes to the shape of the spring mattress. Call this scope-generality (following Baker 2017).
): the explanatory relationship between non-cyclicality and uneven sagging is robust under a wide range of changes to the shape of the spring mattress. Call this scope-generality (following Baker 2017).
Mattress( ) also has the potential to unify a wide range of physically dissimilar phenomena. A wide range of radically different physical processes could give rise to analogous uneven wear in rectangular objects. For each hypothetical case, the fact that
) also has the potential to unify a wide range of physically dissimilar phenomena. A wide range of radically different physical processes could give rise to analogous uneven wear in rectangular objects. For each hypothetical case, the fact that  is non-cyclical would help to explain the uneven wear. This is again a function of the generality of the explanation. Because the fact that
is non-cyclical would help to explain the uneven wear. This is again a function of the generality of the explanation. Because the fact that  is non-cyclical is completely topic general, the explanatory relationship is robust under any change to the underlying physical processes (again, see Baker 2017).
is non-cyclical is completely topic general, the explanatory relationship is robust under any change to the underlying physical processes (again, see Baker 2017).
Appealing to unifying potential appears to help with some of my arguments. For example, in §4, I argued that increasing the number of physically dissimilar phenomena unified by a mathematical explanation does not increase its explanatory power. As we move from a possible world in which photodegradation does not occur to the actual world, we get an increase in the number of actual phenomena unified by Mattress but no increase in explanatory power. But the range of possible phenomena Mattress
but no increase in explanatory power. But the range of possible phenomena Mattress has the potential to unify remains unchanged across these two possibilities, so the fact that we see no change in explanatory power is to be expected on the present form of m-unificationism. In §5, I argued that we cannot recognise the extent to which putative mathematical explanations unify by considering them in isolation, making a mystery of our ability to recognise mathematical explanation. But the unifying potential of a mathematical explanation is a function of its scope and topic generality, which can be recognised by considering an explanation in isolation.
has the potential to unify remains unchanged across these two possibilities, so the fact that we see no change in explanatory power is to be expected on the present form of m-unificationism. In §5, I argued that we cannot recognise the extent to which putative mathematical explanations unify by considering them in isolation, making a mystery of our ability to recognise mathematical explanation. But the unifying potential of a mathematical explanation is a function of its scope and topic generality, which can be recognised by considering an explanation in isolation.
The first thing to say about this alternative form of m-unificationism is that it deserves its own in-depth discussion. To spell it out properly, important questions need answers. For example: Are there any constraints on what we can include in the range of potentially-unified phenomena? Should they be possibilities that are ‘nearby’ in some specified sense? Until questions like these are answered, and we are in possession of a worked-out version of the view, it will be difficult to determine with any certainty how the proposal fares. Unfortunately, there is not space here to provide an in-depth discussion. But I would like to stress that, if there turns out to be an acceptable version of m-unificationism along these lines, that will do nothing to undermine the significance of this paper. My conclusion that understanding mathematical explanation as a matter of actual unification is misguided will stand, and that is a significant result.
That said, there is reason to doubt that we are better off in appealing to unifying potential. For one thing, the move does nothing to address one of my arguments from §4. Recall that appealing to the fact that  is dihedral, rather than the fact that
is dihedral, rather than the fact that  is non-cyclical, makes for a deeper explanation of the uneven sagging on my mattress. Here, we have an increase in explanatory power with no increase in unifying potential. Furthermore, the advantage regarding my other arguments of §4 seem short lived, since we can run analogous arguments regarding merely possible physical phenomena. That is, we can argue that differences in the number of possible phenomena explanations can unify do not correspond to differences in explanatory power.
is non-cyclical, makes for a deeper explanation of the uneven sagging on my mattress. Here, we have an increase in explanatory power with no increase in unifying potential. Furthermore, the advantage regarding my other arguments of §4 seem short lived, since we can run analogous arguments regarding merely possible physical phenomena. That is, we can argue that differences in the number of possible phenomena explanations can unify do not correspond to differences in explanatory power.
Consider physically similar phenomena first. There will be a (perhaps vague) limit to how many sides an ordinary-sized regular polygonal spring mattress can be made to have. Suppose we are in possession of a reliable means of locating the limit. Let us consider our reactions to different epistemic possibilities concerning its outcome. For all we know, the limit could be \(\approx 100\) sides, or it could be \(\approx 50\) sides. On the present form of m-unificationism, these outcomes correspond to a difference in explanatory power. However, it seems that the explanatory power of Mattress is completely insensitive to this difference. This suggests that the potential to unify physically similar phenomena is not proportional to explanatory power.
is completely insensitive to this difference. This suggests that the potential to unify physically similar phenomena is not proportional to explanatory power.
Consider now physically dissimilar phenomena. Suppose there were a reliable way of counting how many possible physical processes there are (or could be) that could give rise to uneven wear on rectangular objects. On the present form of m-unificationism, the higher the count, the more explanatory Mattress will be. But that seems wrong. The explanatory power Mattress
will be. But that seems wrong. The explanatory power Mattress seems completely insensitive to the outcome of such a count.
seems completely insensitive to the outcome of such a count.
Am I targeting a straw man? The total number of possibilities unified surely does not matter. What matters is that all relevant possibilities are unified. I agree with this latter sentiment. If an explanation is not robust across all of the possibilities that it intuitively should be, that is a sign that the explanation is not correct, or at least not best. If, however, an explanation is robust across all relevant possibilities, that is a sign we are on the right track. But all this suggests is that the potential to unify all relevant possibilities is a symptom of good explanation. In contrast, only the present form of m-unificationism seems committed to the claim that a larger total number of possibilities unified means greater explanatory power, which is why I chose to target this claim. If this is a straw man, there must be a better way of characterising unifying potential, in which case I would like to see it.
There is also reason to doubt that we are any better off with respect to the epistemological objection raised in §5. While scope and topic generality can be recognised by considering an explanation in isolation, these features are not sufficient for mathematical explanation. We require further conditions on what it is to potentially unify in an explanatory way. To illustrate, consider again the following example:
Trains: Train T arrives at station \(S_2\) at 3:00 pm, after leaving station \(S_1\) at 2:00 pm. Why? Because \(S_1\) and \(S_2\) are 10 km apart, T travels at 10 kph, and \(\frac{10}{10} = 1\).
This is intuitively a non-explanatory application of mathematics, but it exhibits both scope and topic generality. To see that it exhibits scope generality, note that what matters for the explanation is not that the speed is 10 kph and the distance is 10 km specifically, but rather that these two numerical values are identical. The mathematical relationship between the speed n (in kph) and distance m (in km) that matters is that \(\frac{m}{n} = 1\). The connection between this relationship and the arrival time is robust across a vast range of different distance and speed pairs. To see that Trains exhibits topic generality, note that the fact that \(\frac{10}{10} = 1\) places no constraints on the physical processes responsible for the movement of the train.
Trains has the potential to unify a wide range of physically similar and physically dissimilar phenomena. This is not surprising. The generality of a mathematical explanation is a result of its mathematical presentation, and there is no reason to think that mathematics would not contribute the same generality wherever it is deployed. We must therefore place further conditions on what it is to potentially unify in an explanatory way. But there is no reason to think that these conditions will be more easily recognisable in relation to potential unification than they are in relation to actual unification.
For example, following Baron (2020), we might appeal to the absence of a unifying physical feature across the range of possible application. That would make Mattress a counterexample, and raise the familiar epistemological issue. Presumably, our mistake with respect to Mattress
a counterexample, and raise the familiar epistemological issue. Presumably, our mistake with respect to Mattress would be due to how difficult it is to recognise the presence or absence of a unifying physical feature across a range of possible application. But this mistake is far too easy to make, making a mystery of the presumed reliability of our explanatory judgements. Pending further discussion, it seems that appealing to unifying potential leaves the proponent of m-unificationism no better off.
would be due to how difficult it is to recognise the presence or absence of a unifying physical feature across a range of possible application. But this mistake is far too easy to make, making a mystery of the presumed reliability of our explanatory judgements. Pending further discussion, it seems that appealing to unifying potential leaves the proponent of m-unificationism no better off.
7 Conclusions
The prospects for m-unificationism look dim. It enjoys no antecedent intuitive support (§2); it entails something we have good reason to doubt (§4); and any articulation of it that aspires to empirical adequacy courts a serious epistemological problem (§5). This is reason enough to conclude that m-unificationism is sorely misguided, and that we would be better off looking elsewhere for a theory mathematical explanation.
The good news is, by process of elimination, our conclusion takes believers in mathematical explanation one step closer to finding the right theory. Better still, it provides a guiding principle that will help with the search. We should avoid placing what is constitutive of mathematical explanation beyond that to which our explanatory judgements could plausibly be sensitive. Whatever constitutes mathematical explanation, it must be something that suitably-trained individuals are capable of recognising.
My discussion also provides non-believers with fodder for a divide and conquer strategy. If, in a similar fashion, it can be shown that attributing an explanatory role to mathematical facts makes a mess of whatever theory of scientific explanation one appeals to, that will provide a powerful reason for thinking that mathematical explanation (as I have characterised it here) exists nowhere in science.
A final upshot of my discussion is that it scuppers a certain means of supporting mathematical platonism. The enhanced indispensability argument turns on the premise that mathematics plays an indispensable explanatory role in science. Some have appealed to the unifying power of mathematics in support of this premise, presupposing that increasing mathematical unification increases explanatory power (see Baker 2009: 621, 2017: 199; Baker and Colyvan 2011: 331; Colyvan 2002: 71–72). In light of my discussion, such appeals should be treated with suspicion.
References
Baker, A. (2005). Are there genuine mathematical explanation of physical phenomena? Mind, 114, 223–238.
Baker, A. (2009). Mathematical explanation in science. British Journal for the Philosophy of Science, 60, 611–633.
Baker, A. (2017). Mathematics and explanatory generality. Philosophia Mathematica, 25, 194–209.
Baker, A., & Colyvan, M. (2011). Indexing and mathematical explanation. Philosophia Mathematica, 19, 323–334.
Bangu, S. (2008). Inference to the best explanation and mathematical realism. Synthese, 160, 13–20.
Bangu, S. (2017). Scientific explanation and understanding: Unification reconsidered. European Journal for Philosophy of Science, 7, 103–126.
Baron, S. (2014). Optimisation and mathematical explanation: Doing the Lévy Walk. Synthese, 191, 459–479.
Baron, S. (2016). Explaining mathematical explanation. The Philosophical Quarterly, 66, 458–480.
Baron, S. (2019). Mathematical explanation by law. The British Journal for the Philosophy of Science, 70, 683–717.
Baron, S. (2020). Counterfactual scheming. Mind, 129, 535–562.
Baron, S., Colyvan, M., & Ripley, D. (2017). How mathematics can make a difference. Philosophers’ Imprint, 17, 1–29.
Barrantes, M. (2020). Explanatory information in mathematical explanations of physical phenomena. Australasian Journal of Philosophy, 98, 590–603.
Bartelborth, T. (2002). Explanatory unification. Synthese, 130, 91–107.
Colyvan, M. (2001). The Indispensability of Mathematics. Oxford: Oxford University Press.
Colyvan, M. (2002). Mathematics and aesthetic considerations in science. Mind, 111, 69–74.
Colyvan, M. (2010). There is no easy road to nominalism. Mind, 119, 285–306.
Colyvan, M. (2013). Road work ahead: Heavy machinery on the easy road. Mind, 121, 1031–1046.
Craver, C. F., & Povich, M. (2017). The directionality of distinctively mathematical explanations. Studies in History and Philosophy of Science Par A, 63, 31–38.
Daly, C., & Langford, S. (2009). Mathematical explanation and indispensability arguments. The Philosophical Quarterly, 59, 641–658.
Friedman, M. (1974). Explanation and scientific understanding. Journal of Philosophy, 71, 5–19.
Gijsbers, V. (2007). Why unification is neither necessary nor sufficient for explanation. Philosophy of Science, 74, 481–500.
Jones, T. (1995a). How the unification theory of explanation escapes asymmetry problems. Erkenntnis, 43, 229–240.
Jones, T. (1995b). Reductionism and the unification theory of explanation. Philosophy of Science, 61, 21–30.
Jones, T. (2012). Unification. In S. Psillos & M. Curd (Eds.), The Routledge companion to the philosophy of science (2nd ed., pp. 97–106). New York: Routledge.
Kitcher, P. (1981). Explanatory unification. Philosophy of Science, 48, 507–531.
Kitcher, P. (1989). Explanatory unification and the causal structure of the world. In P. Kitcher & W. C. Salmon (Eds.), Minnesota studies in the philosophy of science, Volume 13 : Scientific explanation (pp. 410–505). Minneapolis: University of Minnesota Press.
Knowles, R., & Saatsi, J. (2019). Mathematics and explanatory generality: Nothing but cognitive salience. Erkenntnis,. https://doi.org/10.1007/s10670-019-00146-x.
Lange, M. (2013). What makes a scientific explanation distinctively mathematical? The British Journal for the Philosophy of Science, 64, 485–511.
Lange, M. (2017). Because without cause: Non-causal explanations in science and mathematics. Oxford: Oxford University Press.
Leng, M. (2010). Mathematics & Reality. Oxford: Oxford University Press.
Leng, M. (2012). Taking it easy: A response to colyvan. Mind, 121, 983–995.
Lyon, A. (2012). Mathematical explanations of empirical facts, and mathematical realism. Australasian Journal of Philosophy, 90, 559–578.
Melia, J. (2000). Weaseling away the indispensability argument. Mind, 109, 455–479.
Pincock, C. (2007). A role for mathematics in the physical sciences. Noûs, 41, 253–275.
Pincock, C. (2015). Abstract explanations in science. The British Journal for the Philosophy of Science, 66, 857–882.
Povich, M. (2019). The narrow ontic counterfactual account of distinctively mathematical explanation. The British Journal for the Philosophy of Science,. https://doi.org/10.1093/bjps/axz008.
Povich, M. (2020). Modality and constitution in distinctively mathematical explanations. European Journal for Philosophy of Science, 10, 1–10.
Saatsi, J. (2011). The enhanced indispensability argument: Representational versus explanatory role of mathematics in science. British Journal for the Philosophy of Science, 62, 143–154.
Saatsi, J. (2016). On the “Indispensable explanatory role” of mathematics. Mind, 125, 1045–1070.
Schurz, G. (1999). Explanation as unification. Synthese, 120, 95–114.
Schurz, G., & Lambert, K. (1994). Outline of a theory of scientific understanding. Synthese, 101, 65–120.
Weber, E. (1999). Unification: What is it, how do we Reach and why do we Want it? Synthese, 188, 479–499.
Woodward, J. (2003). Making things happen: A theory of causal explanation. Oxford: Oxford University Press.
Woodward, J. (2019). Scientific Explanation. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/scientific-explanation/.
Yablo, S. (2013). Explanation, extrapolation, and existence. Mind, 121, 1007–1029.
Acknowledgements
Thanks to Juha Saatsi and two anonymous referees for helpful comments on earlier versions of this paper. Thanks to Emily Shercliff for discussion and support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Knowles, R. Unification and mathematical explanation. Philos Stud 178, 3923–3943 (2021). https://doi.org/10.1007/s11098-021-01631-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-021-01631-2


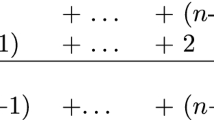

 : To minimise uneven sagging, rectangular spring mattresses must be regularly flipped. I care for my mattress by repeating the same flipping action. There is uneven sagging on my mattress. Why? Because
: To minimise uneven sagging, rectangular spring mattresses must be regularly flipped. I care for my mattress by repeating the same flipping action. There is uneven sagging on my mattress. Why? Because  is non-cyclical.
is non-cyclical. : To minimise uneven sagging, hexagonal spring mattresses must be regularly flipped. Tilly owns a hexagonal mattress, and she cares for her mattress by repeating the same flipping action. There is uneven sagging on Tilly’s mattress. Why? Because
: To minimise uneven sagging, hexagonal spring mattresses must be regularly flipped. Tilly owns a hexagonal mattress, and she cares for her mattress by repeating the same flipping action. There is uneven sagging on Tilly’s mattress. Why? Because  is non-cyclical.
is non-cyclical. : The rectangular rug on my living room floor gets direct sunlight on one side during the day, causing its colours to fade in that area. To minimise uneven fading, the rug should be regularly flipped. I care for my rug by repeating a single flipping action. There is uneven fading on my rug. Why? Because
: The rectangular rug on my living room floor gets direct sunlight on one side during the day, causing its colours to fade in that area. To minimise uneven fading, the rug should be regularly flipped. I care for my rug by repeating a single flipping action. There is uneven fading on my rug. Why? Because  is non-cyclical.
is non-cyclical.